Школьная научно-практическая конференция (сборник материалов)

Вид материала

Документы

Содержание Формулировки теоремы Доказательства теоремы Пифагора Применение теоремы Пифагора

Подобный материал:

• Школьная научно-практическая конференция (сборник материалов), 666.22kb.
• Цивильского района Чувашской республики Школьная научно-практическая конференция школьников, 280.22kb.
• «мир, в котором мы живем» школьная научно-практическая конференция апрель 2010/2011, 63.94kb.
• Школьная научно-практическая конференция «Золотые россыпи», 172.63kb.
• Xxii школьная научно-практическая конференция «Открытия юных», 250.74kb.
• Школьная научно-практическая конференция «Декабрьские чтения» Номинация: физика, 188.73kb.
• Моу гимназия №30 имени Музалева Д. Н. Школьная научно-практическая конференция, 197.15kb.
• Итоги второй школьной конференции, 32.97kb.
• Городская открытая научно-практическая конференция старшеклассников по экономике, 49.41kb.
• Третья школьная научно-практическая конференция Юмор, 203.15kb.

Формулировки теоремы

1.У Евклида эта теорема гласит: В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол.

2. Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.), сделанный Герхардом Клемонским (начало 12 в.), в переводе на русский гласит: Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол.

3. В русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол.

4. Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Доказательства теоремы Пифагора

Существует множество доказательств теоремы Пифагора. Сейчас насчитывается около 367 доказательств. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства. Рассмотрим некоторые из них.

1. Доказательство методом разрезания.

Квадраты, построенные на катетах и на гипотенузе, разрезаются так, что каждой части квадрата, построенного на гипотенузе, соответствует часть одного из квадратов, построенных на катетах. Следует, заметить, что на самом деле доказательство будет неполноценным, пока не доказаны равенства всех соответствующих друг другу частей.


2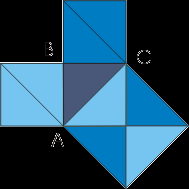. Простейшее доказательство теоремы.

Достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Для треугольника ABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по два.


3. Доказательство через подобные треугольники.

П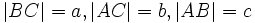усть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения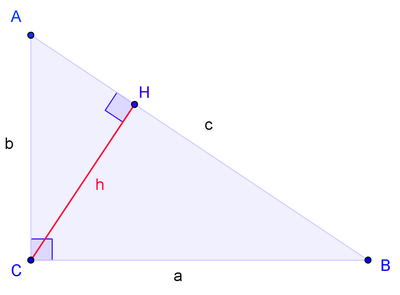




Получаем

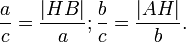
Что эквивалентно

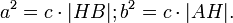
Сложив, получаем

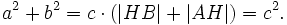
или .

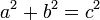4. Доказательство через равнодополняемость.
   

Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.

Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол - 180°.

Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.










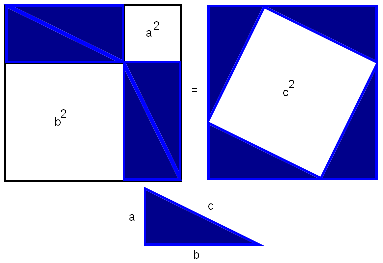
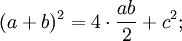
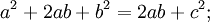
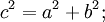
5.Доказательство через равносоставленность.

Квадрат, построенный на гипотенузе, перестановкой преобразуется в два квадрата, построенных на катетах.

Применение теоремы Пифагора

1. Строительство окон.

В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. Способ построения очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины (b/2), для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.

2. Молниеотвод.

Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты.

Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
Решение: по теореме Пифагора h² ≥ a²+b², значит h ≥ (a²+b²)^½.
Ответ: h ≥ (a²+b²)^½

3. Мобильная связь

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например радиусе R=200 км, если известно, что радиус Земли равен 6380 км.)

Решение:
Пусть AB = x, BC=R=200 км, OC= r = 6380 км. OB = OA + AB
OB = r + x. Используя теорему Пифагора, получим ответ.
Ответ: 2,3 км.

Ещё раз хочется сказать о значимости и важности теоремы Пифагора. Ведь не важно то, что Пифагор родился задолго до появления этой теоремы, а важно то, что он доказал эту важнейшую для математики теорему.

Теорема Пифагора встречается очень часто в математике. С помощью этой теоремы можно выражать многие другие величины. Эта теорема является одной из самых значимых, важных и незаменимых теорем.