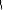Автореферат по теме: «Применение информационных технологий при обучении математике и информатике»
| Вид материала | Автореферат |
- Применение технологий в обучении английскому языку студентов (автореферат), 115.29kb.
- Задачи урока: Практическое применение теоретических знаний по теме «Сечения. Тетраэдр., 48.24kb.
- Использование информационных технологий в обучении математике и информатике студентов, 405.25kb.
- Урок технологии с использованием компьютерных средств обладает своеобразной спецификой., 54.07kb.
- «Применение информационных технологий в математике», 447.24kb.
- Применение информационных технологий при обучении английскому языку в средней школе, 74.08kb.
- Институт информационных технологий Кафедра информационных и коммуникационных технологий, 207.89kb.
- «Применение современных информационных технологий при изучении вопросов нетарифного, 316.46kb.
- Задачи: Выяснить место занимательности на уроках и во внеурочное время в обучении информатике, 64.62kb.
- «Применение информационных технологий при решении задач высшей алгебры», 159.09kb.
2.1 Использование компьютерных средств при активизации познавательной самостоятельности.
Понятие «познавательная самостоятельность» рассматривается как качество личности, сочетающее в себе умение приобретать новые знания и творчески применять их в различных ситуациях.
В условиях широкого использования информационных и коммуникационных технологий (ИКТ) управление познавательной деятельностью, по крайней мере, на функциональном уровне, отличается от традиционного. В Приложении 2 работы приводятся примеры построения структурно-функциональных моделей учебного процесса, по которым можно оценить роль и место ИКТ в нём и явно выделить и классифицировать подпроцессы обучения.
В последнее время в педагогической практике широко используется технология «проектной деятельности». Занимаясь этой проблемой в течении трех лет, я пришла к выводу, что именно применение мультимедиа-проектов дает хорошие результаты в развитии познавательной деятельности ученика. При изучении темы: «Моделирование и формализация» предлагаю учащимся творческое задание по математическому моделированию, а после изучения программы PowerPoint проходит защита проектов, созданных обучающимися на различные темы (см. Приложение № 3 «Фракталы»).
Математическое моделирование – это одним из основных способов познания математической действительности. Такая деятельность даёт хорошие результаты в направлении развития познавательной самостоятельности, где одарённый ребёнок способен самостоятельно исследовать и изучить объекты со всех сторон и получить обобщенные сведения об этих объектах. С другой стороны процесс моделирования является средством формирования у учащегося математической культуры, способствует реализации различных форм представления знаний, развития интереса к предмету и будущей специализации. Существенную роль при моделировании играет применение метода мультимедиа-проектов, который целесообразно осуществить с одарёнными учащимися на занятиях кружка, факультатива по математике, элективных курсах, начиная с 8 класса или при профильном обучении математики. Программу рекомендуется построить так, чтобы систематизация и углубление материала происходили параллельно с изучением школьного курса. Нижеприведенный пример творческой работы обучающегося удобно проводить, интегрируя уроки математики и информатики при изучении, например, темы «Исследование графиков функции»
Учащиеся выполняют задание по исследованию графиков функции, после чего результаты исследования оформляют в форме реферата (см. Приложение 3) и презентации (см. презентация «model»)
При выполнении проекта учащиеся показывают самый высокий уровень самостоятельности - творческий. Он проявляется в ходе выполнения заданий исследовательского характера, когда необходимо овладеть методами и приемами познания, которые позволяют увидеть новую проблему в знакомой ситуации, найти новые способы применения усвоенных знаний. В результате самостоятельной работы на базе имеющихся у учащихся знаний и приемов формируются новые, что свидетельствует о развитии интеллектуальной сферы личности. Цель выполнения проектной работы – углубленное изучение той или иной темы.
Немаловажно и то, что обсуждение результатов выполнения мультимедийного проекта проходит в форме защиты на итоговой конференции. Это в свою очередь требует выработки у учащихся навыков публичного общения, дискутирования, умения аргументированно отстаивать собственную позицию, а если работа над мультимедийным проектом, осуществляется в группе, то это требует овладения особыми навыками коллективной работы и межличностного общения.
В качестве примера приведу схему занятий, где учащиеся выполняют творческое задание (мультимедиа-проект) по теме: «Исследование функции и построению ее графика».
Занятие №1. (вводное)
Организационная составляющая включает постановку цели, разработку плана и этапов выполнения задания, выдачу вариантов задания каждому обучающему, устанавливаются сроки и требования к выполнению и защите творческого задания. Если осуществляется коллективная работа над проектом, то на этом этапе происходит формировании исследовательской группы и выработке систем внутригруппового управления, распределение обязанностей между разработчиками проекта, При этом учащимся отводится главная роль в планировании и проведении работы.
Математическая составляющая включает разбор схемы исследования функции, работу с параметром, уточнение задания, выбор программных средств для осуществления конкретных задач, составляющая по информатике – знакомство с программными средствами, которые будут использоваться при процессе моделирования.
Занятие 2 — 4.
Выполнение обучающимися творческих индивидуальных заданий. На данном этапе я как учитель выступают преимущественно в роли научного руководителя или консультанта.
Уроки 5 — 6 (итоговые).
Отчет работы. Творческое задание учащихся оценивается по следующим пунктам:
- исследование и построение графика функции средствами матанализа;
- использование программного обеспечения для исследований;
- оформление.
Цель проведения данной работы:
- расширение и углубление знаний по вопросам исследования функций и построения графиков;
- развитие самостоятельности при работе с математическим материалом, привитие исследовательских навыков (при работе с параметром);
- изучение основных возможностей графического модуля программной среды;
- формирование элементов компьютерной грамотности обучающихся.
План работы при выполнении творческого задания:
- нахождение области определения функции;
- четность;
- непрерывность, вертикальные асимптоты;
- точки пересечения с осями;
- точки экстремума и монотонность;
- наклонные асимптоты, поведение функции при х → ± ∞;
- выполнение графика функции техническими средствами.
Пример выполнения творческого задания приведён в Приложении 3 и электронной составляющей на CD – диске, презентация «model».
2.2. Разработка уроков с применением ИКТ.
Урок алгебры в 10 классе.
| Тема урока: | Применение производной к исследованию функции. |
| Учебная цель: | Научить применять производную к исследованию функции. |
| Развивающая цель: | Развитие творческой стороны мышления и практического применения возможностей компьютера. |
| Воспитательная цель: | Формировать навыки умственного труда – поиск рациональных путей выполнения работы. |
| Задачи: |
|
| Оборудование: | Карточки для рефлексии настроения и результативности, презентация с дидактическим материалом к уроку (см. приложение 4), компьютеры с установленным графическим калькулятором Математика+1,2 (либо любая другая программа построения графиков). |
Ход урока.
- Рефлексия настроения. Вступительное слово учителя:
Ребята, доброе утро. Я пришёл (шла) к вам на урок вот с таким настроением (показываю изображение солнца)! А какое у вас настроение? У вас на столе лежат карточки с изображением солнца, солнца за тучей и тучи. Покажите, какое у вас настроение. Пример карточек для рефлексии настроения.
Ребята, сегодня у нас урок математики с компьютерным сопровождением. Компьютер всё активнее входит в жизнь человека. Давайте вспомним правила техники безопасности работы за компьютером.
- Работая за компьютером надо следить за осанкой, не сутулиться;
- Взгляд на монитор должен падать перпендикулярно плоскости монитора, расстояние от глаз до монитора должно быть не менее 50 см.
- Дети садятся парами за компьютеры.
- Обсуждение темы занятия.
На слайде презентации предлагаются вниманию учащихся функции (см. рис.).
Обратите внимание, как обозначается функция (
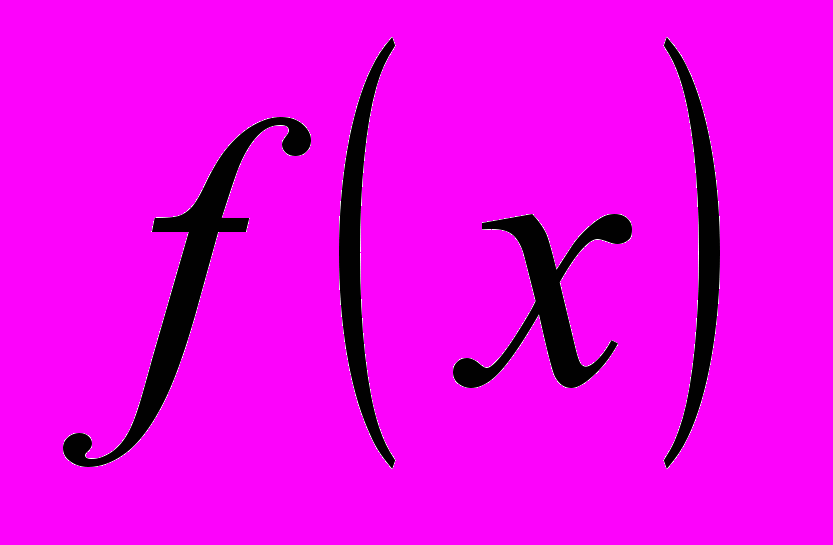). Это обозначение ввёл Леонард Эйлер. Это великий математик, который опубликовал несколько сотен математических работ. Швейцарец по происхождению, очень любил Россию, и любил так сильно, что потерял зрение одного глаза, работая над составлением первых карт России, а потом и вовсе ослеп. Леонард Эйлер верил в великое будущее России!Итак, задание (высвечивается на слайде 2 презентации «algebra 10»): построить графики этих функций на компьютере с помощью программы Математика+, определить по графику точки экстремума указанных функций. Выполнив это задание, ответьте на вопрос: по какому признаку относительно найденных вами значений можно классифицировать эти функции?
Дети, которые справились с заданием, поднимают сигналы (Если дети справились, они поднимают сигналы-карточки с изображением солнца, если кто-то испытывает затруднение, тот поднимает сигнал с изображением тучи.). Дети, у которых затруднения также поднимают соответствующие сигналы. По мере надобности учитель подходит и помогает.
Ответы сверяются по слайду презентации:
а)
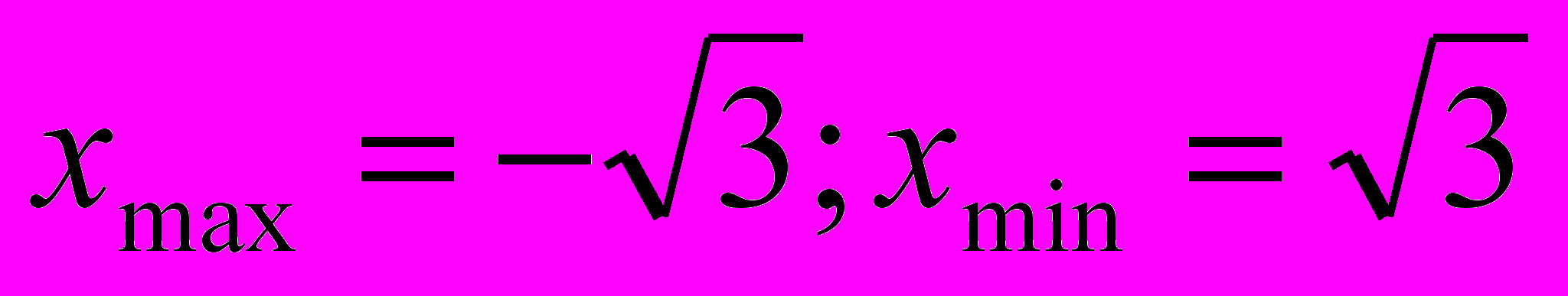;б)
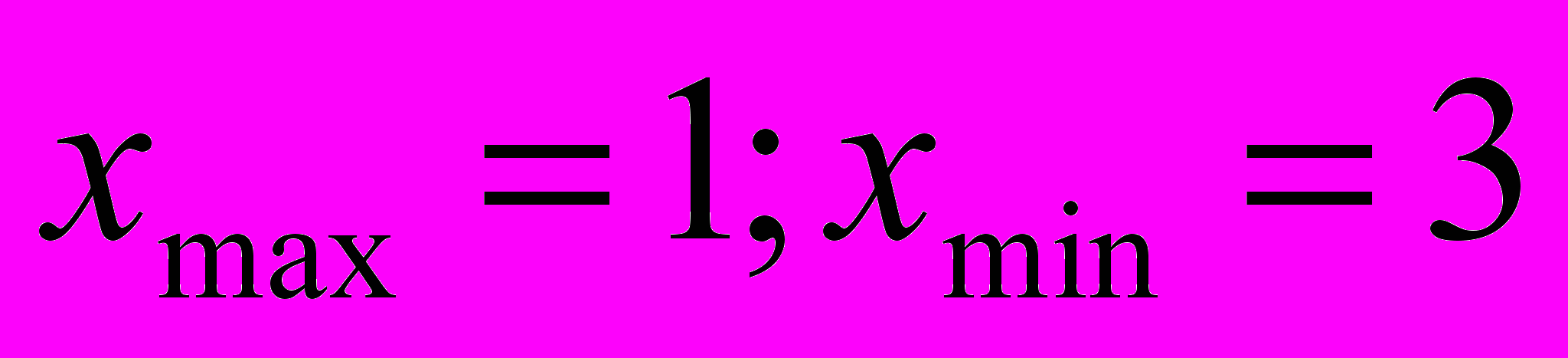;в)
;г)
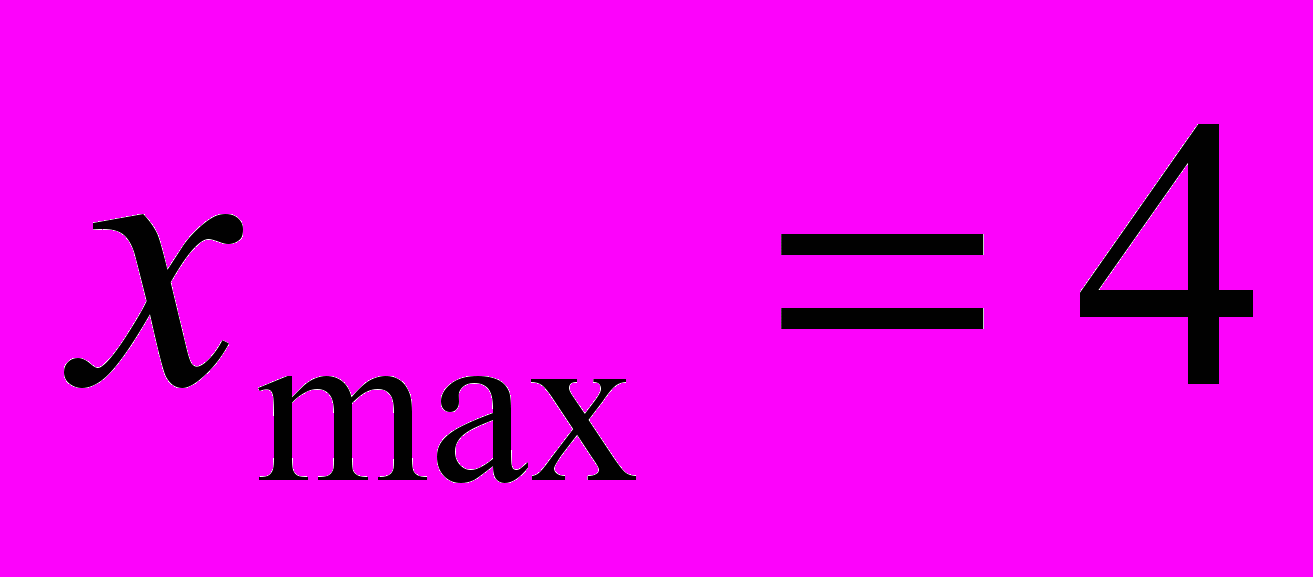.На поставленный вопрос дети отвечают, что для функций б и г найти точки экстремума можно точно, а для функций а и в – лишь приближённо).
Вопрос: Что надо сделать, чтобы найти точное значение точек максимума и минимума? Какой практический шаг вам нужно для этого сделать? (Нужно найти критические точки с помощью производной).
Вопрос: А с какой целью мы находим критические точки? Применяя производную, что мы с вами делаем? (Исследуем функцию).
Вопрос: А ещё что можно найти с помощью производной? (Промежутки возрастания и убывания функции). Какое правило вы знаете, что мы делаем с производной? (Мы находим промежутки знакопостоянства производной).
Вопрос: Какую аналитическую деятельность вы сейчас осуществляли относительно функций? (Исследование).
Вопрос: Для чего нужно исследование функций? (Для построения графиков).
Так какова тема нашего урока? Ребята, вы правильно определили тему нашего урока. Тема нашего занятия – исследование функции и построение графиков с помощью производной.
Как вы думаете, ребята, какова цель нашего урока? Цель нашего урока – научиться применять производную для исследования функции, научиться строить график функции.
Вопрос: Как вы думаете, ребята, зачем нужны графики функций? (Для графического представления зависимости между параметрами физического процесса, для решения уравнений). На каких уроках вы встречали графики? (География, физика). А физика нужна для практики?
- Актуализация знаний, умений, навыков.
Давайте вспомним основные этапы исследования функции. На слайде изображается функция
. Ребята, постройте график этой функции на компьютере. Применяя построенный компьютером график, вспомним основные шаги исследования функции. (Дети вводят в строку программы Математика+ эту функцию, но графика не видят, даже пытаясь изменить масштаб). Почему же компьютер не показывает график? (Подкоренное выражение отрицательно при всех значениях аргумента. Следовательно, важно находить область определения функции). Сформулируем пункты плана (на компьютере учащиеся в текстовом редакторе Word набивают алгоритм исследования функций, который в последствии сохраняется и проверяется учителем). После самостоятельного написания алгоритм исследования функции сверяется со слайдом презентации учителя.
План исследования функций.
1. Область определения функции.
2. Исследование на четность и нечетность.
3. Точки пересечения графика с осью абсцисс; с осью ординат.
4. Точки пересечения графика с осью абсцисс; с осью ординат.
5. Промежутки знакопостоянства.
6. Исследование функции на возрастание и убывание.
7. Точки максимума и минимума.
Прежде чем рассмотреть некоторые примеры применения производной, давайте найдём некоторые производные (Работа у доски).
а)
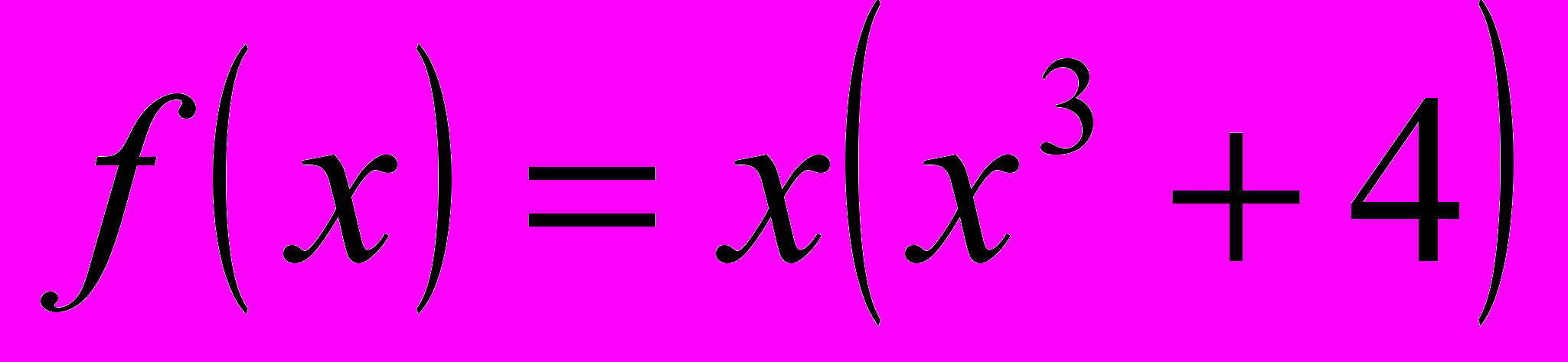; б)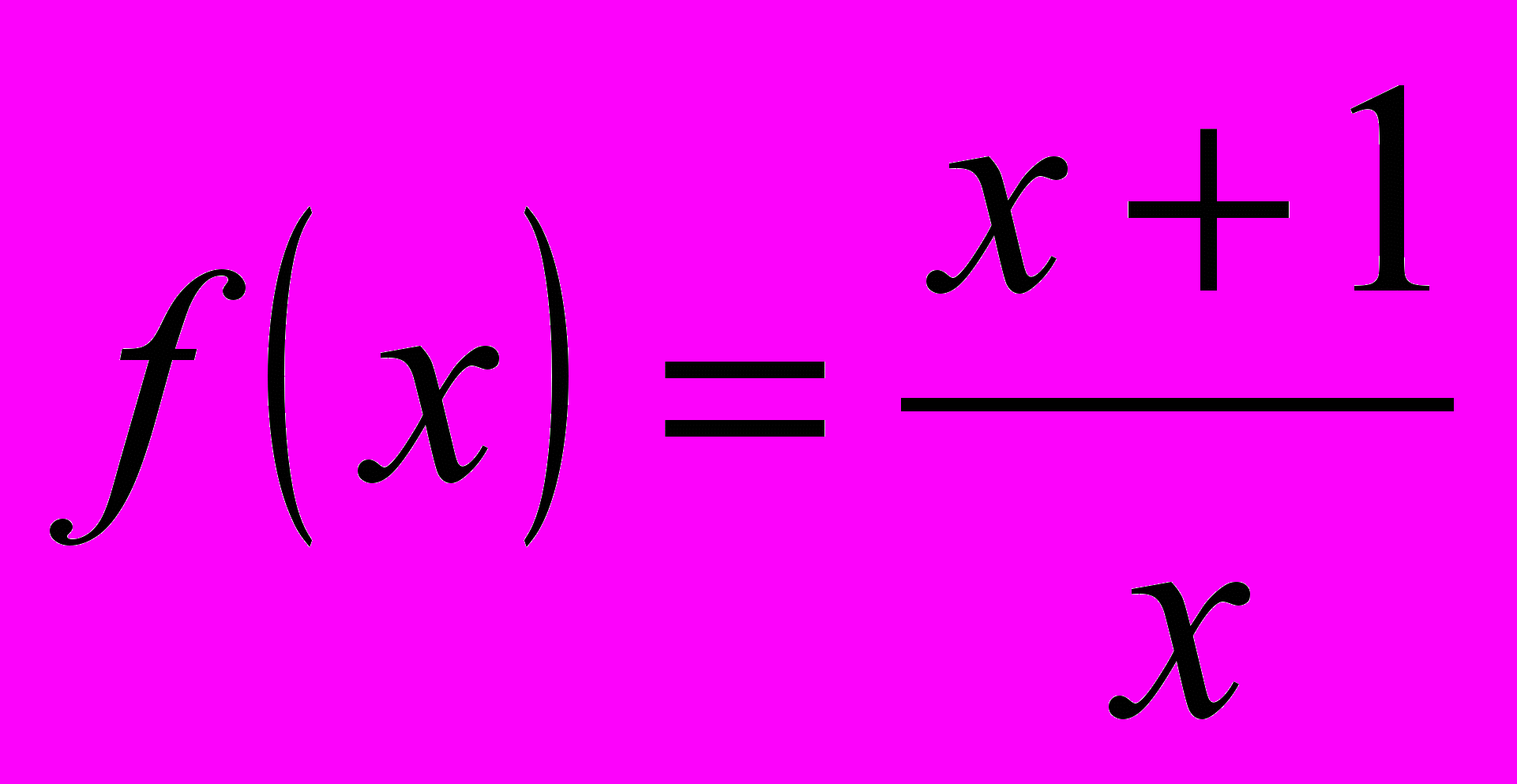 
. Теперь давайте для функции
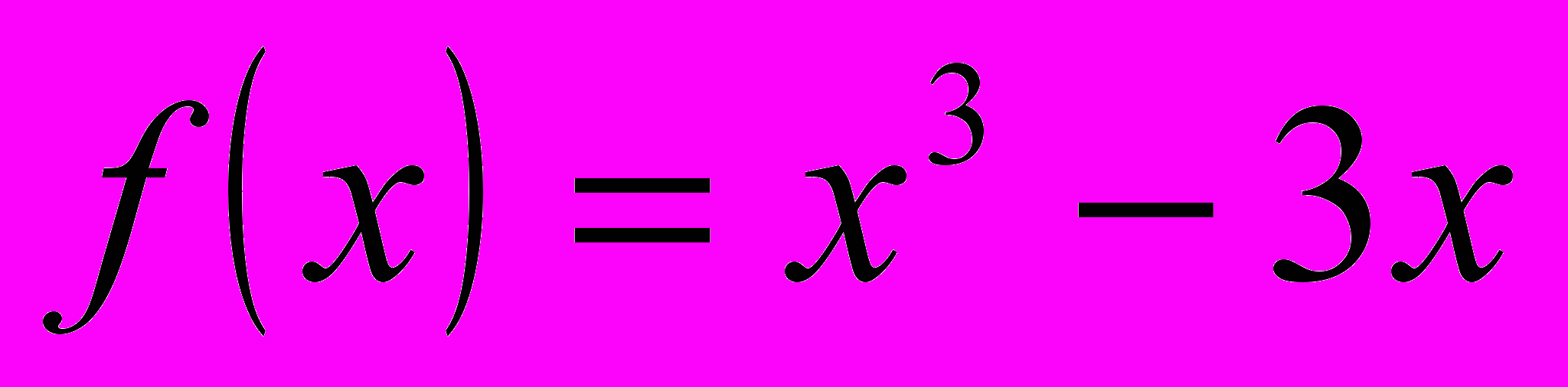выполним все этапы исследования функции. (Дети выполняют шаги плана исследования функции).1.
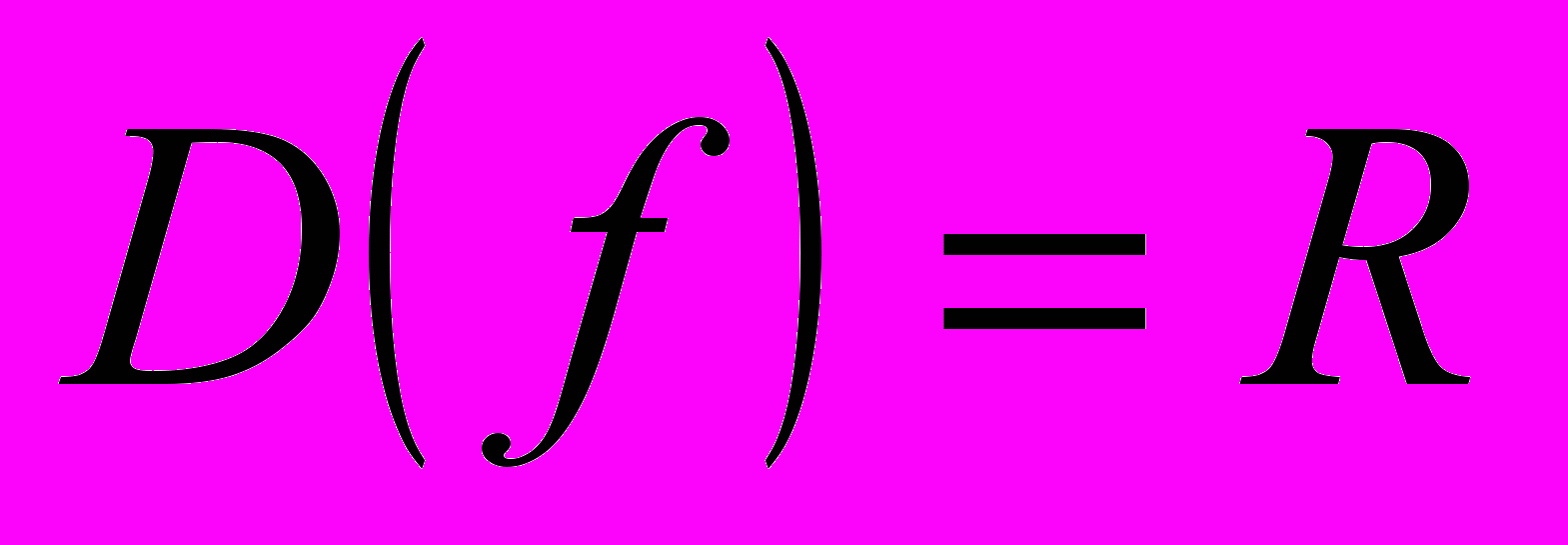. 2. Функция не является ни чётной, ни нечётной.
3.
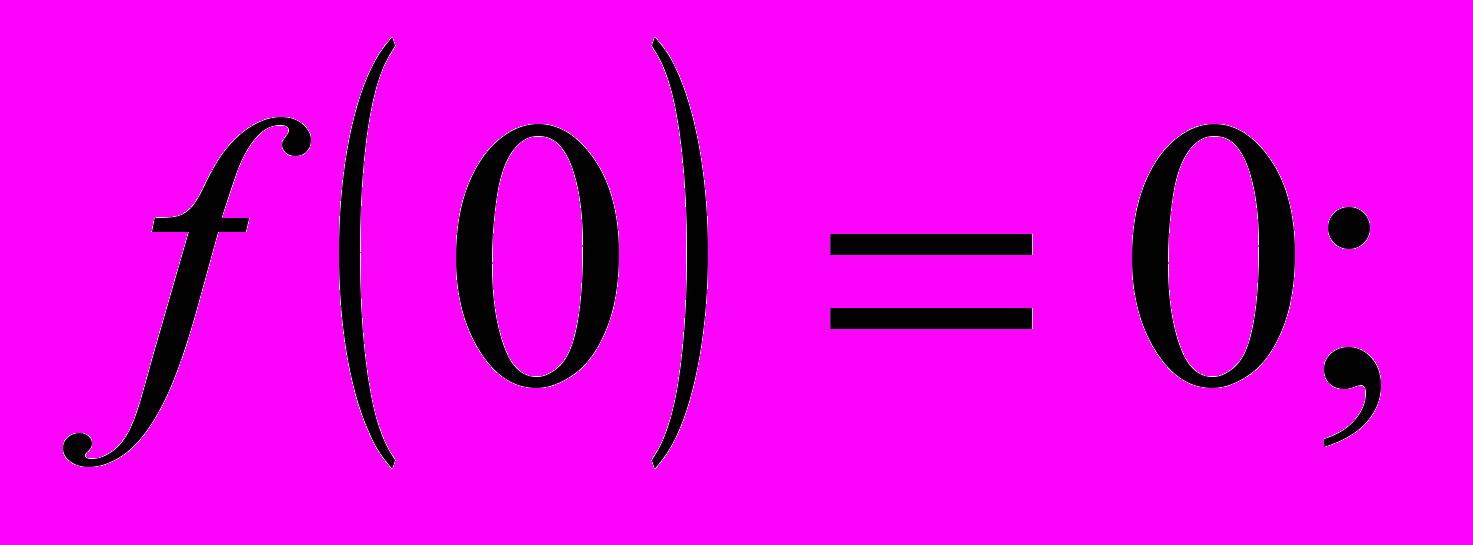
. Координаты точек пересечения графика функции с осями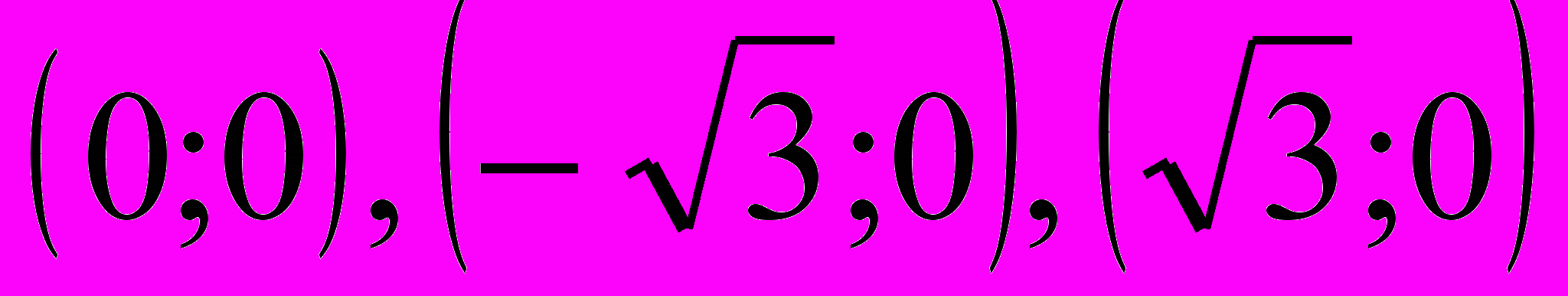
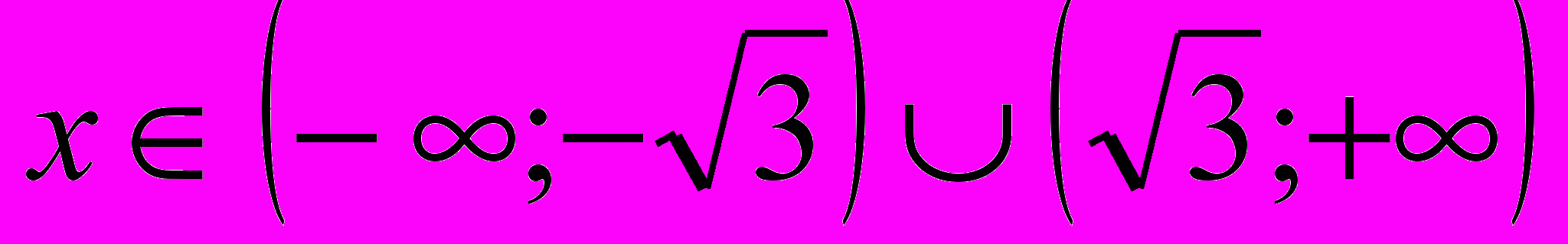
.4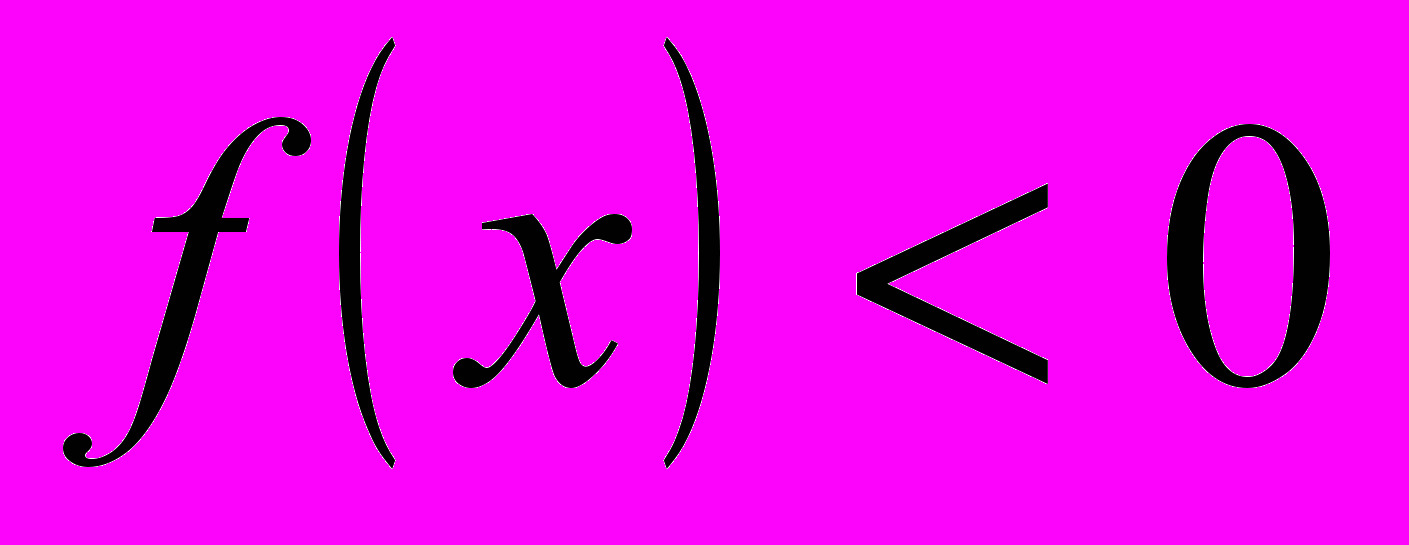. При
; при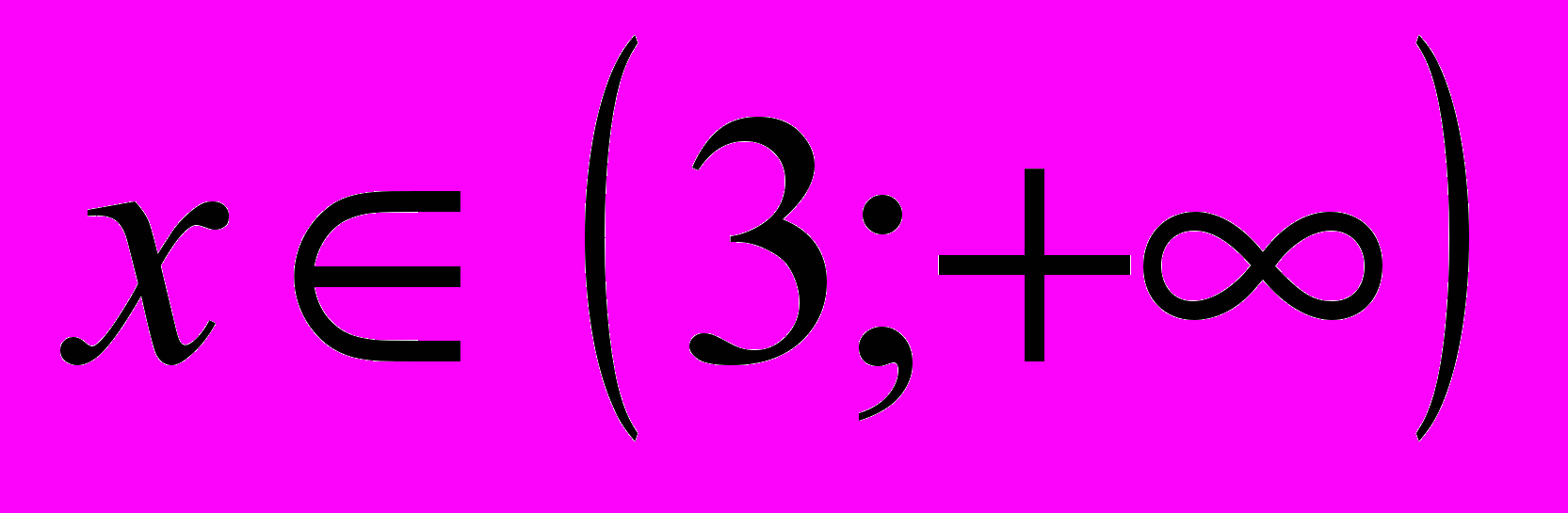 
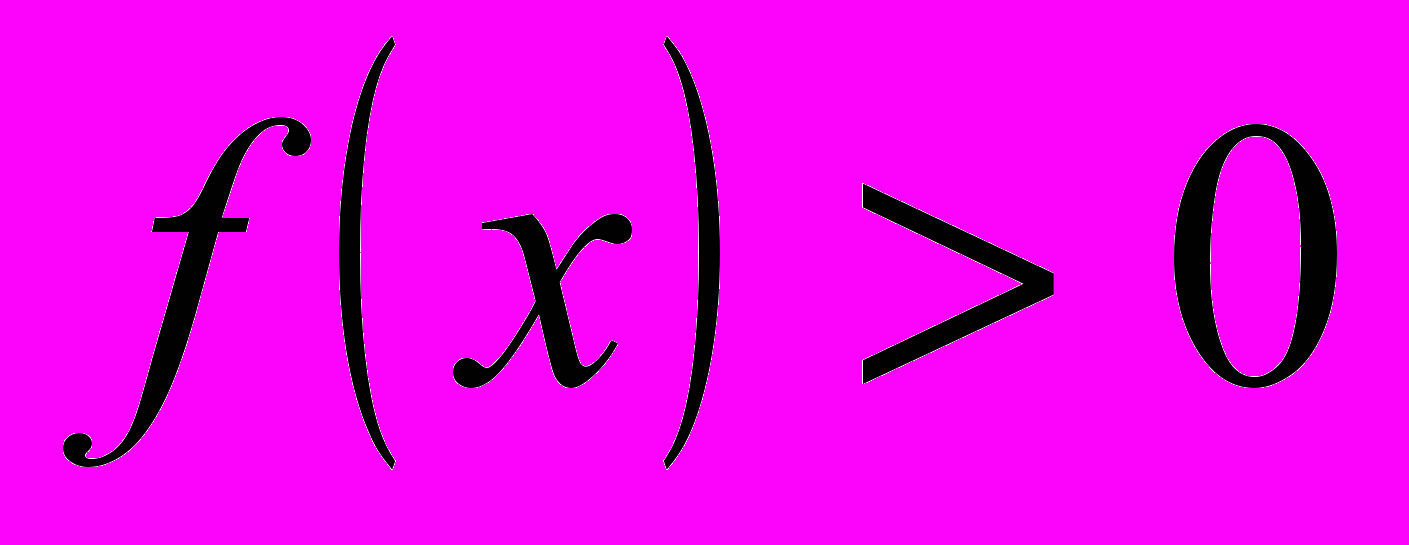.5.
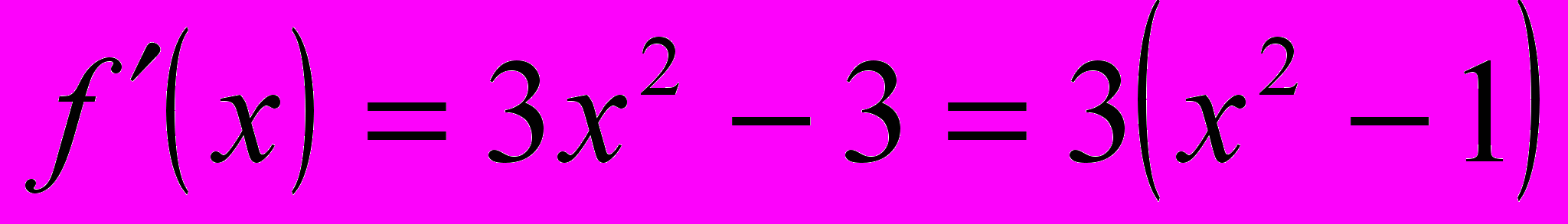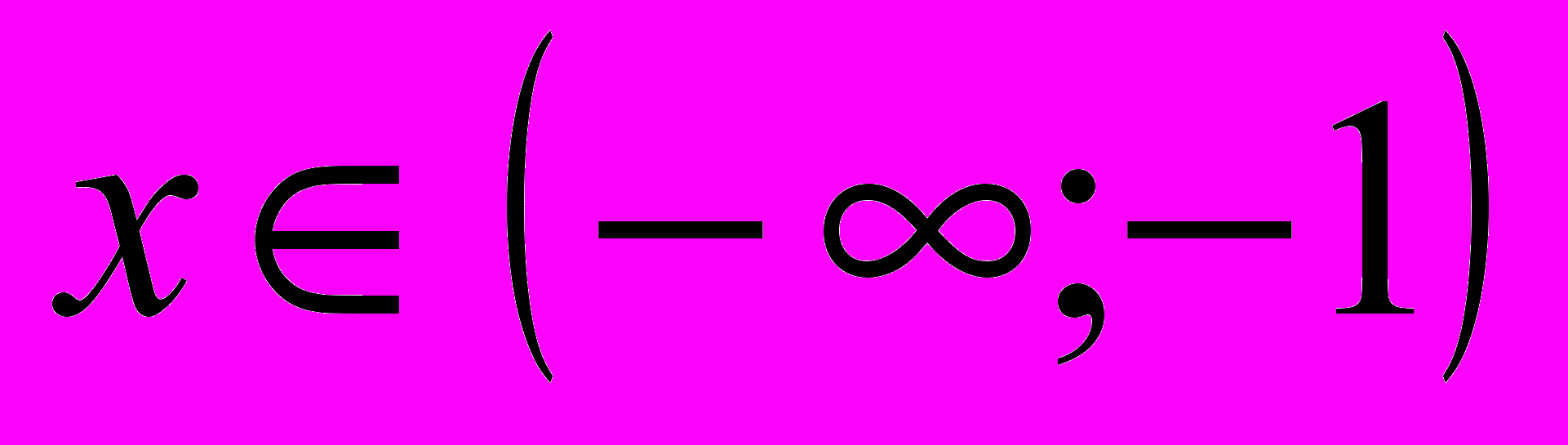. При 
и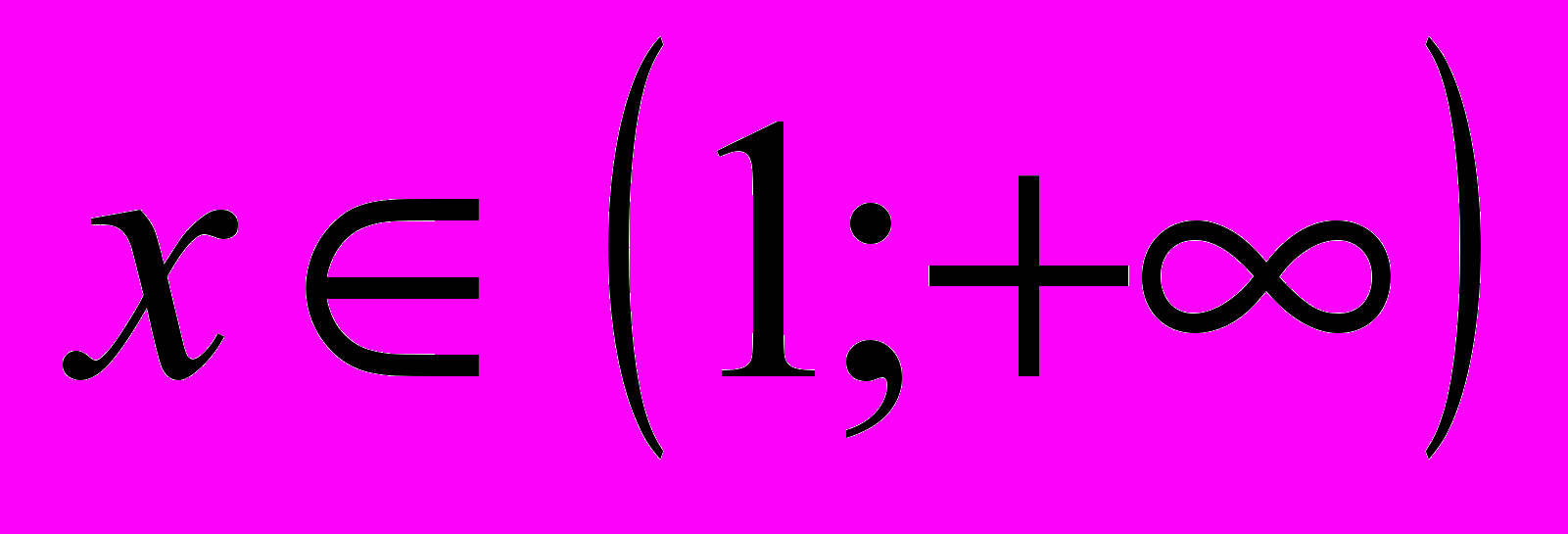 
функция возрастает. При 
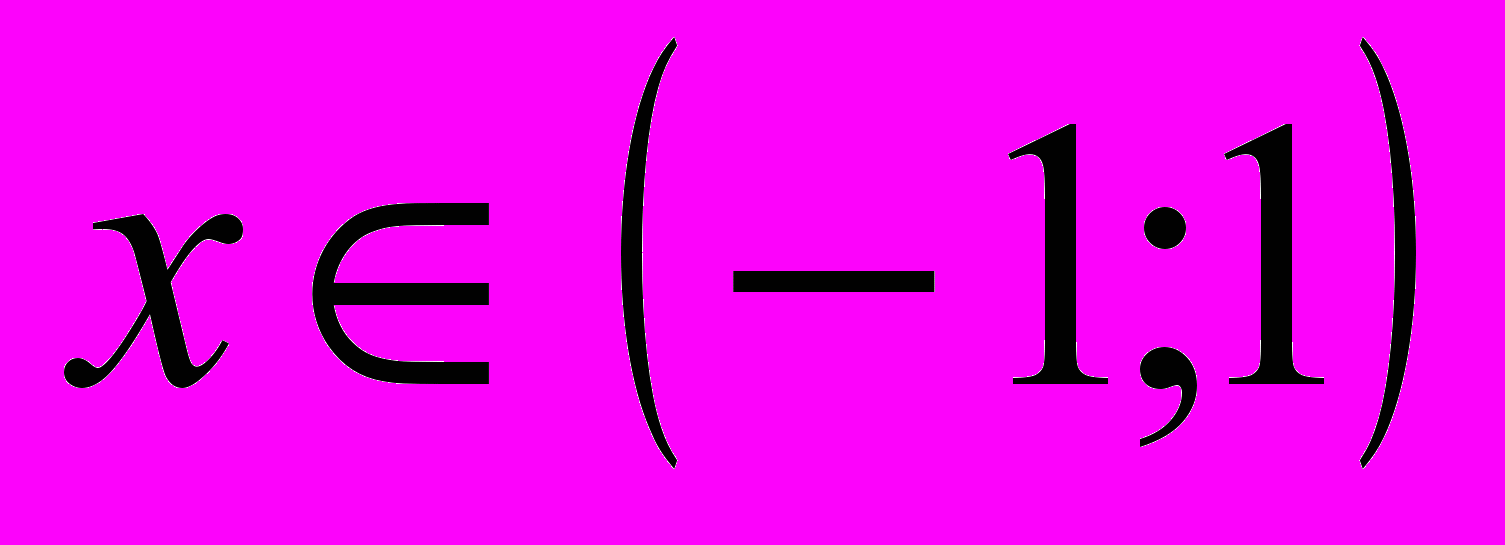функция убывает.6.
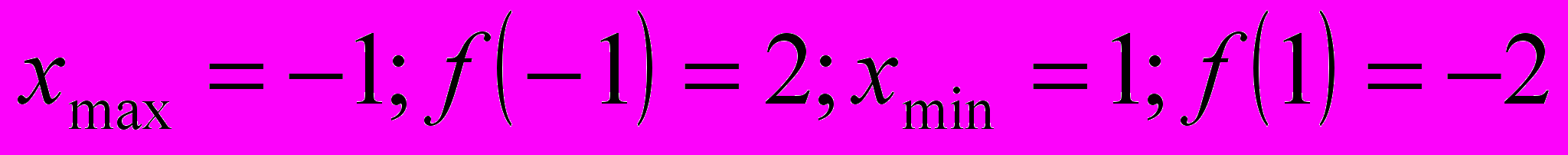.Теперь давайте вспомним, как удобно оформить результат исследования в 5 и 6 пунктах. (В виде таблицы). Заполняется таблица:
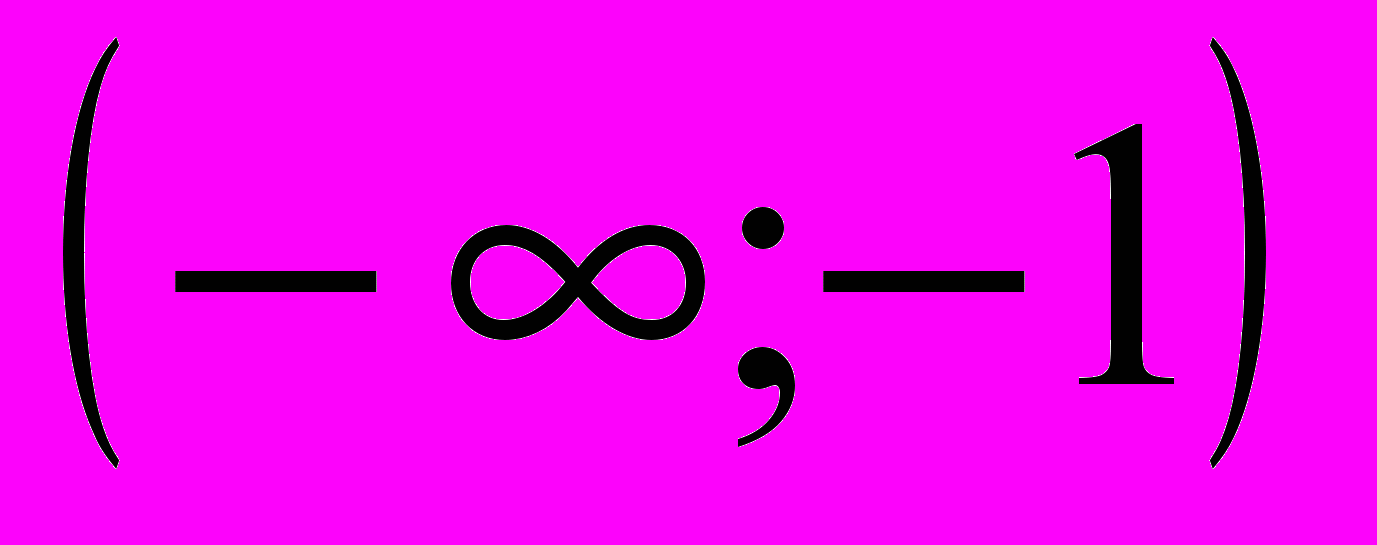| |  | –1 | 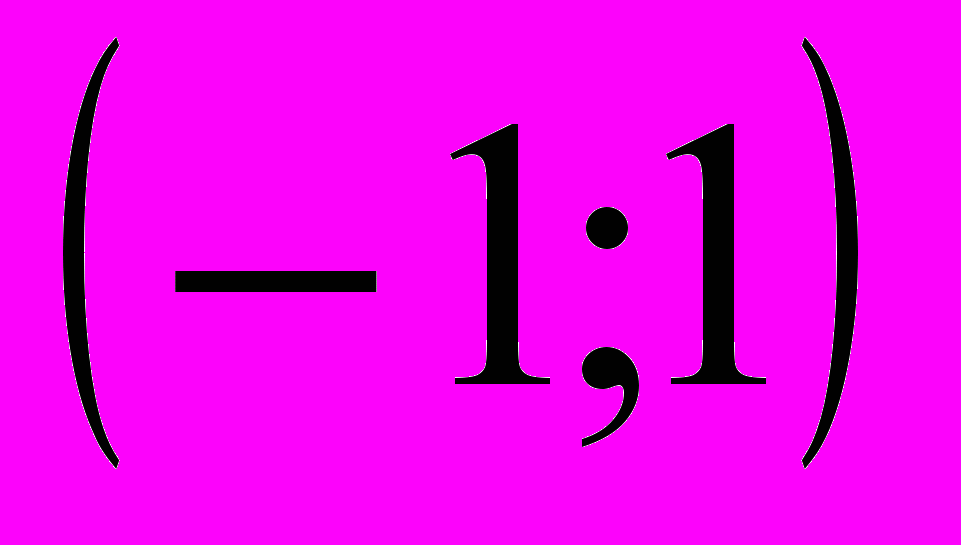 | 1 |  |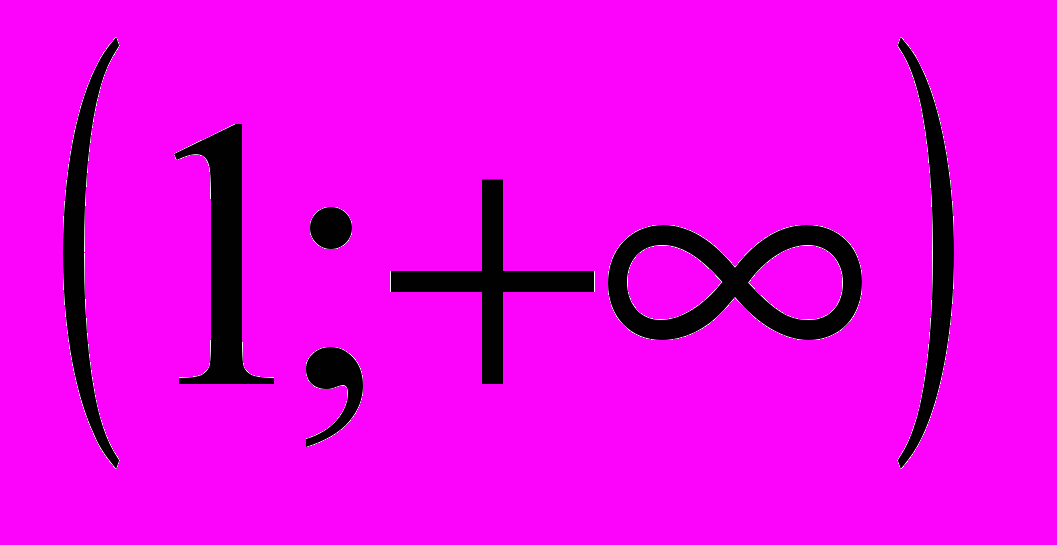
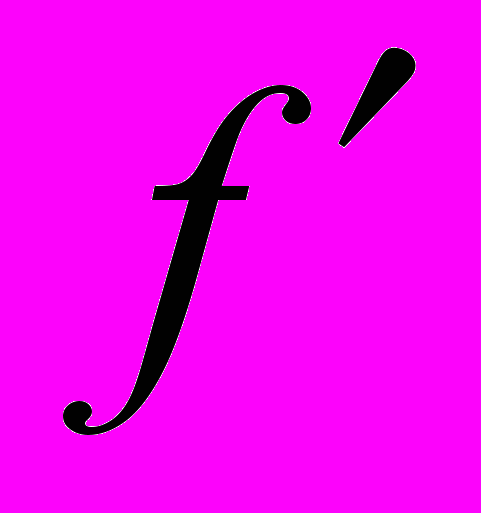 | + | 0 | – | 0 | + |
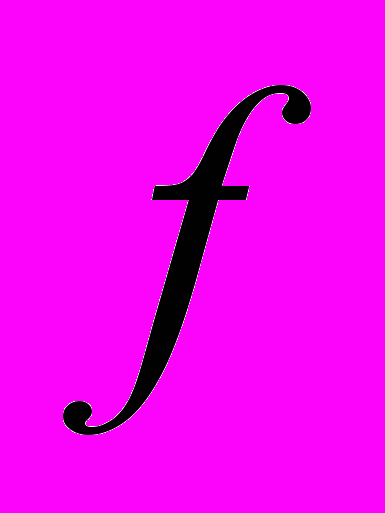 | | 2 | | –2 | |
| | | max | | min | |
7. Для сравнения функция строится на компьютере. Ниже приведен пример построения графика в Excel.
- Самостоятельная работа.
Исследуйте следующие функции, на основе проведённого исследования постройте графики этих функций в тетради, затем проверьте результат с помощью компьютера.
а)
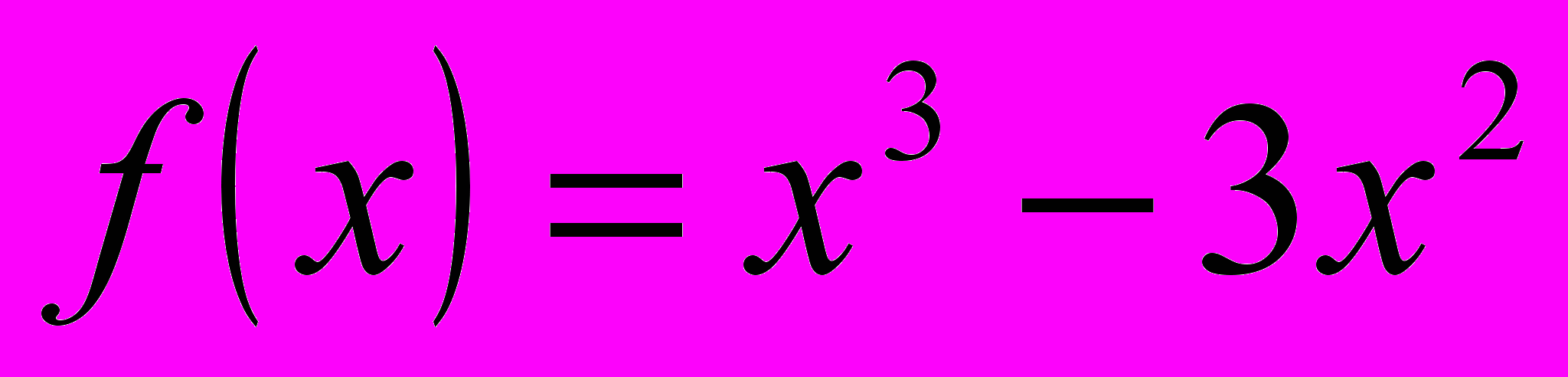; б)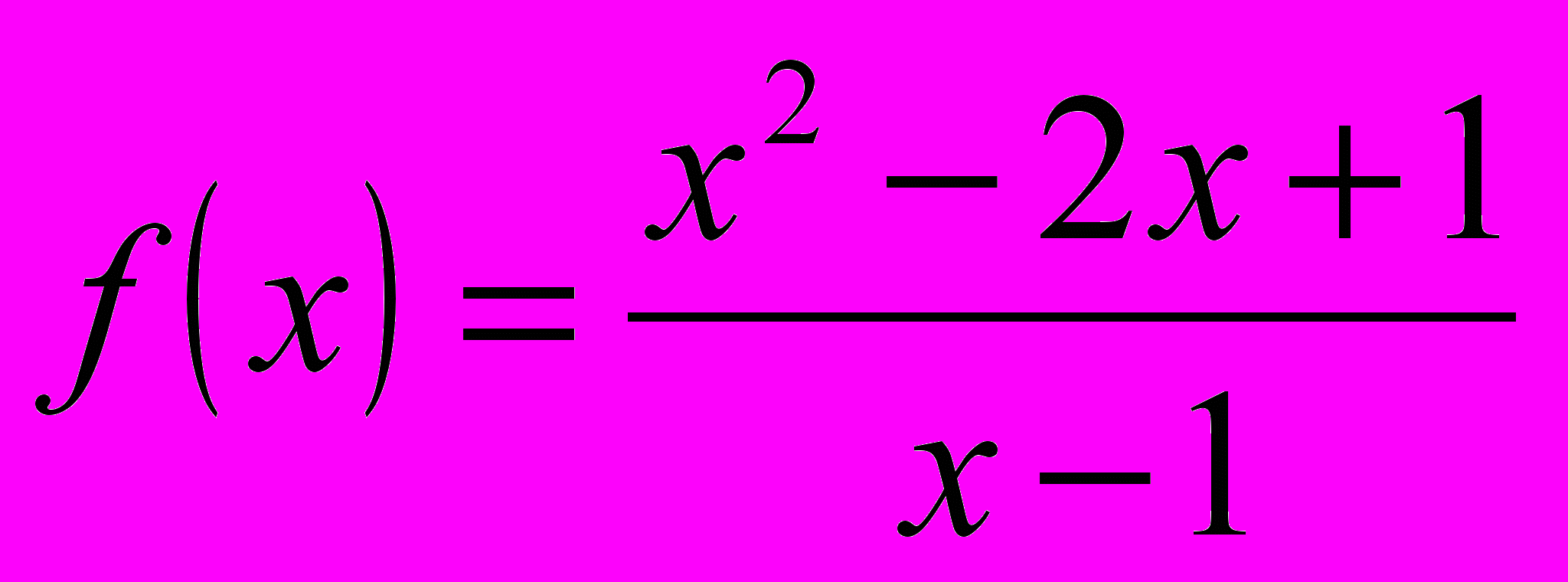 
.Ребята, которые успешно справились с первым, а затем со вторым заданиями поднимают соответствующие сигналы.
- Итог урока.
Вспомним, какова была цель нашего занятия. (Научиться применять производную для исследования функции, научиться строить график функции). Как вы думаете, мы достигли этой цели? (Да, мы научились исследовать функцию, применять для этого производную, научились строить график функции).
Теперь давайте немного пофилософствуем. Что компьютер помог вам сегодня понять? (Компьютер является мощным инструментом, который сильно облегчает человеческую деятельность, но сегодня на многих примерах мы убедились, что компьютер не заменяет человека полностью, по-прежнему высока роль аналитической деятельности человека).
Домашнее задание – творческое. Отыскать функции, описывающие реальные физические процессы, которые вы изучили на уроках физики, и исследуйте эти функции; у кого есть возможность, выдать графики на компьютере.
Урок геометрии в 7 классе.В геометрии компьютер выступает в роли эффективного средства для наглядной иллюстрации понятий, демонстрирования чертежей и рисунков. В школьном курсе геометрии можно выделить три вида чертежей:
1) чертежи, иллюстрирующие содержание вводимого понятия;
2) чертежи, которые образно представляют условие решаемой задачи или рассматриваемого математического предложения;
3) чертежи, иллюстрирующие преобразование геометрических фигур.
По отношению к тексту учебника иллюстрации делятся на:
- ведущие иллюстрации самостоятельно раскрывают содержание учебного материала, заменяя основной текст,
- равнозначные иллюстрации служат целям более глубокого и эффективного усвоения содержания учебного материала. Цель этих иллюстраций — дать определениям геометрических понятий, сформулированных в учебнике в свободной логической форме, адекватную алгоритмическую процедуру получения этих понятий,
- обслуживающие иллюстрации призваны дополнять, конкретизировать содержание текста учебника. Роль обслуживающих иллюстраций — сформировать у учащихся навык поведения под понятие.
Компьютер может сыграть роль средства активного диалога в работе учащихся с моделями геометрических фигур, их развертками, средства формирования у обучающихся конструктивных умений. Рассмотрим пример урока геометрии, где материал приготовленный учителем и ответы учащиеся сделаны на компьютерах, с помощью программного обеспечения Paint (или другие графические редакторы), Word, Microsoft Equation 3.0., «Живая Геометрия».
Тема урока: Четырехугольники и их свойства.
Цели урока:
- повторение определений и свойств различных видов четырехугольников; применение свойств четырехугольников к решению задач;
- развитие логического мышления, памяти, умения подчинять внимание выполнению заданий.
Тип урока: урок совершенствования знаний, умений и навыков.
Форма урока: коллективная система обучения.
Оборудование: экран, мультимедийный проектор, компьютеры, презентация, графический редактор Рaint или электронная программа «Живая геометрия» раздаточный материал (карточки с заданиями).
Ход урока
I. Организационный момент
II. Повторение изученного материала. Работа по группам
Разминка: на экране предлагаются изображения различных четырехугольников (в презентации «geometria 7», на слайдах 2-5 нарисованы прямоугольник, квадрат, ромб, параллелограмм, трапеция). Учащиеся должны дать определение каждого из представленных четырехугольников и перечислить его свойства.
Далее обучающиеся делятся на две группы.
Первая группа: получает задания (на карточках) по построению на компьютере четырехугольников различного типа. Построения производятся в программе Paint. Помимо практического задания по построению на компьютере каждая карточка содержит теоретические вопросы, а также задачу по теме урока (свойства четырехугольников).
Образцы карточек для первой группы:
Карточка 1.
1. Изобразите на экране компьютера все виды четырехугольников.
Назовите свойства этих четырехугольников.
2. Диагональ квадрата равна 7см. Найдите периметр четырехугольника, образованного отрезками, последовательно соединяющими середины сторон данного квадрата.
Карточка 2.
1. Сформулируйте определение параллелограмма. Изобразите на экране компьютера параллелограмм и обозначьте его вершины. Укажите противоположные углы параллелограмма; пару его смежных сторон; диагонали параллелограмма. Сформулируйте свойства параллелограмма.
2. В параллелограмме ABCD проведена биссектриса острого угла А, которая пересекает сторону ВС в точке F, а продолжение стороны CD — в точке Е. Найдите стороны параллелограмма ABCD, если BF = 7 см, СЕ = 2 см.
Карточка №3
Ответить на следующие вопросы:
- Может ли в параллелограмме диагональ равняться стороне?
- Может ли диагональ параллелограмма лежать на биссектрисе угла?
- Может ли в прямоугольнике диагональ равняться стороне?
- Какой четырехугольник можно сложить из четырех спичек?
- Могут ли в трапеции диагонали быть равными?
- Может ли в параллелограмме один угол равняться 40°, другой — 50°?
Образцы карточек для второй группы
Карточка 1.
1. Сформулируйте определение трапеции. Назовите виды трапеции.
Изобразите на экране компьютера равнобедренную трапецию и обозначьте ее вершины. Укажите основание и боковые стороны трапеции; ее диагонали. Сформулируйте свойства равнобедренной трапеции.
2. В равнобедренной трапеции диагональ является биссектрисой острого угла; большее основание равно 8 см, а боковая сторона равна 3 см. Определите периметр трапеции и ее среднюю линию.
Карточка №2.
1. Сформулируйте определение прямоугольника.
Изобразите на экране компьютера прямоугольник и обозначьте его вершины. Перечислите свойства диагоналей прямоугольника.
2. В прямоугольнике ABCD сторона АВ равна 3 см, а сумма диагоналей равна
12 см. Определите угол АСВ.
Карточка №3
Закончить фразы:
- Диагонали, пересекаясь, делят друг друга пополам у ....
- Диагонали равны у ...
- Углы, прилежащие к одной стороне, равны у ...
- Противолежащие углы равны у ...
- Все углы равны у ...
- Диагонали равны и взаимно перпендикулярны у ...
Сразу же после выполнения заданий учитель вместе с учащимися, но уже из противоположных групп, проверяет правильность его выполнения.
III. Подведение итогов урока и домашнее задание
Домашнее задание творческое: нарисовать четырёхугольники на альбомных листах, карандашами или красками, или на компьютере и распечатать.
Yрок математики в 5 классе.
