Конспект лекций по курсу основы алгоритмизации и программирования для студентов всех специальностей и всех форм обучения Минск 2004

Вид материала

Содержание

2.1. Этапы решения задач на ЭВМ
2.2. Понятие алгоритма и способы его записи
2.3. Свойства алгоритмов
2.4. Способы описания алгоритмов

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 24

2.1. Этапы решения задач на ЭВМ

Решение задачи на ЭВМ можно разбить на следующие этапы:

- математическая или информационная формулировка задачи;

- выбор метода (например, численного) решения поставленной задачи;

- построение алгоритма решения поставленной задачи;

- запись построенного алгоритма, т.е. написание текста программы;

- отладка программы - процесс обнаружения, локализации и устранения возможных ошибок;

- выполнение программы - получение требуемого результата.

2.2. Понятие алгоритма и способы его записи

Понятие алгоритма занимает центральное место в современной математике и программировании.

Алгоритмизация - сведение задачи к последовательным этапам действий так, что результаты предыдущих действий используются при выполнении следующих.

Числовой алгоритм - детально описанный способ преобразования числовых входных данных в выходные при помощи математических операций. Существуют нечисловые алгоритмы, которые используются в экономике и технике, в различных научных исследованиях.

Тогда в общем: алгоритм - это строгая и четкая конечная система правил, определяющая последовательность действий над некоторыми объектами и после конечного числа шагов приводящая к достижению поставленной цели.

2.3. Свойства алгоритмов

Дискретность - значения новых величин (данных) вычисляются по определенным правилам из других величин с уже известными значениями.

Определенность (детерминированность) - каждое правило из системы однозначно, а данные однозначно связаны между собой, т.е. последовательность действий алгоритма строго и точно определена.

Результативность (конечность) - алгоритм решает поставленную задачу за конечное число шагов.

Массовость - алгоритм разрабатывается так, чтобы его можно было применить для целого класса задач, например алгоритм вычисления определенных интегралов с заданной точностью.

2.4. Способы описания алгоритмов

Существует несколько способов описания алгоритмов. Наиболее распространенными являются словесное и графическое описания алгоритма.

Словесное описание алгоритма рассмотрим на конкретном примере: пусть необходимо найти наибольший общий делитель для двух целых положительных чисел a и b.

1) Сравнить a и b. Если a
2) Разделить m на d. Обозначить остаток от деления r.

3) Если d=0, то это искомое число. Закончить вычисления. Иначе перейти к пункту 4.

4) Заменить значение m значением d.

5) Заменить d значение значением r.

6) Перейти к пункту 2.

Здесь алгоритм описан с помощью естественного языка, а объекты обработки, являющиеся числами, обозначены буквами.

Например, рассмотрим алгоритм решения квадратного уравнения вида a*x²+b*x+c=0:

1) вычислить D = b*b - 4 * a * c;

2) если D<0, то перейти к 4;

3) вычислить

;

;

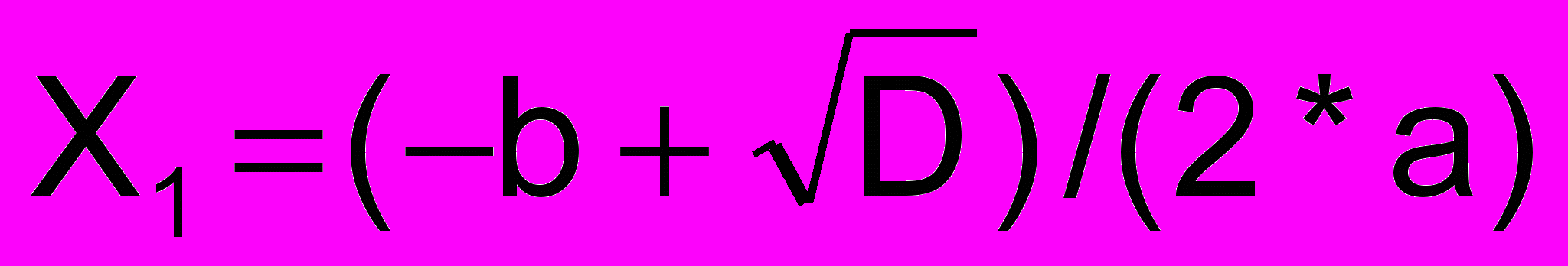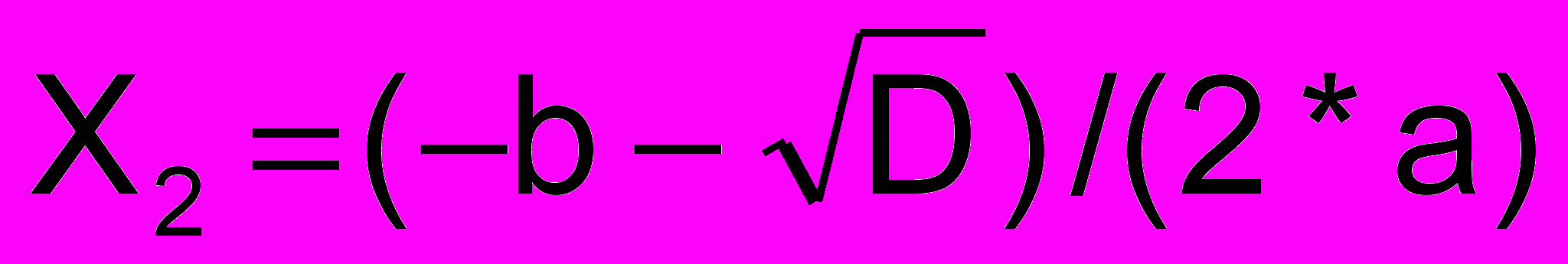4) конец.

2.5. Графическое описание алгоритма

Представление алгоритма в виде схемы, состоящей из последовательности блоков (геометрических фигур), каждый из которых отображает содержание очередного шага алгоритма, называется графическим описанием алгоритма. Внутри фигур кратко записывают действие, выполняемое в этом блоке. Такую схему называют блок-схемой алгоритма.

Правила изображения фигур сведены в единую систему программной документации (ГОСТ 19.701-90). По данному госту – это схема данных, которая отображает путь данных при решении задачи и определяет этапы их обработки.

Схема данных содержит:

- символы данных (могут отображать тип носителя данных);

- символы процесса, который нужно выполнить над данными;

- символы линий, указывающих потоки данных между процессами и носителями данных;

- специальные символы, которые используют для удобства чтения схемы.

2.6. Основные символы схемы алгоритма

Символы ввода-вывода данных:

- данные ввода/вывода (носитель не определен);

- ручной ввод данных с устройства любого типа, например, с клавиатуры;

- отображение данных в удобочитаемой форме на устройстве, например, дисплее.

Символы процесса:

-

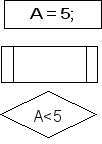процесс - отображение функции обработки данных, т.е. операции приводящей к изменению значения указанного объекта;

- предопределенный процесс - отображение группы операций, которые определены в другом месте, например, в подпрограмме;

- решение - отображение функции, имеющей один вход и ряд альтернативных выходов, их которых только один может быть активизирован после анализа условия: указанного внутри этого символа.

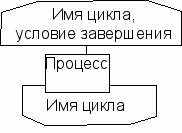
Граница цикла - отображение начала и конца цикла,

или, наоборот, - условие завершения указывают в нижней границе.

Символы линий - отображают поток данных или управления. Линии - горизонтальные или вертикальные, имеющие только прямой угол перегиба. Стрелки - указатели направления не ставятся, если управление идет сверху-вниз или слева-направо.

Специальные символы

Соединитель - используется при обрыве линии и продолжении ее в другом месте (необходимо присвоить название).

Терминатор - вход из внешней среды или выход во внешнюю среду (начало или конец схемы программы).