Geum.ru

Предисловие дорогие друзья !

Вид материалаДокументы

Содержание


Глава 8 рекуррентные соотношения
§46. Реккурентное соотношение как способ задания числовой фун-кции
Рекуррентным соотношением k-го порядка
Для любознательных
Подобный материал:
1   ...   16   17   18   19   20   21   22   23   ...   29

ГЛАВА 8 РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ


В данной главе мы начинаем изучать очень мощный подход, используемый для построения эффективных алгоритмов решения различных задач – динамическое программирование. Здесь мы только слегка коснемся его, рассмотрев способ задания числовых функций при помощи рекуррентных соотношений. Этот способ отличается от уже известных вам из курса математики способов. Мы обсудим его преимущества над другими способами и научимся писать программы, вычисляющие значения функций, заданных рекуррентно.

§46. Реккурентное соотношение как способ задания числовой фун-кции


Легко взглянуть в соседнюю долину,

Взобравшись на высокий перевал!

( Неизвестный автор )

46.1. Из курса математики мы знаем, что функция – это зависимость между двумя величинами, при которой каждому значению первой величины (аргумента функции) соответствует ровно одно значение второй величины. Множество значений, которые может принимать первая величина, называют областью определения функции, а множество значений, которые может принимать вторая величина – областью значений функции. В этом параграфе мы будем рассматривать только функции, область определения которых – это целые числа, принадлежащие некоторому фиксированному отрезку числовой прямой, а область значения – либо все целые, либо все вещественные числа.


Итак, пусть F(n) – это некоторая функция, где n – это целое число из отрезка [a, b], 0 ≤ a < b, a и b – целые. Давайте вспомним, какие способы задания функции F мы уже знаем:

  1. Аналитический. При использовании этого способа функция задается при помощи некоторого математического выражения, значение которого можно вычислить, зная значение переменной n. Например:


F(n) = (n2 + n)/2 (1)

  1. Табличный. Так как количество целых чисел на отрезке [a, b] конечно, то для задания функции F(n) мы можем записать в некоторой таблице ее значения для всех возможных значений переменной n. Например, если a=1 и b=10, то функция (1) может быть задана при помощи следующей таблицы (2):




N
1
2
3
4
5
6
7
8
9
10

F(n)
1
3
6
10
15
21
28
36
45
55



  1. Описательный. Также для задания функции мы можем просто описать ее своими словами. Например:


F(n) – это сумма всех натуральных чисел от 1 до n включительно (3)

  1. Графический. Обычно этот метод используется для описания функций, аргумент у которых принимает вещественные значения, однако при помощи этого способа можно задавать функции и с целым аргументом. При использовании данного способа функция задается при помощи графика в прямоугольной декартовой системе координат, где каждой паре аргумент и соответствующее значение функции ставится в соответствие точка плоскости с соответствующими координатами. По большому счету, данный способ задания функции есть ни что иное, как визуализация табличного метода.



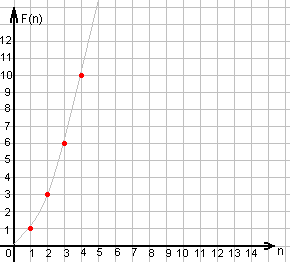
(4)


Интересно заметить, что (1), (2), (3) и (4) на самом деле задают одну и ту же функцию, откуда можно сделать вывод, что одна и та же функция может быть задана несколькими способами.

Теперь, давайте отдалимся от приведенных выше четырех способов задания функций и попробуем придумать еще один способ. Давайте немного «расширим» аналитический способ, позволив в выражении фигурировать задаваемой нами функции F(n) но с меньшими аргументами.

Рассмотрим пример: F(n) = F(n-1)+n. (5)

Совершенно очевидно, что данный способ задания числовой функции не является аналитическим, так как для приведенного примера, чтобы вычислить значение функции для n = 5, необходимо знать значение функции для n = 4, тогда как из определения аналитического способа, чтобы узнать значение функции достаточно знать только значение аргумента.

На самом деле приведенный пример не задает никакую функцию, а задает всего лишь соотношение между значениями данной функции, которое и является примером рекуррентного соотношения первого порядка. Предположим, что n может принимать целые значения от 1 до 10, давайте попробуем вычислить значение функции (5) для n = 3. Известно, что F(3) = F(2) + 3, а F(2) = F(1) + 2, в свою очередь F(1) = F(0) + 1, но ноль не попадает в область определения нашей функции, отсюда следует, что мы не можем вычислить функцию ни для какого значения аргумента. На самом деле не все так плохо, согласитесь, что если заранее задать значение функции для n = 1, то есть задать начальное условие, то мы сможем вычислить функцию для всех наших n от 1 до 10. Давайте положим, что F(1) = 1, тогда F(2) = F(1)+2 = 3, F(3) = F(2) + 3 = 6, и так далее. Давайте теперь попытаемся сформулировать некоторые определения:
  • Рекуррентным соотношением k-го порядка будем называть соотношение вида F(n) = a1*F(n-1) + a2*F(n-2) + … + ak*F(n-k) + G(n), где ai - заранее определенные константы 1 ≤ i ≤ k, а G(n) – некоторая функция заданная аналитическим способом. Примеры:
    1. F(n) = F(n-1) + 1, здесь k = 1, a1 = 1, G(n) = 1;
    2. F(n) = F(n-1) – 2*F(n-2) , здесь k = 2, a1 = 1, a2 = -2, G(n) = 0;
    3. F(n) = 2*F(n-1) – F(n-3) + 7*n, здесь k = 3, a1 = 2, a2 = 0, a3 = -1, G(n) = 7*n;
  • Граничными или начальными условиями для рекуррентного соотношения k – го порядка с областью определения [a,b] (т.е.аргумент n – целое число и a ≤ n ≤ b) называется система состоящая из k- тождеств вида:

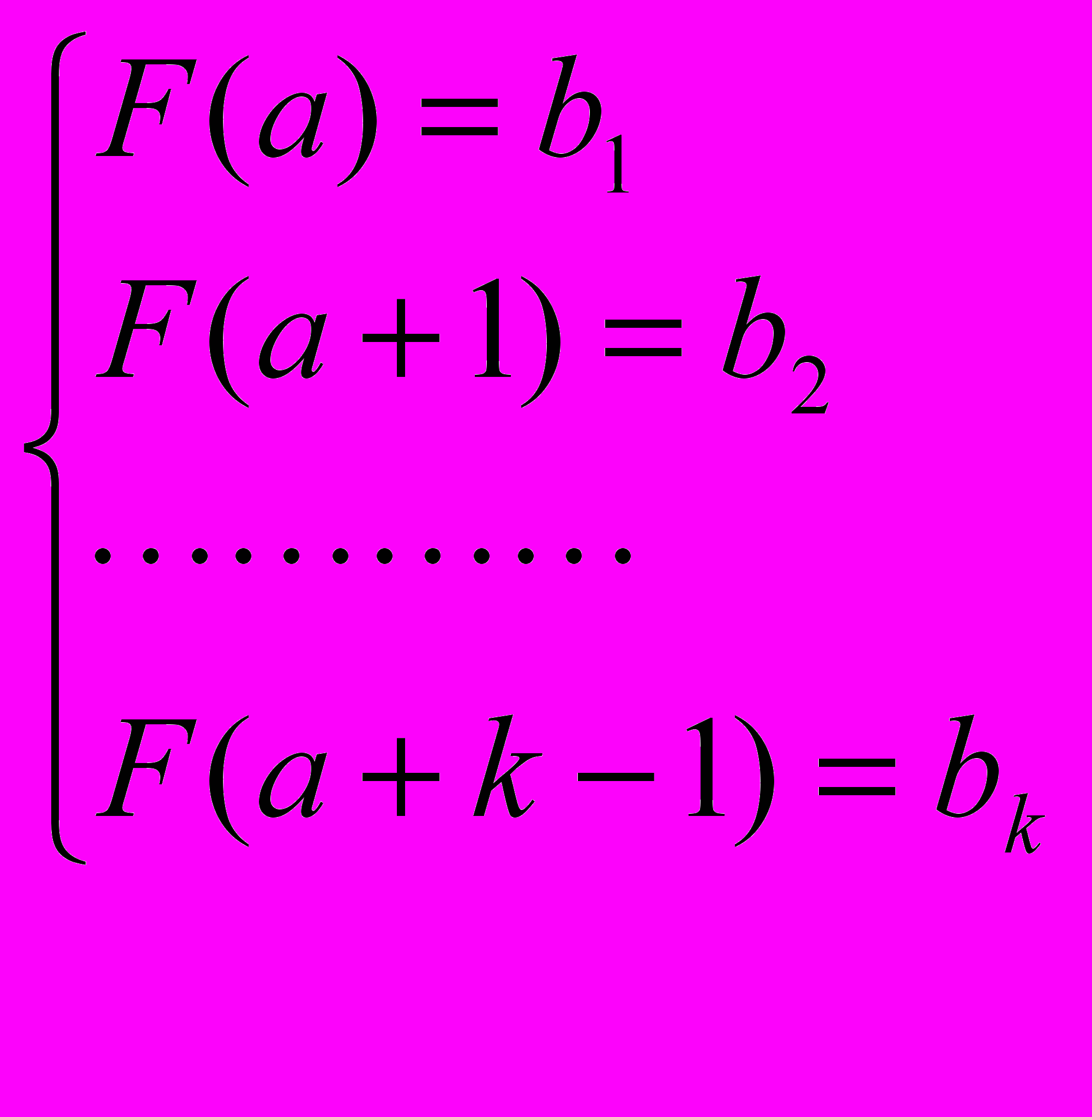, где bi – заданные константы, 1 ≤ i ≤ k
  • Рекуррентное соотношение k-го порядка с заданными граничными условиями называется рекуррентным уравнением.

На самом деле, способ задания функции при помощи рекуррентного уравнения довольно мощный и порой незаменимый метод. Для примера давайте рассмотрим рекуррентное уравнение второго порядка, где область определения – это все положительные целые числа:

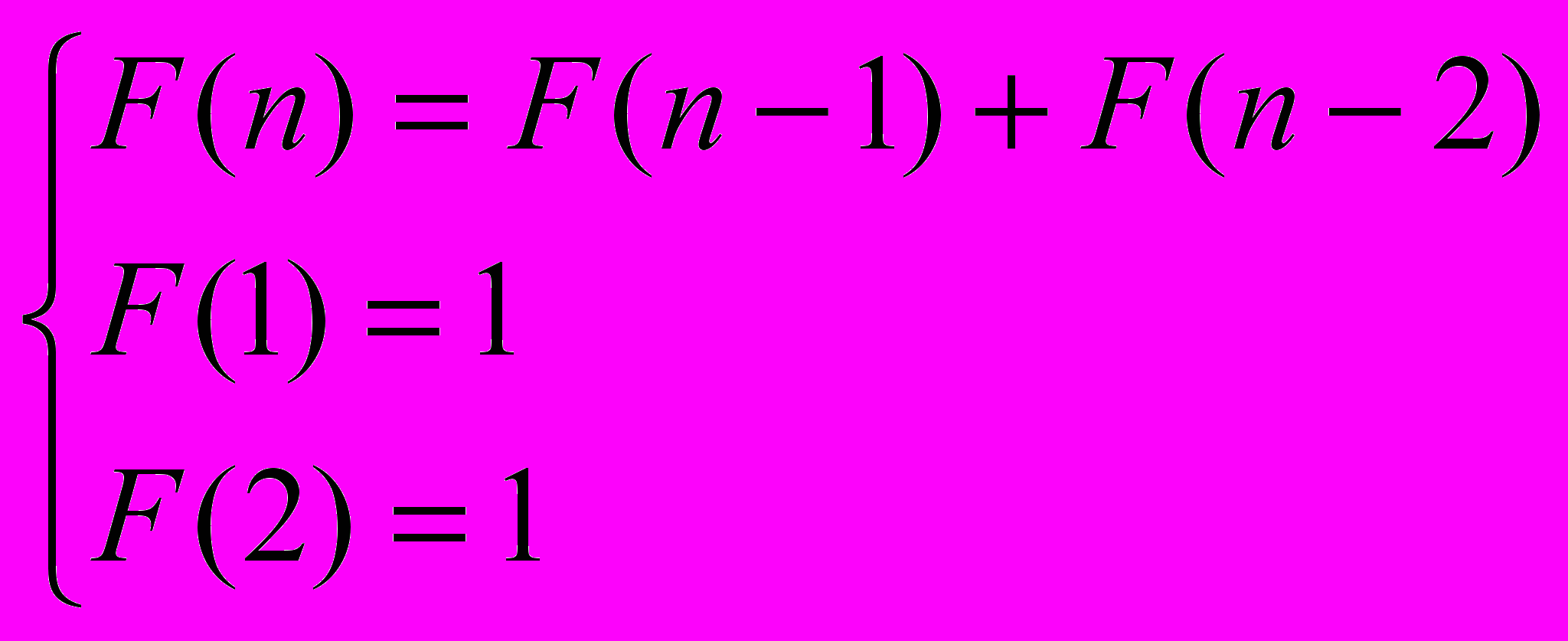(6)

Это рекуррентное уравнение, а вернее все числа из области значения функции носят название – «Числа Фибоначчи». На самом деле числа Фибоначчи можно задать и аналитическим способом :

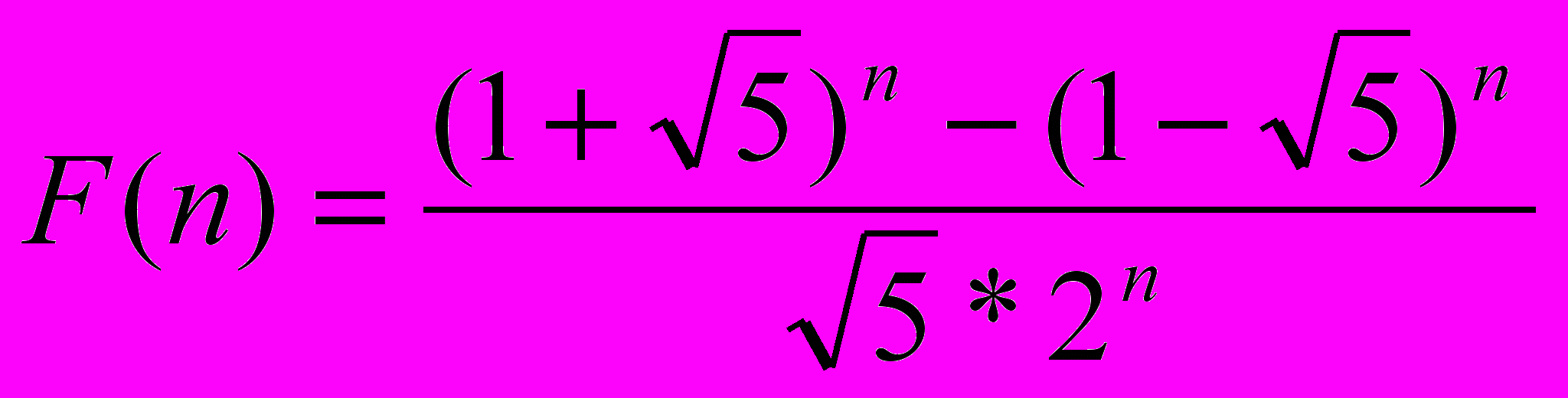(7)

Наверное, многие согласятся, что хоть (6) и (7) задают одну и ту же числовую функцию, но (6) намного проще понять, не говоря уже о том, чтобы вычислить.

Теперь, давайте попробуем научиться программировать рекуррентные соотношения на примере чисел Фибоначчи, предположим, что нам необходимо вычислить и вывести на экран первых 100 чисел Фибоначчи.

1) Первым шагом необходимо определить рекуррентное уравнение, которое будет задавать искомую функцию F(n). Для нашего примера мы уже знаем, что

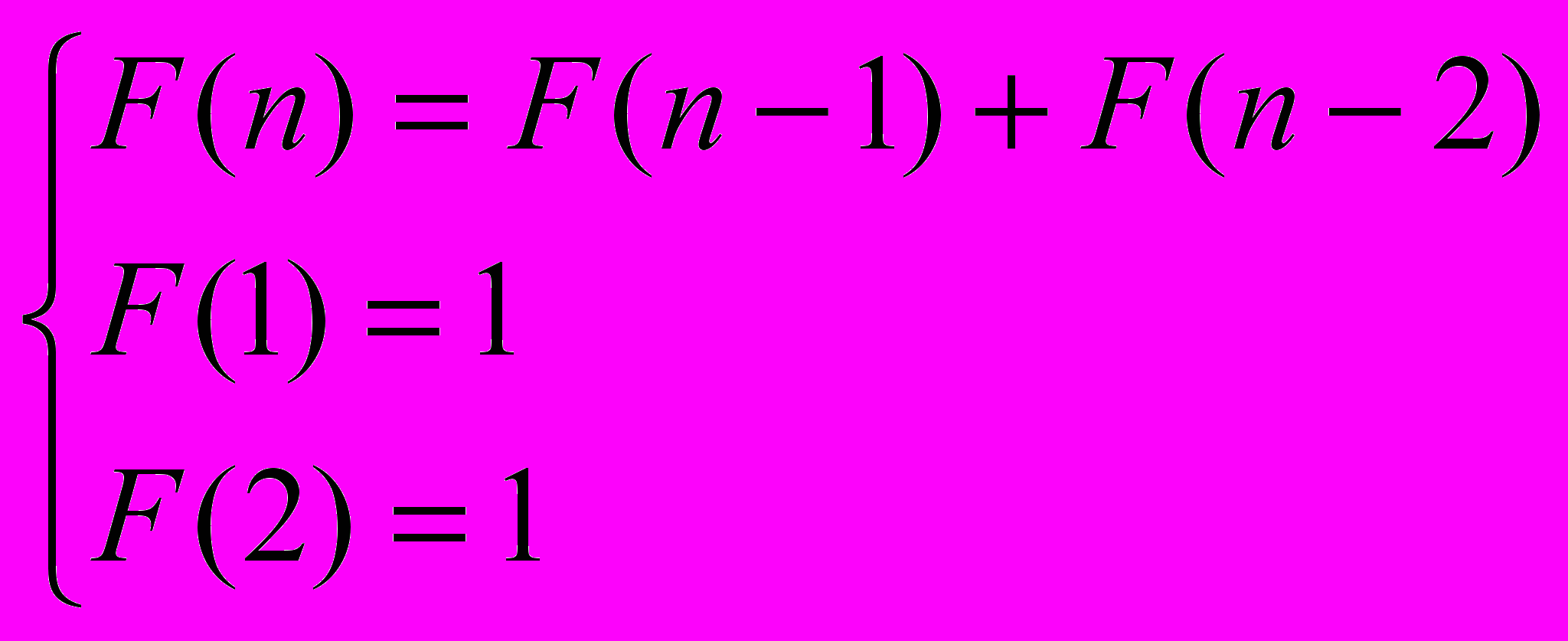
2) Вторым шагом необходимо определить область определения функции. В нашем примере нам необходимо определить первые 20 чисел - поэтому возьмем область определения отрезок [1,20]. После того как нашли область определения, давайте заведем линейный массив соответствующей области определения, т.е. каждому значению аргумента из области определения будет соответствовать ячейка таблицы, в которой будем хранить соответствующее значение функции. Следует отметить, что тип элементов массива зависит от того, какие значения принимает искомая функция. Если функция принимает действительные значения, то массив должен быть типа Real,а если функция принимает целые числа, то типа Integer или LongInt. В нашем случае функция принимает целые числа, поэтому достаточно типа Integer. Объявляем массив:


Var F:Array[1..20] of Integer;


3) Третьим шагом необходимо программно задать граничные условия нашего рекуррентного уравнения. Для (6) необходимо задать значение для n = 1 и для n = 2, те нам просто необходимо соответствующим ячейкам таблицы присвоить заданные значения. Для нашего примера:


F[1]:=1;

F[2]:=1;

4) Четвертым шагом, нам осталось посчитать все еще неопределенные значения функции и вывести результат вычислений, для примера (6) нам необходимо посчитать значения для всех n от 3 до 20 и далее вывести все двадцать чисел на экран.


For i:=3 to 20 do F[i]:=F[i-1] + F[i-2];


For i:=1 to 20 do Writeln(F[i]);


Полный листинг программы по вычислению первых 20 чисел фибоначи:


F:Array[1..20] of Integer; {функция F(n)}

i:Integer; {индекс}


Begin

F[1]:=1;

F[2]:=1;


For i:=3 to 20 do F[i]:=F[i-1] + F[i-2];


For i:=1 to 20 do Writeln(F[i]);

end.


Давайте рассмотрим еще один пример:

Пример126

Ввести с клавиатуры число k и вывести на экран число F(k), где k – целое, 1 ≤ k ≤ 20,




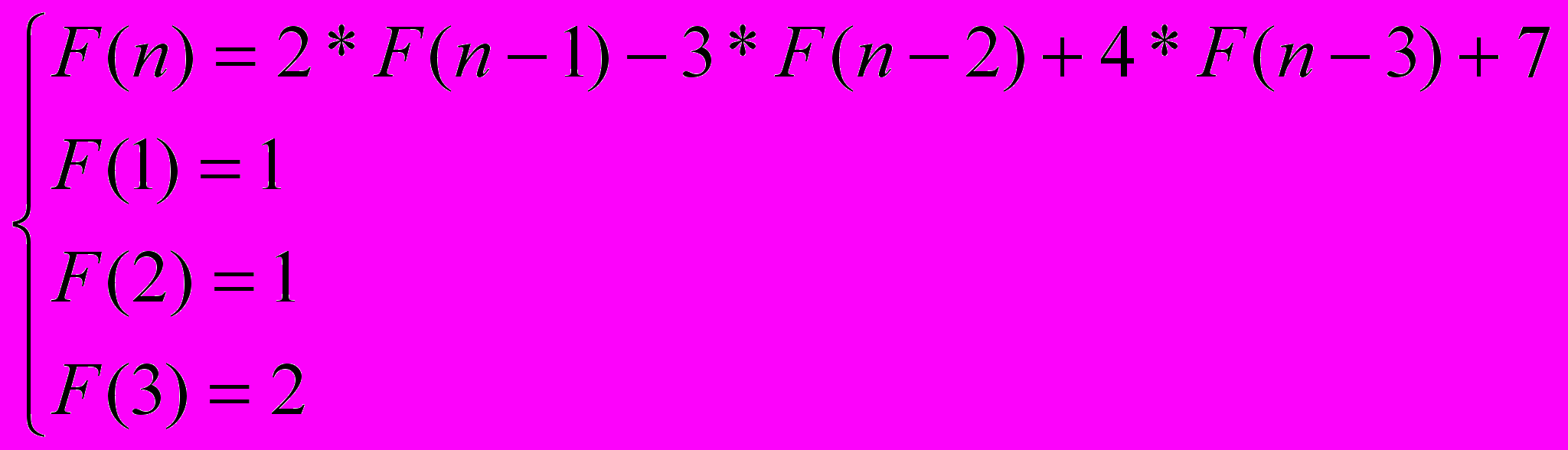
Решение:

Давайте будем писать решение по пунктам, как в предыдущем решении.


1) Рекуррентное уравнение нам уже задано в условии задачи


2) Так как введенное k может принимать произвольные значение от 1 до 20, то будем считать, что область определения отрезок [1,20]. Из рекуррентного уравнения видно, что F принимает целые значения, но возникает вопрос: Какой тип выбрать для массива Integer или LongInt?. На самом деле, если возникает малейшая предпосылка о том, что типа Integer недостаточно, то всегда лучше воспользоваться типом LongInt.Для нашей задачи такие предпосылки есть, поэтому давайте остановимся на типе LongInt.


Var F:Array[1..20] of LongInt;

k,i:LongInt;


3) Перед тем как задавать граничные условия, необходимо ввести данные, если таковые имеются, а после уже задавать начальные данные. В принципе большой разницы нет – ввести данные после определения (инициализации) начальных условий или после, попросту это считается хорошим стилем программирования.

Read(k);

F[1]:=1;

F[2]:=1;

F[3]:=2;


4) Так как нам необходимо вывести только k-е значение функции, то вычисления будем производить до k.


For i:=4 to k do F[i]:=2*F[i-1]–3*F[i-2]+4*F[i-3]+7;

Writeln(F[k]);


Полный листинг программы:


Var F:Array[1..20] of LongInt;{функция F}

k,i:LongInt;{k-аргумент искомого значения F, i - индекс}

Begin

Read(k);

F[1]:=1;

F[2]:=1;

F[3]:=2;

For i:=4 to k do F[i]:=2*F[i-1]–3*F[i-2]+4*F[i-3]+7;

Writeln(F[k]);

end.

46.2. Составление рекуррентных уравнений

На самом деле редко когда встретишь задачу, где сразу уже дано рекуррентное уравнение – обычно задача является текстовой и не понятно, какое же здесь рекуррентное уравнение использовать, а часто даже не ясно вообще решается ли данная задача с помощью рекуррентных уравнений. Скоро вы поймете, что придумать рекуррентное уравнение намного сложнее, чем его запрограммировать. В этом пункте мы уделим внимание выводу рекуррентного уравнения, а точнее шагу номер один при решении задач на рекуррентные уравнения.

Перед тем как учиться составлять рекуррентные уравнения, давайте вспомним такой метод доказательства числовых тождеств как метод математической индукции. Метод математической индукции состоит из трех шагов:

1) Каким то образом( можно даже интуитивно) определяем формулу, которую пробуем доказать .

2) Вручную проверяем для граничных условий верность доказываемой формулы

3) Делаем индуктивное предположение о том, что наша формула «работает» для все n не превосходящих некоторого k. Если после этого нам удается доказать, что формула верна и для n = k+1, то наше предположение верное – формула верна.


Пусть F(n) – это сумма всех натуральных чисел от 1 до n включительно, необходимо найти выражение для вычисления F(n)

1) Предположим F(n) = n*(n+1)/2

2) F(1) = 1*2 / 2 = 1 – это правильно

3) Предположим, что формула верна для всех n от 1 до некоторого k, тогда:

Легко заметить, что если мы знаем F(k), то F(k+1) = F(k) + k + 1 – это верно, так как F(k) – это сумма чисел от 1 до k, а F(k+1) – сумма чисел от 1 до k+1, следовательно F(k)+ k+1 = F(k+1).

Мы показали, что F(k+1) = F(k) + k+1. Так как по нашему предположению F(k) = k*(k+1), то F(k+1) = k(k+1)/2 + (k+1) = k*(k+1)/2 + 2*(k+1) = (k+1)(k+2)/2. Отсюда следует, что формула «работает» и для n = k+1. Следовательно формула верна.

Давайте подумаем, почему же метод математической индукции работает. Согласитесь, что в пункте три мы доказали, что если формула работает для n не превосходящих некоторого k, то формула работает и для n = k+1. Но в пункту 2 мы вручную для граничного (минимального) значения аргумента доказали, что формула работает, следовательно она работает и для следующего значения аргумента. Для нашего примера мы показали, что формула работает для n = 1, тогда по доказанному индуктивному предположению формула работает и для n = 2, а так как работает для n = 2, то работает и для n = 3 и так далее. Получаем мы доказали для все n.

В принципе, если посмотреть на доказательство методом математической индукции, то в пункте доказательства номер один есть неопределенность – согласитесь, если у вас с детства нет математической интуиции, то откуда вам взять формулу, для доказательства?

Различие алгоритмов вывода рекуррентного уравнения от доказательства методом математической индукции заключается в том, что у нас нет первого шага – у нас нет формулы, которую мы хотим доказать, а второе – немного изменится индуктивное предположение и пункты поменяются местами.

Давайте попробуем описать алгоритм вывода рекуррентного уравнение:

1) Предположим, что нам удалось каким-то образом найти значение искомой функции F для всех n не превосходящих некоторого k. Теперь, пытаемся выразить значение F(k+1) через значения функций с аргументом не превосходящим k.

2) Если пункт номер один выполнен, то определяем порядок рекуррентного уравнения, пусть он равен m. Для данного рекуррентного уравнения вручную вычисляем начальные условия.

После этого рекуррентное уравнение готово – приступаем к его программированию.

Давайте рассмотрим несколько примеров.

Пример127

Дано два целых числа a и b 2 ≤ a ≤ 5 , 0 ≤ b ≤ 10. Найти число ab.

Решение

Конечно, данную задачу можно решить и не рекуррентно, но давайте, все же решим ее рекуррентно – это поможет вам более детально понять метод вывода рекуррентного уравнения.

Начнем с того, что введем функцию – пусть F(n) – это an, тогда в ответ нам нужно выдать F(b).

Теперь попробуем вывести само рекуррентное уравнение

1) Предположим, что нам удалось каким-то образом вычислить значения функции F для все n не превосходящих некоторого k. Тогда легко заметить, что F(k+1) = a*F(k).

2) Мы имеем дело с рекуррентным уравнением первой степени и областью определения функции [0,10], следовательно начальные условия состоят из одного равенства, то есть нам необходимо определить F(0) = a0 = 1, для любого a.

Все, рекуррентное уравнение получено, теперь приступаем к алгоритму решения задачи на рекуррентное уравнение.

1. Рекуррентное уравнение. Мы получили его выше, имеем



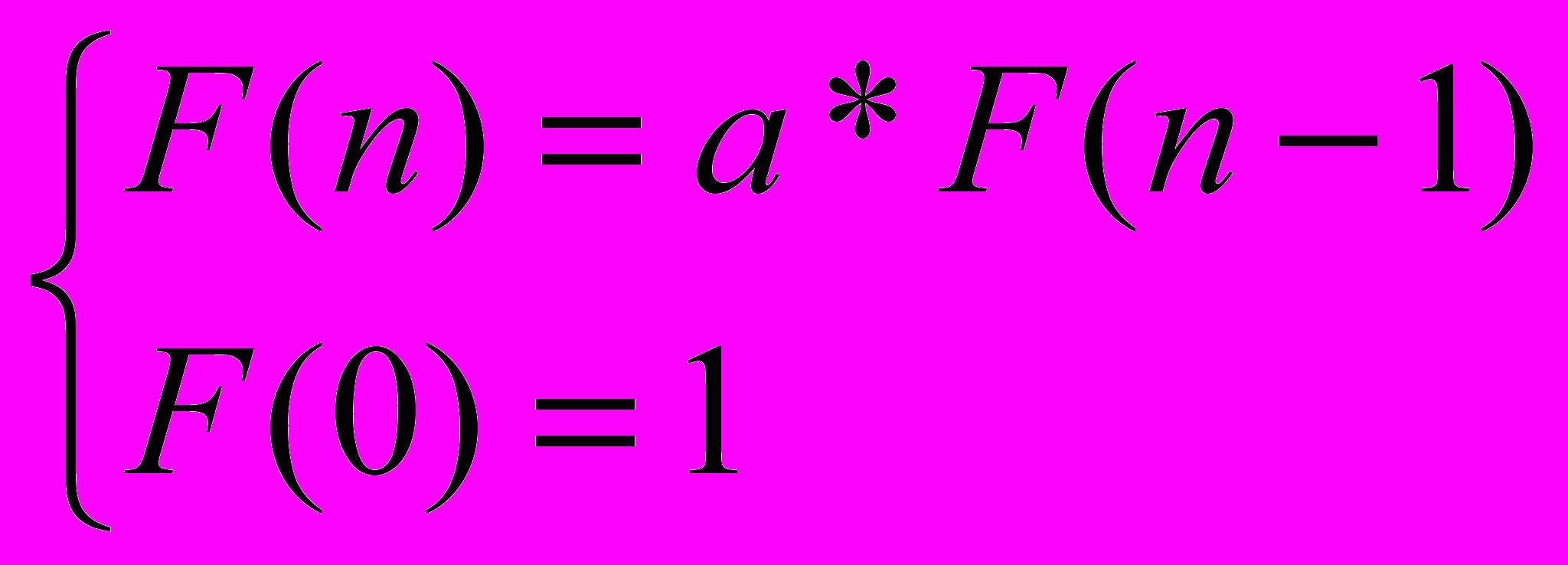
2. Область определения является отрезок [0,10], следовательно массив будет от 0 до 10 типа LongInt.

3. Вводим данные a и b. Задаем начальное условие F[0] = 1

4. Вычисляем для всех n от 1 до b и выводим результат.


Листинг программы:


Var

F:Array[0..10] of LongInt;

a,b,i:LongInt;

Begin

Readln(a,b);

F[0]:=1;

For i:=1 to b do F[i]:=a*F[i-1];

Writeln(F[b]);

end.


Пример128

Определить количество строк длины M ( 1 ≤ M ≤ 40) cостоящих только из символов ‘A’ и ‘B’ у которых нет двух и более рядом стоящих символов ‘B’.

Ввод: Вывод:

2 3

Решение:

Пусть F(n) – количество строк длины n состоящих из символов ‘A’ и ‘B’ и у которых нет двух и более рядом стоящих символов ‘B’. Тогда ответом к задаче будет число F(M) .

1. Предположим, что нам каким-то образом удалось вычислить значение функции для все n не превосходящих некоторого k. Попытаемся выразить F(k+1) через предыдущие значение. Очевидно, что любая строка длинной k+1, которая удовлетворяет условию задачи, может оканчиваться либо на символ ‘A’ либо на символ ‘B’. Давайте рассмотрим два варианта.

A) Предположим, что оканчивается на ‘A’, тогда нам осталось определить количество строк удовлетворяющих условию задачи длинны k, а это не что иное, как F(k).

B) Теперь осталось рассмотреть случай когда строка оканчивается на ‘B’, то есть определить количество строк длинны k+1 удовлетворяющих условию задачи и последним символом в которых является символ ‘B’. Возникает вопрос, почему бы не воспользоваться аналогичными рассуждениями из пункта A, то есть взять все строки удовлетворяющие условию задачи длины k, но в предыдущем пункту у нас не было ограничений на предпоследний символ. А сейчас они есть – так как последний символ у нас по предположению ‘B’, то предпоследним символом не может быть символ ‘B’(по условию задачи), то есть предпоследним символом строки должен быть символ ‘A’. Получим, что теперь нам необходимо определить количество строк длинны k удовлетворяющих условию задачи и последним символом в которых является символ ‘A’. Но как мы показали в предыдущем пункте A, количество таких строк равно F(k-1).

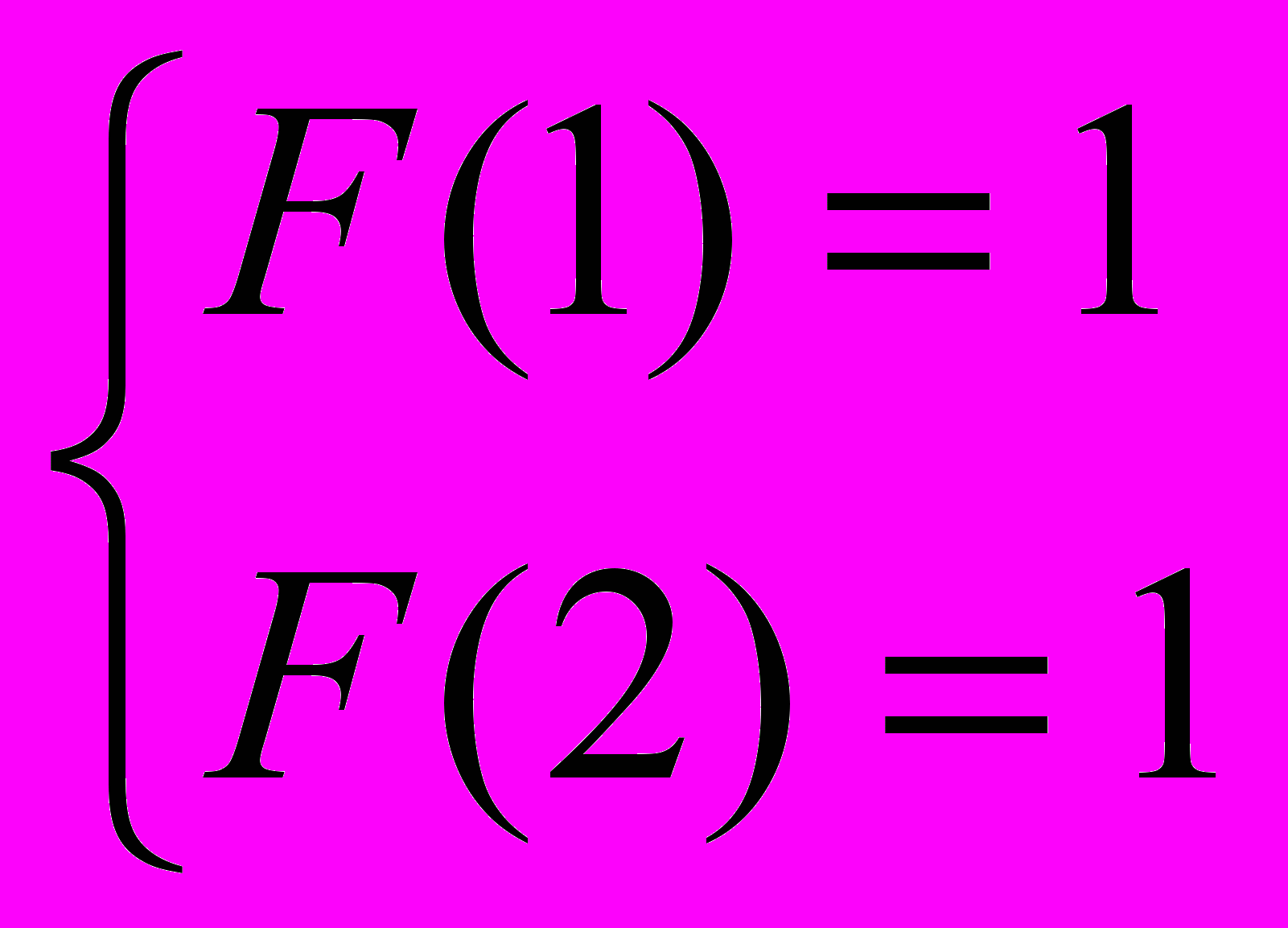
Собрав вместе пункты A и B, получим F(k+1) = F(k) + F(k-1), а это ни что иное, как числа Фибоначчи. Но не стоит сильно радоваться и сразу писать такие начальные условия: , давайте все же найдем начальные условия как и ранее

2. Мы имеем дело с уравнением второго порядка, область определения отрезок [1,40], значит нам необходимо найти F(1) и F(2). Очевидно, что существует две строки длинны один удовлетворяющие условию задачи – это строка ‘A’ и строка ‘B’. Теперь определим количество строк длинны 2 удовлетворяющих условию задачи, найдем их ручным перебором, всего существует 4 строки из символов ‘A’ и ‘B’ – это ‘AA’, ‘AB’, ’BA’ и ‘BB’. Из этих четырех строк не удовлетворяет условию задачи только строка ‘BB’, следовательно F(2) = 2.

То есть получили, что начальные условия данной задачи не совпадают с начальными условиями чисел Фибоначчи, хотя рекуррентные соотношения одинаковы – ничего страшного, так часто бывает. Итак, получаем рекуррентное уравнение:



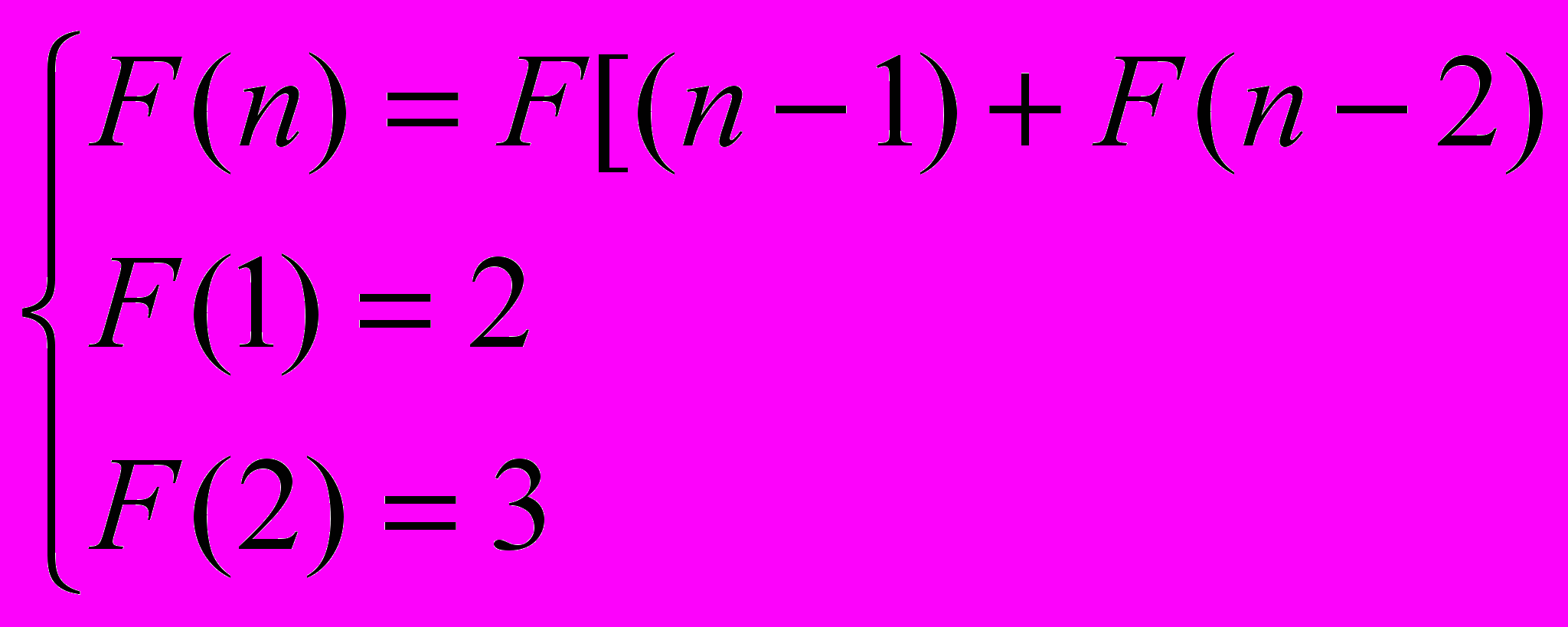
Далее по пунктам расписывать решение рекуррентного уравнения не будем, просто приведем листинг программы:


Var

F:Array[1..40] of LongInt;

M,i:LongInt;


Begin

Read(M);

F[1]:=2;

F[2]:=3;

For i:=3 to M do F[i]:=F[i-1] + F[i-2];

Writeln(F[M]);

end.


Пример129

Определить количество способов укладки коридора длинны M ( 1 ≤ M ≤ 30)плитками 1х2, 2х1 и 2х2. Количество плиток каждого из трех видов неограниченное количество и все три типа плиток имеют различные цвет. Два способа укладки будем называть различными, если существует такая клетка, что цвет этой клетки в этих вариантах различен.

Ввод: Вывод:

2 3


Вопросы и задания.
  1. Дайте определение рекуррентному соотношению?.



  1. Выпишите те выражения, которые являются рекуррентными соотношениями

А) F(n) = F(n-1) + 8

B) F(n) = F(n+2) + F(n-1) + 3

C) F(n) = F(n-2) + F(n-6) + sin(x)

D) F(n) = 7*x + cos(x)

  1. Подумайте, почему для рекуррентного уравнения k-го порядка необходимо чтобы система начальных условий состояла из k равенств (на самом деле можно и больше)?



  1. Запрограммируйте решение рекуррентного уравнения:


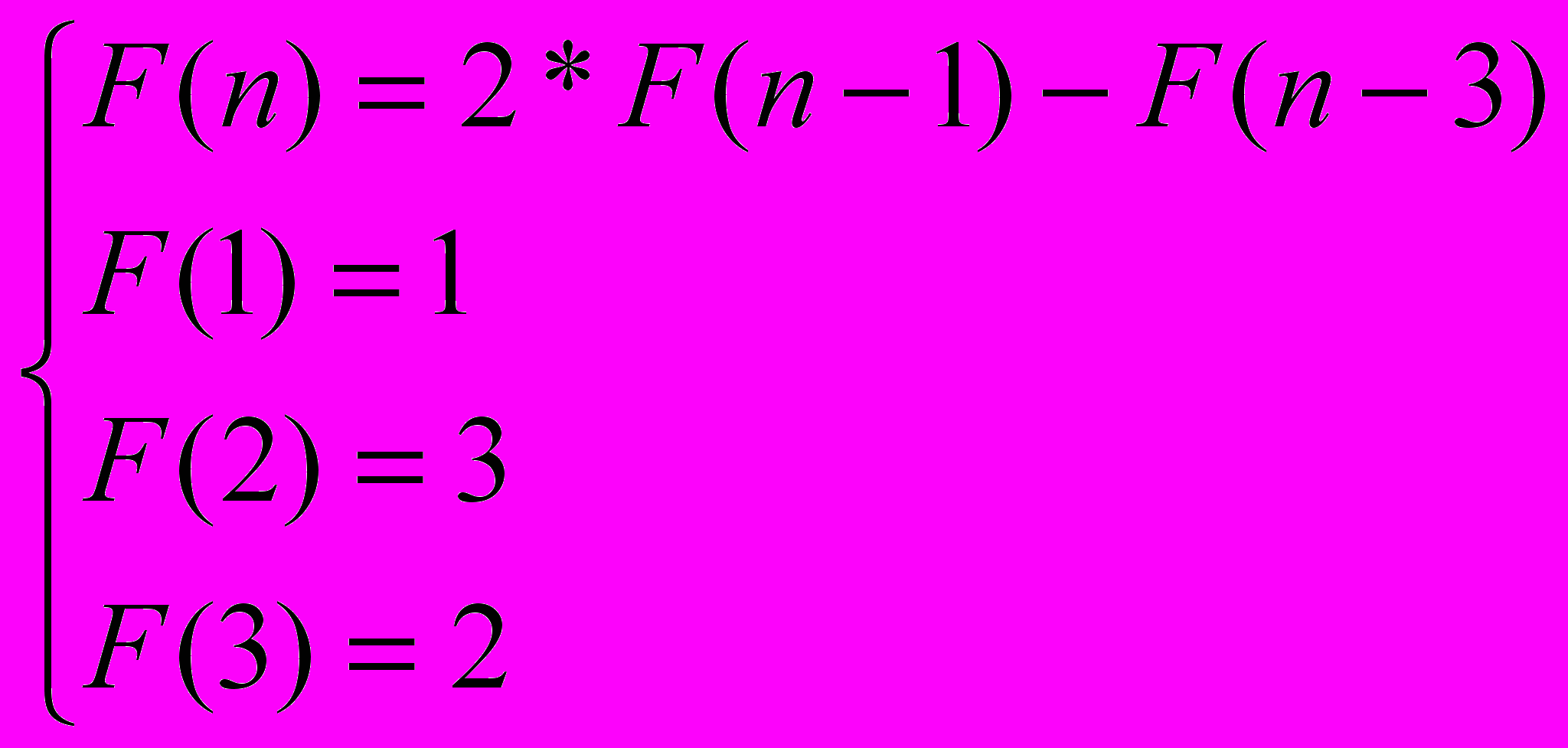
  1. Докажите методом математической индукции, 12+32 +…+(2*N+1)2 = N2



  1. Найти число N! = 1*2*..*N ( 1 ≤ N ≤ 12)

Ввод Вывод
    1. 6

8. Кузнечик находится на первой лесенке, за один ход он может прыгнуть либо на следующею ступеньку или через одну. Определить количество способов, которыми кузнечик может добраться до ступеньки номер M.

Ввод: Вывод:

2 3


7. Определить количество способов укладки коридора длинны M и ширины 2 (1 ≤ M ≤ 30) плитками 1х2, 2х1 и 2х2. Количество плиток каждого из трех видов неограниченное количество и все три типа плиток имеют различные цвет. Два способа укладки будем называть различными, если существует такая клетка, что цвет этой клетки в этих вариантах различен.

Ввод: Вывод:

2 3

9.* Определить количество строк длины M ( 1 ≤ M ≤ 40) состоящих только из символов ‘A’ и ‘B’ у которых нет K и более рядом стоящих символов ‘B’. Первым вводится M а потом K

Ввод: Вывод:

2 1 3


Для любознательных


Определить количество способов укладки коридора длинны M и ширины 3 (1 ≤ M ≤ 30) плитками 1х2, 2х1 и 2х2. Количество плиток каждого из трех видов неограниченное количество и все три типа плиток имеют различные цвет. Два способа укладки будем называть различными, если существует такая клетка, что цвет этой клетки в этих вариантах различен.

Ввод: Вывод:

2 5