Предисловие дорогие друзья !

Вид материала

Документы

Содержание §31. Базовые алгоритмы обработки массивов. Program Ex85; Const Var i: Integer; {Переменная для работы с элементами массива, параметр цикла} Begin End; Procedure Var i, rez: Integer; Begin End; Begin 31.2. Нахождение номеров элементов, обладающих заданным свойством. 31.3. Нахождение количества элементов, обладающих заданным свойством. End; 31.4. Есть ли в данном массиве элементы с данным свойством, или Найти первый (последний) элемент, отвечающий заданным услов Begin i:=l; While (i=0) Do Inc(i); Controll:=(i End; Maximum_i:=maxi; {присвоим имени функции конечный результат} End Var i: Integer; Begin Begin max: =m [ i ] ; {Новое значение максимального элемента) maxi:=i; {Номер максимального элемента в массиве} End 31.6. Изменение значений некоторых элементов. End; Пример 92. End; Пример 93. End; Пример 94. Type mas=array Var i:Byte; {Локальная переменная} Begin §32. удаление элементов массива. ... Полное содержание

Подобный материал:

• К. Бальмонт  Дорогие друзья, сегодня мы в гостях у замечательного русского поэта Константина, 164.76kb.
• Медникова Надежда Александровна учитель начальных классов моу «Уинская сош» Пермский, 91.48kb.
• И в шутку и всерьез Ведущий Добрый день, дорогие друзья! Вот и пришла весна, вот, 339.91kb.
• Играют 2 команды. Вопросы викторины, 53.15kb.
• Летние каникулы в праге, 322.16kb.
• Мои дорогие литературные друзья, 136.81kb.
• Ведущий: Дорогие, друзья! Разрешите поздравить вас с большим и дорогим для всех праздником, 124.29kb.
• Отчет о конференции 17-18 апреля дорогие друзья!, 182.44kb.
• Дорогие друзья и единомышленники, 134.05kb.
• Сценарий для 7-8 классов «Старая сказка на новый лад», 52.44kb.

§31. Базовые алгоритмы обработки массивов.

При работе с элементами массива можно выделить несколько видов задач.

31.1. Нахождение суммы (или произведения) элементов.

Пример 85. Составить программу нахождения суммы элементов массива.

Решение. В параграфе 30 мы уже описали процедуры создания и распечатки массива. Воспользуемся ими для решения задачи. Дополнительно напишем функцию нахождения суммы элементов — Sum1. Находить сумму будем последовательно прибавляя значение элементов. Накапливать значение суммы будем в промежуточной переменной REZ. Программа может быть такой:

Program Ex85;

Const n=30; {Количество элементов массива}

dd=51; {dd используется в генераторе случайных чисел}

Type mas=Array[1..n] Of Integer;

Var A: mas;

s: Integer;{Значение этой переменной s будет равно сумме всех элементов массива}

Procedure Init2(Var m: mas);{Создадим массив с помощью генератора случайных чисел}

Var i: Integer; {Переменная для работы с элементами массива, параметр цикла}

Begin

Randomize; {Инициализация генератора случайных чисел}

For i:=l To n Do {Перебираем все элементы массива}

m[i] :=-25+Random(dd); {Присваивание очередного значения элементу массива }

End;

Procedure Print1(m: mas);

Var i: Integer;

Begin

For i:=l To n Do {Вывод массива }

Write(m[i]: 3) ; {Вывод i-ro элемента}

Writeln;

End;

Function Sum1(m: mas): Integer; {Функция нахождения суммы элементов массива}

Var i, rez: Integer;

Begin

rez:=0; {Начальное значение суммы}

For i:=l To n Do {Перебираем все элементы массива}

rez:= rez +m[i];{К уже найденной сумме прибавляем значение очередного элемента}

Sum1:= rez; {присвоим имени функции конечный результат}

End;

Begin {Основная программа}

Init2(A) ; {Обращение к процедуре формирования массива}

Print1(А); {Вывод массива}

s:=Sum1(A) ; {Нахождение суммы элементов}

Writein('сумма значений элементов равна: ',s); {Вывод результата на экран}

Readln;

End.

Часто встреча­ются различные модификации этой задачи, например, тре­буется найти сумму элементов с заданным свойством.

Пример 86. Найти сумму элементов, кратных заданному числу.

Решение. Изменим функцию Sum1. Будем суммировать не все элементы, а только те, кото­рые удовлетворяют данному условию, то есть только те, которые делятся нацело на заданное число (остаток от деления на данное число равен 0).

Function Sum2 (m: mas): Integer;

Var i, rez, k: Integer;

Begin

Write('Введите число ');Readln(k) ;{Введём заданное число k}

rez:=0; {Начальное значение суммы}

For i:=l To n Do {Нахождение суммы}

If m[i] Mod k =0 Then rez:= rez +m[i];{Если элемент кратен k, то прибавляем его к сумме}

Sum2:= rez; {присвоим имени функции конечный результат}

End;

Остальную часть программы Ex82 предыдущего примера можно ос­тавить без изменений, кроме команды вызова процедуры. Вместо команды

s:=Sum1(A) ;

напишем вызов

s:=Sum2(A) ;

31.2. Нахождение номеров элементов, обладающих заданным свойством.

Пример 87. Найти номера четных элементов.

Решение. Необходимо просмотреть весь массив, и если просматриваемый элемент является четным, то вывести его номер. Опишем процедуру, которой передается данный массив и выводятся нужные номера.

Procedure Nomer_ch(m: mas);

Var i: Integer;

Begin

For i:=l To n Do If m[i] Mod 2=0 Then Write(i:5);

End;

31.3. Нахождение количества элементов, обладающих заданным свойством.

Пример 88. Найти количество положительных и отрицательных элементов в данном массиве.

Решение. Опишем процедуру, которая имеет три параметра — массив и два счетчика, первый — для положительных элементов, второй — для отрицательных, элементы, рав­ные нулю, учитывать не будем.

Procedure Kol_p_o(m: mas; Var kl, k2: Integer);

Var i: Integer;

Begin

kl:=0; k2:=0;

For i:=l To n Do

If m[i]>0 Then Inc(kl)

Else If m[i]<0 Then Inc(k2);

End;

31.4. Есть ли в данном массиве элементы с данным свойством, или Найти первый (последний) элемент, отвечающий заданным условиям. Для решения задач этого типа удобнее использовать циклы с условиями и составлять функции, результат ко­торых имеет логический тип.

Пример 89. Есть ли отрицательный элемент в массиве? Если «да», то вывести его номер первого отрицательного.

Решение. Начинаем просматривать массив с первого элемен­та (i=l) . Пока не просмотрен последний (i<=n) и не найден отрицательный (a[i]>=0), будем перехо­дить к следующему (inc(i)). Таким образом, мы закончим просмотр в одном из двух случаев: первый — просмотрели все элементы и не нашли отрицательно­го, тогда i>n, второй — нашли нужный, при этом i<=n. Опишем функцию, значение которой истина (True) , если в массиве есть отрицательный элемент, и ложь (False), если его нет.

Function Control1(m: mas): Boolean;

Var i: Integer;

Begin

i:=l;

While (i<=n) And (m[i]>=0) Do Inc(i);

Controll:=(i<=n);

End;

Пример 90. Найти номер последнего отрицательного элемента в массиве. Если такой элемент есть, то вывести его номер.

Решение. Последний отрицательный — это первый отрицатель­ный элемент, который встретится при просмотре масси­ва с конца. Если очередной элемент не является отрица­тельным, то нужно уменьшать значение текущего ин­декса, пока он не станет меньше номера первого эле­мента или не будет найден отрицательный элемент. Та­ким образом, можно модифицировать предыдущую функ­цию. Но поскольку надо найти номер элемента, тип ре­зультата будет целым.

Договоримся, что если в массиве нет отрицательного элемента, то значение функции будет равно 0.

Function Control2(m: mas): Integer;

Var i: Integer;

Begin

i: =n;

While (i>0) And (m[i]>=0) Do Dec(i);

Control2:=i;

End;

31.5. Поиск максимального и минимального элементов в массиве. Для поиска максимального элемента необходимо сравнивать каждый элемент массива с уже найденным на предыдущем шаге максимальным значением и при необходимости изменять текущее максимальное значение. Опишем функцию нахождения значения максимального значения.

Function Maximum(m: mas): Integer;

Var i, max, maxi: Integer;

Begin

max:=-32768; {Минимальное значение типа Integer равно -32 768}

For i:=l To n Do {Просмотр всех элементов массива}

If m[i]>max Then {Если данный элемент больше максимального элемента, найденного среди первых i-1 элементов, то}

max: =m [ i ] ; {Новое значение максимального элемента}

Maximum:=max; {присвоим имени функции конечный результат}

End;

Если требуется определить, на каком именно месте находится максимальный элемент, необходимо изменить функцию следующим образом:

Function Maximum_i(m: mas): Integer;

Var i, max, maxi: Integer; {max — хранит максимальное значение, maxi — номер максимального элемента}

Begin

max:=-32768; {Минимальное значение типа Integer равно -32 768}

maxi:=0;

For i:=l To n Do {Просмотр всех элементов массива}

If m[i]>max Then {Если данный элемент больше максимального элемента, найденного среди первых i-1 элементов, то}

Begin

max: =m [ i ] ; {Запомним новое значение максимального элемента)

maxi:=i; {и номер максимального элемента в массиве}

End;

Maximum_i:=maxi; {присвоим имени функции конечный результат}

End;

Если же требуется сохранить и максимальное значение и индекс максимального элемента, тогда необходимо описать следующую процедуру:

Procedure Maximum(m: mas; Var max, maxi: integer);

Var i: Integer;

Begin

max:=-32768; {Минимальное значение типа Integer равно -32 768}

maxi:=0;

For i:=l To n Do {Просмотр всех элементов массива}

If m[i]>max Then {Если данный элемент больше максимального элемента, найденного среди первых i-1 элементов, то}

Begin

max: =m [ i ] ; {Новое значение максимального элемента)

maxi:=i; {Номер максимального элемента в массиве}

End;

End;

Если в массиве несколько элементов имеют максимальное значение, то в переменной maxi будет запоминаться индекс первого из них. Если использовать условие m[i]≥max, то будет запоминаться индекс последнего из максимальных.

Для поиска минимального элемента необходимо заменить знак неравенства в операторе If на противоположный.

31.6. Изменение значений некоторых элементов.

Пример 91. Заменить отрицательные элементы массива на их абсолютные величины.

Решение. Для решения задачи опишем процедуру. Ей будем передавать один параметр — массив, который и будет результатом, при этом значения некоторых элементе могут быть изменены. По определению, модуль (абсолютная величина) отрицательного числа равен противоположному числу, т.е. если А<0, то А=-А. Воспользуемся этим свойством при составлении процедуры.

Procedure Zamena1(Var m: mas);

Var i: Integer;

Begin

For i:=l To n Do

If m[i]<0 Then m[i]:=-m[i] {Если значение элемента отрицательное число, то заменяем его на противоположное}

End;

Пример 92. Прибавить к каждому элементу массива число 25.

Решение. Преобразуем предыдущую процедуру.

Procedure Zamena2(Var m: mas);

Var i: Integer;

Begin

For i:=l To n Do

m[i]:=m[i] + 25; {Прибавляем к каждому элементу число 25}

End;

Пример 93. Если очередной элемент массива четный, то прибавить к нему первый, если нечетный — прибавить последний. Первый и последний элементы не изменять.

Решение. Просмотрим все элементы массива, кроме первого и последнего, и если очередной элемент четный, то есть делится на 2 без остатка, то увеличим его на значение первого элемента, иначе — увеличим его на значение последнего элемента.

Procedure Zamena3(Var m: mas);

Var i: Integer;

Begin

For i:=2 To n-1 Do {Первый и последний элементы не просматриваем}

If a[i] Mod 2=0 Then a[i]:=a[i] + a[l] {если очередной элемент четный, то увеличим его на значение первого элемента}

Else a[i]:=a[i]+a[n]; {иначе — увеличим его на значение последнего элемента}

End;

Пример 94. Дано натуральное число N<2147483648, сколько раз в данном числе встречается каждая цифра.

Решение. Идея решения состоит в следующем:

1. Заведем массив из десяти элементов, пронумеровав их от 0 до 9;
   
2. Каждому элементу массива присвоим начальное значение ноль;
   
3. Выделяя цифры числа, будем увеличивать значение элемента массива на единицу, номер которого соответствует выделенной цифре.
   

Просмотрим процедуру решения задачи.

Type mas=array[0..9] Of Byte; {опишем массив}

var N: LongInt; {Натуральное число}

d:mas; {Результирующий массив}

Cifra:Byte; {Цифра числа}

Procedure PR90(Var b:mas; f:LongInt); {Процедура заполнения массива}

Var i:Byte; {Локальная переменная}

Begin

For i:=0 To 9 Do b[i]:=0; {Обнуление массива}

While f>0 Do {Пока число больше нуля}

Begin

Cifra:=a mod 10; {Получаем очередную цифру}

a:=a div 10; {Отрезаем ее}

Inc(d[Cifra]); {Увеличить значение элемента
End с номером Cifra на единицу}

End;

Вопросы и задания.

1. Как описать переменную типа массив?

2. Как обращаться к элементам массива?

3. С помощью каких конструкций удобно работать с массивами?

4. Изменить знак у максимального по модулю эле­мента массива.

5. Заменить все четные элементы на их квадраты, а нечетные удвоить.

6. Вычесть из положительных элементов элемент с номером kl, а к отрицательным прибавить элемент с номером k2, нулевые элементы оставить без изменения.

7. К четным элементам прибавить А, а из элементов с четными номерами вычесть В.

8. Отрицательные элементы возвести в квадрат.

9. Получить и записать в массив:

1. двадцать первых натуральных чисел, делящихся нацело на 13 или 17 и большими 300 (воспользоваться генератором случайных чисел);
   
2. двадцать первых членов последовательности Фибоначчи (первые два числа равны 1, а каждое следу­ющее равно сумме двух предыдущих).
   

10. Найти среднее арифметичес­кое элементов массива и выяснить, сколько в массиве элементов больших, чем среднее арифметическое.

11. Поменять местами первое положительное число с последним отрицательным в одномерном массиве из N целочисленных элементов.

12. Дан массив. Составить программу вычисления среднего арифметического для каждой пары соседних элементов массива.

13. Дан массив. Все его элементы:

1. увеличить в 2 раза;
   
2. разделить на первый элемент;
   
3. уменьшить на 20;
   
4. умножить на последний элемент.
   

14. Определить сумму элементов массива с K1 по К2 (значения К1 и К2 вводятся с клавиатуры; К2>К1).

15. Дан массив. Напечатать:

1. все неотрицательные элементы;
   
2. все чётные элементы;
   
3. второй, четвёртый и т.д.;
   
4. третий, шестой и т.д.
   

16. Дан массив. Определить на сколько максимальный элемент больше минимального.

17. Дан массив. Найти номера всех элементов:

1. с минимальным значением;
   
2. с максимальным значением.
   

18. Дан массив. Определить количество элементов, больших суммы всех элементов массива, и напечатать их номера.

§32. удаление элементов массива.

Пример 95. Удалить из массива, в котором все элементы различ­ны, максимальный элемент. После удаления максималь­ного элемента, массив "уплотнить", сдвинув все следую­щие за ним элементы влево. Последнему (самому право­му) элементу массива присвоить 0.

Решение. Для того чтобы решить данную задачу, необходимо:

• найти номер максимального элемента k;

• сдвинуть все элементы начиная с (k+1)-го на один эле­мент влево;

• последнему элементу присвоить значение 0.

Рассмотрим решение задачи на конкретном приме­ре. Пусть дан одномерный массив, состоящий из 10 эле­ментов: 6, 3, 4, 7, 11, 2, 13, 8, 1, 5.

Номер максимального элемента равен 7 (k=7), то есть, начиная с 8-го элемента, будем сдвигать элементы на один влево: 7-му элементу присвоим значение 8-го, 8-му присвоим значение 9-го, а 9-му присвоим значение 10-го, на этом сдвиг заканчивается. Таким образом, сдвиг начинается с (k+1)-го элемента и заканчивается n-м (где n — количество элементов в массиве). После этого последнему элементу присвоим 0, тогда массив примет вид: 6, 3, 4, 7, 11, 2, 8, 1, 5, 0.

Примечание. При удалении элемента размерность масси­ва не изменяется.

Составим программу для удаления максимального эле­мента из одномерного массива. Чтобы массив содержал различные числа, изменим процедуру инициализации масси­ва (INIT2). Чтобы последний 0 не выводился на экран, мы мо­дифицируем процедуру вывода Print1 и будем ей пере­давать не только массив, но и количество элементов, ко­торые надо вывести, начиная с первого.

Program Ex95;

Const n=30; dd=51;

Type mas = Array[l..n] Of Integer;

Var A: mas;

k:Integer; {k - номер максимального элемента}

Procedure Init2_R(Var m: mas);

Var i,j: Integer;

F:Boolean; {Переменная для проверки на не совпадения чисел}

Begin

Randomize; {Инициализация генератора случайных чисел}

i:=1; {Начинаем присваивать значения с первого элемента}

While i<=n Do {Пока не заполним весь массив}

Begin

Repeat {Цикл выполняем до тех пор пока не получим число, которого ещё не было}

F:=True; {Предполагаем одинаковых чисел нет}

m[i] :=-25+Random(dd);

For j:=1 To i-1 Do {Проверяем, было ли такое число}

If m[j]=m[i] Then f:=False {Одинаковые есть}

Until f; {Если F=TRUE, то выходим из цикла}

Inc(i); {Следующий элемент массива}

End;

End;

Procedure Print1_1(х:integer;m: mas); {х — количество оставшихся элементов в массиве m}

Var i: Integer;

Begin

For i:=l To х Do {Вывод массива}

Write(m[i]: 4) ; {Вывод i-ro элемента, возможно двухзначное отрицательное число }

Writeln;

End;

Function Maximum_i(m: mas): Integer;

Var i, max, maxi: Integer;

Begin

max:=-32768; {Минимальное значение типа Integer равно -32 768}

For i:=l To n Do {Просмотр всех элементов массива}

If m[i]>max Then {Если данный элемент больше максимального элемента, найденного}

Begin {среди первых i-1 элементов, то}

max: =m [ i ] ; {Новое значение максимального элемента}

maxi:=i; {Номер максимального элемента в массиве}

End;

Maximum_i:=maxi;

End;

Procedure Del_1(kl: Integer; Var m: mas);

Var i: Integer;

Begin

For i:=kl To n-1 Do m[i]:=m[i+l]; {Сдвиг элементов на один влево, i-му элементу присваиваем значение (i+l)-гo}

m[n]:=0; {Последний элемент равен 0}

End;

Begin

Init2_R(A) ; {Заполнение массива А различными числами}

WriteLn(‘первоначальный массив’);

Print1_1(n,A); {Вывод заполненного массива А}

k:=Maximum_i(A); {Поиск номера максимального элемента}

Del_1(k, A) ; {Удаление элемента с номером k}

WriteLn(‘полученный массив’);

Print1_1(n-1, А) ; {Вывод на экран нового массива А}

Readln;

End.

Пример 96. Удалить из массива, в котором значения элементов могут повторяться, все максимальные элементы. После удаления, массив "уплотнить".

Решение. Когда необходимо удалять несколько элементов, то это лучше всего делать с конца массива, так как иначе нужно будет снова возвращаться к элементу, который только что удаляли (эта проблема возникает в том слу­чае, когда подряд идут два максимальных элемента: если первый удалить, то на его место снова встанет макси­мальный элемент). Просматривать массив с конца мож­но при помощи цикла с параметром, который имеет следующий вид:

For i:=B Downto A Do <тело цикла>

Значение переменной i будет уменьшаться на единицу начиная от В до А.

Кроме того, номер максимального элемента запоминать не будем, а просмотрим массив с конца, и если элемент имеет максимальное значение, то удалим его, при этом значение счетчика k будем увеличивать на 1. Для решения этой задачи нам нужен не номер, а значение максимального элемента. В программе это будет выглядеть так:

Program Ex96;

Const n=30; dd=51;

Type mas = Array[l..n] Of Integer;

Var A: mas;

M_a, k, i: Integer; {m_a - значение максимального элемента, k - количество удаленных элементов}

Procedure Init2(Var m: mas);{Создадим массив с помощью генератора случайных чисел}

Var i: Integer; {Переменная для работы с элементами массива, параметр цикла}

Begin

Randomize; {Инициализация генератора случайных чисел}

For i:=l To n Do m[i] :=-25+Random(dd);

End;

Procedure Print1_1(х:integer;m: mas); {n — количество распечатываемых элементов массива m}

Var i: Integer;

Begin

For i:=l To х Do {Вывод массива}

Write(m[i]: 4) ; {Вывод i-ro элемента}

Writeln;

End;

Function Maximum(m: mas): Integer;

Var i, max : Integer;

Begin

max:=-32768;

For i:=l To n Do {Просмотр всех элементов массива}

If m[i]>max Then max:=m[i]; {Новое значение максимального элемента}

Maximum:=max;

End;

Procedure Del_1(kl: Integer; Var m: mas);

Var i: Integer;

Begin

For i:=kl To n-1 Do m[i]:=m[i+l]; {Сдвиг элементов на один влево, i-му элементу присваиваем значение (i+l)-гo}

m[n]:=0; {Последний элемент равен 0}

End;

Begin

Init2(А) ; {Заполнение массива А}

WriteLn(‘первоначальный массив’);

Print1_1(n, А) ; {Вывод заполненного массива А}

m_a:=Maximum(A); {Поиск значения максимального элемента}

k:=0; {Число удалённых элементов}

For i:=n Downto 1 Do {Просмотр всех элементов начиная с последнего}

If A[i]=m_a Then {Если данный элемент имеет максимальное значение, то }

Begin {Удаляем элемент с номером i}

Del_1 (i,A) ;

Inc(k);

End;

WriteLn(‘полученный массив’);

Print1_1(n-k,A); {Вывод нового массива А}

Readln;

End.

Вопросы и задания.

1. Удалить первый отрицательный элемент массива, если такой элемент есть.

2. Удалить все отрицательные элементы массива.

3. Удалить все элементы, большие данного числа А (А вводится с клавиатуры).

4. Удалить все четные элементы, стоящие на нечетных местах.

5. Удалить все повторяющиеся элементы, оставив их первые вхождения, то есть в массиве должны остаться только различные элементы.

6. Удалить последний четный элемент массива.

7. Удалить все элементы, кратные 3 или 5.

8. Удалить все элементы массива начиная с kl-го по k2-й (kl и k2 вводить с клавиатуры). Проверить корректность ввода значений kl и k2 (kl

§33. Вставка и перестановка элементов массива.

33.1. Вставка элементов в одномерный массив

33.1.1. Вставка элемента после элемента с заданным номером

Пример 97. Вставить число 100 после пятого элемента массива.

Решение. Пусть k — номер элемента, после которого мы дол­жны вставить элемент х (k и х будем вводить с клави­атуры). Вставка осуществляется следующим образом:

• первые k элементов массива остаются без изме­нений;

• все элементы, начиная с (k+1)-го необходимо сдви­нуть вправо;

• элементу с номером (k+1) присваиваем значение х.

Рассмотрим конкретный пример. Пусть дан следу­ющий одномерный массив из N (N=10) элементов: 3, -12, 5, 14, 27, -6, 1, -34, 10, -15.

Надо вставить элемент со значением 100 после пято­го элемента массива. Мы получим следующий массив: 3, -12, 5, 14, 27, 100, -6, 1, -34, 10, -15.

Таким образом, после вставки в массиве станет 11 элементов, и это надо учесть при описании типа mas:

Type mas = Array[1..n+1] Of Integer;

Будем выводить массив два раза — до и после встав­ки нового элемента.

Составим теперь основную программу. Сдвиг элементов будем начинать с конца массива.

Program Ex97;

Const n=10; dd=51;

Type mas =Array[1..n+1] Of Integer;

Var A: mas;

y, k:Integer; {y - значение нового элемента k - номер элемента, после которого вставляем}

Procedure Init2(Var m: mas);{Создадим массив с помощью генератора случайных чисел}

Var i: Integer; {Переменная для работы с элементами массива, параметр цикла}

Begin

Randomize; {Инициализация генератора случайных чисел}

For i:=l To n Do m[i] :=-25+Random(dd);

End;

Procedure Print1_1(x:integer;m: mas); {x — количество элементов в массиве m}

Var i: Integer;

Begin

For i:=l To x Do {Вывод массива}

Write(m[i]: 4) ; {Вывод i-ro элемента}

Writeln;

End;

Procedure Insert1(kl, xl: Integer; Var m: mas);

Var i: Integer;

Begin

For i:=n Downto kl+1 Do m[i+l]:=m[i]; {Сдвиг элементов на одну позицию назад}

m[kl+l]:=xl; {Вставка элемента x1 после kl-го}

End;

Begin

Init2(А) ;

Printl_1(n, А); {Вывод начального массива из n элементов}

Writeln('Введите номер элемента, после которого вставлять, ') ;

Write('и значение нового элемента: ');

Readln(k,y) ;

Insert1(k,y,A) ;

Printl_1(n+1,A); {Вывод массива после вставки нового элемента}

Readln;

End.

33.1.2. Вставка элемента перед элементом с данным номером.

Пример 98. Вставить число 100 перед пятым элементом массива.

Решение. Эта задача немного отличается от предыдущей: в предыдущей мы сдвигали вправо все элементы, стоящие после k-го, то есть с (k+1)-го, а на его место записыва­ли новый элемент, в этой — сдвигаем все элементы с k-го, а затем на его место записываем новый.

Пусть дан следующий одномерный массив из N (N=10) элементов: 3, -12, 5, 14, 27, -6, 1, 34, 10, -15. Надо вставить элемент со значением 100 перед пятым элементом массива. Получим следующий массив: 3, -12, 5, 14, 100, 27, -6, 1, 34, 10, -15.

Program Ex98;

Const n=10; dd=51;

Type mas =Array[1..n+1] Of Integer;

Var A: mas;

y, k:Integer; {y - значение нового элемента k - номер элемента, после которого вставляем}

Procedure Init2(Var m: mas);{Создадим массив с помощью генератора случайных чисел}

Var i: Integer; {Переменная для работы с элементами массива, параметр цикла}

Begin

Randomize; {Инициализация генератора случайных чисел}

For i:=l To n Do m[i] :=-25+Random(dd);

End;

Procedure Print1_1(x:integer;m: mas); {x — количество элементов в массиве m}

Var i: Integer;

Begin

For i:=l To x Do {Вывод массива}

Write(m[i]: 4) ; {Вывод i-ro элемента}

Writeln;

End;

Procedure Insert2(kl, xl: Integer; Var m: mas);

Var i: Integer;

Begin

For i:=n Downto kl Do m[i+l]:=m[i]; {Сдвиг элементов на одну позицию назад}

m[kl]:=xl; {Вставка элемента x1 после kl-го}

End;

Begin

Init2(А) ;

Printl_1(n, А); {Вывод начального массива из n элементов}

Writeln('Введите номер элемента, перед которым вставлять, ') ;

Writeln('и значение нового элемента');

Readln(k,y) ;

Insert2(k,y,A) ;

Printl_1(n+1,A); {Вывод массива после вставки нового элемента}

Readln;

End.

33.1.3. Вставка нескольких элементов. Предположим, что необходимо вставлять не один элемент, а по одному элементу после всех элементов с заданным свойством.

Пример 99. Вставить данное число после всех элементов масси­ва, кратных 3.

Решение. Первое, на что необходимо обратить внимание, — это описание массива: на сколько элементов может уве­личиться массив? Максимальное количество элементов, после которых будет вставлен новый элемент, совпада­ет с количеством элементов массива, ведь может слу­читься так, что все элементы массива обладают задан­ным свойством. Поэтому массив может увеличиться максимум в два раза, а значит, соответствующее опи­сание будет следующим:

Type mas = Array[1..2*n] Of Integer;

Если мы будем просматривать элементы массива с начала и вставлять новый элемент после элемента с за­данным свойством, то номер последнего элемента каж­дый раз будет меняться, кроме того, придется пропускать (перепрыгивать) новый (вставленный) элемент, поэтому решение будет не очень эффективным.

Удобнее просматривать массив с конца, тогда встав­ляемый элемент мешать не будет.

Составим программу.

Program Ex99;

Const n=10; dd=51;

Type mas =Array[1..2*n] Of Integer;

Var A: mas;

y, k, i :Integer; {y - значение нового элемента, k — счетчик вставленных элементов}

Procedure Init2(Var m: mas);{Создадим массив с помощью генератора случайных чисел}

Var i: Integer; {Переменная для работы с элементами массива, параметр цикла}

Begin

Randomize; {Инициализация генератора случайных чисел}

For i:=l To n Do m[i] :=-25+Random(dd);

End;

Procedure Print1_1(x:integer;m: mas); {x — количество элементов в массиве m}

Var i: Integer;

Begin

For i:=l To n Do {Вывод массива}

Write(m[i]: 4) ; {Вывод i-ro элемента}

Writeln;

End;

Procedure Insert3(kl, x1: Integer; Var m: mas); {k1 — номер элемента, после которого вставляется число х1}

Var i: Integer;

Begin

{Сдвиг элементов на одну позицию назад, n+k — это в данный момент номер последнего элемента}

For i:=n+k Downto kl+1 Do m[i+l]:=m[i];

m[kl+l]:=xl; {Вставка элемента на место — после kl-го}

Inc(k); {Увеличение счетчика вставленных элементов}

End;

Begin

Init2(А) ;

Print1_1(n,A) ;

Write('Введите вставляемое число');

Readln(y) ;

k:=0;

For i:= n Downto 1 Do {Просматриваем массив с конца}

If A[i] Mod 3=0 Then Insert3 (i,y,A); {Если элемент кратен 3, то вставляем число}

Print1_1(n+k,A); {Вывод массива после вставки в него всех элементов}

Readln;

End.

33.2. Перестановки элементов массива

33.2.1. Перестановка двух элементов

Пример 100. Поменять местами значения двух элементов с номе­рами kl и k2 (где kl и k2 вводятся с клавиатуры).

Решение. Опишем процедуру, которой будем передавать но­мера переставляемых элементов и массив.

Procedure Swap(kl, k2: Integer; Var m: mas);

Var x: Integer;

Begin

X:=m[kl]; m[kl]:=m[k2]; m[k2]:=x;

End;

Примечание. Задача о перестановке двух элементов с за­данными свойствами сводится к этой задаче — надо только найти их номера.

33.2.2. Перестановка нескольких элементов (части) массива.

Пример 101. Дан одномерный массив А, состоящий из 2n эле­ментов. Поменять местами его половины.

Решение. Пусть массив А состоит из 10 элементов, то есть n=5: 1, 12, 23, 3, 7, 13, 27, 6, 9, 11. Тогда если мы поменяем местами его половины, то получим такой массив А: 13, 27, 6, 9, 11, 1, 12, 23, 3, 7. Заметим, что мы меняем местами элементы с номерами 1 и n+1, 2 и n+2 и так далее; последняя пара — n и 2n. Легко заметить и то, что элемент с номером i меняется местами с элементом с номером n+i. Поэтому, исполь­зуя процедуру Swap из примера 97, можно в основной про­грамме применить цикл:

For i:=l To n Do Swap(i,i+n,A);

Вопросы и задания.

1. Вставить элемент с данным значением после пер­вого отрицательного элемента массива.
   
2. Вставить элемент с данным значением перед по­следним отрицательным элементом массива.
   
3. Вставить в массив два элемента с данными значе­ниями: первый — после максимального элемента, вто­рой — перед максимальным элементом (удобнее всего вставлять элементы именно в таком порядке).
   
4. Вставить по одному элементу с данным значени­ем перед всеми элементами массива, кратными задан­ному числу.
   
5. Вставить по одному элементу с данным значени­ем перед всеми отрицательными элементами массива.
   
6. Вставить два элемента с данными значениями: пер­вый — после всех элементов, больших данного числа Р, а второй — перед всеми элементами, большими данно­го числа Р (Р вводится с клавиатуры).
   
7. Вставить элемент со значением А перед всеми эле­ментами, большими А, а элемент со значением В — после всех элементов, меньших В.
   
8. Поменять местами:
   

a) первый и максимальный элементы массива;

b) второй и минимальный элементы массива;

c) первый и последний отрицательный элементы массива.

9. Дан одномерный массив А, состоящий из 2n эле­ментов. Поменять его половины следующим образом: первый элемент поменять с последним, второй — с пред­последним и так далее.
   
10. Дан одномерный массив В, состоящий из 2n элементов. Переставить его элементы по следующему правилу:
    

a) b[n+l], b[n+2],..., b[2n], b[l], b[2],.... b[n];

b) b[n+l], b[n+2],..., b[2n], b[n], b[n-l], ..., b[l];

c)b[l], b[n+l], b[2], b[n+2],..., b[n], b[2n];

d) b[2n], b[2n-l],..., b[n+l], b[l], b[2],..., b[n] .

11. Дан одномерный массив. Переставить в обрат­ном порядке элементы массива, расположенные между минимальным и максимальным элементами.
    
12. Дан массив. Сравнить первый и второй элементы. Если второй элемент меньше первого, то поменять их местами. Затем то же самое сделать со вторым и третьим, … предпоследним и последним. Какое число окажется в результате в последнем элементе массива?
    

Для любознательных

Петя очень любит футбол. А еще больше он любит делать ставки на игры. Всего в турнире участвовало 4 команды. В начале сезона он поставил ставки на 1-ую команду . И вот остался один матч, команда №1 играет с командой №2. Есть результаты 5 сыгранных матчей. И Петя хочет определить, какой результат обеспечит 1-ой команде единоличную победу в турнире и сможет ли она вообще победить. За победу в матче дается 3 очка, за ничью - 1, за поражение – 0. Команда, набравшая большее количество очков считается победителем.

Ввод: 5 строк, в каждой из которых находится 4 числа: 1-ое и 2-ое числа – номера команд, игравших в матче. 3-ее и 4-ое – счет матча (например: 2 4 1 2 – 2-ая команда проиграла 4-ой со счетом 1:2, 4-ая команда набрала 3 очка, 2-ая - 0).

Вывод: Единственное число.

1 – если 1-ой команде можно даже проиграть, но она все равно победит в турнире.

2 - если нельзя проигрывать, но достаточно сыграть вничью.

3 – если обязательно нужно выигрывать для победы в турнире.

4 – если при выигрыше матча, 1-ая команда разделит 1-ое место с другими командами (т.е. несколько команд (в том числе и 1-ая) будут иметь одинаковое количество очков).

0 – если не удастся при любом исходе матча занять первое место (т.е. у какой-нибудь команды будет больше очков, чем у первой команды).

Пример:

input.txt output.txt


1 3 5 0 4

1 4 1 2

2 3 2 0

2 4 4 1

3 4 3 3

§34. Методы сортировки.

Под сортировкой понимают перераспределение элементов массива в некотором определенном порядке. Цель сортировки — облегчить последующий поиск элементов в таком упорядоченном массиве. Если каждый следующий элемент не больше предыдущего, такой порядок расположения чисел называют не возрастающим (убывающим). Порядок, при котором в массиве первым элементом является самое маленькое число, а каждый следующий не меньше предыдущего, называют не убывающим (возрастающим).

Выбранный метод сортировки должен экономно использовать доступную память машины. Существенным критерием выбора нужного метода является его экономичность, т.е. время работы. Хорошей мерой эффективности может служить число необходимых сравнений элементов.

Рассмотрим методы сортировки на основе решения следущей задачи: упорядочить элементы линейного массива в порядке невозрастания их значений.

34.1. Сортировка выбором. Этот метод сортировки основан на следующих принципах.

1. Выбираем максимальный элемент.
   
2. Меняем его местами с первым элементом (ïîñëå ýòîãî íàè­áîëüøèé ýëåìåíò áóäåò ñòîÿòü íà ñâî¸ì ìåñòå).
   
3. Дальше рассматриваем только неотсортированную часть массива, ïîâòîðèòü ïï. 1-2 ñ îñòàâøèìèñÿ n-1 ýëåìåíòàìè, íàéòè ìàêñèìàëüíûé ýëåìåíò è ïîìåíÿòü åãî ìåñòàìè ñо вторым элементом и этот процесс повторяем с оставшимися элементами до тех пор, пока не останется один элемент, óæå ñòîÿùèé íà ñâî¸ì ìåñòå.
   

Âñåãî ïîòðåáóåòñÿ n-1 ðàç âûïîëíèòü ýòó ïîñëåäîâàòåëüíîñòü äåéñòâèé.  ïðîöåññå ñîðòèðîâêè áóäåò óâåëè÷èâàòüñÿ îòñîðòèðîâàííàÿ ÷àñòü ìàññèâà, à íåîòñîðòèðîâàííàÿ, ñîîòâåòñòâåíî, óìåíüøàòüñÿ.

Количество сравнений при этом равно: (N—1)+(N—2)+(N—3)+...+1=N(N—1)/2=(N²—N)/2.

Алгоритм метода будет следующим:

For i:=1 to N-1 do {Отсекаем отсортированные элементы таблицы}

Begin

max:= A[i]; K:=i; {Ищем максимальный элемент}

For j:=i+1 to N do {в оставшейся части таблицы}

If A[j]>max then {}

Begin {}

Max:= A[j]; K:=j; {}

End; {}

If i<>k then begin {если индекс максимального отличен от индекса первого}

A[k]:=A[i]; A[i]:=max; {элемента в оставшейся не отсортированной части}

End; {таблицы, то меняем их местами}

Рассмотрим этот процесс на примере.

I \J	1	2	3	4	5	6
1	3	1	2	9	8	5
	9	1	2	3	8	5
2	9	1	2	3	8	5
	9	8	2	3	1	5
3	9	8	2	3	1	5
	9	8	5	3	1	2
4	9	8	5	3	1	2
	9	8	5	3	1	2
5	9	8	5	3	1	2
	9	8	5	3	2	1

Значение I изменяется от 1 до 5.

На первом шаге находим максимальный элемент — 9, меняем его с первым.

На втором шаге отсекаем из рассмотрения уже отсортированный элемент. находим максимальный элемент — 8, меняем его с первым в оставшейся части таблицы.

На третьем шаге отсекаем из рассмотрения уже отсортированный элемент. находим максимальный элемент — 5, меняем его с первым в оставшейся части таблицы.

На четвёртом шаге отсекаем из рассмотрения уже отсортированный элемент. находим максимальный элемент — 3, но менять его не имеет смысла — он на первом месте. Оставим его там.

На пятом шаге отсекаем из рассмотрения уже отсортированный элемент. находим максимальный элемент — 2, меняем его с первым в оставшейся части таблицы.

Всё, массив отсортирован.

Äëÿ ïðîãðàìíîé ðåàëèçàöèèè ýòîãî ïðîöåñà íåîáõîäèìî îðãàíèçî­âàòü öèêë ïî äëèíå ðàññìàòðèâàåìîé ÷àñòè ìàññèâà, êîòîðàÿ èçìåíÿ­åòñÿ îò 1 до n.  êà÷åñòâå íà÷àëüíîãî çíà÷åíèÿ ìàêñèìóìà ðàçóìíî âçÿòü çíà÷åíèå первого ýëåìåíòà ðàññìàòðèâàåìîé ÷àñòè.

Òåïåðü ìîæåì çàïèñàòü àëãîðèòì ñîðòèðîâêè:

for i:=1 to n-1 Do

Begin

íàéòè ìàêñèìàëíîå çíà÷åíèå èç à[i],..., à[n];

çàïîìíèòü èíäåêñ максимального в ïåðåìåííîé k;

åñëè i<>k ïîìåíÿòü ìåñòàìè à[i] è a[k]

End;

Îïèøåì ýòîò процесс ïîäðîáíî â âèäå ïðîöåäóðû:

Procedure sort1 (Var m:mas); {ïîñêîëüêó â ïðîöåñå ðàáîòû ïðîöåäóðû ìàññèâ èçìåíÿåòñÿ, ôîð­ìàëüíûé ïàðàìåòð m îïèñûâàåòñÿ êàê ïàðàìåòð-ïåðåìåííàÿ}

Var i, j, k: Integer;

max: Integer; {Çíà÷åíèå ìàêñèìàëüíîãî ýëåìåíòà ðàññìàòðèâàåìîé ÷àñòè ìàññèâà}

Begin

For i:=1 to n-1 Do {öèêë ïî äëèíå ðàññìàòðèâàåìîé ÷àñòè ìàññèâà}

Begin {ïîèñê ìàêñèìàëüíîãî ýëåìåíòà è åãî íîìåðà â òåêóùåé ÷àñòè ìàññèâà}

k:=i; max:=m[i]; {íà÷àëüíûå çíà÷åíèÿ ìàêñèìàëüíîãî ýëåìåíòà è åãî èíäåêñà â ðàñìàòðèâàåìîé ÷àñòè ìàññèâà}

For j:=i+1 To n Do

If m[j]>max Then Begin k:=j; max:=m[j] End;

If i<>k then begin {если индекс максимального отличен от индекса первого}

m[k]:=m[i]; m[i]:=max; {элемента в оставшейся не отсортированной части}

End; {таблицы, то меняем их местами}

End;

34.2. Сортировка обменом. Этот метод сортировки основан на следующих принципах.

1. Сравниваем первые два элемента. Если первый меньше второго, то меняем их местами.
   
2. Сравниваем второй и третий и т.д., при необходимости меняя их местами.
   
3. Просматриваем массив сначала, уменьшая на единицу количество просматриваемых элементов. Массив будет отсортирован после просмотра, в котором участвуют только первый и второй элементы.
   

Такой метод известен под названием «метод пузырька». Число сравнений в этом алгоритме также равно (N²—N)/2. Алгоритм метода опишем в процедуре:

Procedure sort2(Var m:mas);

Var i,j,x:Integer; {i—íîìåð ïðîñìîòðà (èçìåíÿåòñÿ îò 1 äî n-1), j — íîìåð ðàññìàòðèâàåìîé ïàðû, x —ïðîìåæóòî÷íàÿ ïåðåìåííàÿ äëÿ ïåðåñòàíîâêè ìåñòàìè ýëåìåíòîâ}

Begin

For i:=1 To n-1 Do {отсекаем отсортированные элементы}

For j:=1 To n-i Do {просматриваем не отсортированную часть}

If m[j]>m[j+1] Then {если j-ый элемент меньше j+1-го, то}

Begin x:=m[j]; m[j]:=m[j+1]; m[j+1]:=x End {меняем их местами}

End;

Улучшения этого алгоритма напрашиваются сами собой. Можно запоминать, были или не были перестановки в процессе некоторого просмотра. Если в последнем просмотре перестановок не было, то алгоритм можно заканчивать. Можно запоминать не только сам факт, что обмен имел место, но и положение (индекс) последнего обмена. Просмотры можно заканчивать на этом индексе и не идти дальше.

Procedure sort2_1(Var m:mas);

Var i,j,x,k,r:Integer; {i—íîìåð ïðîñìîòðà (èçìåíÿåòñÿ îò 1 äî n-1), j — íîìåð ðàññìàòðèâàåìîé ïàðû, x —ïðîìåæóòî÷íàÿ ïåðåìåííàÿ äëÿ ïåðåñòàíîâêè ìåñòàìè ýëåìåíòîâ, r — правая граница просмотра, k — «адрес» последнего обмена}

P:Boolean; {«выключатель» работы программы}

Begin

P:=true; K:=N-1; {P:=true — включаем режим работы цикла}

While P do {пока возможны обмены соседних элементов}

Begin {выполняем цикл}

P:=false; R:=K; { P:=false — выключаем режим работы цикла; R:=K — правая }

For j:=1 to R do {граница просмотра}

If m[j]< m[j+1] then { если j-ый элемент меньше j+1-го, то }

Begin {}

x:= m[j]; m[j]:= m[j+1]; m[j]:=x; {меняем их местами}

P:=true; {раз был обмен, то включаем режим работы цикла }

K:=j; {К — запоминаем, где произошёл обмен}

End; {Для IF}

End; {Для WHILE }

End; {Для PROCEDURE}

Можно ещё улучшить этот метод, если чередовать направление последовательных просмотров. Такая сортировка называется «шейкерной».

Procedure sort_ Shejker (Var m:mas);

Var i, j, x, k, k1, L, r:Integer; {i—íîìåð ïðîñìîòðà (èçìåíÿåòñÿ îò 1 äî n-1), j — íîìåð ðàññìàòðèâàåìîé ïàðû, x —ïðîìåæóòî÷íàÿ ïåðåìåííàÿ äëÿ ïåðåñòàíîâêè ìåñòàìè ýëåìåíòîâ, r — правая граница просмотра, L — левая граница просмотра, k — «адрес» последнего обмена при просмотре слева направо, k1 — «адрес» последнего обмена при просмотре справа налево}

P:Boolean; {«выключатель» работы процедуры}

begin

p:=true; k:=n-1; {P:=true — включаем режим работы цикла, К — Правая граница просмотра }

k1:=1; {левая граница просмотра}

while p do {пока возможны обмены соседних элементов}

begin

p:=false; r:=k; L:=k1;

for j:=L to r do{просматриваем элементы на участке, где был обмен, слева направо}

if m[j]
begin

x:=m[j];m[j]:=m[j+1]; m[j+1]:=x; {меняем их местами}

k:=j; {запоминаем место обмена}

end;

r:=k; {Обновляем правую границу просмотра}

if p then begin p:=false; {Если обмены были}

for j:=r downto L+1 do {просматриваем элементы справа налево}

if m[j]>m[j-1] then { если j-1-ый элемент меньше j-го, то }

begin

x:=m[j]; m[j]:=m[j-1]; m[j-1]:=x; {меняем их местами}

p:=true; {раз был обмен, то включаем режим работы цикла }

k1:=j; {запоминаем место обмена}

end; {Для IF m[j]>m[j-1]…}

end; {Для IF Р…}

end; {Для WHILE }

end; {Для PROCEDURE}

Вопросы и задания.

1. Опишите метод сортировки выбором.
   
2. Опишите метод сортировки обменом.
   
3. Äàí ëèíåéíûé ìàññèâ À[1..N], ñîäåðæàùèé öå­ëûå ÷èñëà. Упорядочить его:
   

1. методом пузырька в порядке возрастания;
   
2. методом пузырька в порядке возрастания модулей;
   
3. методом выбора в порядке возрастания, при помощи поиска минимального элемента;
   
4. методом выбора в порядке возрастания, при помощи поиска одновременно минимального и максимального элементов;
   
5. переставив все нулевые элементы в конец массива. Порядок ненулевых элементов может быть произвольным;
   
6. так, чтобы все чётные числа стояли в начале массива, а нечётные в конце;
   
7. так, чтобы все положительные числа стояли в начале массива, а отрицательные в конце;
   
8. так, чтобы все положительные числа стояли в начале массива, а отрицательные в конце (относительный порядок следования элементов должен сохраняться);
   
9. в порядке возрастания количества цифр в числах, входящих в массив (сначала однозначные, затем двузначные и т.д.). порядок расположения чисел с одинаковым количеством цифр должен сохраниться неизменным;
   
10. в порядке возрастания количества цифр в числах, входящих в массив (сначала однозначные, затем двузначные и т.д.). числа с одинаковым количеством цифр располагаются также в порядке возрастания.
    

§35. Методы сортировки (продолжение).

35.1. Cокращение области поиска. двоичный поиск. Рассмотрим следующую задачу.

Пример 102. Два девятиклассника, Вова и Петя, играют в следующую игру. Петя берёт «Толковый словарь русского языка» и загадывает слово. Вова, чтобы угадать слово, может задавать Пете вопросы. Но только такие, на которые Петя может ответить «Да» или «Нет». Необходимо определить, какие вопросы должен задавать Вова. Какое минимальное количество вопросов ему потребуется задать, чтобы угадать слово.

Самым простым и самым продолжительным по времени решением будет проверка всех слов, находящихся в словаре.

Поступим по другому. Раскроем словарь посредине. Вопрос, который следует задать: «В первой (или во второй) части словаря находится слово?» В результате такого действия количество страниц уменьшится вдвое. Поступим аналогичным образом с выбранной половиной: разделим её снова пополам и опять количество страниц уменьшится вдвое. Продолжаем поступать так, пока не найдём нужную страницу. Затем также поступим со словами на странице, пока не найдём нужное слово. Убедитесь самостоятельно, что для угадывания любого слова достаточно задать не более 16 вопросов.

такой метод поиска называется двоичным поиском. Встречаются и другие названия этого метода: бинарный поиск, логарифмический поиск, метод деления пополам, дихотомия.

В программировании такой поиск применяют для нахождения элемента Х в отсортированном массиве.

Основная идея заключается в следующем.

Пусть массив отсортирован в порядке возрастания. Находим средний элемент массива

A[m] (m=(N+1) div 2)

и сравниваем его с элементом Х. Если средний элемент равен Х, то поиск заканчивается. Если он больше Х, то все элементы с индексами большими или равными m можно не рассматривать. Если же средний элемент меньше Х, то исключаются элементы с индексами, меньшими или равными m.

При выполнении данного алгоритма придется на каждом шаге пересчитывать границы поиска. Поиск будет продолжаться до тех пор, пока элемент не будет найден, либо пока левая и правая границы поиска не совпадут, что соответствует отсутствию элемента в массиве.

Количество операций сравнения на единицу больше показателя степени, в которую нужно возвести число 2, чтобы получилось число больше или равное количеству элементов в массиве.

Ðàññìîòðèì ïðèìåð. Ïóñòü x=6, à ìàññèâ à ñîñòîèò èç 10 ýëåìåíòîâ:

3 5 6 8 12 15 17 18 20 25

1-é øàã: íàéä¸ì íîìåð ñðåäíåãî ýëåìåíòà:

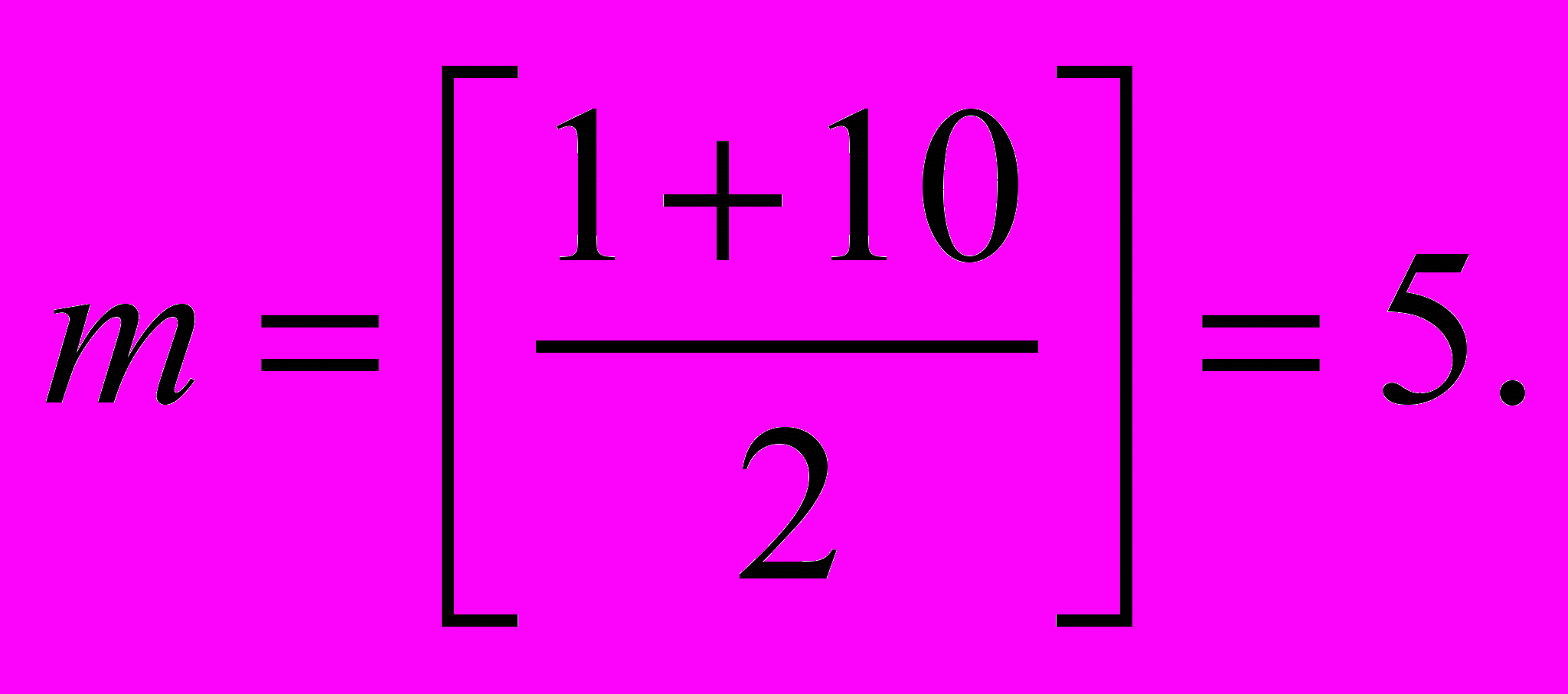Квадратные скобки показывают, что надо взять целую часть от деления. Òàê êàê 6
3 5 6 8 12 15 17 18 20 25;

2-é øàã: ðàññìàòðèâàåì ëèøü ïåðâûå 4 ýëåìåíòà ìàññèâà; íàõîäèì èíäåêñ ñðåäíåãî ýëåìåíòà ýòîé ÷àñòè:



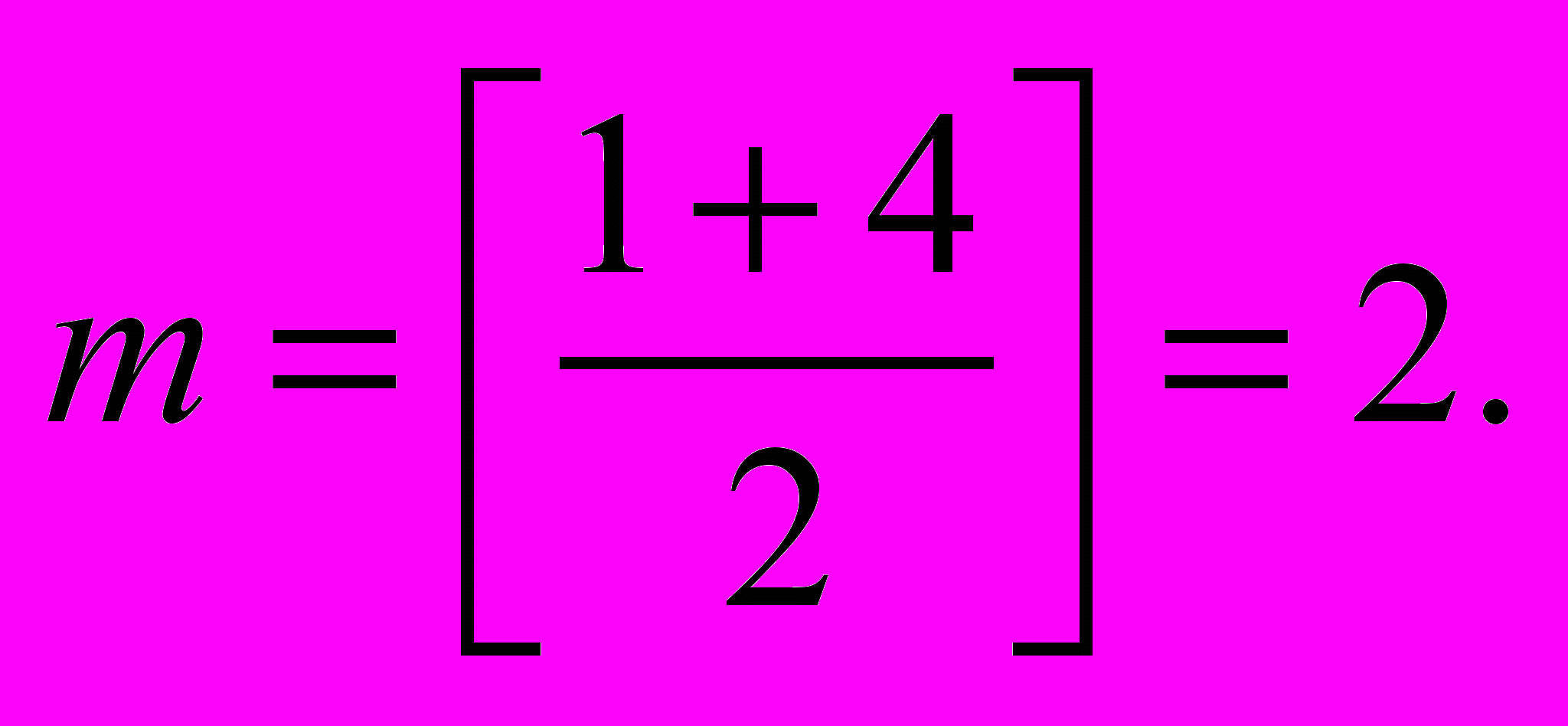
6>a[2], ñëåäîâàòåëüíî, ïåðâûé è âòîðîé ýëåìíòû èç ðàññìîòðåíèÿ èñêëþ÷àåì:

3 5 6 8 12 15 17 18 20 25;

3-é øàã: ðàññìàòðèâàåì äâà ýëåìåíòà; çíà÷åíèå 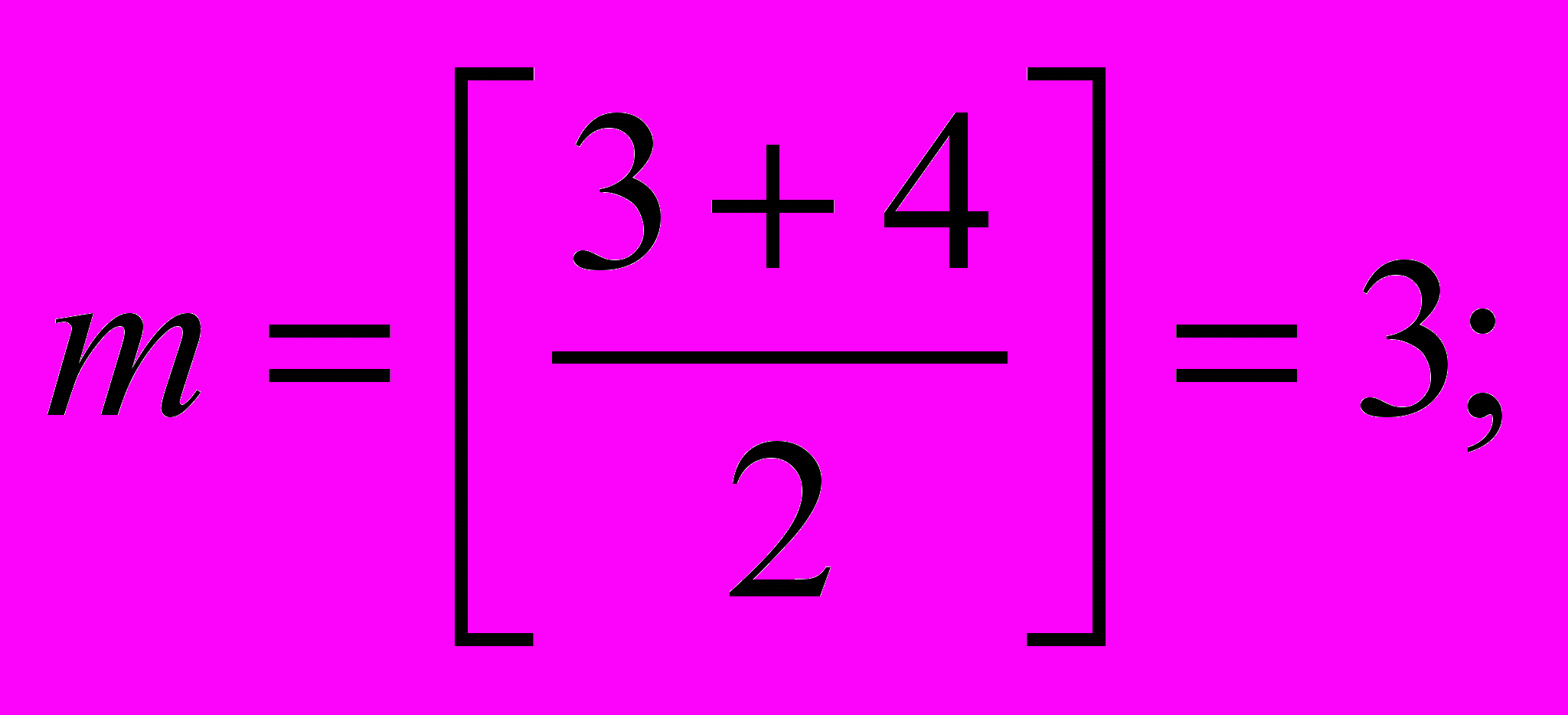а[3]=6! Ýëåìåíò íàéäåí, åãî íîìåð — 3:

3 5 6 8 12 15 17 18 20 25.

Ïðèìå÷àíèå. Âîîáùå ãîâîðÿ, âûáîð çíà÷åíèÿ m ìîæíî îñóùåñòâëÿòü ñëó÷àéíûì îáðàçîì, êîððåêòíîñòü àëãîðèòìà îò ñïîñîáà âûáîðà m íå çàâèñèò. Íî íà ýôôåêòíîñòü àëãîðèòìà âûáîð m âëèÿåò, òàê êàê ìû õî­òèì íà êàæäîì øàãå èñêëþ÷èòü èç äàëüíåéøåãî ðàññìîòðåíèÿ êàê ìîæíî áîëüøå ýëåìåíòîâ. Îïòèìàëüíûì áóäåò âûáîð ñðåäíåãî ýëåìåíòà, ïîòîìó ÷òî ïðè ýòîì â ëþáîì ñëó÷àå áóäåò èñêëþ÷àòüñÿ ïîëîâèíà ìàññèâà.

 îáùåì ñëó÷àå çíà÷åíèå 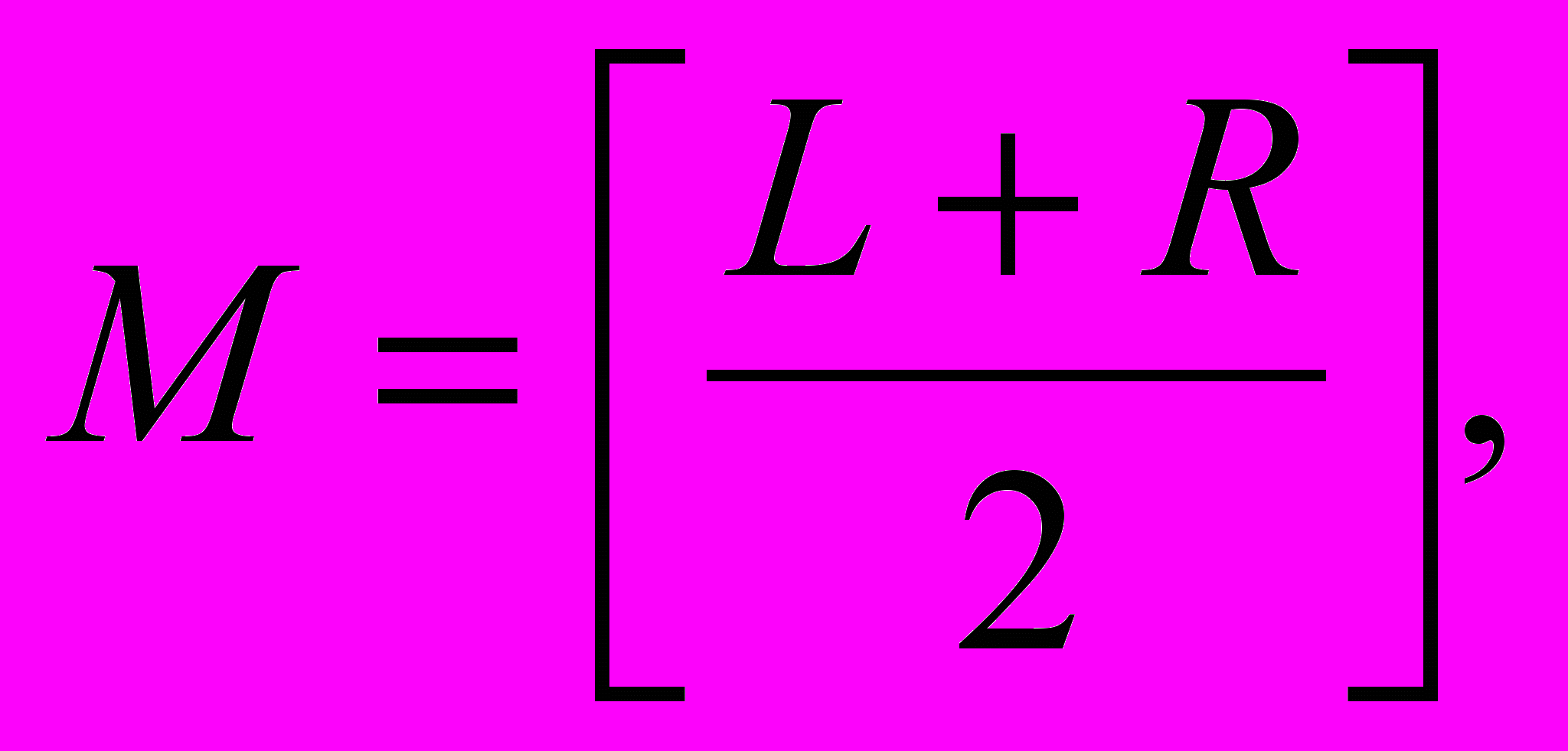ãäå l — èíäåêñ ïåðâîãî, à r — èíäåêñ ïîñëеäíåãî çëåìåíòà ðàññìàòðèâàåìîé ÷àñòè ìàññèâà.

Íèæå ïðèâåäåí ôðàãìåíò ïðîãðàììíîé ðåàëèçàöèè áèíàðíîãî ïîèñêà.

L:=1;R:=N;P:=false;

While (L<=R) and (P=false) do

Begin

M:=(R+L) div 2;

If A[m]=X then P:=true

Else If A[m]>X then L:=m+1 Else R:=m-1;

End;

Ìîæíî òàêæе ðåàëèçîâàòü áèíàðíûé ïîèñê ñ èñïîëüçîâàíèåì ôèê­òèâíîãî "áàðüåðíîãî" ýëåìåíòà. Íèæå ïðèâåäåí ôðàãìåíò ïðîãðàìû, â êîòîðîì ïðåäëàãàåì ðàçîáðàòüñÿ ñàìîñòîÿòåëüíî:

Begin

à[0]=õ

l:=1; r:=n

repeat

m:=( l+r) Div 2;

If l >r Then m:=0

Else if a[m]
Else r:=m-1;

Until a [m]=x;

Ans:=m;

End;

 îòëè÷èå îò ïîñëåäîâàòåëüíîãî ïîèñêà, êîòîðûé òðåáóåò âðåìå­íè, ïðîïîðöèîíàëüíîãî êîëè÷åñòâó ýëåìåíòîâ ìàññèâà, áèíàðíûé ïîèñê òðåáóåò çíà÷èòåëüíî ìåíüøèõ âðåìåííûõ çàòðàò. Íàïðèìåð, ïðè n=2⁴⁰ áèíàðíûé ïîèñê âûïîëíÿåòñÿ äîñòàòî÷íî áûñòðî, â òî âðåìÿ êàê ïîñëå­äîâàòåëüíûé ïîèñê òðåáóåò çíà÷èòåëüíîãî âðåìåíè. Êðîìå òîãî, íåò àë­ãîðèòìà, êîòîðûé òðåáîâàë áû ñðàâíåíèé ìåíüøå, ÷åì ïîèñê ìåòîäîì ïî­ëîâèííîãî äåëåíèÿ.

35.2. Сортировка вставками. все сортировки, рассмотренные ранее, требуют (N²-N)/2 операций сравнения. Используя дихотомический поиск, количество операций сравнения можно сократить.

Будем просматривать элементы массива А, начиная со второго. Каждый новый элемент A[i] будем вставлять на подходящее место в уже упорядоченную совокупность A[1], ..., A[i—1]. Это место определяется последовательными сравнениями элемента A[i] с упорядоченными элементами A[1], ..., A[i—1].

Такой метод сортировки называется сортировкой простыми вставками. Он тоже требует порядка (N²—N)/2 операций сравнения.

Если для поиска места элемента в упорядоченной совокупности воспользоваться методом двоичного поиска, то количество операций сравнения будет гораздо меньше. Такой алгоритм сортировки называется сортировка бинарными вставками:

For i:=2 to n do

Begin

L:=1;R:=i;

While L
Begin

M:=(R+L) div 2;

If A[m]>A[i] then L:=m+1 Else R:=m;

End;

K:=R;X:=A[i];

For j:=i downto k+1 do A[j]:=A[j-1];

A[K]:=X;

End;

Цикл While L
Пример. (Элемент, который вставляем, подчёркнут.)

1. 1, 9, 2, 4, 3, 6, 5, 0
   
2. 9, 1, 2, 4, 3, 6, 5, 0
   
3. 9, 2, 1, 4, 3, 6, 5, 0
   
4. 9, 4, 2, 1, 3, 6, 5, 0
   
5. 9, 4, 3, 2, 1, 6, 5, 0
   
6. 9, 6, 4, 3, 2, 1, 5, 0
   
7. 9, 6, 5, 4, 3, 2, 1, 0
   
8. 9, 6, 5, 4, 3, 2, 1, 0
   

Для вставки элемента в нужное место все элементы, стоящие за ним, сдвигаем до позиции, которую занимал вставляемый на данном шаге элемент.

Вопросы и задания.

1. В чём заключается идея двоичного поиска?
   
2. Задан массив А упорядоченный по возрастанию. Прочитать из файла N неупорядоченных чисел и вставить их в массив А, не нарушая упорядоченности. Использовать метод бинарных вставок.