Предисловие дорогие друзья !

Вид материала

Документы

Содержание §25. Пользовательские процедуры. Begin Раздел операторов End Количество, порядок и тип формальных и фактичес­ких параметров должны в точности совпадать. Var i:Integer; {В разделе описатний описан параметр цикла i) Begin Begin и заканчивается служебным словом End Program Ex65; Var Var z: Integer; Begin Program Ex66; Var End. Пример 67. Begin S:=0; {Начальное значение суммы цифр} While Program Ex67; Var §26. Пользовательские функции. 26.2. Описание функции. Begin S:=0; While Program Ex68; Var Begin k:=0; While Program Ex69; Var End. Пример 70. Begin {тело функции} rez:=l; {начальное значение факториала} For Program Ex70; Var ... Полное содержание

Подобный материал:

• К. Бальмонт  Дорогие друзья, сегодня мы в гостях у замечательного русского поэта Константина, 164.76kb.
• Медникова Надежда Александровна учитель начальных классов моу «Уинская сош» Пермский, 91.48kb.
• И в шутку и всерьез Ведущий Добрый день, дорогие друзья! Вот и пришла весна, вот, 339.91kb.
• Играют 2 команды. Вопросы викторины, 53.15kb.
• Летние каникулы в праге, 322.16kb.
• Мои дорогие литературные друзья, 136.81kb.
• Ведущий: Дорогие, друзья! Разрешите поздравить вас с большим и дорогим для всех праздником, 124.29kb.
• Отчет о конференции 17-18 апреля дорогие друзья!, 182.44kb.
• Дорогие друзья и единомышленники, 134.05kb.
• Сценарий для 7-8 классов «Старая сказка на новый лад», 52.44kb.

§25. Пользовательские процедуры.

25.1. Повторение

1. Из каких разделов состоит программа?

2. Является ли заголовок программы обязательным?

3. Какие разделы описаний вы уже знаете?

4. Каким служебным словом начинается раздел описа­ния констант? Приведите пример описания константы.

5. Каким служебным словом начинается раздел опи­сания типов? Приведите пример описания типа.

6. Каким служебным словом начинается раздел описания переменных? Приведите пример описания пере­менных.

7. Как оформляется тело основной программы?

8. Какие операторы вы знаете?

25.2. Описание процедуры. Оператор вызова процедуры. Описание процедуры начинается с заголовка, кото­рый является обязательным (в отличие от заголовка про­граммы). Заголовок состоит из служебного слова Procedure, за которым следуют имя процедуры, образованное по правилам языка Паскаль. Например:

Procedure PRIM (<Служебная информация — параметры>);

Раздел описаний

Begin

Раздел операторов

End;

Раздел описаний процедуры подобен разделу описаний основной программы, и может состоять из разделов меток, констант, типов, переменных и, в свою очередь, процедур и функций. В языке Паскаль допускается отсутствие раздела описаний.

Служебная информация в круглых скобках рядом с именем процедуры тоже может отсутствовать.

Раздел операторов заключается в операторные скобки BEGIN и END, причём после END в отличие от основной программы ставится точка с запятой.

Вызывается процедура по её имени, например:

PRIM(Список_параметров);

25.3. Параметры. Выясним, какая служебная информация находится в круглых скобках рядом с именем процедуры.

Подпрограмма реализует некоторый частный алгоритм, который вызывается в основной программе. Для реализации алгоритма подпрограмме могут понадобиться некоторые данные из основной программы. Обработав эти данные, подпрограмма возвращает результат основной программе, если в этом есть необходимость. Передавать информацию из основной программы в подпрограмму и наоборот мы можем только через переменные, которые носят специальное название — формальные параметры.

Чтобы лучше разобраться, что же такое формальные параметры, рассмотрим такой пример. В некотором цехе производится сборка автомобилей. Рядом с цехом находится мастерская, в которой изготавливаются болты, необходимые для сборки. Цех и мастерская соединены окнами, через которые в мастерскую поступают заготовки и возвращаются готовые болты. Так вот, формальные параметры можно сравнить с этими окнами. Те из них, через которые данные только поступают в подпрограмму, называют параметры-значения. Те, через которые данные возвращаются в основную программу из процедуры, называют параметры-переменные.

формальные параметры указываются рядом с именем процедуры в круглых скобках. Список параметров формально определяет количество переменных, которое необходимо для обмена информацией, и их тип. При этом, как и в разделе описания переменных, указывается имя переменной и через двоеточие её тип. Этого достаточно для их объявления.

Параметры-переменные (результат работы процедуры) отличаются от параметров-значений тем, что перед ними стоит служебное слово Var.

При каждом обращении к процедуре мы должны поместить в параметры некоторые значения. Эти значения называются фактическими параметрами.

Фактические параметры — это параметры (данные), кото­рые передаются процедуре при ее вызове.

Количество, порядок и тип формальных и фактичес­ких параметров должны в точности совпадать.

В качестве формальных параметров могут быть только переменные с указанием их типа. В качестве фактических параметров могут быть константы, переменные, выражения без указания их типа.

Процедура может содержать несколько операторов и несколько результатов выполнения. Каждый результат обозначается своим именем. В основной программе после вызова процедуры мы можем пользоваться этими результатами, сохраняя те же имена или давая другие.

Пример 65. Составить программу для вычисления аⁿ, целые чис­ла a и n (n>= 0) вводятся из файла.

Решение. В языке Паскаль отсутствует стандартная функция возведения в степень. Составим процедуру для вычисления степени целого числа.

Procedure Stepen(x,у: Integer; Var st: Longint); {Заголовок процедуры}

Var i:Integer; {В разделе описатний описан параметр цикла i)

Begin {тело процедуры)

st:=l; {st — результат, присвоим ему начальное значение равное 1}

For i:=l To у Do st:=st*x; {Последовательно умножая st на х, получаем значение n-й степени числа х}

End; {Конец процедуры}

Первая строчка описания — это заголовок процеду­ры, который начинается со слова Procedure. Процеду­ра названа именем Stepen. В скобках записан список формальных параметров, то есть перечислены переменные с указанием их типа. Мы используем три параметра: пер­вый (х) — основание степени, то есть число, которое надо воз­вести в степень; второй (у) — показатель степени, третий (st) — результат. Первые два формальных параметра — парамет­ры-значения (аргументы), третий — параметр-переменная (результат), и перед ним указано слово Var. Все они описаны как целые (х и у — переменные типа Integer, a st — типа Longint, так как значение степени числа может получиться достаточно большим).

После заголовка процедуры идёт раздел описаний. В нашем примере имеется только описание одной пе­ременной i (параметр цикла).

Далее идет раздел операторов (тело процедуры). Оно начинается служеб­ным словом Begin и заканчивается служебным словом End, после которого стоит точка с запятой (в конце программы после последнего End ставится точка). В теле процедуры вычисляется степень числа х при помощи цикла For.

В программе процедуры и функции описываются после раздела описания переменных программы, но до начала ее основной части, то есть до оператора Begin, начинаю­щего эту часть.

Вся программа для решения нашей задачи может иметь следующий вид;

Program Ex65;

Var a, n: Integer;

s: Longint;

F1,F2:Text;

Procedure Stepen (х,у: Integer; Var st: Longint) ;

Var i:Integer;

Begin

st:=l;

For i:=l To у Do st:=st*x;

End;

Begin

Assign(F1,’Input.txt’); {назначаем входной файл}

Assign(F2,’Output.txt’); {назначаем выходной файл}

Reset(F1); {открываем входной файл для чтения}

Rewrite(F2); {открываем выходной файл для записи}

Readln(F1,a,n); {считываем из файла значение основания и показателя степени}

Stepen (а,n,s); {обращение к процедуре}

Writeln(F2,s); {выводим в файл значение степени}

Close(F2); {закрываем файл}

End.

Процедура вызывается как оператор, состоящий из имени процедуры (Stepen) и фактических параметров (а, n, s), которые записаны в скобках. В нашем примере фор­мальные параметры х, у и st принимают значения фактических параметров а, n и s соответственно. Пос­ле завершения работы процедуры переменные а и n сохранят те же значения, что и при вызове процедуры, а s полу­чит новое значение.

Пример 66. Даны две целые переменные. Поменять местами их значения.

Решение. Поменять местами значения двух переменных можно несколькими способами. Один из них — используя промежуточную переменную. Напишем процедуру, соответствующую этому способу.

Procedure Swap (Var x,y: integer);

Var z: Integer;

Begin

z:=x; x:=y; y:=z;

End;

Процедура называется Swap. У нее имеется два фор­мальных параметра, которые являются параметрами-переменными, так как необходимо поменять значения переменных и запомнить изменения. Эти параметры яв­ляются результатами выполнения процедуры.

В процедуре описана переменная z, которая исполь­зуется как промежуточная.

Вся программа имеет вид:

Program Ex66;

Var a, b: Integer;

F1,F2:Text;

Procedure Swap (Var х, у:Integer);

Var z: Integer;

Begin

z:=x; x:=y; y:=z;

End;

Begin

Assign(F1,’Input.txt’); {назначаем входной файл}

Assign(F2,’Output.txt’); {назначаем выходной файл}

Reset(F1); {открываем входной файл для чтения}

Rewrite(F2); {открываем выходной файл для записи}

Readln(а, b) ; {считываем из файла значения переменных}

Swap(а, b); {обращение к процедуре}

Writeln(F2, а, ' ', b) ; {выводим в файл новые значения переменных}

Close(F2); {закрываем файл}

End.

Пример 67. Написать процедуру, подсчитывающую сумму цифр натурального числа. Используя ее, определить, у какого из двух данных чисел сумма цифр больше.

Решение. Мы уже решали похожую задачу, только в ней не требовалось написать процедуру, и мы считали количество цифр, а не их сумму.

Надо выделять последнюю цифру числа до тех пор, пока число не станет равным нулю. При этом каждый раз суммируя цифры (начальное значение суммы — 0).

Procedure Sum(x: Longint; Var S: Byte);

Begin

S:=0; {Начальное значение суммы цифр}

While x > 0 Do {Пока в числе есть цифры}

Begin

S:=s+x mod 10; {Прибавляем последнюю цифру к сумме}

x:=x div 10; {И удаляем её из числа}

End;

End;

Вся программа имеет вид:

Program Ex67;

Var a, b: LongInt;

s1, s2: byte;

F1,F2:Text;

Procedure Sum(x: Longint; Var S: Byte);

Begin

S:=0;

While x > 0 Do

Begin

S:=s+x mod 10;

x:=x div 10;

End;

End;

Begin

Assign(F1,’Input.txt’); {назначаем входной файл}

Assign(F2,’Output.txt’); {назначаем выходной файл}

Reset(F1); {открываем входной файл для чтения}

Rewrite(F2); {открываем выходной файл для записи}

Readln(а, b) ; {считываем из файла значения переменных}

Sum(а, s1); {обращение к процедуре}

Sum(b, s2); {обращение к процедуре}

{Вывод результата в зависимости от значения сумм цифр чисел}

If s1 > s2 then Writeln(F2, а, ' имеет большую сумму цифр, чем ', b)

Else If s1 < s2 then Writeln(F2, b, ' имеет большую сумму цифр, чем ', a)

Else Writeln(F2, а, ' имеет такую же сумму цифр, что и ', b);

Close(F2); {закрываем файл}

End.

Вопросы и задания.

1. Дайте определение процедуры.
   
2. Может ли быть процедура без параметров?
   
3. Как называются параметры, определяемые в заголовке программы?
   
4. Какие параметры называются фактическими?
   
5. Каково соответствие между фактическими и формальными параметрами?
   
6. Написать процедуру нахождения НОД двух чисел. Используя эту процедуру найти НОД трёх чисел, НОД четырёх чисел.
   
7. Используя процедуру, рассмотренную в приме­ре 2, упорядочить по возрастанию значения трех пере­менных — а, b и с.
   
8. Даны координаты трех вершин треугольника. Написать процедуру нахождения длины отрезка. Найти длины всех его сторон, используя написанную процедуру.
   
9. Дано натуральное число. Найти все его делители и подсчитать их количество.
   
10. Даны три натуральных числа. Написать процедуру определения числа делителей натурального числа. При помощи этой процедуры, определить у которого из них больше всего делителей.
    
11. Натуральное число называется совершенным, если оно равно сумме своих делителей, за исключением самого этого числа. Например: 6=1+2+3. Найти все совершенные числа на отрезке от 1 до n. N вводится с клавиатуры.
    
12. Даны два натуральных числа. Написать процедуру переворачивания числа. Используя эту процедуру определить, являет­ся ли одно число перевертышем другого.
    
13. Сократить дробь a/b (a, b — натуральные числа).
    
14. Даны 4 натуральных числа a, b, c, d. Написать программу, вычисляющую сумму обыкновенных дробей в виде x/y=a/b+c/d.
    
15. Натуральное число из n цифр является числом Армстронга, если сумма его цифр, возведённых в n-ю степень, равна самому числу (153=1³+5³+3³). Получить все числа Армстронга для n=2, 3, 4.
    
16. Найти все натуральные числа, не превосходящие заданного N, которые делятся на каждую из своих цифр.
    
17. Дано натуральное число N. Выяснить, можно ли представить его в виде произведения трёх последовательных натуральных чисел
    
18. Возвести дробь a/b (a, b — натуральные числа) в степень N (N — натуральное).
    

§26. Пользовательские функции.

26.1. Повторение.

1. Что такое подпрограмма? Для чего используются подпрограммы? Перечислите преимущества использо­вания подпрограмм.

2. Запишите структуру процедуры.

3. Что такое формальные и фактические пара­метры?

4. Как записывается вызов процедуры?

26.2. Описание функции. если подпрограмма имеет только один выводимый параметр (результат), то её можно оформить в виде функции.

Функция, как и процедура, может содержать несколько операторов, несколько входных параметров (аргументов), но результат её выполнения только один. Этот единственный результат обозначается именем функции и передаётся в основную программу.

Заголовок функции состоит из слова Function, за которым указывается имя функции, затем в круглых скобках записывается список формальных параметров, далее ставится двоеточие и указывается тип результата функции.

В теле функции обязательно должен быть хотя бы один оператор присваивания, в левой части которого стоит имя функции, а в правой — ее значение. Иначе значение функции не будет определено.

Таким образом, общий вид описания функции сле­дующий (в квадратных скобках записана необязательная часть; функция, как и процедура, может не иметь параметров):

Function Имя[(Список формальных параметров)]: Тип результата;

Раздел описаний

Begin

Раздел операторов — тело функции, в котором обязательно должен быть оператор присваивания: Имя_функции:=значение

End;

Вызывается функция по её имени с указанием фактических параметров. При этом вызов функции можно делать непосредственно внутри выражения, подобно тому, как используются стандартные встроенные функции, например, квадрат — SQR(X).

Для того, чтобы лучше разобраться с особенностями написания процедур и функций, рассмотрим ещё раз задачу из предыдущего параграфа, и сравним, что общего, и каковы различия при использовании процедур и функций.

Пример 68. Написать функцию, подсчитывающую сумму цифр натурального числа. Используя ее, определить, у какого из двух данных чисел сумма цифр больше.

Решение. Для сравнения запишем функцию и процедуру рядом.

Procedure Sum(x: Longint; Var S: Byte); Begin S:=0; While x > 0 Do Begin S:=s+x mod 10; x:=x div 10; End; End;

Function Sum(x: Longint): Byte; Var S: Byte; Begin S:=0; While x > 0 Do Begin S:=s+x mod 10; x:=x div 10; End; Sum:=S; End;

Первая строка — это заголовок процедуры (Procedure) и функции (Function). В заголовке процедуры описаны два формальных параметра х — число, у которого нужно определить сумму цифр, и S — результат работы процедуры — сумма цифр. В заголовке функции только один формальный параметр х — число, у которого нужно определить сумму цифр. Но зато указывается тип функции — ведь она и будет возвращать результат работы. Далее в функции описывается промежуточная переменная S — сумма цифр. Алгоритм нахождения суммы цифр и в функции и в процедуре один и тот же. В конце функции идёт обязательная команда присваивания полученного значения имени функции.

Вся программа с использованием функции может выглядеть так:

Program Ex68;

Var a, b: LongInt;

s1, s2: byte;

F1,F2:Text;

Function Sum(x: Longint): Byte;

Var S: Byte;

Begin

S:=0;

While x > 0 Do

Begin

S:=s+x mod 10;

x:=x div 10;

End;

Sum:=S;

End;

Begin

Assign(F1,’Input.txt’); {назначаем входной файл}

Assign(F2,’Output.txt’); {назначаем выходной файл}

Reset(F1); {открываем входной файл для чтения}

Rewrite(F2); {открываем выходной файл для записи}

Readln(а, b) ; {считываем из файла значения переменных}

s1:=Sum(а); {обращение к функции}

s2:=Sum(b); {обращение к функции}

{Вывод результата в зависимости от значения сумм цифр чисел}

If s1 > s2 then Writeln(F2, а, ' имеет большую сумму цифр, чем ', b)

Else If s1 < s2 then Writeln(F2, b, ' имеет большую сумму цифр, чем ', a)

Else Writeln(F2, а, ' имеет такую же сумму цифр, что и ', b);

Close(F2); {закрываем файл}

End.

Теперь посмотрим, какие отличия появятся в командах вызова в основной программе:

Sum(а, s1); Sum(b, s2);

s1:=Sum(а); s2:=Sum(b);

Слева вызов процедуры, а справа — функции. Различия очевидны. Ещё одно замечание. После выполнения процедуры, мы сможем работать только с переменными S1 и S2, а если использовалась функция, то можно работать как с переменной (в примере), так и с самой функцией, тогда команда сравнения будет выглядеть так:

If Sum(а) > Sum(b) then Writeln(F2, а, ' имеет большую сумму цифр, чем ', b)

Else If Sum(а) < Sum(b) then Writeln(F2, b, ' имеет большую сумму цифр, чем ', a)

Else Writeln(F2, а, ' имеет такую же сумму цифр, что и ', b);

Следует заметить, что в данном случае такой способ использования функции нерационален, так как в первом случае мы только два раза обращаемся к функции, а во втором — четыре. Количество исполняемых операторов увеличивается вдвое.

Рассмотрим ещё одну похожую задачу.

Пример 69. Написать функцию, подсчитывающую количество цифр натурального числа. Используя ее, определить, в каком из двух данных чисел больше цифр.

Решение. Мы уже решали похожую задачу, только в ней не требовалось писать функцию. Надо выделять последнюю цифру числа до тех пор, пока число не станет равным нулю. При этом каждый раз счетчик увеличивается на 1 (начальное значение счет­чика — 0). Надо выделять последнюю цифру числа до тех пор, пока число не станет равным нулю. При этом каждый раз счетчик увеличивается на 1 (начальное значение счет­чика — 0).

Function Kol(x: Longint): Byte;

Var k: Byte;

Begin

k:=0;

While x <> 0 Do

Begin

Inc(k);

x:=x div 10;

End;

Kol:=k;

End;

В заголовке функции указано ее имя — Kol. Функции передается только один параметр (х) — целое число, количество цифр которого надо найти. Результат — тоже целое число. В разделе переменных описана перемен­ная k — счетчик цифр. В теле функции с помощью цикла While и выполняются указанные выше действия (увели­чивается значение счетчика и удаляется последняя цифра).

Еще раз заметим, что память для переменной k, которая является локальной, выделяется только тогда, когда начинает свою работу функция. Поэтому её необходимо «обнулять». После заверше­ния работы функции эта часть памяти освобождается, и значение k будет не определено.

Ввод и вывод данных в программе осуществляется с помощью текстовых файлов.

Program Ex69;

Var nl, n2:.Longint; kl, k2: Byte;

F1,F2:Text;

Function Kol (x: Longint): Byte;

Var k: Byte;

Begin

k: =0;

While x<>0 Do

Begin

Inc(k);

x:=x div 10;

End;

Kol:=k;

End;

Begin

Assign(F1,’Input.txt’);

Assign(F2,’Output.txt’);

Reset(F1);

Rewrite(F2);

Readln(F1, nl, n2) ;

kl:= Kol (nl); {количество цифр первого числа}

k2:= Kol (n2); {количество цифр второго числа}

If kl=k2 Then Writeln(F2, 'Одинаковое количество цифр')

Else If kl>k2 Then Writeln(F2, 'В первом числе цифр больше')

Else Writeln(F2, 'Во втором числе цифр больше') ;

Close(F2);

End.

Пример 70. Найти разность двух факториалов F=m!-k! Напомним, что n! представляет собой произведение n чисел натурального ряда 123…n. Вычисление n! оформим в виде функции FACT, а затем будем обращаться к ней последовательно передавая значения m и k.

Решение. Опишем функцию для вычисления факториала чис­ла п.

Function fact (n:Integer):Longint; {заголовок функции}

Var i: Integer; {раздел описаний: I — параметр цикла}

rez: Longint; {rez — промежуточная переменная для получения факториала}

Begin {тело функции}

rez:=l; {начальное значение факториала}

For i:=l To n Do rez:=rez*i; {вычисление факториала}

fact:=rez; {присваивание значения имени функции}

End;

Первая строчка в описании функции — это ее заголо­вок. Служебное слово Function (функция) указывает на то, что именем fact названа функция. В скоб­ках записан список формальных параметров функции, состо­ящий из одной переменной целого типа. Далее в заголовке указан тип значения функции. В данном примере резуль­тат функции fact — длинное целое число.

За заголовком функции следует описательная часть функции, которая, как и у программы, может состоять из разделов описания переменных, констант, типов. В данном примере имеется только раздел описания пере­менных. В нем описаны переменные i (параметр цикла) и rez (для накопления значения факториала).

Далее идет раздел операторов (тело функции). Ре­зультат присваивается имени функции, таким образом, функция получает свое значение.

В тексте программы описания функций всегда следу­ют за разделом описания переменных и до начала основ­ной части, как и описания процедур. После того как функция описана, ее можно использовать в программе.

Ввод и вывод данных в программе осуществляется с помощью текстовых файлов.

Program Ex70;

Var m, k: Integer; F: Longint;

F1, F2: Text;

Function fact(n:Integer):Longint;

Var i: Integer; rez: Longint;

Begin

rez:=l;

For i:=l To n Do rez:=rez*i;

fact:=rez;

End;

Begin

Assign(F1,’Input.txt’);

Assign(F2,’Output.txt’);

Reset(F1);

Rewrite(F2);

Readln(F1, m, k);

F:= fact(m)-fact(k);

Writeln(F2,F);

Close(F2);

End.

При вычислении значения F программа дважды обращается к функции: FACT(m) и FACT(k).

Вопросы и задания.

1. Назовите основные отличия в описании процедур и функций.
   
2. Каким образом производится вызов функции в программе?
   
3. Что лучше процедура или функция?
   
4. Найти сумму цифр числа.
   
5. Найти первую цифру числа.
   
6. Найти количество делителей числа.
   
7. Найти числа из промежутка от А до В, у которых больше всего делителей.
   
8. Найти сумму всех делителей числа.
   
9. Определить, является ли число совершенным (ис­пользовать функцию из предыдущего задания, изменив ее, если это необходимо).
   
10. Составьте программу, проверяющую, является ли данное число палиндромом (перевёртышем, т.е. читается одинаково слева направо и справа налево).
    
11. Определить, является ли данное число автоморфным. Автоморфным называется число, квадрат которо­го заканчивается им самим. Например, автоморфным является число 6, так как его квадрат 36 заканчивается на 6, или число 25 — его квадрат 625.
    
12. Используя функцию из предыдущей задачи, най­ти все автоморфные числа из промежутка от А до В.
    
13. Составить программу нахождения наибольшего об­щего делителя нескольких чисел, используя функцию нахож­дения НОД двух чисел (см. §20).
    
14. Составить программу, вычисляющую наимень­шее общее кратное четырех чисел (использовать функ­цию из предыдущего задания).
    
15. Даны четыре числа. Вывести на экран наибольшую из первых цифр заданных чисел. Например, если а = 25, b = 730, с = 127, d = 1995, то надо напечатать цифру 7.
    
16. Даны шесть различных чисел. Определить максимальное из них. (Определить функцию, находящую максимум из двух различных чисел.)
    

§27. Рекурсия и рекурсивные программы.

Рекурсия не является чем-то сверхсложным,

а просто является еще одним способом программирования, которым можно пользоваться успешно или злоупотреблять, как и всем остальным.

( Д. Баррон )

В программировании имеется возможность обращения процедуры или функции к самой себе. Выполнение такого вызова ничем не отличается от выполнения вызова любой другой подпрограммы. При этом получается, что циклическую часть программы можно составить без оператора цикла.

Алгоритм, который в процессе работы обращает­ся сам к себе, называется рекурсивным. А способ обращения процедуры или функции к самой себе называют рекурсией. Для иллюст­рации понятия рекурсия часто приводят пример с те­левизором, на экране которого изображен этот же телевизор, на экране второго — опять телевизор и так далее.

Максимальное число рекурсивных вызовов подпрограммы без возвратов, называется глубиной рекурсии. Глубина рекурсии ограничена. Её величину можно изменить с помощью специальной команды языка Паскаль.

Рассмотрим решение задач, которые можно решить, используя рекурсию.

Пример 71. Написать процедуру, определяющую глубину рекурсии.

Решение. При обращении к подпрограмме, система должна знать, куда необходимо вернуться после окончания выполнения подпрограммы. Для этого адрес возврата записывается в специальный отдел оперативной памяти, называемый стеком. Размер стека можно изменять с помощью следующей команды, называемой директивой компилятора, {$M Steck, Min, Max}. Стандартные значения, задаваемые при загрузке Турбо Паскаля, следующие: {$M 16384,0,655360}. Увеличивая число 16384 на блоки, кратные 1024, можно увеличить глубину рекурсии.

Разберёмся теперь с тем, как определить глубину рекурсии. Напишем следующую программу:

Program Ех71_1;

Procedure Slovo;

Begin

WriteLn('Вас приветствует рекурсия');

Slovo

End;

Begin

Slovo

End.

По экрану побежит строка «Вас приветствует рекурсия», но через некоторое время произойдёт аварийное завершение программы из-за ошибки «Error 202: Stack overflow error» смотри приложение 7. Произошло переполнение стека. Но мы так и не определили, какова же глубина рекурсии. Для этого изменим нашу программу следующим образом:

Program Ех71_2;

Var i: longint;

Procedure Slovo;

Begin

Inc (i);

WriteLn('Вас приветствует рекурсия:', i);

Slovo

End;

Begin

I:=0;

Slovo

End.



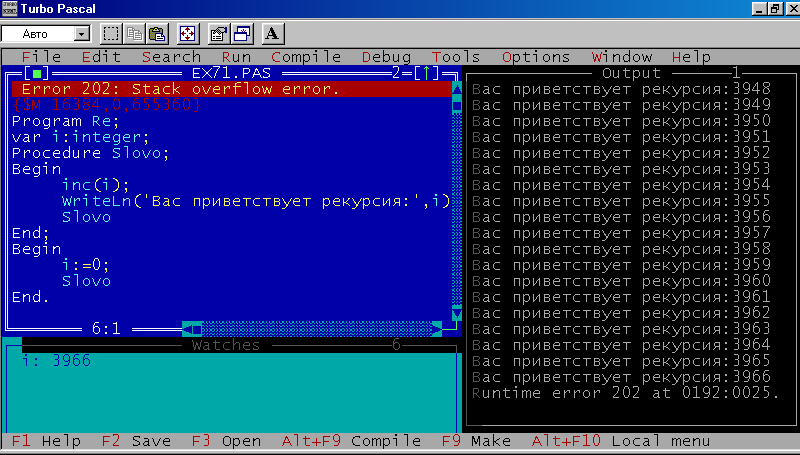
Рис. 15

Теперь после фразы «Вас приветствует рекурсия» через двоеточие будет распечатываться всё увеличивающееся число. В момент прерывания программы оно равно 3966. Это число и определяет глубину рекурсии. Увеличивая или уменьшая размер стека, вы можете изменять глубину рекурсии. поэксперементируйте самостоятельно.

Изменим ещё раз нашу программу:

Program Ех71_2;

Procedure Slovo(i: longint);

Begin

WriteLn('Вас приветствует рекурсия:', i);

Slovo(i+1);

End;

Begin

Slovo(0)

End.

Обратите внимание, что глубина рекурсии изменилась.

Некоторые из задач являются рекурсивными по оп­ределению, поэтому рекурсивные алгоритмы их получе­ния буквально повторяют соответствующие определения.

Пример 72. Рассмотрим ещё один вариант нахождения факториала числа.

Решение. Для того чтобы вычислить N!, надо последовательно умножать все натуральные числа (такой процесс ещё называют итерацией — повторением). Реализовывать такой процесс вы уже умеете:

Factorial:=1;

For I:=1 to N do

Factorial:=I*Factorial;

Но с другой стороны, вычислить N! можно перемножив (N—1)! на N, при этом следует учесть, что 1! = 1 (в математике также принято считать, что 0!=1). Например, 5!=1·2·3·4·5=1!·2·3·4·5=2!·3·4·5=3!·4·5=4!·5. Определение факториала в этом случае можно записать так:



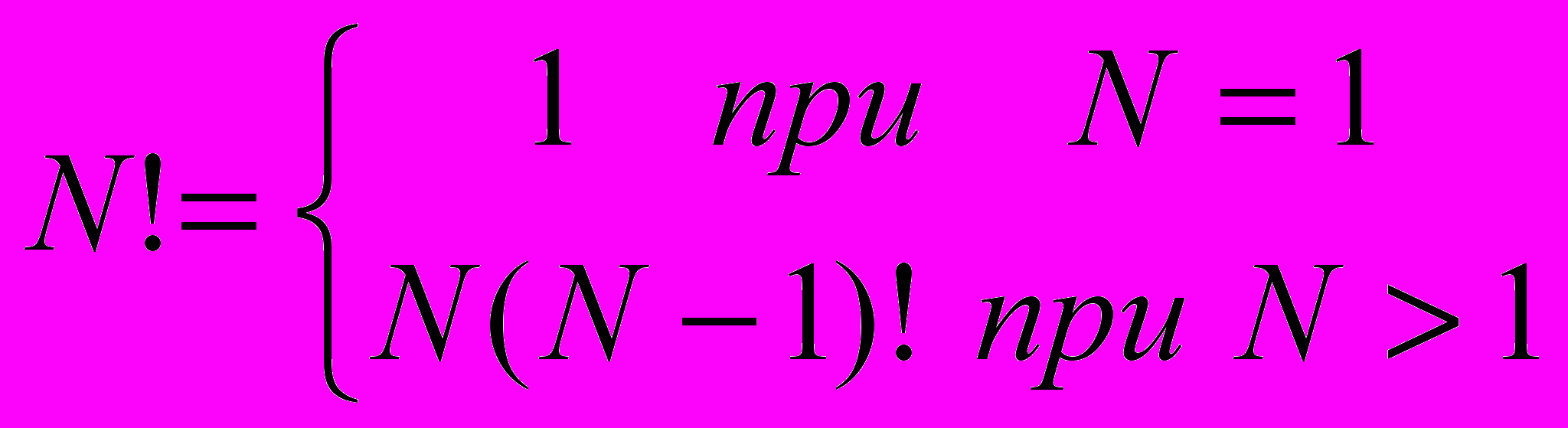
Для вычисления факториала опишем новую функцию.

Function factorial(n: Integer): Longint;

Begin

If n=l Then factorial:=l Else factorial:=n*factorial (n-1) ;

End;

Рассмотрим последовательность вызовов этой функ­ции для n=5. Первый вызов функции происходит в основной программе, например, а:=factorial (5). Отметим, что при каждом обращении к функции будет создаваться свой набор локальных переменных (в данном случае в функции factorial имеется всего одна локальная переменная n). Для каждой локальной переменной на время работы функции выделяется память. После завер­шения работы функции эта память освобождается, и пе­ременные удаляются.

Так как n1, то управление передается на ветку Else и функции factorial присваивается значение n*factorial(n-1), то есть 5*factorial(4). Про­исходит второй вызов функции factorial, с парамет­ром 4. Этот процесс повторяется до тех пор, пока значе­ние параметра не станет равным 1. Тогда условие n=1 истинно, а поэто­му значение функции factorial=l. Таким образом, n=l — это условие окончания рекурсии. Управление пе­редается в точку вызова, то есть в предыдущую функцию для n=2. factorial:=n*factorial(n-1), значит, factorial:=2*1, следовательно, factorial (2) = 2. Возвращаемся назад, поднимаясь "вверх" по цепочке ре­курсивных вызовов. Таким образом, получаем значение factorial (5)=120.




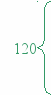
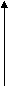
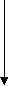5*factorial(4) 5*24=120

4*factorial(3) 4*6=24

3*factorial(2) 3*2=6

2*factorial(1) 2*1=2

1

Программа решения задачи может выглядеть так:

Program Ex72;

Var n: Byte; {как мы выясним в дальнейшем, значение факториала увеличивается очень быстро, и поэтому размерности BYTE нам достаточно для исходного числа}

F1,F2:Text;

Function factorial(n: Byte): Longint;

Begin

If n=l Then factorial:=l Else factorial:=n*factorial (n-1) ;

End;

Begin

Assign(F1,’Input.txt’);

Assign(F2,’Output.txt’);

Reset(F1);

Rewrite(F2);

Readln(F1, n) ;

Writeln(F2, factorial(n));

Close(F2);

End.

Пример 73. В 1228 г. итальянский математик Фибоначчи сформулировал интересную задачу: «Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения».

Решение. Эта задача сводится к нахождению двеннадцатого числа из последовательности чисел Фибоначчи

1, 1, 2, 3, 5, 8, 13, 21, …,

где каждый последующий член равен сумме двух предыдущих, за исключением первых двух членов.

запишем рекурсивную формулировку задачи. В общем виде она будет выглядеть так:



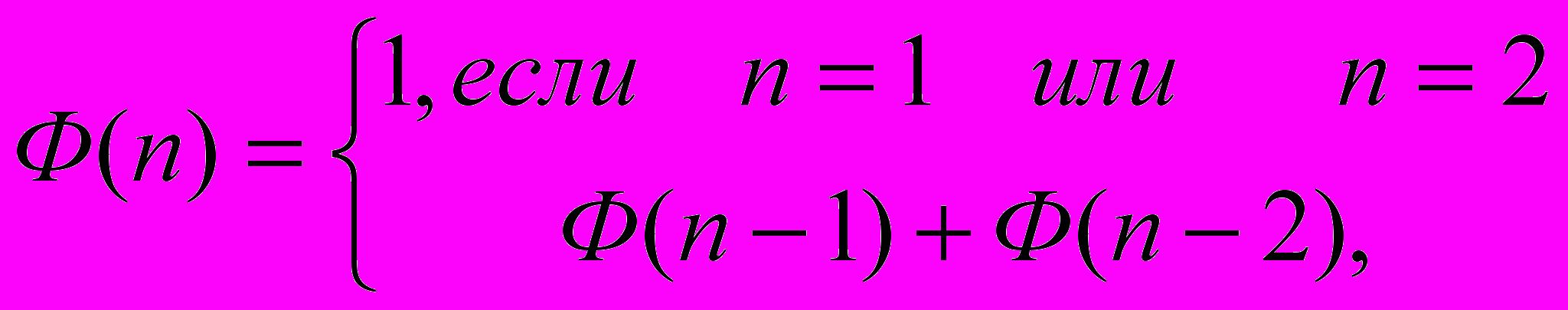
Программа решения задачи может выглядеть так:

Program Ex73;

Var

F2: Text;

Function fib (n: Byte): Longint;

Begin

If (n=l) or (n=2) Then fib:=l Else fib:=fib (n-1)+ fib (n-2) ;

End;

Begin

Assign(F2,’Output.txt’);

Rewrite(F2);

Writeln(F2, fib(12));

Close(F2);

End.

В формулировках некоторых задач рекурсия не присутст­вует в явном виде, но их можно свести к рекурсивным.

Пример 74. Сложение двух чисел. Пусть надо сложить два целых числа а и b, а можно только прибавлять или вычитать 1. Тогда:

если b = 0, то а + b = а;

если b > 0, то a + b = (a + 1) + (b — 1);

если b < 0, то а + b = (а — 1) + (b + 1).

Решение. Можно дать следующее рекурсивное определение операции сложения двух чисел:



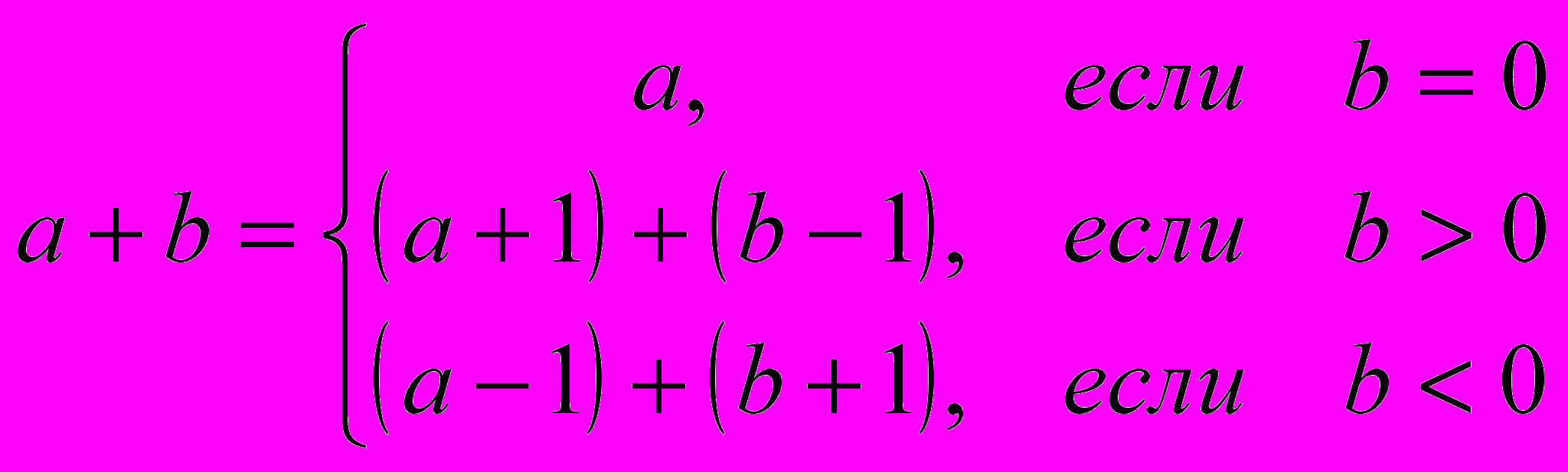
Опишем соответствующую функцию:

Function Sum(a, b: Integer): Integer;

Begin

If b=0 Then Sum:=a

Else If b>0 Then Sum:=Sum(a+l, b-1) Else Sum:=Sum(a-l, b+1 );

End;

Поясним ее на следующих таблицах:

a	b	Примечание	a	b	Примечание
4 5 6 7	3 2 1 0	b>0, a:=a+1; b:=b-1 a:=a+1; b:=b-1 a:=a+1; b:=b-1 Так как b=0, то Sum=7	4 3 2 1	-3 -2 -1 0	B<0, a:=a-1; b:=b+1 a:=a-1; b:=b+1 a:=a-1; b:=b+1 Так как b=0, то Sum=1

Полностью решение задачи запишите самостоятельно.

Пример 75. Найти НОД двух натуральных чисел.

Решение. Рассмотрим еще один способ реа­лизации алгоритма Евклида. Напомним, что такое алгоритма Евклида. Пусть имеются два натуральных числа а и b. Если а=b, то НОД(a, b)=a. Если a>b, то НОД(a, b) = HOД(a-b, b). Если а то НОД (a, b)=НОД(a, b-а).

Рассмотрим конкретный пример: найдем наиболь­ший общий делитель чисел 123 и 36 (см. таблицу).

a	b	Примечание
123	36	Так как а>b, а:=а—b
87	36	a:=a—b
51	36	а:=а—b
15	36	Так как b>а, b:=b—а.
15	21	b:=b-а
15	6	а:=а—b
9	6	a:=а—b
3	6	b:=b—а
3	3	Так как а=b, НОД:=a

Function NOD(a,b: Integer): Integer;

Begin

If a=b Then NOD:=a

Else If a>b Then NOD:=NOD(a - b, b) Else NOD:=NOD(a, b - a) ;

End;

Задание. Написать рекурсивную функцию нахождения НОД двух натуральных чисел, используя вариант алгоритма Евклида с применением нахождения остатков от деления.

Пример 76. Перевести натуральное число из десятичной систе­мы счисления в двоичную.

Решение. Переведем число 23 в двоичную систему счисления. Для этого разделим его на 2, получим целую часть и остаток от деления. Целую часть снова делим на 2 и получаем целую часть и остаток. Так делаем до тех пор, пока целая часть не станет меньше делителя (то есть пока она не станет равной 1).

23	2
22	11	2
1	10	5	2
	1	4	2	2
		1	2	1
			0

Теперь, начиная с этой единицы, выписываем в обратном порядке все остатки от деления. Это и будет запись числа 23 в двоичной системе счисления:

23₁₀ =10111₂.

Опишем соответствующую процедуру:

Procedure Rec(n: Integer);

Begin

If n>l Then Rec(n div 2);

Write(n mod 2) ;

End;

Прорисуем вызовы процедуры для числа 23. Первый вызов процедуры производится в основной программе.

1 вызов (n=23)

If 23>l Then Rec(23 div 2);

If 11>l Then Rec(11 div 2) ;

If 5>l Then Rec(5 div 2);

If 2>l Then Rec(2 div 2);

If 1>l Then Rec(n div 2); {условие не выполняется, последовательно выходим из рекурсии, распечатывая по пути остатки}

Write(1 mod 2) ; 1

Write(2 mod 2) ; 0

Write(5 mod 2) ; 1

Write(11 mod 2) ; 1

Write(23 mod 2) ; 1

Результат: 10111.

Первая цифра (1) выводится на экран из последнего вызова процедуры Rec, следующая цифра (0) — из предпоследнего и так далее, последняя (1) — из первого. Таким образом, вывод очередной цифры происходит перед выходом из очередного экземпляра процедуры Rec.

Приведём пример решения ещё одной задачи, чтобы показать, насколько красивым бывает решение с использованием рекурсии.

Пример 77. В конце XIX века в Европе появилась игра под названием "Ханойские башни". Реквизит игры состоит из 3 игл, на которых размещается башня из колец. Цель игры - перенести башню с левой иглы (1) на правую (3), причем за один раз можно переносить только одно кольцо, кроме того, запрещается помещать большее кольцо над меньшим. Составить алгоритм решения данной задачи (количества колец - N<10).



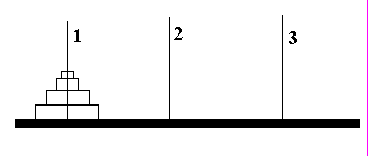
рис. 16

Решение. Суть решения явно просматривается из текста программы. В рекурсивной процедуре используются следующие переменные: High — номер кольца, FromI — номер иглы, на которой первоначально лежат кольца, ToI — номер иглы, на которую нужно переложить все кольца, WorkI — промежуточная (рабочая) игла.

Äëÿ èãðû ñ 30 äèñêàìè òðåáóåòñÿ 2³⁰-1 õîäîâ. Íî 2¹⁰ ðàâíî 1024, èëè ïîðÿäêà 10³. Ñëåäîâàòåëüíî, 2³⁰ ïîðÿäêà 10⁹. Предположим, что компьютер за одну секунду выполняет 10⁶ ходов. Потребуется порядка 0.27 часа для решения задачи.

Program Ех77; { Ханойские башни }

Var N: Integer;

Procedure MoveTown(High,FromI,ToI,WorkI: Integer);

Begin

If High>0 Then Begin

MoveTown(High-1,FromI,WorkI,ToI); {Рекурсия}

{ Вывод }

Writeln('Перенести кольцо ',High,' с иглы ',FromI,' на иглу ',ToI);

MoveTown(High-1,WorkI,ToI,FromI); { Рекурсия }

End;

End;

BEGIN

{ Ввод }

Write('Количество колец = ');

ReadLn(N);

{ Решение }

MoveTown(N,1,3,2); {Первый вызов функции.}

END.

При n=3 в процессе работы программы на экране появятся последовательно сообщения:

Перенести кольцо 1 с иглы 1 на иглу 3

Перенести кольцо 2 с иглы 1 на иглу 2

Перенести кольцо 1 с иглы 3 на иглу 2

Перенести кольцо 3 с иглы 1 на иглу 3

Перенести кольцо 1 с иглы 2 на иглу 1

Перенести кольцо 2 с иглы 2 на иглу 3

Перенести кольцо 1 с иглы 1 на иглу 3

Главное требование к рекурсивным программам заключается в том, что вызов рекурсивной подпрограммы должен выполняться по условию, которое на каком-то вызове станет ложным. Когда оно станет ложным, начнётся рекурсивный возврат из подпрограммы.

Вопросы и задания.

1. Что называется рекурсией?
   
2. Какие программы называются рекурсивными?
   
3. Для данных четырёх натуральных чисел a, b, c, d найти наибольший общий делитель и наименьшее общее кратнае, воспользовавшись рекурсивной функцией нахождения НОД двух чисел.
   
4. Вывести на экран в обратном порядке цифры натурального числа N. При решении задачи использовать рекурсивную функцию..
   
5. Без циклов вывести натуральные числа от К до 1 и снова до К.
   
6. Написать рекурсивную программу нахождения суммы цифр заданного натурального числа.
   
7. Написать рекурсивную программу нахождения количества цифр заданного натурального числа.
   
8. Написать рекурсивную программу нахождения числа, которое образуется из данного натурального числа при записи его цифр в обратном порядке.
   

Для любознательных

Используя рекурсию подтвердите или опровергните следующие интересные свойства чисел Фибоначчи.

Квадрат любого числа F_n на единицу отличается от произведения F_n-1* F_n+1. Знак разности F_n² - F_n-1 * F_n+1 при переходе от n к n+1 изменяется на противоположный.

Для любых четырёх последовательных членов ряда Фибоначчи A, B, C и D справедливо соотношение C²–B²=A*D.

Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60. Если от каждого числа брать по две последние цифры, то они также образуют последовательность с периодом, равным 300.

Каждое третье число Фибоначчи делится на 2, каждое четвертое – на 3, каждое пятое – на 5, каждое шестое – на 8 и т.д., делители сами образуют ряд Фибоначчи.

Если не считать F₄=3, то всякое число Фибоначчи, которое простое, имеет простой индекс (например, число 253 простое, и индекс его, равный 13, также прост) К сожалению, обратное утверждение справедливо не всегда: простой индекс отнюдь не означает, что соответствующее число Фибоначчи простое. Первым примером служит F₁₉=4181. Индекс его прост, но само число разлагается на множители: 4181=37*113.

Единственным квадратом среди чисел Фибоначчи является F₁₂=144, причем его значение совпадает с квадратом индекса.

§28. Составление программ с использованием пользовательских процедур и функций.

Все хорошие принципы уже записаны.

Теперь нужно только использовать их.

( Б. Паскаль )

Пример 78. Что будет выведено на экран в результате работы программы?

Program Ех78;
Var a,b,c,d : Integer;
Function f ( Var b : Integer; c : Integer): Integer;
Var d : Integer;
Begin
        a:=2; b:=b+1; d:=3; c:=b-a;
        Writeln(a,b,c,d); f:=d;
End;
Begin
        a:=0; b:=0; c:=0; d:=0;
        d:=f(a,b); Writeln(a,b,c,d);
End.

В результате работы программы на экран будет выведено следующее:

3303

3003

разберёмся, откуда взялись эти числа.

Первоначально переменные принимают следующие значения:

a=b=c=d=0

Затем происходит вызов функции, которой передаются фактические параметры a и b, равные нулю.

Первая команда функции присваивает глобальной переменной а значение 2. автоматически изменяется значение локальной переменной b, оно тоже становится равным 2.

Следующая команда увеличивает это значение на единицу: B=3.

Переменная d тоже глобальная. Ей присваивается значение 3.

Значение переменной с равно нулю: 3-3=0.

Выдаём на экран число 3303.

Присваиваем функции значение 3.

Возвращаемся в основную программу.

Теперь значения переменных следующие: а=3, b=0, с=0, d=f(a,b)=3.

Выдаём на экран число 3003.

На этом программа заканчивает свою работу.

Как видите использование одинаковых имён локальных и глобальных переменных приводит к непредсказуемым результатам!

Пример 79. Среди трехзначных чисел найти такие, в которых сумма факториалов цифр равнялась бы самому числу.

program Ех79;

var a,b,c,i,s1,s2,s3:integer;

procedure fak(x:integer; var s:integer);

var j:integer;

begin

s:=1;

for j:=1 to x do s:=s*i;

end;

begin

for i:=100 to 999 do

begin

a:=i div 100;

b:=(i-a*100) div 10;

c:=i - a*100 - b*10;

fak (a,s1);

fak (b,s2);

fak (c,s3);

if s1+s2+s3=i then writeln (i);

end;

end.

Пример 80. рассмотрим работу программы с многократным вложенным вызовом функции:

Program Ех80;

var

s : integer;

function N(x : integer) : integer;

begin

N:=x*x

end;

begin

s:=N(N(3)+N(N(2)))

end.

Здесь используется следующий порядок вызовов функции N:

- вычисляется N(2);

- вычисляется N(результат от N(2));

- вычисляется N(3);

- суммируются значения, полученные в 2-х предыдущих пунктах;

- вычисляется N(результат из предыдущего пункта).

Пример 81. Вычислить значение суммы

S = 1/1! + 1/2! + ... + 1/k!

Решение. Можно, конечно, каждый раз вычислять очередное p!, затем 1/p!, и полученное слагаемое добавлять к сумме. Но обратим внимание на следующее очевидное равенство:

1/(p+1)! = (1/p!)/(p+1),

и процедура вычисления запишется следующим образом

function S (k : integer) : real;

var I,p:integer;

rez: real;

begin

rez:=1; p:=1; {rez = p = 1/1!}

for i:=2 to k do

begin
p:=p/i;
rez:=rez+p;
end;

S:=rez;

End;

Пример 82. Возвести число А в натуральную степень n за как можно меньшее количество умножений.

Решение. Можно, конечно, число A умножить само на себя n-1 раз, но для этого надо выполнить n-1 операцию умножения. Рассмотрим метод, требующий меньшего числа умножений (он, однако, не всегда дает минимальное число умножений).

Если n - четное (n=2m), то будем вычислять Aⁿ, используя тождество A^2m=(A^m)²; если же n=2m+1, то A^2m+1=(A^2m)*A=((A^m)²)*A. Таким образом, возведение A в 13 степень будет выглядеть следующим образом:

(A¹³)=((A⁶)²)*A=(((A³)²)²)*A=(((A*A*A)²)²)*A

и вычисление требует 5 операций умножения.

Используя данный метод, для возведения в степень n потребуется гораздо меньше операций умножения.

Программа на Паскале может выглядеть так:

program Ех82;

var A,N: integer;

function power(Х: integer): integer;

begin

if Х>1 then if odd(Х) {N нечетно?}

then power:=SQR(power(Х div 2))*A {Рекурсивный вызов}

else power:=SQR(power(Х div 2)) {функции}

else power:=A {Выход из рекурсии}

end;

begin

read(A,N);
writeln(power(N));
end.

Задания.

1. Вычислить значение выражения b=2.7^K+(a+1)⁵, используя функцию нахождения xⁿ (n - натуральное).
   
2. Найти количество чисел взаимно-простых с а на промежутке от 2 до а-1.
   
3. Выяснить является ли треугольник, заданный своими координатами вершин равносторонним. Поиск сторон осуществлять в функции.
   
4. Являются ли N натуральных введенных чисел простыми? Определение простое ли число осуществлять в функции.
   
5. Дан прямоугольник со сторонами a, b. Не используя циклы выяснить, на сколько квадратиков, длины сторон которых являются натуральными числами, можно разрезать данный прямоугольник, каждый раз отрезая квадрат максимально большей площади.
   
6. Составить программу для нахождения наибольшего общего делителя четырёх натуральных чисел
   
7. Составить программу для нахождения наименьшего общего кратного трёх натуральных чисел
   
8. Составить программу для нахождения суммы наименьшего и наибольшего из трёх чисел.
   
9. Составить программу для вычисления суммы факториалов всех нечётных чисел от 1 до 9.
   
10. даны две дроби 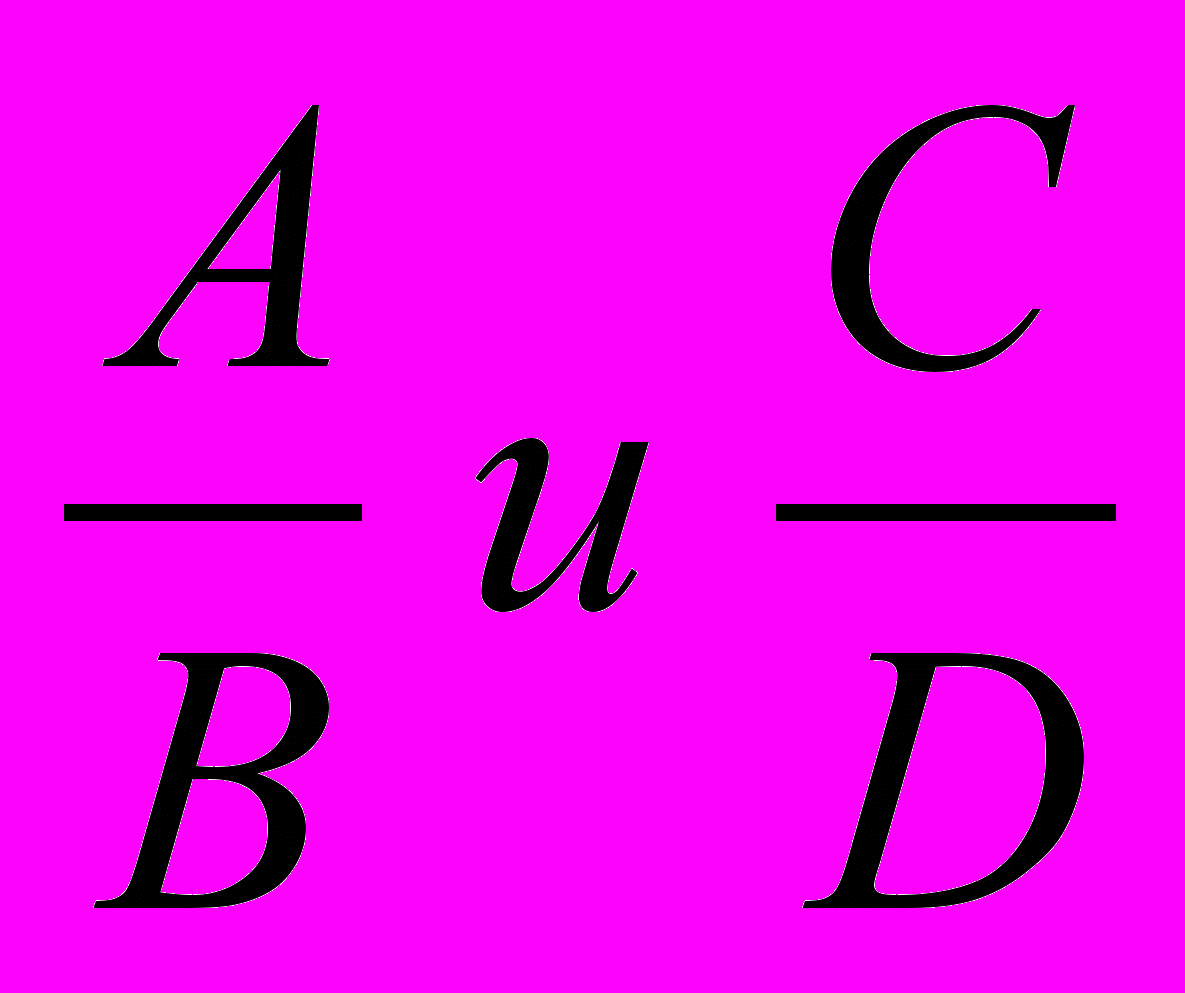(А, В, С, D —натуральные числа). Составить программу для деления дроби на дробь. Результат должен быть несократимой дробью.
    
11. даны две дроби 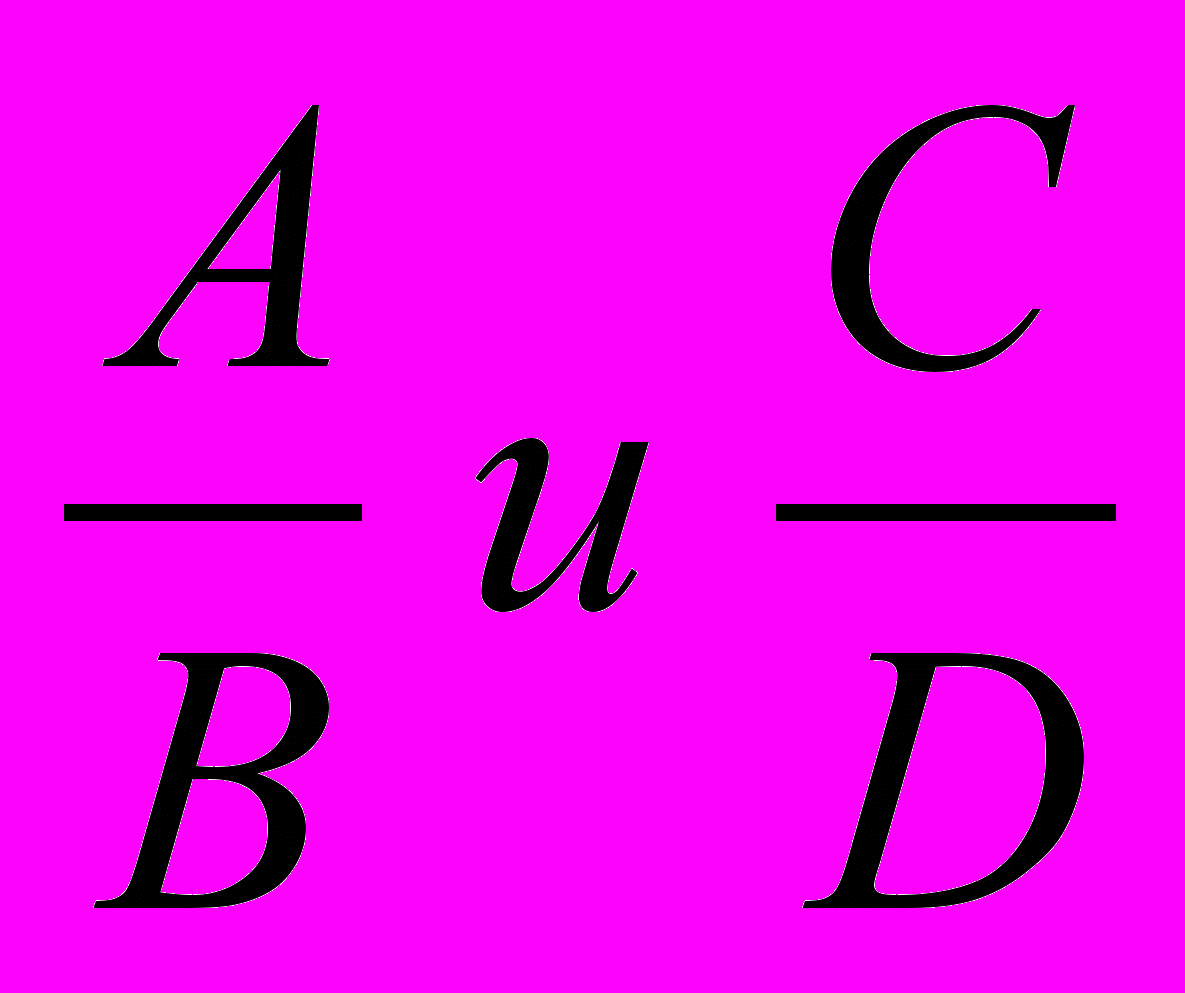(А, В, С, D —натуральные числа). Составить программу для умножения дроби на дробь. Результат должен быть несократимой дробью.
    
12. даны две дроби 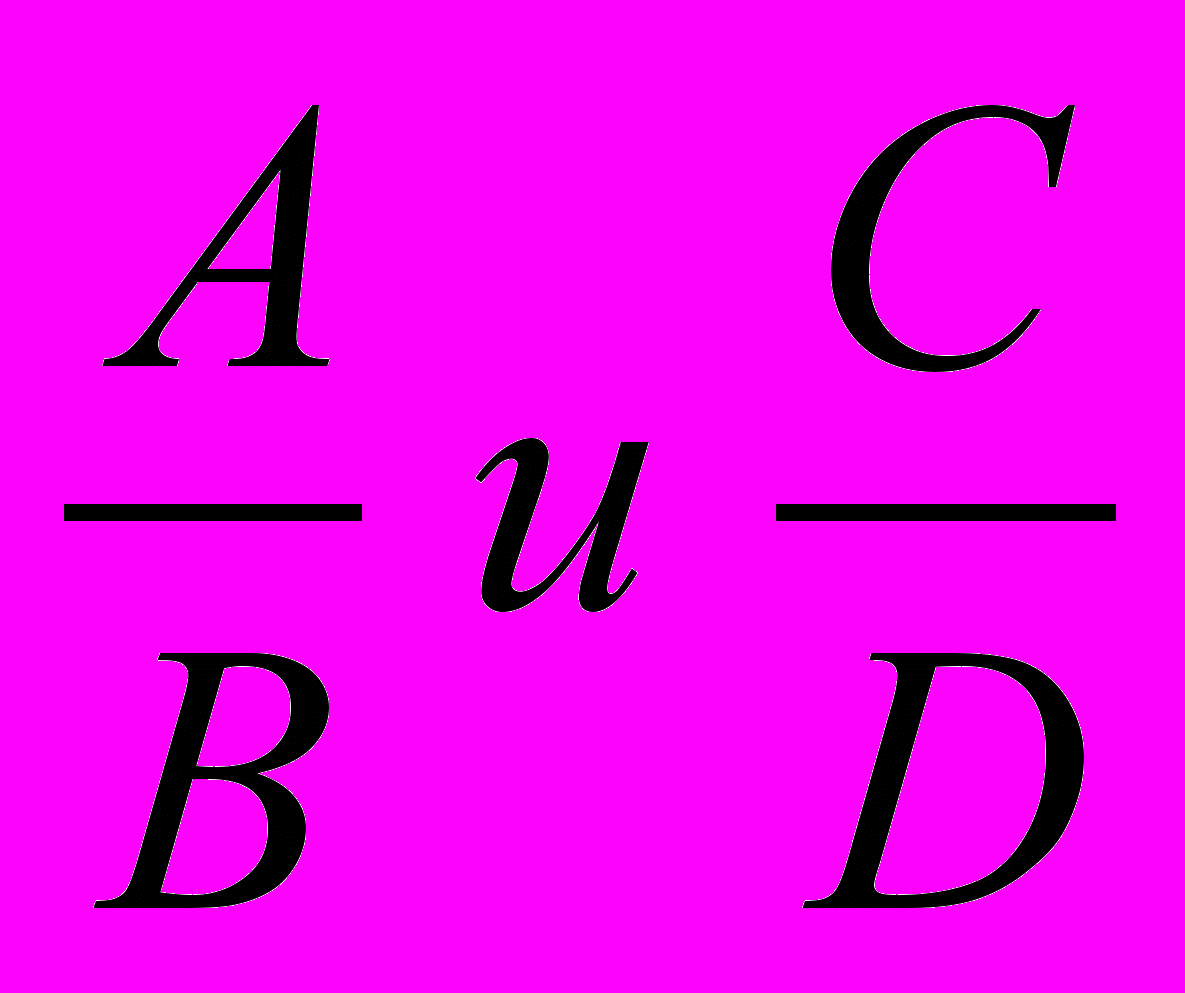(А, В, С, D —натуральные числа). Составить программу для вычитания из первой дроби второй. Результат должен быть несократимой дробью.
    
13. даны две дроби 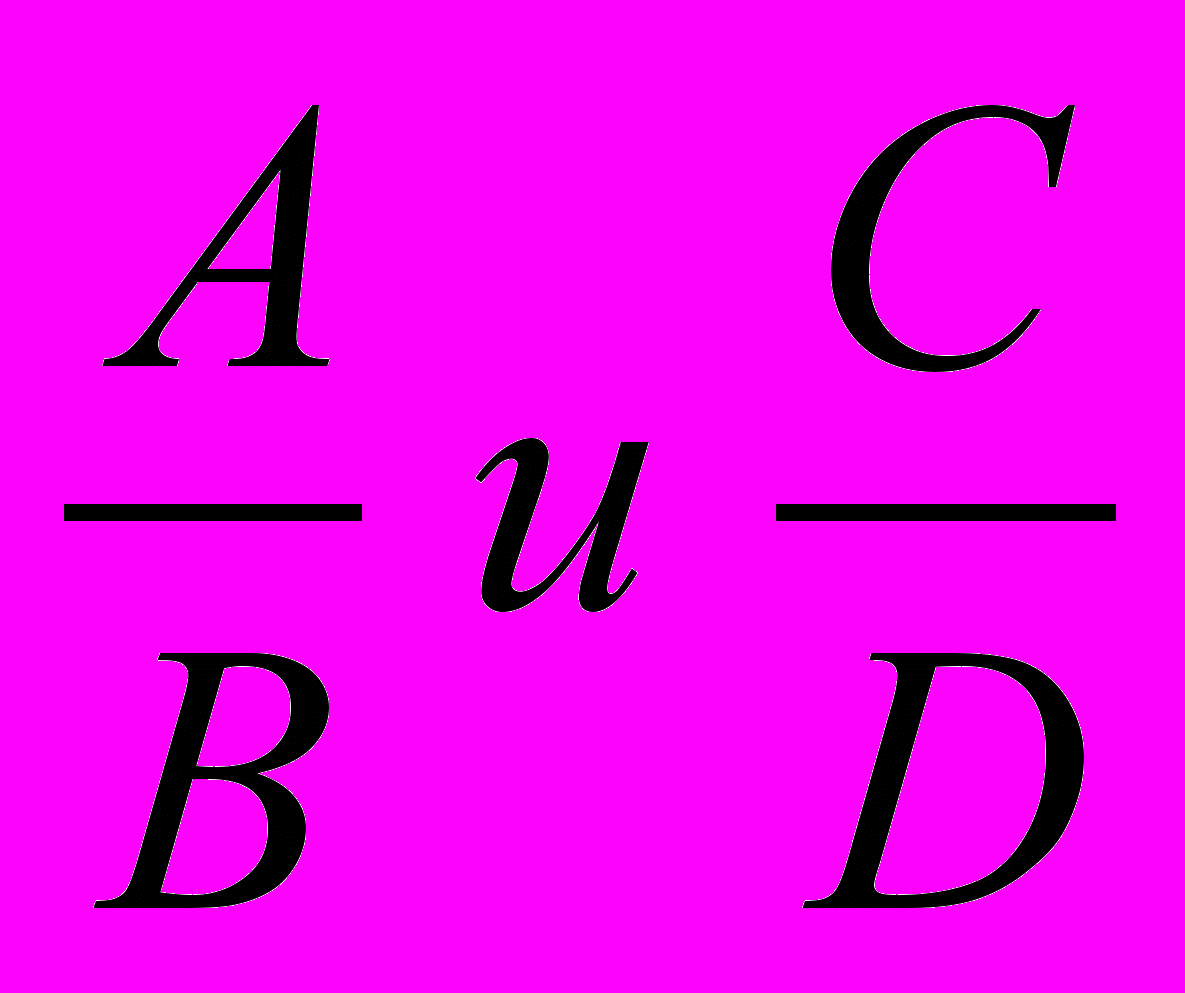(А, В, С, D —натуральные числа). Составить программу для сложения этих дробей. Результат должен быть несократимой дробью.
    

Следующие задачи решить, используя рекурсивную подпрограмму.

14. Найти сумму цифр натурального числа.
    
15. Подсчитать количество цифр в заданном натуральном числе.
    

§29. Основные принципы структурного программирования.

Структурное программирование – это дисциплина,

которую программист навязывает сам себе

(Э. Дейкстра)

29.1. Что такое структурное программирование? Программирование можно определить как «проектирование, кодирование и тестирование программы». Добавляя слово «структурное», можно сказать, что структурное программирование — это «проектирование, написание и тестирование программы в соответствии с зарание определённой дисциплиной». Структурное программирование включает три главные составляющие: последовательное построение алгоритма, модульное программирование, структурное кодирование.

Одна из целей структурного программирования — избавиться от плохой структуры программ. Другая цель — создавать программы, которые можно было бы понимать, сопровождать и модифицировать без участия авторов.

При реализации структурного подхода к программированию используют метод последовательного уточнения. Различают два подхода: уточнение сверху вниз и уточнение снизу вверх.

29.2. Ïîñëåäîâàòåëüíîå ïîñòðîåíèå àëãîðèòìà.

1) Ìåòîä ïîñëåäîâàòåëüíîãî óòî÷íåíèÿ ñâåðõó âíèç.

Метод вычленения вспомогательного алгоритма может быть успешно использован в процессе поиска и разработки нового алгоритма тогда, когда вспомогательный алгоритм ещё неизвестен.

Процесс последовательного построения алгоритма может выглядеть следующим образом. Алгоритм сначала формулируется в самых “крупных” командах, при этом в записи алгоритма могут использоваться команды, выходящие за рамки возможностей исполнителя. Затем на каждом последующем этапе отдельные детали алгоритма уточняются (детализируются), при этом недоступные исполнителю команды записываются как вызовы вспомогательных алгоритмов. После этого так же строятся вспомогательные алгоритмы. Процесс продолжается до тех пор, пока все алгоритмы не будут состоять из команд, понятных исполнителю. Такой способ построения алгоритма называется методом последовательного уточнения сверху вниз. Он лежит в основе структурного программирования. Его иногда называют методом пошаговой детализации.

2) Ìåòîä ïîñëåäîâàòåëüíîãî óòî÷íåíèÿ ñíèçó ââåðõ.

Он напоминает предыдущий метод, но процесс осуществляется в обратном порядке: сначала формируются вспомогательные алгоритмы низшего уровня, затем на порядок выше и т.д. до основного алгоритма.

Рассмотрим, как применяется метод пошаговой детализации на примере вычисления значения выражения:

.

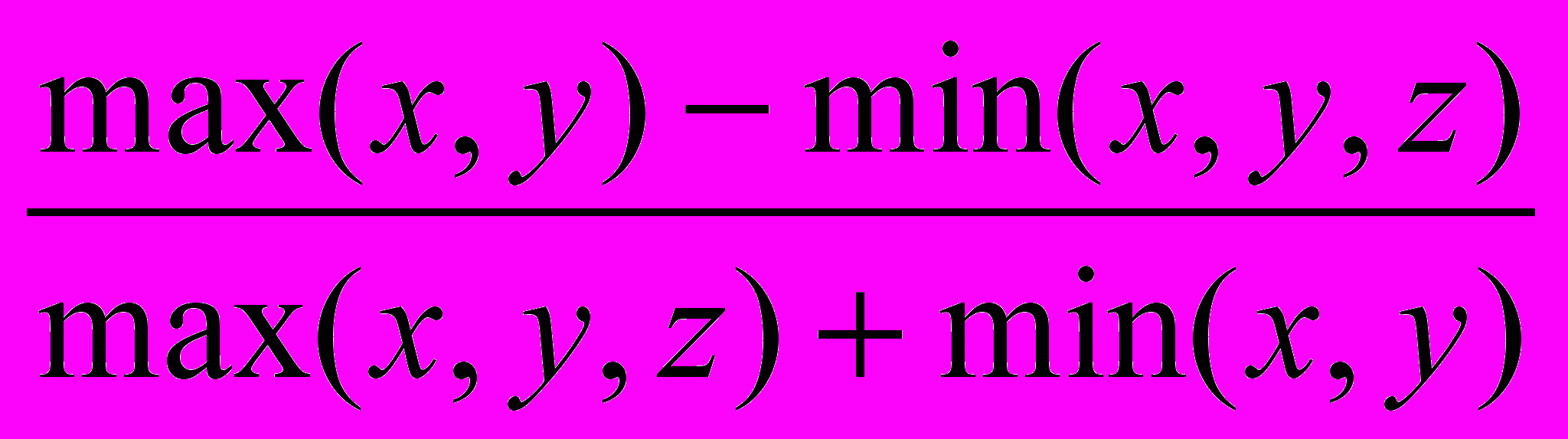В языке Паскаль отсутствуют функции нахождения максимального и минимального значения из заданных.

Покажем, как можно построить алгоритм, используя метод последовательного уточнения сверху вниз. Каждый новый этап будет последовательно уточнять предыдущий алгоритм.

I. Этап.

Вычислить значение выражения.

II. Этап.

Найти a=max(x,y).

Найти b=min(x,y,z).

Найти c=max(x,y,z).

Найти d=min(x,y).

Вычислить значение выражения (a-b)/(c+d).

III. Этап.

Найти a=max(x,y).

Найти b=min(min(x,y),z).

Найти c=max(max(x,y),z).

Найти d=min(x,y).

Вычислить значение выражения (a-b)/(c+d).

IV. Этап.

Функция max для двух чисел.

Функция min для двух чисел.

Найти a=max(x,y).

Найти b=min(min(x,y),z).

Найти c=max(max(x,y),z).

Найти d=min(x,y).

Вычислить значение выражения (a-b)/(c+d).

Осталось только описать вспомогательные подпрограммы.

V. Этап.

Функция max для двух чисел.

Если a>b то max:=a

Иначе max:=b

Конец функции

Функция min для двух чисел.

Если a
Иначе min:=b

Конец функции

Найти a=max(x,y).

Найти b=min(min(x,y),z).

Найти c=max(max(x,y),z).

Найти d=min(x,y).

Вычислить значение выражения (a-b)/(c+d).

29.3. Структурированные программы на языке Паскаль. Следующий этап структурного программирования — собственно написание программы, в основе которого лежит метод структурного кодирования. Этот метод позволяет получать программы более удобные для тестирования, модификации и использования. Он основан на принципе, что любая программа может быть написана с использованием ограниченного набора базисных структур. Эти структуры следующие:

1) последовательность двух или более операторов;

2) условный переход к одному из двух операторов (IF … THEN … ELSE …);

3) повторение операторов, пока условие истинно (WHILE).

К ним добавляют ещё:

4) повторение операторов пока условие ложно (REPEAT … UNTIL);

5) выбор из множества вариантов (CASE).

Написать структурированную программу на языке Паскаль не вызывает трудностей, поскольку он содержит все перечисленные структуры.

29.4. Стиль программирования. Может создаться впечатление, что поскольку программа будет обрабатываться машиной, то главное, чтобы она была правильной. В этом случае машина разберётся в программе, какой бы запутанной она ни была. Всё верно, кроме одного: всё же в первую очередь программы читаются людьми, разработчиками, пользователями и многими другими. И здесь уже на первое место выступает не просто правильность программы, но и её удобочитаемость.

Стиль программирования — это выражение опыта общения людей, занимающихся разработкой и использованием программ, опыта, выработанного в результате многолетней практики такого общения. Он включает в себя следующее:

1. Комментарии. Программы с комментариями значительно легче понимать и разбирать.
   
2. Выбор имён переменных. Правильный выбор имён переменных позволяет сделать программу гораздо понятнее, уменьшить число комментариев к ней.
   
3. Размещение операторов. От того как мы разместим операторы в программе, зависит наглядное восприятие программы. Для выявления структуры программы следует делать отступы разных уровней от левого края программы.
   

Вопросы и задания.

1. Что такое структурное программирование?
   
2. В чём состоит метод пошаговой детализации алгоритмов?
   
3. Написать программу вычисления значения выражения:
   

.
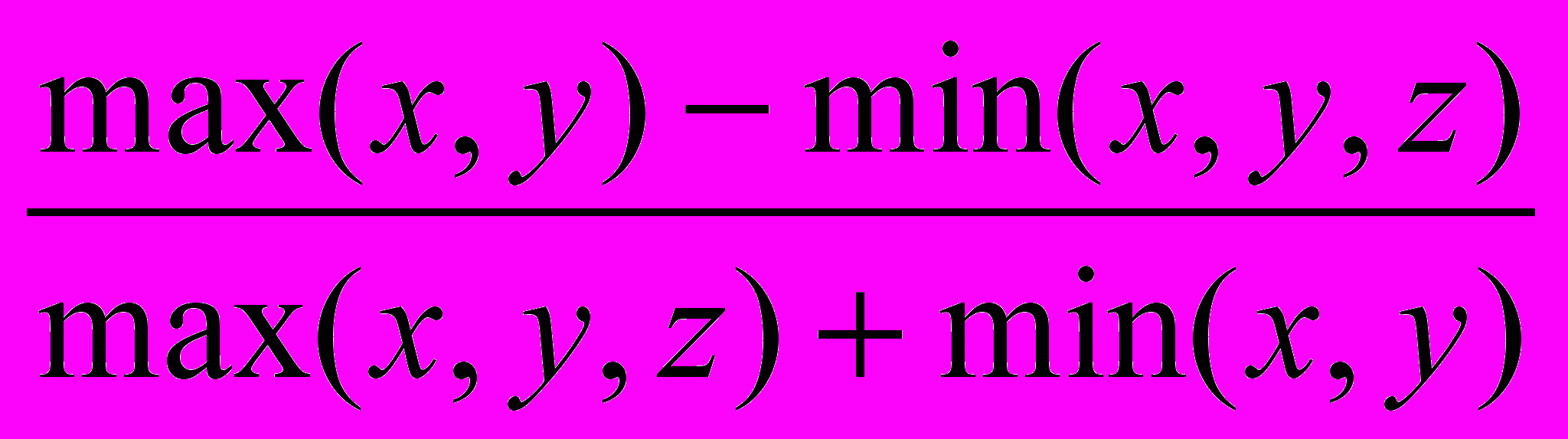