Предисловие дорогие друзья !
| Вид материала | Документы |
- К. Бальмонт Дорогие друзья, сегодня мы в гостях у замечательного русского поэта Константина, 164.76kb.
- Медникова Надежда Александровна учитель начальных классов моу «Уинская сош» Пермский, 91.48kb.
- И в шутку и всерьез Ведущий Добрый день, дорогие друзья! Вот и пришла весна, вот, 339.91kb.
- Играют 2 команды. Вопросы викторины, 53.15kb.
- Летние каникулы в праге, 322.16kb.
- Мои дорогие литературные друзья, 136.81kb.
- Ведущий: Дорогие, друзья! Разрешите поздравить вас с большим и дорогим для всех праздником, 124.29kb.
- Отчет о конференции 17-18 апреля дорогие друзья!, 182.44kb.
- Дорогие друзья и единомышленники, 134.05kb.
- Сценарий для 7-8 классов «Старая сказка на новый лад», 52.44kb.
ГЛАВА 7 АЛГОРИТМЫ ЦЕЛОЧИСЛЕННОЙ АРИФМЕТИКИ
§41. поиск делителей числа, простые и составные числа. Взаимнопростые числа.
Раньше теория чисел была классическим примером красивой, но совершенно бесполезной областью чистой математики. Сейчас же теоретико-числовые алгоритмы широко используются – прежде всего, в различных криптографических схемах, где нужны большие простые числа, а нахождение простых чисел связано с понятием делимости натуральных чисел.
41.1. Делители и кратные. 20 яблок можно разделить поровну между 4 ребятами. Каждый получит по 5 яблок. А если надо разделить (не разрезая) 20 яблок между 6 ребятами, то каждый получит по 3 яблока, а ещё 2 яблока останутся. Говорят, что число 4 является делителем числа 20, а число 6 не является делителем числа 20.
делителем натурального числа a называют натуральное число, на которое а делится без остатка. В этом случае число a представимо в виде произведения
a= k*d,
где k — натуральное число. говорят, что число а делится без остатка на число d, или, короче, число а делится на число d. Из формулы следует, что число а также делится на число k, т.е. k — делитель числа а. Выражения ” d является делителем a “, “a делится на d “, “ a кратно d “ являются синонимами. Обычно перечисляют только положительные делители, например, делители числа 36 (их девять) – это числа 1, 2, 3, 4, 6, 9, 12, 18 и само число 36; а число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12.
число 1 является делителем любого натурального числа.
Числа, делящиеся без остатка на 2, называют чётными, а числа, которые при делении на 2 дают остаток 1, называют нечётными. Из однозначных чисел числа 0, 2, 4, 6 и 8 чётны, а числа 1, 3, 5, 7 и 9 нечётны. Поэтому и цифры 0, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9 — нечётными.
Любое натуральное число чётно лишь в том случае, когда в разряде единиц стоит чётная цифра, и нечётно, когда в разряде единиц стоит нечётная цифра. Например, числа 60, 84, 196 чётные, а числа 3, 57, 185 нечётные.
Пусть на столе лежат пачки печенья, в каждой из которых по 8 печений. Не раскрывая пачек, можно взять 8 печений, 16 печений, 24 печенья, а 18 печений так взять нельзя. Числа 8, 16, 24 делятся на 8, а 18 на 8 не делится. Говорят, что числа 8, 16, 24 кратны числу 8, число 18 не кратно числу 8.
Кратным натуральному числу а называют натуральное число, которое делится без остатка а.
Любое натуральное число имеет бесконечно много кратных. Например, первые пять чисел, кратных 8, такие: 8, 16, 24, 32, 40. наименьшим из кратных натурального числа является само это число.
Для определения кратности чисел пользуются следующим свойством: если число а делится на число b, то остаток от деления равен 0. Поэтому достаточно проверить остаток от деления числа а на число b:
If a mod b = 0 then Writeln(a,’ делится на ’,b)
Else Writeln(a,’ не делится на ’,b);
41.2. Простые и составные числа. Число 17 делится только на 1 и само на себя. Другими словами, число 17 имеет только два делителя: 1 и 17. У числа 12 шесть делителей: 1, 2, 3, 4, 6 и 12. число 25 имеет три делителя: 1, 5 и 25.
Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число. Натуральное число называют составным, если оно имеет более двух делителей.
Число 1 имеет лишь один делитель: само это число. Поэтому его не относят ни к простым, ни к составным числам. Наименьшим простым числом является число 2. Это единственное чётное простое число. Остальные простые числа являются нечётными. Первыми десятью простыми числами являются 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Число 78 составное, потому что, кроме 1 и 78, оно делится, например, ещё на 2. Так как 78:2=39, то 78=2·39. Говорят, что число 78 разложено на множители 2 и 39. Любое составное число можно разложить на два множителя, каждый из которых больше 1. простое число так разложить на множители нельзя.
Для того чтобы найти все делители числа a>1, нужно попытаться делить данное число на все отличные от 1 числа, меньшие данного. Если число не разделилось ни на одно из них, то оно является простым.
Запишем процедуру нахождения всех делителей числа. Массив В будем использовать для хранения делителей числа а, количество делителей будем хранить в нулевой ячейке массива В. Сначала поместим в массив единицу и само число.
TYPE MAS=ARRAY [0..100] OF INTEGER
Procedure Deliteli(a: integer; Var B: mas);
Var i: integer;
Begin
Fillchar(B,sizeof(B),0); {«Обнуляем» массив делителей}
B[1]:=1;B[2]:=a;
B[0]:=2;
For i:=2 to a-1 do
If a mod i = 0 then {Если I — делитель числа, то}
Begin
Inc(B[0]); {Увеличиваем счётчик делителей}
B[B[0]]:=i; {сохраняем делитель}
End;
После выполнения алгоритма в нулевой ячейке массива В будет находиться количество делителей, а в последующих ячейках будут находиться все делители числа а.
Если учесть тот факт, что делитель не может превышать а div 2, то это ускорит работу программы в два раза.
Если требуется только определить, простое число или составное то можно улучшить алгоритм. В самом деле, цикл для i от 2 до а-1 выполняется а-2 раза. Однако для проверки простоты числа а достаточно выполнить данный цикл
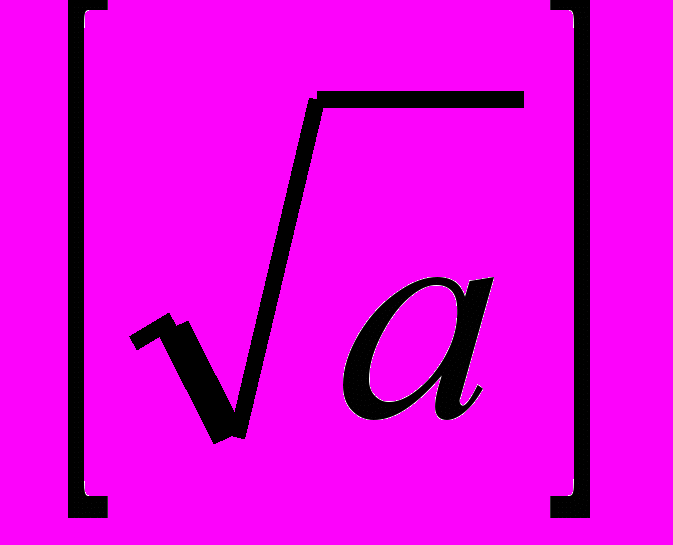 раз (
раз (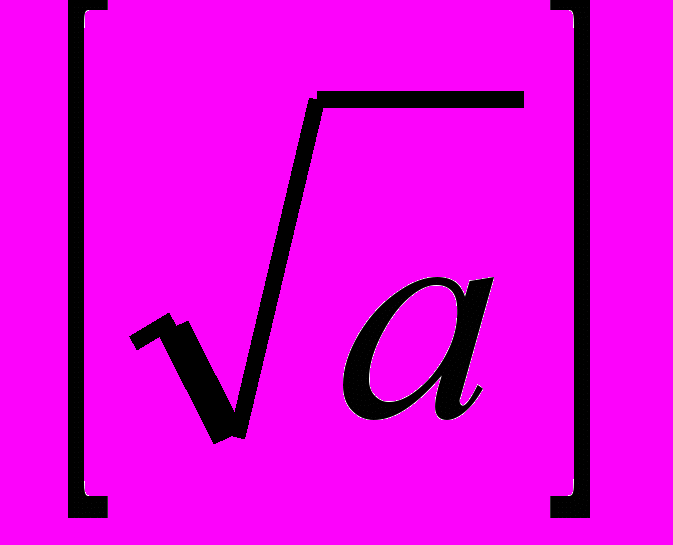 — целая часть от корня квадратного из а). это вытекает из следующих соображений: если а число составное, его можно представить в виде а=bc, где
— целая часть от корня квадратного из а). это вытекает из следующих соображений: если а число составное, его можно представить в виде а=bc, где 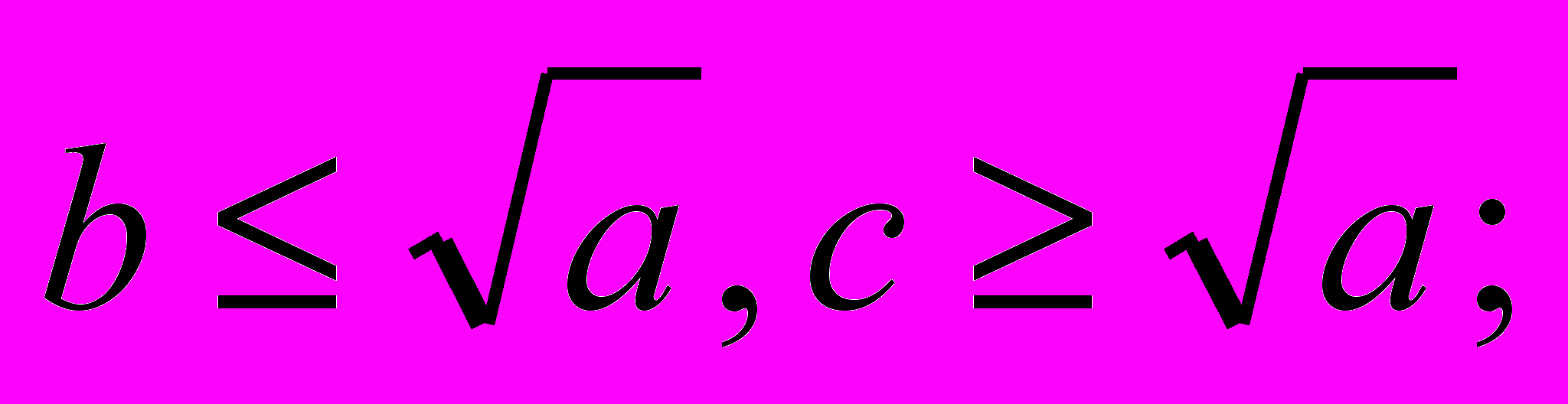 если а делится на b, то оно будет делиться и на с; если а не делится ни на одно число меньшее или равное
если а делится на b, то оно будет делиться и на с; если а не делится ни на одно число меньшее или равное 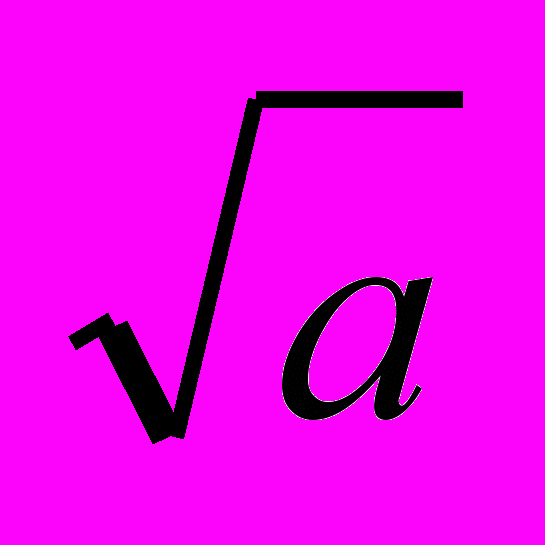 , то оно не будет делиться ни на какое другое число. Запишем функцию, определяющую простое число или нет:
, то оно не будет делиться ни на какое другое число. Запишем функцию, определяющую простое число или нет:Function Prostoe(a: integer): Boolean;
Var d: integer;
P: Boolean;
Begin
d:=2; {Первый делитель числа}
P:= false; {Признак простого числа}
While (d*d<=a) and (a mod d<>0) do d:=d+1;
If (d*d>a) and (a<>1) then P:=true;
Prostoe:=P;
End;
Древнегреческий математик Евклид в своей книге «Начала» доказал, что простых чисел бесконечно много, т.е. за каждым простым числом есть ещё большее простое число.
Для отыскания простых чисел другой греческий математик — Эратосфен придумал такой способ. Он записывал все числа от 1 до какого-то числа, а потом вычёркивал единицу, которая не является ни простым, ни составным числом. Следующее число 2, это простое число. Оставляем его и вычёркиваем все числа кратные 2. Для этого достаточно вычеркнуть каждое второе число, начиная счёт с 3. Первым невычеркнутым числом будет 3. Это простое число. Оставляем его и вычёркиваем все числа, кратные 3, т.е. каждое третье число, начиная счёт с 4. (При счёте необходимо учитывать и ранее вычеркнутые числа, поэтому некоторые числа вычёркиваются второй раз). После этой операции первым невычеркнутым, а значит простым, будет число 5. Оставляем это число и вычёркиваем все числа, кратные 5, т.е. каждое пятое число, начиная счёт с 6. Затем переходим к следующему невычеркнутому числу 7 и т.д. В конце концов оставались невычеркнутыми лишь простые числа:
| | 2 | 3 | | 5 | | 7 | | | |
| 11 | | 13 | | | | 17 | | 19 | |
| | | 23 | | | | | | 29 | |
| 31 | | | | | | 37 | | | |
| 41 | | 43 | | | | 47 | | | |
| | | 53 | | | | | | 59 | |
Так как греки делали записи на покрытых воском табличках или на натянутом папирусе, а числа не вычёркивали, а выкалывали острой палочкой (стилом), то таблица в конце вычислений напоминала решето. Поэтому метод Эратосфена называют решетом Эратосфена: в этом решете «отсеиваются» простые числа от составных.
Запишем фрагмент программы для поиска первых N простых чисел, пользуясь описанным методом. Для хранения чисел создадим массив B[1..N]. Сначала занесём в него число 2 и все нечётные числа, так как все чётные, кроме числа 2, являются составными. Затем будем заменять нулями все числа, кратные 3. После этого найдём первое ненулевое число после числа 3, и будем заменять нулями все числа кратные ему. Так продолжаем до тех пор, пока не просмотрим весь массив.
фрагмент программы выглядит так:
B[1]:=2;
N:=(n+1) div 2;
For i:=2 to n do B[i]:=2*i-1; {первоначальное заполнение массива}
J:=2;
While j<=n do begin
I:= j+B[j]; {индекс первого обнуляемого}
While i<=n do begin {обнуление чисел, кратных текущему}
B[i]:=0;
I:=i+B[j];
End;
Inc(j);
While (B[j]=0)and(j<=n) do{ поиск очередного ненулевого числа}
Inc(j);
End;
Этот алгоритм работает достаточно быстро, но для хранения чисел требуется слишком большой массив.
Улучшенный алгоритм работает дольше, но для его работы требуется массив меньшего размера, так как в массив будут заноситься только простые числа. Вначале в массив поместим число 2. Рассматривая очередное нечётное число, будем делить его на предшествующие ему простые числа. И если ни на одно из предшествующих простых чисел текущее не делится, то оно само является простым.
B[1]:=2;j:=2;i:=3;
While i<=n do begin
K:=1;
D: =trunc(sqrt(i))+1);
while (B[k]<=d) and(i mod B[k]<>0) and(k
inc(k);
if B[k]>d then
begin
B[j]:=i;
inc(j);
end;
i:=i+2;
end;
41.3. Взаимнопростые числа. Найдём наибольший общий делитель чисел 24 и 35 (как это делается, описано в §20, пример 47). Видим, что НОД(24, 35)=1.
натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Запишем функцию проверки, являются ли два числа взаимнопростыми или нет:
Function Vz_pr(n, m:integer): Boolean
Var Nod : integer;
Begin
While n<>m Do
If n>m Then N:=n - m Else M:= m - n ;
If n=1 Then Vz_pr:=TRUE Else Vz_pr:=FALSE;
End;
Вопросы и задания.
- Определить, является ли данное число чётным.
- Два натуральных числа называются дружественными, если каждое из них равно сумме всех делителей другого, кроме самого этого числа. Найти все пары дружественных чисел, лежащих в диапазоне от n до k.
- Найти натуральное число из диапазона от n до k, которое имеет наибольшее количество делителей.
- Разложить дробь p/q на сумму дробей вида 1/n. Например, при p=3, q=7
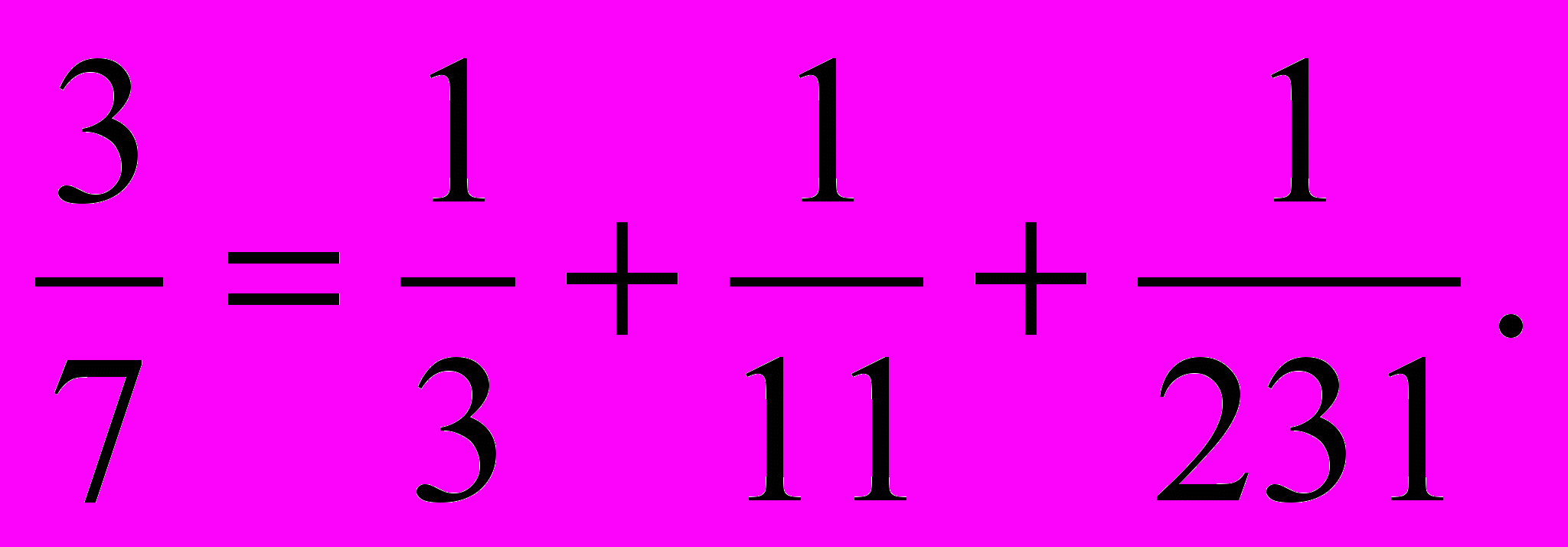
- Найти все совершенные числа, меньшие N. Число совершенно, если оно равно сумме своих делителей, за исключением самого числа (например, 6=1+2+3).
- Любую целочисленную денежную сумму, большую 7 р., можно выплатить без сдачи трёшками и пятёрками (докажите). Для данного n>7 найти все такие целые неотрицательные a и b, что 3a+5b=n.
- Сообщество роботов живёт по следующим законам:
- один раз в начале года они объединяются в группы по 3 или по 5 роботов;
- за год группа из 3 роботов собирает 5 новых, а группа из 5 роботов собирает 9 новых;
- роботы объединяются так, чтобы собрать за год наибольшее количество роботов; каждый робот живёт 3 года после сборки.
Известно начальное количество роботов. Все они только что собраны. Сколько роботов будет через N лет?
- Два двузначных числа, записанных одно за другим, образуют четырёхзначное число, которое делится на их произведение. Найти эти числа.
- Найти натуральные числа из отрезка [n; k], количество делителей у которых является произведением двух простых чисел.
- Дано натуральное число n. Найти четвёрки простых чисел меньших n, принадлежащих одному десятку (например, 11, 13, 17, 19).
- Дано натуральное число n. Выяснить, имеются ли среди чисел n, n+1, …, 2*n числа-близнецы, т.е. простые числа, разность между которыми равна 2.
§42. разложение натурального числа на простые множители.
Ч
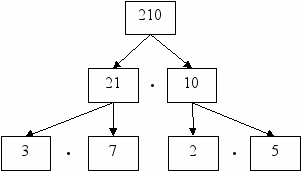
исло 210 является произведением чисел 21 и 10. Значит, 210=21·10. Числа 21 и 10 составные. Их тоже можно представить в виде произведения: 21=3·7, 10=2·5. Получаем: 210=3·7·2·5. теперь в произведении 3·7·2·5 все множители — простые числа. Таким образом, число 210 разложено на простые множители:
Число 210 можно разложить на простые множители иным способом: 210=30·7=10·3·7=5·2·3·7. Получились те же самые множители, только записанные в другом порядке. Обычно записывают множители в порядке их возрастания: 210=2·3·5·7.
Всякое составное число можно разложить на простые множители. При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.
Запишем фрагмент программы, осуществляющий разложение числа на простые множители. Алгоритм разложения будет следующим. Данное число будем делить сначала на 2, а затем только на нечётные числа. Если какое-то нечётное число является составным, то число а на него не разделится (так как а уже разделилось на простые числа, произведение которых равно данному, и они меньше данного). Простые множители будем хранить в массиве В, k — номер текущего простого множителя, d — число на которое делим.
K:=0;
d:=2;
while a>1 do
if a mod d=0 then {Если а делится на d, то}
begin
inc(k); {увеличиваем счётчик}
B[k]:=d; {сохраняем очередной простой делитель}
A:=a div d; {делим число а на простой делитель d}
End
Else {иначе (если а не делится на d)}
If d=2 then inc (d) {и если d=2, то увеличим d на 1}
Else inc(d,2); {если же d2, то увеличиваем d на 2 (получаем следующее нечётное число)}
после выполнения программы первые k элементов массива В будут содержать простые числа, произведение которых равно а.
В разложении числа на простые множители могут быть равные числа. Например: 360=2·2·2·3·3·5. Объединяя равные множители, получим: 360=23·32·5. Произведение в правой части равенства называют каноническим разложением натурального числа.
В общем виде имеем формулу вида
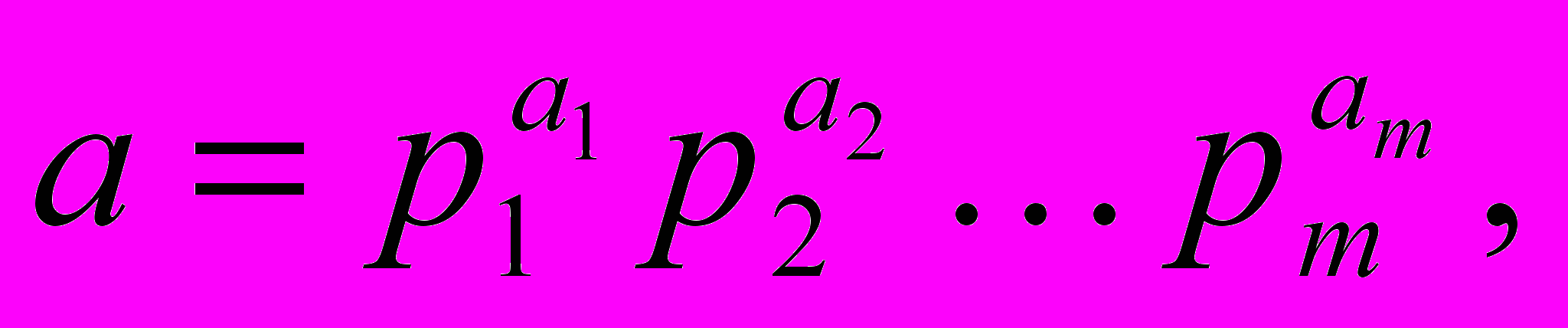
где pi —различные простые числа, а ai — некоторые натуральные числа.
вопросы и задания.
- Измените программу разложения на простые множители, чтобы она находила все простые делители числа (p1, p2, … pm).
- Вывести в порядке возрастания натуральные числа до 1000, которые имеют из простых делителей только числа 2, 3 или 5. Вывести также количество найденных чисел.
- Дано число. Вывести на экран его каноническое разложение.
- Дано четное натуральное число N. Верно ли, что предыдущее и последующее ему числа являются простыми.
- Среди простых чисел, не превосходящих n, найдите такие числа, в двоичной записи которых содержится максимальное количество единиц.
§43. Представление чисел. выделение цифр числа.
43.1. Представление чисел. В десятичной системе счисления любое натуральное число может быть записано в виде суммы разрядных слагаемых, т.е. в виде суммы единиц, десятков, сотен, тысяч и т.д. Например, 6487=61000+4100+810+7.
цифры 6, 4, 8, 7 являются цифрами числа 6487, а 1000, 100, 10 — это разрядные единицы. Каждая разрядная единица является степенью числа 10, поэтому представление чисел в виде суммы разрядных слагаемых чаще записывают так: 6487=6103+4102+8101+7100. Вид числа в левой части равенства будем называть обычным представлением числа в десятичной форме. При написании программ такие числа хранятся в стандартных величинах числовых типов. При работе с числами в обычном представлении мы не имеем возможности непосредственно обращаться к цифрам этого числа, однако иногда это бывает необходимо. Например, если требуется произвести некоторые действия с цифрами числа, то число представляют в виде массива цифр. Такое представление будем называть табличным представлением числа.
Размещение цифр числа в массиве возможно двумя способами. Связано это с тем, что разряды чисел нумеруются справо налево, а число читается слева направо, поэтому цифры числа можно располагать в массиве, начиная с первой (старший разряд), а можно — начиная с последней (младший разряд). Порядок, при котором цифра старшего разряда является первым элементом массива, назовём прямым. Обратным назовём порядок, при котором первый элемент в массиве является цифрой младшего разряда.
Можно задавать число и как литерную величину, тогда мы получим доступ к каждой отдельной цифре, однако с ними, без преобразования в числовой тип, нельзя выполнять арифметические операции.
Рассмотрим способы преобразования обычного представления числа в табличное и наоборот.
43.2. Преобразование числа из обычного представления в табличное. пусть задано число в обычном представлении, необходимо получить табличное представление данного числа.
как видно из представления числа в виде суммы разрядных слагаемых, каждое слагаемое, кроме последнего, разделится на 10 без остатка. Поэтому остаток от деления числа на 10 будет равен последней цифре числа. Эту цифру мы помещаем в массив. Если мы размещаем в массиве цифры числа, начиная с последней, то первому элементу массива присваивается значение полученной цифры. Если размещаем цифры, начиная с первой, то полученную цифру помещаем в элемент массива с индексом, равным количеству цифр в числе (количество цифр необходимо подсчитать до того, как начнём получать сами цифры). Далее находим целую часть от деления исходного числа на 10 (или, говоря другими словами, отбрасываем последнюю цифру числа) и снова находим остаток от деления полученного числа на 10, это и будет следующая цифра. Так продолжается до тех пор, пока в числе не останется ни одной цифры.
Данный алгоритм размещает цифры числа в массив в обратном порядке. Для хранения цифр числа N будем использовать массив В, k — номер текущей цифры в массиве В.
K:=0;
While N>0 do {Пока число содержит цифры}
Begin
Inc(k); {Указатель на след.свобод. ячейку}
B[k]:=N mod 10; {Помещаем цифру в массив}
N:=N div 10; {Отбрасываем цифру}
End;
первые k элементов массива В содержат цифры числа N, записанные в обратном порядке.
Изменим алгоритм для получения цифр числа в прямом порядке.
K:=0;
N1:=N; {Сохраняем значение аргумента}
While N>0 do {Пока число содержит цифры}
Begin
Inc(k); {Считаем цифру }
N:=N div 10; {Отбрасываем цифру}
End;
M:=K; {Сохраняем количество цифр}
N:=N1; {Восстанавливаем значение аргумента}
While N>0 do {Пока число содержит цифры}
Begin
B[k]:=N mod 10; {Помещаем цифру в массив}
N:=N div 10; {Отбрасываем цифру}
dec(k); {Указатель на следующую свободную ячейку}
End;
Первый цикл WHILE считает количество цифр в числе, второй — получает цифры числа. Переменная N1 служит для того, чтобы сохранить значение исходного числа, так как внутри циклов переменная изменяет своё значение. Если бы не было восстановлено значение переменной N1, то второй цикл не выполнился бы ни разу (так как значение N1 равнялось бы 0). В переменной m сохраняется количество цифр числа, что, вообще говоря, не всегда обязательно.
43.3. Преобразование табличного представления числа в обычное. решим обратную задачу, т.е. получим обычное представление числа из табличного.
Пусть некоторое число а задано своими цифрами:
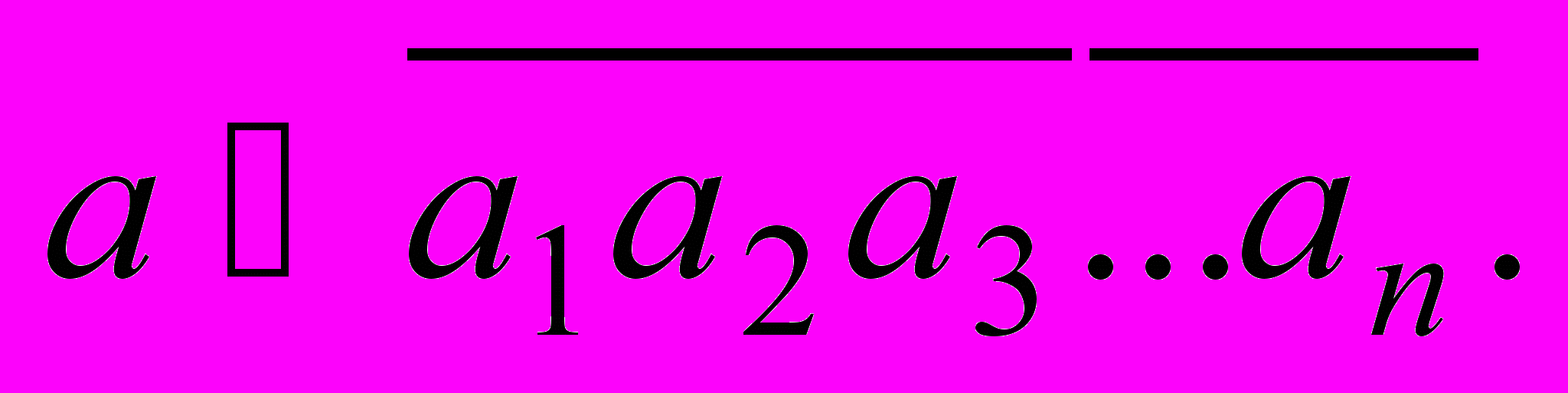
черта сверху означает, что а1, а2, а3, …, аn — цифры числа а (а1 — цифра старшего разряда). Запишем это число в виде суммы разрядных слагаемых:
а= а110n-1+а210n-2+а310n-3+ …+аn-110+аn.
для того чтобы получить значение числа а, необходимо вычислить значение выражения, стоящего в правой части равенства. Для этого проделаем следующее преобразования: вынесем 10 за скобки из тех слагаемых, для которых это возможно. Продолжим действовать таким образом до тех пор, пока это будет возможно:
а=а110n-1+а210n-2+а310n-3+…+аn-110+аn = 10(а110n-2+а210n-3+а310n-4, …, аn-1)+аn =
=10(10(а110n-3+а210n-4+а310n-5+…)+аn-1)+аn=…=10(10…(10(а110+а2)+ а3)+…+аn-1)+аn.
теперь для вычисления значения числа а достаточно:
- первую цифру числа умножить на 10 и к произведению прибавить вторую цифру;
- полученную сумму умножиить на 10 и прибавить следующую цифру;
- пункт 2) выполнять до тех пор, пока не используем все заданные цифры числа.
Описанный выше алгоритм называется схемой Горнера. Работа алгоритма рассмотрена для случая, когда цифры числа расположены в массиве в обратном (а1 — цифра младшего разряда) порядке.
Число будем получать в переменной а. цифры числа хранятся в массиве В (элемент В[1] содержит цифру младшего разряда).
A:=0;
For i:=k downto 1 do A:=A*10+B[i];
для получения числа а, цифры которого заданы в прямом порядке (а1 — цифра старшего разряда), можно воспользоваться схемой Горнера, начиная обработку с первого элемента массива.
A:=0;
For i:=1 to k do
A:=A*10+B[i];
Можно воспользоваться и другим алгоритмом. Каждая цифра должна умножаться на соответствующую ей разрядную единицу: первая — на 1, вторая — на 10, третья — на 100 и т.д. каждая следующая разрядная единица в 10 раз больше предыдущей. Число а будем накапливать следующим образом: будем брать очередную цифру, умножать её на соответствующую ей разрядную единицу и прибавлять полученное произведение к уже накопленному числу. Разрядную единицу увеличим в 10 раз. Так продолжаем до тех пор, пока не используем все цифры числа.
В переменной r будем хранить значение разрядной единицы, цифры числа будем хранить в массиве В.
A:=0;R:=1;
For i:=1 to k do
Begin
A:=A+B[i]*R;
R:=R*10;
End;
Этот алгоритм для случая, когда цифры заданы в обратном порядке.
A:=0;
For i:=1 to k do
Begin
A:=A*10+B[i];
End;
А этот алгоритм для случая, когда цифры заданы в прямом порядке.
43.4. Работа с «длинными» числами. Диапазон представления целых чисел (Integer, Word, LongInt) ограничен, о чем не раз уже говорилось (впрочем, для действительных величин это замечание тоже актуально). Поэтому при решении задач всегда приходится действовать с оглядкой, — как бы не допустить возникновения ошибки выхода за диапазон или переполнения. Например, вычисляя факториал (n! = 1 * 2 * 3 * … * n), в диапазоне представления величин типа Integer удастся правильно получить только 7! = 5040, а в диапазоне представления типа LongInt — 12! = 479001600. Для больших значений, конечно, можно использовать действительные типы данных, но это уже не гарантирует точного результата. Поэтому полезно для получения точных значений при действиях с многозначными числами разработать другие способы представления таких чисел, алгоритмы выполнения арифметических и других операций, процедуры ввода и вывода результатов и т.д.
Для решения задач необходимо уметь выполнять следующие действия:
1) ввод "длинного" числа;
2) собственно действия над двумя "длинными" числами;
3) вывод "длинного" числа;
4) определение количества цифр в записи числа.
Каждую из подзадач реализуем в виде отдельной подпрограммы. Начнем с ввода. Наиболее естественным способом представления многозначного числа является запись каждого его разряда в виде отдельного элемента линейного массива. Пока мы имели дело с числами. Если же вводимое число длиннее допустимых размеров, его необходимо вводить как строку и затем преобразовать в таблицу.
Пример 124. Написать программу ввода длинного числа и вывода его в массив.
Решение. В представленной программе преобразование числа, введённого как строка, осуществляется в процедуре PR с помощью оператора CASE. Это не самое оптимальное решение, но зато самое наглядное. Символы, соответствующие цифрам, преобразуются в цифры числа и записываются в массив.
Вывод полученного массива цифр осуществляется прямо в основной программе с помощью цикла FOR.
program Ex124;
type mas=array[0..1000] of integer;
var a:mas;
i:integer;
s:string;
f1,f2:text;
procedure pr(n:string;var a:mas);
var i,j:integer; k:longint;
begin
fillchar(a,sizeof(a),0);
j:=0; {так как число записывается в обратном порядке, то j указывает в какую ячейку пишем цифру}
k:=length(n);
a[0]:=k; {количество цифр храним в нулевой ячейке}
for i:=k downto 1 do
case n[i] of {другой вариант преобразования — воспользоваться кодами}
'1': begin inc(j);a[j]:=1;end; {символов и функцией ORD,}
'2': begin inc(j);a[j]:=2;end; {но на наш взгляд представленный способ более наглядный}
'3': begin inc(j);a[j]:=3;end;
'4': begin inc(j);a[j]:=4;end;
'5': begin inc(j);a[j]:=5;end;
'6': begin inc(j);a[j]:=6;end;
'7': begin inc(j);a[j]:=7;end;
'8': begin inc(j);a[j]:=8;end;
'9': begin inc(j);a[j]:=9;end;
'0': begin inc(j);a[j]:=0;end;
end;
end;
begin
assign(f1,'input.txt');
assign(f2,'output.txt');
reset(f1);
rewrite(f2);
readln(f1,s);
pr(s,a);
for i:=a[0] downto 1 do {Вывод массива цифр в файл}
write(f2,a[i]);
Close(f2);
End.
Вместо оператора Case в процедуре PR, преобразования числа из строки символов в массив разрядов, можно использовать процедуру VAL:
…
For i:=k downto 1 do
Begin
Val(n[i],a[j],cod);
If cod=0 Then Inc(j);
End;
…
Таким образом, длинное число записано в массив, где впереди (в качестве элементов с большими номерами) стоят незначащие нули. При выполнении действий и выводе ответа они не учитываются. Нулевой разряд массива содержит количество значащих цифр.
Вопросы и задания.
- Какой порядок расположения цифр числа в массиве называется прямым? Какой обратным?
- Как получить цифры числа в обратном порядке? В прямом порядке?
- Как получить число из массива цифр?
- Что такое схема Горнера?
- Дано натуральное число N. Чему равна сумма его цифр? (Число может быть очень большим.)
- Дано натуральное число N. Верно ли, что сумма его цифр является нечётной (чётной)? (Число может быть очень большим.)
- Дано натуральное число N. Верно ли, что это число содержит ровно К одинаковых цифр? Если да, то укажите эти цифры. (Число может быть очень большим.)
- Дано натуральное число N. Сколько раз в нём встречается самая большая из цифр? Какая это цифра? (Число может быть очень большим.)
- Дано натуральное число N. Выбросить из записи числа N все цифры, равные 3, оставив при этом прежним порядок остальных цифр. Например, из 630231637839 получим 60216789. (Число может быть очень большим.)
- Дано натуральное число N. Выбросить из записи числа N все цифры, равные 3 и 6, оставив при этом прежним порядок остальных цифр. Например, из 635231637839 получим 521789. (Число может быть очень большим.)
- Дано натуральное число N. Выбросить из записи числа N все чётные (нечётные) цифры.
44. делимость чисел.
для того чтобы определить, делится ли одно число на другое, нужно найти остаток от деления одного числа на другое и проверить, равен ли он нулю. Если остаток равен нулю, то число делится, иначе — нет. Таким образом, проверка на делимость сводится к нахождению остатка от деления одного числа на другое. Для чисел в обычном представлении остаток находится с помощью стандартной операции mod.
Рассмотрим, как найти остаток от деления числа, заданного в виде массива цифр, на число, заданное непосредственно.
В десятичной системе счисления число представимо в виде:
а=a1·10n-1+a2·10n-2+ … + an-1 ·10+an,
где a1, a2, …, an-1, an — цифры числа а, причём 0а<10, 1in.
пусть нам требуется найти остаток от деления числа а на число m.
Прежде чем это делать, укажем на некоторые свойства остатков. Пусть c, d, n — некоторые натуральные числа, тогда
- (c+d) mod n = ((c mod n) + (d mod n)) mod n;
(5+7) mod 3=12 mod 3 =0
((5 mod 3)+(7 mod 3)) mod 3= (2+1) mod 3=0
- (cd) mod n = (c(d mod n)) mod n = ((c mod n)d) mod n;
(5*7) mod 3=35 mod 3=2
(5*(7 mod 3)) mod 3=(5*1) mod 3=2
((5 mod 3)*7) mod 3= (2*7) mod 3= 14 mod 3=2
- cd mod n = ((cd-1 mod n)c) mod n.
53 mod 4 =125 mod 4=1
((52 mod 4)*5) mod 4=((25 mod 4)*5) mod 4=(1*5) mod 4=1
Доказательство свойства 1):
Пусть с1=c div n, c2=c mod n, d1=d div n, d2=d mod n; тогда c=с1·n+c2,d=d1·n+d2; (c+d) mod n=(с1·n+c2+d1·n+d2) mod n=((с1+d1)·n+c2+d2) mod n=(c2+d2) mod n= =((c mod n)+(d mod n)) mod n.
Доказательства свойств 2) и 3) — аналогичны.
найдём остаток от деления числа а на число m, применив сначала свойство 1), а затем, к каждому слагаемому — свойство 2).
а mod m=( a1·10n-1+a2·10n-2+ … + an-1 ·10+an) mod m = ((a1·10n-1) mod m +(a2·10n-2) mod m + … + (an-1 ·10) mod m +an mod m) mod m = ((a1·(10n-1 mod m) mod m) +(a2·(10n-2 mod m) mod m) + … + (an-1 · (10 mod m) mod m) +an mod m) mod m.
Из последнего равенства вытекает алгоритм нахождения остатка. Находим остаток от деления очередной разрядной единицы на число m, пользуясь свойством 3). Умножаем полученное число на значение цифры, соответствующей данной разрядной единице, прибавляем к тому, что получили на предыдущих шагах, и снова находим остаток от деления на m. Так продолжаем до тех пор, пока не используем все цифры числа а.
Значение остатка будем накапливать в переменной s, значение остатка разрядной единицы — в переменной r, цифры числа а хранятся в массиве В (в обратном порядке), k — количество цифр в числе.
S:=0;
R:=1;
For i:=1 to k do
begin
S:= (s+B[i]*r) mod m;
r:= r*10 mod m;
end;
Этот алгоритм можно применять для получения остатка от деления числа а на число m и в том случае, когда число а, заданное в виде массива цифр, записано в любой позиционной системе счисления (цифры числа должны быть записаны своими десятичными аналогами). Для этого достаточно число 10 заменить основанием системы счисления р. остаток от деления будет получен в десятичной системе счисления.
Для получения остатка от деления можно также воспользоваться схемой Горнера.
Пример 125. Дано натуральное число в k-ичной системе счисления (2£k£36).
Требуется написать программу, которая находит остаток от деления этого числа на заданное натуральное число m.
Технические требования:
Входной файл: INPUT.TXT
Выходной файл: OUTPUT.TXT
Ограничение по времени тестирования: по 1 секунде на один тест.
Формат входных данных:
Входной файл INPUT.TXT содержит в первой строке числа k и m, записанные через пробел. Во второй строке задается число n – количество цифр в заданном числе, а в третьей - его цифры. Числа k, m, n записываются в десятичной системе счисления. Для записи цифр числа в системе счисления с основанием, большим 10, используются латинские заглавные буквы (10 – A, 11 – B, …, 36 – Z). Число m не превышает 32767, а в задаваемом числе не более 10000 цифр.
Формат выходных данных:
Выходной файл OUTPUT.TXT должен содержать одно искомое число, записанное в десятичной системе счисления.
Пример файла входных данных:
10 2
2
17
Пример файла выходных данных (для приведенного выше входного файла):
1
решение. Для решения задачи воспользуемся соотношениями. Одно из них называется схемой Горнера для вычисления значения числа по его цифрам в q-ичной системе счисления N=((…(an*q+an-1)*q+…)*q+a2)*q+a1, где n – количество цифр в числе. Другое следует из свойств операции остаток от деления - (a*b) mod m=((a mod m)*(b mod m)) mod m и (a+b) mod m=((a mod m)+(b mod m)) mod m. Эти соотношения использованы в нижеприведенной программе.
Program Ex125;
var
m, k, n, i : integer;
ost : longint;
c : char;
cifru : string;
begin
cifru:='0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ';
assign(input,'input.txt'); reset(input);
assign(output,'output.txt'); rewrite(output);
readln(k,m);
readln(n);
ost:=0;
for i:=1 to n do
begin
read(c);
ost:=(ost*k+pos(c,cifru)-1) mod m
end;
write(ost)
end.
Запишем трассировку программы для k=10, m=3, n=5, и число 14572:
| шаг i | c | pos(c,cifru) | (ost*10+pos(c,cifru)-1) mod 3 | ost | |
| | | | | | 0 |
| | ‘1’ | 2 | (0*10+2-1) mod 3 | 1 mod 3 | 1 |
| | ‘4’ | 5 | (1*10+5-1) mod 3 | 14 mod 3 | 2 |
| | ‘5’ | 6 | (2*10+6-1) mod 3 | 25 mod 3 | 1 |
| | ‘7’ | 8 | (1*10+8-1) mod 3 | 17 mod 3 | 2 |
| | ‘2’ | 3 | (2*10+3-1) mod 3 | 22 mod 3 | 1 |
Результат: 1.
Вопросы и задания.
- Какие свойства остатков вы знаете?
- Как найти остаток от деления числа, заданного в виде массива цифр, на число, заданное непосредственно?
- Как можно использовать схему Горнера для нахождения остатка от деления числа, заданного в виде массива цифр, на число, заданное непосредственно?
- Найти остаток от деления числа, записываемого с помощью К семёрок, на число А.
- Число называется простым, если оно делится без остатка только на единицу и само себя. Число называется сверхпростым, если оно простое, а также являются простыми все числа, получающиеся всевозможными перестановками его цифр. Например, сверхпростым является число 13, так как числа 13 и 31 простые. Требуется написать программу, которая определит все сверхпростые числа, меньшие заданного натурального N.
