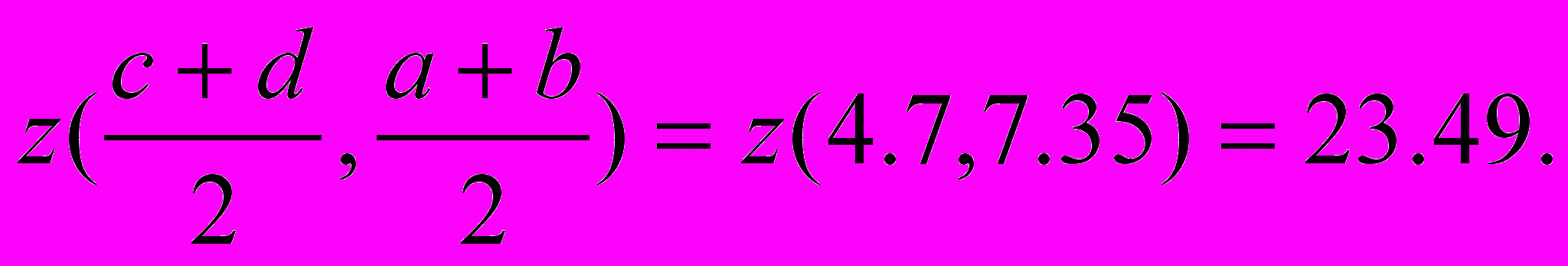Geum.ru

Использование программных массивов для обработки большого числа однотипных данных (на примере одномерного и двумерного массивов)

Вид материалаДокументы

Содержание


Picture Box
Имя объекта
Печатать матрицу
Подобный материал:

Работа № 6

Использование программных массивов для обработки большого числа однотипных данных (на примере одномерного и двумерного массивов)

Цель работы: изучение и использование понятия программного массива как обобщения понятия переменной при программировании процедур на языке VB 6, создание проектов, в программных модулях которых целесообразно использовать одномерные и многомерные программные массивы.

Контрольные вопросы:
  1. Как объявляется одномерный массив? Что такое индекс массива и диапазон изменения индекса?
  2. Как можно находить максимальный (или минимальный) элемент массива чисел? Значение индекса максимального (или минимального) элемента?
  3. В чем заключается идея «пузырьковой» сортировки одномерного массива чисел?
  4. Приведите примеры алгоритмов сортировки одномерного массива, более эффективных, чем алгоритм «пузырьковой» сортировки.
  5. Как можно использовать понятие динамического массива для ввода по одному элементу в одномерный массив произвольной (заранее не известной) длины?
  6. Как с помощью двумерного массива можно хранить и обрабатывать матрицу значений функции двух переменных f(x, y)?
  7. Как можно использовать понятие динамического массива для загрузки в двумерный массив значений цвета «точек» произвольного изображения?

Пример 6.1. Рассмотрим приложение, демонстрирующее «пузырьковую» сортировку одномерного массива чисел. Для определенности, будем считать, что числа в массиве целые, в диапазоне от 0 до 1000. Всего в массиве 100 чисел, которые создаются случайно, с помощью функции Rnd, например, так: X = CInt(Rnd * 1000).

На рис 6.1 показано окно приложения, на котором 2 поля списка и 2 команды меню: Заполнить массив и Сортировать массив.

Щ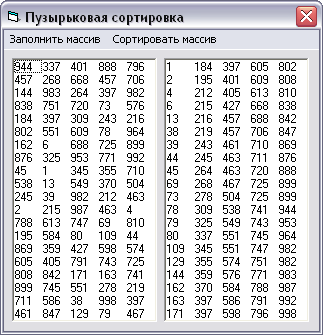елчок 1-й команды вызывает заполнение 1-го поля случайными числами, а щелчок 2-й команды – заполнение 2-го поля.


Рис. 6.1. Результат «пузырьковой» сортировки массива чисел


Опуская описание этапа проектирования интерфейса, представим лишь программный код:

Dim B(99) As Integer


Private Sub mnuLoad_Click()

List1.Clear: List2.Clear

Randomize

For i = 0 To 99

B(i) = CInt(1000 * Rnd)

List1.AddItem B(i)

Next i

End Sub


Private Sub mnuSort_Click()

List2.Clear

For i = 0 To 98 ‘ Алгоритм пузырьковой сортировки:

For j = i + 1 To 99

If B(j) < B(i) Then

A% = B(i): B(i) = B(j): B(j) = A

End If

Next j

Next i

For i = 0 To 99

List2.AddItem B(i)

Next i

End Sub

Пример 6.2. Рассмотрим приложение, которое демонстрирует возможность двумерного динамического массива хранить изображения произвольного размера с целью их обработки.

На экранной форме приложения 2 элемента Picture Box (Picture1 и Picture2) и 4 команды меню (рис. 6.2). Предварительно, на этапе проектирования, в первое графическое поле загружается изображение из графического файла произвольного формата. Чтобы размер графического окна автоматически «подстроился» под размер загружаемого изображения, его свойство AutoSize следует установить равным True.

При загрузке формы ее размеры и расположение обоих графических окон должны настроиться автоматически.

После щелчка команды меню To Array графические окна масштабируются в соответствии с размерами изображения в пикселях, динамический массив для хранения данных о цвете каждой «точки» изображения переопределяется, после чего в него заносятся данные, получаемые в ходе сканирования изображения.

Остальные команды меню относятся к обработке изображения – их действия не нуждаются в комментариях.

Отметим лишь, что меню From Array имеет подменю:

None,

To LeftRight,

To UpDown,

To LeftRight & UpDown.

(Назначение этих команд соответствует их мнемонике.)

Рис. 6.2. Вид окна после отработки команд меню:

To Array, To Negative, From Array → To LeftRight

Для реализации компьютерного интерфейса заполняется следующая таблица свойств:

Имя

объекта

Класс

объекта
Свойство

объекта
Значение свойства

Form1
Form
Caption
“Двумерный динамический массив”

MinButton
False

MaxButton
False

mnuToArray
Menu Command
Caption
“To Array”

mnuToNegative
Menu Command
Caption
“To Negative”

mnuToGrey
Menu Command
Caption
“To Grey”

mnuFromeArray
Menu Command
Caption
“From Array”

mnuNone
Menu Command
Caption
“None”

mnuToLeftRight
Menu Command
Caption
“To Left-Right”

mnuToUpDown
Menu Command
Caption
“To Up-Down”

mnuToLR-UD
Menu Command
Caption
“To Left-Right And Up-Down”

Picture1
PictureBox
AutoSize
True

Picture2
PictureBox
AutoSize
False

Ниже приводится код процедур лишь для некоторых команд меню из приведенной таблицы. Составление кода процедур для остальных команд – тема задания 2 данной работы.

Dim p() As Long

Dim w As Long, h As Long, i As Long, j As Long

Dim r As Byte, g As Byte, b As Byte


Private Sub Form_Load()

w = Picture1.Width: h = Picture1.Height

Width = 2 * Picture1.Width + 900

Height = Picture1.Height + 1200

Picture2.Width = Picture1.Width

Picture2.Height = Picture1.Height

Picture2.Left = Picture1.Width + 450

Picture2.Top = Picture1.Top

End Sub


Private Sub mnuToArray_Click()

w = w \ 15: h = h \ 15

Picture1.Scale (0, 0)-(w, h): Picture2.Scale (0, 0)-(w, h)

ReDim p(w, h)

For i = 1 To h - 1

For j = 1 To w - 1

p(j, i) = Picture1.Point(j, i)

Next j

Next i

End Sub


Private Sub mnuNone_Click()

For i = 1 To h - 1

For j = 1 To w - 1

Picture2.PSet (j, i), p(j, i)

Next j

Next i

End Sub

В ходе выполнения данной работы студент должен выполнить 3 задания.

Задание 1. В процессе выполнения задания студенты, взяв за основу проект из примера 6.1, реализуют и изучают действие различных алгоритмов сортировки одномерного числового массива.

Вариант 1. Внести единственное изменение в проект приложения, представленного в примере 6.1: вместо «пузырьковой» сортировки применить сортировку вставкой. (Алгоритм представлен в пособии [2], стр. 79 – 80.)

Вариант 2. Внести единственное изменение в проект приложения, представленного в примере 6.1: вместо «пузырьковой» сортировки применить сортировку выбором максимального элемента. (Алгоритм представлен в пособии [2], стр. 78 – 79.)

Задание 2. В ходе выполнения задания студенты, взяв за основу проект из примера 6.2, осваивают возможность обработки изображения с помощью двумерного массива.

Для обоих вариантов потребуется процедура «разложения» цвета точки изображения c на 3 его составляющих: красную, зеленую и синюю (r, g, b). Для этого следует решить уравнение с тремя неизвестными: 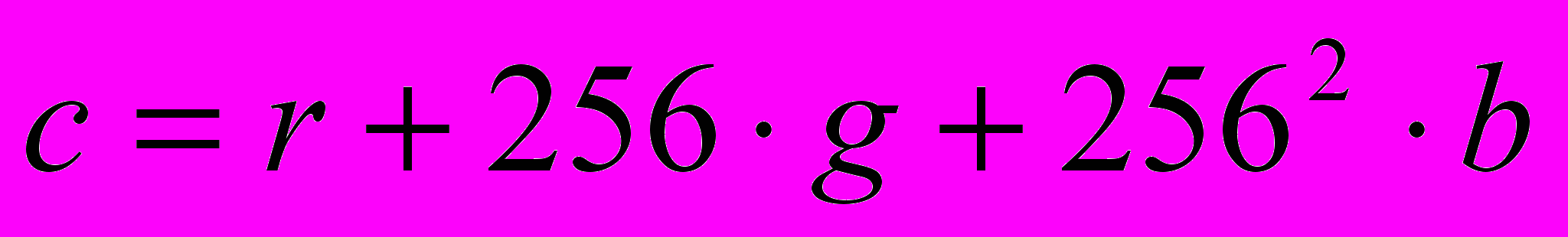. В целых числах это уравнение решается с помощью следующей процедуры:

Private Sub Separate(c As Long, r As Byte, g As Byte, b As Byte)

cc& = c

If cc > 0 Then

r = cc Mod 256: cc = cc \ 256: g = cc Mod 256: b = cc \ 256

Else

r = 0: g = 0: b = 0

End If

End Sub

Вариант 1. Реализовать алгоритм преобразования цветного изображения в черно-белое (написать процедуру для команды меню mnuToGrey из примера 6.2), а также алгоритм преобразования «позитивного» изображения в «негативное» (написать процедуру для команды меню mnuToNegative из примера 6.2).

Указание: Цвет каждой точки изображения – это элемент массива p(j,i) – значение типа Long. Преобразование этого значения в значение «серого» цвета означает следующее:

Separate p(j, i), r, g, b

gr = 0.33 * r + 0.33 * g + 0.33 * b

p(j, i) = RGB(gr, gr, gr)

Преобразование значения p(j,i) в значение «негативного» цвета:

Separate p(j, i), r, g, b

p(j, i) = RGB(255 - r, 255 - g, 255 - b)

Вариант 2. Реализовать алгоритм преобразования исходного изображения в отраженное относительно вертикальной оси (написать процедуру для команды меню mnuToLeftRight из примера 6.2). Реализовать также алгоритм преобразования исходного изображения в отраженное относительно горизонтальной оси (написать процедуру для команды меню mnuToUpDown из примера 6.2), а также алгоритм, совмещающий эти два преобразования (mnuToLR-UD из примера 6.2).

Указание: Цвет каждой точки изображения – это элемент массива p(j,i) – значение типа Long.

1-й индекс массива для исходного изображения меняется от 1 до w-1, где w – ширина изображения в пикселях. При построении «отраженного» изображения (рис. 6.2) этот индекс должен меняться от w-1 до 1:

Picture2.PSet (w - j, i), p(j, i)

2-й индекс массива для исходного изображения меняется от 1 до h-1, где h – высота изображения в пикселях. При построении «перевернутого» изображения этот индекс должен меняться от h-1 до 1:

Picture2.PSet (j, h - i), p(j, i)

Для обоих преобразований одновременно:

Picture2.PSet (w - j, h - i), p(j, i)

Задание 3. В ходе выполнения задания студенты приобретают навык использования двумерного массива для обработки матрицы чисел, представляющей значения функции двух переменных.

Для определенности, в обоих вариантах задания рассматривается одна функция - гиперболический параболоид:



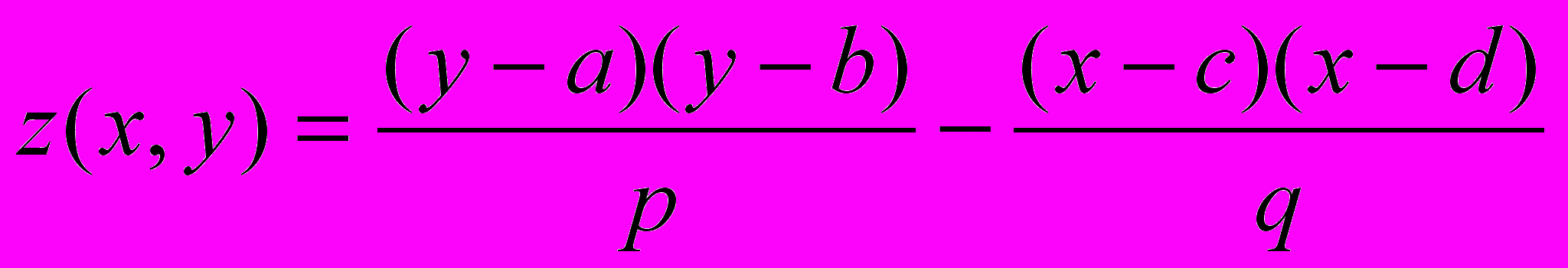
с одним и тем же набором значений параметров:

Const a As Double = 5.2, b As Double = 9.5, p As Double = 1.1

Const c As Double = -1.3, d As Double = 10.7, q As Double = 1.3

Значения этой функции должны быть вычислены и помещены в двумерный массив z(x, y), где x - номер столбца, а y - номер строки матрицы. На рис. 6.3 показана матрица указанных значений с 8 столбцами и 15 строками.



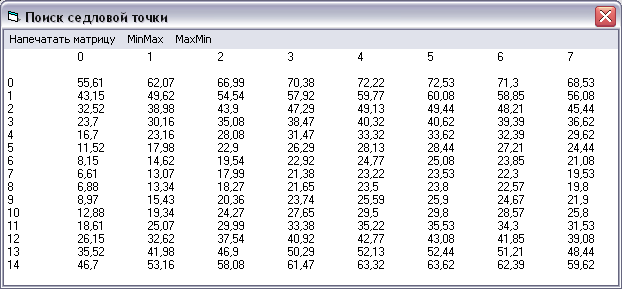
Рис. 6.3. Матрица значений гиперболического параболоида для целочисленных аргументов x = [0, 7], y = [0, 14]

Код процедуры для команды меню Печатать матрицу:

Private Sub mnuPrint_Click()

Cls

Print "",

For x = 0 To 7

Print x,

Next x

Print: Print

For y = 0 To 14 ' 15 строк

Print y,

For x = 0 To 7 ' 8 столбцов

z(x, y) = (y - a) * (y - b) / p - (x - c) * (x - d) / q

z(x, y) = Round(z(x, y), 2)

Print z(x, y),

Next x

Print

Next y

End Sub

Вариант 1. Написать процедуру для команды меню MinMax, с помощью которой «седловая точка» (x0, y0) гиперболического параболоида ищется как минимум по строкам максимумов по столбцам матрицы:



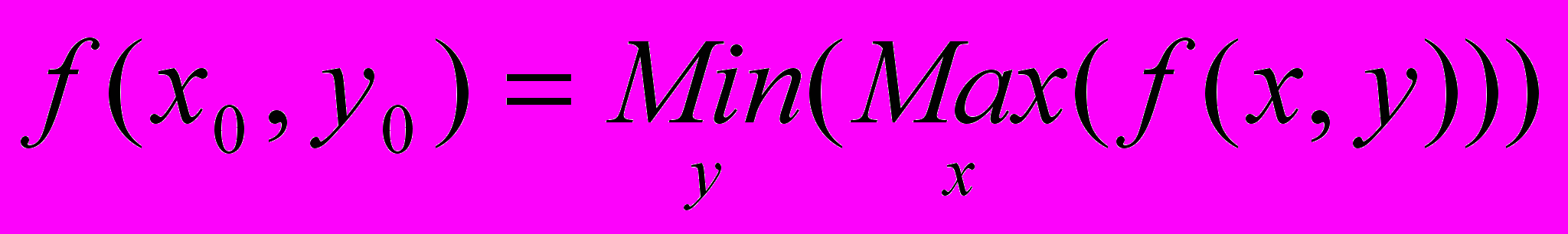
Вариант 2. Написать процедуру для команды меню MaxMin, с помощью которой «седловая точка» (x0, y0) гиперболического параболоида ищется как максимум по столбцам минимумов по строкам матрицы:



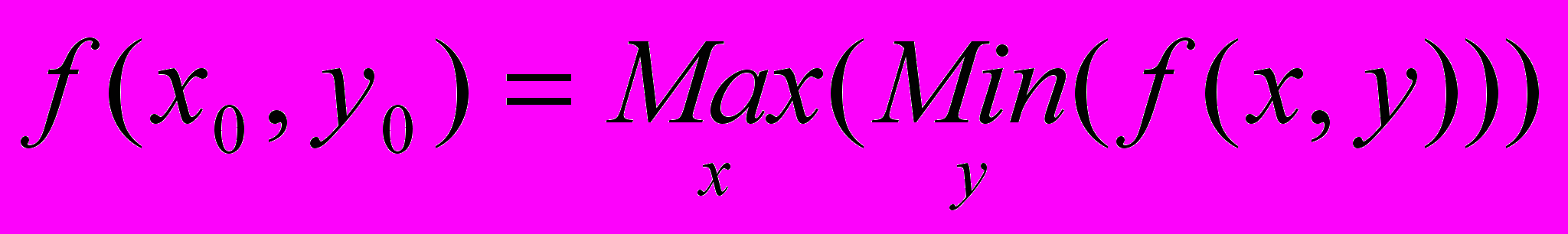
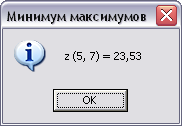
О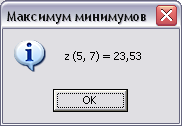чевидно, что результаты работы процедур 1-го и 2-го вариантов должны совпасть (рис. 6.4).


Рис. 6.4.


Отметим, что полученный результат хорошо согласуется с теоретическим значением: