Практикум по птицеводству издание второе, дополненное
| Вид материала | Практикум |
- Головин Е. Сентиментальное бешенство рок-н-ролла. (Второе издание, исправленное и дополненное), 1970.65kb.
- С. Б. Борисов Человек. Текст Культура Социогуманитарные исследования Издание второе,, 7455.38kb.
- К. С. Гаджиев введение в политическую науку издание второе, переработанное и дополненное, 7545.88kb.
- Очерки российского сектоведения Сборник Издание 2-е, дополненное, 10804.55kb.
- Православная Церковь и Сектанты. Часть Общие вопросы, 6403.26kb.
- Программа дисциплины Экономика и менеджмент муниципального образования для специальности, 110.29kb.
- В. П. Грузинов, В. Д. Грибов экономика предприятия издание второе, дополненное, 2824.54kb.
- Учебник для вузов издание второе, переработанное и дополненное, 6890.79kb.
- Линь Хоушен, Ло Пэйюй 300 вопросов о цигун Секреты китайской медицины, 4960.19kb.
- Учебник 3-е издание, переработанное и дополненное, 10138.23kb.
Занятие 16
НАСЛЕДУЕМОСТЬ ПРОДУКТИВНЫХ ПРИЗАКОВ СЕЛЬСКОХОЗЯЙСТВЕННОЙ ПТИЦЫ
РАСЧЕТ КОЭФФИЦИЕНТА НАСЛЕДУЕМОСТИ
Цель занятия – познакомиться с характером наследования основных продуктивных признаков сельскохозяйственной птицы, освоить расчет коэффициента наследуемости методом дисперсионного анализа.
Содержание занятия
При комплексном подходе к оценке птицы важно значение основных генетических параметров хозяйственно полезных признаков. В основе характеристики продуктивных и племенных качеств птицы лежат генетические положения о фенотипе и генотипе.
Генотип представляет собой совокупность всех локализованных в хромосомах генов организма. В результате взаимодействия генотипа и условий внешней среды складывается фенотип особи. Для определения генотипа необходимо изучение предков либо потомков данной особи, либо тех и других вместе.
Фенотип складывается из совокупности всех внешних и внутренних структур и функций организма, которые могут быть описаны и изучены морфологическими и зоотехническими методами (например, яйценоскость, масса яйца, живая масса, скорость оперяемости, склонность к насиживанию, обмускуленность киля и т. д.).
В фенотипе никогда не реализуются все генотипические возможности, поскольку фенотип каждого организма есть лишь частный случай проявления его генотипа в тех условиях внешней среды, в которых происходит его развитие. В этой связи наследуемость рассматривается как влияние генотипического разнообразия родителей на фенотипическое разнообразие потомства по каждому признаку. В свою очередь, фенотипическое разнообразие признака у потомства основывается, с одной стороны, на разнообразии генотипической информации полученной от родителей, а с другой – на разнообразии условий жизни, в которых эта информация реализуется.
Для определения степени влияния наследуемости на изменчивость признака применяется коэффициент наследуемости, указывающий, какая доля фенотипической изменчивости признака обусловлена влиянием генотипа.
В практике используется несколько методов расчета коэффициента наследуемости признака. Однако наилучшим методом измерения степени наследуемости является дисперсионный анализ, позволяющий определить величину фенотипической изменчивости признака и разложить ее на составляющие величины генетической и паратипической (средовой) изменчивости.
При обработке с помощью дисперсионного анализа однофакторного комплекса (или двухфакторного) получают основные величины его дисперсий – Cy, Cx, Cz, сущность которых заключается в следующем:
Cy – фенотипическая дисперсия, показывающая общее фенотипическое разнообразие признака у потомков по всему комплексу (общая сумма квадратов) (Cph);
Cx – генотипическая дисперсия, показывающая разнообразие генотипической информации родителей (межгрупповая сумма квадратов) (Cн);
Cz – паратипическая дисперсия, отражающая ту часть фенотипического разнообразия, которое обусловлено влиянием внешней среды (внутригрупповая сумма квадратов) (CЕ).
Общее фенотипическое разнообразие признака складывается из доли разнообразия, обусловленного генетической информацией, и из доли разнообразия, отражающего возможность реализации генетической информации в данных условиях среды:
Cy = Cx + Cz или Cph = Cн + CЕ.
Таким образом, коэффициент наследуемости признака (h2), определяющий долю разнообразия значений признака, обусловленную генетической информацией, в общем фенотипическом его разнообразии может быть найден по формуле
h2 = Cx/Cy, или h2 = Cн /Cph,
Это наиболее широко используемый и точный прием вычисления h2 дисперсионным методом.
Может применяться также и другой способ, при котором изменчивость признака выражается величиной вариансы S2, и коэффициент наследуемости рассчитывается по формуле
h2 = (Sx)2/(Sy)2 .
Этот метод применяется реже, поскольку он иногда дает минусовые значения коэффициента наследуемости.
Величина h2 колеблется в пределах от 0 до 1 (табл. 19).
Чем выше величина коэффициента наследуемости, тем в большей степени фенотипическая изменчивость обусловлена наследственностью, тем выше генетическое разнообразие в данной популяции. Малая величина h2 говорит о сниженном генетическом разнообразии, что может быть, в частности, следствием длительного и тесного инбридинга.
На величину коэффициента наследуемости влияют колебания во внешних условиях (особенно в условиях кормления и содержания). При неблагоприятных условиях среды существенно возрастает доля паратипической изменчивости признака, а следовательно, снижается величина коэффициента наследуемости. Более того, высокопродуктивные особи при плохих условиях могут оказаться менее продуктивными, чем особи с худшей наследственной потенцией. Благоприятные и стабильные условия среды способствуют повышению коэффициента наследуемости.
Величина коэффициента наследуемости по тому или иному признаку оказывает большое влияние на результативность селекции в данном стаде. При высоком значении коэффициента наследуемости селекционируемого признака в данной популяции массовый отбор по фенотипу может оказаться эффективным средством улучшения этого признака, особенно в оптимальных условиях среды.
Таблица 19
Коэффициенты наследуемости некоторых признаков у птицы
(по обобщенным данным)
| Признак | Пределы колебаний коэффициентов наследуемости |
| Куры | |
| Яйценоскость яичных кур | 0,09-0,22 |
| Яйценоскость мясных кур | 0,19-0,43 |
| Интенсивность яйценоскости | 0,19-0,22 |
| Длина цикла яйценоскости | 0,14-0,49 |
| Половая зрелость | 0,10-0,56 |
| Масса яйца | 0,31-0,81 |
| Оплодотворенность яиц | 0,11-0,13 |
| Выводимость яиц | 0,03-0,16 |
| Выживаемость молодняка | 0,05-0,16 |
| Выживаемость взрослой птицы | 0,03-0,13 |
| Живая масса в 7-8 нед. | 0,20-0,60 |
| Живая масса взрослой птицы | 0,32-0,06 |
| Скорость оперения | 0,25-0,42 |
| Индекс формы яйца | 0,10-0,62 |
| Толщина скорлупы | 0,14-0,58 |
| Мраморность скорлупы яйца | 0,27-0,41 |
Продолжение таблицы 19
| Цвет скорлупы | 0,35-0,80 |
| Индекс белка | 0,26-0,60 |
| Индекс желтка | 0,54-0,55 |
| Масса белка яиц | 0,16-0,68 |
| Масса желтка яиц | 0,00-0,16 |
| Цвет желтка | 0,00-0,21 |
| Наличие кровяных пятен | 0,10-0,50 |
| Угол груди молодняка в 7-8 нед. | 0,10-0,62 |
| Убойный выход | 0,17-0,44 |
| Индейки | |
| Яйценоскость | 0,16-0,40 |
| Массаяйца | 0,55-0,91 |
| Выводимость яиц | 0,12-0,18 |
| Живая масса | 0,33-0,50 |
| Длина киля | 0,28 |
| Ширина груди | 0,26 |
| Длина голени | 0,43 |
| Гуси | |
| Масса печени | 0,63 |
| Живая масса | 0,50 |
| Половая зрелость | 0,28-0,40 |
| Яйценоскость | 0,09-0,14 |
| Выводимость яиц | 0,04-0,23 |
| Масса яиц | 0,38 |
| Утки | |
| Живая масса в 50-дневном возрасте | 0,10-0,65 |
| Яйценоскость | 0,29-0,53 |
| Оплодотворенность яиц | 0,17 |
| Масса яйца | 0,52-0,59 |
| Выводимость яиц | 0,14 |
| Убойный выход | 0,59 |
| Масса тушки | 0,78 |
| Масса мускулатуры | 0,50-0,88 |
При низком значении h2 селекция потомков по фенотипу родителя будет мало результативной, массовая селекция не принесет большого успеха. В этих случаях племенная работа должна основываться на индивидуальном подборе и отборе, анализе сочетаемости, линейном разведении.
Как показывают данные табл.19, высокими коэффициентами наследуемости у кур обладают такие показатели, как живая масса, качество яиц, мясная продуктивность молодняка и некоторые другие. Следовательно, перспективно совершенствование этих признаков путем простой массовой селекции.
В отношении признаков, характеризующихся низкой наследуемостью (оплодотворяемость яиц, выводимость молодняка), эффективность массового отбора гораздо ниже. Такие признаки, как яйценоскость и половая скороспелость, имеют промежуточные величины наследуемости (h2=0.2-0.3), поэтому массовый отбор в некоторых случаях может быть эффективным.
Поскольку коэффициент наследуемости того или иного признака может существенно колебаться в зависимости от степени селекционированности стада и характера условий среды, в практической селекционной работе необходим постоянный контроль популяции по этому показателю.
Методика расчета
Расчет коэффициента наследуемости дисперсионным анализом основывается на том, что наследуемость рассматривается как генетическое влияние родителей на тот или иной признак у потомства. Исходя из этого в комплекс включаются данные изучаемого продуктивного признака. Систематизированные данные содержатся в табуляграммах.
В качестве примера в табл.20 представлены данные по яйценоскости для расчета коэффициента наследуемости.
В целях некоторого упрощения расчетов варианты могут быть преобразованы путем уменьшения на определенное число, в данном случае на 100. В дальнейшем каждая варианта записывается как величина
х' = х - 100
Расчет коэффициента наследуемости приведен в алгоритме (табл.21).
Порядок расчета следующий:
1. Преобразованные варианты возводятся в квадрат.
2. Все варианты по потомкам одного родителя суммируются с получением Σх, затем получается общая сумма всех вариантов ΣΣх.
3. По потомкам каждого родителя получается квадрат суммы (Σх)2.
4. Делением квадрата суммы на число потомков в группе каждого производителя получается частная подсобная величина Σh; затем — сумма частных подсобных величин ΣΣh.
5. Получив сумму квадратов Σх2 по потомкам каждого родителя, рассчитывают общую сумму квадратов ΣΣх2 по всему комплексу.
6. Рассчитывается общая подсобная величина Н=ΣΣх2/N
7. На основании полученных подсобных величин нетрудно рассчитать значение дисперсий факториальной (Сx), случайной (Сz) и общей (Су).
Таблица 20
Яйценоскость кур – потомков отдельных петухов
| Номера петухов-отцов | ||||
| 3915 | 6929 | 6906 | 6919 | 3984 |
| Яйценоскость дочерей, шт. яиц | ||||
| 207 | 187 | 210 | 192 | 193 |
| 200 | 188 | 178 | 213 | 188 |
| 169 | 177 | 164 | 218 | 211 |
| 205 | 191 | 155 | 198 | 226 |
| 172 | 172 | 129 | 183 | 197 |
| 180 | 232 | | 221 | 199 |
| 157 | 200 | | 188 | 214 |
| 172 | 206 | | 210 | 224 |
| | 200 | | | |
| | 219 | | | |
| | 179 | | | |
| | 207 | | | |
.
8. Коэффициент наследуемости рассчитывается как отношение дисперсии факториальной (генотипической) к общей (фенотипической).
9. Сделав несложные расчеты чисел степеней свободы (ν) и варианс (S2), получают значение критерия Фишера (F) как отношение вариансы факториальной к случайной. Сопоставление полученного значения F со стандартным значением критерия Фишера в таблице справочника позволяет заключить о степени достоверности полученного коэффициента наследуемости (табл.22)
Cx=ΣΣh-H Cz=ΣΣx2-ΣΣh Cy=ΣΣx2-H
Cx=364511-357945=6566 Cx=6566
Cz=376893-364511=12382 Cz=12382
Cy=376893-357945=18948 Cy=18948
Проверка: 6566+12382=18948
h2=Cx /Cy=6566/18948=0,346; h2=0.346
F=Sx2/Sz2=1641,5/343,9=4,8
Полученное значение критерия Фишера (F) сравнивается со стандартными значениями по специальной таблице. Для значений чисел степеней свободы факториального 4 и случайного 36 стандартные значения критериев Фишера по трем уровням значимости равны 2,6 - 3,9 - 5,4. Расчетное значение 4,8 превышает величину критерия стандартного 3,9 для второго уровня значимости.
| Таблица 21 | Алгоритмы расчета h2 | Номера петухов-отцов | 3984 | Яйценоскость дочерей (x'=x-100) | X2 | 8649 7744 12321 15876 9404 9801 12966 15373 |
| X | 93 88 111 126 97 99 114 124 | |||||
| 6919 | X2 | 8464 12769 13924 9604 6889 14641 7744 12100 | ||||
| X | 92 113 118 98 83 121 88 110 | |||||
| 6906 | X2 | 12100 6084 4096 3025 841 | ||||
| X | 110 78 64 55 29 | |||||
| 6929 | X2 | 7569 7744 5929 8281 5184 17424 10000 11236 10000 14161 6241 11449 | ||||
| X | 87 88 77 91 72 132 100 106 100 119 79 107 | |||||
| 3915 | X2 | 11449 10000 4761 11025 5184 6400 3249 5184 | ||||
| X | 107 100 69 105 72 80 57 72 |
| Продолжение табл.21 | r=5 | N=41 | ΣΣx=3831 | | ΣΣh=364511 | ΣΣx2=376893 | x'=93,4; x=193,4 | H=(ΣΣx)2/N=(3831)2/41=14676561/41=357945 | |
| Номера петухов-отцов | 3984 | 8 | 852 | 725904 | 90738 | 92142 | 106,5 | ||
| 6919 | 8 | 823 | 677329 | 84666 | 86135 | 102,9 | |||
| 6906 | 5 | 336 | 112896 | 22579 | 26146 | 67,2 | |||
| 6929 | 12 | 1158 | 1340964 | 111747 | 115218 | 96,5 | |||
| 3915 | 8 | 662 | 438244 | 54781 | 57252 | 82,8 | |||
| Обозначение параметров | n | Σx | (Σx2) | Σh=(Σx2)/n | Σx2 | xi | |||
Таблица 22
Сводная таблица
| показатель | разнообразие | ||
| x | z | y | |
| C | 6566 | 12382 | 18948 |
| h2 | 0,346 | 0,654 | 1,00 |
| ν | r-1=4 | N-r=36 | N-1=40 |
| S2=C/N | 1641.5 | 343.9 | - |
| F=Sx2/Sz2 | 4.8 | Fst=2.6-3.9-5.9 | |
Вывод. В данной популяции кур коэффициент наследуемости яйценоскости (h2) равен 0.346 и достоверен при P>0,99.
Практические задания
Материалы и оборудование
- Калькуляторы.
- Справочная таблица стандартных значений критерия Фишера. В табл.23 приводятся данные о продуктивности потомков группы родителей одной популяции. Используя эти материалы, студенты выполняют некоторые из следующих работ.
Работа 1. Рассчитать коэффициент наследуемости яйценоскости в потомстве петуха 200710, принимая за градации классы матерей;
Рассчитать коэффициент наследуемости массы яйца в потомстве петуха 200710;
Рассчитать коэффициент наследуемости живой массы в потомстве петуха 200710.
Работа 2. На основе приведенных данных табуляграммы рассчитать коэффициент наследуемости яйценоскости, принимая за градации классы петухов 200710,310901 и 311507:
а) рассчитать коэффициент наследуемости массы яйца;
в) рассчитать коэффициент наследуемости живой массы кур.
Работа 3. На основании полученных коэффициентов наследуемости сделать заключение о направлении селекционной работы с данной группой птицы.
Таблица 23
Данные табуляграммы
| Номер несушки | Номер матери | Номер отца | Живая масса, кг | Масса яйца, г | Яйценоскость за 9 мес. | | |||||
| 710 | 23009 | 200710 | 1,7 | 54,1 | 164 | | |||||
| 711 | 23009 | 200710 | 1,7 | 50,9 | 230 | | |||||
| 714 | 23009 | 200710 | 1,8 | 57,3 | 214 | | |||||
| 721 | 23009 | 200710 | 1,5 | 57,5 | 190 | | |||||
| 752 | 23009 | 200710 | 1,7 | 53,3 | 110 | | |||||
| 710 | 23009 | 200710 | 1,6 | 53,3 | 226 | | |||||
| 730 | 23012 | 200710 | 1,8 | 56,5 | 207 | | |||||
| 755 | 23012 | 200710 | 1,5 | 59,1 | 198 | | |||||
| 766 | 23012 | 200710 | 1,6 | 57,7 | 181 | | |||||
| 791 | 23012 | 200710 | 1,6 | 54,3 | 210 | | |||||
| 799 | 23012 | 200710 | 1,6 | 55,2 | 151 | | |||||
| 716 | 23012 | 200710 | 1,7 | 56,1 | 217 | | |||||
| 719 | 23020 | 200710 | 1,6 | 56,2 | 175 | | |||||
| 720 | 2302 | 200710 | 1,6 | 53,9 | 222 | | |||||
| 739 | 23020 | 200710 | 1,7 | 55,8 | 169 | | |||||
| 742 | 23020 | 200710 | 1,8 | 60,0 | 188 | | |||||
| 767 | 23071 | 200710 | 1,5 | 55,3 | 175 | ||||||
| 774 | 23071 | 200710 | 1,6 | 51,4 | 207 | ||||||
| 7402 | 23071 | 200710 | 1,6 | 53,2 | 194 | ||||||
| 7411 | 23071 | 200710 | 1,7 | 54,2 | 214 | ||||||
| 7413 | 23071 | 200710 | 1,6 | 49,8 | 170 | ||||||
| 717 | 23018 | 200710 | 1,7 | 55,0 | 180 | ||||||
| 777 | 23018 | 200710 | 1,6 | 57,5 | 208 | ||||||
| 732 | 23018 | 200710 | 1,7 | 55,2 | 197 | ||||||
| 741 | 23018 | 200710 | 1,5 | 51,1 | 197 | ||||||
| 757 | 23018 | 200710 | 1,6 | 52,2 | 193 | ||||||
| 2815 | 18511 | 310901 | 1,6 | 54,2 | 147 | ||||||
| 2822 | 18511 | 310901 | 1,5 | 56,0 | 113 | ||||||
| 2825 | 18511 | 310901 | 1,7 | 56,9 | 228 | ||||||
| 2829 | 18511 | 310901 | 1,5 | 51,7 | 239 | ||||||
| 2835 | 18511 | 310901 | 1,5 | 56,7 | 205 | ||||||
| 2814 | 25526 | 310901 | 1,6 | 56,0 | 245 | ||||||
| 2818 | 25526 | 310901 | 1,6 | 54,3 | 146 | ||||||
| 2841 | 25526 | 310901 | 1,5 | 55,4 | 198 | ||||||
| 2855 | 25526 | 310901 | 2,0 | 55,4 | 134 | ||||||
| 2811 | 25529 | 310901 | 1,6 | 56,2 | 255 | ||||||
Продолжение таблицы 23
| 2828 | 25529 | 310901 | 1,5 | 54,1 | 228 |
| 2855 | 25529 | 310901 | 2,0 | 55,9 | 189 |
| 2859 | 25529 | 310901 | 1,7 | 57,6 | 109 |
| 4307 | 23302 | 311507 | 1,8 | 64,4 | 198 |
| 4316 | 23302 | 311507 | 1,5 | 59,5 | 215 |
| 4318 | 23302 | 311507 | 1,7 | 61,0 | 145 |
| 4320 | 23302 | 311507 | 1,6 | 59,6 | 243 |
| 4336 | 23302 | 311507 | 1,6 | 56,9 | 209 |
| 4302 | 23361 | 311507 | 1,6 | 57,4 | 174 |
| 4331 | 23361 | 311507 | 1,7 | 52,0 | 196 |
| 4341 | 23361 | 311507 | 1,5 | 56,3 | 180 |
| 4346 | 23361 | 311507 | 1,6 | 57,0 | 151 |
| 4361 | 23361 | 311507 | 1,8 | 55,6 | 190 |
| 4327 | 23372 | 311507 | 1,6 | 50,9 | 162 |
| 4329 | 23372 | 311507 | 1,5 | 53,3 | 129 |
| 4342 | 23372 | 311507 | 2,0 | 55,5 | 227 |
| 4356 | 23372 | 311507 | 1,5 | 54,4 | 166 |
| 4359 | 23372 | 311507 | 1,6 | 58,1 | 118 |
Контрольные вопросы
- Как вы определите наследуемость признака с позиции учения о генотипе и фенотипе организма?
- Зависит ли фенотипическое разнообразие признака от условий внешней среды?
- Что такое коэффициент наследуемости? Посредством отношения каких величин он определяется?
- На каких положениях основывается расчет коэффициента наследуемости методом дисперсионного анализа?
- Каков порядок расчета коэффициента наследуемости методом дисперсионного анализа?
- В каких пределах колеблется величина коэффициента наследуемости?
- Какие продуктивные признаки сельскохозяйственной птицы характеризуются высокими значениями коэффициента наследуемости? Какие признаки имеют низкое значение?
- Всегда ли значение коэффициента наследуемости определенного признака остается постоянным? Какие факторы влияют на его величину?
- Какое значение для селекционной работы с конкретной популяцией птицы имеет значение величины коэффициента наследуемости?
Занятие 17
Расчет эффекта селекции в птицеводстве
Цель занятия — освоить метод расчета ожидаемого эффекта селекции, т. е. теоретически возможного увеличения признака в последующих поколениях птицы при применении того или иного уровня отбора.
Содержание и методика занятия
Для селекционера важно уметь заранее предвидеть, какой эффект в увеличении конкретного признака может быть получен у потомства в результате селекции при определенном уровне отбора. Важно ориентировочно прогнозировать, сколько поколений и сколько лет потребуется для доведения продуктивности птицы до желаемых показателей при принятом уровне отбора и численности отбираемых для селекции особей, если условия кормления и содержания благоприятны. Для этих целей рассчитывается эффект селекции. который представляет собой обусловленный селекцией сдвиг генетической средней в данной популяции за определенный временной период (за одно или несколько поколений, за один год или несколько лет). Величина селекционного эффекта зависит от интенсивности селекции, измеряемой селекционным дифференциалом, от коэффициента наследуемости признака и интервала между поколениями.
Селекционный дифференциал (d) равен разности между средними показателями селекционируемого признака в популяции и средними показателями его у отобранной для дальнейшего воспроизводства птицы. Селекционный дифференциал может быть выражен в виде равенства
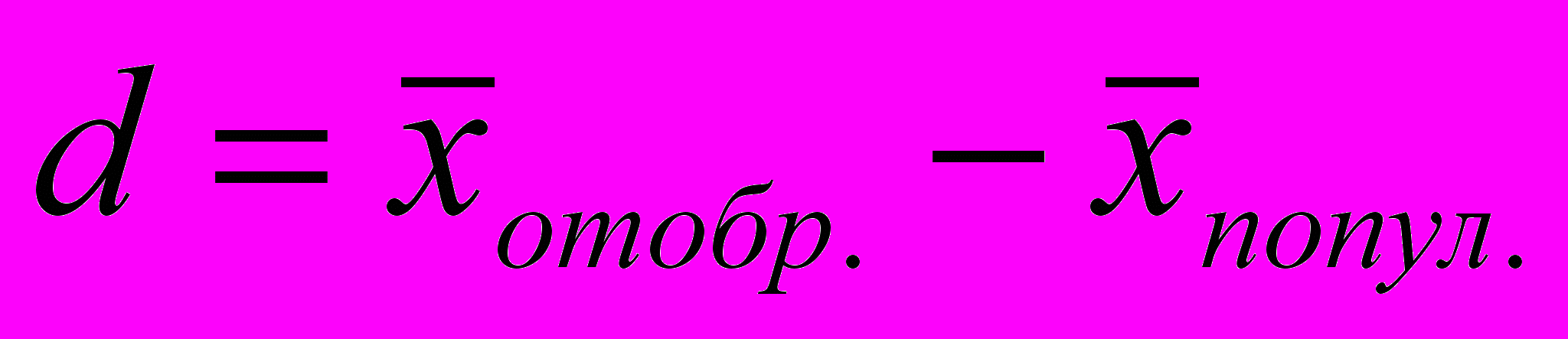
В этом случае селекционный дифференциал выражается именованной величиной соответственно признаку.
Селекционный дифференциал может быть выражен в условных единицах с помощью квадратического отклонения S, характеризующего фенотипическую изменчивость признака. В этом случае селекционный дифференциал показывает интенсивность отбора, он называется интенсивностью селекции и обозначается символом i.
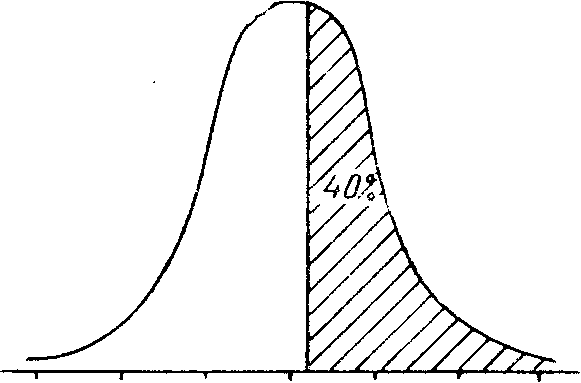
Величина i может быть вычислена по специальной таблице, в которой обозначаются доля отбираемых на племя особей и число квадратических отклонений с учетом знака, характеризующее отличие минимального значения признака от средней арифметической в популяции (табл. 24). Пользуясь данными табл. 24. можно определить интенсивность селекции по планируемой численности отбираемых из популяции особей, так же как, зная интенсивность селекции, можно определить количество особей, оставляемых для воспроизводства (рис. 25).
Таблица 24
Таблица для нахождения интенсивности селекции
| Доля особей, используемых на племя (b) | Число средних квадратических отклонений, характеризующее отличие минимального значения признака от средней в популяции (t) | Интенсивность селекции в стандартных еденицах (i) | Доля особей, используемых на племя (b) | Число средних квадратических отклонений, характеризующее отличие минимального значения признака от средней в популяции (t) | Интенсивность селекции в стандартных еденицах (i) |
| 0,95 0,90 0,85 0,80 0,75 0,70 0,65 0,60 0,55 0,50 | -1,64 -1,28 -1,04 -0,84 -0,67 -0,52 -0,39 -0,25 -0,13 -0,00 | 0,1094 0,1954 0,2732 0,3504 0,4249 0,4970 0,5688 0,6445 0,7193 0,7978 | 0,45 0,40 0,35 0,30 0,25 0,20 0,15 0,10 0,05 0,01 | 0,13 0,25 0,39 0,52 0,67 0,84 1,04 1,28 1,64 2,33 | 0,8791 0,9667 1,0563 0,1617 1,27481,4015 1,5486 1,7590 2,0800 2,6400 |
На селекционный эффект существенное влияние оказывает величина коэффициента наследуемости: низкая наследуемость обусловливает уменьшение селекционного эффекта, при коэффициенте наследуемости, равном нулю, селекция не дает результатов.
-3s -2s -1s x +1s +2s +3s -3s -2s -1s x +1s +2s +3s
b = 0,70; t = -52; i = 0,4970 b = 0,40; t = 0,25; i = 0,9667
Рис. 25 Связь интенсивности селекции и доли популяции, используемой на племя
Интервал между поколениями представляет собой промежуток времени между рождением родителей и потомков. У кур смена поколений требует 1,5 года. Однако при отборе на основании учета яйценоскости за первые 4 мес. продуктивности интервал между поколениями сокращается до 1 года.
Для расчета эффекта селекции могут быть использованы две формулы разной степени сложности. Зная величину коэффициента наследуемости и величину селекционного дифференциала, можно вычислить эффект селекции на одно поколение по формуле (1)
∆g=h2•d.
Эта формула удобна в тех случаях, когда известно среднее значение признака в популяции и группе птицы, отобранной для воспроизводства. Использование формулы иллюстрируется следующим примером.
Пример. В генетическом центре, где ведется селекция на повышение яйценоскости, средняя яйценоскость в популяции равна 221 яйцу при среднем квадратическом отклонении 15 яиц и коэффициенте наследуемости 0,18. Яйценоскость в группе, отобранной для воспроизводства, намечается не ниже 245 яиц. При указанном уровне отбора селекционный дифференциал составит;
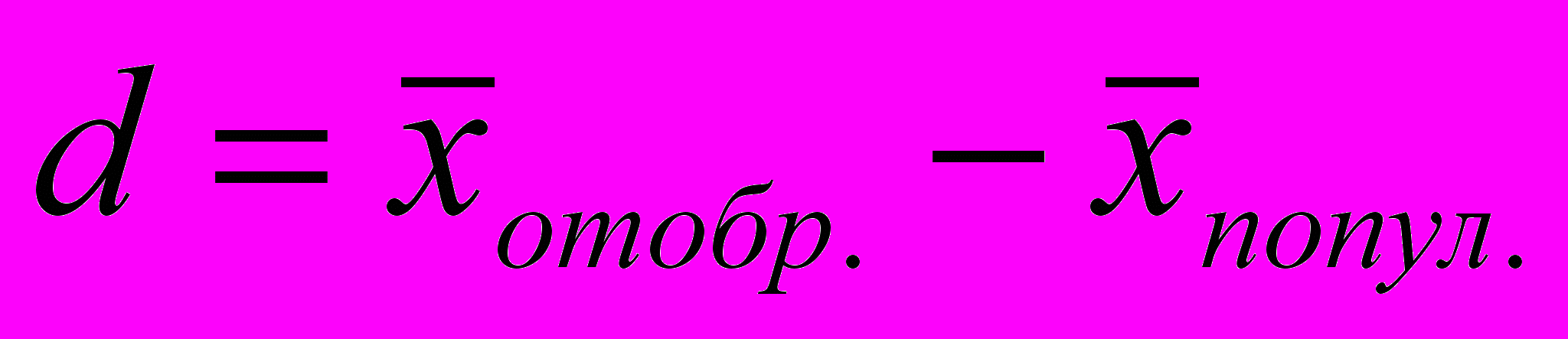= 245 – 221 = 24 яйца. Эффект селекции на одно поколение равен: 0,18•24==4,23 яйца.Рассчитанный эффект селекции указывает, что яйценоскость дочерей кур, отобранных для воспроизводства, может быть на уровне 221+4,3==225,3 яйца. С учетом интервала между поколениями может быть определен эффект селекции за 1 год:
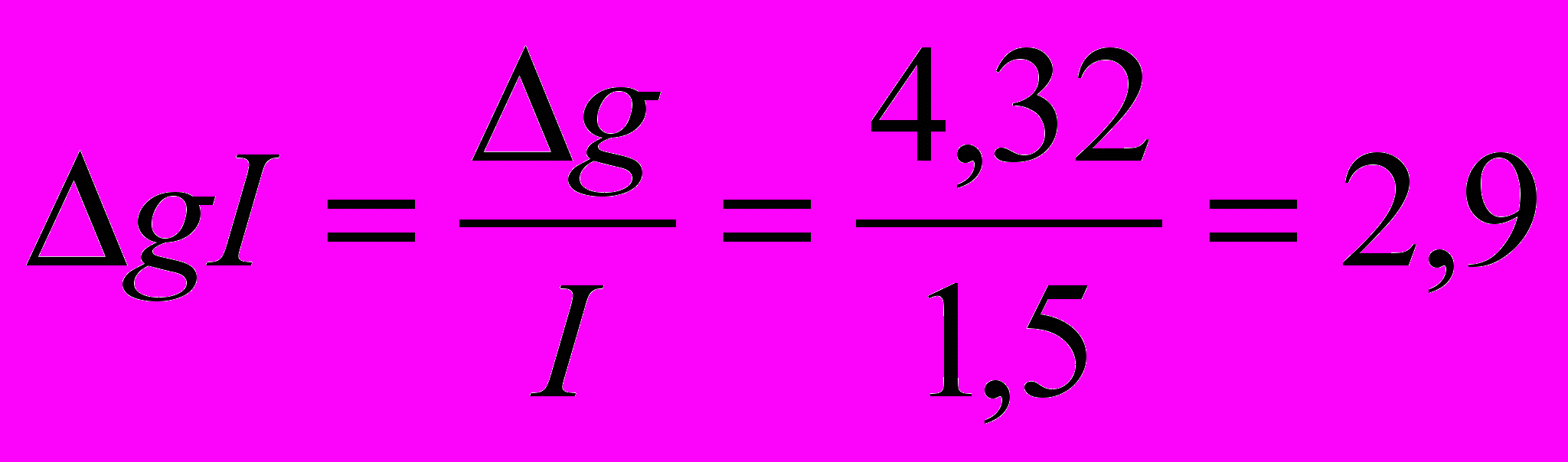
Другая формула расчета эффекта селекции
∆g = h2 • i • S (2)
основана на использовании специальной таблицы и позволяет прогнозировать не только генетический сдвиг в популяции, но и необходимое для этого «селекционное давление», т. е. определить, какая часть популяции должна быть отобрана для дальнейшего воспроизводства. Используя указанную формулу, вначале необходимо определить выраженную в средних квадратических отклонениях разницу минимального значения признака и группе отбора и средней яйценоскостью в популяции:
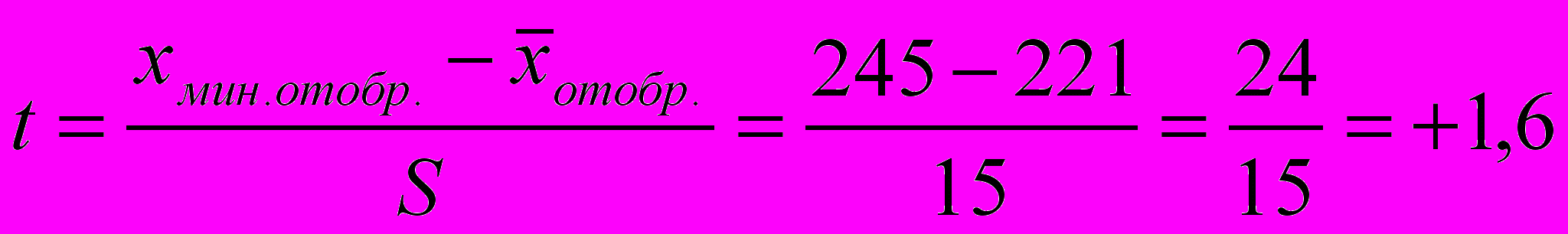
Из табл. 24 находим, что при. t = +1,6 интенсивность селекции i равна 2,08, тогда
∆g = 0,18• 2,08 • 15 = 5,62
Эффект селекции за одно поколение составляет 5,62 яйца, а яйценоскость дочерей кур, отобранных для воспроизводства, может быть на уровне 221+5,62==226,62 яйца. Полученные значения близки рассчитанным по формуле (1). Имеющиеся различия обусловлены тем, что для упрощения расчета в обоих случаях принималась цифра 245, хотя в первом случае она рассматривалась как средняя яйценоскость в группе отбора, а во втором — как минимальный показатель продуктивности при отборе птицы для воспроизводства. При данном расчете, пользуясь табл. 24, определяем, что для достижения планируемого эффекта селекции в группу воспроизводства должно быть отобрано всего 5% кур селекционируемой популяции (b = 0,05). При всех прочих заданных значениях может быть рассчитан также средний уровень продуктивности в отбираемой для воспроизводства материнской группе кур с использованием формулы
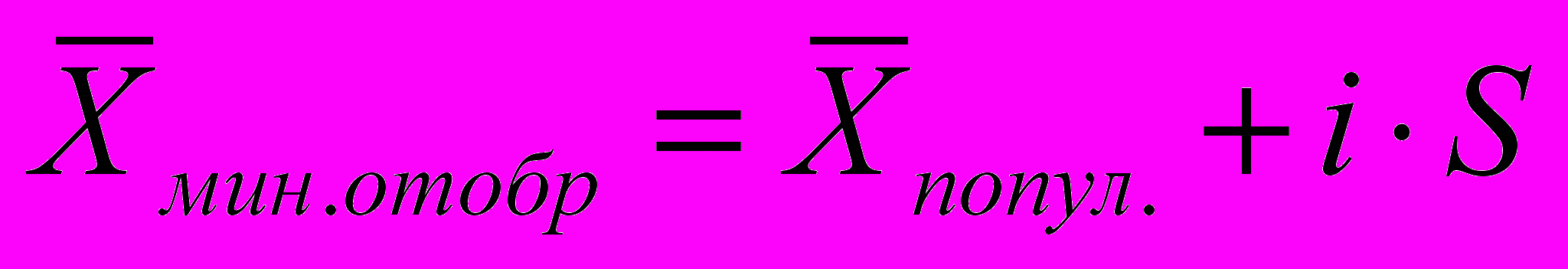
Эта яйценоскость в приведенном примере составляет
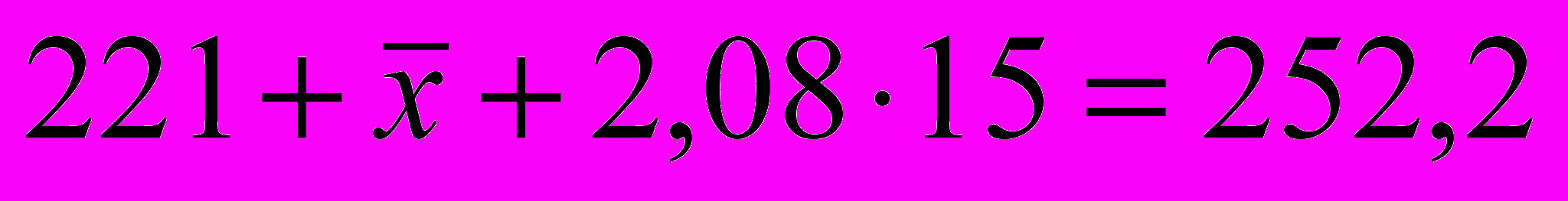яйца. В указанном расчете эффект селекции за один год составляет 5,62/1,5=3,75 яйца. Если планом племенной работы предусматривается довести эффект селекции до 15 яиц, на это потребуется 4 года (15/3,75=4), или 2,7 поколений кур (4/1,5=2,7).В свою очередь, когда ведется селекционная работа в течение нескольких поколений, ожидаемый эффект селекции вычисляется путем суммирования селекционных дифференциалов всех поколений.
При расчете эффекта селекции по продуктивным признакам, ограниченным полом (яйценоскость, масса яйца), условно принимают, что влияние отцов на проявление признака у потомства определяется по яйценоскости их сестер и полусестер. Рассмотренные выше методы расчета полностью приложимы к этим случаям. При определении же селекционного эффекта по признаку, имеющему •промежуточный (между обоими родителями) характер, необходимо. учитывать значение этого признака как у кур, так и у петухов. В этом случае формула расчета эффекта селекции принимает вид
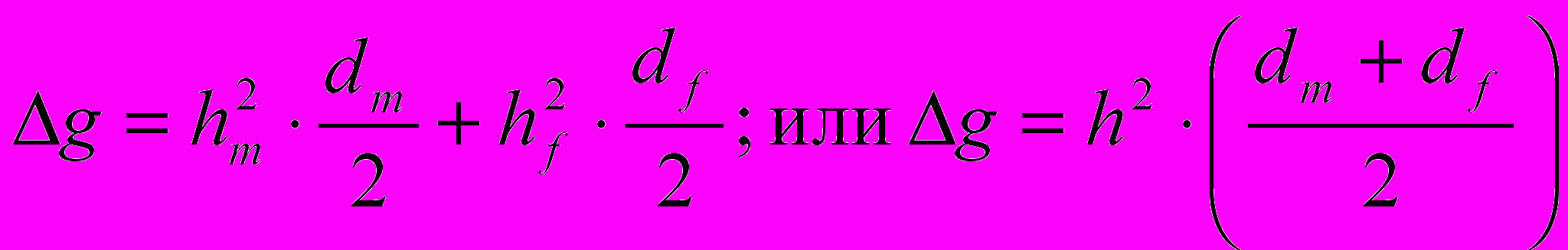(3)Где hm 2 и hf 2 - коэффициенты наследуемости признака по петухам и по курам; dm и df — селекционный дифференциал по петухам и курам.
При одновременной селекции на несколько признаков (n), каждому из которых придается равное значение, селекционный дифференциал
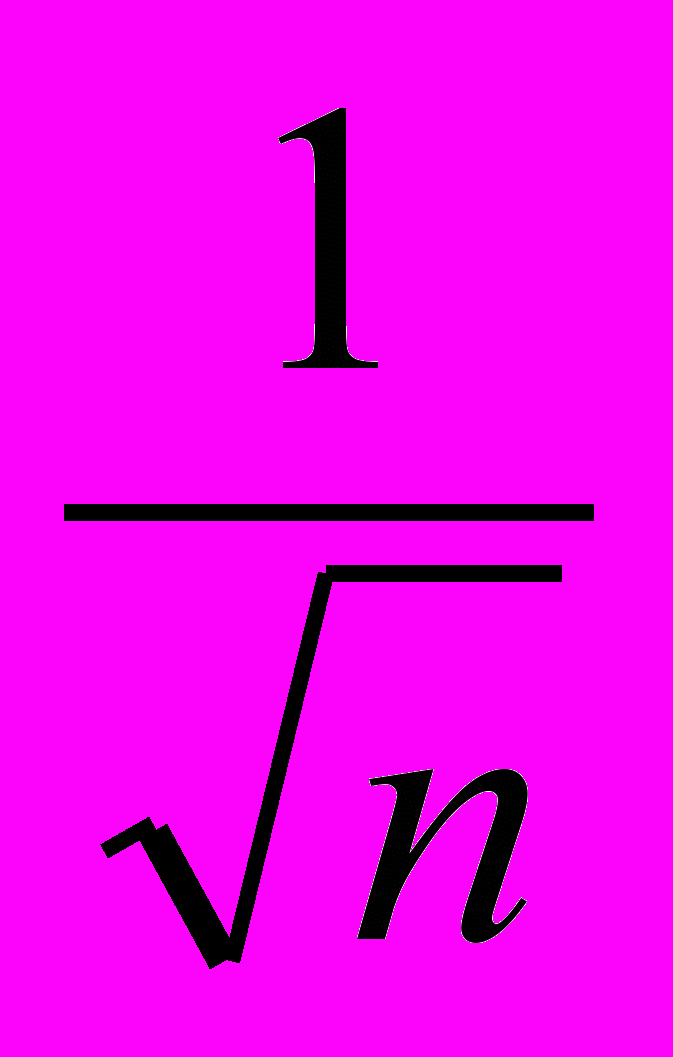для каждого из них составит той величины, которую он имел. бы при, селекции только по этому признаку: при селекции на четыре признака он будет вдвое меньше, чем при селекции на. один. Следует иметь в виду, что нецелесообразно распылять селекционное давление, распределяя его на большее количество признаков, чем это экономически оправдано. В этой связи представляет интерес использование селекционных индексов.Практические задания
Работа 1.Яйценоскость в популяции кур 236 яиц, среднее квадратическое отклонение 25 яиц, коэффициент наследуемости 0,20. В выведенную селекционную группу отбираются куры, имеющие яйценоскость не ниже 250 яиц. Определить: эффект селекции, долю отобранной группы в популяции, яйценоскость кур отобранной группы и яйценоскость их дочерей.
Работа 2. Используя исходные данные, приведенные в работе 1, сделать аналогичные расчеты при условии, что в селекционную группу отбираются куры, имеющие яйценоскость не ниже 230 яиц.
Работа 3. Яйценоскость в популяции кур 202 яйца, среднее квадратическое отклонение 20 яиц, коэффициент наследуемости 0,16. Сколько потребуется лет для доведения эффекта селекции до 18 яиц при ежегодном отборе в группу для воспроизводства 30% кур популяций?
Работа 4. Масса яйца в популяции кур составляет в среднем 57,5 г при среднем квадратическом отклонении 1,95 и коэффициенте наследуемости 0,60. В группу для воспроизводства отбираются куры, несущие яйца средней массой не ниже 60 г.
Определить: эффект селекции за одно поколение, долю, которую отобранная группа должна составлять в популяции; массу яиц кур отобранной группы и массу яиц их дочерей.
Работа 5. Масса яиц кур в популяции в возрасте 300 дней составляет 56,6 г при среднем квадратическом отклонении 1,80 и коэффициенте наследуемости 0,45. Сколько потребуется лет для доведения эффекта селекции до 5,5 г при отборе в группу для воспроизводства 20% кур популяции?
Контрольные вопросы
- Что такое эффект селекции? Для чего нужно его определять?
- От каких факторов зависит эффект селекции?
- Что такое селекционный дифференциал? В каких единицах он может быть выражен? Что такое «интенсивность селекции»? Как она может быть найдена?
- Как связан эффект селекции с коэффициентом наследуемости?
- Что такое интервал между поколениями?
- Напишите по памяти формулы расчета эффекта селекции
- разной степени сложности.
- По каким этапам ведется расчет эффекта селекции с использованием специальной таблицы?
- Как определить яйценоскость дочерей кур, отобранных в селекционную группу?
- Как определить среднюю яйценоскость кур, отобранных в селекционную группу?
- II. Как рассчитать, сколько лет (или поколений) потребуется для достижения намеченного эффекта селекции?
- Как определить, какую часть в популяции кур должна составлять селекционная группа для достижения намеченного эффекта селекции? Какие исходные данные необходимо иметь для этого?
- В чем состоит различие расчета эффекта селекции для признаков, ограниченных полом, и признаков, характерных для обоих родителей.
- Как изменяются селекционные дифференциалы при одновременной селекции по нескольким признакам?