Конспект лекций Утверждено редакционно-издательским советом университета Омск 2002

Вид материала

Конспект

Содержание 3.1. Общие закономерности процессов механического разрушения 3.2. Процессы механического разрушения металлов и сплавов 3.3. Процессы механического разрушения полимерных материалов 3.4. Механизм образования и развития трещин 3.5. Влияние характера изменения нагрузки 3.6. Адсорбционное понижение прочности под действием

Подобный материал:

• Конспект лекций Рекомендовано в качестве учебного пособия Редакционно-издательским, 1023.31kb.
• Рекомендовано в качестве конспекта лекций Редакционно-издательским советом Томского, 1088.59kb.
• Прокурор в уголовном процессе, 2839.04kb.
• Пособие подготовлено на кафедре экономической теории © Новосибирский государственный, 754.49kb.
• Методические указания к выполнению практических занятий по дисциплине "Осложнения, 1155.63kb.
• Учебно-методическое пособие по выполнению, структуре, оформлению и защите дипломной, 941.58kb.
• Нефтяное товароведение, 1449.59kb.
• Общая и, 861.29kb.
• Методические указания к оформлению курсовых и дипломных проектов (работ) для студентов, 364.72kb.
• Методические указания к курсовому и дипломному проектированию Москва 2007, 873.19kb.

^ 3.1. Общие закономерности процессов механического разрушения


До недавнего времени считались общепринятыми классические представления о пластической деформации и разрушении материалов как о критических событиях, наступающих тогда, когда действующие в материале напряжения достигают некоторой критической величины _кр. Согласно этим представлениям при напряжениях, меньших предела упругости, пластическая деформация вообще не может развиваться, а разрушение тела происходит (практически мгновенно) только тогда, когда напряжения достигнут предела прочно-


14

сти. Однако в последнее время этому взгляду противопоставляется другой подход, согласно которому разрушение материала рассматривается не как критическое событие, а как постепенный кинетический термоактивационный процесс, развивающийся в механически напряженном материале во времени с момента приложения к нему нагрузки, в том числе меньше критической. Разрушение является безактивационным процессом лишь при очень низких температурах (близких к абсолютному нулю) или при действии напряжений, равных пределу теоретической прочности (прочности атомных связей).

В соответствии с этой кинетической теорией, согласно которой одним из фундаментальных свойств прочности является ее зависимость от времени, деформация и разрушение должны характеризоваться не предельным напряжением, но скоростью деформации и разрушения, а также долговечностью  временем, требующимся для разрушения. Пределы упругости, текучести, прочности

являются с этой точки зрения лишь некоторыми условными характеристиками.

Скорость процессов механического разрушения нагруженного твердого тела и, соответственно, время до разрушения зависят от структуры и свойств материала тела, от напряжения, вызываемого нагрузкой, и температуры. Предложен ряд электрических формул, описывающих зависимость времени до разрыва  (или скорости разрушения 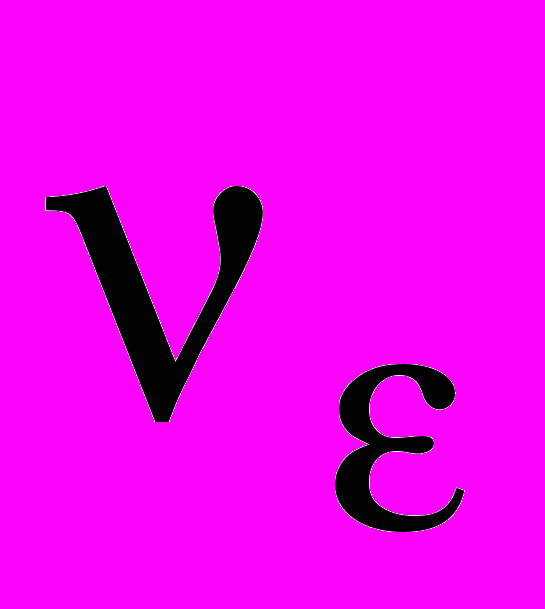) от этих факторов. Наибольшее признание получила установленная экспериментально для многих материалов (чистых металлов, сплавов, полимерных материалов, полупроводников, органического и неорганического стекла и др.) следующая температурно-временная зависимость прочности  зависимость между напряжением , температурой Т и временем  от момента приложения постоянной механической нагрузки до разрушения образца [1,2]:

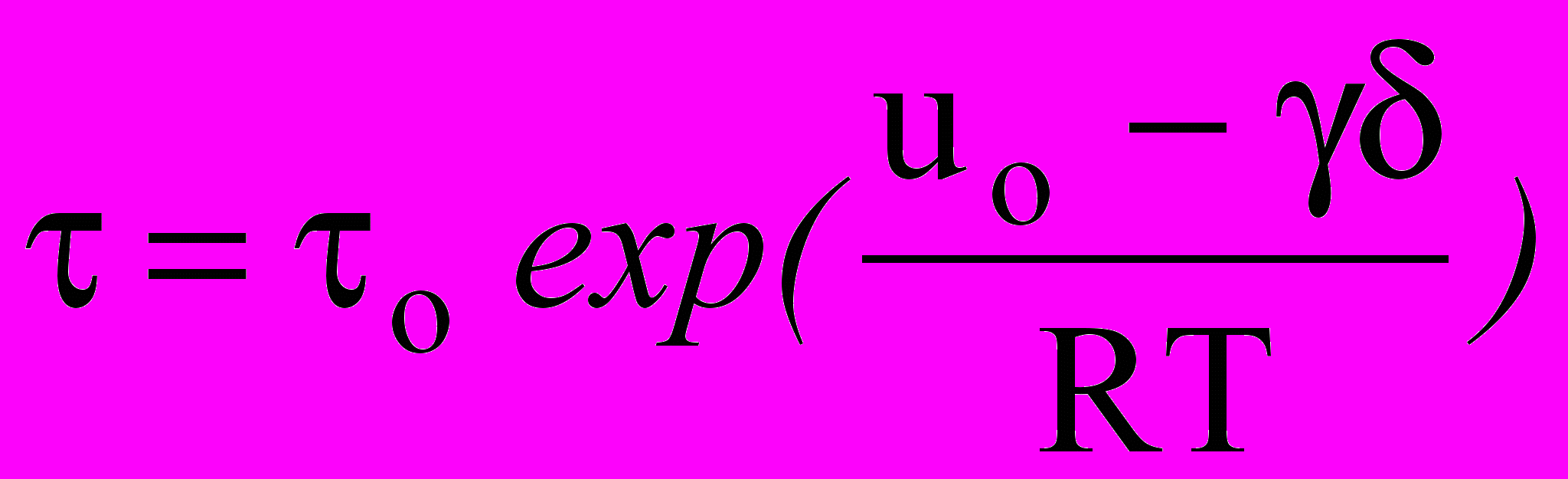, (8)

где _о, u_о,   параметры уравнения, характеризующие свойства материалов.

Для скорости процесса разрушения можно записать:

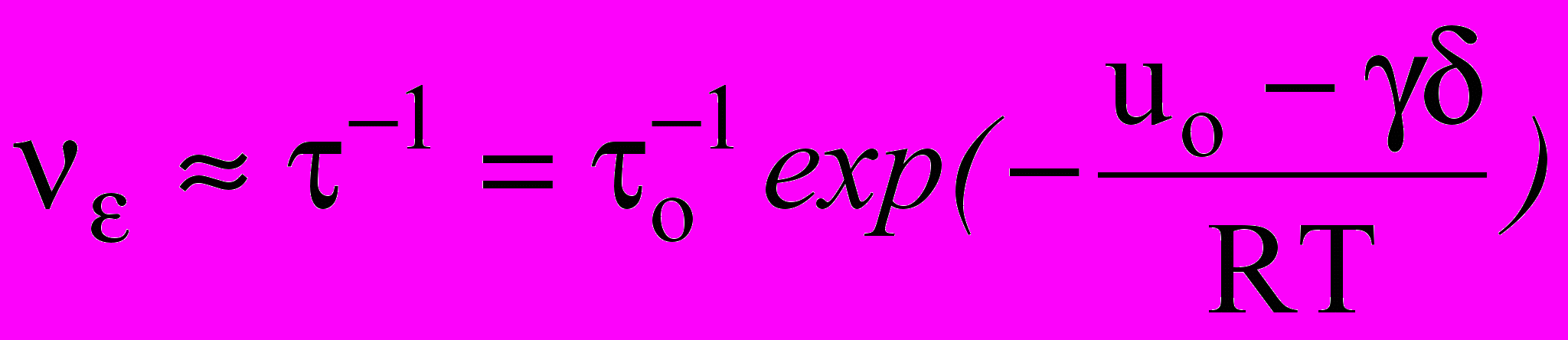. (9)

В уравнениях (8) и (9), характеризующих кинетический процесс разрушения, 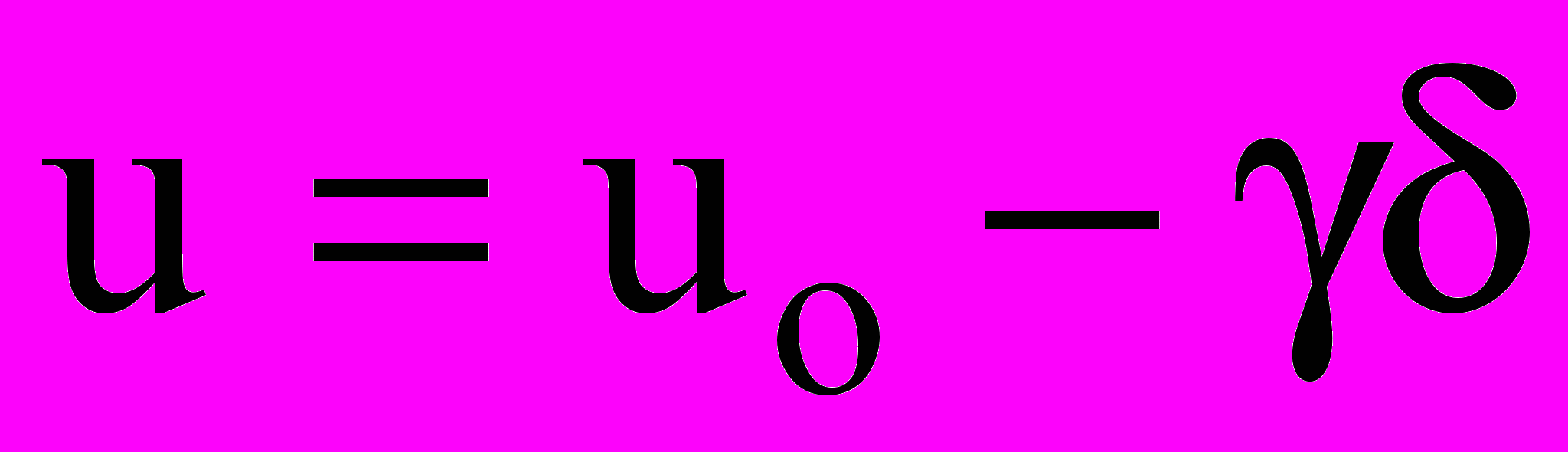имеет смысл энергии активации процесса разрушения, причем u_o представляет собой начальную энергию активации (величину начального энергетического барьера) процесса разрушения при  = 0, постоянную для данного материала в широкой области температур Т и не зависящую от обработки материала (наклепа, термической обработки, легирования и т. д.); 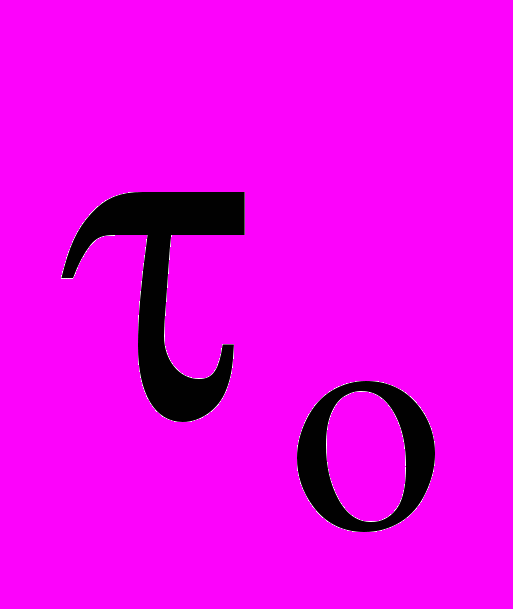и 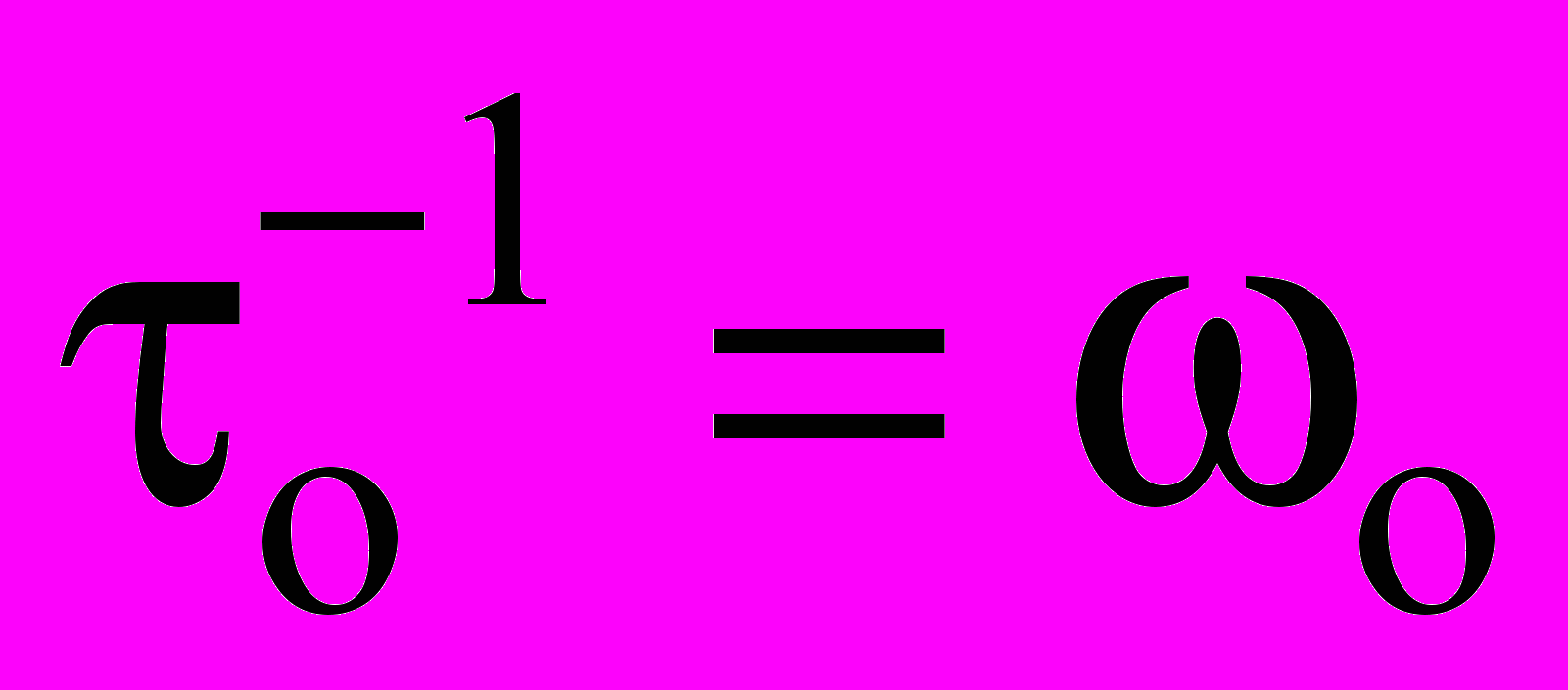– параметры, совпадающие по величине соответственно с периодом и

15

частотой собственных тепловых колебаний атомов в кристаллической решетке твердого тела (равными 10^12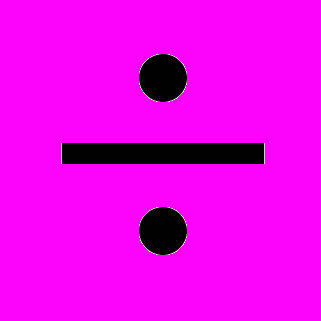10^14 с и 10¹²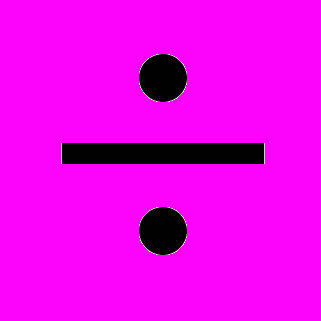10¹⁴ Гц), постоянные для всех исследованных металлов и сплавов, полимеров, ионных кристаллов, не зависящие от обработки материала и условий нагружения;   напряжение материала, обусловленное механической нагрузкой, уменьшающее начальную энергию активации на величину , активирующее таким образом процесс разрушения и создающее направленность процесса;   структурный коэффициент, определяющий степень уменьшения начального энергетического барьера под действием приложенного напряжения (характеристика чувствительности материала к напряжению).

Указанная температурно-временная зависимость прочности проверена в широком интервале напряжений, температур и времени при различных видах напряженного состояния (растяжении, изгибе, кручении), при статических и циклических нагрузках. Справедливость уравнения (8) показана для величины

долговечности  от 10^3 до 10⁷ с; дальнейшее увеличение  всего на порядок (с 10⁷ до 10⁸ с) означает увеличение испытания с нескольких месяцев до нескольких лет.

Зависимости долговечности  материала от напряжения  и температуры Т, аналогичные экспериментально установленной зависимости (8), получены путем теоретического рассмотрения дислокационных механизмов зарождения и развития трещин. Время  разрыва при постоянной нагрузке образцов, изготовленных из одного материала, есть случайная величина (зависящая от случайных размеров и распределения элементарных дефектов в образцах материала), распределяющаяся по некоторому вероятностному закону. Обычно под долговечностью  понимают среднее ее значение.

Хотя временная зависимость отражает внутренний механизм разрушения твердых тел, так как обусловлена тем, что само разрушение представляет собой развивающийся во времени процесс, уменьшению прочности нагруженного образца способствуют побочные процессы, вызываемые агрессивным воздействием среды, действием поверхностно-активных веществ.

Таким образом, зависимость (8) показывает, что разрушение может происходить при напряжениях, меньших предела прочности, и что разрывное напряжение зависит от времени действия приложенной нагрузки и от температуры материала.

Кинетическая теория прочности подчеркивает необходимость учета влияния теплового движения (флуктуации тепловой энергии) на процессы де-

16

формации и разрушения, особенно в их начальной стадии. Процесс разрушения при нагрузках ниже критической не может происходить в отсутствие теплового движения атомов и молекул, которое является фактором, принципиально обусловливающим разрыв материала при нагрузках, меньших критической. Зависимость (8) приводит к выводу, что разрушение следует рассматривать как процесс, в котором за счет тепловых флуктуаций преодолевается энергетический барьер u_о, сниженный в результате действия напряжений на величину . При этом физический смысл величин, входящих в уравнение (8), совпадение величины _о с периодом атомных колебаний показывают, что процесс разрушения представляет собой ряд элементарных актов, связанных с тепловым движением атомов и молекул.


^ 3.2. Процессы механического разрушения металлов и сплавов


Можно считать установленным, что у металлов температурно-временная зависимость прочности, возникновение и развитие микротрещин обусловлены в основном двумя процессами: разрывом межатомных связей за счет тепловых

флуктуаций и направленной диффузией вакансий к трещинам.

Непосредственные измерения величин энергии активации разрушения, энергии самодиффузии, энергии сублимации для ряда металлов и сплавов и исследование характера их изменения показывают, что в области больших напряжений и сравнительно низких температур (меньших 0,5 ,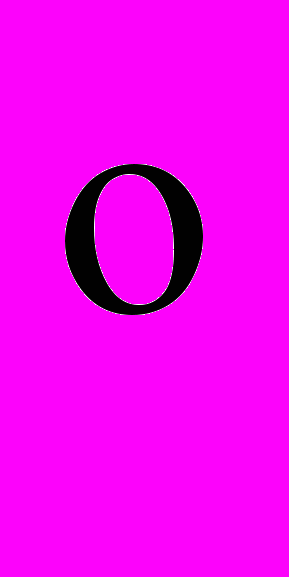К; Т_пл  температура плавления) действует механизм разрушения, обусловленный процессом последовательного флуктуационного разрыва атомных связей в кристаллической решетке, и следовательно, справедлива зависимость (8).

В области малых напряжений и высоких температур действует диффузионный механизм разрушения, основанный на росте трещинки путем притока вакансий или на образовании очагов нарушения связей в месте скопления избыточного числа вакансий, что приводит к температурно-временной зависимости прочности следующего вида [1]:

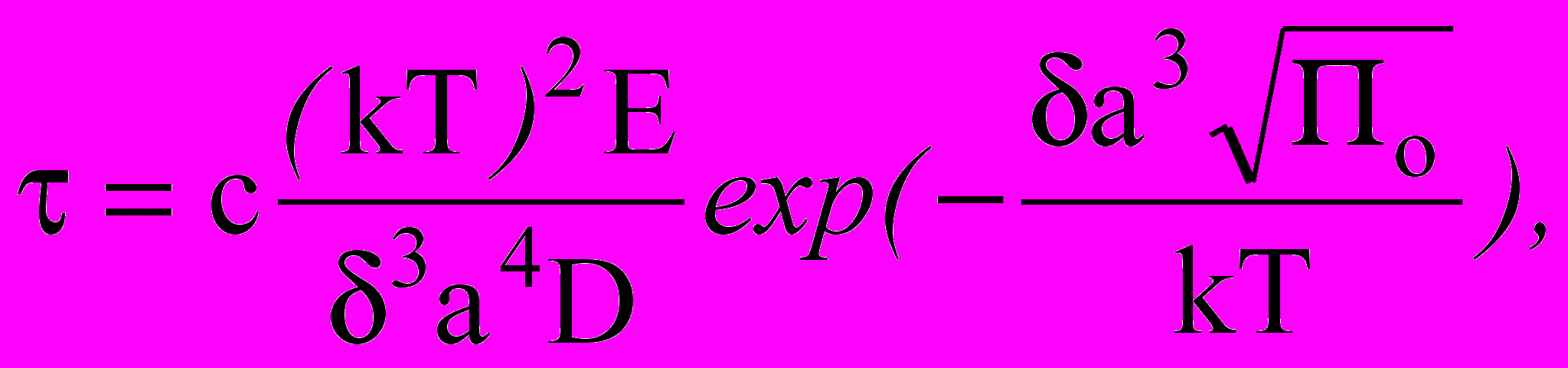(10)

где D  коэффициент объемной диффузии;

П_о  количество объединившихся вакансий;

а  атомный размер;

17

  действующее напряжение;

Е  модуль упругости;

К  постоянная Больцмана;

С  численная константа порядка единицы.

Параметры u_о, _о, , входящие в уравнение (8), полностью характеризующие в «низкотемпературной» области прочностные свойства металлов и сплавов во времени (при процессах разрушения и деформации), являются недостаточными для описания этих свойств при переходе в «высокотемпературную» область, где проявляется новый фактор  дифференционная подвижность атомов, влияние которого на механизм разрушения становится при некоторых условиях преобладающим.


^ 3.3. Процессы механического разрушения полимерных материалов


Процессы, вызывающие разрушение нагруженного полимерного материала, представляют собой процессы разрыва внутримолекулярных химических связей в результате тепловых флуктуаций, т. е. процессы термодиструкции полимерных цепей, активированные механическими напряжениями. Для полимерных материалов температурно-временная зависимость прочности (8) определяется кинетикой постепенного флуктуационного разрыва химических связей. Энергия активации процесса разрушения полимеров, уменьшающаяся под действием напряжения, соответствует энергии активации термодиструкции; при этом величина u_о в формуле (8) представляет собой энергию активации процесса термодиструкции полимерных цепей в ненапряженном полимере, равную энергии химической связи между атомами в полимерной цепочке.

Большое практическое значение имеет знание закономерностей разрушения составных материалов, армированных волокнами. Механизм разрушения этих материалов представляется следующим. Вследствие того, что волокна имеют дефекты, распределенные по их длине, разрушение волокон происходит в некоторых случайных точках (сечениях) при нагрузках, меньших, чем общая разрушающая нагрузка для составного материала. В месте разрушения волокна возникает концентрация напряжений, которая при увеличении нагрузки может вызвать появление небольших местных трещин в связующем (основном) материале. В процессе дальнейшего нагружения за счет сдвига связующего материала смежные трещины соединяются друг с другом. Этот процесс разрыва во-


18

локон, возникновения местных трещин в основном материале и соединения смежных трещин продолжается непрерывно до общего разрушения составного материала.


^ 3.4. Механизм образования и развития трещин


Локальный характер разрыва твердых тел показывает, что кинетика разрушения (и долговечность материала) определяется прежде всего развитием трещин разрушения. Механизм процесса разрушения при длительном воздействии нагрузки сводится к постепенному росту микротрещин до критического размера в результате флуктуационного разрыва атомных связей в вершине (устье) трещины. Таким образом, развитие микротрещин в напряженном теле представляет собой сущность процесса разрушения.

Исследования показывают, что трещины образуются вскоре после приложения нагрузки обычно на различного рода дефектах: включениях, неоднородностях, царапинах, и их развитие занимает основную часть времени до разрыва (например, в меди на развитие видимых трещин до разрыва затрачивается 90 % времени, в пластмассах–до 99 % ). Обычно различают две стадии роста трещины: стадию медленного роста с увеличивающейся скоростью (стадию ускоренного роста), преобладающую по времени, и стадию быстрого роста с постоянной предельной скоростью, близкой к скорости звука в материале. Длительность этой стадии составляет незначительную долю по сравнению с длительностью ускоренной стадии и временем разрыва образца.

Время до разрушения (долговечность под нагрузкой) определяется скоростью роста трещин на ускоренной стадии [1]


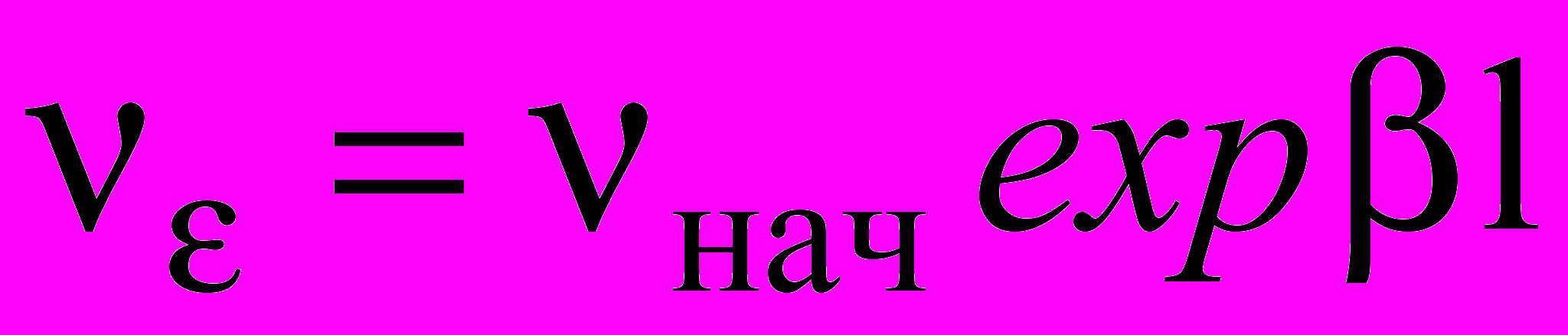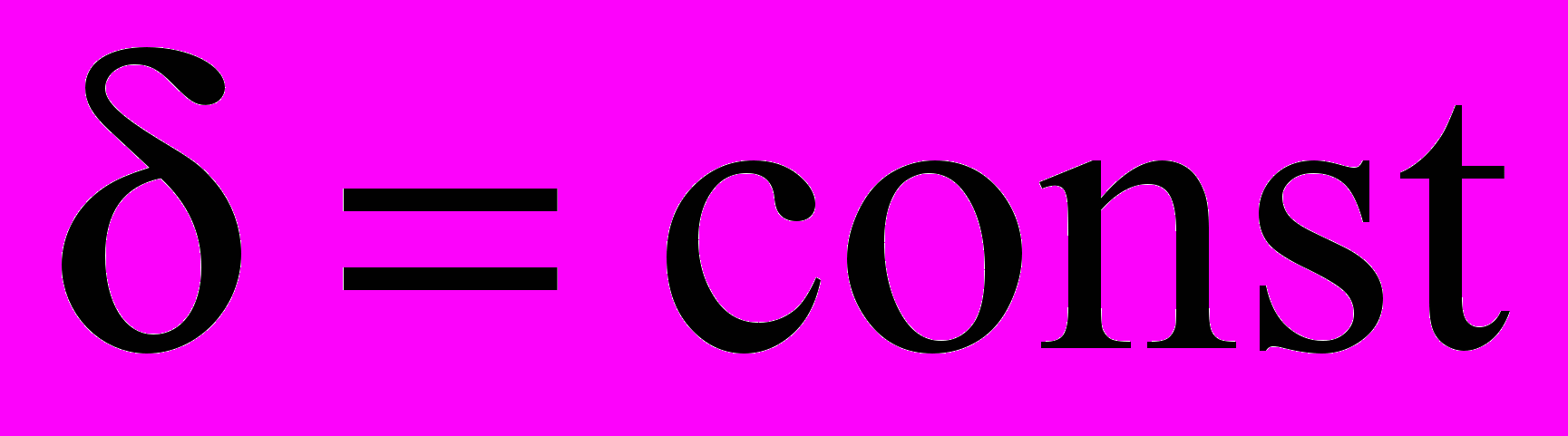при и 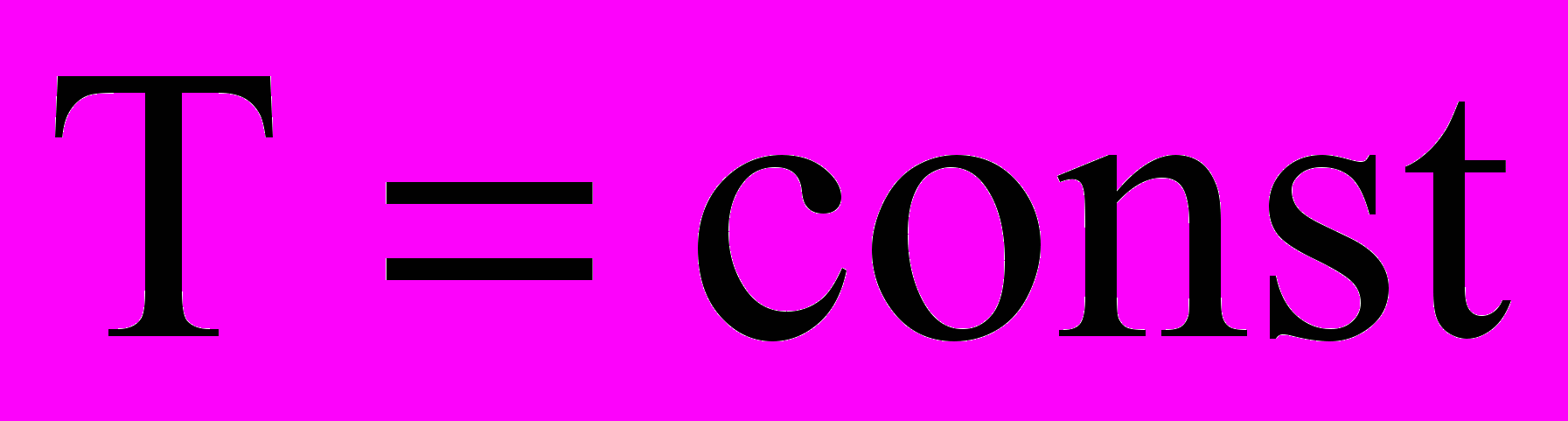; (11)

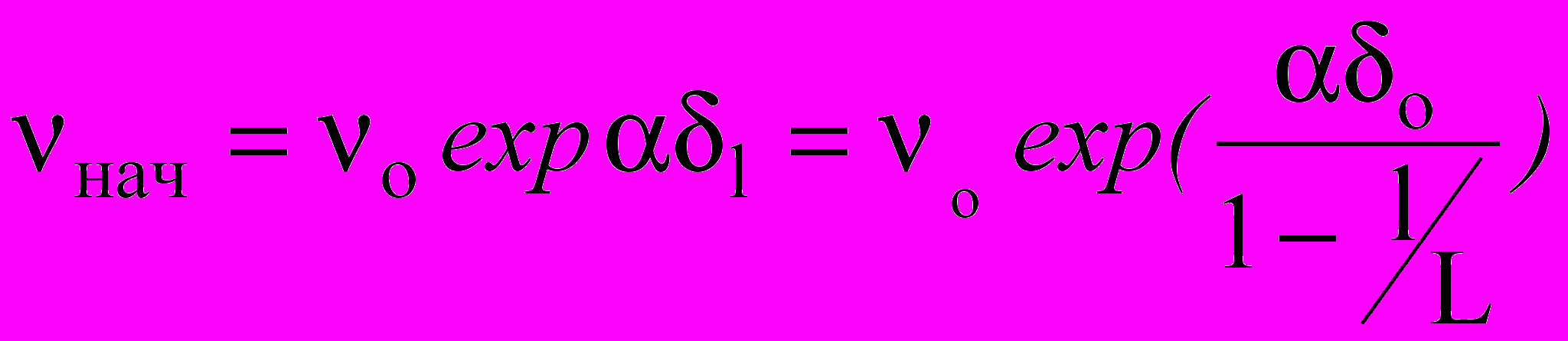, (12)


где 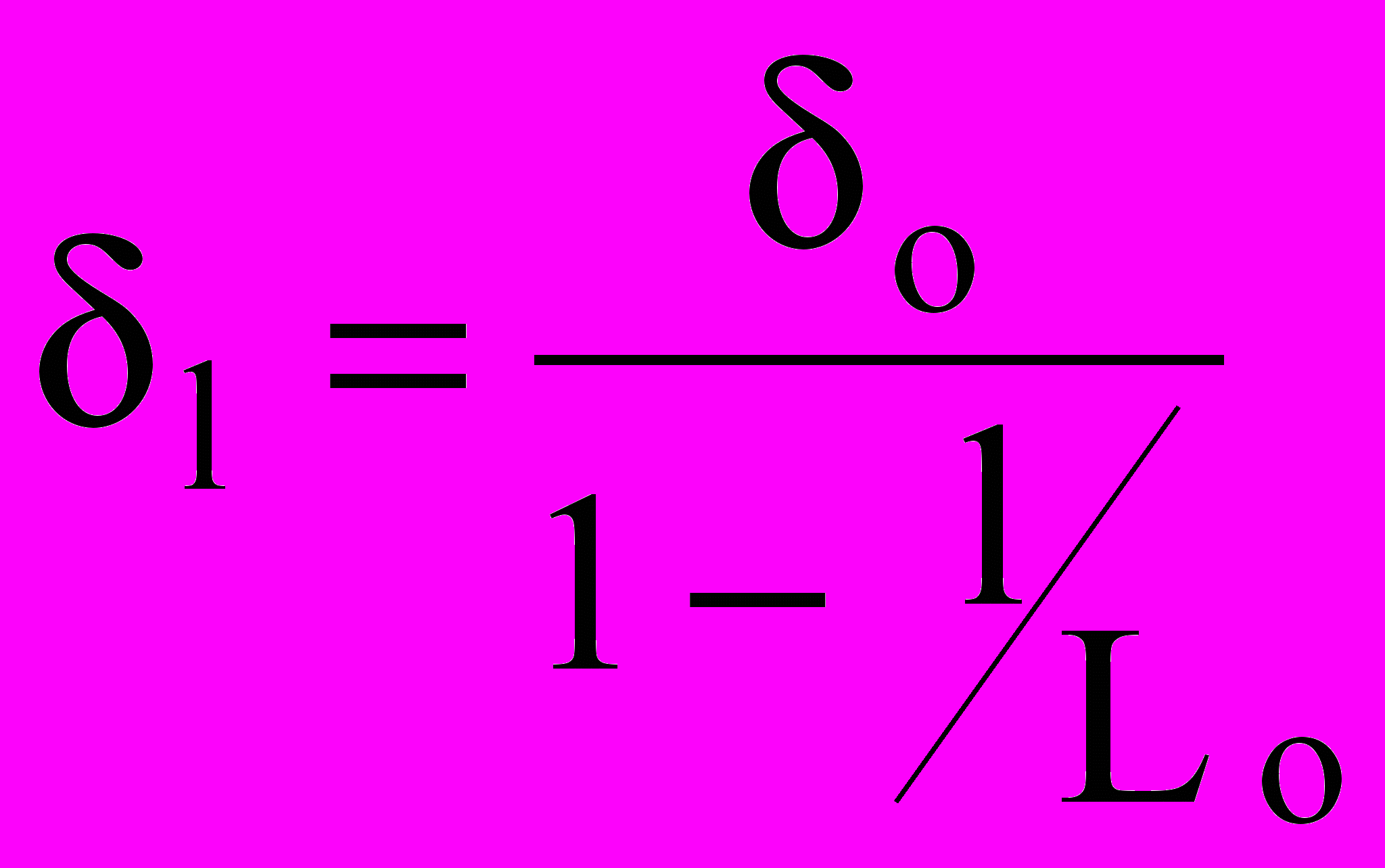 среднее напряжение в оставшейся неразорванной части образца;

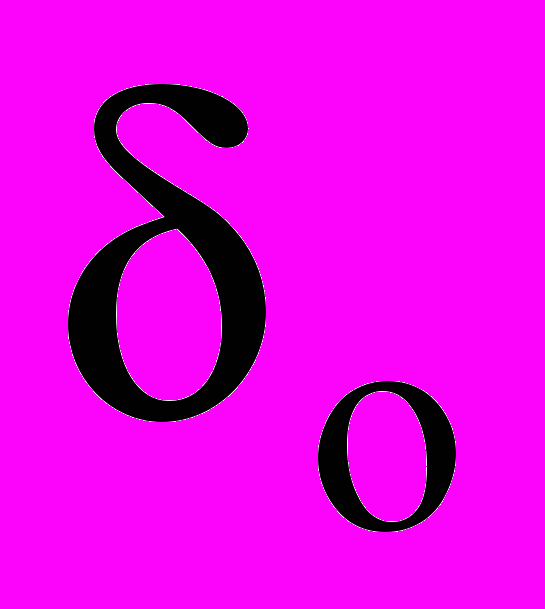 среднее приложенное напряжение;

L  ширина образца;

l  длина трещины;

19

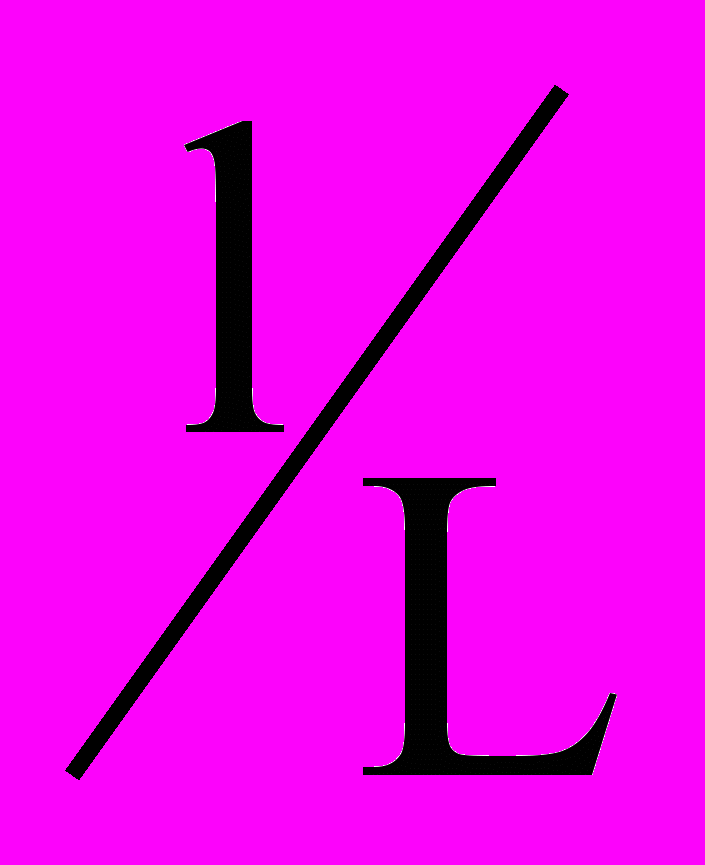 относительная длина трещины;

 и _о  постоянные, определяемые свойствами материала;

  коэффициент, характеризующий самоускорение процесса разрыва при

данных значениях напряжения и температуры.

Экспоненциальная связь между скоростью роста трещины и напряжением определяет лавинообразный характер развития трещин; увеличение длины трещины под действием постоянной нагрузки приводит к постепенному увеличению напряжения 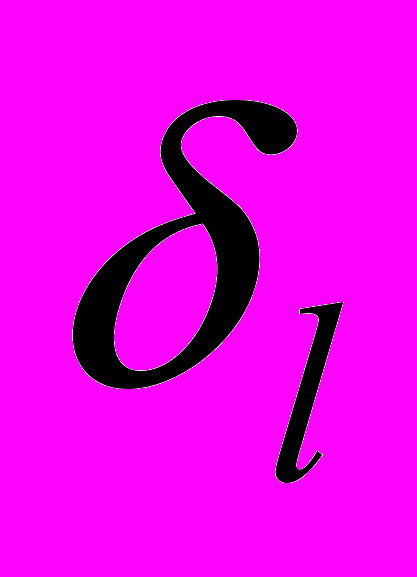, что, в свою очередь, согласно уравнению (12) резко увеличивает скорость роста трещины и вызывает самоускорение процесса ее развития. Такой характер зависимости скорости распространения трещины объясняет, почему имеющиеся в материале дефекты, создавая локальные перенапряжения, тем самым становятся центрами разрушения. Исследования свидетельствуют об отсутствии порогового напряжения для начала роста трещины.

На основании уравнений (11), (12), записанных в дифференциальной форме 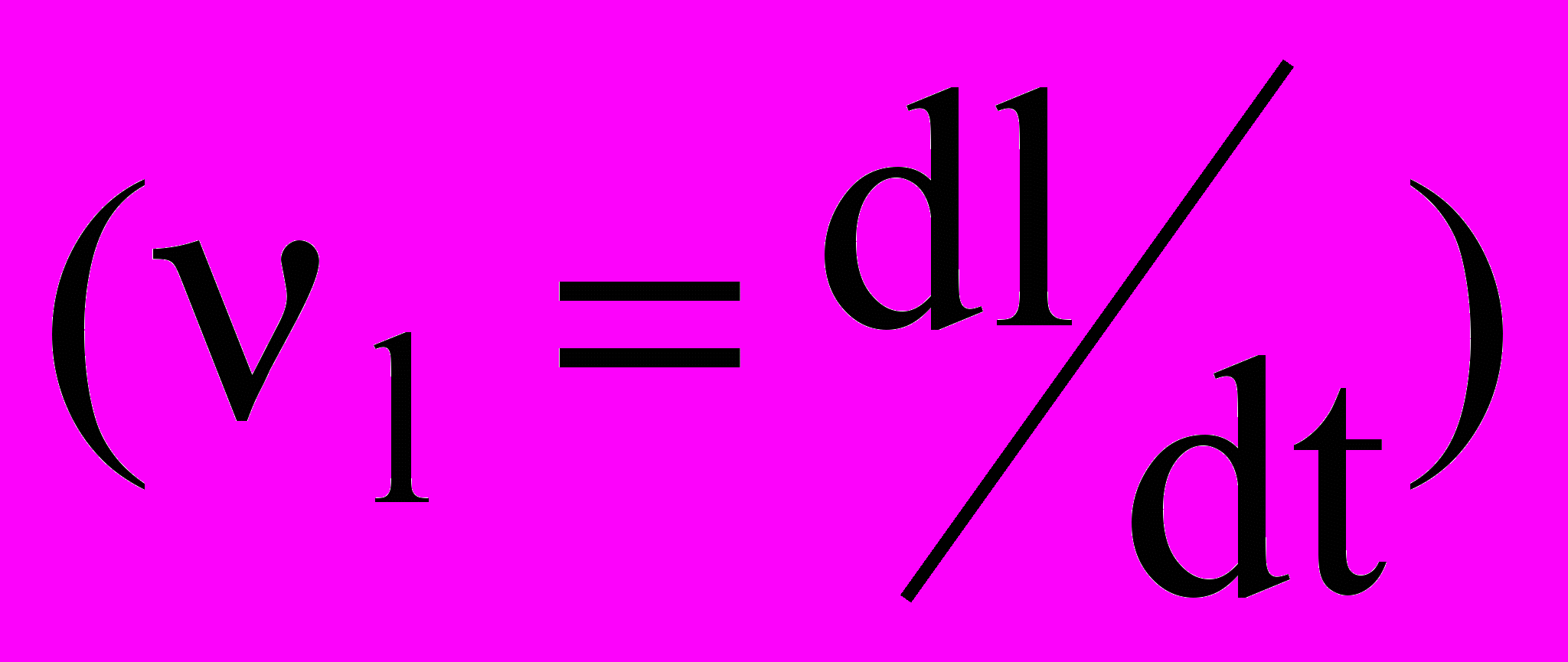, полагаем, что при t = 0 длина трещины 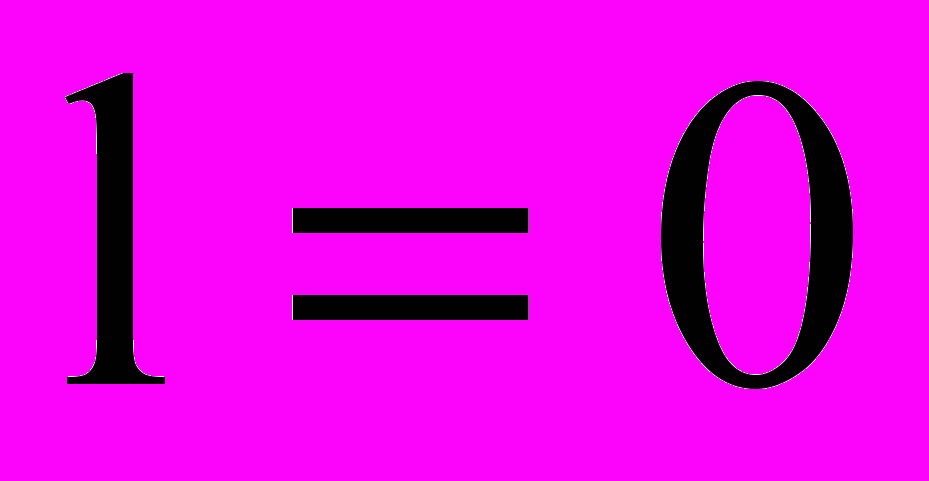, а по истечении времени  трещина пересечет весь образец, т. е.

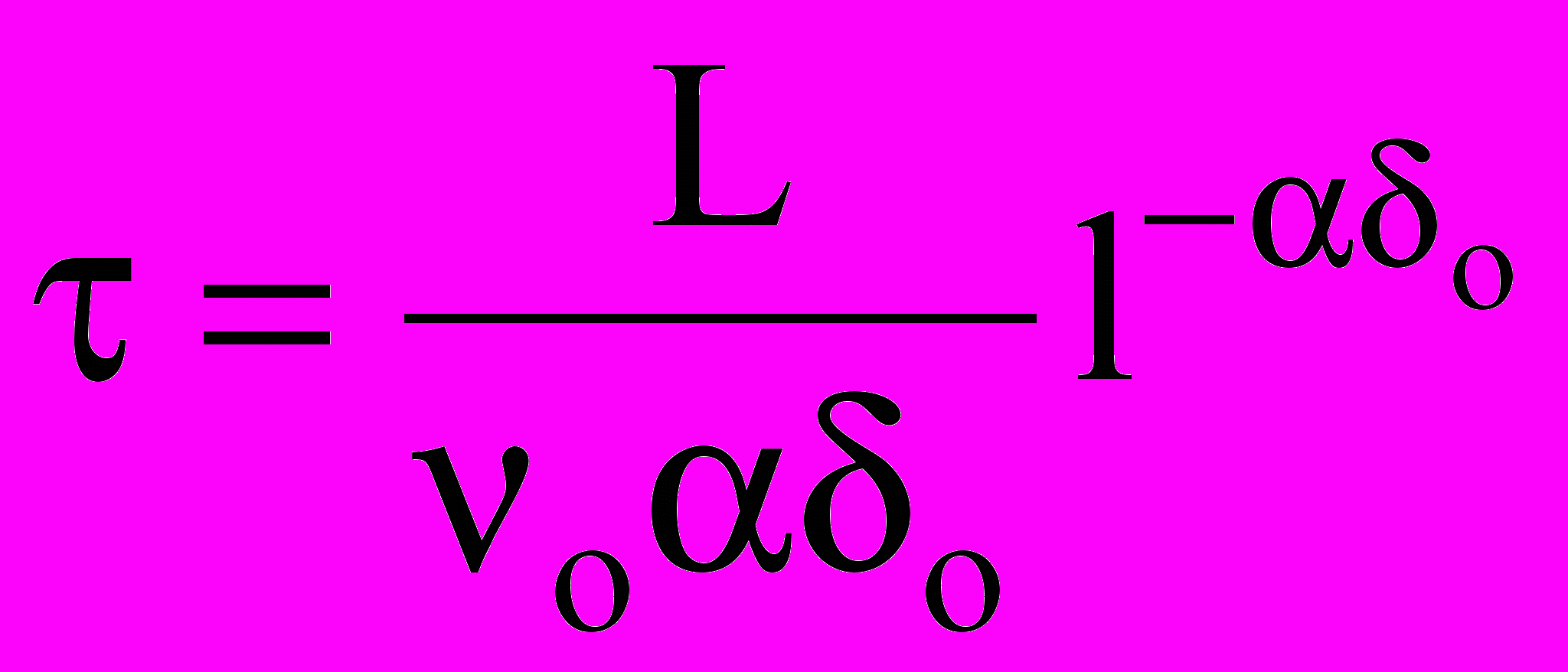. (13)

Значения времени , необходимые для разрушения (разрыва) образца, вычисленные по скорости роста трещин (11), совпадают со значениями времени, полученными при эксперименте. В пределе при мгновенном приложении нагрузки, создающей среднее напряжение, равное теоретической прочности ( = _теор)_, все связи в сечении будут разрываться одновременно и  будет близко к _0.

Время до разрушения зависит от формы и размеров нагруженного образца (детали). Переход от одной формы образца к другой, хотя и не изменяет основных выводов, но меняет вид получаемых аналитических зависимостей.

^ 3.5. Влияние характера изменения нагрузки

на разрушение материалов


Процессы разрушения материалов сводятся, главным образом, к постепенному росту деформаций и трещин, к постепенному накоплению локальных дефектов, которое становится возможным вследствие необратимого характера

последовательных случайных единичных нарушений (необратимости каждого

20

парциального влияния нагрузки). Необратимость процесса накопления повреждений подтверждается результатами опытов с прерыванием нагрузки и последующим нагружением; при этом суммарное время пребывания под нагрузкой до разрушения в среднем равно долговечности образцов материала при непрерывном нагружении.

В случае изменяющегося во времени напряжения  произвольной последовательности напряжений _i, каждому из которых соответствует долговечность (_i), причем время действия каждого напряжения равно t_i  разрыв образца произойдет тогда, когда сумма относительных уменьшений долговечности (располагаемого ресурса) станет равной единице. Для случая дискретной зависимости напряжений  от времени t, когда напряжение в отдельных интервалах времени остается постоянным, изменяясь только при переходе от одного интервала к другому, условия разрушения образца будут такими:

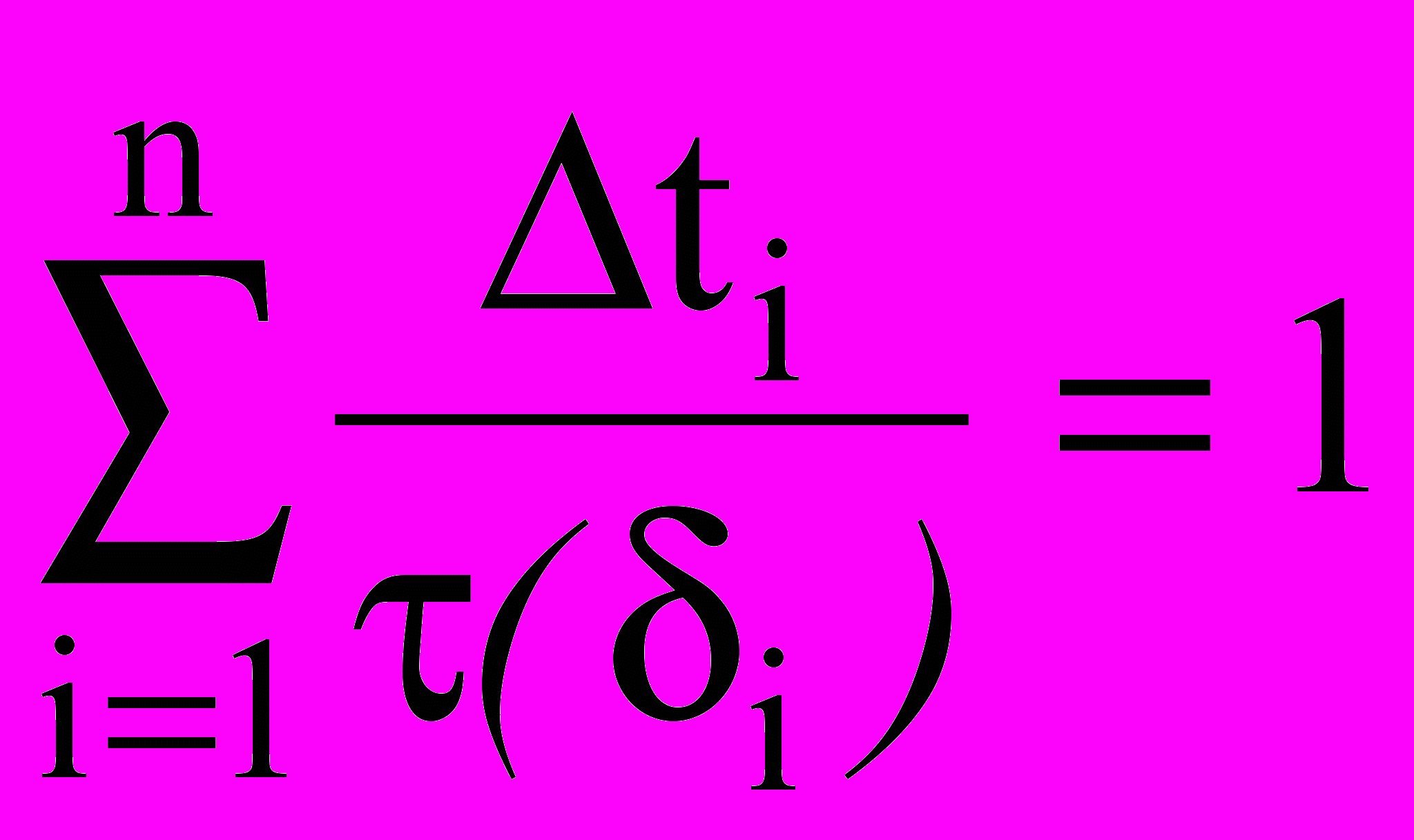; (14)

если напряжение является непрерывной функцией времени (t) , условие разрыва образца имеет вид:

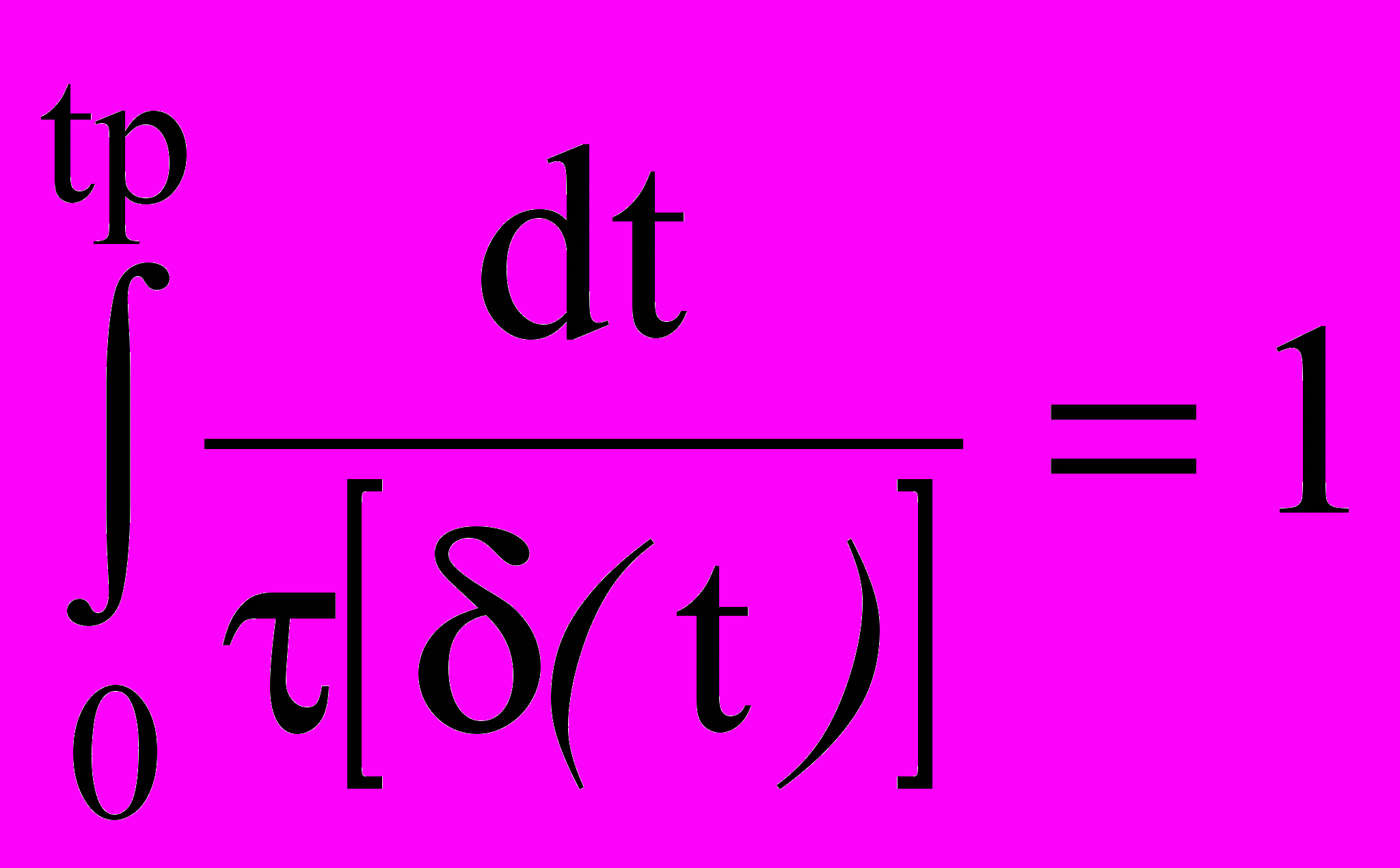, (15)

где t_p  время до разрушения образца;

(t)  временной режим нагружения;

(t)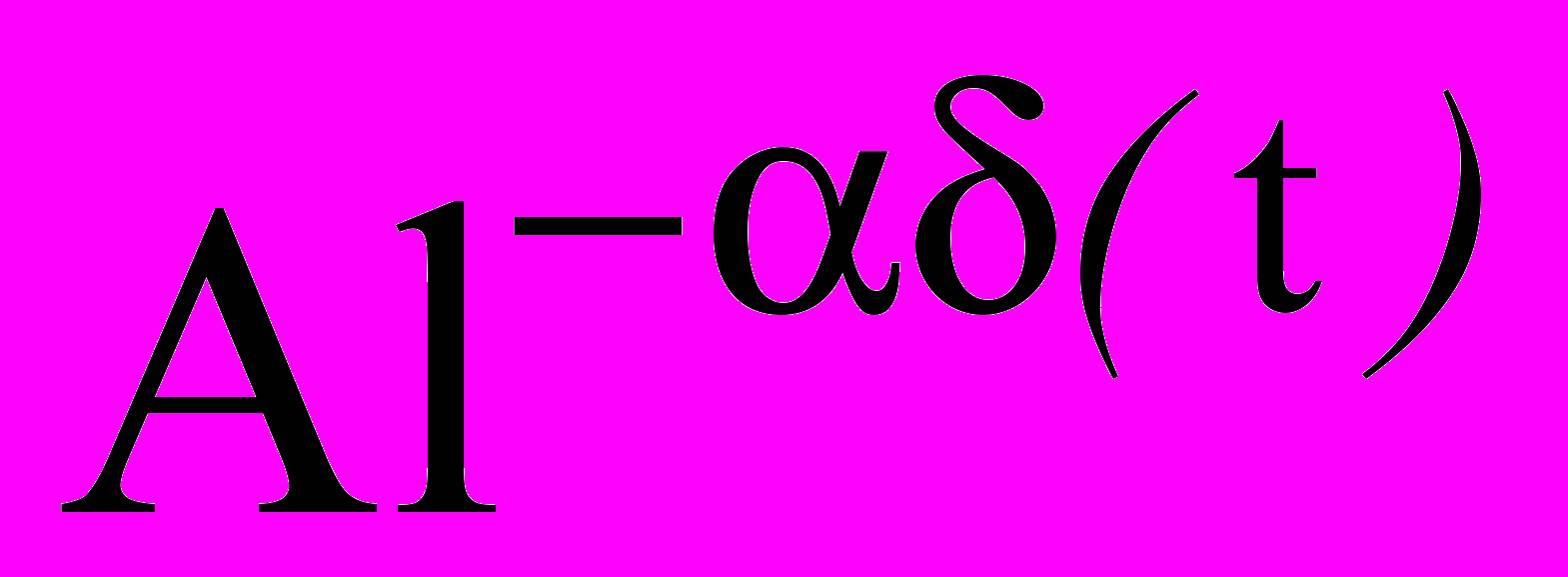=  долговечность при данном напряжении.

Условия (14), (15) характеризуют принцип наложения или суммирования парциальных разрушений; отдельные локальные разрушения суммируются вплоть до предельного состояния, когда трещина достигает критической величины и происходит разрушение образца.

Процессы разрушения при циклическом режиме нагружения, для которого давно установлена временная зависимость прочности, и при статическом нагружении обычно противопоставляются друг другу; предполагается, что закономерности разрушения при циклическом и статическом нагружении различны. Однако кинетическая теория разрушения твердых тел дает основание считать, что, хотя характер изменения внешней нагрузки оказывает влияние на процессы деформации и разрушения, существует определенная общность процессов разрушения независимо от условий нагружения; процессы разрушения обусловлены одинаковым механизмом.

Скорость нагружения существенно влияет на механизм разрушения твер-

21

дого тела. При медленном увеличении нагрузки происходит упругая деформа-

ция, затем – пластическое течение твердого тела и, наконец, – его разрыв. Медленное возрастание механического напряжения может сопровождаться протеканием вторичных процессов в твердых телах и соответствующими обратимыми и необратимыми изменениями свойств тела. При большой скорости нарастания механического напряжения обычно происходит хрупкое разрушение большинства материалов.


^ 3.6. Адсорбционное понижение прочности под действием

поверхностно-активных веществ


Процессы разрушения, протекающие в твердом теле, существенно зависят от его физико-химического взаимодействия с окружающей средой. Установлено, что долговечность, например, меди и алюминия в вакууме до 10^5 мм рт. ст. увеличивается соответственно в 20 и 10 раз по сравнению с долговечностью в обычной атмосфере. Воздействие почти всех активных сред начинается с адсорбции элементов среды (молекул или ионов) на поверхности твердого тела. Таким образом, адсорбционный механизм влияния среды является первичным (предшествующим всем другим видам влияния внешней среды на свойства материалов) и наиболее универсальным.

Адсорбционное влияние окружающей среды обусловлено, главным образом, двумя факторами:

а) влиянием физико-механического состояния поверхности твердых тел (металлов и неметаллов) на их механические свойства. Характеристики пластической деформации, сопротивление ползучести, усталостная прочность и внутреннее трение значительно изменяются в зависимости от состояния поверхности. Прочность твердых тел пропорциональна их поверхностной энергии, следовательно, факторы, вызывающие уменьшение свободной поверхностной энергии, т. е. уменьшение работы образования новых поверхностей, вызывают тем самым более или менее значительное снижение прочности;

б) действием так называемых поверхностно-активных (адсорбционно-активных) веществ (ПАВ), снижающих поверхностную энергию твердого тела. Понижение свободной поверхностной энергии, связанное с адсорбцией, лежит в основе изменений механических свойств (прочности и пластичности) твердых тел под влиянием поверхностно-активных веществ (эффект Ребиндера). Поскольку разрушение можно рассматривать как процесс образования новых по-

22

верхностей (поверхностей трещин и разломов), то, следовательно, адсорбция

поверхностно-активных веществ, уменьшая работу, необходимую для образования новых поверхностей, снижает сопротивление разрушению.

Различают внешний и внутренний адсорбционные эффекты. Внешний вызывается адсорбцией поверхностно-активных веществ на внешней поверхности твердого тела, что приводит к снижению предела текучести и коэффициента упрочнения. Внутренний адсорбционный эффект возникает в результате адсорбции поверхностно-активных веществ на поверхности дефектов внутри твердого тела, следствием чего является снижение прочности и хрупкость.

Принято различать проявление адсорбционного понижения прочности под влиянием органических поверхностно-активных веществ, жидких металлов и электролитов.

Органические ПАВ  спирты, высшие жирные кислоты, канифоли, мыла и т. д.  имеют значительную по величине дифильную молекулу (состоящую из какой-либо полярной группы  СООН, ОН, NH₂, SH, CN, NO₂, CHO и т. п., обладающей большим дипольным моментом, и неполярного углеводородного радикала), которая не может диффундировать в решетку металла. Действие органических ПАВ чисто поверхностное, причем эти вещества незначительно снижают уровень поверхностной энергии металла (не более 10  15 % от исходного); их называют слабыми поверхностно-активными веществами. Расплавленные легкоплавкие металлы, атомы которых по величине соизмеримы с константой решетки твердого металла, могут диффундировать в него и способны значительно снизить уровень поверхностной энергии твердого металла; эти поверхностно-активные вещества носят название сильных.

Ионы электролитов, склонные к специфической адсорбции на поверхности твердого металла, заряжают эту поверхность, но из-за значительного размера обычно не могут внедриться в решетку, причем ионы галогенов сильно снижают уровень поверхностной энергии металла, тогда как другие ионы, например, сульфатные, слабо влияют на уровень поверхностной энергии (аналогично слабым ПАВ).

Разупрочняющее действие ПАВ связано с наличием микротрещин на поверхности, возникающих в процессе деформации или имевшихся еще до приложения нагрузки. ПАВ физически адсорбируются на поверхности тела, внедряясь во все дефекты, мигрируя к основанию трещины. В результате создается большое давление, величина которого определяется уравнением, выведенным для давления, развивающегося в капиллярах:

23


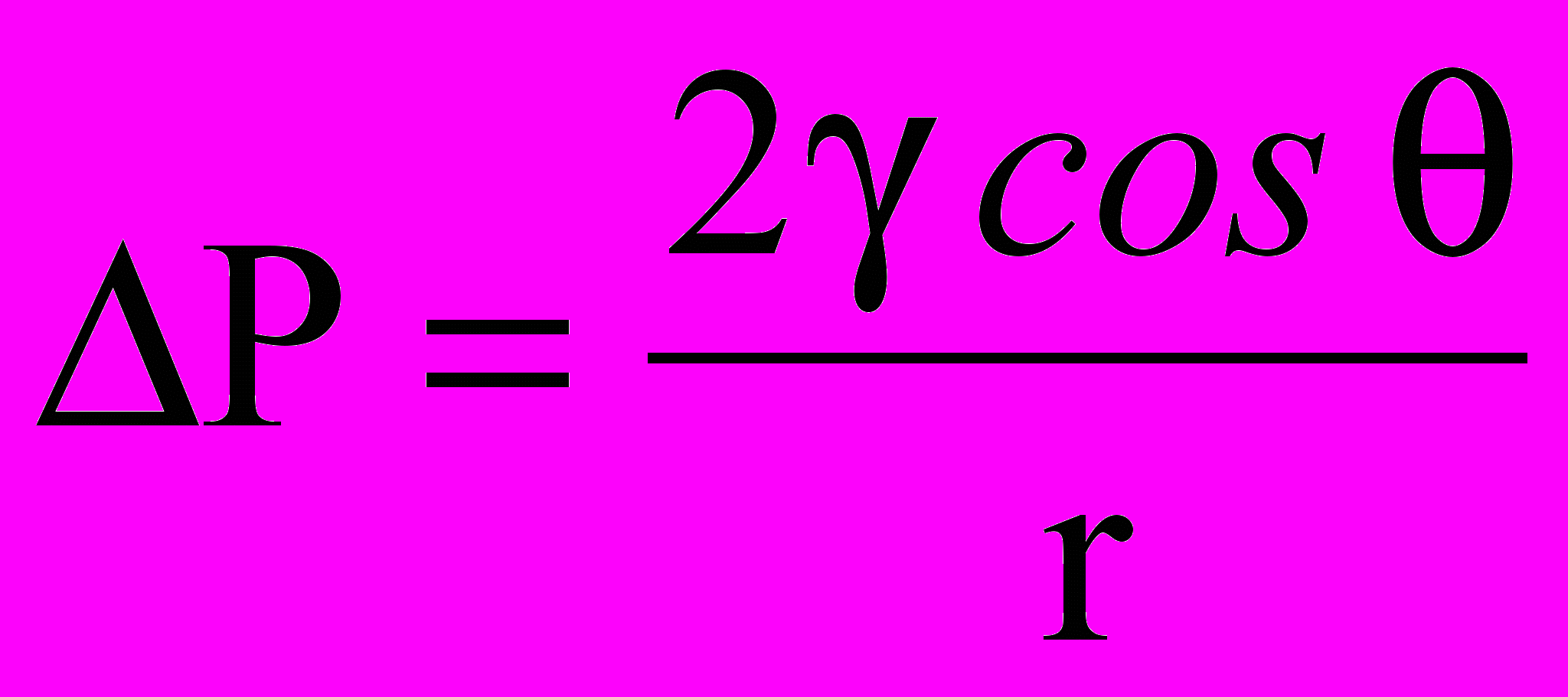, (16)

где   давление поперек мениска;

r  радиус поры;

  угол контакта, характеризующий степень смачивания;

  свободная поверхностная энергия.

Когда материал смачивается полностью (cos = 1), 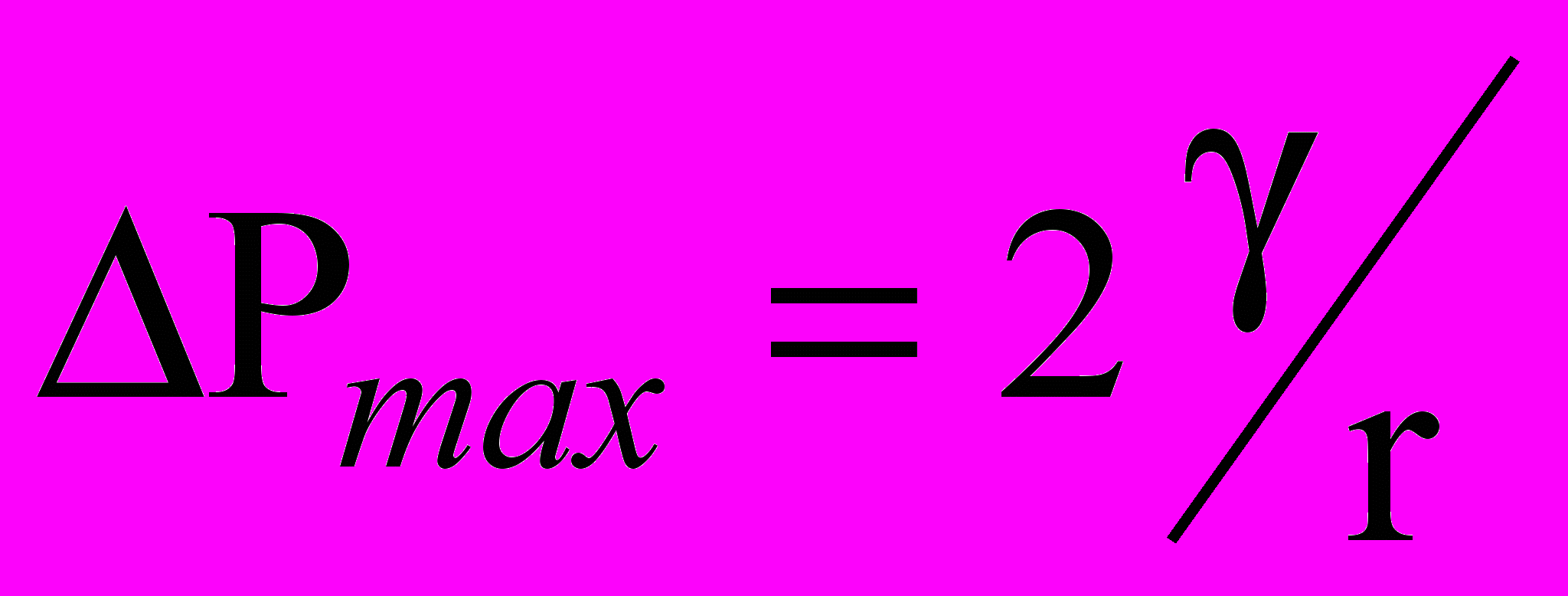. При малом значении r давление может быть очень большим.