Г. Г. Яновский Официальные оппоненты: доктор технических наук, профессор

Вид материала

Содержание

Г.Г. Яновский
В.Х. Харитонов
Цели и задачи исследования.
Методы исследования.
Научная новизна
Практическая ценность
Реализация результатов работы
Апробация работы и публикации
Личный вклад автора
Структура и объем работы
ОСНОВНОЕ Содержание работы
В первой главе
Вторая глава
P должен иметь значение между 0 и 1; строки P
Описание МККС с n состояниями
Вектор предельных
Марковских моделей с двумя состояниями

Подобный материал:

На правах рукописи

Томашевич

Виктор Сергеевич

Исследование процесса потерь кадров в беспроводных локальных сетях

05.12.13

Системы, сети и устройства телекоммуникаций

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук

САНКТ-ПЕТЕРБУРГ

2010

Работа выполнена в Санкт-Петербургском государственном университете телекоммуникаций им. проф. М.А. Бонч-Бруевича.

Научный руководитель: доктор технических наук, профессор

Г.Г. Яновский

Официальные оппоненты: доктор технических наук, профессор

М.А. Сиверс

кандидат технических наук

Т.В. Иванова

Ведущая организация: ФГУП «ЛОНИИР»

Защита состоится «___»___________2010 г. в _____часов на заседании диссертационного совета ДХХХ.ХХХ.ХХ при Санкт-Петербургском государственном университете телекоммуникаций им. проф. М.А. Бонч-Бруевича по адресу: 191186, Санкт-Петербург, наб. р. Мойки, 61, ауд. 205.

С диссертацией можно ознакомиться в библиотеке университета.

Отзыв на автореферат, заверенный печатью учреждения, просим высылать по вышеуказанному адресу на имя секретаря диссертационного Совета.

Автореферат разослан «___»_____________2010 г.

Ученый секретарь диссертационного совета,

проф. В.Х. Харитонов

общая характеристика работы

Актуальность работы.

В последние пятнадцать лет наблюдается резкий рост числа сетей локального масштаба на базе беспроводных технологий связи. Широкое распространение в этих сетях получили системы на базе стандарта IEEE 802.11. Появление новых беспроводных технологий передачи информации и новые требования к качеству обслуживания абонентов ставят перед исследователями принципиально новые задачи. Системы стандарта IEEE 802.11 (далее, 802.11), применяемые для построения беспроводных локальных сетей, исследовались в большом числе работ известных отечественных и зарубежных авторов, в том числе в работах В. М. Вишневского, С. Л. Портного, А. П. Ляхова, W. Turin, W.C. Jakes, M. Zorzi и др.

Вместе с тем ряд проблем в системах стандарта 802.11 остается нерешенным. Так, при изучении характеристик беспроводных систем связи важно использовать достоверные канальные модели. Результаты, получаемые при исследовании моделей, могут применяться при разработке механизмов более эффективной эксплуатации (например, для повышения эффективности использования энергетических ресурсов), либо для точной настройки параметров существующих протоколов. Вместе с тем анализ публикаций по системам 802.11 показывает недостаточную глубину исследований процесса потерь в реальных беспроводных системах 802.11, ограниченный анализ моделей путем имитационного моделирования только физического уровня, использование при анализе предположений об отсутствии частотной селективности гладкости канала и др. Частичному восполнению данных пробелов и посвящена настоящая диссертационная работа, что и определяет ее актуальность.

Цели и задачи исследования.

В связи с вышеизложенным целью диссертационной работы является разработка методов описания процесса потерь с помощью Марковских моделей для получения характеристик потерь на канальном уровне, исходя из результатов экспериментальных измерений, проведенных в реальных системах 802.11.

Основные положения данной работы сформулированы на примере протокола беспроводной локальной сети IEEE 802.11b. Тем не менее, большинство полученных результатов может быть использовано в беспроводных локальных сетях всего семейства 802.11.

Для достижения поставленной цели в ходе выполнения теоретических и экспериментальных исследований необходимо решить следующие задачи:

на базе реальной системы 802.11b, развернутой внутри здания, провести экспериментальные исследования по сбору данных, описывающих потери на канальном уровне в исследуемой системе, при различных условиях относительно типа здания, расположения приемников по отношению к передатчику, различных скоростей передачи и размера кадра;
разработать метод построения модели потерь кадров в виде Марковского канала с конечными состояниями (МККС);

на основе полученных экспериментальных данных определить достоверность модели МККС и методов определения параметров МККС с использованием статистических критериев;

разработать метод построения модели потерь кадров в форме скрытой Марковской модели (СММ) с использование алгоритма Баума-Вэлша для определения параметров СММ;

на основе полученных экспериментальных данных определить достоверность модели СММ и методов определения параметров СММ с использованием статистических критериев.

Методы исследования. При получении основных результатов диссертационной работы использовались методы теории вероятностей, теории случайных процессов, в частности, Марковских процессов, методика проведения экспериментальных исследований, а также методы имитационного моделирования с использованием пакетов Matlab и OPNET Modeler.

Научная новизна диссертационной работы заключается в следующем.

1. Проведены экспериментальные исследования реальной системы стандарта 802.11b, в результате которых получены трейсы (последовательности), характеризующие процесс потерь в данной системе беспроводной связи.

2. Для описания процесса потерь предложена модель МККС. Показано, что традиционный метод определения характеристик МККС на основе огибающей замираний характеризуется существенными ошибками.

3. Представлен метод определения параметров МККС на базе экспериментальных данных и проведена проверка достоверности параметров модели МККС с использованием критерия Колмогорова-Смирнова.

4. Для описания процесса потерь предложена модель СММ, использующая экспериментальные данные. Для определения параметров модели применяется алгоритм Баума-Велша, позволяющий получить оценки параметров на базе итерационной процедуры. Для проверки достоверности параметров модели СММ был применен критерий Колмогорова-Смирнова.

Практическая ценность диссертационной работы. В работе проведено экспериментальное исследование конкретной системы 802.11 b в реальных условиях при наличии различных факторов (скорость передачи данных, размер кадра, диапазон частот, метод доступа к среде, мощность при передаче между двумя станциями). Результаты исследования и разработанные модели являются достаточно общими; они могут быть распространены на другие системы этого семейства – 802.11a, d, e, g, h, n и др. при создании беспроводных локальных сетей и использованы как на этапе проектирования, так и на этапе эксплуатации таких сетей.

Реализация результатов работы. Основные результаты диссертационной работы использованы в разработках ФГУП ЛОНИИС, ОАО «Гипросвязь СПб» и в учебном процессе СПбГУТ им. проф. М.А. Бонч-Бруевича, что подтверждается соответствующими актами внедрения.

Апробация работы и публикации. Результаты диссертационной работы докладывались и обсуждались на международных семинарах JASS’2005 и «IEEE Russia Northwest section» (St-Petersburg, 2005), а также на научно-технических конференциях и семинарах СПбГУТ им проф. М.А. Бонч-Бруевича.

По теме диссертационной работы опубликовано 7 печатных работ, из них 1 работа опубликована в перечне изданий, рекомендуемых ВАК.

Основные положения, выносимые на защиту.

Разработка методики проведения экспериментальных исследований системы 802.11b в здании с использованием соответствующих аппаратно-программных средств.
Разработка метода построения модели потерь кадров в системе 802.11b в виде Марковского канала с конечными состояниями.
Разработка метода построения модели потерь кадров в системе 802.11b в виде скрытой Марковской модели
Проверка достоверности определения параметров Марковских моделей на базе статистических критериев.

Личный вклад автора. Основные результаты теоретических и прикладных исследований получены автором самостоятельно. В работах, опубликованных в соавторстве, соискателю принадлежит основная роль при постановке и решении задач и в обобщении полученных результатов.

Структура и объем работы. Диссертационная работа включает пять глав, заключение, приложения и список литературы. Вся работа изложена на ХХХ страницах текста, включающих в себя 16 страниц приложений, 32 рисунка, 19 таблиц. Количество библиографических ссылок – 72.

ОСНОВНОЕ Содержание работы

Во введении обоснована актуальность темы исследования, сформулированы цели и задачи работы, перечислены результаты, полученные в диссертации, определены практическая ценность и области применения результатов, приведены сведения по апробации работы и представлены основные положения, выносимые на защиту.

В первой главе диссертационной работы проведен обзор современного состояния моделирования беспроводных каналов связи. На основании опубликованных работ рассматривается применение Марковских моделей для потерь кадров или пакетов, которые происходят вследствие процесса замираний сигнала. Марковские модели, предложенные ранее, предполагали использование упрощенных условий для определения параметров моделей. В частности, рассматривались достаточно простые схемы модуляции, такие как двоичная фазовая манипуляция (BPSK) или относительная фазовая манипуляция (DPSK), что позволяло упростить процесс конструирования моделей. При определении параметров моделей предполагалось, что канал не является частотно-селективным. Подобные предположения допустимы для систем сотовой связи, где используются простые схемы модуляции; однако в системах, используемых в беспроводных локальных сетях, применяются сложные схемы модуляции, работающие в частотно-селективных каналах. В таких случаях неясно, каким образом можно определить характеристики Марковских моделей или понять, являются ли они адекватными для того, чтобы оценить потери кадров в беспроводном канале. Эти соображения и определяют содержание следующих четырех глав диссертации.

Вторая глава посвящена описанию моделей, предложенных для описания процесса замираний в беспроводных каналах. В ряде работ для моделирования замираний было предложено использовать Марковский процесс с конечными состояниями (МККС), модель которого является развитием модели Гилберта-Эллиота. В диссертации рассматриваются характеристики и ограничения модели Марковского канала с конечными состояниями (МККС).

На Рис. 1 показано, как получаемое отношение С/Ш может быть использовано при создании модели МККС. Отношение С/Ш разбивается на n интервалов, или уровней. Затем каждый из интервалов соотносится с состоянием Марковского процесса. Первый интервал начинается с уровня нулевого значения отношения С/Ш, тогда как последний интервал обычно включает в себя все значения принимаемого отношения С/Ш, которые превышают определенный порог. На Рис. 2 показана модель МККС, представляемая Марковской цепью с n состояниями. В этой модели имеется возможность переходов только в такие же состояния или в смежные состояния. На рисунке вероятности перехода в такие же состояния (p_ii) и вероятности перехода в смежные состояния (p_ij) указаны рядом с каждой из стрелок.

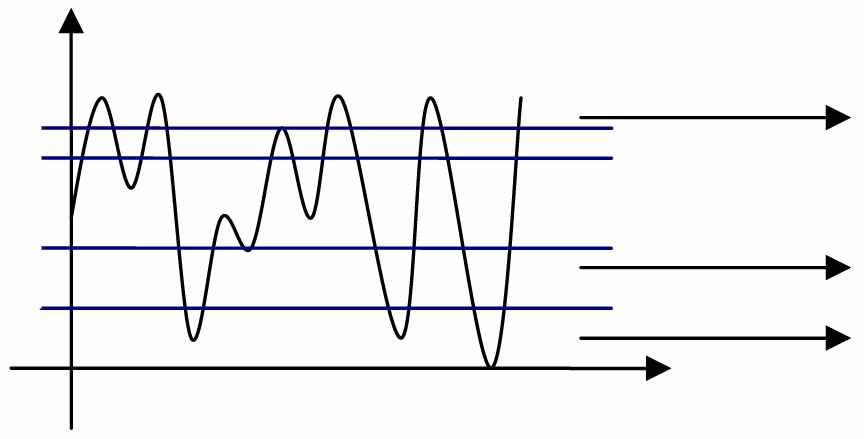Интервал, соответствующий состоянию n

Интервал, соответствующий состоянию 1

Интервал, соответствующий состоянию 0

Время

Рисунок 1. Разбиение отношения С/Ш на уровни

и соответствие каждого уровня состояниям МККС

Элементы, представленные в Табл. 1, подчиняются определенным ограничениям. Любой элемент матрицы переходных вероятностей P должен иметь значение между 0 и 1; строки P должны составлять единицу, и элементы e должны иметь значения между 0 и 0,5.

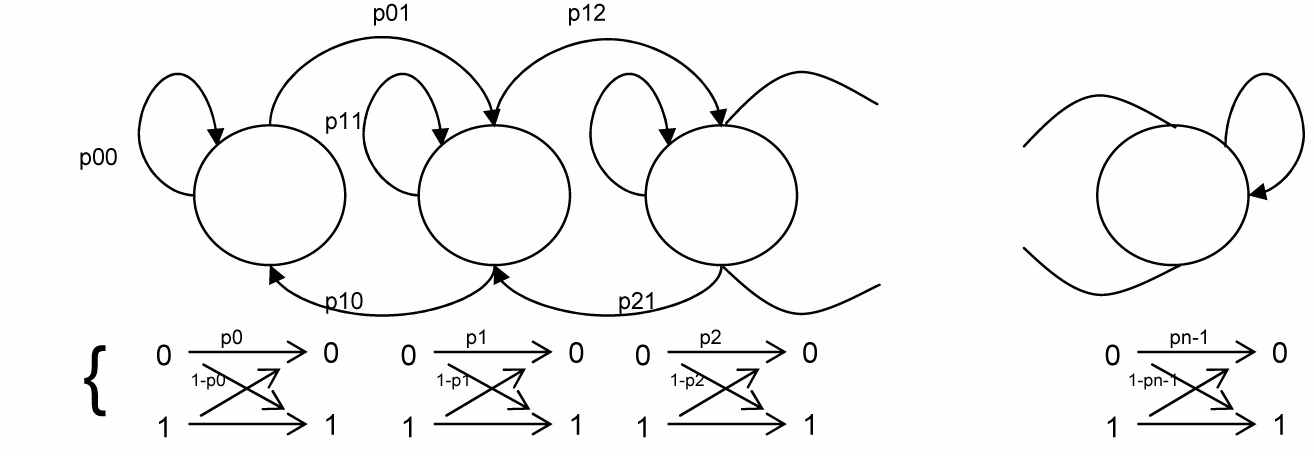
Состояние 1

Состояние 2

Состояние n-1

Состояние 0

Состояния двоичного симметричного канала

Рисунок 2. Модель Марковского канала с конечными состояниями

В Главе 2 рассматривается проблема точности определения параметров модели МККС в зависимости от числа состояний, схем модуляции и кодирования на точность определения параметров МККС. На основе детального анализа опубликованных работ, касающихся схем разбиения значений отношения С/Ш показано, что модель с двумя состояниями дает вполне приемлемые результаты с точки зрения точности параметров МККС. Кроме того, в диссертации показано, что модель МККС является достаточно точной для широкого набора схем модуляции и коррекции ошибок, и выбор схем модуляции и кодирования не влияет на точность определения параметров МККС.

Табл. 1 Элементы, необходимые для описания Марковского канала с конечными состояниями (МККС)

Компонента	Обозначение	Описание МККС с n состояниями
Матрица переходных вероятностей	P	Матрица n×n, представляющая вероятности переходов между состояниями или переходов в то же самое текущее состояние
Вектор предельных вероятностей	π	Вектор 1×n, представляющий предельные вероятности при нахождении в любом из n состояний (дополнительно, π P = π и )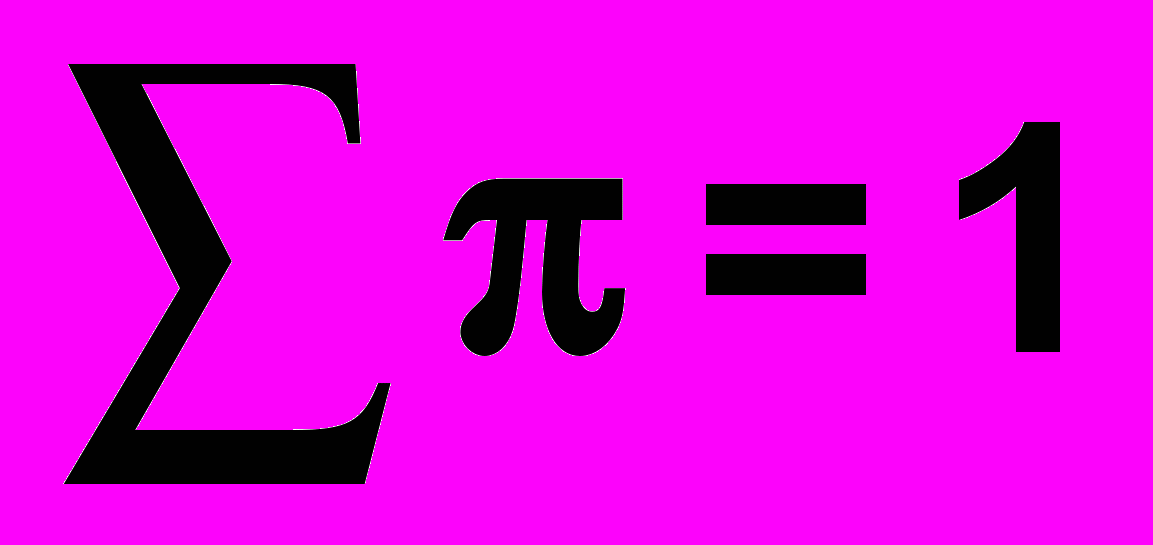
Вектор перекрестных вероятностей	е	Вектор 1×n, представляющий перекрестные вероятности между различными состояниями при наличии символа ошибки в каждом из n состояний

В ряде работ было показано, что применение МККС для моделирования радиоканалов с замираниями, является адекватным в условиях очень медленных замираний, то есть для коротких периодов времени. В тех случаях, когда необходимо учитывать эффект долговременной памяти канала, модель МККС оказывается неприемлемой. Здесь необходимо использовать модели Марковских цепей с большей памятью, однако, поскольку количество состояний возрастает экспоненциально с увеличением памяти, данный подход оказывается практически неосуществимым. В подобных случаях могут быть использованы другие подходы.

В диссертации предлагается использовать в таких случаях подход, основанный на скрытых Марковских моделях (СММ). Далее в Главе 2 обсуждается возможность использования скрытых Марковских моделей, являющихся вероятностными функциями Марковских цепей, для описания процесса потерь в каналах с релеевскими замираниями. Вначале мы обсудим общие понятия и характеристики, относящиеся к СММ и затем рассмотрим, как СММ используются для моделирования замираний.

Модель СММ характеризуется следующими элементами:

набором состояний Марковской цепи представляемым в виде S = {1, 2, … , n} с количеством состояний в модели, равным n. Несмотря на то, что эти состояния называются "скрытыми", в практических приложениях они связаны с некоторым физическим событием.
набором H наблюдаемых выходных символов в любом состоянии, представляемым как H ={,..} с m элементами, где m - размер алфавита.
матрицей P = {p_ij} распределения переходных вероятностей, где p_ij = Pr[текущее состояние = j | предыдущее состояние = i] = Pr [s_j | s_i ]
матрицами B распределения вероятностей наблюдаемого символа. Матрицы B являются диагональными матрицами, чьи элементы b_j представляют собой вероятности p{h | s_j}, где h ∈H.
вектором π финальных вероятностей.

Для нас представляют интерес методы, в которых СММ применяются для описания процесса замираний или потерь кадров. Один из таких методов описан в работе W. Turin, R. Van Nobelen, "Hidden Markov Modeling of Flat-Fading Channels", IEEE Journal on Selected Areas in Communications, Vol. 16, No. 9, pp. 1234-1238, December 1998. Этот метод, использующий аппроксимацию многомерных плотностей вероятностей, определяет, каким образом можно регулировать параметры модели с тем, чтобы максимизировать вероятность наличия определенной наблюдаемой последовательности. В более определенном смысле, если задана последовательность O, такая, что O = O₁, O₂, … , O_T (O_i∈H), то каким образом можно представить ее наиболее точное описание, основываясь на параметрах модели? Это означает, что мы пытаемся максимизировать вероятность p(O| θ), где модель представляет собой θ = (P, B, π). Наблюдаемая последовательность, которая используется для расчета параметров модели, называется обучающей последовательностью.

К сожалению, отсутствует оптимальный способ оценки параметров модели для получения решения при использовании этого метода. Однако имеются пути для того, чтобы локально максимизировать p(O| θ) при использовании итерационной процедуры. Одной из таких итерационных процедур является метод Баума-Велша, который мы будем использовать для нахождения неизвестных параметров СММ. На Рис. 3 показан принцип действия метода Баума-Велша. Первое приближение решения обозначено как θ . Это первое приближение генерируется при использовании экспериментальных данных и вычислении элементов матриц π, P, B путем подсчета общих и отдельных переходов, а также выходных символов для каждого состояния. После того, как будет вычислено θ, производится вычисление второго приближения модели, обозначенного

, с использованием уравнений для повторной оценки. Второе приближение используется снова для повторной оценки модели с применением уравнений повторной оценки. Эта процедура повторяется многократно до тех пор, пока различие между новыми значениями параметров и старыми значениями не станут несущественными. В частности, при получении результатов, представленных в диссертации, процедура была остановлена, когда значения матрицы переходных вероятностей P изменялись на величину менее 10^-4 между последовательными итерациями.

Элементы матрицы P переходных вероятностей можно вычислить путем разбиения отношения С/Ш и подсчета общего числа переходов и отдельных переходов между состояниями, которые происходят в течение данного временного интервала. Отношения числа отдельных переходов к общему числу переходов дают искомые значения. Элементы матриц B могут быть вычислены путем подсчета количества раз, когда для каждого состояния генерируется отдельный символ h_i, и деления этих величин на общее число символов, наблюдаемых для каждого состояния. Таким способом, на базе алгоритма Баума-Велша определяется распределение длительностей состояний канала с релеевским распределением замираний. В последующих главах диссертации показано применение СММ для описания данных, полученных в результате эксперимента.

Определение первой аппроксимации θ=( π, P, B)

Получение

θ =

Использование (π, P, B) для вычисления

с использованием уравнений для повторной оценки

Рисунок 3. Блок-схема, иллюстрирующая вычисление параметров СММ

В предыдущей главе были рассмотрены теоретические основы моделей МККС и СММ для беспроводных каналов. В Главе 3 вначале описывается методика проведения экспериментов с целью получения характеристик процесса кадров в реальной системе стандарта 802.11b. На основе получаемых экспериментальных последовательностей, содержащих кадры с ошибками и кадры без ошибок, строятся соответствующие гистограммы, пример которых приведен на Рис. 4. Эти гистограммы получены при следующих условиях: длина кадра = 1000 байтов; скорость передачи 11 Мб/с; средняя величина отношения С/Ш в приемнике = 34 дБ; число переданных кадров = 100 000.

Рядом с каждой из гистограмм на рисунке представлены основные параметры распределений, полученные в результате анализа: среднее, максимальное и минимальное значения, величина стандартного отклонения и количество выборок. Имея подобную информацию, можно описать процесс потерь кадров, используя модель, которая генерирует последовательности с распределениями, аналогичными распределениям, показанным на Рис. 3.

Затем в Главе 3 рассматривается построение Марковских моделей. Модель МККС строится двумя способами - в соответствии со стандартным методом построения модели на основе характеристик огибающей замираний и с использованием данных, полученных в результате эксперимента. Целью построения данной модели является установление длительности каждого из состояний, соответствующих приему кадров без ошибок (так наз. «хорошие» состояния) и кадров с ошибками («плохие» состояния) – см. Рис. 5.

Построение Марковских моделей с двумя состояниями, таких, как модель на Рис. 5, на основе характеристик огибающей является достаточно известным. В диссертации проведено построение такой модели и установлено следующее. Во-первых, в описанном подходе нет способа, чтобы непосредственно связать длительности состояний и реальное значение среднего отношения С/Ш принимаемого сигнала. Это означает, что изменения величины сигнала считаются одинаковыми для каждого значения отношения С/Ш. Во-вторых, отсутствуют четкие указания относительно того, каким должно быть значение глубины замираний p. Еще один недостаток данного подхода в том, что нет способа учитывать такие характеристики, как размер кадра и скорость передачи, при определении параметров модели. Предполагается, что модель будет одинаковой для всех значений длины кадров и скоростей передачи. Все это определяет невысокую точность аналитической модели МККС для потерь кадров.

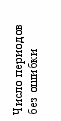
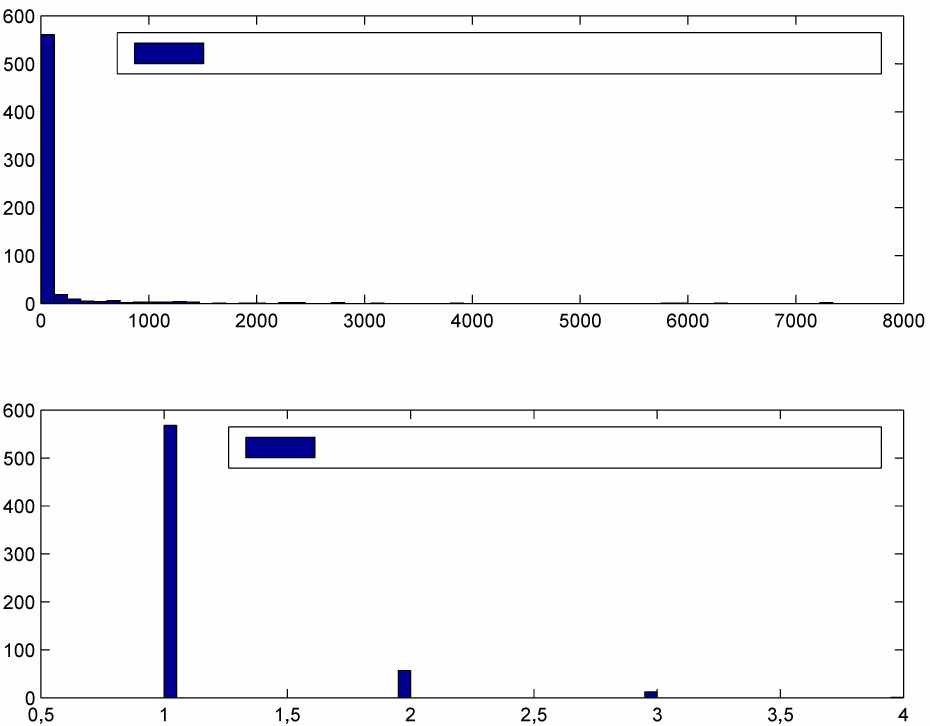
среднее: 158,2884; макс.: 7345; мин.: 1;

ст. откл.: 688,8775; число выборок: 638

среднее: 1,1317; макс.: 4; мин;.1;

ст. откл.: 0,402; число выборок: 638

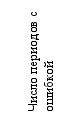
Длина кодового блока для периодов с ошибкой [в кадрах]

Рисунок 4. Результаты эксперимента, полученные при отношении С/Ш 34 дБ

для системы 802.11b

«Хорошее» состояние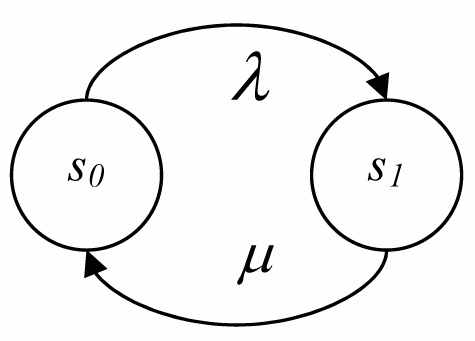

«Плохое» состояние

Рисунок 5. Марковская модель с двумя состояниями - «хорошим» (

) и «плохим» (

),

и с интенсивностями переходов λ и μ

Определение параметров модели МККС, основанное на использовании экспериментальных данных, может быть выполнено путем непосредственного выделения значений длительностей состояний (1/λ и 1/μ) из распределений периодов с ошибками и без ошибок, полученных из трейсов. Затем модель МККС может быть построена путем введения этих значений в пакет программ моделирования, например, такой как OPNET Modeler, который содержит подпрограмму для генерации геометрически распределенных периодов времени.

Рис. 6 иллюстрирует процесс расчета длительности состояний для модели Рис. 5. На рисунке представлен расчет значения

, определяющего длительность «хорошего» состояния. Аналогичный подход может быть использован для вычисления

, длительности «плохого» состояния.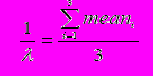

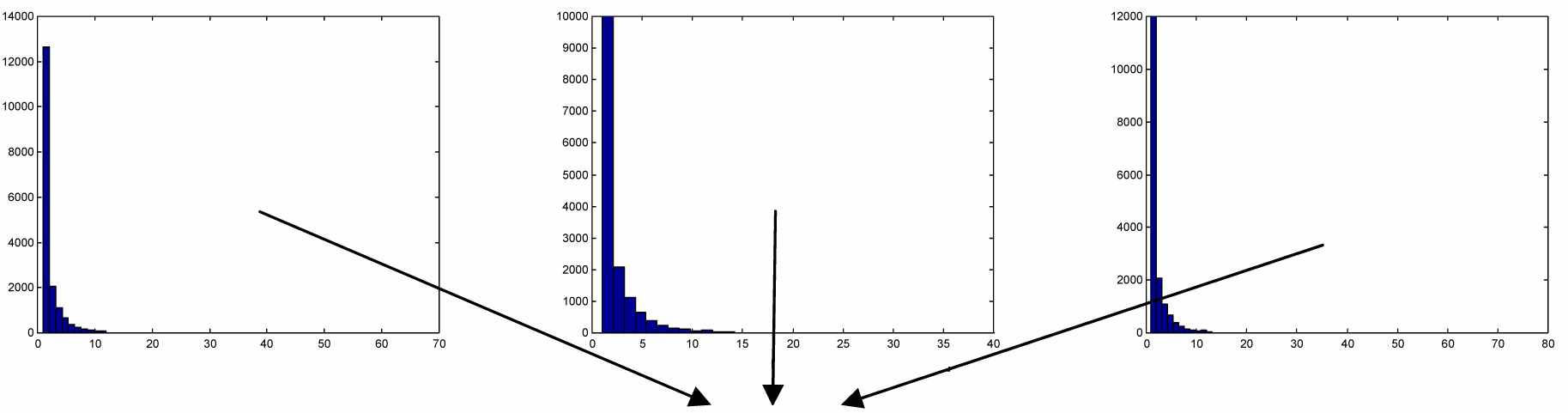
среднее₁ = 2,2894

среднее₂ = 2,2101

среднее₃ = 2,1100

Длина кодового блока

для периодов без

ошибок (в кадрах)

Длина кодового блока

для периодов без

ошибок (в кадрах)

Длина кодового блока для периодов без ошибки (в кадрах)

Рисунок 6. Расчет длительности «хорошего» состояния для модели с двумя состояниями

на основе экспериментальных данных

В диссертации проведено сравнение двух методов построения модели МККС для процесса потерь кадров и показано, что метод построения на основе экспериментальных данных позволяет более точно решить поставленную задачу.

Для моделирования процесса потерь кадров на базе скрытой Марковской модели (СММ) необходимо иметь "скрытую" переменную, которая обладает Марковским свойством. Отношение С/Ш традиционно использовалось в качестве такой «скрытой переменной», и ее Марковские свойства интенсивно изучались в ряде работ. Однако в наборах трейсов, полученных в процессе экспериментов, значения отношения С/Ш недоступны. Поэтому для построения СММ мы будем использовать индикатор уровня принимаемого сигнала (ИУРС), имеющийся в экспериментальных данных. Далее в этой главе показано, что параметр ИУРС в полученных данных обладает Марковскими свойствами.

Процесс конструирования СММ на базе экспериментальных данных состоит из анализа трейсов и вычисления первого приближения для переменных π, P, B модели СММ. Эти переменные, полученные в результате первого приближения, будут представлять первое приближение модели θ, которое необходимо для реализации алгоритма Баума-Велша, описанного выше. При наличии этих переменных имеется возможность генерировать данные, которые будут представлять потери кадров. Чтобы получить переменные, характеризующие модель СММ, необходимо выполнить следующие шаги.

1. Выбор Марковской переменной для базового скрытого процесса. В нашем случае в качестве такой переменной используется параметр ИУРС, доступный в трейсах.

2. Выбор метода разбиения для ИУРС:

a. выбор количества состояний;

b. выбор схемы разбиения;

3. Разбиение ИУРС

4. Получение первого приближения для величин π, P и B

Количество состояний определяет число интервалов, на которое будет разбит параметр ИУРС. После проведения анализа данных ИУРС было определено, что с учетом имеющихся данных могут быть построены только модели с двумя состояниями. В диссертации показано, что нет необходимости рассматривать число состояний больше двух, т.к. результаты, получаемые при двух состояниях, достаточно точно моделируют процесс потерь кадров.

Как показано в Главе 2, эффект разных схем разбиения не является критическим в отношении выходных данных. Поэтому была выбрана простая схема разбиения, в которой наблюдаемый диапазон значений ИУРС был разделен на два интервала одинаковой ширины. Границы интервалов были рассчитаны, используя следующие выражения:

для состояния s₀: [max ИУРС/2, max ИУРС];

для состояния s₁: [min ИУРС, max ИУРС/2].

Экспериментальные трейсы

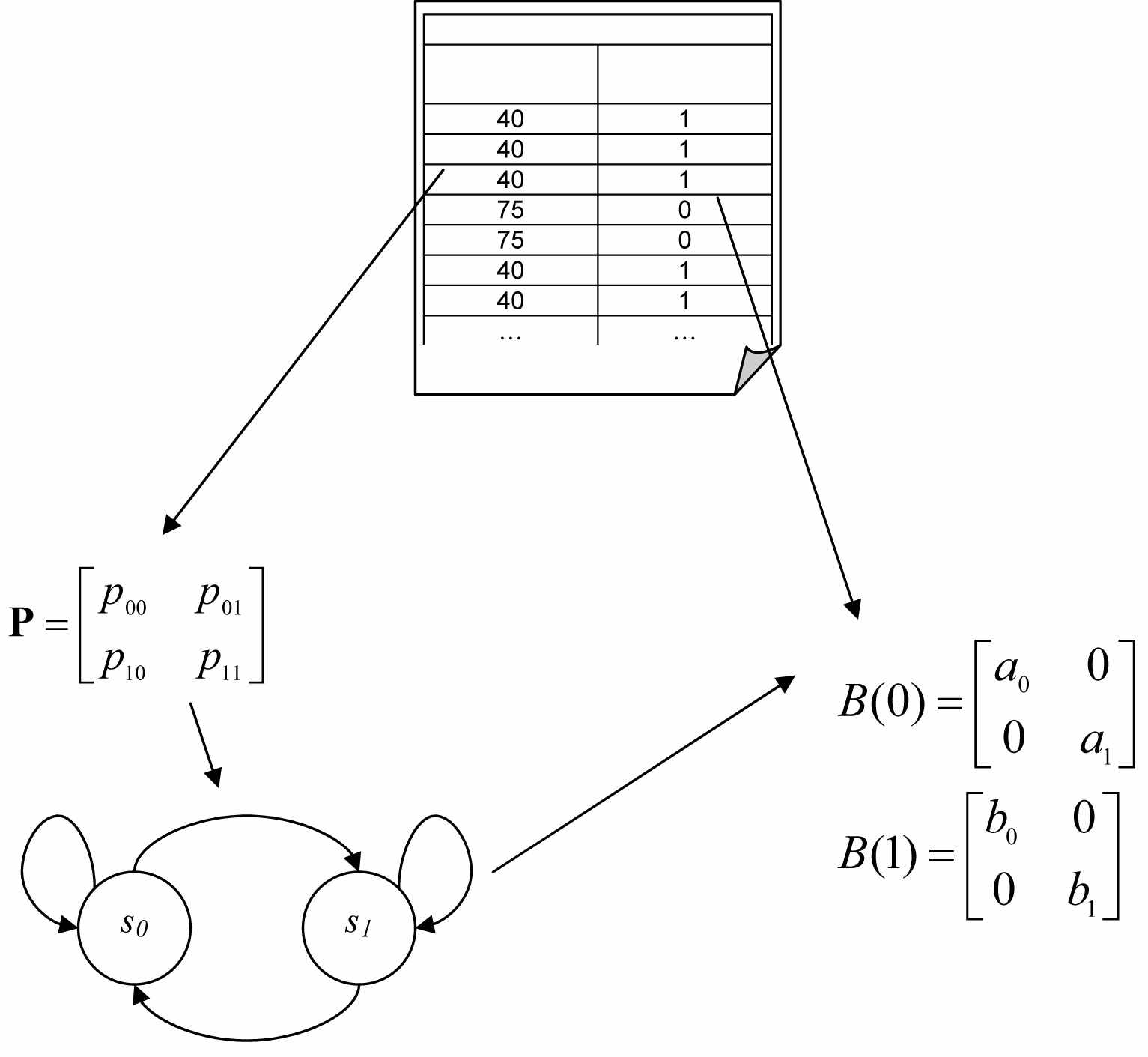
ИУРС (%)

Кадр

с ошибкой

1. Разбиение и
подсчет

2. Подсчет и проверка, в каком состоянии появляется кадр

Р
Построение Марковской цепи
исунок 7. Построение первой аппроксимации СММ для потерь кадров

на базе экспериментальных трейсов

Структура выполняемых процедур по разбиению показана на Рис. 7. Анализируя значения ИУРС в принятых экспериментальных трейсах, можно подсчитать переходы между двумя состояниями и получить матрицу переходных вероятностей P, а затем определить вектор π. При анализе столбца, в котором указано, был ли получен кадр с ошибкой или без ошибки и соответствующее состояние ИУРС в Марковской цепи, можно получить матрицы B. С помощью этих трех элементов мы находим первую аппроксимацию модели. Затем можно использовать алгоритм Баума-Велша для получения "оптимальной" СММ, которая будет представлять наблюдаемый процесс потери кадров.

В Табл. 2. суммируются свойства описанных Марковских моделей с учетом способов их построения.

Таблица 2. Обзор свойств Марковских моделей, описывающих процесс потери кадров

Модель	Метод описания характеристик	Преимущества	Ограничения
Марковская модель с двумя состояниями	На основе огибающей замираний	Дает описание модели, когда нет экспериментальных данных. Однако эта модель не является точной.	Не имеется указаний, как охарактеризовать модель, если заданы среднее значение отношения С/Ш, размер кадров или скорости передачи. Предполагается, что длительности состояний описываются геометрическим распределением
Марковская модель с двумя состояниями	На основе экспериментальных данных	Для определения характеристик требуется только длительность состояний Экспериментальные данные содержат информацию о среднем отношении С/Ш, размере кадра и скорости передачи данных	Должны иметься в наличии экспериментальные данные Предполагается, что длительности состояний описываются геометрическим распределением
Скрытая Марковская модель	На основе экспериментальных данных	После получения первой модели она может "обучена" с использованием алгоритма Баума-Велша и отличаться более хорошим приближением к экспериментальным данным	Описание характеристик и реализация включают в себя больше параметров, чем модель МККС с двумя состояниями Должны иметься в наличии экспериментальные данные Степень структурирования значений ИУРС ограничивает число состояний для скрытой переменной

Затем в Главе 3 рассматриваются методы проверки достоверности Марковских моделей с использованием критерия Колмогорова-Смирнова. Для проверки достоверности в диссертации предлагается применить прикладные пакеты Matlab (v6.5) и OPNET Modeler (v10.5p11).

В Главе 4 представлен анализ большого числа экспериментальных данных для локальных сетей, работающих по стандарту IEEE 802.11b, полученных на площадках, где выполнялись измерения. Представлены экспериментальные результаты для двух различных типов сред - офиса и жилого помещения. Экспериментальные данные (трейсы), полученные при проведении экспериментов, содержат значительный объем данных (приблизительно 4 Гбайта). По этой причине важно исследовать влияние каждого из факторов на распределения ошибок – отношения С/Ш, скорости передачи и длины кадров, в связи с чем была разработана методика анализа большого объема экспериментальных данных.

Анализ экспериментальных трейсов для систем 802.11b выявил аналогичные тенденции для обеих исследуемых площадок - офисного и жилого помещений. В частности, на обеих площадках по мере того, как среднее значение отношения С/Ш в приемнике падает, распределения периодов без ошибок имеют укороченные хвосты распределений, в то время как для периодов с ошибками наблюдаются более длинные хвосты распределений. Причина этого состоит в том, что при более низком среднем значении отношения С/Ш процент кадров с ошибками возрастает, поэтому растет вероятность появления длинных периодов последовательного прихода кадров с ошибками.

Форма распределения периодов без ошибок и периодов с ошибками изменяется с изменением скорости передачи данных. При более низкой скорости передачи данных процент кадров с ошибками оказывается меньше, чем при высоких скоростях, причем распределение периодов при низких скоростях не сохраняет экспоненциальную форму при больших отношениях С/Ш.

Еще одной общей характеристикой результатов экспериментов является изменение процента кадров с ошибками при изменении длины кадра. По мере того, как длина кадра растет, процент кадров с ошибками также повышается. Этот результат является ожидаемым, поскольку для более длинных кадров имеется более высокая вероятность поражения ошибками по сравнению с более короткими кадрами. В Табл. 3 суммируются результаты экспериментов для системы 802.11b. В заключительной части главы проведено исследование взаимодействия между перечисленными выше тремя факторами на основе факторного анализа.

В Главе 5 представлены результаты проверки достоверности моделей потерь кадров. В отличие от других известных работ по проверке моделей потерь кадров в беспроводных системах связи в диссертационной работе используются экспериментальные данные, а не результаты имитационного моделирования. В этой главе выходные данные, полученные при использовании Марковских моделей с конечными состояниями, а также скрытых Марковских моделей, анализируются с использованием методов, описанных в Главе 3, включая и применение пакетов Matlab и OPNET Modeler.

Таблица 3. Обзор результатов экспериментов для системы 802.11b

Характеристика	Наблюдаемый результат	Примечания
Хвост распределения периодов без ошибок	Укорачивается с уменьшением среднего отношения С/Ш в приемнике	Максимальные выборки, вносящие вклад в возникновение длинных хвостов распределения, не имеют значительных значений кумулятивных (накопительных) частот. В частности, выборки, создающие длинные хвосты, вносят 1% или меньше в значение кумулятивной частоты
Хвост распределения периодов с ошибками	Возрастает с уменьшением среднего отношения С/Ш в приемнике	См. примечание к предыдущему пункту
Распределения периодов без ошибок и с ошибками при низкой скорости передачи данных	Не описываются экспонентой при большом среднем отношении С/Ш и низкой скорости передачи данных. По мере того, как скорость передачи растет, появляется экспоненциальная огибающая	При работе с низкой скоростью (например, 1 Мбит/с или 5,5 Мбит/с) в приемнике, расположенном близко к передатчику, наблюдается очень небольшое число кадров с ошибками
Процент кадров с ошибками в фиксированной точке расположения	Растет с увеличением скорости передачи и длины кадра. Снижается при увеличении среднего отношения С/Ш	___

Проведенные исследования с использованием экспериментальных данных по определению длительности «хороших» и «плохих» состояний на базе модели МККС с двумя состояниями показали, что метод, основанный на огибающей замираний, подходит только для небольшого диапазона рабочих значений скорости передачи, отношения С/Ш, длины кадров. Для сравнения распределений потерь кадров использовался критерий Колмогорова-Смирнова для двух независимых выборок. Было установлено, что форма распределений, получаемых из модели МККС и из экспериментальных данных будет совпадать при низких скоростях передачи (1 и 2 Мбит/с) и не будет совпадать при скоростях 5 и 11 Мбит/с. Это расхождение наблюдалось более, чем в 20% случаев. Это явление определяется тем, что при низких скоростях передачи процент кадров с ошибками оказывается ниже 0,1%, и согласование распределений, имеющих негеометрический вид, с Марковскими моделями оказывается несложным, так как ошибки возникают спорадически. В условиях низкой скорости передачи модель генерирует значительные периоды без ошибок и короткие периоды со спорадическим появлением ошибок.

Описание скрытых Марковских моделей для представления потерь кадров в системе 802.11b было проведено в соответствии с процедурой, разработанной в Главе 3. Экспериментальные трейсы, содержащие информацию, обеспечивают первое приближение модели, которое затем используется для применения алгоритма Баума-Велша. Для сравнения распределений периодов с ошибками и периодов без ошибок был использован критерий Колмогорова-Смирнова для двух независимых выборок. Было показано, что более, чем в 90% случаев распределения, получаемые из модели СММ и из экспериментальных данных, совпадают. Эти результаты позволяют сделать выводы о том, что модель на базе СММ дает более точные результаты, чем модель МККС.

В Табл. 4 представлены методы проверки достоверности, используемы в диссертации.

Таблица 4. Методы проверки достоверности

Метод проверки достоверности	Процесс, проверяемый на достоверность	Испытываемая модель
Критерий Колмогорова-Смирнова с двумя выборками: сравнение выходных данных модели и экспериментальных данных для определения распределений	Потери кадров	Модель МККС, характеризуемая данными из огибающей замираний
	Потери кадров	Модель МККС, характеризуемая экспериментальными данными
	Потери кадров	Модель СММ, характеризуемая экспериментальными данными
Таблица сопряженности признаков с двумя входами	Марковское свойство значений ИУРС	Проверка достоверности процесса СММ

В Приложении А описаны детали проводимого эксперимента, такие как выбор площадок, различные конфигурации расположения передатчиков и приемников, спецификация получаемых трейсов, ограничения, влияющие на процесс получения данных. В Приложении Б представлены детали использования прикладного пакета OPNET Modeler, применяемого в диссертации при анализе экспериментальных трейсов и создании выходных данных для моделей МККС или СММ.

Заключение

В процессе проведенных в диссертационной работе исследований получены следующие основные результаты.

Приведен детальный обзор методов, на базе которых строились ранее модели потерь кадров. Этот обзор позволил выявить ограничения, характерные для традиционных моделей. В частности, показано, что марковские модели с простыми схемами модуляции (BPSK, DPSK) не являются применимыми в беспроводных локальных сетях, где используются сложные схемы модуляции в частотно-селективных каналах.
Для описания процесса потерь кадров в беспроводных локальных сетях представлена модель марковского канала с конечными состояниями (МККС). Показано, что модель МККС с двумя состояниями дает приемлемые значения параметров МККС и не требуется увеличивать число состояний. Также установлено, что точность определения параметров модели МККС не зависит от набора схем модуляции, коррекции ошибок и кодирования.
Описаны алгоритмы получения параметров процесса потерь кадров в системе 802.11b с использованием модели МККС: на основе характеристик огибающей (аналитическая модель) и на базе экспериментальных данных. Определены недостатки первого подхода и показано преимущество второго подхода при определении параметров процесса потерь кадров.
Другой подход, разработанный в диссертации для исследования процесса потерь кадров, базируется на скрытых марковских моделях (СММ). Для нахождения распределения длительности состояний канала при использовании СММ предложен метод, основанный на алгоритме Баума-Велша. Метод основан на построении СММ с использованием индикатора уровня принимаемого сигнала (ИУРС), доступного из экспериментальных данных (трейсов). Важным результатом работы является доказательство свойство марковости ИУРС, необходимое при использовании в СММ в качестве «скрытой переменной».
Проведен анализ большого массива экспериментальных данных (более 4 Гб) при функционировании системы 802.11b в двух типах сред – жилом и офисном помещениях. Экспериментальные исследования показали, что в обоих типах помещений получаются аналогичные результаты для распределений периодов с ошибками и без ошибок при учете влияния трех факторов – отношения С/Ш, скорости передачи данных и длины кадров
Проверка достоверности модели потерь кадров на основе МККС показала, что распределения периодов с ошибками и без ошибок, получаемые из этой модели, в относительно большом числе случаев не будут совпадать с распределениями, получаемыми из экспериментальных данных. В результате применения критерия Колмогорова-Смирнова получено, что распределения, полученные из модели и из эксперимента, различаются более, чем в 20% случаев. В то же время применение скрытых марковских моделей приводит к более точным результатам, чем применение марковских моделей с двумя состояниями. Модели СММ обеспечивают соответствие теоретических распределений периодов с ошибками и периодов без ошибок с экспериментальными более, чем в 90% случаев.
Представлены процедуры построения марковских моделей для имитационного моделирования на базе пакетов Matlab и OPNET Modeler. Описанные процедуры позволяют построить модели на базе установления соотношений между численными результатами таких параметров систем 802.11 как отношение С/Ш, скорость передачи и длина кадров.

Список публикаций по теме диссертации