Комплекс условий с овокупность условий, в которых рассматривается данное событие. Испытание
| Вид материала | Документы |
- 1. Случайные события,их вероятность, 757.49kb.
- Безопасности и условий охраны, 424.09kb.
- Комплекс условий неорганической среды, влияющих на организмы. Абсорбция, 329.84kb.
- Московский Государственный Горный Университет Кафедрв Истории и Социологии реферат, 207.32kb.
- Методические указания к практическим занятиям по курсу «Безопасность труда» для студентов, 406.59kb.
- Аннотация программы учебной дисциплины «Методы обеспечения комфортных условий жизнедеятельности», 18.08kb.
- Устав Организации Объединенных Наций подтверждает право людей всего мира на создание, 89.08kb.
- «согласовано» «утверждаю», 747.11kb.
- Конспект лекций 2006 Классификация условий труда по показателям тяжести и напряжённости, 260.44kb.
- Система управления охраной труда в омской области – основа для создания здоровых, 175.22kb.
2 ОСНОВЫ ВЕРОЯТНОСТНЫХ МЕТОДОВ МОДЕЛИРОВАНИЯ СИСТЕМ
2.1 Понятия о случайных событиях, величинах и функциях
Событие - всякий факт, который может произойти в данных условиях.
Комплекс условий - совокупность условий, в которых рассматривается данное событие.
Испытание - реализация определенного комплекса условий на практике.
В зависимости от связи между событиями и соответствующими комплексами условий различают достоверные, невозможные и случайные события.
Достоверным называется такое событие, которое наступает каждый раз при реализации данного комплекса условий (Обозначение U).
Невозможным называется событие, которое никогда не наступает при реализации данного комплекса условий (Обозначение ).
Случайным называется событие, которое может либо наступить при реализации данного комплекса условий, либо не наступить (Обозначение А, В, С...).
Частота события А - отношение числа испытаний, в которых появилось данное событие m(А), и общего числа испытаний n:
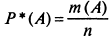
Вероятность события - количественная мера степени возможности появления события для заданного комплекса условий.
Частоту, вычисленную при достаточно большом числе испытаний, можно считать близкой к соответствующей вероятности (по закону больших чисел)
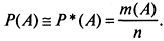 ( - статистический способ определения вероятности).
( - статистический способ определения вероятности).Для случайного события А:
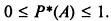 и 0<Р(А)<1.
и 0<Р(А)<1.Вероятность невозможного события
 .
.Для любого события А вероятность противоположного события
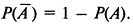
Случайные события могут быть представлены через случайные величины (СВ).
СВ - величина, которая в результате испытания (реализации определенного комплекса условий) может принять то или иное значение, причем до испытания неизвестно, какое именно.
Типы СВ:
Дискретная – СВ, имеющая конечное или счетное множество значений;
Непрерывная – СВ, множество значений которой представляет собой множество всех точек, принадлежащих какому-либо интервалу числовой оси.
СВ смешанного типа - СВ, для которых наряду с участками непрерывных значений имеются отдельные, изолированные значения (например, время ожидания в очереди).
Закон распределения СВ - соотношение, позволяющее определить вероятность появления СВ в любом интервале.
Основные формы закона распределения: ряд распределения, функция распределения, плотность распределения.
Ряд распределения - таблица, в которой перечислены возможные значения СВ и соответствующие им вероятности.
Пусть хi — i-e значение случайной величины Х, и Pi — вероятность появления i-го значения случайной величины X. Тогда ряд распределения имеет вид:
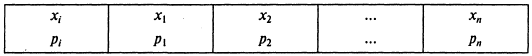
Эмпирический ряд распределения - таблица, в которой перечислены наблюдаемые значения (фактические реализации) случайной величины (хi) и соответствующие им частоты (mi).

Ряд распределения не может служить характеристикой непрерывной СВ, т.к. ее значения нельзя перечислить.
Функция распределения СВ X - функция аргумента х, равная вероятности того, что СВ Х примет любое значение, меньшее х:
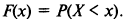
Вероятность попадания случайной величины в полузамкнутый интервал [а, b) равна разности значений функции распределения в точках b и а:
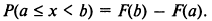
Функция распределения дискретной СВ:
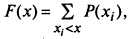
где суммирование распространяется на значения xj, которые меньше х..
Функция распределения дискретной СВ увеличивается скачками каждый раз, когда Х при своем изменении проходит через какое-нибудь из возможных значений х, причем величина скачка равна вероятности этого значения.
Функция распределения непрерывной СВ
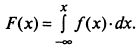
где f(x) – плотность распределения.
Плотность распределения f(x) - предел отношения вероятности попадания случайной величины на малый участок к длине этого участка при ее неограниченном уменьшении

Плотность распределения применяется для непрерывной СВ, т.к. в этом случае нельзя использовать в качестве характеристики вероятность появления ее отдельных значений.
Вероятность попадания непрерывной СВ на произвольный участок [а, b)
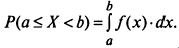
График плотности распределения (кривая распределения) совместно с осью абсцисс ограничивает площадь, равную единице (т.к.
 ).
).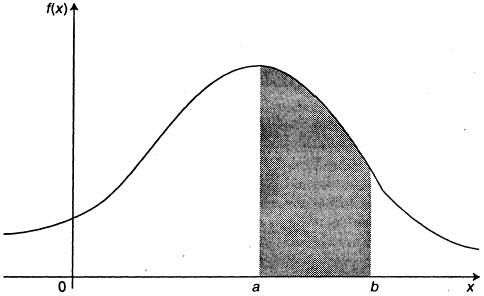 (заштрихована
(заштрихована 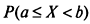 ).
).2.2 Числовые характеристики СВ
Характеристики положения:
Среднее значение - величина, относительно которой группируются всевозможные значения СВ.
Математическое ожидание (МО) - теоретическая характеристика СВ.
МО дискретной СВ
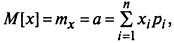
где хi - возможные значения случайной величины Х,
Pi —вероятность появления i-го возможного значения СВ Х.
Эмпирическая средняя - эмпирическая характеристика СВ
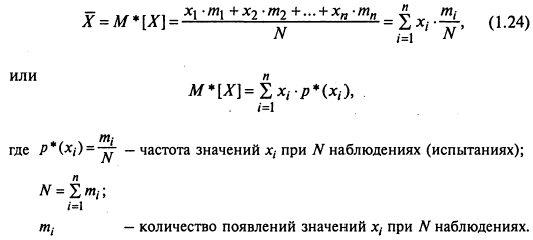
Эмпирическая средняя СВ по мере увеличения испытаний (наблюдений) стабилизируется относительно математического ожидания.
МО непрерывной СВ
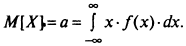
Медиана (Me) СВ - величина, относительно которой равновероятно получение большего или меньшего значения СВ:
Р(Х > Me) = Р(Х < Me).
Мода (Мо) дискретной СВ - ее значение, обладающее наибольшей вероятностью.
Мода непрерывной СВ - такое значение, которое отвечает максимальной плотности распределения.
Математическое ожидание, медиана и мода совпадают только в частном случае при симметричном распределении.
Характеристики рассеяния:
Дисперсия - МО квадрата отклонений СВ от своего МО
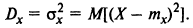
Дисперсия дискретной СВ
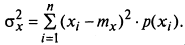
Дисперсия непрерывной СВ
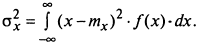
Среднее квадратическое отклонение
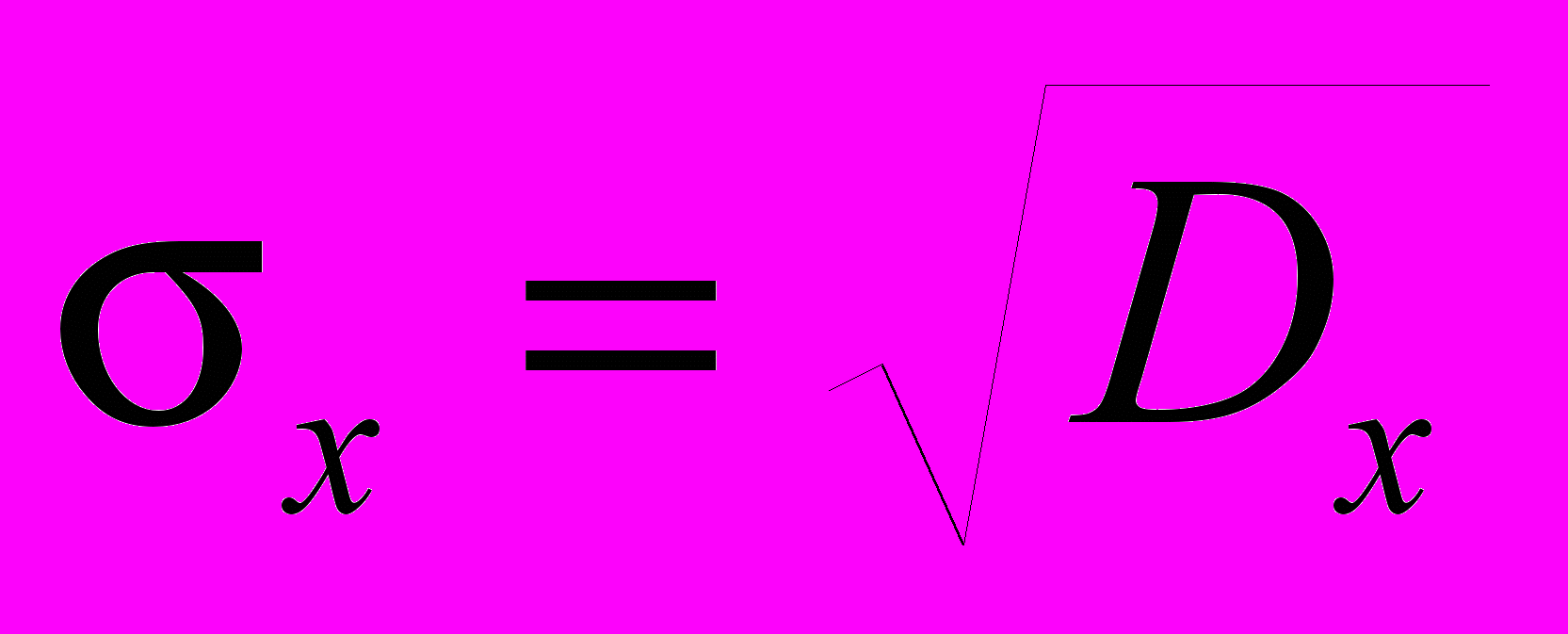 .
.Эмпирические значения характеристик рассеивания:

Коэффициент вариации - относительная характеристика рассеивания
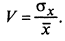
2.3. Статистическая оценка законов распределения СВ
Обработка статистического материала производится для нахождения законов распределения СВ.
Рассмотрим некоторую СВ X.
Статистическая выборка - совокупность из п определенных значений СВ Х, которые она принимает при функционировании системы в течение некоторого времени t.
Если расположить отдельные значения СВ X в возрастающем или убывающем порядке и указать относительно каждого значения, как часто оно встречалось в данной совокупности, то получится эмпирическое распределение СВ, или вариационный ряд, на основании которого определяются аналитическая форма неизвестной плотности вероятности f(х), функция распределения F(x) и оцениваются входящие в нее параметры.
Построение вариационного ряда.
1. Диапазон значений непрерывной СВ X разбивается на интервалы. Оптимальная длина интервала
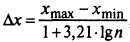 .
.Число интервалов
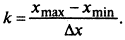
2. Подсчитывается количество значений mi СВ Х, приходящееся на каждый интервал, и определяется частота ее попадания в данный интервал по формуле
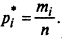
3. Строится вариационный (статистический) ряд

Вариационные ряды могут быть изображены графически в виде полигона распределения (чаще для дискретных СВ) и гистограммы (для непрерывных СВ).
Построение полигона распределения:
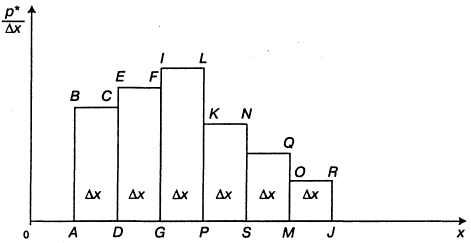
1. В выбранных масштабах на оси абсцисс наносится шкала для фактических значений СВ X, на оси ординат — для частот
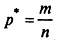 .
.2. Наносят точки Mi с координатами хi и
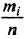 .
.3. Точки
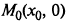 ,
, 
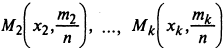 ,
, 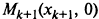 соединяют ломаной линией.
соединяют ломаной линией. Многоугольник
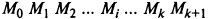 - полигон распределения.
- полигон распределения.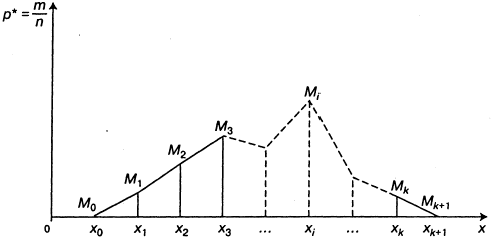
Построение гистограммы распределения
1. В выбранных масштабах на оси абсцисс наносится шкала для реализаций случайной величины X, на оси ординат — величины
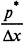 .
.2. Строят прямоугольники ABCD, DEFG, ..., основания которых соответствуют ширине интервала х, а высоты равны отношениям -
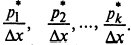
Многоугольник ABCEF... QORJA - гистограмма распределения.
При уменьшении интервалов х гистограмма будет приближаться к графику плотности распределения СВ.
2.4. Основные законы распределения случайных величин
Полигон и гистограмма есть реализация распределения выборочной совокупности при ограниченном числе наблюдений (N), а предельная кривая при N—> является распределением генеральной совокупности - теоретическим распределением. Отдельные распределения поддаются точному аналитическому описанию.
Дискретные законы распределения
А. Биномиальное распределение. Распределение числа X появления события А в серии из n испытаний. В каждом испытании возможны два исхода: наступление или ненаступление события А. Пусть р - вероятность наступления события А в каждом испытании. Распределение числа появления события А определяется формулой Бернулли
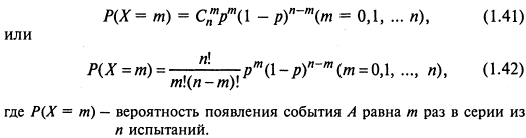
Определяется двумя параметрами р и п.
МО биномиально распределенной СВ
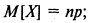
Дисперсия биномиально распределенной СВ
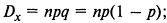
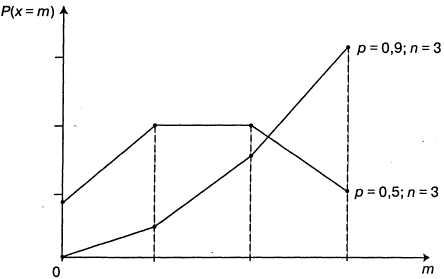
Б. Распределение Пуассона - предельный случай биномиального распределения. Пусть в биномиальном распределении
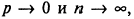 тогда плотность вероятности биномиального распределения выражается законом Пуассона:
тогда плотность вероятности биномиального распределения выражается законом Пуассона: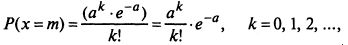
Распределение Пуассона зависит только от одного параметра — математического ожидания М[Х] = а.:
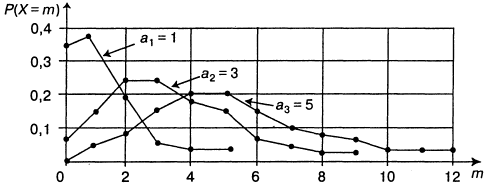
Непрерывные законы распределения
В. Нормальное распределение – наиболее известно. Полностью характеризуется математическим ожиданием и дисперсией. Кривая f(x) симметрична относительно математического ожидания.
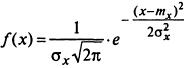
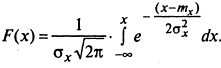

Г. Гамма-распределение и распределение Эрланга. Неотрицательная СВ X имеет гамма-распределение, если
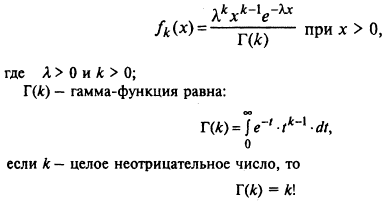
МО СВ X, подчиненной гамма-распределению
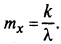
Дисперсия СВ X
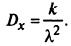
При целом k>1 гамма-распределение превращается в распределение Эрланга k-го порядка
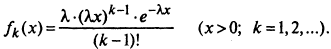
Закону Эрланга k-го порядка подчинена сумма независимых случайных величин, каждая из которых распределена по показательному закону с параметром .
При k=1 гамма-распределение превращается в показательное распределение с параметром .
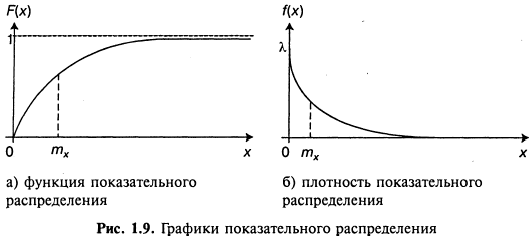
Д. Показательное распределение.
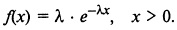
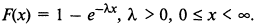
- параметр распределения,
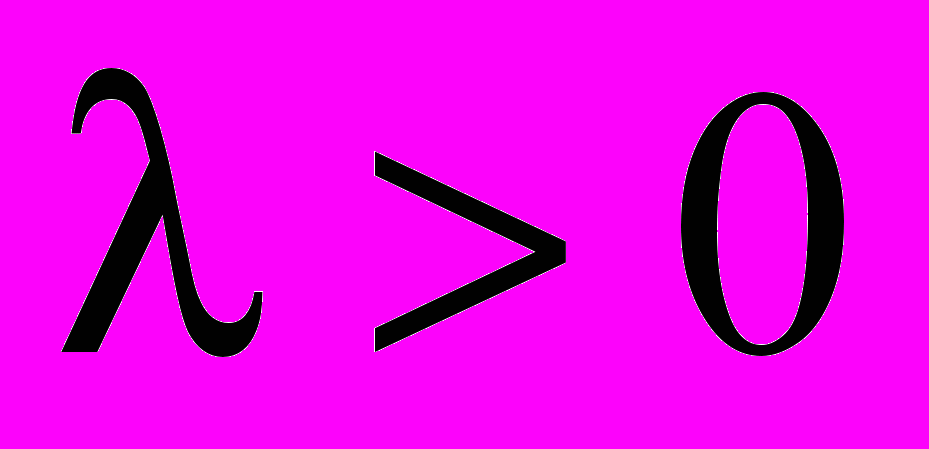 .
.
МО СВ X
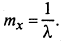
Дисперсия СВ X
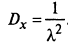 откуда
откуда 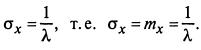
Е. Непрерывная СВ Х имеет равномерное распределение на отрезке [а, b], если на этом отрезке плотность распределения постоянна, а вне его — равна нулю:
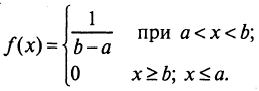
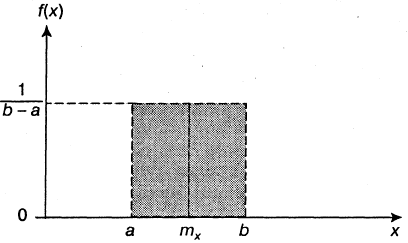
МО СВ Х
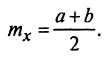
Дисперсия и СКО СВ X

2.5. Выбор теоретического закона распределения СВ
В любом статистическом распределении присутствуют элементы случайности, и, как следствие, экспериментальные точки гистограммы обычно колеблются от опыта к опыту около неизвестной кривой истинного распределения.
При наличии числовых характеристик СВ (математического ожидания, дисперсии, коэффициента вариации) законы ее распределения могут быть приближенно определены по табл.
Законы распределения СВ в зависимости от коэффициента вариации
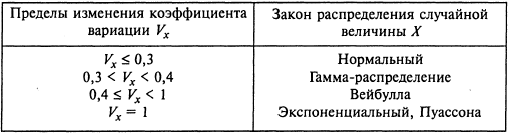
Для более точного определения теоретического закона распределения проводят построение теоретической кривой распределения.
Оно состоит в подборе такой функций теоретического распределения f(x), которая обеспечивала бы максимальное приближение теоретических данных к эмпирическим
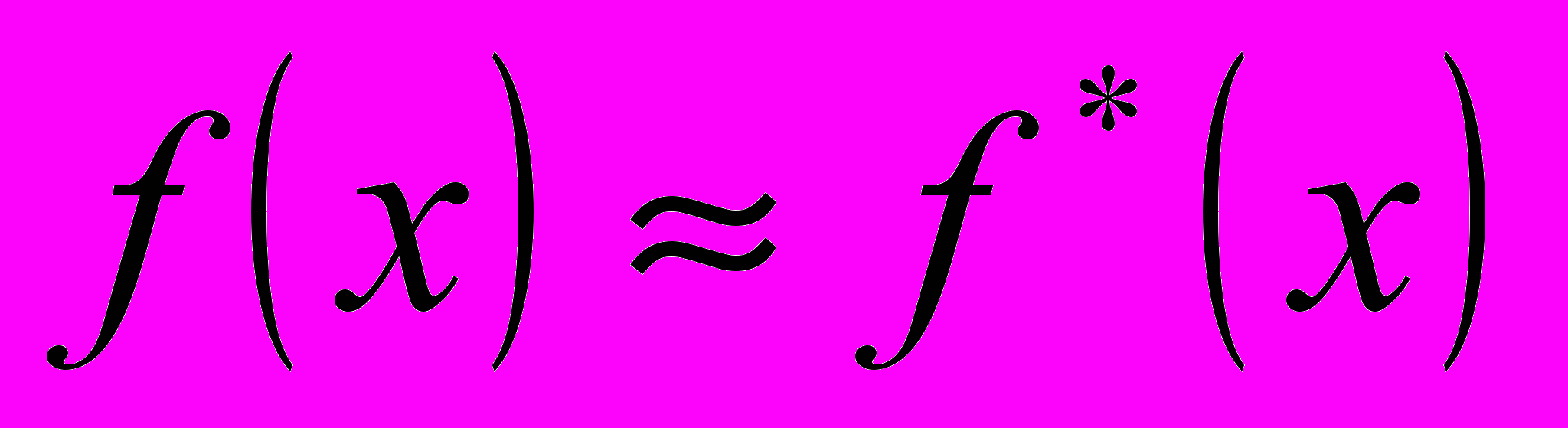 . Для оценки правдоподобия этого приближения используется несколько критериев согласия проверяемых гипотез относительно вида функции f(x), например, критерий
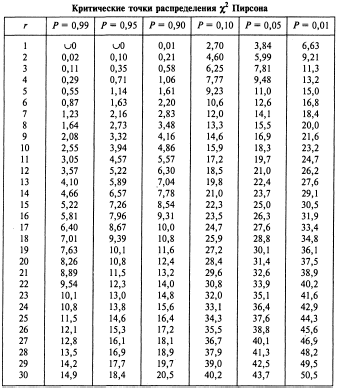
. Для оценки правдоподобия этого приближения используется несколько критериев согласия проверяемых гипотез относительно вида функции f(x), например, критерий 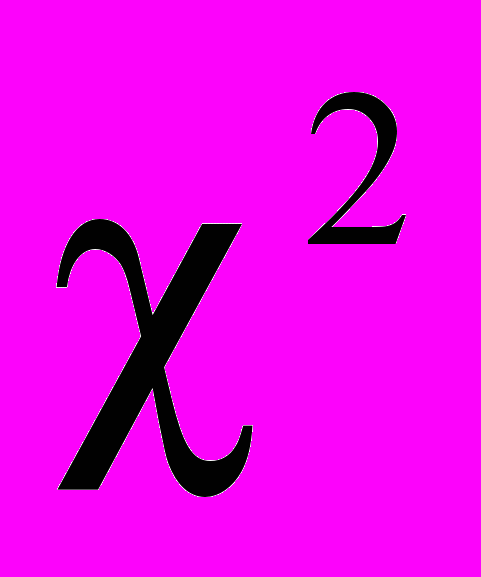 Пирсона.
Пирсона.Мера расхождения между теоретическим законом распределения и статистическим распределением:
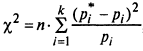
где k - число интервалов статистического ряда;
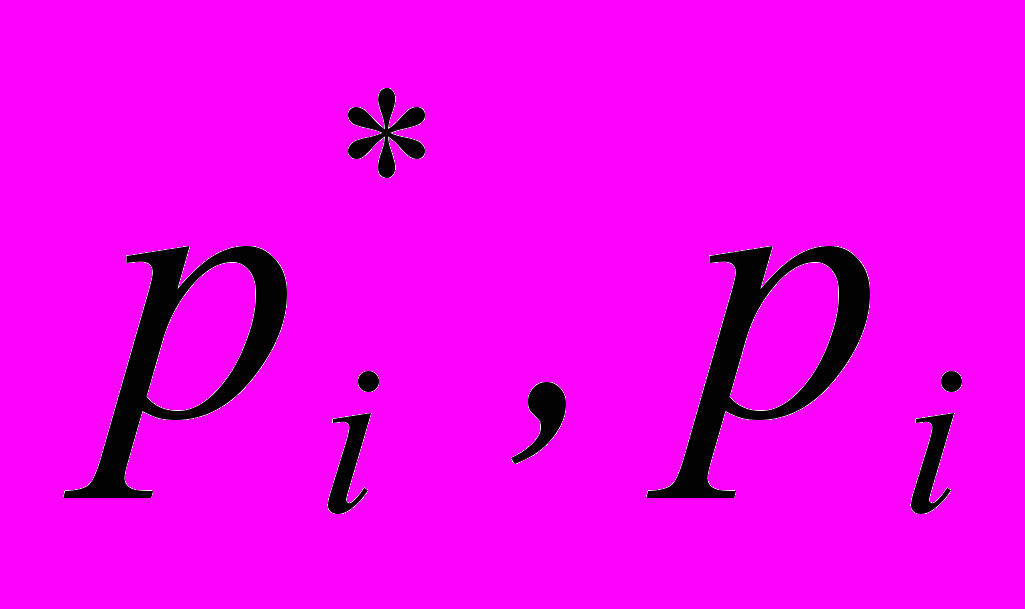 — соответственно, статистическая и теоретическая вероятности попадания случайной величины Х в i-й интервал.
— соответственно, статистическая и теоретическая вероятности попадания случайной величины Х в i-й интервал.С учетом
 получим
получим 
Полученное расхождение
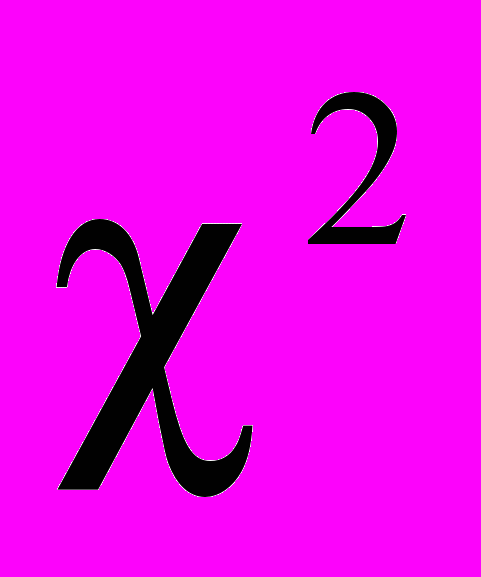 может объясняться двумя причинами: 1) ограниченный объем выборки, в этом случае расхождение случайно; 2) наличие существенной разницы между теоретическим и статистическим распределениями, в этом случае нужно отвергнуть выбранное теоретическое распределение.
может объясняться двумя причинами: 1) ограниченный объем выборки, в этом случае расхождение случайно; 2) наличие существенной разницы между теоретическим и статистическим распределениями, в этом случае нужно отвергнуть выбранное теоретическое распределение.Для выявления причины вводится величина - мера расхождения теоретического и статистического распределений за счет число случайных факторов.
Далее находится вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического распределений будет не меньше, чем фактическое значение
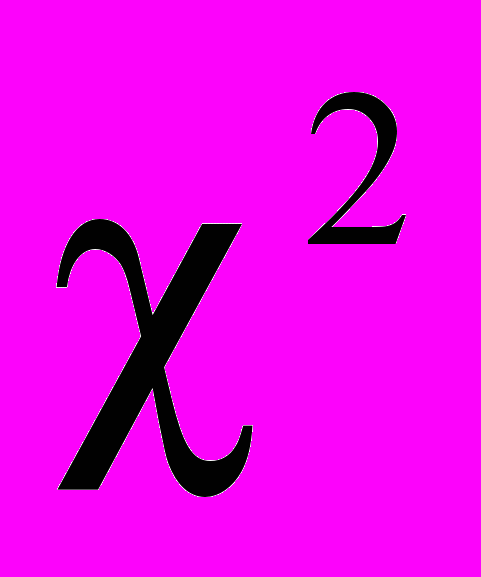 для данной выборки
для данной выборки 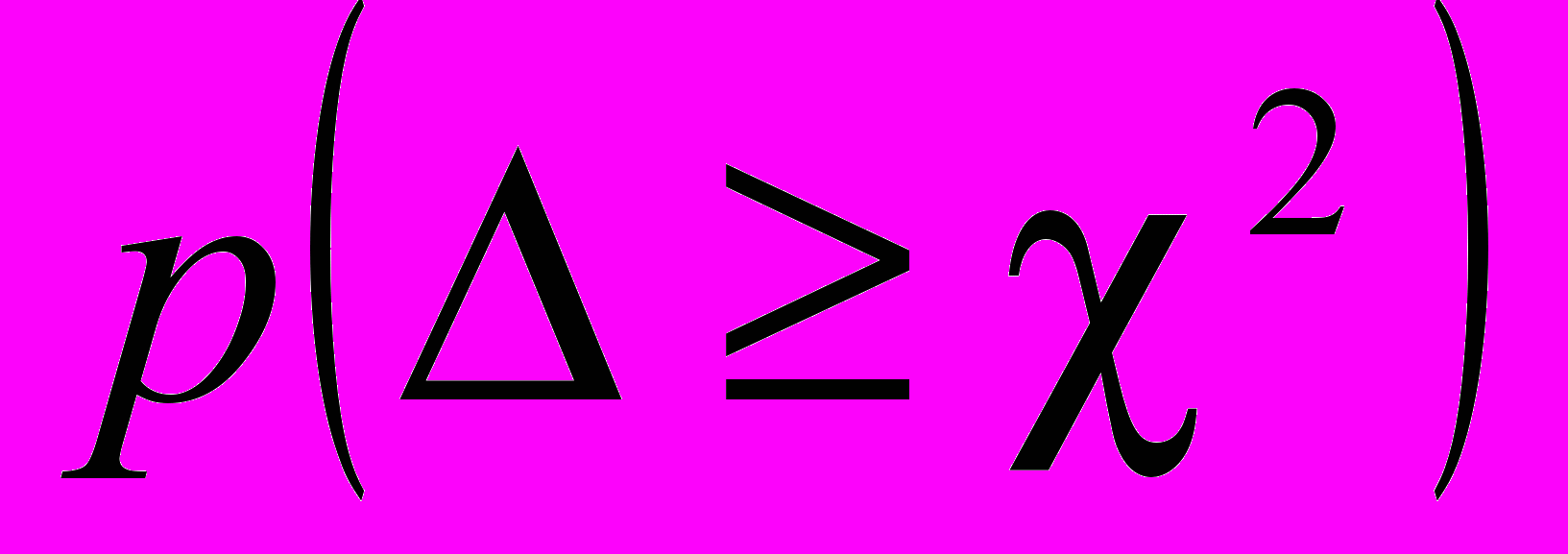 .
. Величина
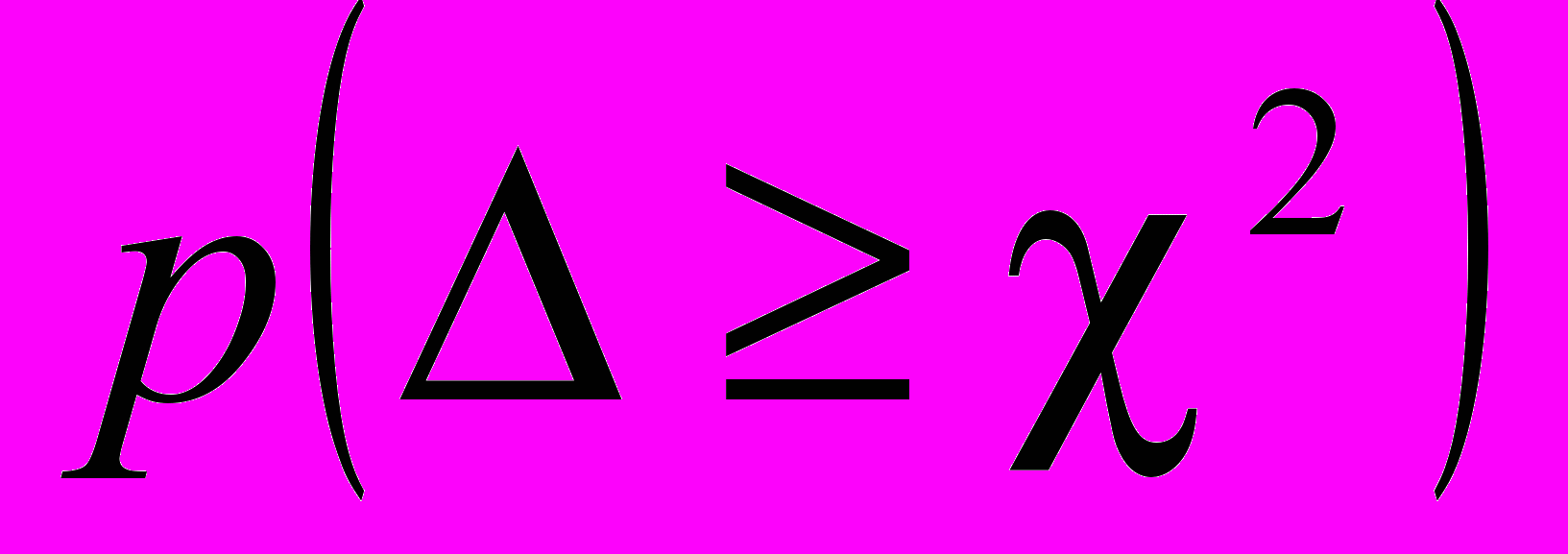 определяется по таблицам при известных r и
определяется по таблицам при известных r и 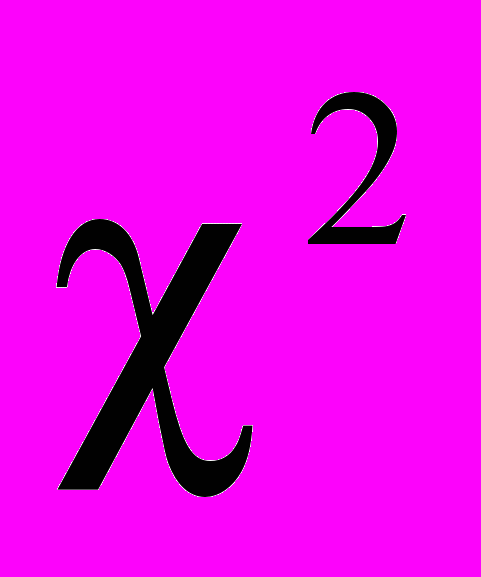 .
.r - число степеней свободы
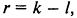
где l — число статистических характеристик (средняя, дисперсия и т. д.), использованных при вычислении теоретического распределения.
Если вероятность p мала (меньше 0,1), то выбранное теоретическое распределение считается неудачным.
Критерий
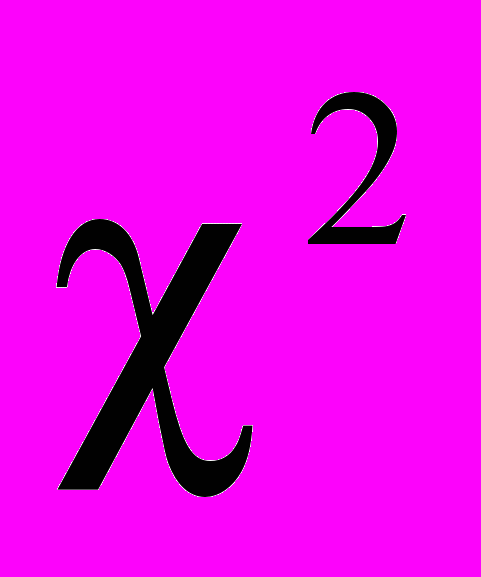 Пирсона применим в тех случаях, когда объем выборки
Пирсона применим в тех случаях, когда объем выборки 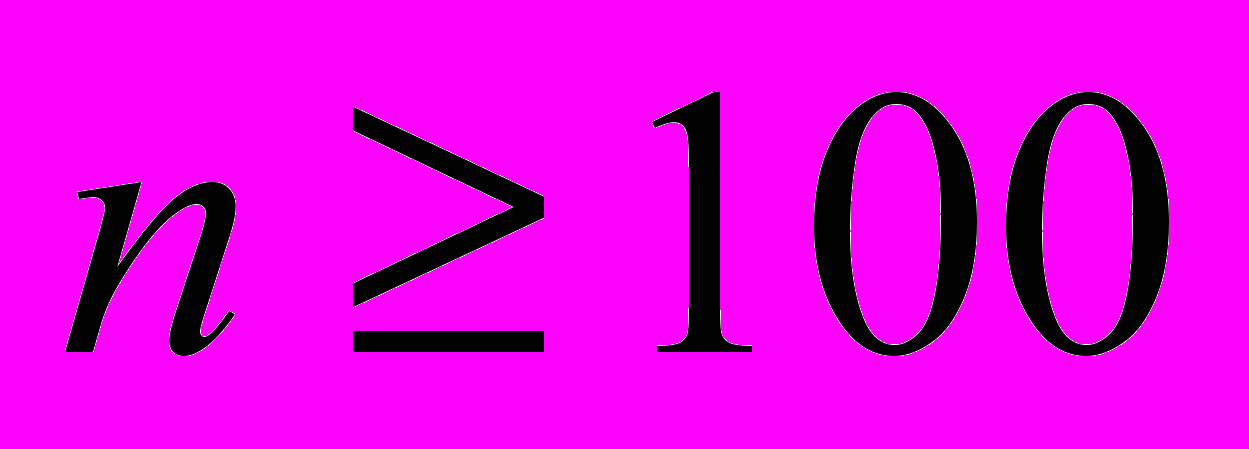 и в каждом интервале число наблюдений
и в каждом интервале число наблюдений 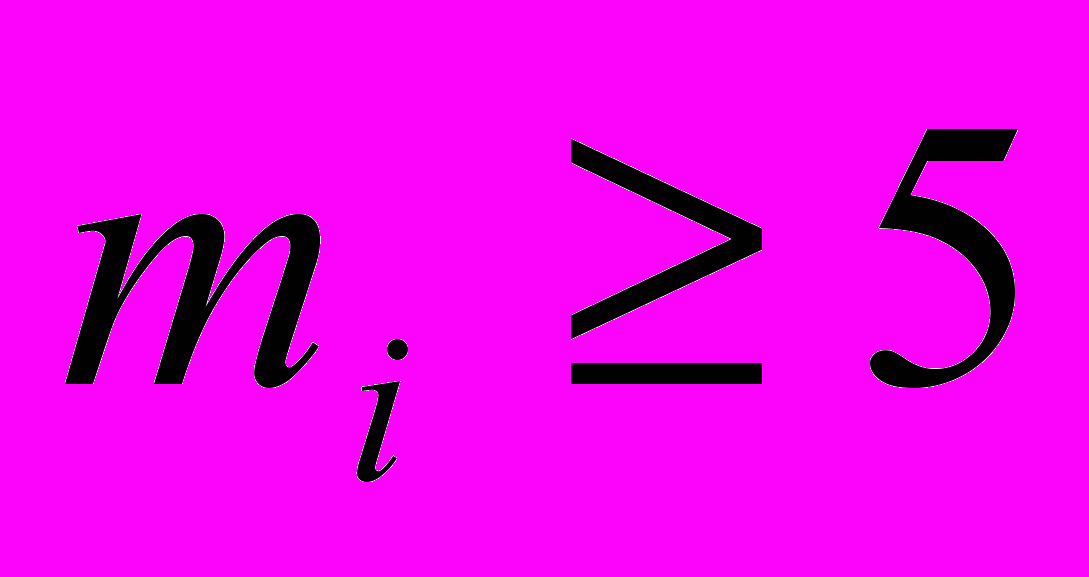 .
.