Geum.ru

Программа дисциплины «Теория алгоритмов и эволюционные вычисления»

Вид материалаПрограмма дисциплины

Содержание


Целью данной дисциплины
Тема 2. Машина Тьюринга и нормальные алгорифмы Маркова как формализации понятия «алгоритм»
Тема 3. Алгоритмическая разрешимость и неразрешимость
Тема 4. Модели вычислений и меры сложности
Тема 5. Классы сложности P
Тема 7. Алгоритмы комбинаторной оптимизации на графах
Тема 8. Потоковые алгоритмы
Тема 9. Полиномиальные алгоритмы теории расписаний
Тема 10. Точные и приближенные алгоритмы
Тема 11. Генетические алгоритмы и эволюционные вычисления
Рекомендации по использованию информационных технологий
Тематический расчет часов
Наименование тем
Типовые задачи для подготовки к контрольной работе
Подобный материал:





Программа дисциплины
«Теория алгоритмов и эволюционные вычисления»


для направления 080700.62 – Бизнес-информатика



Утверждена

Учебно-методическим Советом ПФ ГУ-ВШЭ


Председатель_______________ Володина Г.Е.


«_______»_________________________2010г.



Одобрена на заседании кафедры
Информационных технологий в бизнесе
протокол _______________________________


Зав. кафедрой_______________Казаченко Т.А.


«______»__________________________2010 г.




Пермь 2010

  1. Обязательный минимум содержания дисциплины по ГОС

Дисциплина «Теория алгоритмов и эволюционные вычисления» относится к национально-региональному компоненту основной образовательной программы подготовки бакалавра бизнес-информатики. Её содержание обеспечивает подготовку выпускника в соответствии с квалификационной характеристикой, установленной государственным образовательным стандартом для направления 080700.62 – Бизнес-информатика.
  1. Пояснительная записка
  1. Автор программы: к.ф.-м.н., доцент В.В. Морозенко
  2. Требования к студентам:

Приступая к изучению данной дисциплины, студент должен обладать знаниями математики и информатики в объеме общеобразовательной школы, а также знаниями, полученными при изучении курсов «Дискретная математика», «Основы программирования», «Информатика и программирование», «Теория информационных технологий и систем», «Логика».
  1. Аннотация:

Программа составлена в соответствии с требованиями ГОС к обязательному минимуму содержания основной образовательной программы подготовки бакалавра бизнес-информатики.

Дисциплина «Теория алгоритмов и эволюционные вычисления» относится к национально-региональному компоненту цикла общепрофессиональных дисциплин.

Целью данной дисциплины является изучение важнейших разделов теории алгоритмов, методов анализа сложности алгоритмов и обоснования их корректности, методов разработки алгоритмов для решения сложных вычислительных задач и оценивания их эффективности. Изучение данной дисциплины углубляет знания, полученные студентами при изучении курсов «Информатика и программирование» и «Дискретная математика».

Содержание программы дисциплины «Теория алгоритмов и эволюционные вычисления» должно обеспечить базовую подготовку студентов в процессе формирования устойчивых теоретических знаний и практических навыков разработки и анализа алгоритмов для дальнейшей учебной, научной и профессиональной деятельности.

Задачи:
    • познакомить студентов с основами теории алгоритмов, их математическими моделями;
    • дать знания о существующих эффективных алгоритмах для решения наиболее известных задач комбинаторной оптимизации, об их сложности и требованиям к памяти;
    • познакомить с классификацией оптимизационных задач и алгоритмов для их решения, особенностями задач комбинаторной оптимизации большой размерности;
    • дать представление об эволюционных вычислениях, как эффективном методе решения сложных вычислительных задач.

Курс призван повысить общую эрудицию студентов, дать им возможность ориентироваться в данной предметной области, подготовить к применению теоретических знаний при решении различных задач оптимизации, при изучении и разработке средств поддержки принятия решений.
  1. Учебная задача курса:

В результате изучения курса студент должен:
  • Знать:
  • наиболее известные алгоритмы для работы с различными структурами данных;
  • точные и приближенные подходы к решению типовых задач, возникающих в области бизнес-информатики;
    • особенности точных, приближенных, эволюционных, эвристических, переборных, «жадных» алгоритмов.
  • Уметь:
  • анализировать существующие алгоритмы с точки зрения их эффективности и применимости для решения прикладных задач;
  • разрабатывать новые алгоритмы для решения конкретных задач в области бизнес-информатики;
  • оценивать сложность разработанных алгоритмов и обосновывать их корректность.
  • Иметь представление:
  • об областях применения теории алгоритмов;
  • о различных формализациях понятия «алгоритм»;
  • о различных методах классификации существующих алгоритмов;
  • об алгоритмически неразрешимых проблемах.
  • Обладать навыками:
  • применения известных и разработки собственных алгоритмов для решения практических задач с учетом требований к точности, времени работы алгоритма и вычислительным ресурсам;
    • формализации конкретных практических проблем в сфере бизнес-информатики и их сведения к известным модельным задачам.

Студенты должны получить знания о существующих эффективных алгоритмах для решения наиболее известных задач комбинаторной оптимизации, методах их разработки и анализа в объеме, достаточном для успешного изучения курсов «Оптимизация и математические методы принятия решений», «Нечеткая логика и нейронные сети», «Распределенные алгоритмы и параллельное программирование», «Криптографические методы защиты» и др.
  1. Формы контроля:
  • Текущий контроль: в соответствии с учебным планом предусмотрено проведение одной контрольной работы.
  • Промежуточный контроль – работа на семинарских занятиях.
  • Итоговый контроль: зачет проводится в соответствии с учебным планом.
  • Итоговая оценка: складывается в соответствии с «Положением о рейтинге», принятым в ПФ ГУ ВШЭ.
  1. Содержание программы дисциплины

Раздел 1. ОСНОВЫ ТЕОРИИ АЛГОРИТМОВ

Тема 1. Рекурсивные функции как формализация понятия «алгоритм»

Простейшие рекурсивные функции, операции суперпозиции и примитивной рекурсии. Обоснование примитивной рекурсивности некоторых элементарных функций. Частично-рекурсивные функции и предикаты. Операция минимизации. Примеры всюду определенных и частичных рекурсивных функций и предикатов, функция Аккермана. Существование нерекурсивных функций.

Тема 2. Машина Тьюринга и нормальные алгорифмы Маркова как формализации понятия «алгоритм»

Интуитивное понятие алгоритма. Машина Тьюринга, устройство и функционирование. Простейшие машины Тьюринга. Операции над машинами Тьюринга. Вычислимые по Тьюрингу функции, примеры. Совпадение классов частично-рекурсивных и вычислимых по Тьюрингу функций. Формулы, подстановки, схемы. Функции, вычислимые с помощью нормальных алгорифмов Маркова, примеры. Операции над алгорифмами Маркова.

Тема 3. Алгоритмическая разрешимость и неразрешимость

Сопоставление различных формализаций понятия «алгоритм». Тезисы Черча, Тьюринга, Маркова. Кодирование машин Тьюринга. Алгоритмическая разрешимость и неразрешимость проблемы. Примеры алгоритмически разрешимых и неразрешимых проблем. Алгоритмические проблемы самоприменимости, применимости, останова, их алгоритмическая неразрешимость. Разрешимые и перечислимые множества. Нумерация алгоритмов. Теоремы Клини и Райса.

Тема 4. Модели вычислений и меры сложности

Комбинационная сложность, меры комбинационной сложности, сложность «в худшем» и «в среднем». Методы получения верхних и нижних оценок сложности, асимптотические оценки. Соотношения между памятью и временем. Трудные комбинаторные задачи. Приближенные методы и алгоритмы. Алгоритмы гарантированного функционирования. Эвристические и комбинированные алгоритмы. Генетические алгоритмы и эволюционные вычисления.

Тема 5. Классы сложности P и NP

Задачи распознавания. Недетерминированные вычисления. Два подхода к определению недетерминированных машин Тьюринга. Классы P и NP. Соотношение между ними. Примеры задач из классов P и NP. Полиномиальная сводимость и NP-полные задачи, примеры. Задача о «выполнимости КНФ» и теорема Кука. Методы доказательства NP-полноты. NP-трудные задачи. Подходы к решению NP-полных и NP-трудных задач.

Раздел 2. ТОЧНЫЕ И ПРИБЛИЖЕННЫЕ МЕТОДЫ И АЛГОРИТМЫ

Тема 6. Комбинаторные алгоритмы

Рекурсивные алгоритмы, примеры. Исследование сложности рекурсивных алгоритмов с помощью рекуррентных соотношений. Матричный метод решения систем рекуррентных соотношений. Производящие функции, операции над ними, использование для решения рекуррентных соотношений. Алгоритмы генерации комбинаторных объектов. Теория перечисления Пойа и теорема Бернсайда для подсчета числа комбинаторных объектов.

Тема 7. Алгоритмы комбинаторной оптимизации на графах

Задача о максимальном паросочетании в графе. Чередующиеся цепи. Метод «волны» для поиска чередующихся цепей. Теорема Бержа. Алгоритм поиска максимального паросочетания с помощью чередующихся цепей. Задача о совершенном паросочетании. Чередующееся дерево. Метод «волны» для поиска чередующихся деревьев. Теорема Холла. Алгоритм поиска совершенного паросочетания с помощью чередующихся деревьев. Задача о назначениях. Матрица затрат и её свойства. Диагональная редукция матрицы затрат. Венгерский алгоритм для решения задачи о назначении.

Тема 8. Потоковые алгоритмы

Поток в двухполюсной сети. Величина потока. Задача о максимальном потоке в двухполюсной сети. Разрез сети. Пропускная способность разреза. Теорема Форда-Фалкерсона. Остаточная сеть. Алгоритм поиска максимального потока в двухполюсной сети с помощью остаточной сети. Стоимость потока в двухполюсной сети. Задача о максимальном потоке минимальной стоимости в двухполюсной сети. Остаточная сеть. Алгоритм поиска максимального потока минимальной стоимости путем устранения циклов отрицательной стоимости в остаточной сети. Сведение задачи о максимальном паросочетании в двудольном графе к задаче о максимальном потоке в измененном графе.

Тема 9. Полиномиальные алгоритмы теории расписаний

Граф предшествования. Построение расписания минимальной стоимости для независимых заданий и одного исполнителя. Построение расписания минимальной длительности для системы единичных заданий с древовидным графом предшествования и несколькими идентичными исполнителями. Построение расписания минимальной длительности с прерываниями для системы независимых заданий. Труднорешаемые задачи теории расписаний. Конвейерная задача. Алгоритм Джонсона.

Тема 10. Точные и приближенные алгоритмы

Метод ветвей и границ. Задача о рюкзаке, её точное решение методом ветвей и границ. Приближенные алгоритмы, оценки их погрешности. Приближенный алгоритм для задачи о рюкзаке с гарантированной погрешностью. Динамическое программирование. Задача о минимальном покрытии, её точное решение с помощью динамического программирования. Задача коммивояжера. Метод ветвей и границ для точного решения задачи коммивояжера. Алгоритм Литтла. Приближенный алгоритм Кристофидиса для евклидовой задачи коммивояжера.

Тема 11. Генетические алгоритмы и эволюционные вычисления

Кодирование объектов. Определение фенотипа объекта по его генотипу. Основные генетические операции: кроссовер, отбор, мутация. Фитнесс-функция. Схема работы эволюционного алгоритма на примере задачи коммивояжера. Шаблоны. Теорема шаблонов. Настройка эволюционного алгорита. Стратегии отбора. Модели эволюционных вычислений: Genitor, СНС, Hybrid Algorithms, Island Models, Cellular Genetic Algorithms. Эволюционное программирование.
  1. Учебно-методическое обеспечение дисциплины
  1. Литература:

Базовый учебник:

Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, 2-е издание. М.: Издательский дом «Вильямс», 2005.

Основная:
  1. Гладков Л.А., Курейчик В.В., Курейчик В.М. Генетические алгоритмы. М.: ФИЗМАТЛИТ, 2006.
  2. Иванов Б.Н. Дискретная математика. Алгоритмы и программы: Учеб. пособие. М.: Лаборатория Базовых Знаний, 2002.
  3. Игошин В.И. Математическая логика и теория алгоритмов: Учеб. пособие. М.: Академия, 2004.
  4. Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы. М.: Издательский дом «Вильямс», 2000.

Дополнительная:
  1. Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности / Г.К.Вороновский, К.В.Махотило, С.Н.Петрашев, С.А.Сергеев. – Х.: ОСНОВА, 1997.
  2. Мальцев А.И. Алгоритмы и рекурсивные функции. М.: Наука, 1986.
  3. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы: теория и практика. М.: Мир, 1980.
  4. Сигал М.Х., Иванова А.П. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы: Учеб. пособие. М.: ФИЗМАТЛИТ, 2002.
  5. Судоплатов С.В., Овчинникова Е.В. Математическая логика и теория алгоритмов: Учебник. М.: ИНФРА-М; Новосибирск: Изд-во НГТУ, 2004.
  6. Успенский В.А., Семенов А.Л. Теория алгоритмов: основные открытия и приложения. М.: Наука, 1987.



  1. Тематика заданий по различным формам текущего контроля:


Приложение 1. Примерный перечень задач для подготовки к контрольной работе

Приложение 2. План семинарских занятий

Приложение 3. Тематика контрольных работ

Приложение 4. Перечень вопросов для самоконтроля студентов
  1. Методические рекомендации (материалы) преподавателю:

На лекциях рекомендуется иллюстрировать материал примерами, показывающими все этапы решения задачи: формализацию и построение математической модели, разработку алгоритма, доказательство его корректности, нахождение его сложности, написание программы, её отладку и тестирование, выполнение программы на реальных входных данных.

На практических занятиях используются следующие методы обучения и контроля усвоения материала:
    1. написание контрольной работы по теоретической части курса;
    2. разработка алгоритмов для конкретных задач и их практическая реализация в виде программного продукта с последующей отладкой и тестированием.

При оценке выполненных заданий особое внимание рекомендуется обратить на оценки разработанных программ (получение теоретических оценок, сравнение проведенных экспериментов с результатами, полученными различными способами).
  1. Методические указания студентам:

Студенту рекомендуется следующая схема подготовки к контрольной работе:
  1. проработать конспект лекций;
  2. проанализировать основную и дополнительную литературу, рекомендованную по изучаемому разделу;
  3. проанализировать варианты решений, предложенные преподавателем на практических занятиях;
  4. при затруднениях сформулировать вопросы к преподавателю.

При подготовке рекомендуется использовать электронные учебные материалы, имеющиеся в медиатеке.

Выполненные задания должны сопровождаться данными анализа результатов (теоретическими оценками, сравнением результатов, полученных различными способами).
  1. Рекомендации по использованию информационных технологий

Часть практических занятий по разделу «Точные и приближенные методы и алгоритмы» проводятся в компьютерном классе. Программное обеспечение сети должно поддерживать возможность
  1. доступа к материалам для подготовки, размещаемым на сервере;
  2. разработки, тестирования, отладки программ, написанных на языке Pascal или C++;
  3. оформления отчетов по выполненным заданиям с помощью текстовых редакторов.


Авторы программы: _________________________________/В.В. Морозенко /


  1. Тематический расчет часов



№
Наименование тем



Аудиторные часы
Самостоятельная работа
Всего часов

Лекции
Семинарские или практические занятия
Всего


Рекурсивные функции как формализация понятия «алгоритм»
2
2
4
2
6


Машина Тьюринга и нормальные алгорифмы Маркова как формализации понятия «алгоритм»
2
2
4
2
6


Алгоритмическая разрешимость и неразрешимость
2
0
2
2
4


Модели вычислений и меры сложности
2
0
2
2
4


Классы сложности P и NP
2
0
2
2
4


Комбинаторные алгоритмы
2
2
4
4
8


Алгоритмы комбинаторной оптимизации на графах
2
2
4
10
14


Потоковые алгоритмы
2
4
6
10
16


Полиномиальные алгоритмы теории расписаний
2
6
8
10
18


Точные и приближенные алгоритмы
2
2
4
10
14


Генетические алгоритмы и эволюционные вычисления

2
2
4
10
14




Всего
22
22
44
64
108



Авторы программы: __________________________________________ /В.В. Морозенко /

Приложение 1


Примерный перечень задач для подготовки к контрольной работе


По дисциплине предусмотрена одна контрольная работа по теме «Основы теории алгоритмов». По темам и уровню сложности приведенные задачи соответствуют контрольным заданиям. Для подготовки к контрольной необходимо выполнить все домашние задания и разобрать примеры, приведенные в лекциях. Примерный перечень заданий:
    1. для заданной всюду или частично определенной функции построить вычисляющую её машину Тьюринга;
    2. доказать рекурсивность заданной функции;
    3. к заданной паре всюду определенных рекурсивных функций применить операцию примитивной рекурсии;
    4. к заданной не всюду определенной рекурсивной функции одного или двух аргументов применить операцию минимизации по одному из аргументов.


Типовые задачи для подготовки к контрольной работе
  1. Для всюду определенной функции



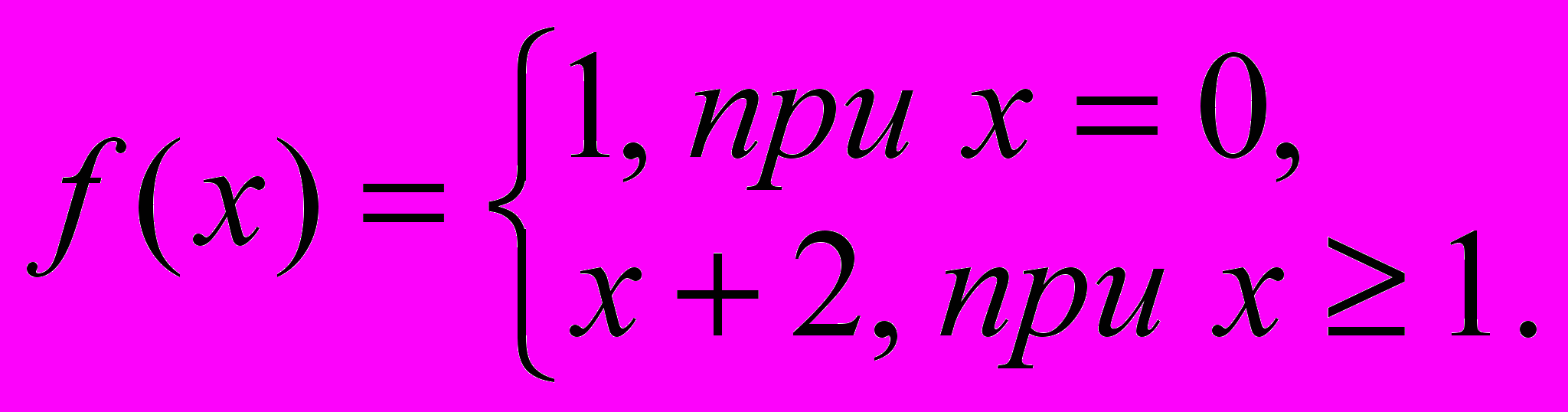
построить вычисляющую (и правильно вычисляющую) её машину Тьюринга.
  1. Для частично определенной функции



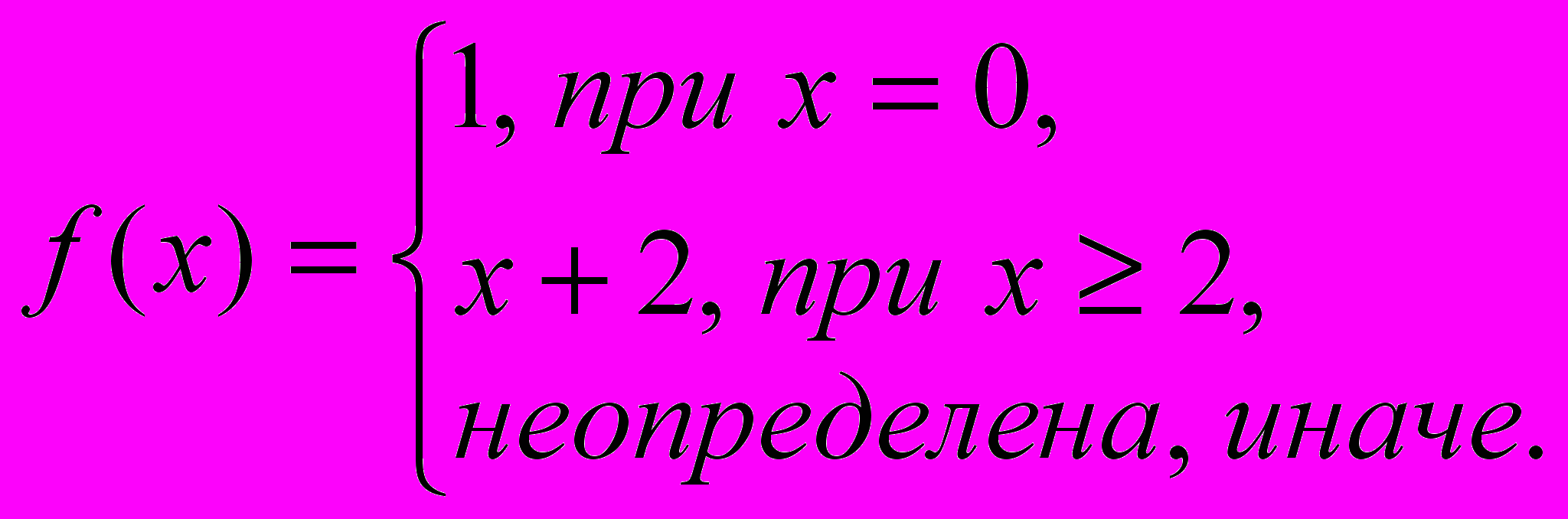
построить вычисляющую (и правильно вычисляющую) её машину Тьюринга.
  1. Какие функции f(x) и f(x,y) вычисляет (не обязательно правильным образом) машина Тьюринга, заданная программой? Исправить программу так, чтобы машина вычисляла обе функции правильным образом.
q1
q2
q3
q4
q5
q6

0



0Rq4
0Rq4






ΛLq6

1
1Rq2
1Rq3
1Rq3
0Rq5
1Rq6
1Sq0

Λ



ΛRq2
1Sq0



ΛLq6
ΛSq0


Ответ:





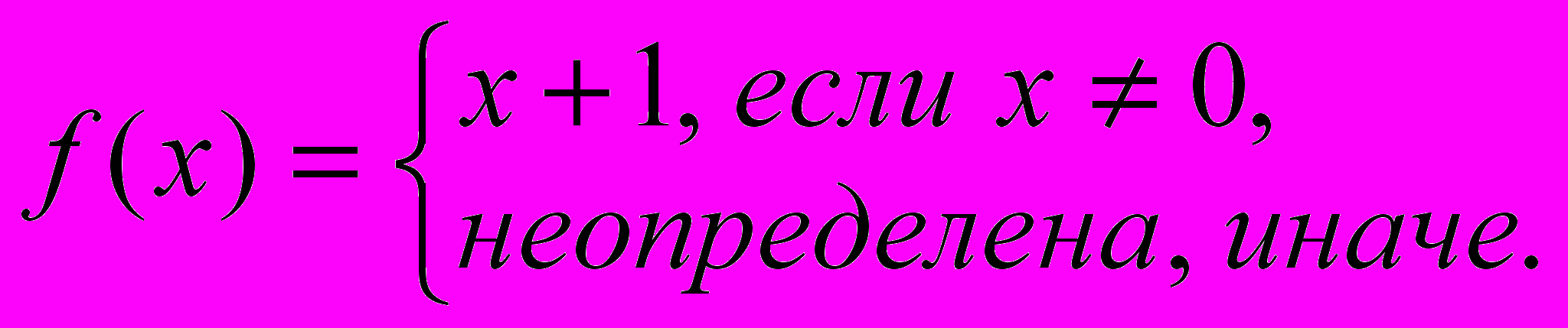
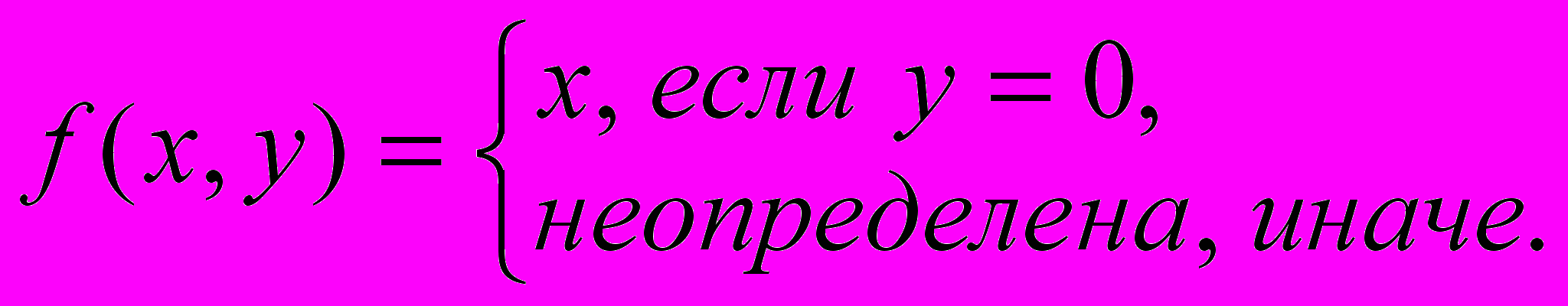
Указание:
  1. на ленте в начальный момент написан либо один массив из единиц, либо несколько массивов из единиц, разделенных одним нулем, а слева и справа от этих массивов лента заполнена пустыми символами Λ;
  2. в начальный момент времени головка машина Тьюринга видит левую крайную единицу массива из единиц;
  3. считается, что машина Тьюринга вычисляет функцию правильным образом, если выполняются два условия:

а) если f(x) определено, то машина вычисляет это значение, записывает его в виде массива из единиц, стирает все остальные символы и останавливается напротив крайней левой единицы этого массива;

б) если f(x) неопределено, то машина зацикливается (не останавливается).
  1. считается, что машина Тьюринга просто вычисляет функцию (не обязательно правильным образом), если выполняются два условия:

а) если f(x) определено, то машина вычисляет это значение, записывает его в виде массива из единиц, стирает все остальные символы и останавливается (неважно – где);

б) если f(x) неопределено, то машина либо зацикливается, либо останавливается и оставляет на ленте все что угодно, но не массив из единиц.
  1. Доказать рекурсивность заданной функции:

а) 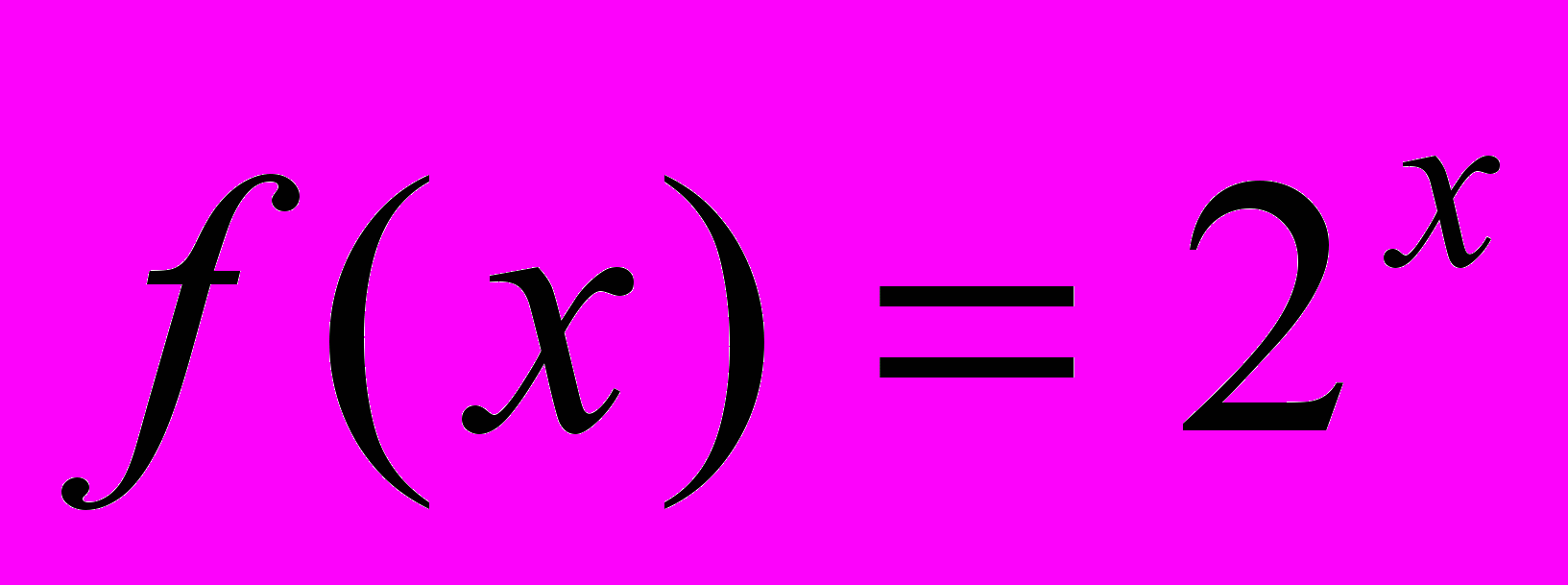; б) .
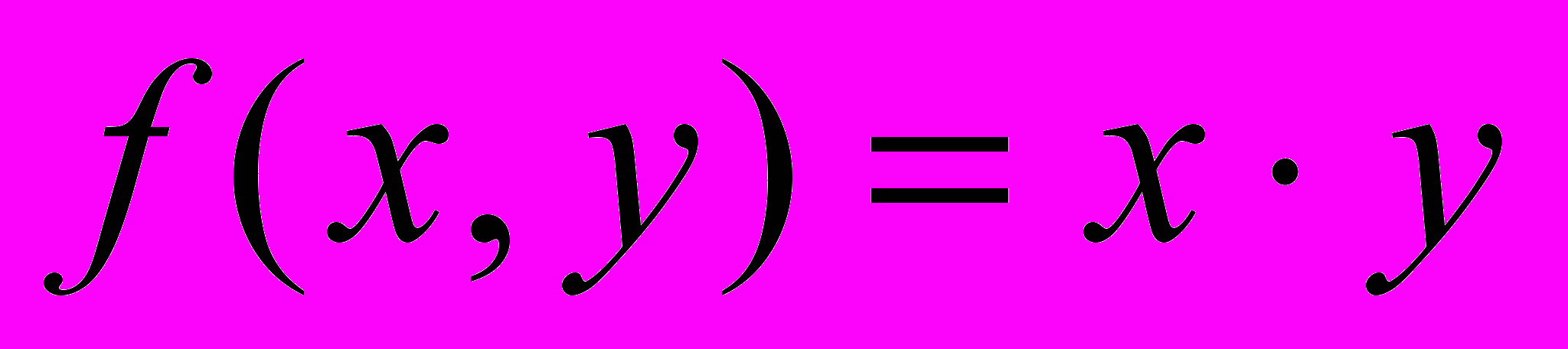  1. К заданной паре всюду определенных рекурсивных функций применить операцию примитивной рекурсии:

а) 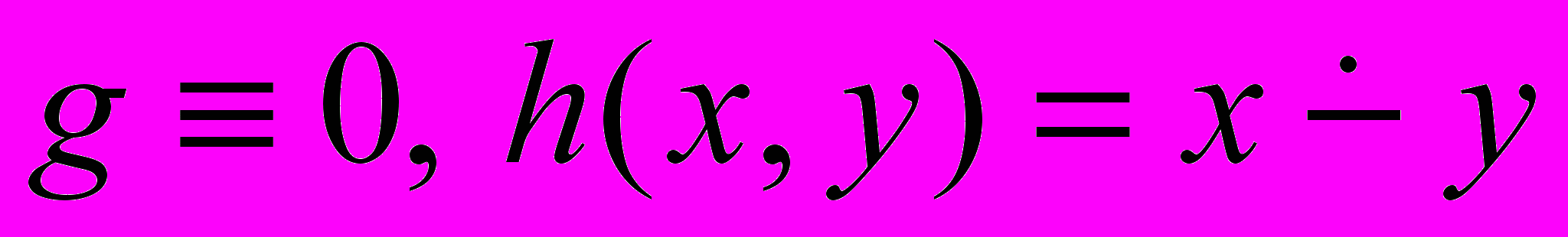; б) .

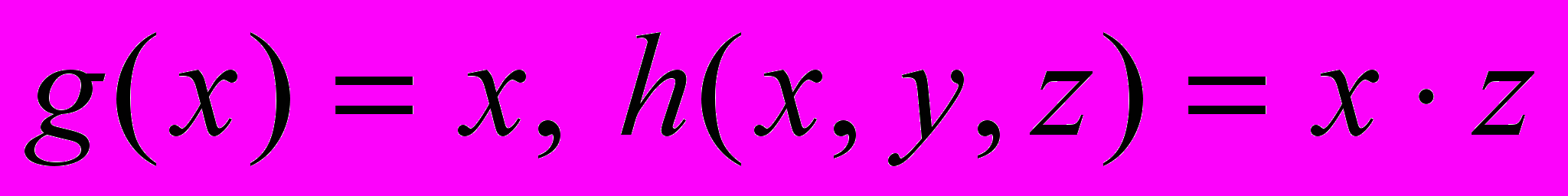Указание: Функция 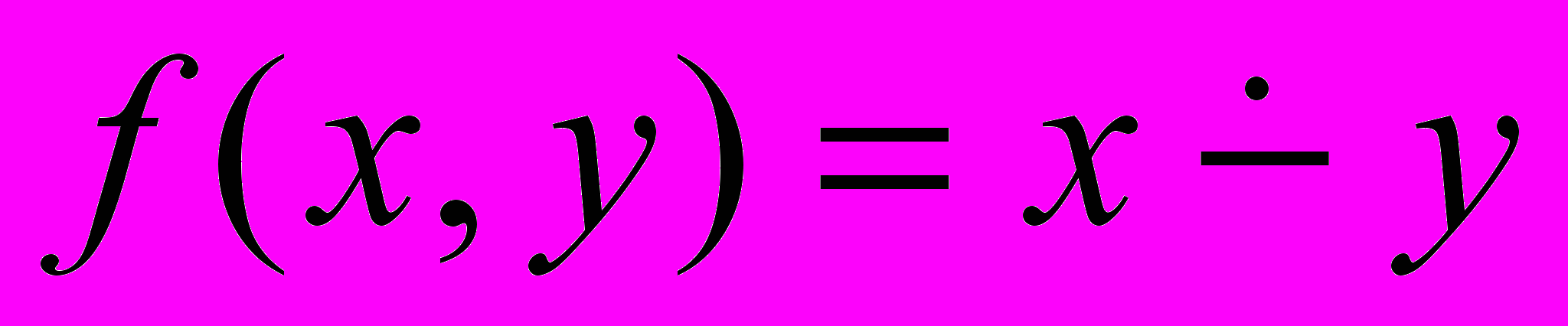называется усеченной разностью и определяется следующим образом: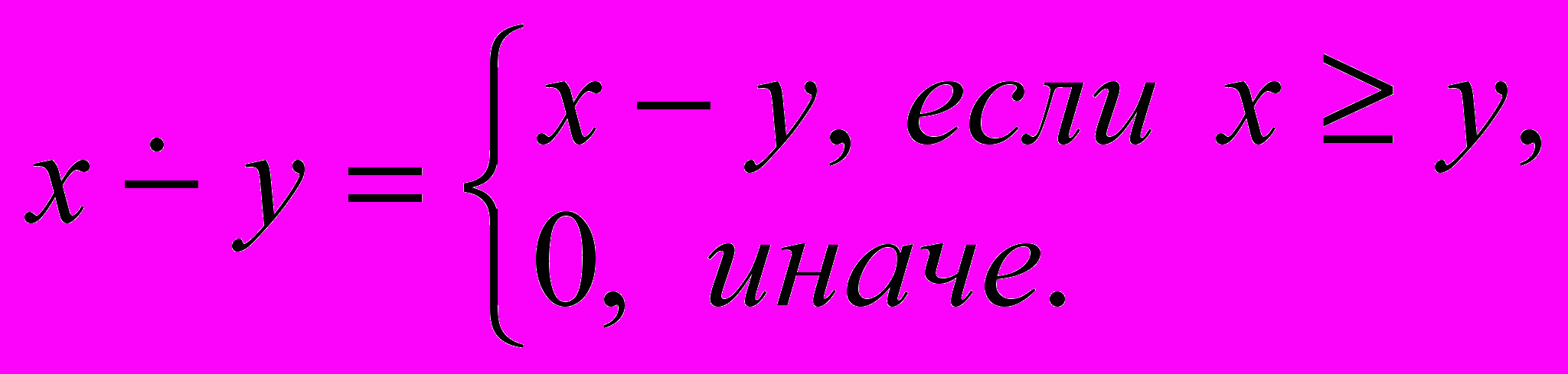


  1. К заданной не всюду определенной рекурсивной функции одного или двух аргументов применить операцию минимизации по одному из аргументов:

а) ;

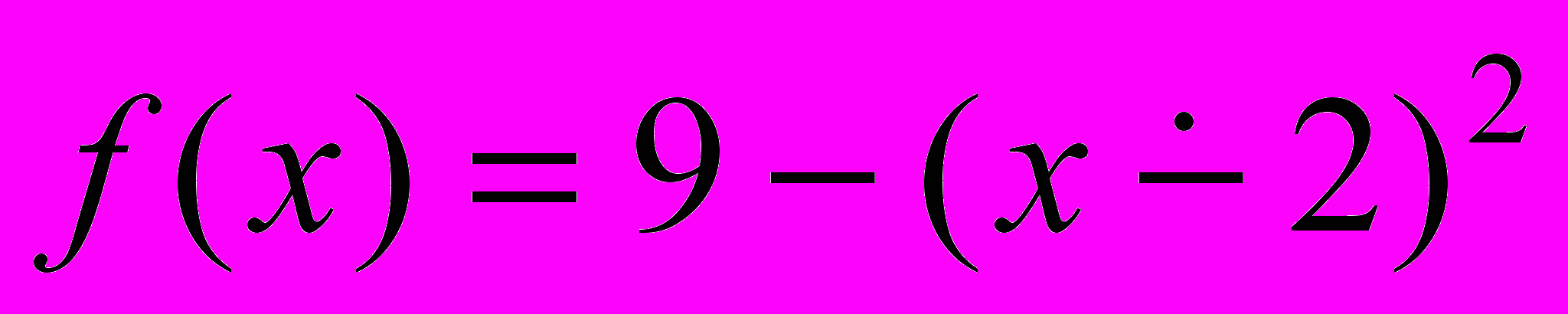Указание: Функция 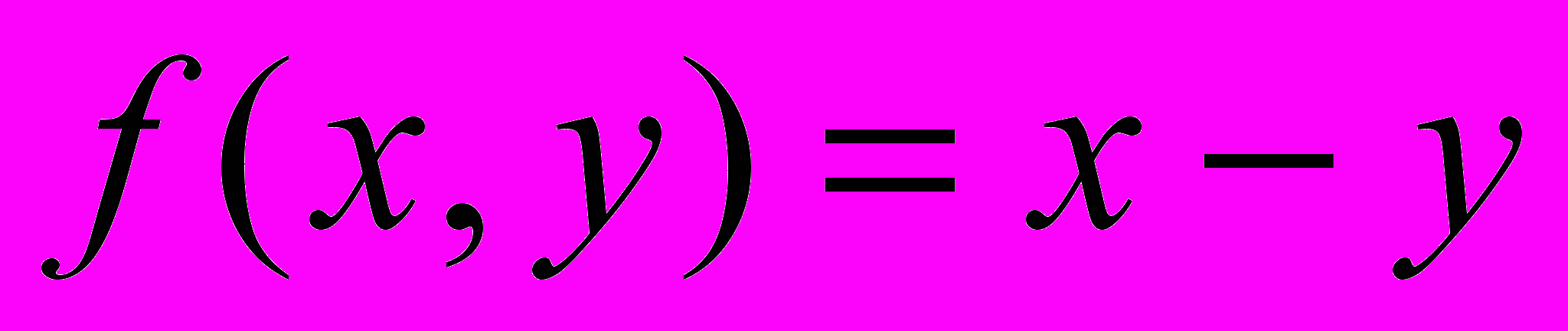определяется следующим образом: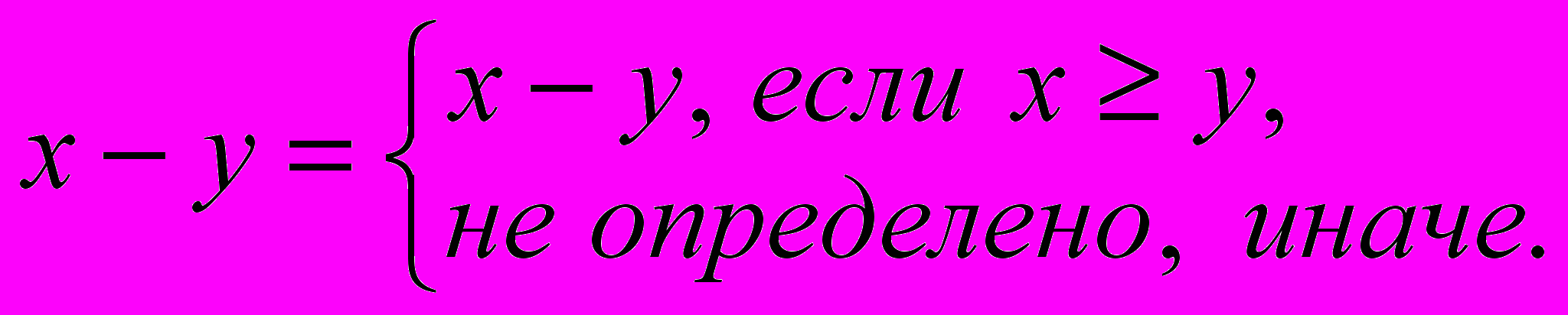



б) 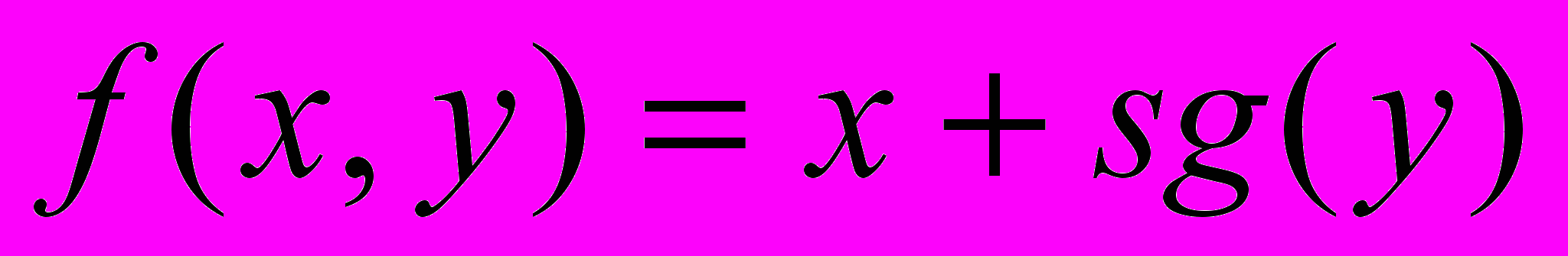(по переменной х);

в) 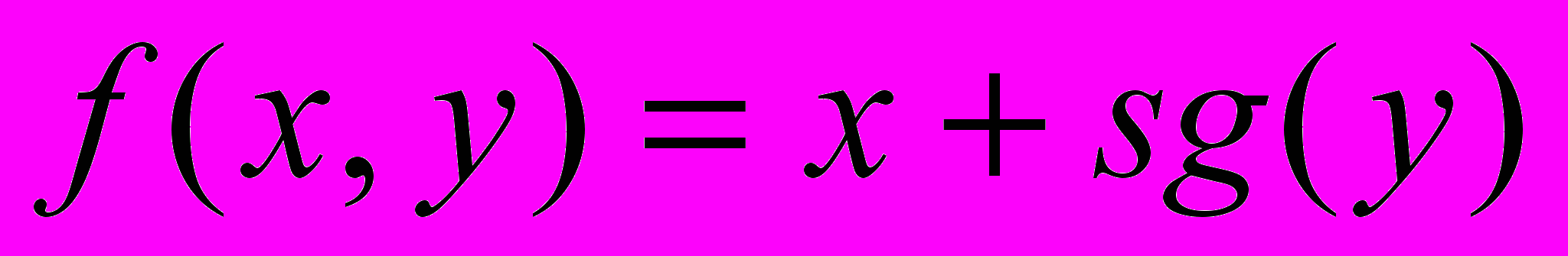(по переменной у).

Указание: Функция 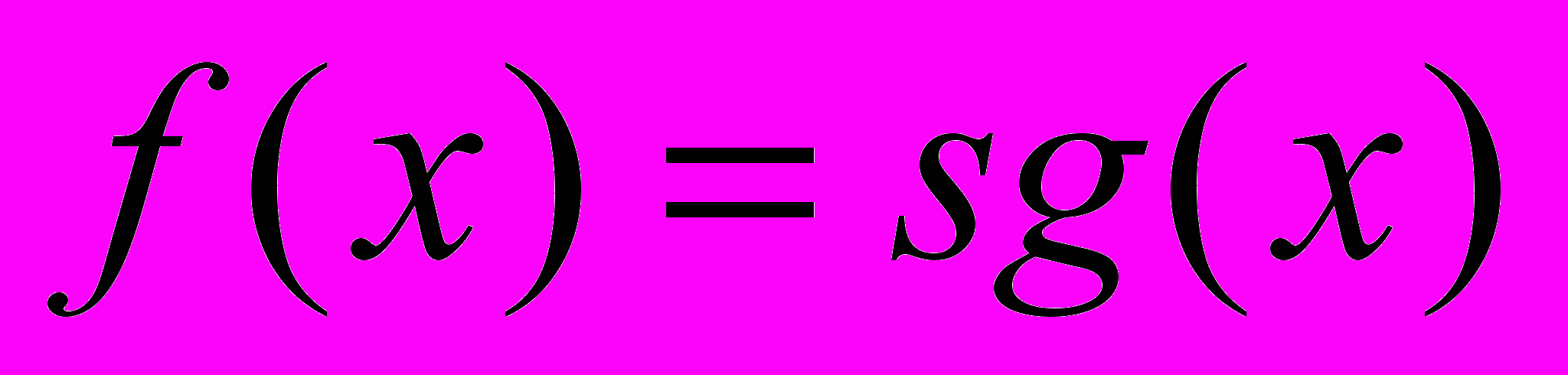называется сигнум и определяется следующим образом: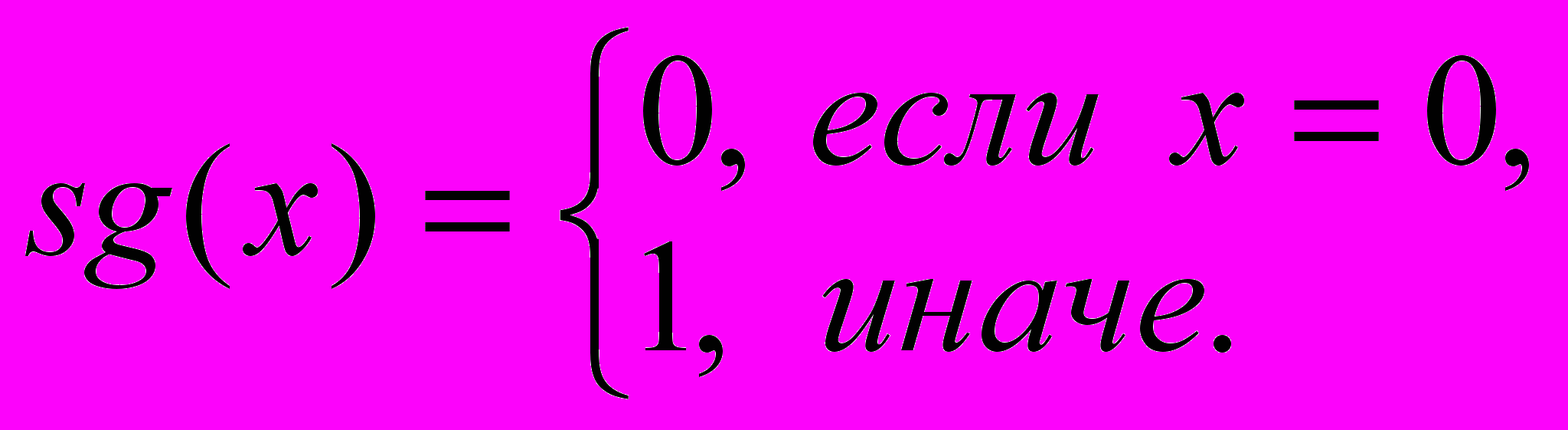


  1. Используя функции 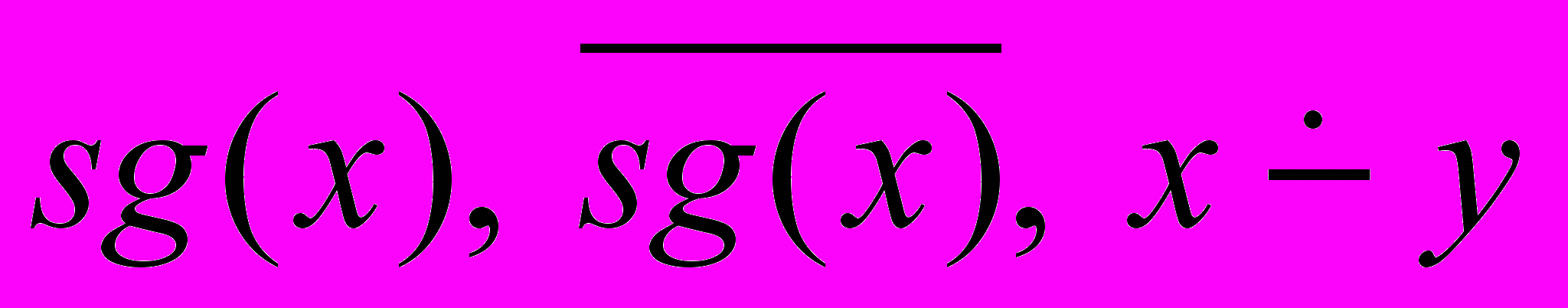, задать формулой функцию:

а) 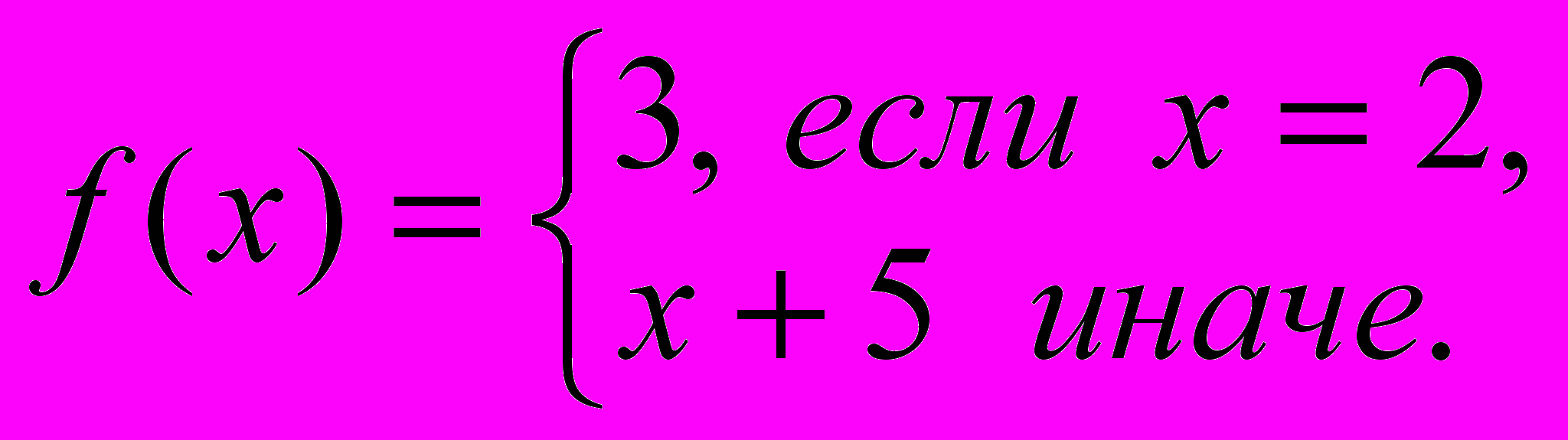б)

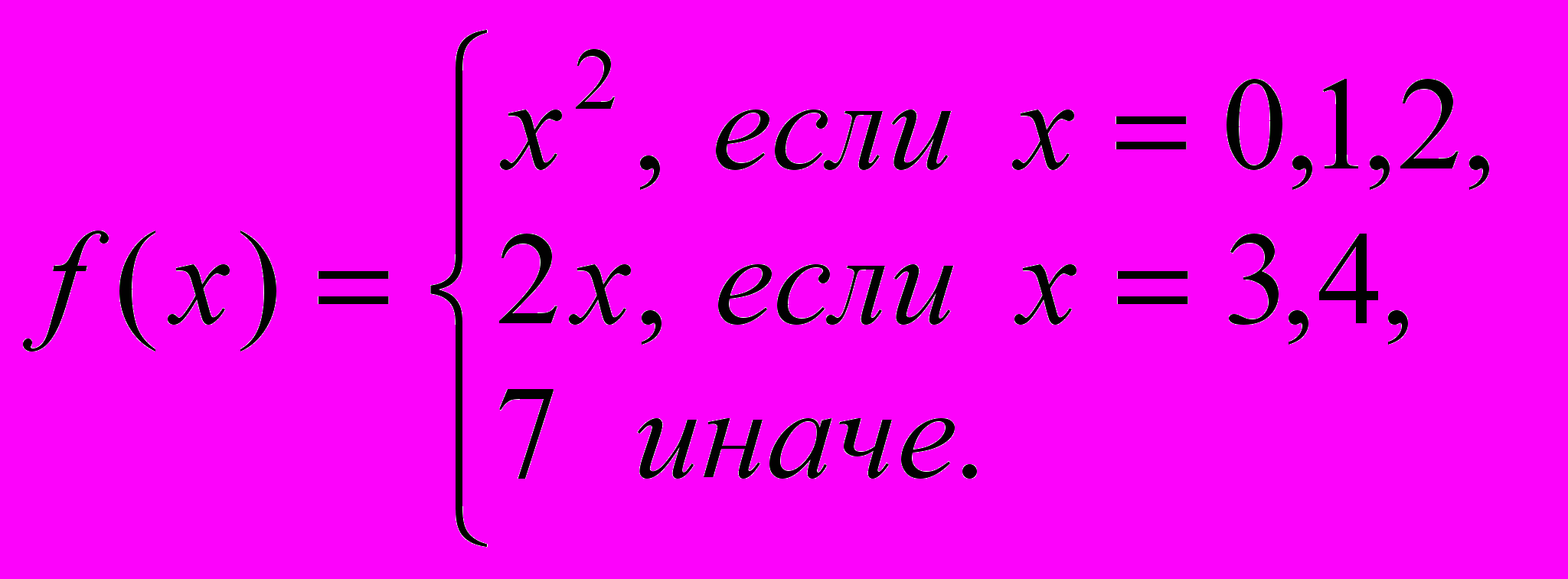
Указание: Функцию



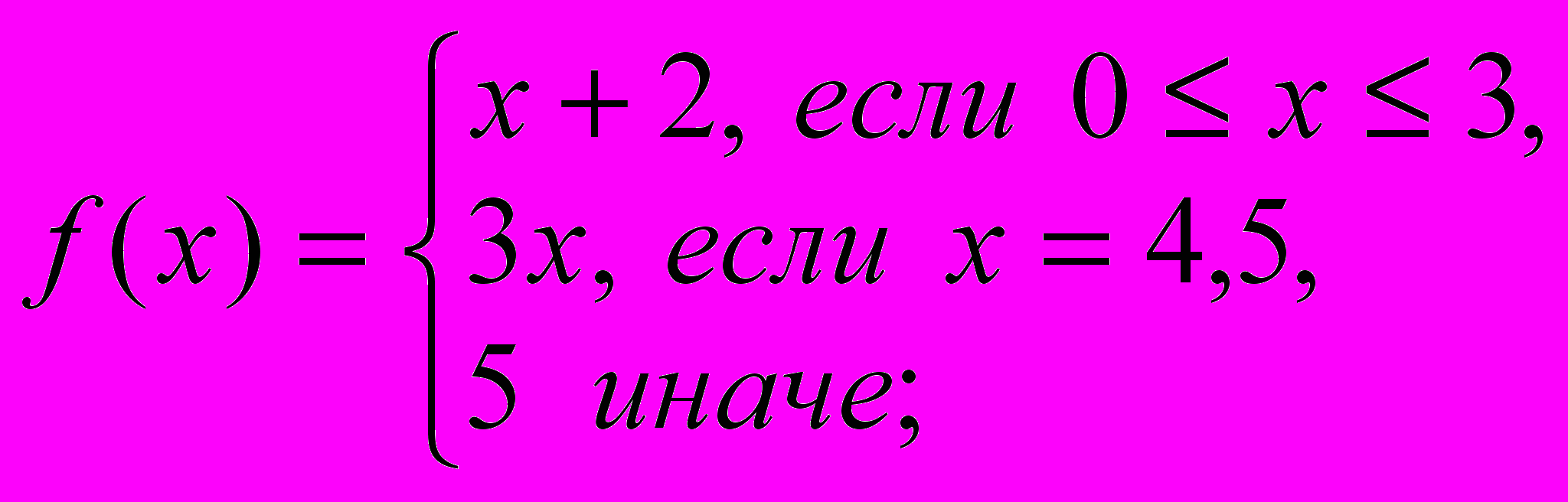
можно задать формулой .

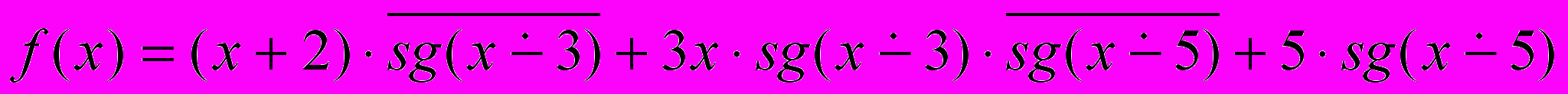Приложение 2


План семинарских занятий


Раздел 1. Тема 1. Рекурсивные функции как формализация понятия «алгоритм».

На семинаре предполагается разбор и самостоятельное решение следующих задач:
  • к заданным рекурсивным функциям применить операции суперпозиции, примитивной рекурсии, минимизации;
  • доказать, что заданная функция является примитивно-рекурсивной;
  • доказать, что заданная функция является рекурсивной.

Раздел 1. Тема 2. Машина Тьюринга и нормальные алгорифмы Маркова как формализации понятия «алгоритм».

На семинаре предполагается разбор и самостоятельное решение следующих задач:
  • для заданной функции написать программу вычисляющей её машины Тьюринга;
  • к заданным машинам Тьюринга применить операции суперпозиции, подключения, итерации;
  • по заданной программе машины Тьюринга выяснить, какую функцию она вычисляет;
  • написать алгорифм Маркова для заданного преобразования символьной строки.

Раздел 1. Тема 6. Комбинаторные алгоритмы.

На семинаре предполагается разбор и самостоятельное решение следующих задач:
  • решить заданное неоднородное рекуррентное соотношение методом неопределенных коэффициентов;
  • решить заданную неоднородную систему рекуррентных соотношений методом исключения и матричным методом;
  • решить заданное неоднородное рекуррентное соотношение с помощью производящей функции;
  • найти сложность заданного рекурсивного алгоритма, составив рекуррентное соотношение для числа операций, выполняемых данным алгоритмом.

Раздел 2. Тема 7. Алгоритмы комбинаторной оптимизации на графах.

На семинаре предполагается разбор и самостоятельное решение следующих задач:
  • применить алгоритм поиска максимального паросочетания для заданного графа;
  • применить алгоритм поиска совершенного паросочетания для заданого графа;
  • применить венгерский алгоритм для решения задачи о назначении с заданной матрицей затрат.

Раздел 2. Тема 8. Потоковые алгоритмы.

На двух семинарах по этой теме предполагается разбор и самостоятельное решение следующих задач:
  • в заданной двухполюсной сети найти все разрезы и вычислить их пропускные способности;
  • для заданной двухполюсной сети найти величину максимального потока с помощью теоремы Форда-Фалкерсона;
  • для потока, заданного в двухполюсной сети, построить остаточную сеть;
  • для заданной двухполюсной сети найти максимальный поток с помощью остаточной сети;
  • найти стоимость потока, заданного в двухполюсной сети;
  • найти циклы отрицательной стоимости в остаточной сети для заданного потока в двухполюсной сети;
  • найти максимальный поток минимальной стоимости в заданной двухполюсной сети;
  • заданную задачу комбинаторной оптимизации свести к задаче о максимальном потоке или к задаче о максимальном потоке минимальной стоимости.

Раздел 2. Тема 9. Полиномиальные алгоритмы теории расписаний.

На трех семинарах по этой теме предполагается разбор и самостоятельное решение следующих задач:
  • с помощью алгоритма Демукрона выполнить топологическую сортировку ориентированного графа, задающего отношение предшествования между работами (заданиями);
  • найти расписание выполнения заданного комплекса работ в кратчайшие сроки при условии, что некоторые работы могут выполняться параллельно и между ними существует отношение предшествования, указать «критические» работы;
  • найти самое дешевое расписание для заданного комплекса работ при условии, что работы независимы, известны их длительности и материальные затраты за каждую единицу времени с момента начала выполнения работ до завершения данной работы, имеется один исполнитель;
  • используя «уровневую стратегию», найти расписание выполнения заданного комплекса работ в кратчайшие сроки при условии, что работы зависимы (граф зависимостей является деревом, ориентированным к корню), имеется несколько идентичных исполнителей, все работы единичной длительности, прерывания работ запрещены;
  • используя «уровневую стратегию» и лексикографическую сортировку, найти расписание выполнения заданного комплекса работ в кратчайшие сроки при условии, что работы зависимы (граф зависимостей является произвольным ориентированным графом без ориентированных циклов), все работы единичной длительности, имеется два идентичных исполнителя, прерывания работ запрещены;
  • найти расписание выполнения заданного комплекса работ в кратчайшие сроки при условии, что работы зависимы (граф зависимостей является произвольным ориентированным графом без ориентированных циклов), имеется 2 идентичных исполнителя, длительности работ - произвольные положительные числа, прерывания работ допускаются;
  • используя «ленточную стратегию», найти расписание выполнения заданного комплекса работ в кратчайшие сроки при условии, что работы независимы, имеют произвольную длительность, имеется произвольное число исполнителей, допускаются прерывания;
  • используя стратегию «разделения процессоров», найти расписание выполнения заданного комплекса работ в кратчайшие сроки при условии, что работы зависимы (граф зависимостей - лес), длительности работ – произвольны, число исполнителей – любое, исполнители универсальны и идентичны, допускаются прерывания;
  • используя стратегию «разделения процессоров и времени», найти расписание выполнения заданного комплекса работ в кратчайшие сроки при условии, что работы независимы, длительности работ – произвольные, число исполнителей – любое, исполнители универсальны, но имеют разную производительность, допускаются прерывания;
  • используя алгоритм Джонсона, решить конвейерную задачу для заданного комплекса независимых работ.

Раздел 2. Тема 10. Точные и приближенные алгоритмы.

На семинаре предполагается разбор и самостоятельное решение следующих задач:
  • методом ветвей и границ решить задачу о рюкзаке для набора предметов с заданными весами и стоимостью;
  • методом ветвей и границ решить задачу коммивояжера для заданной матрицы стоимостей применить (алгоритм Литтла);
  • используя приближенный алгоритм Кристофидиса, решить евклидову задачу коммивояжера для заданной матрицы расстояний;
  • используя динамическое программирование, решить задачу об оптимальном распределении ресурсов между проектами.
  • используя динамическое программирование, решить задачу об оптимальной загрузке транспортного средства неделимыми предметами.

Раздел 2. Тема 11. Генетические алгоритмы и эволюционные вычисления.

На семинаре предполагается разбор и самостоятельное решение следующих задач:
  • выполнить действия, моделирующие работу генетического алгоритма для заданной задачи комбинаторной оптимизации (на примере задачи о рюкзаке и задачи коммивояжера);
  • разработать наиболее подходящую схему бинарного кодирования и генетические операторы для решения заданной задачи комбинаторной оптимизации;
  • разработать наиболее подходящую схему многобуквенного кодирования и генетические операторы для решения заданной задачи комбинаторной оптимизации.



Приложение 3

Тематика контрольных работ


По дисциплине предусмотрена одна контрольная работа по теме «Основы теории алгоритмов». Примерный перечень заданий:
  1. для заданной всюду определенной функции построить вычисляющую её машину Тьюринга;
  2. доказать рекурсивность заданной функции;
  3. к заданной паре всюду определенных рекурсивных функций применить операцию примитивной рекурсии;
  4. к заданной не всюду определенной рекурсивной функции одного или двух аргументов применить операцию минимизации по одному из аргументов.



Приложение 4

Перечень вопросов для самоконтроля студентов

  1. Какая функция называется примитивно рекурсивной?
  2. В чем заключаются операции суперпозиции и примитивной рекурсии?
  3. Что такое частично рекурсивная функция?
  4. Как выполняется операция минимизации?
  5. Как можно закодировать и пронумеровать машины Тьюринга?
  6. Какие функции вычислимы по Тьюрингу? В чем состоит тезис Тьюринга?
  7. Существуют ли невычислимые функции?
  8. Какая функция соответствуют проблеме самоприменимости? Вычислима ли эта функция?
  9. В чем состоит проблема останова и что означает её алгоритмическая неразрешимость?
  10. Что такое разрешимое и перечислимое множество?
  11. Какие проблемы в теории алгоритмов алгоритмически неразрешимы?
  12. В чем смысл теорем Клини и Райса?
  13. Какие существуют оценки эффективности алгоритма? Чем сложность «в худшем» отличается от сложности «в среднем»?
  14. Чем полиномиальные алгоритмы отличаются от экспоненциальных?
  15. Чем нижние оценки сложности алгоритмов отличаются от верхних? Чем отличаются методы их доказательства?
  16. Что такое недетерминированная машина Тьюринга?
  17. Чем отличаются классы задач P и NP?
  18. Какая задача считается NP-полной?
  19. Каковы методы доказательства NP-полноты задачи?
  20. В чем состоят матричный метод и метод исключения неизвестных для решения системы линейных рекуррентных соотношений с постоянными коэффициентами?
  21. Каковы этапы решения неоднородного рекуррентного соотношения с постоянными коэффициентами?
  22. Как полиномиальные производящие функции используются для решения рекуррентных соотношений с переменными коэффициентами?
  23. Как формулируются первая и вторая теоремы Пойа о цикловом индексе группы подстановок?
  24. Что такое максимальное паросочетание и как его можно найти с помощью алгоритма чередующихся цепей?
  25. Что такое совершенное паросочетание и как его можно найти с помощью чередующихся деревьев?
  26. Что такое поток и разрез в сети? Как формулируется теорема Форда–Фолкерсона?
  27. В чем состоит задача о максимальном потоке в сети и как она решается?
  28. В чем состоит задача о максимальном потоке минимальной стоимости и как она решается?
  29. В чем состоит задача о назначениях? Как она решается с помощью венгерского алгоритма?
  30. Каков алгоритм построения расписания минимальной стоимости для независимых заданий и одного исполнителя?
  31. Каков алгоритм построения расписания минимальной длительности для единичных заданий с древовидным графом предшествования?
  32. Каков алгоритм построения расписания минимальной длительности с прерываниями для независимых заданий?
  33. В чем заключается задача о рюкзаке? Как она решается методом ветвей и границ?
  34. В чем заключается приближенный алгоритм для задачи о рюкзаке с гарантированной погрешностью?
  35. Как формулируется задача коммивояжера? Как она решается методом ветвей и границ?
  36. Как формулируется евклидова задача коммивояжера? В чем состоит алгоритм Кристофидиса для её решения?
  37. Что такое «жадный» алгоритм и эвристика? Чем они отличаются?
  38. Какова общая схема работы генетического алгоритма? Каковы его параметры?
  39. Что такое генетические операторы? Какие существуют методы отбора особей?
  40. Как решается задача коммивояжера с помощью генетического алгоритма?