Термин интеллект (intelligence) происходит от латинского intellectus что означает ум, рассудок, разум; мыслительные способности человека
| Вид материала | Документы |
- 1. Основы теории коррозии Термин коррозия происходит от латинского "corrosio", что, 205.52kb.
- Слово "мебель" происходит от латинского "мобилис", что означает "подвижный", 457.09kb.
- Лекция Понятие об интеллекте и интеллектуальных нарушениях. Интеллект, 1197.01kb.
- Теоретический курс: Что означает термин «логика» Каковы объект и предмет логики, 632.78kb.
- Понятие информации, виды информации. Ее свойства, 220.05kb.
- Культура античности древнегреческая цивилизация, 120.53kb.
- М. Ю. Лермонтова 7-10 стр, 331.07kb.
- Проституция одна из форм социально отклоняющегося полового поведения, проявляющегося, 325.9kb.
- Концепция, 230.42kb.
- Роль спекуляции (легальной и нелегальной) в рыночном хозяйстве. Хеджеры и спекулянты, 244.01kb.
Декларативный, процедурный подход языка Пролог. Пролог (Prolog) — язык логического программирования, основанный на логике дизъюнктов Хорна, представляющей собой подмножество логики предикатов первого порядка. Начало истории языка относится к 70-м годам XX века. Будучи декларативным языком программирования, Пролог воспринимает в качестве программы некоторое описание задачи, и сам производит поиск решения, пользуясь механизмом бэктрекинга и унификацией. Пролог относится к так называемым декларативным языкам, требующим от автора умения составить формальное описание ситуации. Поэтому программа на Прологе не является таковой в традиционном понимании, так как не содержит управляющих конструкций типа if … then, while … do; нет даже оператора присваивания. В Прологе задействованы другие механизмы. Задача описывается в терминах фактов и правил, а поиск решения Пролог берет на себя посредством встроенного механизма логического вывода. Декларативный подход: B-> PQ Процедурный подход: Что бы получить В нужно решить P, а затем решить Q. Основные положения пропорциональной логики и логики 1-го порядка. Пропозициональная логика — это формальная теория, основным объектом которой служит понятие логического высказывания. С точки зрения выразительности, её можно охарактеризовать как классическую логику нулевого порядка. Логика высказываний является простейшей логикой, максимально близкой к человеческой логике неформальных рассуждений и известна ещё со времён античности. Знаки 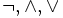 и и 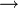 (отрицание, конъюнкция, дизъюнкция и импликация) называются пропозициональными связками. Подформулой называется часть формулы, сама являющаяся формулой. Собственной подформулой называется подформула, не совпадающая со всей формулой. (отрицание, конъюнкция, дизъюнкция и импликация) называются пропозициональными связками. Подформулой называется часть формулы, сама являющаяся формулой. Собственной подформулой называется подформула, не совпадающая со всей формулой. Являясь формализованым аналогом обычной логики, логика первого порядка дает возможность строго рассуждать об истинности и ложности утверждений и об их взаимосвязи, в частности, о логическом следовании одного утверждения из другого, или, например, об их эквивалентности. Рассмотрим классический пример формализации утверждений естественного языка в логике первого порядка. Возьмем рассуждение «Каждый человек смертен. Конфуций — человек. Следовательно, Конфуций смертен». Обозначим «x есть человек» через ЧЕЛОВЕК(x) и «x смертен» через СМЕРТЕН(x). Тогда утверждение «каждый человек смертен» может быть представлено формулой: 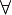 x(ЧЕЛОВЕК(x) → СМЕРТЕН(x)) утверждение «Конфуций — человек» формулой ЧЕЛОВЕК(Конфуций), и «Конфуций смертен» формулой СМЕРТЕН(Конфуций). Утверждение в целом теперь может быть записано формулой: x(ЧЕЛОВЕК(x) → СМЕРТЕН(x)) утверждение «Конфуций — человек» формулой ЧЕЛОВЕК(Конфуций), и «Конфуций смертен» формулой СМЕРТЕН(Конфуций). Утверждение в целом теперь может быть записано формулой:( 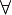 x(ЧЕЛОВЕК(x) → СМЕРТЕН(x)) x(ЧЕЛОВЕК(x) → СМЕРТЕН(x))  ЧЕЛОВЕК(Конфуций) ) → СМЕРТЕН(Конфуций) ЧЕЛОВЕК(Конфуций) ) → СМЕРТЕН(Конфуций)Экспертные системы. Модели представления знаний. Архитектура экспертной системы. Экспертная система — компьютерная программа, способная частично заменить специалиста-эксперта в разрешении проблемной ситуации. ЭС начали разрабатываться исследователями искусственного интеллекта в 1970-х годах, а в 1980-х получили коммерческое подкрепление.В информатике экспертные системы рассматриваются совместно с базами знаний как модели поведения экспертов в определенной области знаний с использованием процедур логического вывода и принятия решений, а базы знаний — как совокупность фактов и правил логического вывода в выбранной предметной области деятельности. Структура ЭС представляет следующую структуру ЭС: Интерфейс пользователя Пользователь Интеллектуальный редактор базы знаний Эксперт Инженер по знаниям Рабочая (оперативная) память База знаний Решатель (механизм вывода) Подсистема объяснений База знаний состоит из правил анализа информации от пользователя по конкретной проблеме. ЭС анализирует ситуацию и, в зависимости от направленности ЭС, дает рекомендации по разрешению проблемы.Как правило, база знаний ЭС содержит факты (статические сведения о предметной области) и правила - набор инструкций, применяя которые к известным фактам можно получать новые факты. В рамках логической модели баз данных и базы знаний записываются на языке Пролог с помощью языка предикатов для описания фактов и правил логического вывода, выражающих правила определения понятий, для описания обобщенных и конкретных сведений, а также конкретных и обобщенных запросов к базам данных и базам знаний. Конкретные и обобщенные запросы к базам знаний на языке Пролог записываются с помощью языка предикатов, выражающих правила логического вывода и определения понятий над процедурами логического вывода, имеющихся в базе знаний, выражающих обобщенные и конкретные сведения и знания в выбранной предметной области деятельности и сфере знаний. Обычно факты в базе знаний описывают те явления, которые являются постоянными для данной предметной области. Характеристики, значения которых зависят от условий конкретной задачи, ЭС получает от пользователя в процессе работы, и сохраняет их в рабочей памяти. Например, в медицинской ЭС факт «У здорового человека 2 ноги» хранится в базе знаний, а факт «У пациента одна нога» — в рабочей памяти. База знаний ЭС создается при помощи трех групп людей: Эксперты той проблемной области, к которой относятся задачи, решаемые ЭС; Инженеры по знаниям, являющиеся специалистами по разработке ИИС; Программисты, осуществляющие реализацию ЭС. Режимы функционирования ЭС может функционировать в 2-х режимах. Режим ввода знаний — в этом режиме эксперт с помощью инженера по знаниям посредством редактора базы знаний вводит известные ему сведения о предметной области в базу знаний ЭС. Режим консультации — пользователь ведет диалог с ЭС, сообщая ей сведения о текущей задаче и получая рекомендации ЭС. Например, на основе сведений о физическом состоянии больного ЭС ставит диагноз в виде перечня заболеваний, наиболее вероятных при данных симптомах. Классификация ЭС по решаемой задаче Интерпретация данных Диагностирование Мониторинг Проектирование Прогнозирование Сводное Планирование Обучение Управление Ремонт Отладка Классификация ЭС по связи с реальным временем Статические ЭС Квазидинамические ЭС Динамические ЭС Этапы разработки ЭС Этап идентификации проблем — определяются задачи, которые подлежат решению, выявляются цели разработки, определяются эксперты и типы пользователей. Этап извлечения знаний — проводится содержательный анализ проблемной области, выявляются используемые понятия и их взаимосвязи, определяются методы решения задач. Этап структурирования знаний — выбираются ИС и определяются способы представления всех видов знаний, формализуются основные понятия, определяются способы интерпретации знаний, моделируется работа системы, оценивается адекватность целям системы зафиксированных понятий, методов решений, средств представления и манипулирования знаниями. Этап формализации — осуществляется наполнение экспертом базы знаний. В связи с тем, что основой ЭС являются знания, данный этап является наиболее важным и наиболее трудоемким этапом разработки ЭС. Процесс приобретения знаний разделяют на извлечение знаний из эксперта, организацию знаний, обеспечивающую эффективную работу системы, и представление знаний в виде, понятном ЭС. Процесс приобретения знаний осуществляется инженером по знаниям на основе анализа деятельности эксперта по решению реальных задач. Реализация ЭС — создается один или нескольких прототипов ЭС, решающие требуемые задачи. Этап тестирования — производится оценка выбранного способа представления знаний в ЭС в целом. Теорема Байеса, наивная Байесовская модель. ссылка скрыта где ссылка скрыта— априорная вероятность гипотезы A; ссылка скрыта— вероятность гипотезы A при наступлении события B (апостериорная вероятность); ссылка скрыта— вероятность наступления события B при истинности гипотезы A; ссылка скрыта— вероятность наступления события B. Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность того, что произошло какое-либо событие (гипотеза), имея на руках лишь косвенные тому подтверждения (данные), которые могут быть неточны. Полученную по формуле вероятность можно далее уточнять, принимая во внимание данные новых наблюдений. Физический смысл Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. События, отражающие действие «причин», в данном случае обычно называют гипотезами, так как они — предполагаемые события, повлекшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную — с учетом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учетом данных о событии). Можно также уточнять вероятность гипотезы, учитывая другие имеющиеся данные (другие произошедшие события). Для учета каждого следующего события нужно в качестве априорной вероятности гипотезы подставлять ее апостериорную вероятность с предыдущего шага. [править] Следствие Важным следствием формулы Байеса является формула полной вероятности события, зависящего от нескольких несовместных гипотез (и только от них!). 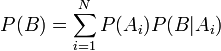 — вероятность наступления события B, зависящего от ряда гипотез Ai, если известны степени достоверности этих гипотез (например, измерены экспериментально). — вероятность наступления события B, зависящего от ряда гипотез Ai, если известны степени достоверности этих гипотез (например, измерены экспериментально).Марковская модель, фильтр Кальмана. С 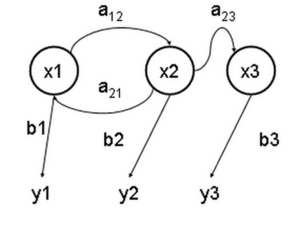 крытая марковская модель (СММ) — статистическая модель, имитирующая работу процесса, похожего на марковский процесс с неизвестными параметрами, и задачей ставится разгадывание неизвестных параметров на основе наблюдаемых. Полученные параметры могут быть использованы в дальнейшем анализе, например, для распознавания образов. СММ может быть рассмотрена как простейшая Байесовская сеть доверия. крытая марковская модель (СММ) — статистическая модель, имитирующая работу процесса, похожего на марковский процесс с неизвестными параметрами, и задачей ставится разгадывание неизвестных параметров на основе наблюдаемых. Полученные параметры могут быть использованы в дальнейшем анализе, например, для распознавания образов. СММ может быть рассмотрена как простейшая Байесовская сеть доверия. Диаграмма переходов в скрытой марковской модели (пример) x —скрытые состояния y — наблюдаемые результаты a — вероятности переходов b — вероятность результата Основное применение СММ получили в области распознавания речи, письма, движений и биоинформатике. Кроме того, СММ применяются в криптоанализе, машинном переводе. Конкретный пример Представим двух друзей, обсуждающих каждый вечер по телефону, что они сегодня делали днём. Ваш друг может делать лишь три вещи: гулять в парке, ходить за покупками или убираться в комнате. Его выбор основывается лишь на погоде, которая была в момент принятия решения. Вы ничего не знаете о погоде в том регионе, где живёт ваш друг, но вы можете, основываясь на его решениях, попытаться предугадать, какая погода была. Погода представима в виде марковской цепи, она имеет два состояния: солнечно или дождливо, но вы не можете сами увидеть её, поэтому она скрыта от вас. Каждый день ваш друг принимает одно из трёх возможных решений: прогулка, покупки или уборка. Вы можете узнать о решении вашего друга, поэтому это наблюдаемое значение. В целом мы получаем СММ. Структура скрытой марковской модели В обычной Марковской модели состояние видимо наблюдателю, поэтому вероятности переходов — единственный параметр. В скрытой марковской модели мы можем следить лишь за переменными, на которые оказывает влияние данное состояние. Каждое состояние имеет вероятностное распределение среди всех возможных выходных значений. Поэтому последовательность символов, сгенерированная СММ, даёт информацию о последовательности состояний. Д 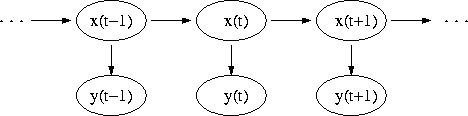 иаграмма, представленная ниже, показывает общую структуру СММ. Овалы представляют собой переменные со случайным значением. Случайная переменная x(t) представляет собой значение скрытой переменной в момент времени t. Случайная переменная y(t) — это значение наблюдаемой переменной в момент времени t. Стрелки на диаграмме символизируют условные зависимости. Из диаграммы становится ясно, что значение скрытой переменной x(t) (в момент времени t) зависит только от значения скрытой переменной x(t − 1) (в момент t − 1). Это называется свойством Маркова. Хотя в то же время значение наблюдаемой переменной . иаграмма, представленная ниже, показывает общую структуру СММ. Овалы представляют собой переменные со случайным значением. Случайная переменная x(t) представляет собой значение скрытой переменной в момент времени t. Случайная переменная y(t) — это значение наблюдаемой переменной в момент времени t. Стрелки на диаграмме символизируют условные зависимости. Из диаграммы становится ясно, что значение скрытой переменной x(t) (в момент времени t) зависит только от значения скрытой переменной x(t − 1) (в момент t − 1). Это называется свойством Маркова. Хотя в то же время значение наблюдаемой переменной . Вероятность увидеть последовательность 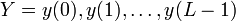 длины L равна длины L равна 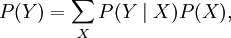 здесь сумма пробегает по всем возможным последовательностям скрытых узлов 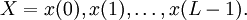 Метод подсчёта полным перебором значений P(Y) очень трудоёмкий для многих задач из реальной жизни в силу того, что количество возможных последовательностей скрытых узлов очень велико. Фи́льтр Ка́лмана — рекурсивный фильтр, оценивающий вектор состояния динамической системы, используя ряд неполных и зашумленных измерений. Назван в честь Рудольфа Калмана.Фильтр Калмана предназначен для рекурсивного дооценивания вектора состояния априорно известной динамической системы, то есть для расчёта текущего состояния системы необходимо знать текущее измерение, а также предыдущее состояние самого фильтра. Таким образом фильтр Калмана, как и множество других рекурсивных фильтров, реализован во временном представлении, а не в частотном. Далее, запись вида 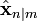 соответствует оценке вектора состояния соответствует оценке вектора состояния 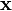 в момент времени (итерации) n, по данным на момент времени m. в момент времени (итерации) n, по данным на момент времени m.Состояние фильтра находится в двух переменных: 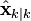 — оценка вектора состояния динамической системы в момент времени k; — оценка вектора состояния динамической системы в момент времени k;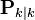 — ковариационная матрица ошибок (мера точности оценивания вектора состояния). — ковариационная матрица ошибок (мера точности оценивания вектора состояния).Работу каждого шага фильтра Калмана можно разделить на два этапа: прогноз и корректировка. Этап прогноза вычисляет вектор состояния, по его же значению на предыдущем шаге работы фильтра. На этапе корректировки в алгоритм поступают данные текущих измерений, которые используются для уточнения прогнозного значения вектора состояния, и вычисления собственно оценки вектора состояния динамической системы. Этап прогноза Вычисление прогнозного значения вектора состояния по априорно известной модели Вычисление прогнозного значения ковариационной матрицы Этап корректировки Вычисление математической невязки прогнозного значения вектора состояния относительно измерений Ковариационная матрица измерений Оптимальный по Калману коэффициент усиления Вычисление оценки вектора состояния через корректировку прогнозного вектора состояния Обновление ковариационной матрицы ошибок. Характеристика нейронных сетей, как инструмент ИИ. Искусственные нейронные сети (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети Маккалока и Питтса. Впоследствии, после разработки алгоритмов обучения, получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др. ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов). Такие процессоры обычно довольно просты, особенно в сравнении с процессорами, используемыми в персональных компьютерах. Каждый процессор подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам. И тем не менее, будучи соединёнными в достаточно большую сеть с управляемым взаимодействием, такие локально простые процессоры вместе способны выполнять довольно сложные задачи. Модели искусственного нейрона. Искусственный нейрон — узел искусственной нейронной сети, являющийся упрощённой моделью естественного нейрона. Математически, искусственный нейрон обычно представляют как некоторую нелинейную функцию от единственного аргумента — линейной комбинации всех входных сигналов. Данную функцию называют функцией активации или функцией срабатывания, передаточной функцией. Полученный результат посылается на единственный выход. Такие искусственные нейроны объединяют в сети — соединяют выходы одних нейронов с входами других. Искусственные нейроны и сети являются основными элементами идеального нейрокомпьютера. 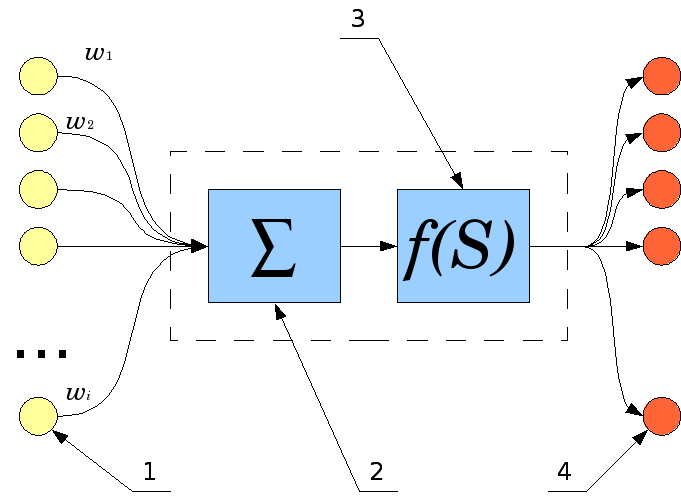 Схема искусственного нейрона: 1.Нейроны, выходные сигналы которых поступают на вход данному. 2.Сумматор входных сигналов 3.Вычислитель передаточной функции 4.Нейроны, на входы которых подаётся выходной сигнал данного 5.wi — веса входных сигналов Классификация нейронов В основном, нейроны классифицируют на основе их положения в топологии сети. Разделяют: Входные нейроны — принимают исходный вектор, кодирующий входной сигнал. Как правило, эти нейроны не выполняют вычислительных операций, а просто передают полученный входной сигнал на выход, возможно, усилив или ослабив его; Выходные нейроны — представляют из себя выходы сети. В выходных нейронах могут производиться какие-либо вычислительные операции; Промежуточные нейроны — выполняют основные вычислительные операции. Основные типы передаточных функций: Линейная передаточная функция С 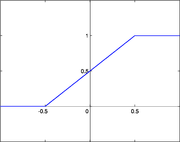 игнал на выходе нейрона линейно связан со взвешенной суммой сигналов на его входе. игнал на выходе нейрона линейно связан со взвешенной суммой сигналов на его входе.f(x) = tx, где t - параметр функции. В искусственных нейронных сетях со слоистой структурой нейроны с передаточными функциями такого типа, как правило, составляют входной слой. Кроме простой линейной функции могут быть использованы её модификации. Например полулинейная функция (если её аргумент меньше нуля, то она равна нулю, а в остальных случаях, ведет себя как линейная) или шаговая (линейная функция с насыщением), которую можно выразить формулой: П 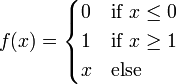 ри этом возможен сдвиг функции по обеим осям (как изображено на рисунке). ри этом возможен сдвиг функции по обеим осям (как изображено на рисунке).Недостатками шаговой и полулинейной активационных функций относительно линейной можно назвать то, что они не являются дифференцируемыми на всей числовой оси, а значит не могут быть использованы при обучении по некоторым алгоритмам. Пороговая передаточная функция Д 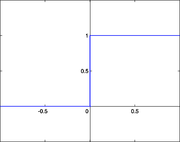 ругое название - Функция Хевисайда. Представляет собой перепад. До тех пор пока взвешенный сигнал на входе нейрона не достигает некоторого уровня T — сигнал на выходе равен нулю. Как только сигнал на входе нейрона превышает указанный уровень — выходной сигнал скачкообразно изменяется на единицу. Самый первый представитель слоистых искусственных нейронных сетей — перцептрон состоял исключительно из нейронов такого типа. Математическая запись этой функции выглядит так: ругое название - Функция Хевисайда. Представляет собой перепад. До тех пор пока взвешенный сигнал на входе нейрона не достигает некоторого уровня T — сигнал на выходе равен нулю. Как только сигнал на входе нейрона превышает указанный уровень — выходной сигнал скачкообразно изменяется на единицу. Самый первый представитель слоистых искусственных нейронных сетей — перцептрон состоял исключительно из нейронов такого типа. Математическая запись этой функции выглядит так: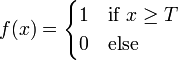 Здесь T = − w0x0 — сдвиг функции активации относительно горизонтальной оси, соответственно под x следует понимать взвешенную сумму сигналов на входах нейрона без учёта этого слагаемого. Ввиду того, что данная функция не является дифференцируемой на всей оси абсцисс, её нельзя использовать в сетях, обучающихся по алгоритму обратного распространения ошибки и другим алгоритмам, требующим дифференцируемости передаточной функции. Сигмоидальная передаточная функция О 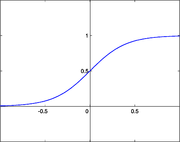 дин из самых часто используемых, на данный момент, типов передаточных функций. Введение функций сигмоидального типа было обусловлено ограниченностью нейронных сетей с пороговой функцией активации нейронов — при такой функции активации любой из выходов сети равен либо нулю, либо единице, что ограничивает использование сетей не в задачах классификации. Использование сигмоидальных функций позволило перейти от бинарных выходов нейрона к аналоговым. Функции передачи такого типа, как правило, присущи нейронам, находящимся во внутренних слоях нейронной сети. дин из самых часто используемых, на данный момент, типов передаточных функций. Введение функций сигмоидального типа было обусловлено ограниченностью нейронных сетей с пороговой функцией активации нейронов — при такой функции активации любой из выходов сети равен либо нулю, либо единице, что ограничивает использование сетей не в задачах классификации. Использование сигмоидальных функций позволило перейти от бинарных выходов нейрона к аналоговым. Функции передачи такого типа, как правило, присущи нейронам, находящимся во внутренних слоях нейронной сети.ссылка скрыта Математически эту функцию можно выразить так: З 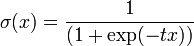 десь t — это параметр функции, определяющий её крутизну. Когда t стремится к бесконечности, функция вырождается в пороговую. При t = 0 сигмоида вырождается в постоянную функцию со значением 0,5. Область значений данной функции находится в ссылка скрыта (0,1). Важным достоинством этой функции является простота её производной: десь t — это параметр функции, определяющий её крутизну. Когда t стремится к бесконечности, функция вырождается в пороговую. При t = 0 сигмоида вырождается в постоянную функцию со значением 0,5. Область значений данной функции находится в ссылка скрыта (0,1). Важным достоинством этой функции является простота её производной:Т 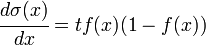 о, что производная этой функции может быть выражена через её значение облегчает использование этой функции при обучении сети по алгоритму обратного распространения. Особенностью нейронов с такой передаточной характеристикой является то, что они усиливают сильные сигналы существенно меньше, чем слабые, поскольку области сильных сигналов соответствуют пологим участкам характеристики. Это позволяет предотвратить насыщение от больших сигналов. о, что производная этой функции может быть выражена через её значение облегчает использование этой функции при обучении сети по алгоритму обратного распространения. Особенностью нейронов с такой передаточной характеристикой является то, что они усиливают сильные сигналы существенно меньше, чем слабые, поскольку области сильных сигналов соответствуют пологим участкам характеристики. Это позволяет предотвратить насыщение от больших сигналов. |
