Х школьные Харитоновские чтения

Вид материала

Документы

Содержание История циклоиды. Это должен знать каждый. Немного о циклоиде. Рис. 3бКривая наикратчайшего по времени спуска. Якоб Бернулли Рис.4Доказатель­ства Бернулли послужили толчком для развития но­вой отрасли математики - вариационного исчисления Рис. 6Эпициклоида и кардиоида Еще одна «родственница» циклоиды. О площадях криволинейных фигур. Вот несколько таких свойств. Ошибка Галилея. Парадоксы странные, но истинные. А проделала явно больший путь, чем точка В. А прошла в промежутке от А Рис. 17Построение циклоиды.

Подобный материал:

• Родительское собрание: хорошо или плохо?, 2396.46kb.
• О некоторых особенностях, 82.63kb.
• Задачи интеллектуального воспитания: Формировать и развивать культуру умственного труда, 53.79kb.
• Рассказывайте детям о ценности чтения. Показывайте связь чтения с их успехами в учебе, 97.26kb.
• Урок литературного чтения по книге для чтения «Капельки солнца», 84.82kb.
• Гребенькова Татьяна Сергеевна, гимназия №19 им. Поповичевой Н. З. Базовый уровень., 62.07kb.
• Итоги исследований. Программы З. П. Гурьян, заведующая сектором развития детского, 604.04kb.
• Программа детского чтения для учащихся 1-4 классов Составитель: Марина Владимировна, 98.98kb.
• Списки для обязательного чтения по программе, 55.48kb.
• Списки для обязательного чтения по программе, 55.84kb.

Х Школьные Харитоновские чтения


Межрегиональная олимпиада школьников

«Будущие исследователи – будущие науки»


«Тайны циклоиды»


Математика


Каштанова Екатерина Алексеевна


с.Ельники

Ельниковского района

Республики Мордовия

МОУ «Лицей», 10 класс


Москаева Надежда Васильевна

учитель математики


Саров 2010

Содержание.


История циклоиды………………………………………………………… 2

Это должен знать каждый……………………………………………………… 3

Немного о циклоиде……………………………………………………… 3

Кривая наикратчайшего по времени спуска…………………………….. 5

Таутохрона………………………………………………………………… 6

Эпициклоида и кардиоида……………………………………………….. 8

Еще одна «родственница» циклоиды…………………………………… 8

О площадях криволинейных фигур…………………………………… 9

Ошибка Галилея………………………………………………………….. 12

Парадоксы странные, но истинные……………………………………... 13

Построение циклоиды…………………………………………………… 15

Заключение……………………………………………………………….. 16

Список используемой литературы……………………………………… 17


История циклоиды.


Рулетта является линией столь обычной, что после прямой и

окружности нет более часто встречающейся линии; она так

часто вычерчивается перед глазами каждого, что надо уди-

вляться тому, как не рассмотрели ее древние, ибо это

не что иное, как путь, описываемый в воздухе гвоздем коле-

са, когда оно катится своим движением с того момента, как

гвоздь начал подниматься от земли, до того, когда непре-

рывное качение колеса не приводит его опять к земле после

окончания целого оборота.

Паскаль


Кривую, «так часто вычерчивающуюся перед глазами каждого», первыми заметили Галилей в Италии и Мерсенн (1588 - 1648) во Франции. В Италии ее назвали циклоидой (это название, означающее «происходящая от круга», принадлежит Галилею), во Франции - рулеттой. Привилось первое название, а рулеттами теперь называют кривые более широкого класса, речь о которых пойдет позднее. Математики XVII века, создававшие общие методы исследования кривых, были очень заинтересованы в новых «подопытных» кривых. Среди этих кривых циклоида заняла особое место. Она оказалась одной из первых трансцендентных кривых (кривых не алгебраического происхождения), для которых удалось найти красивый явный ответ в задачах о построении касательных и вычислении площади. Но больше всего поражало, что циклоида вновь и вновь появлялась при решении самых разных задач, в первоначальной постановке которых она не участвовала. Все это сделало циклоиду самой популярной кривой XVII века:



крупнейшие ученые и Италии, и Франции (Торричелли, Вивиани (1622 - 1703), Ферма (1601 - 1665), Декарт (1596 - 1650), Роберваль (1602 - 1675) ) решали разнообразные задачи о циклоиде, а в 1673 году Гюйгенс констатировал, что «циклоида исследована точнее и основательнее всех других кривых».


Это должен знать каждый.

- Циклоида есть траектория точки, лежащей на ободе катящегося колеса.

- Изучать её начал во второй половине 17 века италь­янец Галилео Галилей. Именно он вывел циклоиду в люди. Впослед­ствии ей заинтересовались другие математики и итальянский физик Торичелли.

- Циклоиду стали применять в различных областях техники. Немецкий физик Гюйгенс построил маятник, который движется по циклоиде.


Немного о циклоиде.


Декартов лист, гипербола, парабола, эллипс, овал Кассини, конхоида - все это алгебраические кривые. Но уже Галилей и Декарт изучали кривую, описыва­емую точкой окружности, катящейся по прямой, - циклоиду («механическую кривую»). Слово «циклои­да» произошло от греческого слова «cykioetdes» - «кру­гообразный». Так назвал эту кривую в 1590 году Га­лилей (рис. 1).

АМ=\0А\


Рис.1

A₁A₂ - основание циклоиды, А₃ - вершина, А₃М -высота циклоиды,

A₁A₂A₃ - арка циклоиды, пря­мая I - линия центров.


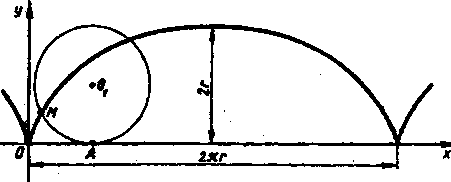
Галилей экспериментально установил, что площадь под одной аркой циклоиды в 3 раза больше площади производящего циклоиду круга, а длина дуги арки равна четырем диаметрам круга.

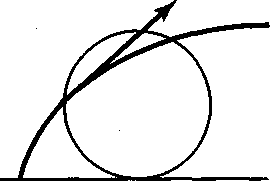Уравнение циклоиды удобно записывать через α - угол поворота окружности, выраженный в радианах (он численно равен пути, пройденному производящей окружностью по прямой): х = гα-rsinα, у =r-r cos α.

У циклоиды много замечательных свойств.
Одно из них: касательная к циклоиде проходит через «верхнюю» точку производящего круга.

Обратим внимание на положение касательной к циклоиде (рис. 2). Если велосипедист едет по мокрой дороге, то оторвавшиеся от колеса капли будут ле­теть по касательной Рис. 2

к циклоиде и при отсутствии щитков могут забрызгивать спину велосипедиста.

Пусть теперь окружность катится по прямой, а точка закреплена на радиусе внутри окружности, то она будет описывать кривую, называемую укороченной циклоидой. (рис. 3а)





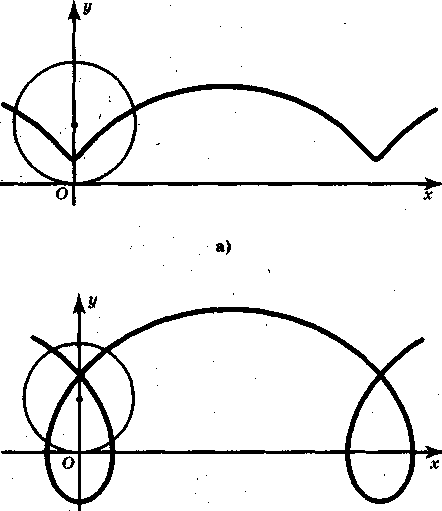
Рис. 3а


Если точка закреплена на продолжении радиуса, то она будет описывать кривую, называемую удлиненной циклоидой. (рис. 3б)




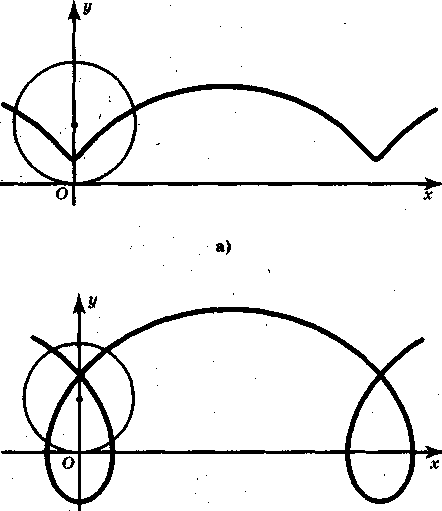
Рис. 3б


Кривая наикратчайшего по времени спуска.


Циклоида имеет ряд замечательных свойств.

За одно из них она получила название брахистохроны. Это слово произошло от греческого «brachistos», что означает «кратчайший» и «chronos», что означает «время», т. е. брахистохрона - это кривая наикратчайшего по вре­мени спуска.







Якоб Бернулли (1654-1705) - профессор математики Базельского университета (с 1687). Широко использовал методы математического анализа при изучении геометричес­ких кривых.

ОПЫТ.

Рассмотрим три отшлифованных желоба, со­единяющих точки А и В (рис. 4). Три полированных металлических шарика скатываются по этим жело­бам. Время наименьшего спуска у шарика, двигаю­щегося по циклоидальному желобу. Это впервые ус­тановили швейцарские математики братья БЕРНУЛЛИ (в 1696 году) точным расчетом.




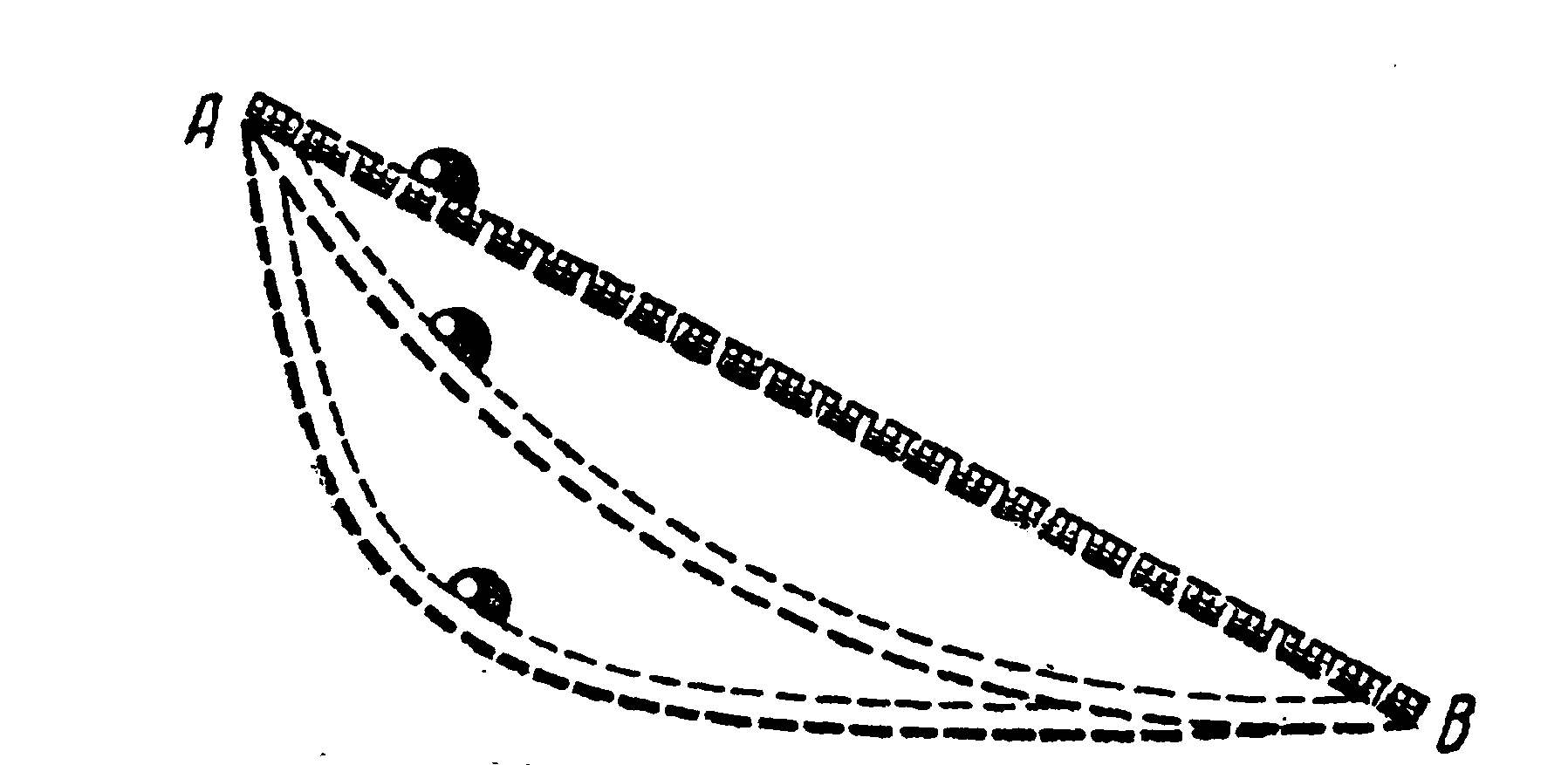
Рис.4


Доказатель­ства Бернулли послужили толчком для развития но­вой отрасли математики - вариационного исчисления, раздела математики, изучающего методы исследова­ния некоторых величин на достижение ими максиму­ма или минимума.


Таутохрона.


Другим синонимом циклоиды является таутохрона (от греческих слов «tautos» - тот же самый, «chronos» - время). Такое название циклоиды связано с истори­ей маятниковых часов, с попыткой ученых создать «идеальный» маятник, т. е. такой маятник, период колебаний которого не зависит от его размаха. Христиан ГЮЙГЕНС, голландский ученый, в 1657 году создал такой маятник.




ХРИСТИАН ГЮЙГЕНС, (1629-1695), голландский математик, физик и астроном. Гюйгенс получил известность благодаря изобретению маятниковых часов. В 1673 в Париже вышел его фундаментальный труд - Качающиеся часы, или о движении маятника, в котором рассматривалось движение тяжелых тел по циклоиде.ссылка скрыта




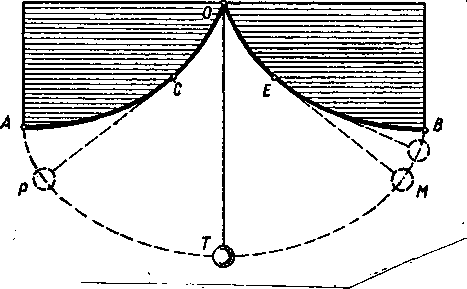
Рис. 5


Он подвесил маятник в острие перевернутой циклоиды (точка О), сделал длину нити равной половине длины арки циклоиды (АО) и дал возможность нити наматываться на циклоидальные «щеки» (ОА и ОВ).

При этих условиях конец маятни­ка (Т) движется по циклоиде (таутохроне), а период колебания не зависит от величины начального откло­нения (рис. 5).

Представим себе ледяную горку, спуск которой имеет форму циклоиды. У этой горы есть интересные свойства. Если в разных точках ее (на разной высоте) стоят готовые к старту спортсмены с салазками (рис. 6), и по команде одновременно эти салазки начинают скользить, то первым к финишу (т. А) придет не спортсмен К, как кажется. Все спортсмены достигнут точки А одновременно! Поэтому ее называют таутохроной - «равновременной».




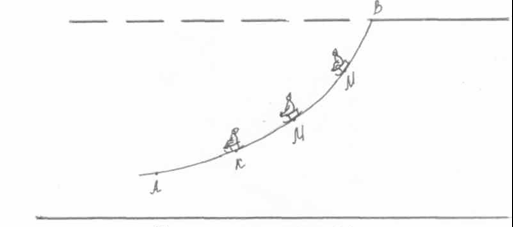
Рис. 6


Эпициклоида и кардиоида.


Древние ученые не знали циклоиду, но они знали и успешно пользовались ее близкой родственницей - эпициклоидой, плоской кривой, описываемой точкой окружности, которая катится без скольжения по дру­гой неподвижной окружности, касаясь ее извне (рис. 7).


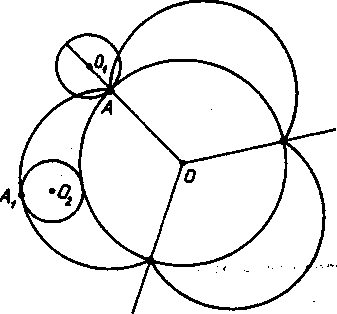
Рис. 8

Рис. 7


Если радиус неподвижной окружности равен ра­диусу подвижной, то эпициклоиду называют кардиои­дой (алгебраическая кривая четвертого порядка) (рис. 8).


Еще одна «родственница» циклоиды.


Другой «родственницей» циклоиды является гипо­циклоида - плоская кривая, описываемая точкой ок­ружности, катящейся внутри и без скольжения по другой неподвижной окружности (рис. 9). В зависи­мости от соотношения длин радиусов подвижной и неподвижной окружностей, получаются различные формы гипоциклоид. Если радиус неподвижной ок­ружности в 4 раза больше радиуса подвижной, то эта гипоциклоида называется астроидой

(рис.10).





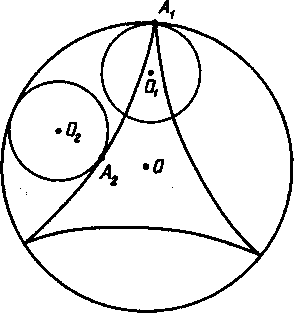
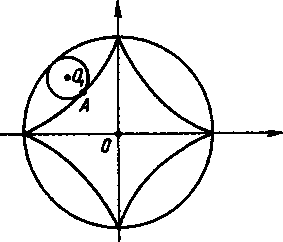
Рис. 9 Рис. 10


Длина астроиды равна 6а, а площадь фигуры, ограниченной ею – S = 3/8а (R = а).


О площадях криволинейных фигур.


Площади некоторых криволинейных фигур умели вычислять еще в Древней Греции. Вначале интересовались лишь квадратурой фигур, т. е. построением для данной фигуры циркулем и линейкой отрезка, длина которого равна ее площади. Как выяснилось позднее, это можно сделать для тех фигур, площадь которых вычисляется при помощи арифметических операций и операции извлечения квадратного корня. Постепенно стали интересоваться фигурами, площади которых вычисляются с помощью произвольных алгебраических операций (алгебраическая квадратура), а затем даже и такими фигурами, в выражениях для площадей которых фигурировало число. Основной метод вычисления площадей состоял в приближении данной фигуры многоугольниками и переходе к пределу; но должно было очень повезти, чтобы эти вычисления удалось довести до явного ответа. Иногда вычисление площади фигуры можно упростить, воспользовавшись какими-нибудь общими свойствами площадей.

Вот несколько таких свойств.

1. При гомотетии фигуры с коэффициентом k площадь ее умножается на k², а при растяжении фигуры относительно некоторой оси с коэффициентом k площадь ее умножается на k.

2. Равносоставленные фигуры (т. е. фигуры, которые можно разрезать на попарно равные части) равновелики (имеют равные площади).

3. Две фигуры, при пересечении которых любой прямой, параллельной некоторой фиксированной прямой, получаются равные отрезки, равновелики (этот принцип сформулировал в 1635 году Кавальери (1598 - 1647) ). Представим себе, что контур фигуры - гибкая лента, а сама фигура составлена из очень тонких жестких слоев, параллельных прямой l («неделимых», по терминологии Кавальери). Рассмотрим преобразования, сохраняющие эти слои, но сдвигающие их друг относительно друга. Все получающиеся при таких преобразованиях фигуры в силу принципа Кавальери будут равновелики.

Перечисленные свойства площадей нуждаются в доказательствах (основная трудность этих доказательств состоит в том, чтобы дать строгое определение площади), но в них легко поверить.



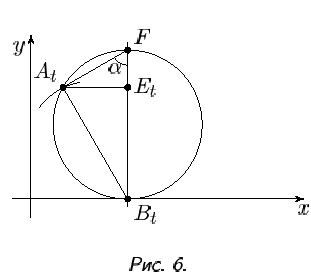
Рис. 11


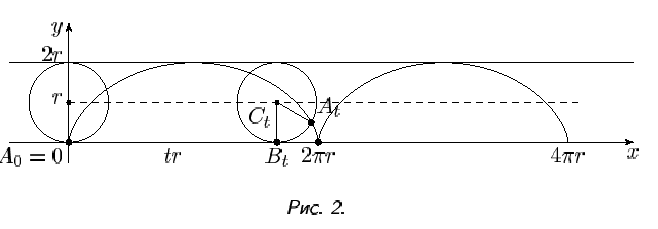
Поскольку все циклоиды подобны, мы ограничимся случаем r = 1. Вслед за Робервалем свяжем с каждой точкой циклоиды A_t (см. рис.11) ее проекцию E_t на вертикальный диаметр производящего круга. Точка E_t имеет координаты x = t; y = 1 - cos t = 1 + sin (t – ^π/₂)



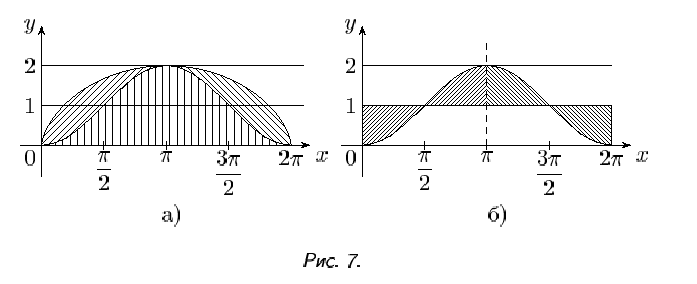
Рис. 12


Кривую, составленную из точек E_t при всевозможных t, Роберваль назвал «спутницей циклоиды». Легко понять, что «спутница циклоиды» - это сдвинутая синусоида (на 1 вверх и на ^π/₂ вправо). Если из всех точек циклоиды опустить перпендикуляры на вертикальные диаметры производящего круга (который у нас «катится» вдоль прямой), то мы и получим синусоиду. С этим обстоятельством связан исторический курьез. Математики с незапамятных времен занимались тригонометрическими функциями, но синусоида впервые появилась лишь в XVII веке, причем не как график синуса, а как «спутница циклоиды» (отчасти это можно объяснить тем, что долго не рассматривали функций неалгебраического происхождения).

«Спутница циклоиды» разбивает ее на три части (рис. 12а): фигуру под синусоидой и две симметричные фигуры, названные «лепестками Роберваля». В силу свойства 2 площадь фигуры под синусоидой равна 2π эта фигура равносоставлена с прямоугольником такой площади (рис. 12б). Рассмотрим один «лепесток». Горизонталь на вы соте y = 1 - cos t пересекает его по отрезку AtEt длины | sin t|. Переместив эти горизонтальные отрезки (при всевозможных t) вдоль своих горизонталей так, чтобы их левые концы попали на одну вертикаль, мы получим полукруг единичного круга (рис. 13).



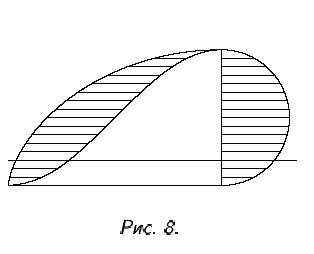
Рис. 13

В силу принципа Кавальери площадь «лепестка» равна площади этого полукруга, т. е. ^π/₂. Значит, площадь фигуры под аркой циклоиды с r = 1 равна 2π + 2 ^π/₂= 3π (и следовательно, 3πr² при r ≠ 1). Вопрос о вычислении площадей сегментов циклоиды является менее элементарным. Гюйгенс не без гордости писал: «Я первый промерил площадь той части циклоиды, которая получится, если отсчитать от вершины ¹/₄ часть оси и провести параллель основанию. Эта часть составляет половину площади правильного шестиугольника, вписанного в образующий круг».





Роберваль Жюль, псевдоним Жиля Персонье (8.8.1602-27.10.1675)- французский математик. ссылка скрытассылка скрыта, как результат перемещения точки, которое складывалось из нескольких более простых движений. Роберваль известен как изобретатель «весов Роберваля».


Ошибка Галилея.


В самом начале XVII века юный Галилей пытался экспериментально проверить свою догадку о том, что свободное падение - равноускоренное движение. Когда он перенес наблюдения с Пизанской башни в лабораторию, ему стало очень мешать то, что тела падают «слишком быстро». Чтобы замедлить это движение, Галилей решил заменить свободное падение тел их движением по наклонной плоскости, предположив, что и оно будет равноускоренным. Проводя эти опыты, Галилей обратил внимание на то, что в конечной точке величина скорости тела, скатившегося по наклонной плоскости, не зависит от угла наклона плоскости, а определяется только высотой H и совпадает с конечной

Рис. 14 скоростью тела, свободно упавшего с той же высоты (как вы хорошо знаете, в обоих случаях |v|2 = 2gH. Изучив движения по наклонным плоскостям, Галилей перешел к рассмотрению движения материальной точки под действием силы тяжести по ломаным линиям.

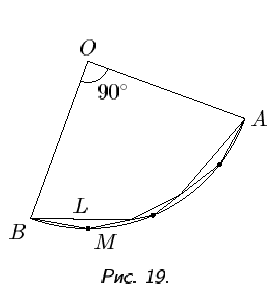
Сравнивая времена движения по различным ломаным, соединяющим фиксированную пару точек A и B, Галилей заметил, что если через эти две точки A, B провести четверть окружности и вписать в нее две ломаные M и L, такие, что ломаная L «вписана» в ломаную M (см. рис. 14), то материальная точка из A в B быстрее попадает по ломаной M, чем по ломаной L. Увеличивая у ломаной число звеньев и переходя к пределу, Галилей получил, что по четверти окружности, соединяющей две заданные точки, материальная точка спустится быстрее, чем по любой вписанной в эту четверть окружности ломаной. Из этого Галилей сделал ничем не аргументированный вывод, что четверть окружности, соединяющая пару заданных точек A, B (не лежащих на одной вертикали), и будет для материальной точки, движущейся под действием силы тяжести, линией наискорейшего спуска (позже линию наискорейшего спуска стали называть брахистохроной). Впоследствии выяснилось, что это утверждение Галилея было не только необоснованным, но и ошибочным.


Парадоксы странные, но истинные.





На рис. 15 изображены две одинаковые монеты. Если мы заставим первую монету катиться по второй так, чтобы она прошла ровно
половину окружности (как указано стрелкой), мы можем ожидать, что, придя к точке,
диаметрально противоположной первоначальной, монета перевернется вниз головой по
сравнению с исходной позицией. Мы убеждены, что, пройдя половину окружности,
монета должна повернуться на 180°. Если же мы проделаем эксперимент с реальной
монетой, то убедимся, что она окажется снова в исходном положении — будто бы она
прошла полную окружность, а не ее половину.

Рис. 15

Рис. 16 показывает, что, когда колесо движется по прямой MN, точки А и В описывают циклоиды. После того как колесо сделает пол-оборота, точка А 1 попадает в положение А 3, а точка В 1 - в положение В 3. В этом положении нет никаких оснований думать, что точки А и В движутся с разной скоростью, поскольку за одно и то же время они проходят одинаковый путь. Но если мы обратимся к точкам А 2 и В 2, в которые попали А и В после того как колесо сделало четверть оборота, мы увидим, что за одно и то же
время точка А проделала явно больший путь, чем точка В. Эта разница в скоростях
компенсируется на второй четверти оборота, когда точка В в промежутке от В 2 к В 3
п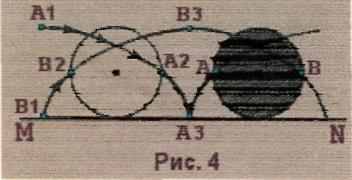роходит тот же самый путь, который точка А прошла в промежутке от А 1 к А 2; ясно,
что путь В 2 В 3 равен пути А I A 2. Значит, за половину оборота обе точки пройдут
одинаковое расстояние. Такое странное поведение циклоиды может служить объяснением

Рис. 16

того факта, что точки колеса, находящиеся на некотором удалении от самой нижней точки, при качении колеса движутся в горизонтальном направлении быстрее, чем точка, соприкасающаяся с дорогой. Можно показать, что точка, соприкасающаяся с дорогой, двигаясь вверх, все больше и больше ускоряется и достигает наибольшей горизонтальной скорости в верхнем своем положении, то есть на максимальном расстоянии от дороги.

Другое интересное свойство циклоиды было открыто Галилеем. Еще раньше было установлено, что площадь круга может быть выражена только с помощью трансцендентного числа ТС. Поскольку численное значение π дается лишь приближенно (хотя и с любой степенью точности, достигаемой суммированием необходимого числа членов бесконечного ряда), следовательно, и площадь круга может быть выражена лишь приближенно. Но замечательно то, что с помощью циклоиды мы можем построить площадь, в точности равную площади круга. Исходя из факта, что длина циклоиды от начальной до конечной точки равна четырем диаметрам порождающей ее окружности, можно показать, что площадь части плоскости между полной дугой циклоиды и прямой, по которой катится окружность, равна трем площадям круга. Отсюда вытекает, что заштрихованные площади справа и слева от окружности (рис. 17) в точности равны площади круга, ограниченного этой окружностью.




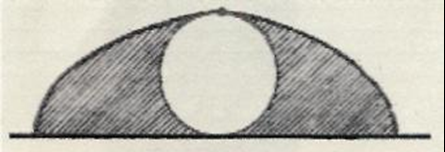
Рис. 17


Построение циклоиды.


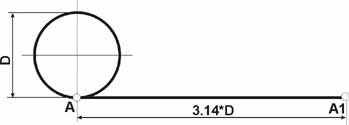
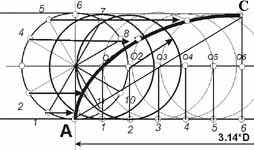
Построение циклоиды можно выполнить следующим образом:

1) Задаем окружность заданного диаметра (через "размер" в "преобразованиях" )

2) От точки А строим отрезок равный длине 3.14х D (также используем "размер" в "преобразованиях" )





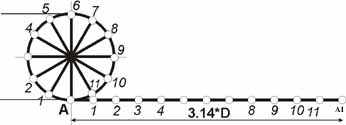
3) Делим окружность на равное число, например, на 12. Для чего от центра окружности провести горизонтальный радиус и повернуть его 11 раз. Точки обозначить снизу по часовой стрелке.


4) Делим отрезок на 12 частей. Для чего точку А (ее окружность) сдвигаем вдоль оси на ¹/₁₂ от AA1.





5) Из точек 1,2,3,... горизонтального отрезка АА1 проводим вертикальные отрезки до пересечения с осью центров





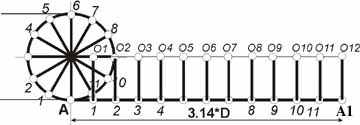
6) Далее описывая из этих центров дуги радиусом R, последовательно отметить точки их пересечения с соответствующими прямыми, параллельными АА1,, как точки, принадлежащие циклоиде. Чтобы провести кривую плавную от точки А до точки С лучше между ними сначала провести отрезок, который заменить кривой и, управляя касательными добиться чтобы она прошла через найденные точки.





Заключение.


Героическая история циклоиды завершилась с концом XVII века. Она так таинственно возникала при решении самых разных задач, что никто не сомневался, что она играет совершенно исключительную роль. Пиетет перед циклоидой держался долго, но прошло время, и стало ясно, что она не связана с фундаментальными законами природы, как, скажем, конические сечения. Задачи, приводившие к циклоиде, сыграли огромную роль в становлении механики и математического анализа, но когда величественные здания этих наук были построены, оказалось, что эти задачи являются частными, далеко не самыми важными. Произошла поучительная историческая иллюзия. Однако, знакомясь с поучительной историей циклоиды, можно увидеть много принципиальных фактов из истории науки.

У всех на руках есть часы. А ведь в них исполь­зуется циклоида, так что, не будь её, что было бы на белом свете? Если вовремя не раздается знакомый звонок будильника, вас ожидает неприятный разговор с начальником. Влюбленные были бы в большой растерянности, если бы из города исчезли все часы. Ценить и беречь время в наш век - самое главное. Я думаю, что одно это полностью доказывает полезность и необходимость этой кривой.


Список используемой литературы.

1. Берман Г. Н. «Циклоида», Наука, 1980г.
   
2. ссылка скрыта», МЦНМО, 2006г.
   
3. Майер В.В., Майер Р.В. «Удивительные свойства циклоиды», Учебная физика, 1998г.
   
4. Берман Г.Н. «Циклоида», Гостехтеориздат, 1954г.
   
5. Научно-популярный физико-математический журнал "Квант",
   

Веров С. , Тайны циклоиды, № 8, 1975г. 

6. Маркушевич А.И., Замечательные кривые, М., 1978 г.