Geum.ru

Блок 1: Рост стоимости вложений за счет присоединения процентов 4

Вид материалаАнализ

Содержание


Функции для определения дюрации
Функции для определения курсовой цены и доходности облигации
Накопдоход( )
Подобный материал:
1   ...   17   18   19   20   21   22   23   24   ...   36

Функции для определения дюрации


Следующие две функции (табл. 2.4) позволяют определить одну из важнейших характеристик облигаций – дюрацию.

Функция ДЛИТ() вычисляет дюрацию D и имеет два дополнительных аргумента:

ставка – купонная процентная ставка (ячейка В6);

доход – норма доходности (ячейка Е4).

Заданная в ячейке В17, функция с учетом размещения исходных данных имеет вид:

=ДЛИТ(E2; B4; B6; E4; B8) (Результат: 9,39).

Таким образом, средневзвешенная продолжительность платежей по 15-летней ОВВЗ седьмой серии со сроком обращения составит 9 лет и около 140 дней (0,39  360).

Функция МДЛИТ( ) реализует модифицированную формулу для определения дюрации MD и имеет аналогичный формат (ячейка В18):

=МДЛИТ(E2; B4; B6; E4; B8) (Результат: 8,39).

Полученный результат на целый год меньше. Напомним, что для бескупонных облигаций дюрация всегда равна сроку погашения.

Следующие функции рассматриваемой группы позволяют определить наиболее широко используемые при анализе характеристики купонных облигаций – цену P и доходность к погашению YTM. Они требуют задания шести обязательных аргументов. Поэтому в дополнение к уже встречавшимся нам аргументам прибавляются:

погашение – стоимость 100 единиц номинала при погашении (ячейка В7);

доход – требуемая норма доходности (ячейка Е4);

ставка – годовая ставка купона (ячейка В6)

цена – цена, уплаченная за 100 единиц номинала (ячейка Е3).

Функции для определения курсовой цены и доходности облигации


Функция ЦЕНА() позволяет определить современную стоимость 100 единиц номинала облигации (т.е. курс), исходя из требуемой нормы доходности на дату ее покупки. В нашем примере она задана в ячейке В19 и имеет следующий формат:

=ЦЕНА(E2; B4; B6; E4; В7; B8) (Результат: 40,06).

Полученная величина 40,06 представляет собой цену облигации, которая обеспечивает нам требуемую норму доходности – 12% (ячейка Е3). Поскольку ее величина меньше средней цены покупки в 34,75 (ячейка Е2), мы также получим дополнительную прибыль приблизительно в 5,30 на каждые 100 единиц номинала при погашении облигации.

Функция ДОХОД() вычисляет доходность облигации к погашению (yield to maturity – YTM). Данный показатель присутствует практически во всех финансовых сводках, публикуемых в открытой печати и специальных аналитических обзорах. В рассматриваемом примере функция для его вычисления задана в ячейке В20:

=ДОХОД(E2; B4; B6; E3; B7; B8) (Результат: 13,63%).

Полученный результат несколько выше требуемой нормы доходности и в целом подтверждает прибыльность данной операции.

Ячейка В21 содержит формулу для расчета текущей (на момент совершения сделки) доходности Y – отношение купонной ставки (ячейка В6) к цене приобретения облигации (ячейка Е3):

=В6/Е3 (Результат: 8,63%).

Таким образом, текущая доходность операции составляет 8,63%, что значительно выше купонной ставки, однако ниже доходности к погашению.

Последним показателем, рассчитанным в электронной таблице (ячейка В22), является величина накопленного купонного дохода НКД на дату сделки. Для его вычисления используется функция НАКОПДОХОД( ):

=НАКОПДОХОД(B3;B11;E2;B6;B7;B8) (Результат: 2,53).

Отметим, что в качестве одного из аргументов здесь используется дата ближайшей (после заключения сделки) выплаты купона (ячейка В11). Данную функцию также удобно использовать при определении суммы дохода, подлежащей налогообложению, которая представляет собой разность между накопленным процентом на момент погашения или перепродажи ценной бумаги и накопленным процентом на момент ее приобретения.

Последние 4 функции этой группы – ДОХОДПЕРВНЕРЕГ(), ДОХОДПОСЛНЕРЕГ(), ЦЕНАПЕРВНЕРЕГ() и ЦЕНАПОСЛНЕРЕГ(), применяются для вычисления цены и доходности облигации в тех случаях, когда период выплаты первого или последнего купона отличается от остальных. При этом в списке аргументов должна быть указана дата выплаты первого (последнего) купона. В остальном, выполняемые ими действия аналогичны рассмотренным выше.

Полученная в результате таблица должна иметь вид рис. 2.9.



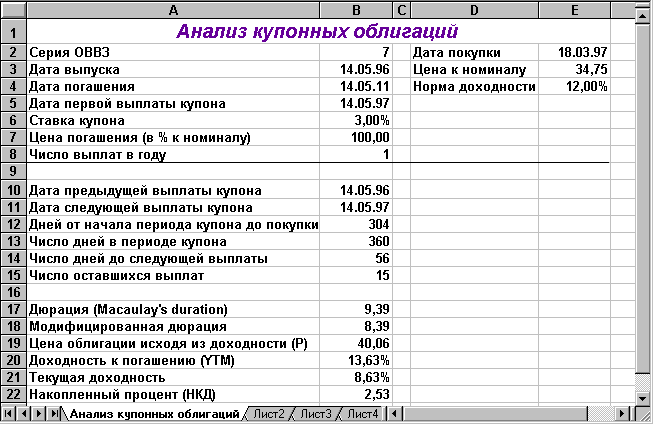
Рис. 2.9. Результаты анализа ОВВЗ седьмой серии

Очистите таблицу от исходных данных (блоки ячеек В2.В8 и Е2.Е4) и сохраните на магнитном диске в виде шаблона BONDCOUP.XLT.

Осуществите проверку работы шаблона на следующем примере.

Пример 2.10

Рассматривается возможность приобретения облигаций внутреннего валютного займа Минфина России третьей серии. Произвести расчет эффективности операции на 18 марта 1997 года исходя из следующих данных .

Дата выпуска ОВВЗ – 14/05/1993 г. Дата погашения – 14/05/1999 г. Купонная ставка – 3%.Число выплат – 1 раз в год. Средняя курсовая цена на дату операции – 85,83. Требуемая норма доходности – 10% годовых.

Полученная в результате таблица должна иметь вид рис. 2.10.



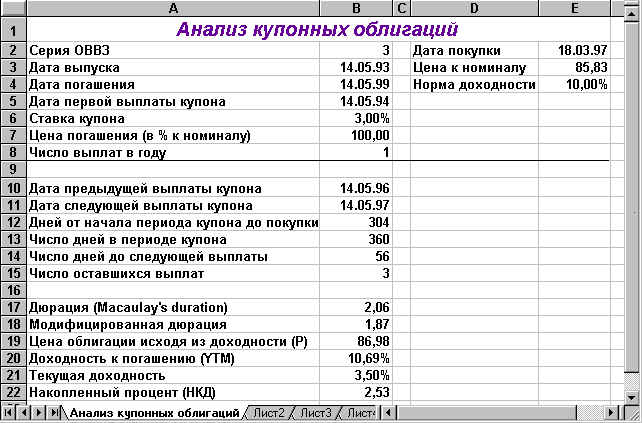
Рис. 2.10. Решения примера 2.10

Большинство из рассмотренных функций можно использовать и для анализа облигаций с плавающей ставкой купона (ОГСЗ, ОФЗ и др.). Однако следует отметить, что результаты расчета доходности к погашению будут справедливы только для текущей ставки купона (т.е. для периода между двумя купонными выплатами).

При окончательном определении величины полученного дохода, т.е. ретроспективном анализе операций с ОГСЗ, ОФЗ и ряда муниципальных бумаг с плавающей ставкой доходности, удобно пользоваться функцией БЗРАСПИС(). Ее можно применять и для приблизительной оценки будущих доходов, предположив, например, что купонная ставка будет изменяться с фиксированным шагом. Альтернативным вариантом является определение доходности YTM по значениям полученных платежей с помощью функции ЧИСТВНДОХ().

Следует отметить, что рассмотренные в данном параграфе фундаментальные зависимости справедливы для любых ценных бумаг, отражающих отношения займа.