Флуктуационные, термо- и электромеханические эффекты в квазиодномерных проводниках с волной зарядовой плотности

Вид материала

Автореферат

Содержание А.Н. Васильев Общая характеристика работы Научная новизна Научная и практическая значимость Основные положения, выносимые на защиту Личный вклад автора Апробация работы. Структура и объем работы Основное содержание работы Глава 2 посвящена изучению спонтанных флуктуаций сопротивления в квазиодномерном соединении TaS3. В разделе 2.1 Т пропорционален доле объёма нормальной фазы. В этом случае ступенька L TP длина когерентности ВЗП может достигать толщины образца, t TP, а также эффективное уменьшение W Главе 5 рассматривается однородная деформация образцов. Вначале (раздел 5.1 Глава 7 посвящена исследованию деформации кручения, возникающей в квазиодномерных проводниках с ВЗП в электрическом поле. В разд Слева: микрофотография образца TaS3 с подвешенным контактом и 6-ю микрозеркалами. Расстояние между контактами - 3.4 мм. Справа В заключении ( Основные результаты диссертации опубликованы в следующих статьях

Подобный материал:

• 4 Механические и электромагнитные колебания и волны 4 Энергия волны. Перенос энергии, 35.27kb.
• Ооо «нпкф «Термо Инжиниринг», 30.22kb.
• Аннотация к научно-образовательному материалу «Современные электромеханические аппараты», 60.95kb.
• План лекции. Рынок труда и занятость. Влияние плотности населения на трудовую занятость, 35.63kb.
• Сс-системы и соответственно повреждающие эффекты стресс-реакции, в механизме устойчивости, 19.64kb.
• Реферат Отчет 65 с., 3 ч., 26 рис., 8 табл., 53 источника, 92.51kb.
• Рейтинг план по дисциплине Электромеханические аппараты автоматики, управления, распределения, 36.34kb.
• 4 образование ядер и атомов, 48.2kb.
• От 20 г, 53.43kb.
• Основные эксплуатационные характеристики медицинских термоконтейнеров производства, 67.16kb.

На правах рукописи



ПОКРОВСКИЙ ВАДИМ ЯРОСЛАВОВИЧ


ФЛУКТУАЦИОННЫЕ, ТЕРМО- И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЭФФЕКТЫ

В КВАЗИОДНОМЕРНЫХ ПРОВОДНИКАХ С ВОЛНОЙ ЗАРЯДОВОЙ ПЛОТНОСТИ.


Специальность 01.04.07 Физика конденсированного состояния


АВТОРЕФЕРАТ


диссертации на соискание ученой степени

доктора физико-математических наук


Москва – 2009


Работа выполнена в Учреждении Российской академии наук Институте радиотехники и электроники им. В.А.Котельникова РАН


Официальные оппоненты: доктор физико-математических наук,

профессор А.Н. Васильев

доктор физико-математических наук,

Н.Н. Кирова

: доктор физико-математических наук,

профессор В.Г. Шавров


Ведущая организация: Институт сверхпроводимости и физики твердого тела

РНЦ «Курчатовский Институт»


Защита состоится «19» марта 2010 г., в 10 ч. 00 мин. на заседании диссертационного совета Д.002.231.01 при Учреждении Российской академии наук Институте радиотехники и электроники им. В.А.Котельникова РАН, по адресу: 125009, Москва, ГСП-9, ул. Моховая 11, стр. 7.


С диссертацией можно ознакомиться в библиотеке ИРЭ им. В.А.Котельникова РАН


Автореферат разослан «___»_____________ 2009 г.


Ученый секретарь диссертационного совета

д.ф.-м.н., профессор С.Н.Артеменко



ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы. Физика систем с пониженной размерностью представляет собой одну из динамично развивающихся областей современной физики. Интерес к этой области связан с активным поиском новых физических явлений, которые могли бы лечь в основу приборов и устройств. Особый интерес представляют физические системы, в которых перенос электрического заряда осуществляется не отдельными электронами, а носит коллективный характер. В качестве примеров можно привести двумерные системы с квантовым эффектом Холла, вигнеровские кристаллы, квантовые проволоки и точки, системы с кулоновской блокадой, а также квазиодномерные проводники с волнами зарядовой и спиновой плотности (ВЗП). Эти системы активно исследуются в настоящее время.

ВЗП возникает в квазиодномерных проводниках в результате пайерлсовского перехода, – самосогласованной деформации решетки и модуляции электронной плотности с волновым вектором, равным удвоенному фермиевскому вектору электронов k_F. Возникновение такой деформации понижает энергию электронной системы одномерного металла, одновременно увеличивая упругую энергию, связанную с возникновением деформации кристаллической решетки. Однако, в одномерных системах при достаточно низких температурах проигрыш энергии при малых деформациях всегда оказывается меньше выигрыша энергии электронной системы. В результате перехода в электронном спектре возникает пайерлсовская щель 2. Под действием электрического поля ВЗП может перемещаться вдоль одномерных цепочек, перенося электрический ток (фрёлиховская проводимость). Взаимодействие ВЗП с дефектами кристаллической решетки и примесями приводит к тому, что скольжение ВЗП возникает лишь при превышении электрическим полем некоторого значения E_t, называемого пороговым полем возникновения нелинейной проводимости. Зацепление ВЗП за примеси называется пиннингом ВЗП.

В электрических полях меньших порогового ВЗП запиннингована, а ее поляризуемость характеризуется гигантской диэлектрической проницаемостью, до 10⁹. Специфическим свойством ВЗП является также её способность деформироваться при внешних воздействиях, скажем при изменении температуры или при приложении электрического поля.

Таким образом, квазиодномерные проводники являются физическим объектом, обладающим уникальными свойствами, обусловленными наличием коллективного состояния – ВЗП. Поскольку пайерлсовский переход является переходом трёхмерного упорядочения и из-за сильных одномерных флуктуаций не описывается теорией среднего поля, в области перехода можно ожидать ряд явлений, не имеющих аналогов в других типах фазовых переходов и требующих специфического описания.

Другое важнейшее свойство ВЗП – её способность деформироваться при воздействии электрического поля и температурном воздействии. Интересно было выяснить, проявляется ли эта деформация в свойствах основной решётки.

Из изложенного выше очевидна актуальность проведения как фундаментальных, так и прикладных исследований в области флуктуационных и деформационных свойств квазиодномерных проводников, причём эти две группы свойств находятся во взаимной связи: флуктуации, проявляющиеся в динамической деформации ВЗП, могут приводить к деформации образцов, например, к особенностям в тепловом расширении.

К началу работы над диссертацией не был исследован ряд свойств квазиодномерных проводников: не исследовались спонтанные флуктуации сопротивления, тепловое расширение нитевидных кристаллов, не ставился вопрос об исследовании неоднородной деформации кристаллов. Среди задач, которые оставались нерешёнными к началу работы над диссертацией, были описание поведения основных параметров в области перехода трёхмерного упорядочения, таких как транспортные свойства, теплоёмкость, модули упругости, тепловое расширение, а также описание спонтанных флуктуаций сопротивления в этой области температур. Не был исследован вопрос о возможном воздействии деформации ВЗП на форму кристалла.


Целью данной диссертационной работы является изучение особенностей свойств квазиодномерных проводников с ВЗП в области пайерлсовского перехода и физических механизмов, определяющих эти свойства, а также влияния воздействии температуры или электрического поля на размеры и форму образцов.


Научная новизна работы заключается в том, что для квазиодномерных проводников с ВЗП автором впервые экспериментально исследованы:

- особенности флуктуаций вблизи пайерлсовского перехода и их связь с динамикой деформации ВЗП;

- воздействие деформации ВЗП на решётку кристалла;

- спонтанные флуктуации сопротивления вблизи пайерлсовского перехода;

- особенности вольт-амперных характеристик образцов ромбического TaS₃ нанометровой толщины в области пайерлсовского перехода;

- тепловое расширение квазиодномерного соединения TaS₃, температурный гистерезис теплового расширения и особенности тепловом расширении вблизи пайерлсовского перехода;

- деформация кручения и изгиба квазиодномерных проводников, возникающая при приложении электрического поля.

Проведён теоретический анализ полученных результатов.

В ходе выполнения перечисленных исследований автором вблизи пайерлсовского перехода были обнаружены спонтанные электрические шумы, особенность в тепловом расширении, размытие вольт-амперных характеристик (ВАХ) тонких образцов TaS₃ в области порога для нелинейной проводимости. Выше перехода в тонких образцах, наоборот, был обнаружен пороговый характер ВАХ. Был обнаружен гистерезис в тепловом расширении квазиодномерных проводников, а также кручение и изгиб в электрическом поле.

Автором предложена модель, связывающая разрушение дальнего порядка ВЗП со спонтанным проскальзывания фазы и образованием областей локального подавления (или сильного возмущения) пайерлсовского состояния. Модель объясняет спонтанные флуктуации сопротивления, размытие ВАХ в области E_t, особенности на температурных зависимостях теплового расширения, теплоёмкости, модуля Юнга и проводимости. Также предложена модель, объясняющая сильную неоднородную деформацию квазиодномерных проводников с ВЗП в электрическом поле.

Автором разработан ряд экспериментальных методик, в том числе оптические методики, позволяющие измерять тепловое расширение и кручение нитевидных образцов.


Научная и практическая значимость работы состоит в том, что полученные в ней результаты расширяют и углубляют физические представления о физике квазиодномерных проводников с ВЗП, создают цельную картину флуктуационных явлений в них, демонстрируют возможность создания неоднородной деформации кристаллической решётки в электрическом поле за счёт её взаимодействия с ВЗП. Обнаружение и исследование кручения квазиодномерных проводников в электрическом поле открывает возможность для создания эффективных актюаторов (приводов) микронного и субмикронного размера, необходимых в микро- и наносистемной технике. Интерференционная методика, разработанная для измерения удлинения нитевидных образцов, может быть применена для исследования различных объектов.

Основные положения, выносимые на защиту:

1) В квазиодномерном проводнике, ромбическом TaS₃, вблизи температуры пайерлсовского перехода, T_P, возникают спонтанные флуктуации проводимости, имеющие спектр типа 1/f. Флуктуации связаны с актами проскальзывания фазы волны зарядовой плотности (ВЗП), имеющими обратимый характер.

2) Тепловое расширение TaS₃ вблизи T_P испытывает особенность, имеющую вид размытой ступени. Сделан вывод, что механизм разрушения трёхмерного порядка ВЗП есть следствие роста вероятности проскальзывания фазы ВЗП с повышением температуры.

3) В образцах квазиодномерного проводника TaS₃ нанометровой толщины при температурах существенно ниже T_P срыв ВЗП с примесей (депиннинг) происходит без резкого порога. Данный эффект является следствием обратимого проскальзывания фазы ВЗП: каждый акт проскальзывания фазы приводит к локальному переносу заряда ВЗП. В то же время, депиннинг в таких образцах сохраняет пороговый вид существенно выше T_P. Это связано с большими длинами флуктуаций параметра порядка ВЗП, достигающими поперечных размеров образцов и определяющими её временную когерентность.

4) Создана оптическая интерференционная методика, позволяющая исследовать удлинение нитевидных кристаллов с чувствительностью не менее 5×10^-7. Обнаружено, что тепловое расширение TaS₃ имеет гистерезис, который достигает 510^-5 и связан с деформацией ВЗП. Упругое взаимодействие ВЗП и основной решётки определяется зависимостью импульса Ферми от деформации решётки.

5) Квазиодномерные проводники под действием электрического поля испытывают деформацию кручения (TaS₃, (TaSe₄)₂I, K_0.3MoO₃) и изгиба (TaS₃), которая обусловлена неоднородной деформацией ВЗП. Зависимость угла кручения от электрического поля носит пороговый гистерезисный характер. Для TaS₃ сдвиговая деформация при этом достигает величины, соответствующей пьезомодулю более 10^-6 м/В.


Личный вклад автора

Большая часть экспериментальных результатов и все теоретические результаты, выносимые на защиту, были получены автором. Автор также проводил обработку экспериментальных данных, написание и оформление публикаций. Использованные в работе соединения квазиодномерных проводников были выращены в ИРЭ им. В.А. Котельникова РАН, а также в лабораториях США, Франции и Швейцарии.


Апробация работы.

Результаты работы докладывались на научных семинарах ИРЭ РАН, Физфака МГУ, Курчатовского института, МИФИ, на Научной сессии Отделения информационных технологий и вычислительных систем (ОИТВС) РАН «Проблемы наносистем и микросистемной техники» 28.09.07, в Лаборатории сверхнизких температур (Гренобль, Франция), в Лаборатории сильных магнитных полей (Вроцлав, Польша), в Университетах Байройта и Хемница (Германия), в Университете Эксетера (Англия), на 25 и 26 Всесоюзных совещаниях по физике низких температур (Ленинград 1988, Донецк 1990), на XI Всесоюзной конференции по физике полупроводников (Кишинев 1988), на 5 и 6 Всесоюзных конференциях по флуктуационным явлениям в физических системах (Паланга 1988, 1991), XXII Международной конференции по физике низких температур (Хельсинки, Финляндия), 13-й Международной конференции по шумам в физических системах и флуктуациям 1/f (Паланга, Литва 1995), на Международных конференциях по физике электронных кристаллов ECRYS'93, ECRYS'02, ECRYS'05, ECRYS'08 (Франция 1993), на 3-й конференции IEEE по НЭМС (Хайнянь, Китай 2008), представлялись для 7-ой рамочной Европейской программе по направлению микро-наносистемы, 26.09.07, 21.10.08.


Публикации. Основные результаты опубликованы в 40 научных работах, в том числе в 29 статьях в реферируемых отечественных (7) и зарубежных (22) журналах; все 29 публикаций – в журналах и изданиях, определенных Высшей аттестационной комиссией. 11 публикаций - в сборниках трудов докладов отечественных и международных конференций и симпозиумов, а также интернет-изданиях.


Структура и объем работы. Диссертация состоит из введения, шести глав и заключения. Общий объем работы 132 страницы, включая 36 рисунков. Список цитированной литературы содержит 87 наименований.


ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ


Во введении обосновывается актуальность работы, даётся краткий обзор основных свойств квазиодномерных проводников с волной зарядовой плотности (ВЗП) в связи с тематикой диссертации, формулируются цели и задачи работы, отмечается новизна и практическая ценность работы, приводятся положения, выносимые на защиту, даны сведения об апробации работы, кратко изложена структура и содержание работы.


Содержание глав 2-4 относится к флуктуационным свойствам квазиодномерных проводников с ВЗП.

Глава 2 посвящена изучению спонтанных флуктуаций сопротивления в квазиодномерном соединении TaS₃.

В разделе 2.1 обосновывается постановка задачи. Даётся обзор флуктуационных свойств, изученных к моменту начала работы над диссертацией. Универсальной теории, описывающей поведение всех физических величин вблизи температуры пайерлсовский перехода – перехода трёхмерного упорядочения ВЗП – пока не создано. Приводятся примеры, показывающие, что предсказания имеющихся теорий существенно расходятся с экспериментом [A25,1]. Очевидно, одной из причин трудностей в описании перехода является необходимость учёта пространственной неоднородности состояния вблизи перехода. Об этом, в частности, свидетельствует теоретическая работа [2], в которой показано, что локальный сдвиг химического потенциала из-за флуктуаций вблизи температуры перехода, T_P, может быть сравним с , и можно ожидать подавления пайерлсовской щели в этой области температур. Поэтому актуальным может быть разработка моделей флуктуаций, имеющих экспериментальное основание и ясный физический смысл, а также сопоставление этих моделей с другими экспериментами.

В разделе 2.2. даётся обзор научных работ, в которых экспериментально и теоретически изучалось явление проскальзывания фазы (ПФ) ВЗП [3-6,А2]. Описывается феноменологическая модель термически активированного ПФ. Модель основана на экспериментальных исследованиях избыточного напряжения, V_ps, возникающего при движении ВЗП в соединениях NbSe₃ [4] и TaS₃ [5]. Это напряжение связано с ПФ и описывается активационной моделью. Согласно модели, ток ВЗП, а значит, и частота ПФ, пропорциональны


exp[-(W-MV_ps)/T], (1)


где W~(3–6)10⁴ K, M~(1-4)×10². Аналогичным соотношением можно описать и релаксацию метастабильных состояний (деформации) ВЗП [6], которая, как известно, носит логарифмический характер [3]. В этом случае в (1) вместо V_ps следует подставить ζ, сдвиг химического потенциала относительно равновесного положения.

Далее обосновываются предпосылки для экстраполяции модели в область более высоких температур. Показано, что при температуре на несколько градусов ниже T_P должны наблюдаться спонтанные флуктуации сопротивления.

Раздел 2.3 посвящён особенностям экспериментальных методик, применявшихся для исследования флуктуаций. Показано, что для описания особенностей поведения основных параметров, характеризующих пайерлсовский переход, таких как теплоёмкость, модули упругости, тепловое расширение, транспортные свойства, следует исследовать образцы не слишком малых размеров, в которых переход не размыт из-за размерного эффекта [7]. Для исследования электрических шумов в таких образцах пришлось применить специальную методику, использующую малошумящий усилитель [А8]. В диапазоне частот, на которых измерялись флуктуации сопротивления, поддерживался режим заданного тока. При этом, однако, использование медленной обратной связи (с обратной постоянной времени ~10^-2 с^-1, т.е. ниже всех частот, на которых проводились измерения) позволило поддерживать постоянную величину смещения, несколько ниже порогового, несмотря на существенное изменение сопротивления с температурой.

С другой стороны, в образцах субмикронной толщины флуктуации выражаются в особых эффектах. В частности, шумы в них имеют вид случайного телеграфного сигнала [А5,А7]. Поэтому, в данном разделе описана также методика приготовления образцов малых размеров, необходимых для исследования таких шумов.


Раздел 2.4 посвящён исследованию спонтанных флуктуаций сопротивления образцов TaS₃.

На Рис. 1 приведена зависимость спектральной плотности шума, S_f, от температуры на частоте 7.7 Гц (кривая А) для образца TaS₃ сечением 0.5 мкм² и длиной 400 мкм [А8]. На образце поддерживалось постоянное напряжение V=35 мВ при значении порогового напряжения V_t60 мВ. Фоновый шум усилителя вычтен. Вблизи перехода, при T_m=213 К, наблюдается максимум шума. Показано, что S_f приблизительно пропорциональна V² при V<V_t. Это означает, что шумы связаны с не зависящими от V флуктуациями сопротив-ления, то есть носят спон-танный характер. На этом же графике приведены темпера-турные зависимости логариф-мической производной со-противления, dlnR/d(1/T), образца (кривая B) и ширины петли гистерезиса R(T), R_heating/R_cooling (кривая C). Температура перехода, T_P, как её принято определять, соответствует максимуму dlnR/d(1/T).

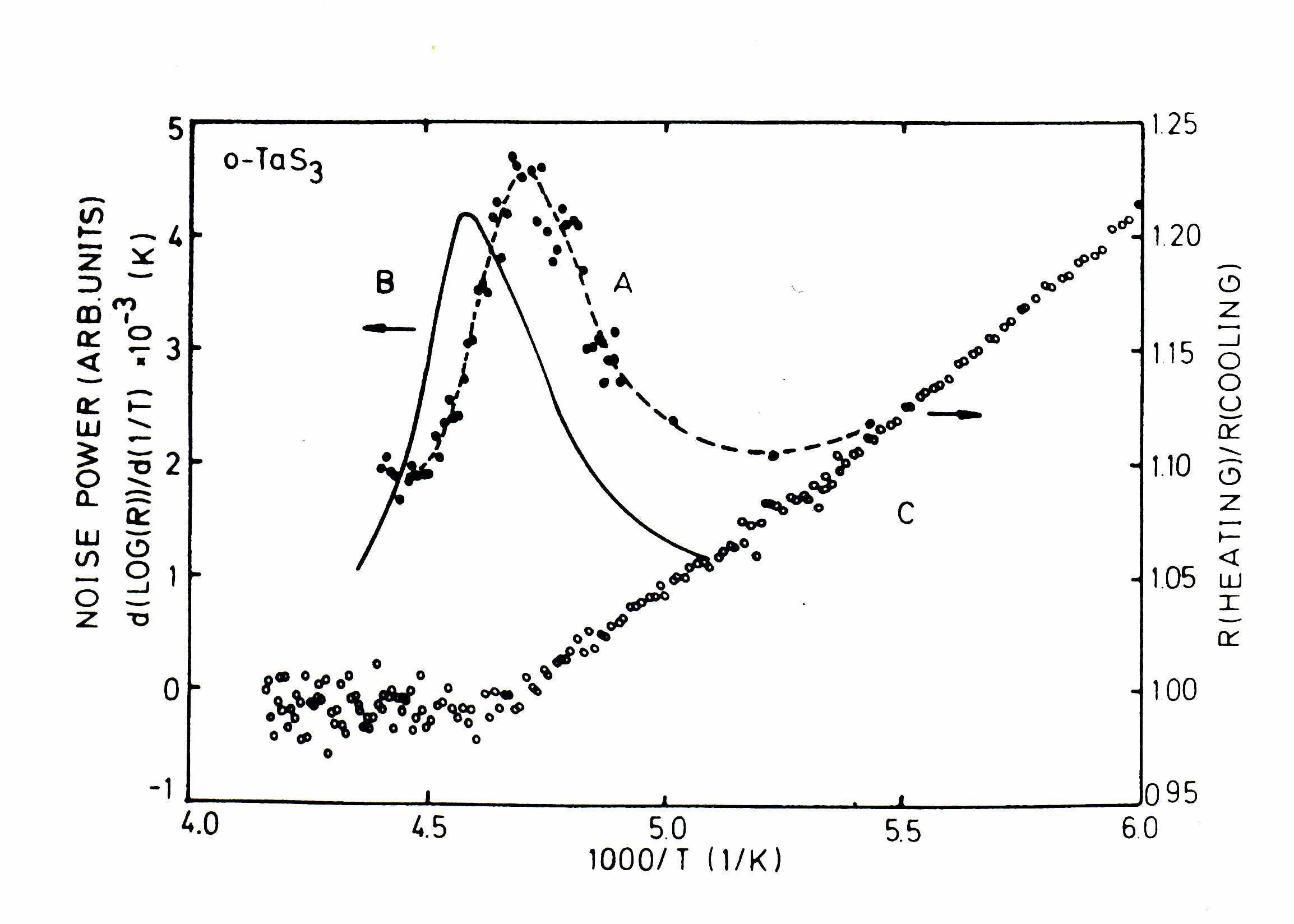Рис.1. Температурные зависимости спектральной плотности шума на частоте 7.7 Гц (А), логарифмической производной сопротивления (В) и ширины петли гистерезиса сопротивления (С) образца TaS3.

Показано, что зависимость S_f(f) можно описать как 1/f^β, где β1.15. С понижением Т наблюдается некоторое увеличение β.

В разделе 2.5 обосновывается связь наблюдаемых флуктуаций сопротивления со спонтанным ПФ. Вначале результаты [А8] сопоставляются с полуэмпирическим соотношением Хоухе [8], дающим оценку величины 1/f–шума для широкого класса материалов. Показано, что величина S_f имеет аномально большое значение. Совпадение температуры, при которой наблюдается максимум шума, с точкой схлопывания петли гистерезиса, а также подобие форм максимума и температурного хода сопротивления в области T_P, указывают на связь флуктуаций с процессом ПФ. Особо отмечаются шумы в образцах субмикронной толщины [А5]: наблюдение спонтанных шумов, имеющих вид случайного телеграфного сигнала, непосредственно доказывает, что шумы связаны со спонтанным обратимым процессом ПФ. Температурная эволюция этих шумов [А5,А7] показывает, что переключения отражают единичные акты ПФ: при низких температурах ПФ проявляются в виде ступенек на R(T), а вблизи T_P, в области исчезновения метастабильных состояний, ступеньки эволюционируют в обратимые переключения сопротивления.

Переключения, связанные с единичным «флуктуатором» имеют лоренцевский спектр. В образцах больших размеров распределение характерных частот отдельных двухуровневых флуктуаторов приводит к размытию лоренцовского спектра [А8]. Этим объясняется спектральная зависимость шума типа 1/f^β и увеличение β с понижением Т. Показано, что согласно (1) ширина максимума должна быть ~1/W в единицах 1/T. Из Рис. 1 можно оценить W~7000 K, что соответствует высоте барьера, характеризующего ПФ.

Для описания пайерлсовского перехода, т.е. процесса разрушения трёхмерного порядка ВЗП с повышением температуры, предлагается экстраполировать процесс термически активированного ПФ до T_P и выше. Для сопоставления этой экстраполяции с экспериментом формулируется модель ПФ, которая в дальнейшем позволит описать поведение различных величин вблизи T_P [А25]. Согласно модели, каждый акт ПФ приводит к временному возникновению области локального подавления (или сильного возмущения) пайерлсовского состояния. Размер такой области можно характеризовать длинами амплитудной когерентности ВЗП, x_i. При этом, однако, надо иметь в виду, что существенное возмущение ВЗП происходит и далеко за пределами этой области, на длинах фазовой когерентности, (L_2π)_i [А4,А6]. С ростом Т концентрация нормальных областей растёт как exp(-W/T). Доля объёма образца, находящаяся в нормальном состоянии

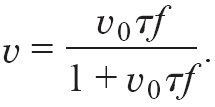, (2)


где 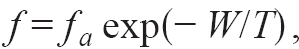f_a- частота попыток, v₀ – объём нормальной фазы, связанный с одним актом ПФ, а  – время его жизни. Это выражение описывает рост v от 0 до 1. Зависимость v от T имеет вид размытой ступени, середина которой (v =1/2) соответствует .


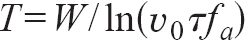В главах 3-4 модель конкретизируется и находит экспериментальное обоснование.