Флуктуационные, термо- и электромеханические эффекты в квазиодномерных проводниках с волной зарядовой плотности
| Вид материала | Автореферат |
- 4 Механические и электромагнитные колебания и волны 4 Энергия волны. Перенос энергии, 35.27kb.
- Ооо «нпкф «Термо Инжиниринг», 30.22kb.
- Аннотация к научно-образовательному материалу «Современные электромеханические аппараты», 60.95kb.
- План лекции. Рынок труда и занятость. Влияние плотности населения на трудовую занятость, 35.63kb.
- Сс-системы и соответственно повреждающие эффекты стресс-реакции, в механизме устойчивости, 19.64kb.
- Реферат Отчет 65 с., 3 ч., 26 рис., 8 табл., 53 источника, 92.51kb.
- Рейтинг план по дисциплине Электромеханические аппараты автоматики, управления, распределения, 36.34kb.
- 4 образование ядер и атомов, 48.2kb.
- От 20 г, 53.43kb.
- Основные эксплуатационные характеристики медицинских термоконтейнеров производства, 67.16kb.
В разделе 3.1 отдельно рассмотрено тепловое расширение TaS3, исследованное автором диссертации [А25]. На Рис. 2 приведены результаты измерения относительного удлинения, δL/L, образца TaS3 вблизи TP Понижение температуры ниже TP приводит к относительному укорочению образца приблизительно на 10-5.
Для описания эффекта предпо-лагается, что рост длины образца с повышением Т пропорционален доле объёма нормальной фазы. В этом случае ступенька L(T) должна описываться соотношением (2). Результат подгонки показан на Рис. 2 сплошной линией. Подгоночное значение W=6500 K хорошо соответствует известной энергии активации ПФ.
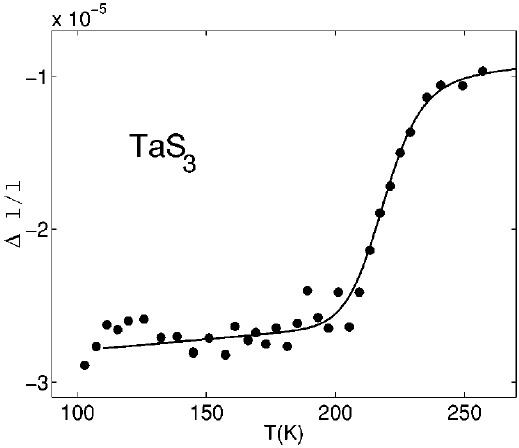 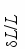 |
| Рис.2. Зависимость δL/L от Т для образца TaS3. Для наглядности плавный ход δL/L, приближенный полиномом второго порядка, вычтен. Сплошной линией показано приближение зависимости соотношением (2) с W=6500 K.. |
В начале раздела описываются результаты измерения сопротивления в зависимости от температуры, R(T). В рамках модели спонтанного ПФ рассчитывается сопротивление смеси двух фаз с разными удельными сопротивлениями, c и n. Для пайерлсовского состояния предполагается
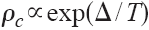 , а для нормального – n =A+BT, где A и B – подгоночные константы. Вклад каждой фазы в сопротивление считается пропорциональным её объёмной доле. В результате удаётся удовлетворительно описать всю зависимости R(T) для TaS3 в области перехода. Выше TP наблюдается некоторое расхождение модели с экспериментом: спад v происходит медленнее, чем следует из (2). Это объясняется тем, что характерные размеры областей пайерлсовского состояния оказываются меньше v0.
, а для нормального – n =A+BT, где A и B – подгоночные константы. Вклад каждой фазы в сопротивление считается пропорциональным её объёмной доле. В результате удаётся удовлетворительно описать всю зависимости R(T) для TaS3 в области перехода. Выше TP наблюдается некоторое расхождение модели с экспериментом: спад v происходит медленнее, чем следует из (2). Это объясняется тем, что характерные размеры областей пайерлсовского состояния оказываются меньше v0.Далее рассмотрена температурная зависимость модуля Юнга Y вблизи TP. Проанализированы результаты для соединения TaS3 из [9], в котором наблюдается минимум Y(T) вблизи TP. Показано, что при приближении к TP отклонение Y(T) от линейного хода хорошо описывается активационной зависимостью с энергией активации W=5600 K, что находится в согласии с моделью ПФ. В рамках модели описана также вся зависимость Y(T) – минимум в области TP. Для этого, кроме того, что вблизи перехода образец разбивается на области двух типов, каждая из которых имеет свой модуль Юнга, учтено, что в пайерлсовских областях ВЗП частично находится в состоянии движения (вследствие термических флуктуаций). Известно, что при движении ВЗП модуль Юнга может заметно снижаеться (для TaS3 на величину до 5% [10]). Поскольку термическое движение ВЗП можно связать со спонтанным ПФ [А4,А6,А17] (подробнее эта связь рассмотрена в главе 4), доля фазы с движущейся ВЗП растёт с повышением T как exp(-W/T). Это объясняет снижение модуля Юнга при приближении к TP снизу. Отмечается также, что в другом соединении с ВЗП, «голубой бронзе» (К0.3MoO3), снижения модуля Юнга при движении ВЗП не наблюдается (δY/Y < 510-5) [10], что, в соответствии с моделью, согласуется с очень слабым снижением Y(T) при T® TP-0 [11,12].
Наконец, рассмотрена особенность в теплоёмкости, cp(T), TaS3 вблизи TP, измеренная в [13]. Эта особенность очень слабая и видна только на температурной производной dcp/dT. Она имеет вид зигзага, что соответствует пику теплоёмкости. Эта особенность также успешно описана в рамках модели ПФ.
Глава 4 посвящена флуктуационным эффектам, специфическим для образцов субмикронных и нанометровых поперечных размеров, проявляющимся в их транспортных свойствах. В разделе 4.1 сообщается о наблюдении эффекта размытия («закругления») вольт-амперных характеристик (ВАХ) тонких образцов TaS3 в области порогового поля вблизи TP (Рис. 3). В таких образцах пайерлсовский переход размыт и понижен на величину ~10 K [7]. Из зависимости R(T) определён флуктуационный вклад в линейную проводимость, δs, – добавка к проводимости s exp(-/T): δs s-s (Рис. 4). Этот вклад описывается зависимостью exp(-W/T), в соответствии с результатами главы 3. Сопоставление температурных зависимостей этого вклада и нелинейной проводимости (Рис. 4) свидетельствует о том, что они имеют общую природу и, следовательно, должны быть связаны со спонтанным ПФ.
В разделе 4.2 показано, как модель ПФ можно обобщить для описания локального движения (крипа) ВЗП, вызванного спонтанным ПФ. Каждый акт ПФ сопровождается локальным крипом (перераспределением фазы) ВЗП на длине порядка фазовой когерентности ВЗП, L2π, в окрестности точки, в которой зародился центр ПФ [А4,А6,А17]. В присутствии внешнего электрического поля крип происходит преимущественно в направлении, определяемом полем. Этот процесс даёт вклад в проводимость ниже Vt. На основании модели выводится соотношение между линейным и нелинейным вкладами в проводимость, которое согласуется с экспериментом. При E Et модель даёт расходимость, не имеющую физического смысла, т.к. в модели не учтено конечное время самого крипа. Ограничиваясь линейным и квадратичным вкладами в ток, получаем соотношение между линейной и нелинейной флуктуационной проводимостью:
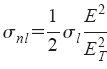 (3)
(3) 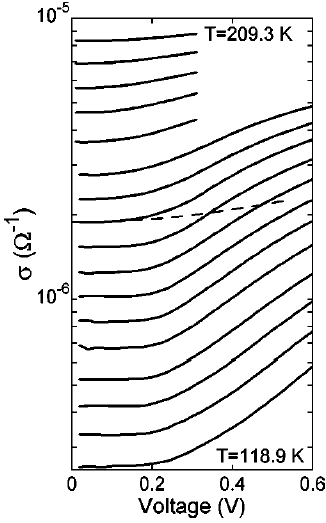 | 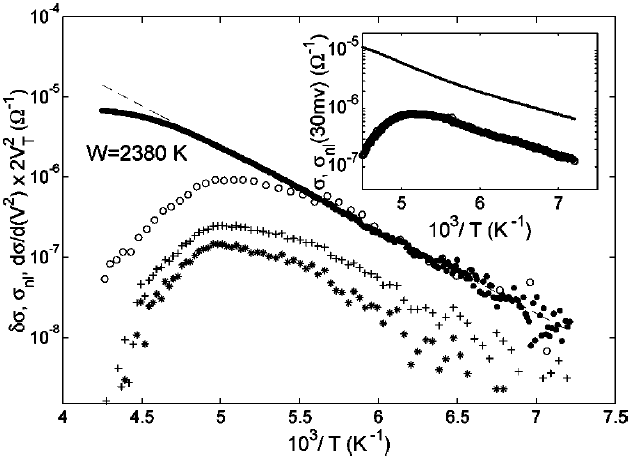 |
| Рис.3. Зависимости проводимости (I/V) при T=209.3, 203.4, 197.4, 191.4, 184.5, 176.8, 171.2, 165.9, 160.1, 154.6, 149.3, 144.3, 139.1, 133.6, 128.8, 123.9 и 118.9 K. Пунктиром показан пример приближения snl(E) уравнением (3). TP=199 K | Рис. 4. Температурные зависимости флуктуационного вклада в линейную проводимость (точки), нелинейной проводимости при двух значениях V<Vt: 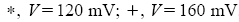 . Пустыми кружками обозначено приближение нелинейной проводимости уравнением (3) с Vt =220 мВ (Et= 480 В/см). На вставке показана полная линейная проводимость (точки) вместе с нелинейной проводимостью при . Пустыми кружками обозначено приближение нелинейной проводимости уравнением (3) с Vt =220 мВ (Et= 480 В/см). На вставке показана полная линейная проводимость (точки) вместе с нелинейной проводимостью при 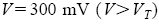 . Наклон линий соответствует энергии активации ~1000 К. . Наклон линий соответствует энергии активации ~1000 К. |
При заданном E/Et нелинейная и линейная флуктуационная проводимость должны иметь одинаковые температурные зависимости, определяемые частотой ПФ, fexp(-W/T). Это видно из Рис. 4 (считая Et const). Соотн. (3) даёт и количественную связь линейной флуктуационной (δs на Рис. 4) и нелинейной проводимости: параметр Et в (3), 480 мВ/см, соответствует экспериментальному значению при низких Т, когда порог достаточно определён. То, что δs начинает отклоняться от активационной зависимости при более высоких температурах, чем snl, объясняется непосредственным вкладом нормальной фазы в линейную проводимость; этот вклад сохраняется при более высоких Т, при которых модель крипа ВЗП, индуцированного ПФ, неприменима.
В заключении раздела отмечается, что модель крипа ВЗП, связанного с ПФ, применима не только к TaS3, но и к другим соединениям (например, NbSe3 [14,15]), где наблюдается размытие порогового поля в тонких образцах вблизи TP. Кроме того, этот эффект должен существовать (и наблюдается [3]) в образцах обычных размеров. Однако его исследование затруднено, т.к. область плавной нелинейности ограничена гораздо более узкими диапазонами температур и напряжений (ниже порогового).
В разделе 4.3 сообщается о наблюдении качественно иного эффекта – появления порогового вклада в нелинейную проводимость в субмикронных образцах TaS3 [А14]. Наиболее выражен пороговый характер проводимости в образцах, имеющих лентообразный вид: ширина – около 2 мкм, толщина – t=0.1-0.2 мкм. Эффект наблюдается при температурах, более чем на 45 К превосходящих TP.
На Рис. 5a показаны зависимости Rd(V) для образца TaS3. Ниже TP (211 К) формы зависимостей типичны для этого соединения. Выше TP величина нелинейности падает, и зависимости обретают более сложную форму. Её можно представить как
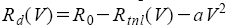 , где второй член описывает пороговый вклад в нелинейность.
, где второй член описывает пороговый вклад в нелинейность. 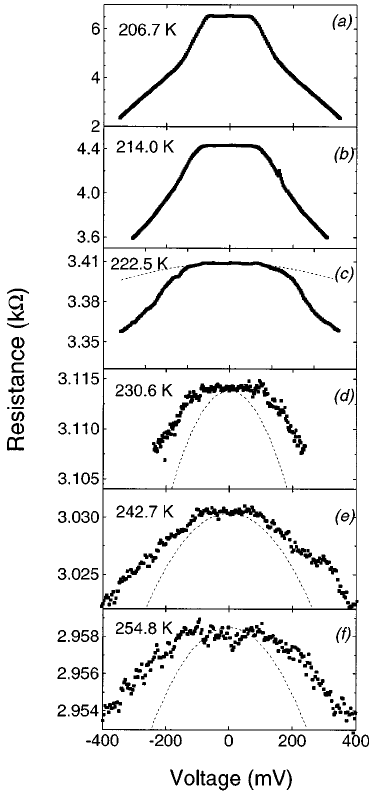 a) | 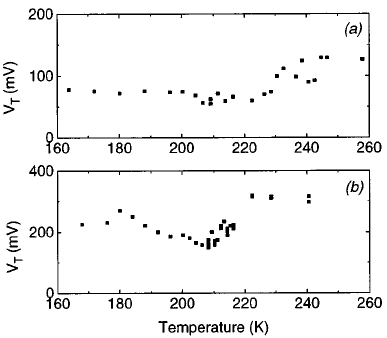 b) |
| Рис.5. a)Зависимости Rd от V при различных Т (указанных на рисунке) для образца TaS3. Пунктиром показан плавный вклад в Rd (V2); на графиках (с)-(f) он вычтен. Длина образца L=140 мкм, ширина – w=2 мкм, площадь сечения – S=0.2 мкм2. b). Температурные зависимости порогового напряжения Vt для двух образцов TaS3: (а) длина L=140 мкм, ширина – w=2 мкм, площадь сечения – S=0.2 мкм2, TP =211 K, (b) L=400 мкм, w=2 мкм, S=0.1 мкм2, TP =210 K. |
Величина Vt (Рис. 5b) относительно слабо зависит от температуры ниже TP, что отличает исследованные образцы от образцов обычных размеров. В то же время, величина порогового нелинейного сопротивления, Rtnl, при заданном V падает с ростом Т на 3 порядка.
Далее показано, что величина Rtnl повторяет температурный ход флуктуационного вклада в линейную проводимость, Rfl, однако при этом изменение Rtnl с температурой в два раза больше (в логарифмическом масштабе), чем изменение Rfl: Rtnl Rfl2.
Из результатов эксперимента следует, что существенно выше TP длина когерентности ВЗП может достигать толщины образца, t. Далее показано, что такое действительно возможно. Хотя доля таких флуктуаций (доменов) при высоких температурах очень мала, именно они первыми начинают движение с ростом поля. Иными словами, домены с поперечным размером l=t определяют нижнюю границу для поля срыва флуктуаций ВЗП и определяют пороговое поле. Поэтому нелинейность может быть слабой, но при этом носит пороговый характер. Слабая зависимость Vt(T) выше TP (Рис. 5b) означает, что внутри больших областей флуктуаций ВЗП при изменении температуры не происходит никаких качественных изменений по сравнению с пайерлсовским состоянием, что является прямым доказательством связи перехода с разрушением трёхмерного порядка, а не с однородным подавлением пайерлсовской щели.
Далее, в предположении лоренцовского вида функции распределения флуктуаций по длинам и степенного спада длины когерентности флуктуаций выше TP, x (T-TP)-1/2, предлагается объяснение связи между линейным флуктуационным и нелинейным пороговым сопротивлением, Rtnl Rfl2. Делается вывод, что, в тонких образцах появляется возможность выделить вклад и исследовать свойства (динамику) самых длинноволновых флуктуаций.
В разделе 4.4 анализируется природа состояния квазиодномерных проводников выше TP, обсуждаются области применимости модели ПФ для описания пайерлсовского перехода, рассматриваются варианты её возможного микроскопического обоснования.
Наиболее вероятное обоснование [А25] основано на предположении, что условием зарождения акта ПФ является начальное подавление пайерлсовского состояния в объёме xi3x||x2. Объём же, в котором происходит возмущение ВЗП (деформация, локальное движение) – гораздо больше, порядка (L2π)i – см. раздел 4.1. При температуре перехода доля этого объёма (v из соотн. 2) становится сравнимой с 1. Оно может быть достигнуто при очень малой концентрации возбуждений. Из условия v=½ получаем оценку
TP ~ W/ln[(L2π)i 3/s], (4)
которая даёт W~24TP, что хорошо соответствует эксперименту. Делаются выводы о характере перехода: 1) переход происходит при очень малой концентрации возбуждений, что согласуется с отсутствием критического поведения, т.е. степенных зависимостей вблизи TP. 2) состояние выше TP можно рассматривать как ВЗП, находящуюся в постоянном флуктуационном движении. Отмечается, что значение TP в данной модели определено несколько условно, скажем, из условия v=1/2.
Далее показано, что модель также может описать размытие и снижение TP, а также эффективное уменьшение W в тонких или примесных образцах (т.е. с высоким Et). Объяснение этих эффектов основано на том, что чем выше Et, тем выше пространственные флуктуации химического потенциала, ζ [А6] т.е. деформации ВЗП. Эти флуктуации понижают W на величину Mζ (соотн. 1), и условие v=1/2 достигается в некоторых точках при более низких температурах.
Главы 5-7 посвящены исследованиям деформации образцов квазиодномерных проводников, связанной с деформацией ВЗП. Исследованы три вида деформации: однородная продольная, кручение и изгиб.
В Главе 5 рассматривается однородная деформация образцов. Вначале (раздел 5.1) приведены соображения, согласно которым можно ожидать чувствительность размеров и формы образцов квазиодномерных проводников к деформации ВЗП. Приводятся экспериментальные работы зарубежных авторов, в которых наблюдалось уменьшение модуля Юнга и модуля сдвига при депиннинге ВЗП [12,16-19]. Результаты свидетельствуют о возможности упругого взаимодействия ВЗП и основной решётки. Анализируется также эксперимент, проведённый американскими авторами, в котором сообщается об изменении длины образцов TaS3 при воздействии электрического поля [20]. Поскольку деформация ВЗП в электрическом поле неоднородна, исследование взаимодействия ВЗП и решётки по удлинению всего кристалла в поле оказывается затруднительным [А12,А21]: основное воздействие поля на решётку также должно быть неоднородным. Для изучения воздействия деформации ВЗП на кристалл в данной работе предлагается два пути: во-первых, можно создать относительно однородное растяжение или сжатие ВЗП, используя термическое воздействие на образцы; во-вторых, можно создавать деформацию ВЗП электрическим полем, но при этом исследовать неоднородные виды деформации образца.
Отдельный раздел (5.2) посвящён описанию оригинальной экспериментальной методики, разработанной для исследования теплового расширения нитевидных образцов [А24]. Приводится краткий обзор методик, применявшихся ранее для этой цели. Делается вывод, что до сих пор не существовало методики, позволяющей с удовлетворительной точностью исследовать тепловое расширение нитевидных образцов.
Предложенная в данной диссертации методика основана на простом принципе. Допустим, образец выгнут в виде арки, слегка приподнятой над подложкой, а концы его зафиксированы (Рис 6а). Длина образца, L, много больше расстояния от его середины до подложки, d. Тогда, при малом удлинении образца изменение d, d, многократно (в отношении ~L/d) превосходит изменение L. Это значит, что, измеряя d, можно детектировать гораздо меньшие изменения L. Предлагается интерференционная методика измерения d.
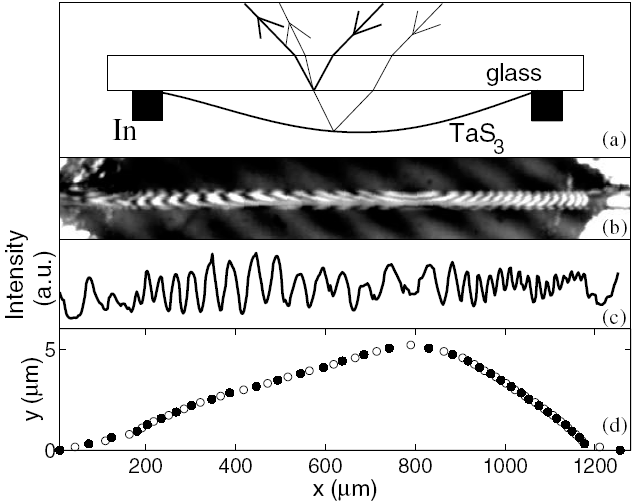 |
| Рис.6. а).Расположение образца на подложке и схема отражений и интерференции лучей лазера (реально, углы падения близки к 90 град). b). Пример полученного интерференционного изображения. c). Профиль сечения изображения. d) Рассчитанный профиль образца. Пустые кружки соответствуют минимумам в сечении (с)), а чёрные – максимумам. |
Для получения абсолютной величины теплового расширения TaS3 отдельно измерялось тепловое расширение материала подложки. Расположение образцов между индиевыми контактами позволило одновременно с тепловым расширением измерять проводимость образцов.
Результаты измерения теплового расширения TaS3 приведены в разделе 5.3. На Рис.7а и b показаны результаты одновременного измерения длины и сопротивления образца TaS3 в зависимости от Т. На обеих зависимостях виден гистерезис ниже TP =214 К. Петля гистерезиса, L(T), достигает δL/L=510-5, что на 1.5 порядка превышает максимальную деформацию, наблюдавшуюся в [20].
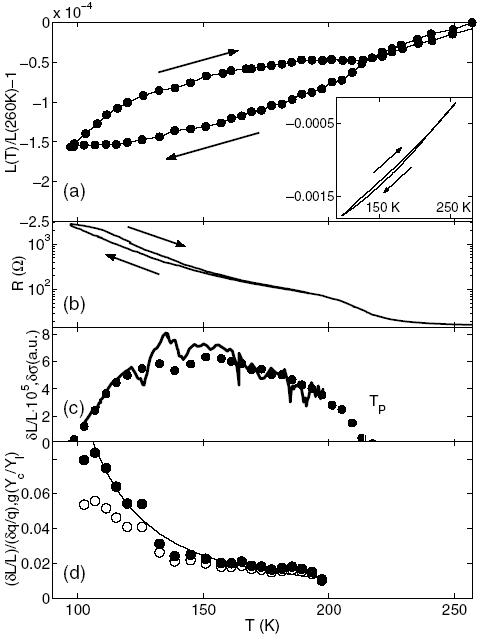 |
| Рис.7. а) Температурная зависимость удлинения, δL/L, относительно материала подложки. Тепловое расширение в абсолютных единицах показано на вставке. b) R(T), измеренная одновременно. с) Температурные зависимости амплитуд петель гистерезиса длины (точки) и проводимости (сплошная линия). d) Отношение 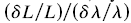 (пустые кружки) и (пустые кружки) и 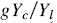 (чёрные кружки), полученные из с). Сплошная линия соответствует Ycexp(470 K/T). (чёрные кружки), полученные из с). Сплошная линия соответствует Ycexp(470 K/T). |
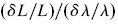 , полученная с учётом температурной зависимости подвижности [21]. При низких температурах δL/L достигает 6% деформации ВЗП. Рост отношения с понижением температуры показывает рост модуля упругости ВЗП.
, полученная с учётом температурной зависимости подвижности [21]. При низких температурах δL/L достигает 6% деформации ВЗП. Рост отношения с понижением температуры показывает рост модуля упругости ВЗП.В разделе 5.4 анализируются результаты исследования гистерезиса теплового расширения TaS3 и предлагается модель взаимодействия ВЗП с решёткой кристалла. Показано, что такое взаимодействие возникает в случае, если при продольной деформации образца изменяется отношение равновесного периода ВЗП, eq к периоду решётки, c. Отмечено экспериментальное указание на такое изменение: это цикл работ [22], из которых следует, что при растяжении образцов TaS3 ВЗП в них может достигнуть 4-хкратной соизмеримости с исходной решёткой. На основе этих работ, а также температурной зависимости q-вектора ВЗП [3] показано, что при растяжении образца eq изменяется в g6 раз быстрее, чем c. Для объяснения такой большой величины g предлагается использовать особенность трихалькогенидов, отмеченную в [23], состоящую в зависимости вида S-S связей от расстояния между атомами серы. При деформации образца возможен переход электронов между валентной и проводящей зонами, что может приводить к изменению ферми-вектора (а значит и q) при деформации образца.
Для определения удлинения образца при деформации ВЗП плотность упругой энергии записывается как сумма упругих энергий, связанных с деформацией ВЗП и образца. Минимизация этой энергии даёт:
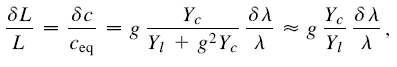 (5)
(5)где δl – исходная деформация ВЗП, Yl и Yc – модули упругости решётки и ВЗП соответственно. Приближение подразумевает, что g2Yc<<Yl. Это соотношение имеет прозрачный физический смысл: кристалл деформируется как пружина, соединённая параллельно с ВЗП через рычаг, отношение плеч которого должно быть равно g. Величина деформации, определяемая (5), согласуется с экспериментальными оценками δl, а также сдвига химического потенциала δζ [5], связанного с деформацией ВЗП.
Далее приводятся результаты исследований неоднородной деформации квазиодномерных проводников в электрическом поле.
Отдельная
