Geum.ru

Флуктуационные, термо- и электромеханические эффекты в квазиодномерных проводниках с волной зарядовой плотности

Вид материалаАвтореферат

Содержание


Глава 7 посвящена исследованию деформации кручения, возникающей в квазиодномерных проводниках с ВЗП в электрическом поле. В разд
Слева: микрофотография образца TaS3 с подвешенным контактом и 6-ю микрозеркалами. Расстояние между контактами - 3.4 мм. Справа
В заключении (
Основные результаты диссертации опубликованы в следующих статьях
Подобный материал:
1   2   3
глава, № 6, посвящена теоретическому расчёту возможного воздействия электрического поля на изменение формы образца. В разделе 6.1 проводится расчёт профиля деформации ВЗП. Рассматривается простейший случай однородного образца, одноосная деформация ВЗП в котором связана с необходимостью ПФ на контактах при движении ВЗП, т.е. с «контактным пиннингом». В этом случае, как известно [3], наблюдается параболическое «провисание» фазы ВЗП, (x), между контактами. В середине наблюдается максимальный набег фазы. Продольное смещение (деформация) самого образца относительно контактов, δx(x), должно повторять профиль «провисания» ВЗП с коэффициентом gYc/YL (5). По аналогии с обратным пьезоэлектрическим эффектом, «пьезомодуль» образца с ВЗП, dc, можно определить как перемещение середины образца, нормированное на приложенное электрическое напряжение. В пренебрежении объёмным пиннингом (V  2Vps) получаем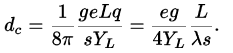

(6)


Здесь s – площадь, приходящаяся на одну проводящую цепочку. Для TaS3 длиной L=2 мм получается dc=510-6 м/В, что на 4–6 порядков превышает значения, известные для пьезоэлектриков. В более типичном случае, V >> 2Vps, получаем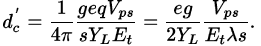

(6’)


Эта величина, несколько меньше оценки (6) приведённой выше оценки, однако весьма велика по сравнению с пьезомодулями известных материалов. В обоих случаях одноосная деформация образца достигает 310-5, а ожидаемое максимальное смещение середины образца равно 2dcVps, что для Vps=3 мВ [1] составляет 300 Å, что можно измерить, например, с помощью атомно-силового микроскопа [А31].

Раздел 6.2 посвящён анализу полученных результатов. Соотношение (6) сопоставляется с оценкой пьезомодуля для ионных пьезоэлектриков. Оказывается, что величина dc по порядку величины в Lc/ раз превосходить пьезомодуль таких материалов, где Lc - длина когерентности, достигающая миллиметров при скольжении ВЗП. Огромная величина dc связана с большой (макроскопической) длиной когерентности ВЗП. В то же время, более точной аналогией рассчитанной деформации является флексоэлектрический эффект [24], при котором электрическое поле вызывает градиент деформации образца 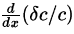, а не саму деформацию δc/c.

Отмечается также, что виды неоднородной деформации квазиодномерных проводников в электрическом поле могут быть различными: помимо продольной, можно ожидать изгиб, сдвиг и т.д. Мотивируется постановка задачи об исследовании кручения.


Глава 7 посвящена исследованию деформации кручения, возникающей в квазиодномерных проводниках с ВЗП в электрическом поле. В разделе 7.1 отмечается, что одна из причин такой постановки задачи является относительная простота экспериментальных методов исследования кручения (т.е. неоднородного сдвига). Приводятся соображения, по которым сдвиговая деформация может быть ещё больше, чем одноосная (6,6’).




Рис.8. Слева: микрофотография образца TaS3 с подвешенным контактом и 6-ю микрозеркалами. Расстояние между контактами - 3.4 мм. Справа: увеличенный фрагмент того же образца. Вставка: схема хода лучей.


Далее описываются оптические экспериментальные методики исследования деформации кручения нитевидных образцов [А35]. Для наблюдения кручения образец был закреплён так, чтобы один из его контактов был свободно подвешен (Рис. 8). Верхний конец вискера (т.е. нитевидного кристалла) прижат к подложке с помощью индия, а другой конец приподнят над ней. К нему с помощью проводящего клея прикреплена тонкая проволока (вискер сверхпроводника Ba2Sr2CuCa2Ox сечением примерно 100.2 мкм2), практически не препятствующая свободному кручению вискера вокруг вертикальной оси. На образец наклеены одно или несколько микрозеркал (тоже вискеры Ba2Sr2CuCa2Ox). Кручение фиксировалось по смещению луча лазера, отражённого от одного из зеркал (вставка к Рис. 8). Образец помещался в оптическом криостате. Изменяя величину тока через образец, мы измеряли угол его кручения, δ(I), и дифференциальное сопротивление Rd.

Для определения угла кручения использовались два варианта оптической методики. В первом варианте отраженный от микрозеркала «зайчик» проецировался на матрицу цифрового фотоаппарата, затем полученное изображение обрабатывалось, и в результате определялся угол кручения. Этот метод был применим только для достаточно медленных измерений, т.к. с его помощью удавалось записывать не более двух изображений в секунду. Вторая методика позволяла напрямую преобразовывать отклонение луча в сигнал на выходе фотодиода, пропорциональный углу отклонения. Эта методика позволила проводить измерение малых углов поворота (~10-3) с высоким временным разрешением (зарегистрированы частоты крутильных колебаний до 200 кГц).

В разделе 7.2 приводятся результаты измерения кручения образцов TaS3 в зависимости от электрического поля и температуры [А35,А39].




Рис.9. Зависимости δj(I) и Rd(I), измеренные одновременно. а) и b) – данные для двух образцов, шкала δj - общая. а) – с использованием цифрового фотоаппарата, b) – с использованием прямого преобразования δj в напряжение. На вставке к а) показана зависимость δj(I) (в произвольных единицах) для образца, полученного из того же кристалла TaS3, но с перевёрнутой осью c. На рисунках b) исходная точка – переохлаждённое состояние – помечены тёмными кружками. Результат свидетельствует об отсутствии вклада термических метастабильных состояний в кручение.
На Рис. 9 показаны одновременно измеренные токовые зависимости угла кручения, , и дифференциального сопротивления, RddV/dI, образца TaS3. На зависимостях Rd(I) виден резкий спад сопротивления при превышении током, I, порогового значения. Одновременно происходит и резкий поворот свободного конца образца: зависимости (I) также носят пороговый характер. При нулевом токе состояние образца может характеризоваться различными углами кручения в некотором диапазоне. Из этого следует, что основная часть деформации кручения связана с деформацией ВЗП, а не с её движением.

В полях выше порогового заметна тенденция к насыщению зависимостей δj(I). Направление кручения определяется направлением тока. Примерно половина образцов закручивалась в одном направлении, а половина – в другом, при одном и том же направлении тока. Неэквивалентность двух направлений вдоль образца указывает на наличие полярной оси внутри образца – вдоль кристаллографического направления c. Структурные данные, однако, относят TaS3 к точечной группе симметрии 222 [3], при которой полярная ось отсутствует. Тем не менее, показано, что направление кручения определяется внутренними свойствами образца и не связано с особенностями приготовления образца и асимметрией контактов. Вероятно, оно определяется направлением роста кристалла (см. вставку к Рис. 9a).

Величина угла кручения растёт приблизительно линейно при удалении от неподвижного контакта. Амплитуда δj, нормированная на длину, уменьшается с увеличением ширины w: δj  w -, где 2-3. Этот результат согласуется с предположением, что вращательной усилие формируется в слое вблизи поверхности: само по себе вращение есть сдвиговая деформация, достигающая максимальной величины на поверхности.

Термическое воздействие не оказывает влияние на угол кручение (Рис. 9b), что показывает, что кручение не связано с однородной деформацией ВЗП. Однако, и «поляризация ВЗП», рассмотренная в главе 6, также не может быть причиной кручения: деформация кручения примерно однородна по длине образца, в то время как знаки деформации ВЗП при её «поляризации» противоположны около разных контактов.

Далее отмечается, что наиболее вероятной причиной кручения можно считать поверхностный пиннинг [5,15,25]. Величина сдвига на поверхности может превышать 10-4. Такой деформации можно условно приписать пьезомодуль (недиагональные компоненты тензора пьезомодуля) >10-6 м/В, что на 4–6 порядков превышает значения, известные для пьезо-электриков.

Рис. 10. Температурные зависимости t для двух образцов TaS3, полученные из осциллограмм переходных процессов, δj(t). Наклон сплошной линии соответствует энергии активации 880 К. Пример δj(t) показан на вставке.
Затем приводится температурная зависимость кручения. Наблюдается спад величины угла с ростом температуры от 80 К до 200 К. Выше 200 К угол кручения не превышает 0.1. Приводятся также частотные зависимости амплитуды кручения, которые свидетельствуют о наличии двух вкладов: медленного (гистерезисного, порогового) и быстрого (практически линейного по току). Температурная зависимость времени релаксации медленного вклада, (T), описывается активационным законом (Рис. 10). Энергия активации, характеризующая зависимость, 900 К, близка к полуширине пайерлсовской щели в TaS3, что с очевидностью свидетельствует о связи кручения с ВЗП [26,27].

Частотной зависимости быстрого вклада не наблюдалось до максимальных частот приложенного электрического поля (~1 кГц), на которых можно было проводить корректные измерения. Наблюдение резонансных пиков кручения до 200 кГц указывает на то, что кручение может возбуждаться на существенно более высоких частотах. В отличие от медленного, быстрый вклад слабо зависел от температуры ниже TP, однако резкий спад его в области TP свидетельствует о том, что он также связан с пайерлсовским состоянием TaS3 [А39].

Рис. 11. Амплитуда кручения TaS3 в зависимости от амплитуды прямоугольного знакопеременного напряжения при различных f, указанных на рисунке. Т=80 К.
Общая картина зависимости кручения от амплитуды и частоты видна из Рис. 11, где показан набор зависимостей амплитуды кручения от напряжения на разных частотах. Видна общая тенденция: для низких частот линейный рост δj(V) переходит к резкому возрастанию в области Vt. С ростом частоты пороговый вклад становится не таким значительным, его появление сдвигается в сторону более высоких напряжений. Начиная с f=9 кГц и выше, на зависимостях остаётся только линейный вклад, который не зависит заметным образом от f (видимый спад амплитуд кручения для f > 12 кГц связан с частотной характеристикой крутильного осциллятора).

В заключении раздела отмечается, что результаты исследования кручения, полученные для соединений квазиодномерных проводников (TaSe4)2I и K0.3MoO3, качественно схожи с результатами для TaS3. В частности, наблюдаются два вклада в кручение: быстрый и медленный.

В разделе 7.3 обосновывается и описывается постановка эксперимента, в котором неоднородная деформация вискеров исследуется с помощью просвечивающего электронного микроскопа (ПЭМ) [А39]. Отмечается, что электрическое поле может создавать различные виды неоднородной деформации. Высокое пространственное разрешение ПЭМ можно использовать для наблюдения малых перемещений, соответствующих изгибной, неоднородной продольной деформации, неоднородному кручению образцов.

Описывается монтаж образцов TaS3 в микрокриостате (T=155 K), помещённом в ПЭМ. Для защиты образца от высокоэнергетических электронов, над ним был закреплён более широкий вискер Ba2Sr2CuCa2Ox, играющий роль экрана. Два индиевых прижимных контакта фиксировали концы образца, оставляя его середину свободной, приподнятой над подложкой. Чтобы наблюдать деформацию, к образцу были приклеены поперечные перекладины – тоже вискеры Ba2Sr2CuCa2Ox, концы которых выступали из-под экрана. На этих вискерах выбирались реперные точки, по перемещению которых можно было изучать деформацию образца. К образцу прикладывалось переменное напряжение. Изображение выводилось на фотоплёнку; при этом направление и амплитуда колебаний вискеров определялась по размытию изображений реперных точек.




Рис. 12. Микрофотографии движущихся фрагментов поперечных вискеров (перекладин), полученные в ТЭМ. (a) ∆y = 20 нм, VAC = 70 мВ, f = 3 Гц; (b) ∆y = 0.8 мкм, VAC = 10 мВ, f = 12 кГц; (c) ∆x = 1 мкм, VAC = 10 мВ, f = 45 кГц
В разделе 7.4 приводятся результаты исследований в ПЭМ. Наблюдалось как продольное, ∆x, (вдоль оси c образца TaS3), так и поперечное, ∆y, смещение перекладин. На Рис. 12 показаны фотографии фрагментов перекладин. По размытию фотографий на Рис.12a,b делается вывод о поперечном смещении в квазистатическом и резонансном режимах, соответственно, что свидетельствует об изгибной деформации TaS3. Смещение ∆x наблюдалось только в резонансных модах и связано с изгибным резонансом самой перекладины. Дополнительный эксперимент показал, что наблюдаемое смещение ∆x также связано с изгибными колебаниями TaS3.

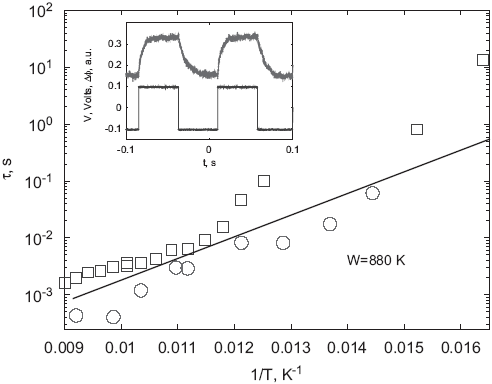
Изгиб связывается с неоднородной в сечении продольной деформацией образца. Относительная величина продольной деформации (разность деформации на краях образца) оценивается как ~10-7. Продольного смещение середины образца (глава 6) не наблюдалось, что связывается с недостаточной чувствительностью методики, а также недостаточно низкой температурой образца (155 К).

В разделе 7.5 делается вывод о связи наблюдаемого кручения и изгиба с деформацией ВЗП, рассматриваются виды деформации ВЗП, обуславливающие деформацию образцов. Отмечается, что центральным результатом данной главы является деформация кручения в электрическом поле, причём её величина согласуется с оценками (6,6’), полученными для неоднородной продольной деформации (глава 6). Связь кручения с деформацией ВЗП очевидна из гистерезисной пороговой зависимости угла кручения от напряжения, δj(V) (Рис. 9) и из температурной зависимости времени его релаксации (Рис. 10).

Наиболее вероятная причина кручения – деформация ВЗП, связанная с поверхностным пиннингом. Сдвиг ВЗП можно оценить по аналогии с расчётом, проведённом в главе 6. Предполагается, что сдвиг ВЗП передаётся решётке кристалла. В формуле (6) при этом следует заменить модуль Юнга на модуль сдвига образца, а длину – на ширину.

Сложнее объяснить пространственное распределение сдвига, соответствующее кручению. Такое распределение может возникнуть, если на каких-то двух противолежащих рёбрах кристалла пиннинг сильнее, чем на двух других. С другой стороны, кручение может отражать лишь часть (неоднородную по сечению) сдвиговой деформации. В любом случае ясно, что большая деформация связана с поперечной когерентностью ВЗП, длина которой многократно превосходит длину, на которой действует поверхностный пиннинг (~(L2π)).

В конце главы делается обобщающий вывод о многообразии возможных видов деформации квазиодномерных образцов в электрическом поле. Эти виды деформации ждут дальнейших исследований, как для TaS3, так и для других соединений.

В ЗАКЛЮЧЕНИИ (Глава 8) содержатся краткие выводы.

Кратко анализируется модель пайерлсовского перехода как следствия спонтанного ПФ и вытекающая из неё природа состояния выше TP, вопрос о корректном определении самой TP. Обсуждаются нерешённые вопросы.

Кратко рассматриваются неясные вопросы, связанные с деформацией образцов в электрическом поле, в частности – о природе полярной оси. Обсуждаются перспективы исследований. В частности, предлагается провести одновременные дифракционные исследования ВЗП и кристаллической решётки.

Отмечается прикладное значение эффекта кручения квазиодномерных проводников в электрическом поле, в частности, при комнатной температуре [А39]: вискеры квазиодномерных проводников являются готовыми крутильными актюаторами, элементами микро- и наноэлектромеханических систем, существенно превосходящими существующие приводы аналогичных размеров по отношению угол поворота/напряжение.

В конце данного раздела выражаются благодарности.


Основные результаты диссертации опубликованы в следующих статьях:

А1. Иткис М.Е., Надь Ф.Я., Покровский. В.Я. ЭДС, возникающая в квазиодномерном проводнике TaS3 под действием лазерного излучения.// ЖЭТФ – 1986. – Т.90. – С. 307-316.

А2. Зайцев-Зотов С.В., Покровский В.Я. Релаксация метастабильных состояний и зарождение металлической фазы в результате образования центров проскальзывания фазы в TaS3.// Сб. трудов XXV Всесоюзной конференции по физике низких температур, Ленинград 1988. – Ч.3. – С. 112-113.

А3. Зайцев-Зотов С.В., Покровский В.Я.. Самолегирование в квазиодномерных пайерлсовских полупроводниках.// Сб. трудов XI Всесоюзной конференции по физике полупроводников, Кишинёв 1988. – Т.1.– С. 60-61.

А4. Pokrovskii V.Ya., Zaitsev-Zotov S.V. Inhomogeneous Spatial Structure of the CDW Metastable States: Step-Like and Continuous Temperature Evolution.// Synthetic Metals – 1989. –V. F439-444. – P. 39.

А5. Зайцев-Зотов С.В., Покровский В.Я. Уединенные двухуровневые флуктуаторы в сверхмалых образцах квазиодномерного проводника TaS3.// Письма в ЖЭТФ – 1989. –Т.49. – С.449-452.

А6. Pokrovskii V.Ya., Zaitsev-Zotov S.V. Critical-State Model for Pinned Charge-Density Waves: Conditions and Consequences of Phase Slip.// Synthetic Metals –1989. –V. 32. – P. 321-328

А7. Pokrovskii V.Ya., Zaitsev-Zotov S.V. Spontaneous Resistance Fluctuations and Transition of the Charge- Density Waves into Disordered State in o-TaS3 Nanosamples.// Europhys. Lett.– 1990. – V.13. – P. 361-366.

А8. Pokrovskii V.Ya., Zaitsev-Zotov S.V. Phase-Slip, Critical Fluctuations and Order-Disorder Transition of the CDW in o-TaS3. // Synthetic Metals. – 1991. – V.41-43. – P. 3899-3904.

А9. Zaitsev-Zotov S.V., Pokrovskii V.Ya., Gill J.C. Mesoscopic Behavior of the Threshold Voltage in Ultra-Small Specimens of o-TaS3.// Journ. Phys. I (France). – 1992. – V. 2 – P. 111-120.

А10. Pokrovskii V. Ya., Zaitsev-Zotov S. V., Monceau P., and Nad' F. Ya. The anomalous growth of resistance fluctuations in o-TaS3 below the liquid-nitrogen temperature.// J.Phys.: Cond. Matter. – 1993. – V. 5. – P. 9317-9326.

А11. Pokrovskii V. Ya., Zaitsev-Zotov S. V., Monceau P., and Nad' F. Ya. Spontaneous Resistance Fluctuations and Their Evolution Near the Threshold in o-TaS3 Below the Liquid-Nitrogen Temperature.// J. Phys IV (France) – 1993. V. 3. – P. 189-192.

А12. Pokrovskii V. Ya., Zaitsev-Zotov S. V. Comment on 'Metastable Length States of a Random System: TaS3'. // Phys. Rev. B. – 1994. – V. 50. – P. 15442-15444.

А13. Артеменко С. Н., Покровский В. Я., Зайцев-Зотов С. В. Электронно-дырочный баланс и полупроводниковые свойства квазиодномерных проводников с волной зарядовой плотности.// ЖЭТФ. – 1996. – Т. 110, №. 3. – С. 1069-1080.

А14. Pokrovskii V. Ya., Zaitsev-Zotov S. V., Monceau P. Threshold nonlinear conduction of thin samples of o-TaS3 above the Peierls transition temperature.// Phys. Rev. B. – 1997. – V. 55 – P. R13377-13380.

А15. Heinz G., Pokrovskii V. Ya, Goldbach M., Kittel A., Parisi J. Imaging the Spatial Structure of Metastable States in a Charge Density Wave System with the Scanning Electron Microscope.// Phys. Lett. A. –1997. – V. 236. – P. 583-588.

А16. Heinz G., Pokrovskii V. Ya, Goldbach M., Kittel A., Parisi J. Deformation of Charge Density Waves in Quasi-One-Dimensional Semiconductors Visualized by Scanning Electron Microscopy.// In: “A Perspective Look at Nonlinear Media in Natural and Social Science”, eds. J. Parisi, S. C. Mueller, and W. Zimmermann (Springer, Berlin). – 1997. – P. 339-347.

А17. Pokrovskii V. Ya., Zaitsev-Zotov S. V. Contributions of the spontaneous phase slippage to the linear and non-linear conduction near the Peierls transition in the thin samples of o-TaS3. // Phys. Rev. B. – 2000. – V. 61. – P. 13261-13265.

А18. Зайцев-Зотов С. В., Покровский В.Я., Монсо П. Переход к одномерной проводимости при уменьшении толщины кристаллов квазиодномерных проводников TaS3 и NbSe3. // Письма в ЖЭТФ. – 2001. Т. 73. – С. 29-32.

А19. Синченко А. А., Покровский В. Я., Зыбцев С. Г. Управление электронным спектром квазиодномерного проводника К0.3MoO3 с помощью микроконтакта. // Письма ЖЭТФ. – 2001. – Т. 74, № 3. – С. 191-194.

А20. Heinz G., Parisi J., Pokrovskii V. Ya., Kittel A. Visualizing the spatial structure of charge density waves via scanning electron microscopy. //Physica B: Condensed Matter. – 2002. – V. 315, № 4. – P. 273-280.

А21. Golovnya A. V., Pokrovskii V. Ya., Shadrin P. M. Coupling of the lattice and superlattice deformations and hysteresis in thermal expansion for the quasi-one-dimensional conductor TaS3.// Phys. Rev. Lett. – 2002. – V. 88. – P. 246401(1-4).

А22. Sinchenko A. A., Zybtsev S. G., Gorlova I. G., Latyshev Yu. I., Pokrovskii V.Ya., Monceau P. On The Critical Current For The Charge-Density Wave Transport.// J.Phys. IV France. – 2002. – V. 12. – P. Pr9-127-128.

А23. Sinchenko A A, Latyshev Yu I, Pokrovskii V Ya, Zybtsev S G., Monceau P. Micro-contact spectroscopy features of quasi-one-dimensional materials with a charge-density wave. // J. Phys. A: Math. Gen. – 2003. – V. 36 – P. 9311–9322.

А24. Golovnya A. V., Pokrovskii V. Ya. Interferometric setup for measurements of expansion of whisker-like samples. // Rev. Sci. Instrum. – 2003. – V. 74, №3. – P. 4418-4422.

А25. Pokrovskii V. Ya., Golovnya A. V., Zaitsev-Zotov S. V. Peierls transition as spatially inhomogeneous gap suppression. // Phys. Rev. B. – 2004. – V. 70, № 11. – P. 113106 (1-4).

А26. Головня А. В., Покровский В. Я. Методика исследования удлинения нитевидных квазиодномерных проводников и перспективы использования их в микроэлектромеханике. // Сб. трудов Молодёжной школы «Микросиситемная техника МСТ-2004». Санкт-Петербург – Таганрог. – 2004. – С. 37-42.

А27. Pokrovskii V. Ya., Gorlova I. G., Zybtsev S. G., Zaitsev-Zotov S. V. Variable-range-hopping-like transverse conductivity of the quasi one-dimensional conductor TaS3. // J. Phys. IV France. – 2005. – V. 131. – P. 185-187.

А28. Pokrovskii V. Ya. Distributed latent heat of the phase transitions in low-dimensional conductors. // J. Phys. IV France. – 2005. – V. 131. – P. 315-318.

А29. Синченко А. А., Покровский В. Я. Деформация волны зарядовой плотности вблизи микроконтакта с нормальным металлом. // ЖЭТФ. – 2005. – Т. 128. – С. 1288-1298.

А30. Sinchenko A. A., Pokrovskii V. Ya. Effect of commensurability on the CDW deformation near a point contact. // J.Phys.IV. – 2005. – V.131 – P. 227-229.

А31. Pokrovskii V. Ya., Meshkov G. B., Gorlova I. G., Zybtsev S. G., Odobesko A. B., Yaminsky I. V. Atomic-Force Microscope as an Instrument for Measurements of Thermal Expansion of Whisker-Like Samples. // In Proceedings of the Workshop „Recent developments in low dimensional charge density wave conductors“, Skradin, Croatia June 29.-July 3. – 2006. – P. 28-29.

А32. Pokrovskii V. Ya., Gorlova I. G., Zybtsev S. G., Zaitsev-Zotov S. V. Universal Variable-Range Hopping Along and Perpendicular to the Chains in the Quasi One-Dimensional Conductor o-TaS3. // In Proceedings of the Workshop „Recent developments in low dimensional charge density wave conductors“, Skradin, Croatia June 29.-July 3. – 2006. – P. 44-45.

А33. Sinchenko A. A., Pokrovskii V. Ya. Effects of strong deformation of a CDW in the vicinity of a point contact with a normal metal. // In Proceedings of the Workshop „Recent developments in low dimensional charge density wave conductors“, Skradin, Croatia June 29.-July 3. – 2006. – P. 16-17.

А34. Покровский В. Я., Зыбцев С. Г., Кузнецов А. П. Деформация квазиодномерных проводников в электрическом поле и методики её исследования. // Труды Научн. сессии МИФИ. М. – 2007. – Т. 4. – С. 37-38.

А35. Pokrovskii V. Ya., Zybtsev S. G., Gorlova I. G. Torsional Strain of TaS3 Whiskers on the Charge-Density Wave Depinning. // Phys. Rev. Lett. – 2007. – V. 98. – P. 206404.

А36 Покровский В. Я. Об огромном воздействии электрического поля на кристаллическую решетку квазиодномерных проводников с волной зарядовой плотности.// Письма ЖЭТФ. – 2007. – Т. 86, № 4 – С. 290-293.

А37 Pokrovskii V. Ya., Zybtsev S. G. Self-sensitive torsional microresonators based on a charge-density wave system. // arXiv:0708.2694v1 [cond-mat.str-el]., 1-10 – Режим доступа: /abs/0708.2694.

А38. Pokrovskii V. Ya., Zybtsev S. G., Gorlova I. G. Enormous torsional strain of one dimensional conductors under electric field: an alternate for the piezoelectric actuators? // Сб. трудов Международной конференции “Functional Materials” ICFM – 2007. Украина, Крым, Партенит. – 2007. – С. 221-222.

А39. Pokrovskii V. Ya., Zybtsev S. G, Loginov V. B., Timofeev V. N., Kolesov D. V., Yaminsky I. V., Gorlova I. G. Deformations of charge-density wave crystals under electric field. // Physica B. –2009. – V. 404. – P. 437–443.

А40. Zybtsev S. G., Pokrovskii V. Ya., Nasretdinova V. F., Zaitsev-Zotov S. V. Gigahertz-range synchronization at room temperature and other features of charge-density wave transport in the quasi-one-dimensional conductor NbS3. // Appl. Phys. Lett. – 2009. – V. 94. – P. 152112 (1-3).


Цитируемая литература

1. D. Staresinic, A. Kis, K. Biljakovic, B. Emerling, J.W. Brill, J. Souletie, H. Berger, and F. Levy, Eur. Phys. J. B 29, 71-77 (2002).

2. S. N. Artemenko, J. Phys. IV 12, Pr9-77 (2002).

3. P. Monceau в «Electronic Properties of Quasi-One-Dimensional Materials», (Reidel, Dordrecht, 1985), Part II, p.139; G. Grüner, Rev. Mod. Phys. 60, 1129 (1988); современное состояние исследований достаточно полно представлено в Трудах Международного симпозиума по электронным кристаллам ECRYS 2008: Physica B Cond. Mat. 404, Issues 3-4, March 2009.

4. J. C. Gill, J. Phys. C 19, 6589 (1986).

5. Д. В. Бородин, С.В. Зайцев-Зотов, Ф.Я. Надь, ЖЭТФ 93, 1394 (1987).

6. S. V. Zaitsev-Zotov, Synth. Met. 41-43, 3923 (1991).

7. С.В. Зайцев-Зотов, «Размерные эффекты и релаксационные явления в квазиодномерных проводниках с волной зарядовой плотности», докторская диссертация, Москва, 1999. С.В. Зайцев-Зотов, УФН 174, 585 (2004).

8. F.N. Hooge, Phys. Lett. A 20, 139 (1969).

9. G. Mozurkewich and R.L. Jacobsen, Synth. Met. 60, 137 (1993).

10. L. C. Bourne and A. Zettl, Solid State Commun. 60, 789 (1986).

11. J. W. Brill, M. Chung, Y. -K. Kuo, X. Zhan, and E. Figueroa, Phys. Rev. Lett. 74, 1182 (1995).

12. J. W. Brill, in Handbook of Elastic Properties of Solids, Liquids, and Gases, edited by M. Levy, H. E. Bass, and R. R. Stern (Academic Press, New York, 2001), Vol. II, pp. 143–162.

13. D. Starešinic, A. Kiš, K. Bilacovic, B. Emerling, J. W. Brill, J. Souletie, H. Berger, and F. Lévy, Eur. Phys. J. B 29, 71 (2002).

14. J. C. Gill, Synth. Met. 43, 3917 (1991).

15. McCarten, D. A. DiCarlo, M. Maher, T. L. Adelman, and R. E. Thorne, Phys. Rev. B 46, 4456 (1992).

16. G. Mozurkewich, Phys. Rev. B 42, 11183 (1990).

17. J.W. Brill and W. Roark, Phys. Rev. Lett 53, 846 (1988); Phys. Rev. B 36, 2969 (1987).

18. R.L. Jacobsen and G. Mozurkewich, Phys. Rev. B 42, 2778 (1990).

19. Z.G. Xu and J.W. Brill, Phys. Rev. B 45, 3953 (1992).

20. S. Hoen, B. Burk, A. Zettl, and M. Inui, Phys. Rev. B 46, 1874 (1991).

21. Ю.И. Латышев, Я.С. Савицкая и В.В. Фролов, Письма ЖЭТФ 38, 541 (1983).

22. В.Б. Преображенский, А.Н. Талдёнков, И.Ю. Кальнова, Письма ЖЭТФ 40, 182 (1984); V. B. Preobrazhensky, A. N. Taldenkov, and S. Yu. Shabanov, Solid State Commun. 54, 1399 (1985).

23. A. Meerschaut, J. Physique 44, C3-1615 (1983).

24. А.К. Таганцев, УФН 152, 423 (1987).

25. J. C. Gill, Europhys. Lett. 11, 175 (1990).

26. D. Starešinić, K. Biljaković, W. Brütting, K. Hosseini and P. Monceau, Phys. Rev. B 65, 165109 (2002).

27. L. Ladino, J. W. Brill, M. Freamat, M. Uddin, and D. Dominko, Phys. Rev. B 74, 115104 (2006).

Copyright © 2023. All rights Reserved.