Курс лекций по дисциплине «теория фирмы» тема основные подходы к природе фирмы

Вид материала

Курс лекций

Содержание Тема 5. эластичность спроса и предложения Эластичность предложения и фактор времени Тема 6. производство 2. Закон убывающей предельной производительности Общий или совокупный продукт (TP) Средний продукт (AP) Предельный продукт (МР) Тема 7. выбор производственной технологии 2. Виды изоквант 3. Изокоста и равновесие производителя 4. Эффект от масштаба производства и «путь развития»

Подобный материал:

• Фирмы изучаемые вопросы, 281.62kb.
• Правительстве Российской Федерации по адресу: 125468, г. Москва, Ленинградский проспект,, 715.82kb.
• Трансформация фирмы в процессе развития институтов современной экономики: теория, методология,, 561.4kb.
• Рабочая программа по дисциплине «Финансы фирмы» Условное обозначение рабочей программы, 191.86kb.
• Электронные таблицы. Назначение и основные функции, 40.06kb.
• М. В. Ломоносова Кафедра экономики и экономической географии стран Азии и Африки программа, 83.17kb.
• А. А. Исаев имидж фирмы опорный конспект, 122.2kb.
• Эволюция теория фирмы. Современная трактовка, 112.1kb.
• Курс лекций для студентов заочного факультета самара, 1339.16kb.
• А. А. Задоя микроэкономика курс лекций, 195.46kb.

ТЕМА 5. ЭЛАСТИЧНОСТЬ СПРОСА И ПРЕДЛОЖЕНИЯ

1. Понятие эластичности. Эластичность спроса по цене и по доходу
   

Под эластичностью понимается реакция экономического показателя на изменение какого-либо фактора или группы факторов. При изучении спроса очень важно знать, как сильно изменится спрос при изменении цены на данный товар. Об этом дает представление эластичность спроса по цене.

Эластичность спроса по цене – это реакция спроса на изменение цены, которая показывает, в какой мере изменяется спрос в ответ на подорожание или удешевление товара. Измеряется эластичность спроса по цене с помощью коэффициента эластичности, который рассчитывается по формуле

,

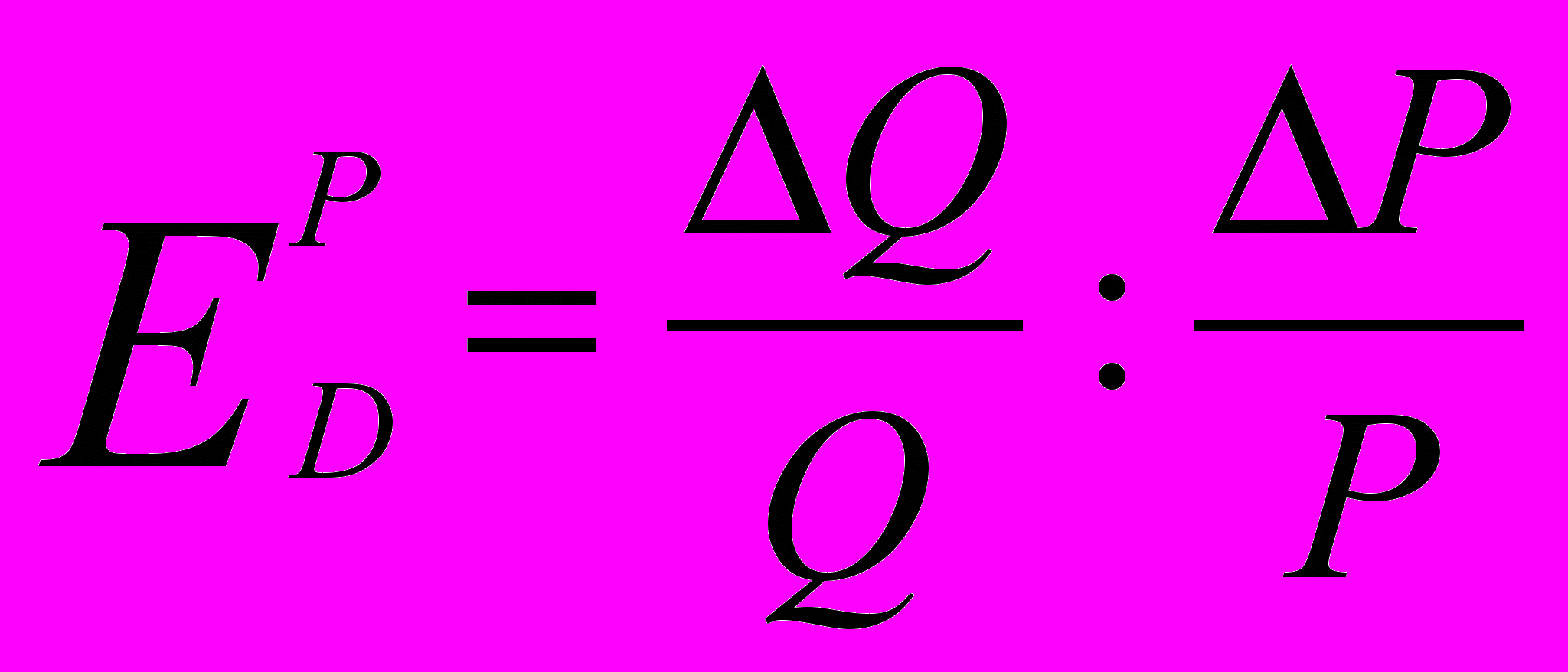где Q – величина спроса; ∆Q/Q – процентное изменение величины спроса; Р – цена; ∆Р/Р – процентное изменение цены.

Эластичность спроса по цене показывает, насколько процентов изменится спрос в случае изменения цены на 1%.

Различают точечную и дуговую эластичность.

Точечная характеризует относительное изменение объема спроса при бесконечно малом изменении цены (как правило, менее 5%) и определяется по формуле:

.


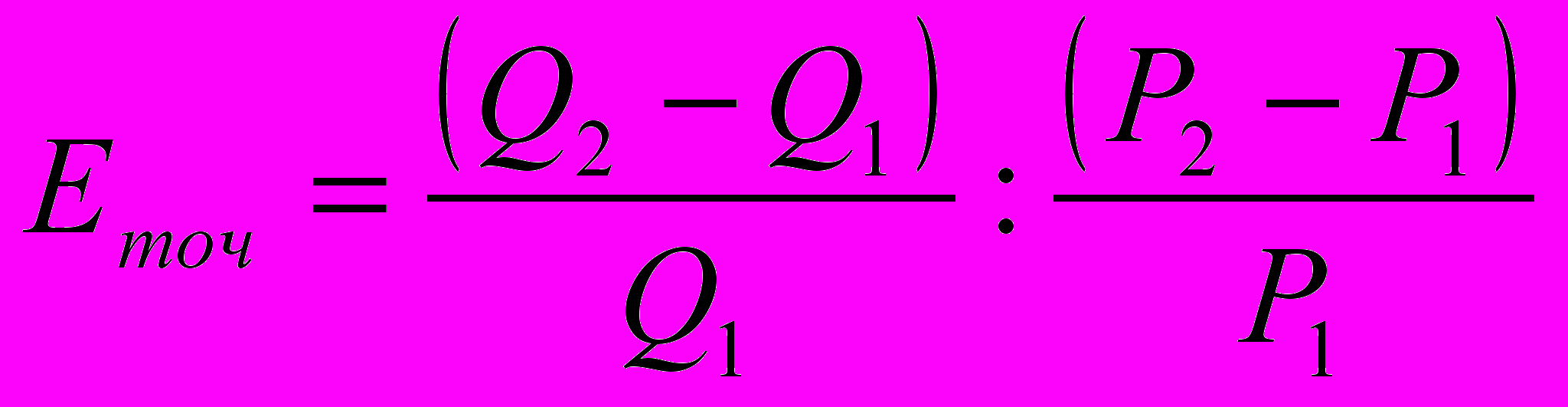Дуговая эластичность есть показатель средней реакции спроса на значительное изменение цены товара (превышающее 5%):

.


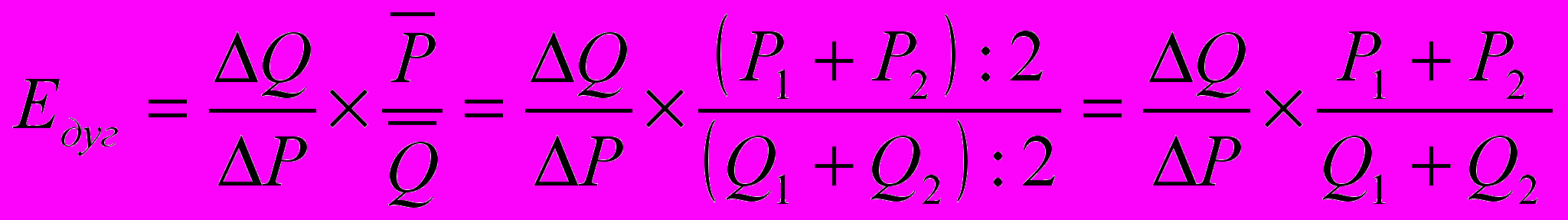Эластичность спроса по цене исследуют производители и продавцы товара для того, чтобы посмотреть, как изменится их общая выручка от продажи товара при изме­нении цены на него, и как это скажется на прибыли.

Определение эластичности спроса позволяет рассчитать, когда и в каких пределах можно манипулировать це­нами.

Рассмотрим, как меняется общая выручка при изме­нении цены товара при трех различных значениях коэффициента эластичности спроса по цене.

Первый случай – единичная эластичность спроса по цене. Спрос на такие товары изменяется точно так же, как цена, в результате общая выручка остается неизменной.







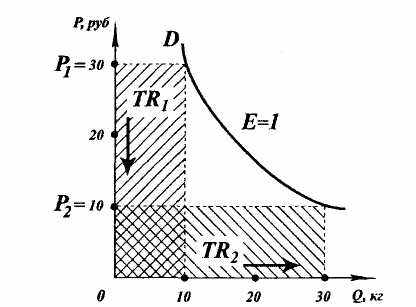
Рис. 1.5. Единичная эластичность спроса по цене


В случае единичной эластичности спроса по цене (Е = 1) общая выручка от продажи данного товара при повышении или снижении цены на него не изменяется.

Это значит, что продавец может свободно манипулировать ценой, в случае необходимости, например, под давлением конку­рентов или правительства решать проблему ускорения сбыта и т. д. При этом его общий доход, а значит и размер прибыли, не пострадают.

Второй случай - высокая эластичность спроса по цене. Для таких товаров характерен коэффициент эластичности по модулю больше единицы (Е > 1). Спрос на такие товары изменяется в большей мере, чем цена, поэтому в случае небольшого снижения цены объем продаж и общая выручка серьезно вырастут. И наоборот. При не­большом повышении цены общая выручка будет значительно со­кращаться.




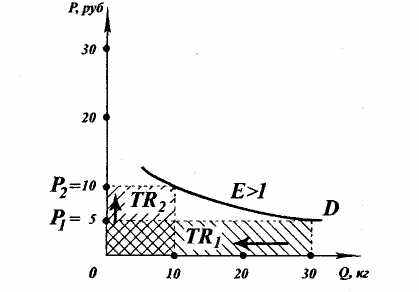
Рис. 2.5. Высокая эластичность спроса по цене


В случае понижения цены возможен обратный эффект: спрос, а, следовательно, и общая выручка увеличиваются в боль­шей мере, чем снижается цена. Это показывает, что при неболь­шом снижении цены на товары с высокой эластичностью спроса можно увеличить выручку от их продажи. Как правило, товары с высокой эластичностью по цене имеют множество суб­ститутов, а также не являются предметами первой необходимо­сти. Снижать на них цены выгодно. Повышение же цен, напро­тив, приведет к уменьшению общей выручки и, соответственно, к сокращению или потере прибыли.

Третий случай – низкая эластичность спроса по цене. Это товары, спрос на которые слабо реагирует на изменение цены. Прежде всего, это товары повсе­дневного спроса, занимающие ведущее место в потреблении. У таких товаров коэффици­ент эластичности меньше единицы (Е < 1). В этом случае при из­менении цены на товар общая выручка изменяется в меньшей степени, чем цена.



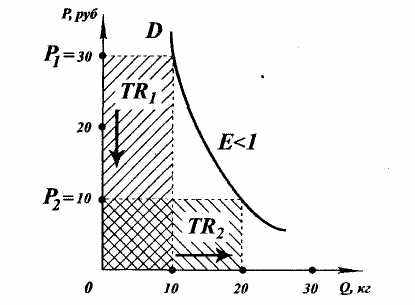
Рис. 3.5. Низкая эластичность спроса по цене


Например, спрос на эксклюзивные товары весьма устойчив и об­ладает низкой эластичностью по цене. На такие товары цену выгодно повышать, а снижать опасно, так как не следует ждать расширения спроса, адекватного изменению цены.

Еще одна характеристика спроса — эластичность спроса по до­ходу, которая показывает, как изменяется спрос в зависимости от изменения дохода покупателя. Как правило, спрос на товар уве­личивается, если вырос доход покупателя. Однако, если товар низкокачественный, то с ростом дохода потребителя спрос на этот товар уменьшается, а спрос на высококачественный товар растет.

Коэффициент эластичности спроса по доходу рассчитывает­ся по следующей формуле:

.

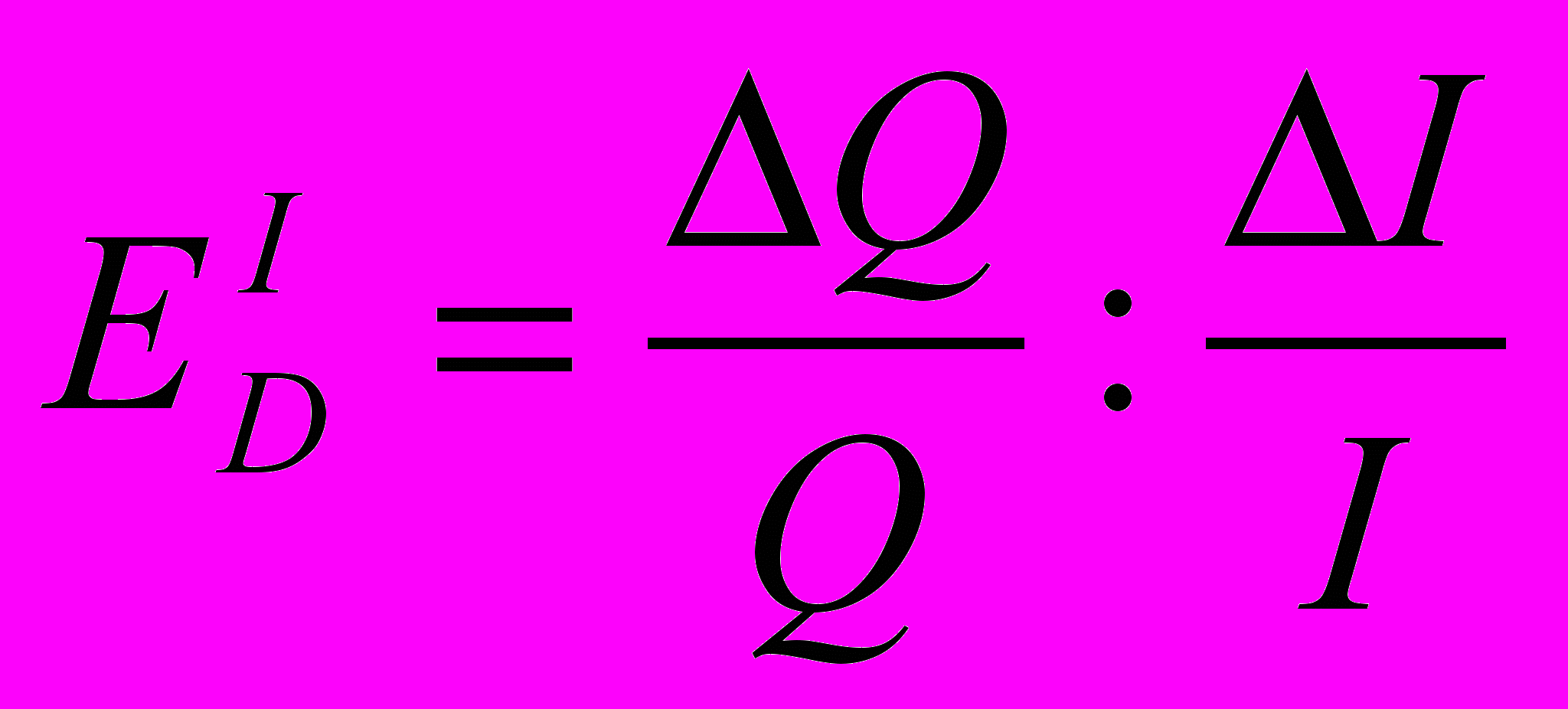Как видим, данное выражение аналогично формуле эластич­ности спроса по цене, куда вместо цены подставляется значение дохода — I (income).

2. Эластичность предложения и фактор времени
   

Производители, как и покупатели, тоже реагируют на изме­нение рыночной цены на свою продукцию. Но если при повы­шении цены покупатель, как правило, уменьшает величину спроса, то производитель, заметив, что товар раскупается по бо­лее высокой цене, чем ожидалось, станет расширять предложе­ние, и наоборот. В микроэкономике такая реакция предло­жения на изменение рыночной цены товара называется эластич­ностью предложения по цене.

Производитель при повышении цены на свою про­дукцию стремится расширить объем продаж потому, что издержки (затраты) производителя на еди­ницу выпуска при изменении цены товара остаются на прежнем уровне. Следовательно, при подорожании товара увеличивается разница между рыночной ценой товара (доходом производителя) и издержками производителя, т. е. увеличивается прибыль.

Поэтому, когда на рынке складывается более высокая цена, именно возможность увеличить прибыль стимулирует фирму к расширению предложения.

Однако реакция производителя на изменение рыночной це­ны (эластичность предложения) зависит от фактора времени. Чем большим периодом времени располагает производитель, тем боль­ше возможность маневрировать объемами производства и изме­нять величину предложения. Для рас­ширения предложения фирме необходимо либо распродать нако­пившиеся товарные запасы, либо выпустить дополнительную продукцию, на что требуется отрезок времени, равный по продол­жительности производственному циклу того или иного товара.

В связи с этим микроэкономика рассматривает три случая эластичности предложения фирмы — мгновенная, крат­косрочная и долгосрочная реакции на изменение рыночной цены товара.

В первом случае производитель не мо­жет мгновенно отреагировать на повышение рыночной цены и увеличить объем запланированной поставки товара на рынок. Поэтому сразу (мгновенно) объем продаж не расширится в ответ на благоприятное изменение рыночной конъюнктуры. Значит, при мгновенной реакции величина предложения остается на прежнем уровне.

В случае эластичности предложения в краткосрочном пе­риоде, производитель уже располагает не­большим отрезком времени для подстройки под новую ситуа­цию. При повышении цены на рынок могут быть выпущены то­варные запасы или расширен выпуск путем увеличения загрузки уже имеющихся мощностей (станков, оборудования). Тогда предложение сможет отреагировать небольшим расшире­нием в ответ на повышение цены.

Таким образом, в краткосрочном периоде фирмы располагают некоторым временем, чтобы увеличить выпуск, но в рамках своих производственных возможностей, т.е. обладают большей эла­стичностью по цене по сравнению с мгновенной ситуацией.

В долгосрочном периоде предложение обладает еще более высокой эластичностью по цене. Так, производители при росте спроса, а, следовательно, и цены на их продукцию, бу­дут наращивать свои производственные мощности, расширять рамки производственных возможностей своих фирм, значитель­но увеличив объем выпуска.

Более того, ценовой сигнал, распространяя информацию о повышении среднеотраслевой прибыли, привлекает в отрасль но­вых производителей, и объем выпуска увеличивается еще больше. Все это делает высокой эластичность общеотраслевого предложе­ния по цене на конкурентном рынке. Поэтому в долгосрочном периоде небольшому увеличению спроса соответствует значи­тельное расширение предложения.


ТЕМА 6. ПРОИЗВОДСТВО


1. Производственная функция. Понятие и виды

Под производством понимается деятельность по использованию факторов производства (ресурсов) с целью достижения наилучшего результата. Если объем использования ресурсов известен, то максимизируется результат и наоборот, если известен результат, которого необходимо достичь, то максимизируется объем ресурсов.

Под затратами понимается все, что фирма (производитель) закупает для дальнейшего использования в целях получения необходимого результата.

Выпуск подразумевает любое благо (продукция или услуга), изготовленное фирмой для продажи.

Деятельность фирмы может означать как производственную, так и коммерческую деятельность.

В рамках теории фирмы в целях упрощения представления деятельности принято считать, что фирма производит одно благо.

Поэтому экономическая деятельность фирмы описывается производственной функцией, включающей в себя переменные для выпуска одного вида товара или услуги:

Q = f (F₁, F₂, F₃, … F_n), где

Q – максимальный объем производства при заданных затратах;

F₁, F₂, F₃, … F_n – количество использованных факторов.

В затраты включаются все используемые факторы производства (труд, материалы, оборудование, уровень технико-организационных знаний, при рассмотрении с/х производства учитывается еще один фактор – земля).

При микроэкономическом анализе предполагается, что уровень организационно–технических знаний фиксирован, а все материальные факторы объединяют в один фактор – капитал. Поэтому производственная функция включает в себя два фактора, от которых зависит выпуск продукции: труд и капитал.

Q = f (L, K)

Следовательно, производственная функция характеризует техническую зависимость между количеством применяемых ресурсов и максимальным объемом выпуска продукции в единицу времени.

Производственная функция описывает множество технологически эффективных способов производства, каждый из которых характеризуется определенной комбинацией ресурсов, необходимых для получения единицы продукции при данном уровне технологии. Как технологическое соотношение производственная функция может быть определена только эмпирическим путем посредством изменения фактических показателей.

Производственная функция имеет ряд особенностей или свойств:

1) факторы производства являются взаимодополняющими;

2) отсутствие одного из факторов делает производство невозможным;

3) производственная функция, использующаяся на макроуровне, именуется функцией Кобба-Дугласа:

Q = f (k*K^*L^), где

Q - максимальный объём выпуска продукции;

K - затраты капитала;

L – затраты труда;

,  - эластичность выпуска по затратам соответствующих факторов (капитала и труда); k – коэффициент пропорциональности или масштабности в отрасли.

4) производственная функция непрерывна и не имеет ограничений по времени, а следовательно, свидетельствует о непрерывности производственного процесса.


Виды производственных функций:

Производственные функции бывают статические и динамические.

Статические производственные функции имеют следующий вид:

Y = f (x₁,x₂,…x_n)

Они не включают в себя показатель времени, т.е. не содержат время как фактор, изменяющий основные производственные характеристики изучаемой зависимости.

Среди статических производственных функций наиболее часто встречаются линейные функции (y = a₀ + a₁x₁ + a₂x₂) и функция Кобба-Дугласа.

Динамические производственные функции имеют следующий вид:

y = f (t , x_i (t) …х_n(t)), где:

x_i (t) – представляет собой динамику изменения определенного производственного фактора в зависимости от времени;

t – представляет собой временную независимую переменную, которая в неявном виде отражает воздействие всех неучтенных факторов на результативность показателя у.

Рассмотрим графическое представление производственной функции. Графиком двухфакторной функции Q = f (L,K) является изокванта, которая представляет собой линию постоянного уровня выпуска. Т.е. изокванта - есть кривая равного продукта или множество возможных комбинаций факторов труда и капитала, при котором достигается один и тот же выпуск продукции.



Рис. 1.6. Двухфакторная производственная функция


Чем дальше от начала координат расположена кривая, тем больше выпуск продукции.

Карта изоквант представляет собой набор изоквант, каждая из которых показывает максимальный объем выпуска продукции при использовании определенного сочетания факторов производства.



Рис. 2.6. Карта изоквант


К свойствам изоквант относят:

1) отрицательный наклон; 2) вогнутость к началу координат; 3) никогда не пересекаются; 4) показывают различные уровни производства. Чем дальше от начала координат расположена изокванта, тем больший объем выпуска продукции она показывает.


2. Закон убывающей предельной производительности

Для представления закона убывающей предельной производительности следует рассматривать производство с одним переменным фактором. Примем в качестве переменного фактора труд, а постоянного фактора – капитал:

Q = f (L, K_const)

Существует определенный предел роста объемов производства при увеличении одного фактора, в то время как остальные остаются постоянными. Это свойство производственной функции называется законом убывающей отдачи или производительности.

Чтобы отразить влияние переменного фактора (L) на производство и графически проиллюстрировать данный закон необходимо ввести следующие понятия:

Общий или совокупный продукт (TP) – это количество экономического блага, произведенное с использованием некоторого количества переменного ресурса и возрастающее по мере возрастания одного из факторов.

Средний продукт (AP) – это отношение общего продукта к количеству используемого в производстве переменного фактора, или количество дополнительной продукции, получаемой при использовании дополнительной единицы переменного продукта.

АР = ТР/х, где х – переменный фактор, в нашем случае это L.

Предельный продукт (МР) – это отношение изменения общего продукта к изменению переменного фактора или количество дополнительной продукции, полученной при использовании дополнительной единицы переменного ресурса.

МР = ТР/х

Совокупный продукт (TP) с ростом использования в производстве переменного фактора будет увеличиваться, однако данный рост будет иметь определенный размер в рамках заданной технологии.



Рис. 3.6. Динамика производительности по совокупному продукту


При неизменном состоянии техники на первой стадии производства (от 0 до А) увеличение затрат труда способствует все более полному использованию капитала, т.е. и предельная и общая производительность возрастает и это выражается в росте среднего и предельного продукта. При этом МРАР. Если на первой стадии (от 0 до А) совокупный продукт возрастает медленнее, чем использование переменного фактора, то на второй стадии (отрезок АВ) совокупный продукт растет быстрее, чем использованное количество переменного фактора.



Рис. 4.6. Динамика производительности по среднему и предельному продукту


В точке А предельный продукт достигает своего максимума. На второй стадии - отрезок АВ - величина предельного продукта уменьшается и в точке В становится равной среднему продукту. Здесь справедливо равенство МР = АР.

На третьей стадии (отрезок ВС) предельный продукт меньше среднего продукта (МРАР), в результате чего совокупный продукт растет медленнее, чем затраты переменного фактора и при наступлении четвертой стадии (после точки С) предельный продукт становится меньше нуля (МР0).

В результате прирост переменного фактора приводит к уменьшению выпуска совокупной продукции. Однако, чтобы данный закон действовал, необходимо чтобы все единицы переменного фактора были качественно однородны и добавление все новых и новых единиц не вело к качественному изменению технологий.

Таким образом, закон предельной производительности (отдачи) гласит, что с ростом использования какого-либо производственного фактора (при неизменности остальных) рано или поздно достигается такая точка, в которой дополнительное применение переменного фактора, ведет к относительному или даже абсолютному снижению объема выпуска продукции, т.е. увеличение одного из факторов приводит к последовательному снижению отдачи его применения.

Заметим, что данный закон никогда не был доказан теоретически, а выведен исключительно экспериментальным путем. Первоначально он базировался на сельскохозяйственной отрасли, затем был применен для других отраслей производства. Закон предельной производительности носит относительный характер, так как может быть применим лишь на краткосрочном отрезке времени, когда хотя бы один из факторов производства остается неизменным. Во-вторых, технический прогресс постоянно совершенствуется, поэтому раздвигает границы применения данного закона.


ТЕМА 7. ВЫБОР ПРОИЗВОДСТВЕННОЙ ТЕХНОЛОГИИ


1. Предельная норма технологического замещения. Изокванта

Рассмотрим производственную функцию, состоящую из двух переменных факторов: Q = ƒ (L,K) (от других ресурсов мы абстрагируемся, а объем производства является величиной постоянной). При заданной технологии один и тот же выпуск продукции может быть обеспечен с большим применением капитала (как в точке А) или с большим привлечением труда (как в точке D). Возможны и промежуточные варианты (точки B и С). Если мы соединим все сочетания ресурсов, использование которых обеспечивает одинаковый объем выпуска продукции, то получатся изокванты.

Р
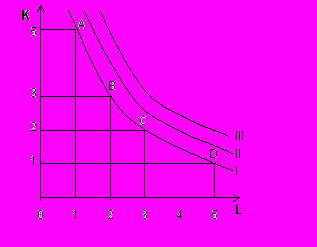
ис. 1.7. Производственная функция (изокванта)


Изокванта является непрерывной линией, т.е. число возможных комбинаций ресурсов будет бесконечным, что обеспечивает гибкость принимаемых фирмой решений по организации производства продукции.

Количественное соотношение изменения одного фактора (X) к изменению другого (Y) называется предельной нормой технологического замещения:

,

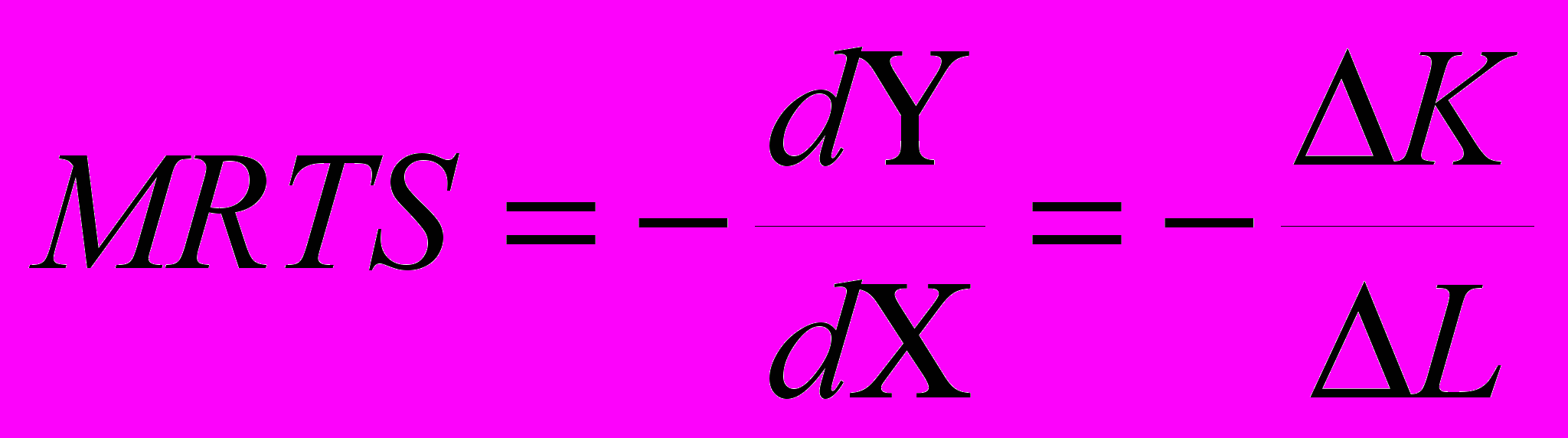т.е. увеличение затрат одного фактора (L) компенсируется уменьшением затрат другого (К). Рассмотрим, как изменяется MRTS при росте затрат с 1 до 5. С увеличением затрат труда уменьшаются затраты капитала. Это означает, что уменьшается предельная производительность труда и увеличивается предельная производительность капитала, т.е.







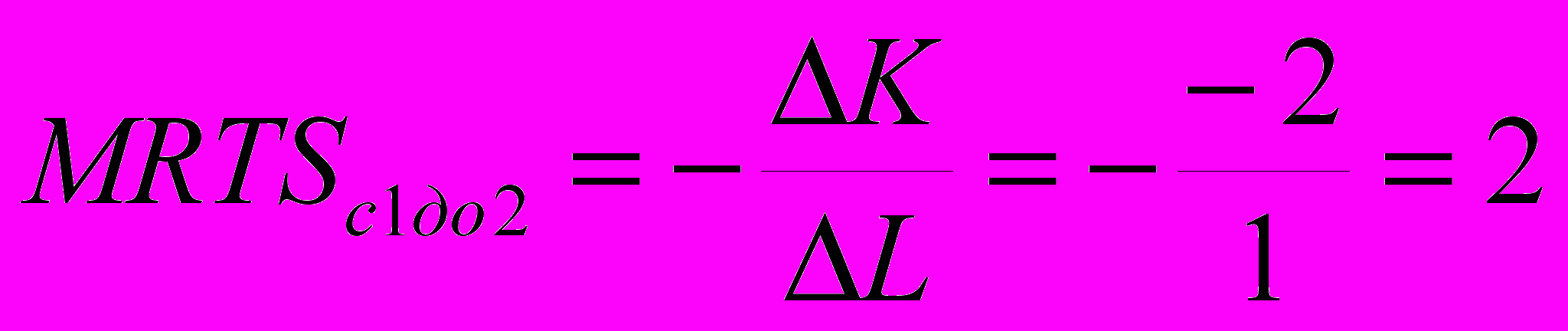
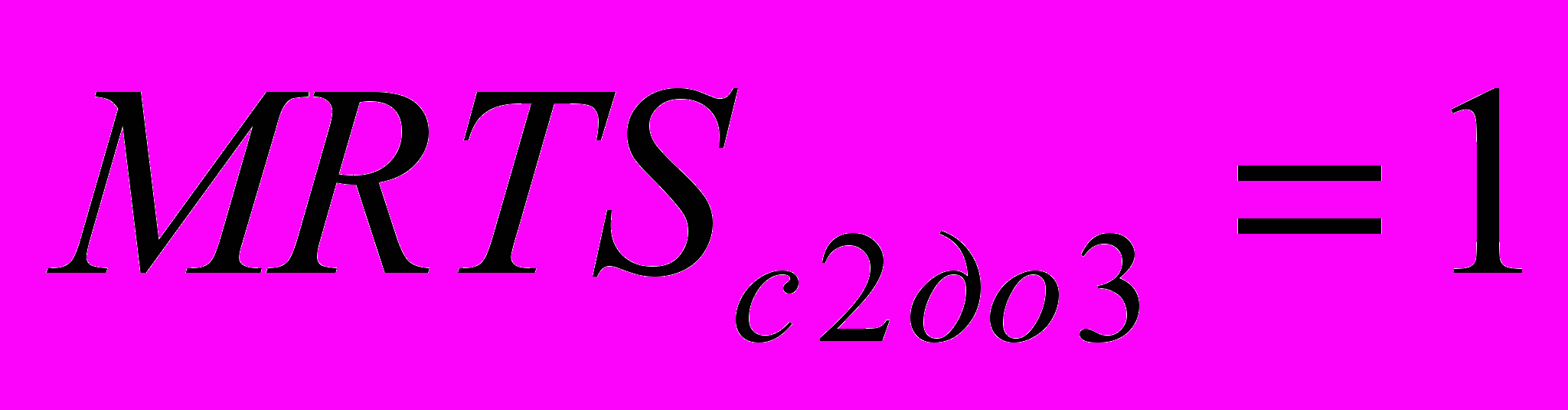
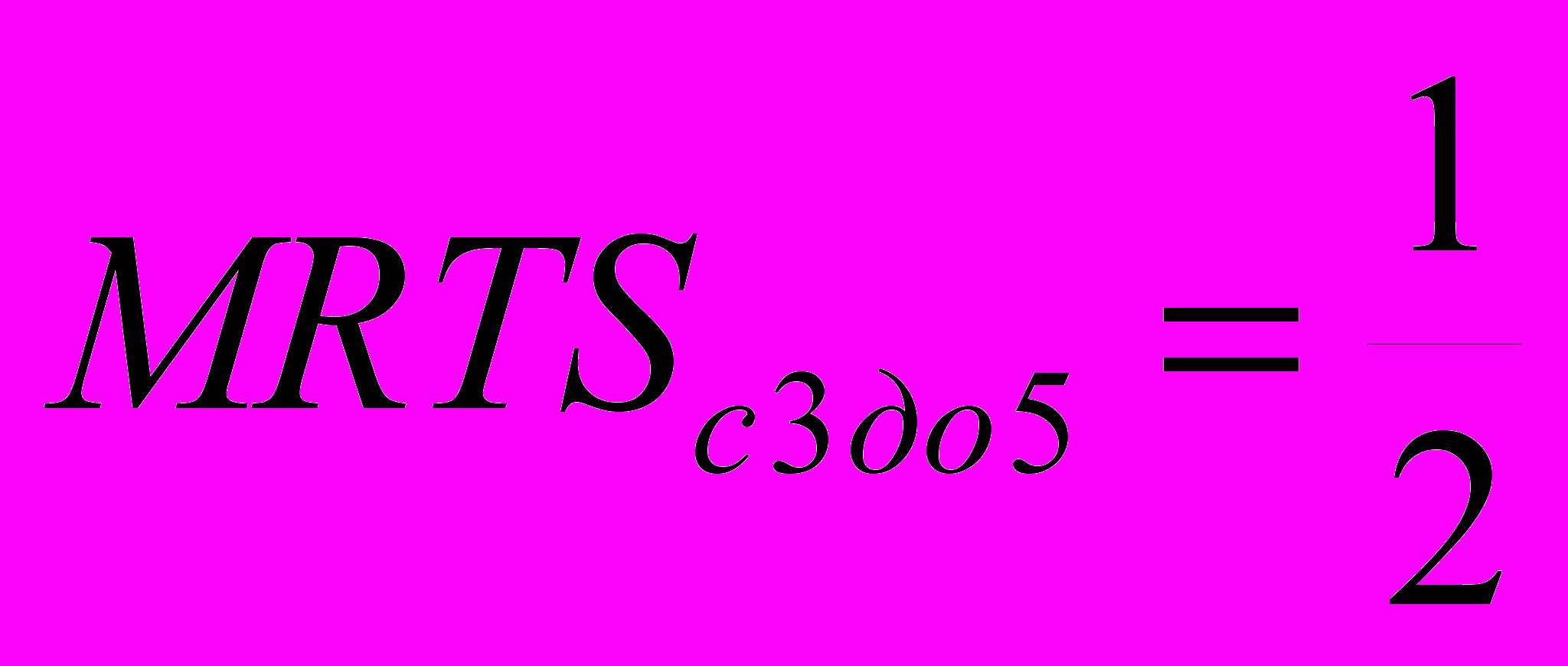
Минус свидетельствует о том, что с увеличением затрат одного фактора уменьшаются затраты другого.

Уменьшение предельной нормы технологического замещения свидетельствует о том, что эффективность использования любого ресурса ограничена. В нашем случае по мере замены капитала трудом отдача последнего снижается. Причем, прирост совокупного продукта при замещении одного фактора другим для изокванты равен нулю:

.


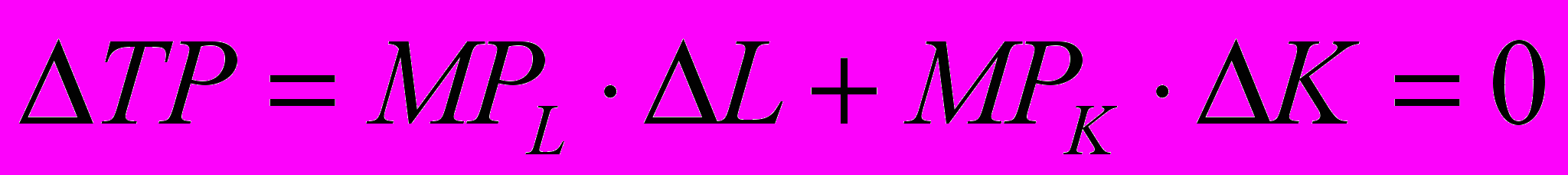2. Виды изоквант

Различают следующие виды изоквант:

1. Линейная. Два переменных фактора идеально взаимозаменяемы и MRTS постоянно во всех точках.
   

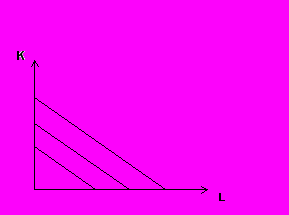
Рис. 2.7. Линейная изокванта

2. Изокванта Леонтьева. Два переменных фактора жестко дополняют друг друга и MRTS = 0. При этом капитал и труд применяются в единственно возможном соотношении. Замещение одного фактора другим невозможно.
   

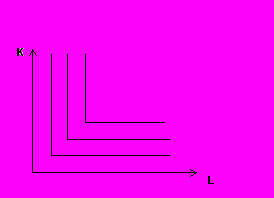
Рис. 3.7. Изокванта Леонтьева

3. Ломаная. MRTS сверху вниз убывает, причем на некоторых отрезках она может практически приближаться к нулю.
   

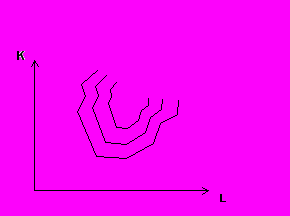
Рис. 4.7. Ломаная изокванта

4. Непрерывная изокванта.
   

Наиболее распространенный вид. MRTS убывает сверху вниз. Считается, что факторы производства несовершенно замещаемы.




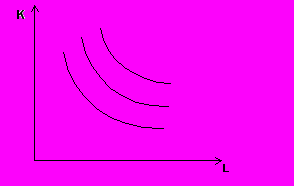
Рис. 5.7. Непрерывная изокванта


3. Изокоста и равновесие производителя

Анализ с помощью изоквант имеет для производителя очевидные недостатки, т.к. использует только натуральные показателя затрат ресурсов и выпуска продукции.

Максимизировать выпуск при данных издержках позволяет прямая равных издержек или изокоста. Если P_K - цена фактора производства К, P_L - цена L, то располагая определенным бюджетом С, производитель может купить Х единиц фактора L и Y единиц фактора К. Общие затраты производителя при этом составляют:

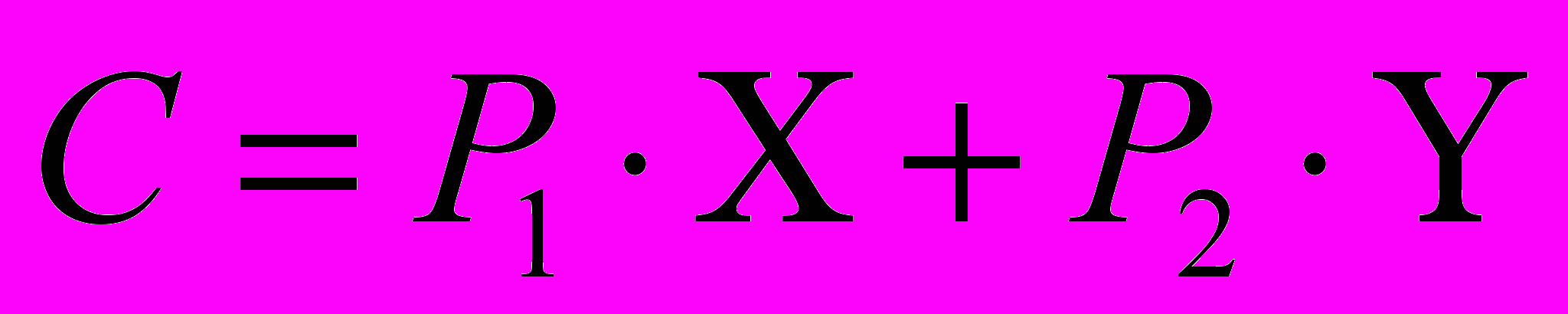, где

P_1,P₂ – цена на факторы производства.

Для труда и капитала: 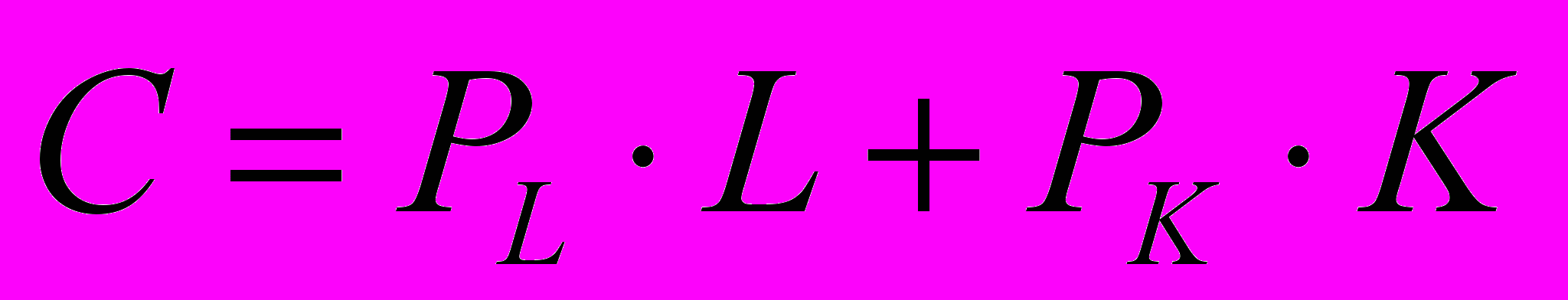, где

P_L – цена фактора труда

L – количество единиц труда.

Это уравнение прямой представляет комбинации ресурсов, использование которых ведет к одинаковым затратам, израсходованным на производство.

Линии равных затрат предприятия называется изокостой (С).




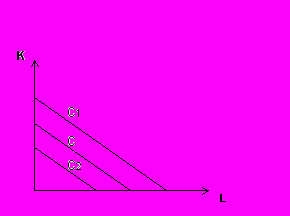
Рис. 6.7. Изокоста


Рост бюджета производителя или снижение цен ресурсов сдвигает изокосту вправо, а сокращение бюджета или рост цен – влево. Касание изокванты с изокостой определяет положение равновесия производителя, поскольку позволяет достичь максимального объема производства при имеющихся ограниченных средствах, которые можно затратить на покупку ресурсов.

Р
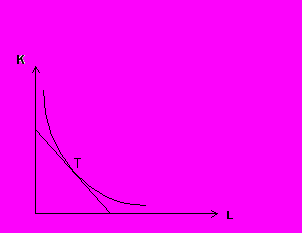
ис. 7.7. Пересечение изокванты и изокосты


Учитывая, что в точке Т изокванта и изокоста имеют одинаковый наклон и что наклон изокванты измеряется предельной нормой технологического замещения, можно записать условие равновесия, как

.


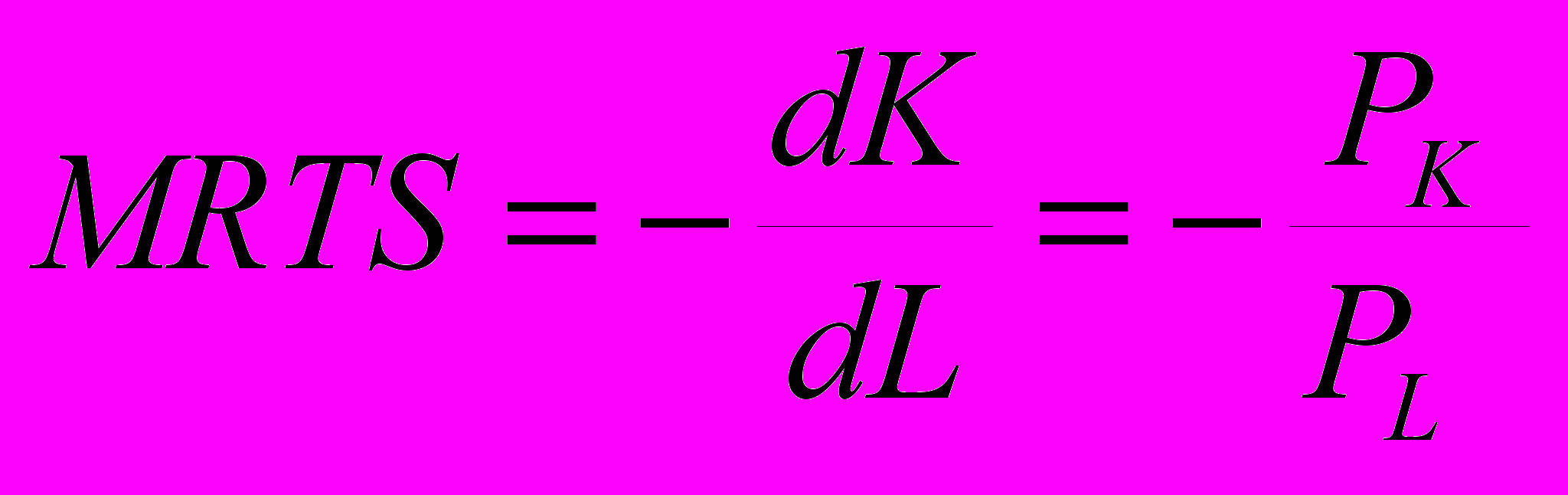4. Эффект от масштаба производства и «путь развития»

Предположим, что цены ресурсов остаются неизменными, тогда как бюджет производителя постоянно растет. Соединив точки пересечения изоквант с изокостами, мы получим линию OS – «путь развития» эта линия показывает темпы роста соотношения между факторами в процессе расширения производства.

Р
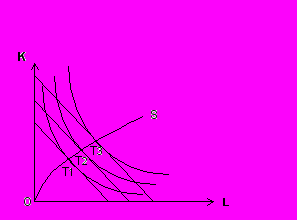
ис. 8.7. Кривая «путь развития»


На нашем рисунке труд в ходе развития производства используется в большей мере, чем капитал. Форма кривой «путь развития» зависит от:

1) от формы изоквант; 2) от цен на ресурсы (соотношение между которыми определяет наклон изокост).

Линия «путь развития» может быть прямой или кривой, исходящей из начала координат.

Если расстояние между изоквантами уменьшается, это свидетельствует о том, что существует возрастающая экономия от масштаба, т.е. увеличение выпуска достигается при относительной экономии ресурсов.

Р
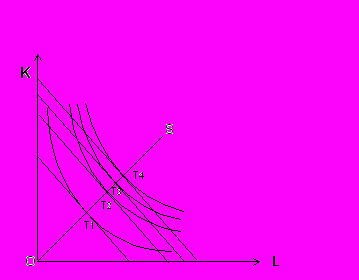
ис. 9.7. Возрастающая экономия от масштаба


Если расстояние между изоквантами увеличивается, это свидетельствует об убывающей экономии от масштаба.






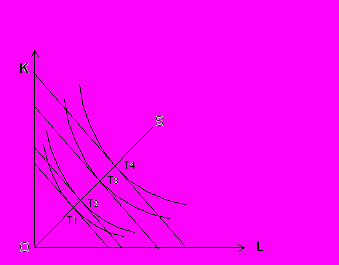
Рис. 10.7. Убывающая экономия от масштаба


В случае, когда увеличение производства требует пропорционального увеличения ресурсов, говорят о постоянной экономии от масштаба.





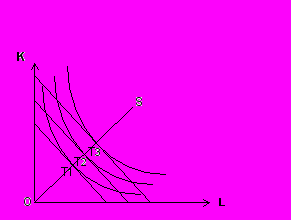
Рис. 11.7. Постоянная экономия от масштаба


Таким образом, анализ с помощью изоквант позволяет не только экономно использовать имеющиеся ресурсы для достижения данного объема производства, но и определить минимально эффективный размер предприятия в отрасли.

В случае возрастающей экономии от масштаба фирме необходимо наращивать объем производства, так как это приводит к относительной экономии имеющихся ресурсов. Убывающая экономия от масштаба свидетельствует о том, что минимально эффективный размер предприятия уже достигнут и дальнейшее наращивание производства нецелесообразно. Тем самым анализ выпуска с помощью изоквант позволяет определить техническую эффективность производства. Пересечение изокванты с изокостой позволяет определить не только технологическую, но и экономическую эффективность и выбрать оптимальную технологию производства (трудо- или капиталосберегающую, энерго- или материалосберегающую и т.д.), позволяющую обеспечит максимальный выпуск продукции при тех денежных средствах, которыми располагает производитель для организации производства.