Geum.ru

Урок n 19

Вид материалаУрок

Содержание


L1:=true; L2:=false; L3:=L1
OR - логическое ИЛИ (логическое сложение - дизъюнкция).
Задача. Дополните программу вычисления площади треугольника по
Каждому символу приписывается целое число в диапазоне 0...255.
Символьная константа (литера) - это символ, заключенный в апост
Символьную константу можно обозначить именем и задать в разделе
ORD(X)-определяет порядковый номер символа X, например ORD('R')=82.
Строковые данные задаются описателем string. Пример строковой пе
Пример: Объединение двух строк.
Таблица настройки цветов в модуле CRT Turbo Pascal
HighVideo - устанавливает включение яркости.
ClrScr - производит очистку экрана.
Sound(1500) - включение звукового сигнала частотой 1500 Гц.
Пример подключения модуля CRT
Program Gas
Pascal, обеспечивающих полное управление графическими режимами
SetColor(14) - установка цвета рисуемых линий.
Rectangle(25,100,100,200) - рисование прямоугольной рамки
Circle(300,250,80) - рисование окружности (X, Y, R), где X, Y
PieSlice(100,100,30,120,70) - рисование сектора окружности
...
Полное содержание
Подобный материал:
Урок N 19

Данные логического, символьного и строкового типа в Turbo Pascal.

Библиотека (модуль) CRT и Graph.

Работа с файлами в Turbo Pascal.

Построение графиков функций. Численные методы.

Логический тип переменных называется булевым. Он основан на ма-

тематической логике, в которой применяются две константы: 1 (ис-

тина) и 0 (ложь). В языке Turbo Pascal тоже есть две логические

константы: TRUE (истина) и FALSE (ложь). Их можно использовать в

явном виде или обозначать именем в разделе CONST, например:

const

T=true;

F=false;

L=true;

Логическая переменная тоже может принимать два значения TRUE и

FALSE. Описание логической переменной имеет тип BOOLEAN, например:

var L,A,C:boolean;

В разделе операторов логическому типу переменной можно присвоить

значение логической константы, например:

L1:=true; L2:=false; L3:=L1;

В языке Turbo Pascal для сравнения переменных, принимающих чис-

ленные значения, существуют следующие операции отношений:

 

< меньше,

<= меньше или равно,

= равно,

<> не равно,

> больше,

>= больше или равно.

 

Операции с данными логического типа

 

В языке Turbo Pascal есть логические операции:

OR - логическое ИЛИ (логическое сложение - дизъюнкция).

AND - логическое И (логическое умножение - конъюнкция).

NOT - логическое отрицание НЕ.

 

Пример программы с использованием логических операций.

Задача. Дополните программу вычисления площади треугольника по

формуле Герона исследованием существования треугольника, если

заданы его три стороны.

 

program tangle;

var a,b,c,p,S,Q:real;

begin

writeln('Вычислите площадь треугольника по трем сторонам');

writeln('и проведите его анализ.');

writeln('Введите стороны треугольника a,b,c:');

read(a,b,c);

p:=(a+b+c)/2;

S:=sqrt(abs(p*(p-a)*(p-b)*(p-c)));

if (a>=(b+c)) or (b>=(a+c)) or (c>=(a+b))

then writeln('Треугольник не существует.')

else if (a=b) and (b=c)

then writeln('Треугольник равносторонний, его площадь S=',s)

else if (a=b) or (b=c) or (a=c)

then writeln('Треугольник равнобедренный, его площадь S=',s)

else writeln('Треугольник разносторонний, его площадь S=',s);

if (a*a=(b*b+c*c)) or (b*b=(a*a+c*c)) or (c*c=(a*a+b*b))

then writeln('Треугольник прямоугольный.');

writeln('Для выхода из программы введите число 1.');

readln(Q);

end.

 

Данные символьного типа в Turbo Pascal

Язык TP может обрабатывать не только числа, но и символы. Это

даёт возможность представлять в программах тексты и выполнять над

ними некоторые операции, обрабатывать различные ведомости, доку-

менты, справочники и т.д.

Значениями символьного типа является всё множество символов ПК.

Каждому символу приписывается целое число в диапазоне 0...255.

Это число служит кодом внутреннего представления символов. Для

кодировки используется код ASCII (Американский стандартный код

для обмена информацией).

Символьная константа (литера) - это символ, заключенный в апост-

рофы, например: 'A', 'R', '+', '7'. Внешние апострофы являются

признаком символьной константы, которая занимает 1 байт памяти.

Символьную константу можно обозначить именем и задать в разделе

констант, например:

Const

sim='A';

A='B';

S='+';

D1='T';

Символьная переменная принимает значение одного символа. В раз-

деле переменных она обозначается описателем CHAR (символьный тип),

например:

Var

B1,B2,R:CHAR;

BUKVA:CHAR;

Допускается использование символьных данных в операторе присваи-

вания, например: BUKVA:='A'; R:='*'; B1:='S';

Операции. Так как символы языка упорядочены, то к символьным

данным применимы операции отношений (сравнений): <,<=,=,<>,>,>=.

Поэтому 'A'<'B'; '+'<'-'; '*'<'4'. Результатом операции сравнения

является логическая константа TRUE (истина) или FALSE (ложь).

К символьным данным можно применять встроенные функции:

ORD(X)-определяет порядковый номер символа X, например ORD('R')=82.

CHR(X)-определяет символ, стоящий по порядковому номеру Х, напри-

мер: CHR(68)='D';

PRED(X)-определяет предыдущий символ по отношению к Х, например:

PRED('N')='M';

SUCC(X)-определяет последующий символ по отношению к Х, например:

SUCC('R')='S'.

 

Пример программы вывода на экран символов (букв) от A до Z:

 

program Simbol; {Данные символьного типа}

uses crt;

var i:Char;

begin

clrscr;

writeln('Вывод на экран букв от A до Z:');

for i:='A' to 'Z' do

write(' ',i);

writeln;

writeln('Выход-любая клавиша.');

readkey;

end.

 




Строковые данные

Строковые данные - это последовательность символов произвольной

длины (до 255 символов). Размер строки указывают в квадратных

скобках, но если размер не указан, то он считается равным 255.

Строковые данные задаются описателем string. Пример строковой пе-

ременной:

var

str1: string[80];

str2: string;

 

Строковая константа:

const

January: string[10]='Январь';

 

Для строковых данных применимы операции объединения (конкатена-

ции) и сравнения.

Пример: Объединение двух строк.

program ObStr;

var

str, str1, str2: string[80];

begin

....

str1:='Turbo';

str2:='Pascal';

str:=str1+str2; {В переменной str - 'Turbo Pascal'}

....

end.

 

Пример программы, позволяющей соединить два слова в одно:

 

program Stroka1; {Строковые переменные}

uses crt;

var x,y,z:string[255];

begin

clrscr;

writeln('Программа, объединяющая два слова в одно.');

writeln('Введите 1-е слово:');

readln(x);

writeln('Введите 2-е слово:');

readln(y);

z:=x+y;

writeln(z);

writeln('Выход-любая клавиша.');

readkey;

end.

 




Библиотека (модуль) CRT в Turbo Pascal.

 

Библиотека CRT позволяет менять цвета и яркость экрана, производить

его очистку, управлять звуковым генератором компьютера.

Подключение модуля CRT производится директивой USES CRT, которая

указывается в разделе описаний. CRT - аббревиатура, означающая

"Электронно-лучевая трубка".

 

Таблица настройки цветов в модуле CRT Turbo Pascal

Константа

Число

Цвет

Процедуры

Black
0
Черный
TextColor, TextBackGround

Blue
1
Синий
TextColor, TextBackGround

Green
2
Зеленый
TextColor, TextBackGround

Cyan
3
Голубой
TextColor, TextBackGround

Red
4
Красный
TextColor, TextBackGround

Magenta
5
Фиолетовый
TextColor, TextBackGround

Brown
6
Коричневый
TextColor, TextBackGround

LightGray
7
Ярко-серый
TextColor, TextBackGround

DarkGray
8
Темно-серый
TextColor

LightBlue
9
Ярко-синий
TextColor

LightGreen
10
Ярко-зеленый
TextColor

LightCyan
11
Ярко-голубой
TextColor

LightRed
12
Ярко-красный
TextColor

LightMagenta
13
Ярко-фиолетовый
TextColor

Yellow
14
Желтый
TextColor

White
15
Белый
TextColor

Blink
128
Мерцание
TextColor (как слогаемое)

 




Основные директивы модуля CRT

Uses CRT - подключение модуля CRT.

TextColor - устанавливает цвет символов.

TextBackGround - устанавливает цвет фона (только 8 неярких цветов).

HighVideo - устанавливает включение яркости.

LowVideo - устанавливает выбор низкой яркости.

NormVideo - восстановление того цветового оформления, которое было

на момент начала работы программы.

ClrScr - производит очистку экрана.

ReadKey - обеспечивает задержку изображения и выход из программы при

нажатии любой клавиши, например Esc, Enter, Пробел.

Sound(1000) - включение звукового сигнала частотой 1000 Гц.

Sound(1500) - включение звукового сигнала частотой 1500 Гц.

Delay(1000) - установка (задержка) звучания на время 1 с (1000 мс).

Delay(2000) - установка (задержка) звучания на время 2 с.

NoSound - отключение звукового сигнала.

Пример подключения модуля CRT:

USES CRT;

BEGIN

TextColor(14); {Задаёт желтые символы текста}

TextBackGround(5); {Задаёт фиолетовый фон}

HighVideo; {Устанавливает включение яркости}

ClrScr; {Очищает экран}

 

Пример: TextColor(14+128); {Задаёт мерцание символов желтого цвета}

 

Пример программы, использующей модуль CRT:

 

Program Gas;

uses CRT;

var N:integer;

begin

TextColor(14);

TextBackGround(1);

highvideo;

clrscr;

writeln('Законы состояния идеального газа.');

writeln;

writeln('Рассмотрим случаи (здесь число N - номер случая), когда:');

writeln('1) T=const, N=1.');

writeln('2) V=const, N=2.');

writeln('3) P=const, N=3.');

writeln('4) P,V,T=varia, N=4.');

writeln('5) Быстрое сжатие или расширение');

writeln('в теплоизолированном сосуде Q=0, N=5.');

write('Введите число N=');

read(N);

writeln;

if N=1 then

writeln('Изотерм. процесс, T=const, PV=const-закон Бойля-Мариотта.');

if N=2 then

writeln('Изохорный процесс, V=const, P/T=const-закон Шарля.');

if N=3 then

writeln('Изобарный процесс, P=const, V/T=const-закон Гей-Люсака.');

if N=4 then

writeln('P,V,T=varia, PV=(M/Mo)RT-уравнение Менделеева-Клайперона.');

if N=5 then

writeln('Адиабатный процесс, Q=0, (PV)Г-уравнение Пуассона.');

if N>5 then writeln('Другие случаи здесь не рассматриваются.')

else

writeln;

writeln('Выход - любая клавиша.');

readkey;

TextColor(7);

TextBackGround(0);

clrscr;

end.

 




Библиотека (модуль) Graph в Turbo Pascal 7.0.

Модуль Graph представляет собой библиотеку подпрограмм Turbo

Pascal, обеспечивающих полное управление графическими режимами

различных мониторов - CGA, EGA, VGA, SVGA. Библиотека содержит

более 50 графических процедур и функций, как базовых (рисование

точек, линий, окружностей и т.п.), так и расширяющих возможностей

базовых (многоугольники, закрашивание фигур, вывод текста и др.).

Для запуска программ, использующих модуль Graph, должен быть

доступен драйвер egavga.bgi. Для компиляции программ должен быть

доступен модуль GRAPH.TPU.

 

Основные директивы модуля GRAPH

Uses GRAPH - подключение модуля GRAPH.

InitGraph(gd,gm,'c:\tp7\') - инициирование графического режима,

указываем gd-графический драйвер, gm-графическую мода и полный

путь файла поддержки графики egavga.bgi: c:\tp7\.

ClearDevice - очистка экрана в графическом режиме.

SetColor(14) - установка цвета рисуемых линий.

SetBkColor(1) - установка цвета фона.

SetLineStyle(0,0,3) - установка толщины линий.

SetFillStyle(5,11) - установка стиля и цвета закраски. Число сти-

лей закраски = 0-11.

PutPixel(300,250,15) - рисование точки (X, Y, C), где X, Y -коор-

динаты точки, C - цвет точки. С=0-15.

Line(25,100,100,200) - рисование отрезка прямой линии

(X1,Y1,X2,Y2), где X1,Y1-координаты начала отрезка; X2,Y2-коор-

динаты конца отрезка прямой линии.

Rectangle(25,100,100,200) - рисование прямоугольной рамки

(X1,Y1,X2,Y2), где X1,Y1 и X2,Y2 - координаты соответственно

начала и конца диагонали левого верхнего угла.

Bar(20,70,210,50) - рисование закрашеннго прямоугольника

(X1,Y1,X2,Y2), где X1,Y1 и X2,Y2 - координаты соответственно

начала и конца диагонали левого верхнего угла.

Circle(300,250,80) - рисование окружности (X, Y, R), где X, Y -

координаты центра окружности, R - радиус окружности.

Arc(300,250,135,45,60) - рисование дуги окружности (X,Y,Ф1,Ф2,R),

где Ф1,Ф2 - начальный и конечный углы дуги. X,Y,R - см. выше.

PieSlice(100,100,30,120,70) - рисование сектора окружности

(X,Y,Ф1,Ф2,R).

Ellipse(300,250,0,360,95,40)-рисование эллипса (X,Y,Ф1,Ф2,R1,R2).

Ф1,Ф2 - начальный и конечный углы. R1, R2 - радиусы эллипса.

Sector(400,100,90,290,200,80)- рисование сектора эллипса

(X,Y,Ф1,Ф2,R1,R2).

FillEllipse(X,Y,R1,R2) - рисование закрашенного эллипса

(или окружности при R1=R2).

OutTextXY(25,30,'Текст.') - вывод текста (X, Y, 'Текст').

CloseGraph - закрытие графического режима.

 

Ниже приведены примеры программ, использующих модуль Graph и

Graph0 (модуль Graph0 - графика для начинающих, упрощенный модуль

Graph). Из комментариев к ним можно узнать о конкретном использо-

вании основных директив модуля Graph при создании простейших гра-

фических изображений.

 

Пример 1.

 

Program Ris1;

uses Crt,Graph;

var gd,gm:integer; {gd-графический драйвер, gm-графическая мода}

begin

gd:=detect; {Автоматически определяем графический драйвер}

InitGraph(gd,gm,'c:\tp7\'); {Инициируем графический режим, указы-

ваем полный путь файла egavga.bgi}

SetLineStyle(0,0,3); {Задаем толщину линии}

SetColor(LightMagenta); {Задаем цвет линии}

SetFillStyle(1,LightGreen); {Задаем стиль и цвет закраски}

PieSlice(100,100,30,120,70); {Рисуем сектор окружности, X,Y,Ф1,Ф2,R}

SetColor(White); {Задаем цвет линии}

SetFillStyle(5,11); {Задаем стиль и цвет закраски}

Sector(400,100,90,290,200,80); {Рисуем сектор эллипса, X,Y,Ф1,Ф2,R1,R2}

Readkey; {Обеспечиваем задержку изображения и выход из программы при

нажатии любой клавиши, например Esc, Enter, Пробела}

CloseGraph {Закрываем графический режим}

end.

 

Пример 2.

 

Program Grafika;

uses Crt,Graph,Graph0; {Подключаем модули CRT, GRAPH, GRAPH0}

begin

Init('c:\tp7\'); {Указываем полный путь файла egavga.bgi}

SetColor(14); {Задаем цвет рисуемых линий}

SetLineStyle(1,0,ThickWidth); {Задаем тройную толщину линии}

SetBkColor(1); {Задаем цвет фона}

Circle(300,250,120); {Рисуем окружность, X, Y, R}

SetColor(11);

Circle(300,250,100);

SetColor(13);

Circle(300,250,80);

SetColor(10);

Arc(300,250,135,45,60); {Рисуем дугу, X, Y, Ф1, Ф2, R}

SetColor(12);

Ellipse(300,250,0,360,95,40); {Рисуем эллипс, X, Y, Ф1, Ф2, R1, R2}

PutPixel(300,250,15); {Рисуем точку, X, Y, C}

SetColor(15);

OutTextXY(25,30,'Графика в Turbo Pascal.'); {Вывод текста, X, Y, 'Текст'}

SetColor(11);

OutTextXY(160,450,'Для выхода из программы нажмите Esc.');

SetFillStyle(1,14); {Задаем вид закраски (0-11) и цвет закраски С}

Bar(20,70,210,50); {Рисуем закрашенный прямоугольник, X1,Y1,X2,Y2}

SetColor(11);

Rectangle(25,100,100,200); {Рисуем прямоугольную рамку, X1,Y1,X2,Y2}

SetColor(14);

Line(25,100,100,200); {Рисуем прямую линию, X1,Y1,X2,Y2}

Readkey;

CloseGraph;

end.

 

Здесь X, Y, X1, Y1, X2, Y2 - координаты основных точек на экране;

Ф1, Ф2 - углы дуг, круговых и эллиптических секторов;

R, R1, R2 - радиусы окружностей, эллипсов, дуг и секторов.

С - цвет линий (0-15).

 

Пример 3. Флаг России.

 

program Flag_RUS;

uses CRT,Graph,Graph0;

begin

Init('c:\tp7\');

SetFillStyle(1,15);

Bar(0,0,320,50);

SetFillStyle(1,1);

Bar(0,51,320,101);

SetFillStyle(1,4);

Bar(0,102,320,152);

ReadKey;

CloseGraph;

end.

 

Примеры программ построения графиков функций:

 

1. Построение графика параболы в декартовых координатах (путь

S(t)=gt2/2 при свободном падении тела). Построение производится

по точкам.

 

Program Put3;

uses Crt,Graph,Graph0;

var t1,S,H,n:integer;Y,g,dt,t:real;

begin

Init('c:\tp7\');

SetColor(14);

OutTextXY(25,30,'Путь S(t)=gt2/2 при свободном падении.');

OutTextXY(25,50,'Выход - любая клавиша.');

SetColor(10);

Line(0,470,550,470);

Line(0,0,0,470);

g:=9.81;

t:=0;

n:=100;

repeat

Y:=g*t*t/2;

dt:=1/(n+1);

t:=t+dt;

t1:=round(6*t);

S:=round(Y);

H:=round(470-S/70);

PutPixel(t1,H,11);

until t>80;

Readkey;

CloseGraph;

end.

 

2. Построение графика функции (улитки Паскаля) в полярных коорди-

натах. Если в прямоугольных (декартовых) кординатах задают точку

A на плоскости по её координатам x, y, то в полярных координатах

точку задают по её радиус-вектору R и углу fi между вектором R и

осью X (смотрите чертёж на рисунке). Функция в декартовых коорди-

натах имеет вид y=f(x), в полярных координатах R=F(fi). Связь

между декартовыми и полярными координатами: x=R*cos(fi),

y=R*sin(fi), R=SQRT(x*x+y*y).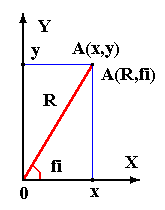



 

Program Ulitka;

uses crt, graph, graph0;

const xc=320; yc=175; k=0.775;

var fi,dfi,R,a:real; x1,y1,x2,y2,n:integer;

Function F(fi:real):real;

begin F:=a/2+a*cos(fi);

end;

begin

clrscr;

writeln('Улитка Паскаля: R=1+a*cos(fi).');

write('Введите коэффициент a=0.5-2; a=');

read(a);

a:=100*a;

write('Введите число точек n>=100; n=');

read(n);

init('C:\TP7\');

cleardevice;

outtextxy(10,10,'Улитка Паскаля: R=1+a*cos(fi).');

setcolor(10);

line(xc,0,xc,349);

line(0,yc,639,yc);

dfi:=2*pi/n;

x1:=xc; y1:=yc; fi:=0;

while fi<2*pi+dfi do

begin

R:=F(fi);

x2:=xc+round(R*cos(fi));

y2:=yc+round(k*R*sin(fi));

setcolor(11);

line(x1,y1,x2,y2);

x1:=x2; y1:=y2; fi:=fi+dfi;

end;

outtextxy(10,30,'Выход - любая клавиша.');

readkey;

closegraph;

end.

 

Здесь построение графика функции производится с помощью отрезков

прямых линий, которые при большом их числе превращаются в кривую

линию. В программе для построения графика функции используется

процедура Function, что позволяет строить графики других функций,

не меняя программы (универсальный алгоритм), а заменив только вид

самой функции R=F(fi). Например, если подставить R=a*(1-cos(fi)),

то мы получим кардиоиду. Аналогично можно построить график спира-

ли Архимеда R=a*fi и т.д.

 




Работа с файлами в Turbo Pascal

При работе с файлами в TP используются следующие процедуры:

assign(var F; name: string); - устанавливает соответствие между

файлом и файловой переменной, окрывает все другие поцедуры работы

с файлами. F -переменная любого файлового типа, name - полное имя

файла.

close(var F); - окончание процедур работы с файлами (закрытие

файла).

rewrite(var F: file); - создаёт и открывает новый файл.

reset(var F: file); - открывает существующий файл.

append(var F: text); - открывает существующий текстовый файл и

позиционирует указатель обработки на конец файла. После этого

можно дополнять текстовый файл информацией, начиная с конца стро-

ки.

erase(var F); - удаляет неоткрытый внешний файл любого типа, за-

даваемый переменной F.

rename(var F: newname: string); - переименовывает неоткрытый файл

F любого типа. Новое имя задаётся строкой newname.

Текстовый файл можно рассматривать как последовательность симво-

лов, разбитую на строки длиной от 0 до 256 символов. Для описания

используется стандартный тип text: var F: text; (F - файловая пе-

ременная).

Стандартные типы данных не требуют описания в разделе type в от-

личие от типов, образованных пользователем. Формат раздела:

type <имя типа> = <значение типа>;

Имя и значение типа даёт пользователь. Пример: type fil=text;

 

Рассмотрим работу с файлами в TP на примерах.

 

Пример 1. Запись текстового файла на диск и ввод в него текста.

 

program wtf;

type fil=text;

var f1:fil; name:string[35]; txt:string;

begin

write('Введите имя файла для записи текста>');

readln(name);

writeln;

assign(f1,name);

rewrite(f1);

writeln('Введите текст для записи (для окончания-Enter):');

writeln;

repeat

write(':>');

readln(txt);

writeln(f1,txt);

until txt='';

close(f1);

writeln;

writeln('Ввод окончен, нажмите Enter.');

readln;

end.

 

Пример 2. Запись результата вычисления в текстовый файл.

 

program wtf1;

uses crt;

type fil=text;

var f1:fil; name:string[35]; txt:string;

var i,n:real;s,q:real;

begin

clrscr;

writeln('Для вычисления суммы ряда S=1+1/4+1/9+...+1/n2,');

write('введите n=1,2,3...: n=');

read(n);

i:=1;

S:=1;

while i<>n do

begin

i:=i+1;

s:=s+1/(i*i);

end;

writeln('Сумма членов ряда равна S=',s);

name:='rezult.txt';

txt:='Сумма ряда S=1+1/4+1/9+...+1/n2 равна: S=';

writeln;

assign(f1,name);

rewrite(f1);

writeln(f1,txt,s,' при n=',n:9:0);

close(f1);

writeln('Ваш результат будет записан в файл rezult.txt');

writeln('Для выхода из программы нажмите Enter.');

readkey;

end.

 

Пример 3. Чтение последовательности длиной до 35 символов из

текстового файла example.txt (его содержимое, например,

"23456 Всем привет!"

 

Функция Eoln(var F: text) возвращает булевское значение True,

если текущая файловая позиция находится на маркере конца строки

или вызов Eof(F) возвратил значение True. Во всех других случаях

значение функции будет False.

Функция Eof(var F: text) возвращает булевское значение True, ес-

ли указатель конца файла находится сразу за последним компонен-

том. В противном случае - False.

 

program wtf2;

var F: text; St: string[35];

begin

assign(F, 'example.txt'); {Файл example.txt должен существовать!}

reset(F);

while not Eoln(F) do begin {Проверка конца строки}

read(F,St);

writeln('St = ',St); {Вывод на экран}

end;

readln(F); {Переход к следующей строке}

close(F);

writeln('Вывод символов из файла окончен. Для выхода - Enter.');

readln;

end.

 




Численные методы и связанные с ними задачи.

Рассмотрим некоторые характерные для численных методов задачи,

для решения которых удобно использовать программирование на TP.

 

Пример 1. Вычислите приближенно определенный интеграл по формуле

прямоугольников. Подынтегральная функция f(x)=sin(x). Пределы ин-

тегрирования a=0; b=pi.

 

program INTEGRAL1;

var i,n:integer; a,b,S,h,x,Y:real;

begin

writeln('Подынтегральная функция f(x)=sin(x). Пределы a=0; b=pi.');

write('Введите число членов ряда приближения: n=');

read(n);

a:=0; b:=pi;

h:=(b-a)/n;

S:=0;

for i:=1 to n do

begin

x:=a+i*h-h/2;

S:=S+h*sin(x)

end;

writeln('Приближенное значение интеграла равно: I=',S);

writeln('Для выхода из программы введите число 1.');

readln(Y);

end.

 

Пример 2. Вычислите выражение S=sqrt(1+sqrt(2+sqrt(3+sqrt(4+...)))

с максимальной точностью.

 

program zp1;

var j,n:integer;s0,s1:real;

begin

s0:=0;

s1:=1;

n:=1;

while s0<>s1 do

begin

s0:=s1;

n:=n+1;

s1:=0;

for j:=n downto 1 do

s1:=sqrt(j+s1);

end;

writeln('Ответ: значение выражения S=',s1);

writeln('Для выхода из программы - Enter.');

readln

end.

 

Пример 3. Вычислите с точностью e (e<<1) сумму ряда

S=sin(x)=x-x3/3!+x5/5!-x7/7!+...+(-1)(n-1)*x(2*n-1)/(2*n-1)!

Это разложение функции S=sin(x) в ряд Тейлора.

 

program zp2;

var i:integer;x,y,S,e,q:real;

begin

write('Введите x=');

read(x);

write('Введите величину точности e=');

read(e);

i:=1;

S:=x;

y:=x;

while abs(y)>e do

begin

i:=i+1;

y:=-y*x*x/((2*i-2)*(2*i-1));

S:=S+y;

end;

writeln('Ответ: Сумма ряда S=',S);

writeln('Для сравнения и проверки S=sin(x)=',sin(x));

writeln('Для выхода из программы введите любое число.');

readln(q);

end.

 

Пример 4. Решение уравнения F(x)=sin(x)-x+0.25=0 методом простых

итерраций. Суть этого метода заключается в следующем. Пусть Xo -

исходное приближённое значение корня уравнения F(x)=0, которое

может быть переписано в виде x=f(x). Тогда в качестве следующего

приближения примем x1=f(Xo). В качестве следующего приближения

возьмём x2=f(x1). Продолжая процесс дальше, в качестве n-го приб-

лижения необходимо положить Xn=f(X(n-1)). Итеррационный процесс

будет сходиться и мы в итоге указанной процедуры найдем корень

уравнения, если ABS(f'(x))<1. В противном случае процесс расхо-

дится и мы не найдём решение этим методом. При нахождении исход-

ного значения корня Xo следует учитывать, что в окрестности корня

функция F(x) меняет знак.

Данное уравнение можно решить только приближённо и лишь численны-

ми методами. Заданная точность e=1e-9. Начальное значение корня

x=1. Получаемый в процессе решения результат x=1.1712296519 прев-

ращает уравнение в тождество с большой точностью.

 

program iterac;

label m1;

var i:integer; x,x1,e,q:real;

begin

e:=1e-9;

x:=1;

for i:=1 to 30 do

begin

x1:=sin(x)+0.25;

if abs(x1-x)<=e then goto m1;

x:=x1;

end;

m1: writeln('Ответ: x =',x1);

writeln('Для выхода введите любое число.');

readln(q);

end.

 

Пример 5. Решение уравнения F(x)=cos(x)-x=0 методом Ньютона.

Согласно методу Ньютона, корень уравнения равен x1=x-F(x)/F'(x).

Этот численный метод часто используется как основной, а также в

тех случаях, когда уравнение не удаётся решить методом простых

итерраций. Чтобы метод сходился и приводил к результату необходи-

мо, чтобы начальное значение x было выбрано достаточно близко к

корню и в окресности корня значение F'(x) не было слишком большим

и F'(x) не было слишком близко к нулю. Последнее условие F'(x)<>0

означает, что никакие два корня не находятся слишком близко один

к другому.

В данном примере начальное значение корня x=0.7. Корень x=0.73908.

 

program Newton;

uses crt;

var x,x1,e:real; i:integer;

begin

clrscr;

i:=1;

e:=1E-3;

x:=0.7;

repeat

i:=i+40;

x:=x+i*e;

x1:=x+(cos(x)-x)/(sin(x)+1);

until abs(x-x1)>=e;

writeln('Ответ: x=', x1);

writeln('Проверка решения: F(x)=cos(x)-x =', cos(x1)-x1);

writeln('Выход - любая клавиша.');

readkey;

end.

 




Вопросы

1. Что такое данные логического типа и как они используются?

2. Какие существуют операции отношений над переменными в Turbo

Pascal?

3. Какие существуют операции над данными логического типа?

4. Что такое данные символьного типа?

5. Что такое данные строкового типа?

6. Что такое библиотека CRT в Turbo Pascal и как она используется?

7. Какие директивы модуля CRT вы знаете?

8. Как очищается экран и задается цвет текста и цвет фона?

9. Как устанавливается и отключается звуковой сигнал?

10. Что такое модуль Graph и какие директивы модуля Graph Вы знаете?

 

Задания

1. Воспроизведите самостоятельно и проанализируйте приведенную

выше программу исследования треугольника.

2. Составьте программу, определяющую наибольшее из трёх чисел.

3. Составьте программу, определяющую наименьшее из трёх чисел.

4. Введите в приведенные выше программы модуль CRT и задайте цвет

текста и цвет фона, а затем поменяйте их. Примените команду

очистки экрана.

5. Введите в приведенные выше программы модуль CRT и задайте

включение звука, измените частоту и длительность его звучания.

Попытайтесь исполнить простейшую мелодию, а затем отключите

звук.

6. Создайте простейшие изображения (окружность, линия, прямоу-

гольник, эллипс) при помощи модуля Graph Turbo Pascal.

7. Нарисуйте треугольник с вписанной и описанной окружностями.

8. Нарисуйте квадрат с диагоналями и с вписанной в него окруж-

ностью.

9. Нарисуйте Солнце.

10. Нарисуйте пятиконечную звезду, вписанную в окружность.

11. Нарисуйте график функции (параболы, гиперболы и т.д.).

12. Решите уравнение методом простых итерраций:

exp(x)+x=0 (Ответ: x=-0.567)

13. Решите следующие уравнения методом Ньютона:

2*x3-5*x2+5*x-3=0 (Ответ: x=1.5);

x3-x2-x-2=0 (Ответ: x=2);

exp(x)+x-3=0 (Ответ: x=0.792)

14. Вычислите простейшие определённые интегралы методом прямоугольников от следующих функций:

cos(x) от 0 до pi/2 (Ответ: S=1)

1/x от 1 до e (Ответ: S=1)

4/(1+x2) от 0 до 1 (Ответ: S=pi)

exp(x) от 0 до 1 (Ответ: S=e-1).