Построение базы знаний нечеткого логического контроллера

Вид материала

Содержание

Construction of the knowledge base of the indistinct logic controller
Анық емес логика контроллерін құрастыру қорындағы қаблеттілігі
2. Нахождение оптимальной траектории
3. Построение нечеткого контроллера

Подобный материал:

ПОСТРОЕНИЕ БАЗЫ ЗНАНИЙ НЕЧЕТКОГО ЛОГИЧЕСКОГО КОНТРОЛЛЕРА

Атанов С.К., к.т.н, доцент кафедры компьютерные системы Казахского агротехнического университета им. С.Сейфуллина, г. Астана

Резюме

Рассмотренная в статье проблема создания базы правил представляет одну из важнейших задач при построении нечеткого логического контроллера.

В данной работе реализован принцип максимума скорости управление для замкнутой системы регулирования. Переход из временной области, в фазовое пространство системы позволил применить полученное решение для построения нечеткого контроллера.

CONSTRUCTION OF THE KNOWLEDGE BASE OF THE INDISTINCT LOGIC CONTROLLER

The resume

The problem of creation of base of rules considered in article represents one of the major problems at construction of the indistinct logic controller.

In the given work the principle of a maximum of speed management for the closed system of regulation is realized. Transition from time area, in phase space of system has allowed applying the received decision to construction of the indistinct controller.

Анық емес логика контроллерін құрастыру қорындағы қаблеттілігі

Түйін

Мақалада қарастырылған базаны жасау ережесінің проблемасы анықемес логикалық контроллерді құру үшін маңызды есеп болып табылады. Берілген жұмыста тұйық реттелу жүйесі үшін басқару жылдамдығының максимум принципі қолданылады. Анық емес контроллерді құруға арналған алынған есеп уақыттық облыстан фазалық кеңістіктің жүйесіне ауысуын қолдануға мүмкіндік береді

1. Введение

Проблема создания базы правил представляет одну из ключевых задач при построении нечеткого логического контроллера. Для её решения используется интервьюирование опытного оператора, либо фиксирование решений, принимаемых оператором в различных ситуациях, либо, наконец, желательная траектория управления, полученная из каких-либо соображений.
В данной работе в качестве желаемой траектории принято найденное по принципу максимума [1] оптимальное по быстродействию управление для замкнутой системы регулирования. Осуществлен переход из временной области, в которой найдено оптимальное управление, в фазовое пространство системы, что позволило непосредственно применить полученное решение для построения нечеткого контроллера.

2. Нахождение оптимальной траектории

Рассмотрим задачу коррекции качества переходного процесса путем динамического изменения в определенных пределах параметров ПИД-регулятора. Структурная схема системы регулирования с ПИД-регулятором показана на рис.1.

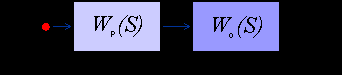Рис.1

Здесь W₀(S) и W_p(S) - передаточные функции объекта и регулятора соответственно. Для линейного объекта n - порядка и ПИД-регулятора с передаточной функцией

W_p(S)= K₁+K₂/S+K₃S (2.1)

уравнение системы имеет вид

(2.2)
Введем переменную

(2.3)

и запишем уравнения движения в векторной форме

(2.4)
Здесь X и B-(n+1) - мерные векторы; A - матрица; u - скаляр. Для матрицы A и элементов вектора B имеем следующие соотношения:

(2.5)
b₁ = 1;
b₂ = b₃ = ... = b_n-1 = 0;

Предполагается, что параметры ПИД-регулятора в процессе управления можно изменять в некоторых интервалах

. (2.6)
Пусть при u = u(t) и некоторых допустимых значениях параметров K_i система может быть переведена из состояния X(t₀) = X⁰ в заданное состояние X(t₁) = X¹. Ставится задача перевода системы (2.5) из состояния X⁰ в состояние X¹ за минимальное время t₁ - t₀ путем динамического изменения параметров K_i при выполнении условий (2.6). В соответствии с принципом максимума вводим сопряженную систему

(2.7)

и определяем параметры K_i из условия максимума функции

(2.8)

по K_i при условиях (2.6). Оставляя в (2.8) только члены, содержащие искомые параметры K_i, приходим к задаче максимизации по K_i функции

. (2.9)

Введем параметры

. (2.10)
Учитывая положительность коэффициента a_n, из (2.5), (2.6) и (2.9) получаем оптимальные значения коэффициентов K_i:

(2.11)
Соотношения (2.11), (2.4), (2.5) и (2.7) образуют замкнутую систему уравнений, описывающую оптимальный переходный процесс при соответствующем выборе

- начальных условий для сопряженной системы (2.7). Выбор этих условий производится исходя из требования прохождения управляемой системы (2.7) через точку X(t₁) = X¹ в некоторый момент t = t₁. Сопряженная система в соответствии с (2.11) определяет только моменты смены знаков управляющих параметров. В свою очередь эти моменты зависят от X⁰, u, X¹. Однако, для режима перевода управляемой системы из одной точки статического равновесия X⁰ в другую точку статического равновесия u при ступенчатом изменении X¹ моменты переключений управляющих параметров остаются фиксированными для данной системы и могут быть рассчитаны заранее.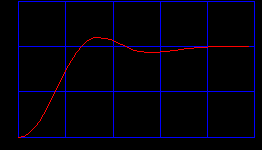

Рис.2

На рис.2 показаны результаты моделирования описан-ного выше способа управления для объекта третьего по-рядка, состоящего из трех апериодических звеньев. (Т1=0,1с, Т2=0,2с, Т3=0,7с) Предложенный метод коррекции переходного процесса дает хорошие результаты, но его реализция с помощью задания оптимальной программы пере-ключений чрезвычайно чувствительна даже к малым изменениям параметров объекта и действию возмущений.
Преодоление указанных недостатков можно искать на пути определения K_i в зависимости от фазовых координат системы с использованием методов нечеткого управления

3. Построение нечеткого контроллера

Основная функция, возлагаемая на нечеткий контроллер - формирование корректирующих поправок к коэффициентам K₁, K₂ и K₃ ПИД-регулятора в зависимости от текущих координат системы. В этом случае ПИД-регулятор с корректирующим нечетким контроллером представляет собой нелинейную систему.
Разработка нечеткого контроллера сводится к решению нескольких задач:

- выбору входных лингвистических переменных на основе анализа поведения замкнутой системы в рассчитанном ранее оптимальном режиме (см. рис. 2); - назначению для каждой из лингвистических переменных набора лингвистических значений (термов); - выбору для каждого из термов аппроксимирующего нечеткого множества; - созданию базы правил контроллера на основе анализа совокупности значений "входные переменные - управление", полученной для оптимального режима; - принятию адекватного проблеме механизма нечеткого вывода и выбору эффективного метода преобразования полученного нечеткого управления в "четкий" выходной сигнал.

Процедура обработки входной (четкой) информации в контроллере вкратце может быть описана следующим образом:

- текущие значения входных переменных преобразуются в лингвистические (фазифицируются); - на основании полученных лингвистических значений и с использованием базы правил контроллера производится нечеткий логический вывод, в результате которого вычисляются лингвистические значения выходных переменных; - заключительным этапом обработки является вычисление "четких" значений управляющих параметров (дефазификация).

Для решения рассматриваемой задачи необходима нечеткая система управления с несколькими входами и тремя выходами. Функциональная схема системы управления с использованием динамически корректируемого ПИД-регулятора приведена на рис. 3.

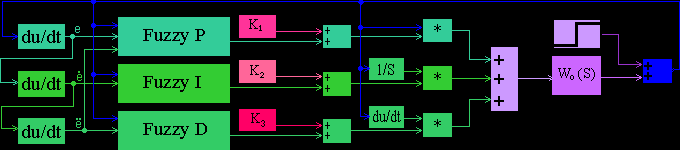рис. 3.

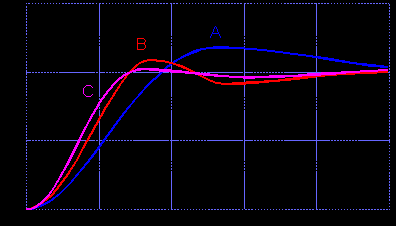
Каждый нечеткий контроллер, вырабатывающий поправки к соответствующим коэффициентам регулятора в реальном масштабе времени, реализует закон управления, рассчитанный в п.2 настоящей работы. На рис. 4. приведены законы изменения поправок для P-, I- и D-термов ПИД-регулятора; а на рис. 5 - значения ошибки e x 1 и ее производных

как функции времени. Нечеткий контроллер реализует соответствующие законы управления как функции фазовых координат системы.
В качестве примера реализации основных этапов разработки нечеткого контроллера на рис. 6. а-д представлены лингвистические термы и связанные с ними нечеткие множества для переменных "ошибка" и ее первой, второй и третьей производных, а также "выход", cоответственно.

Результаты моделирования отклика на единичный скачок для системы с традиционным ПИД-регулятором (a), систем с оптимальной коррекцией во временной области (b) и нечеткой коррекцией (c) приведены на рис. 7. Исходные (опорные) значения параметров K_i ПИД-регулятора рассчитаны методом Циглера-Николса

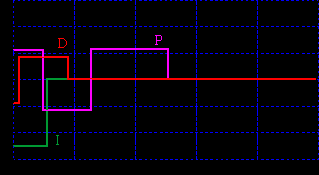Рис. 4	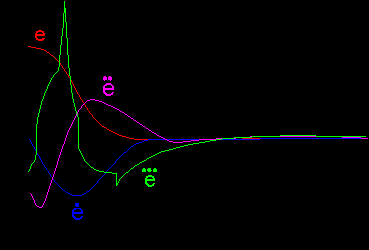Рис.5
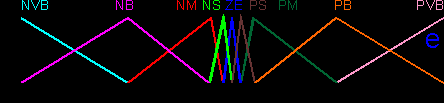Рис. 6а

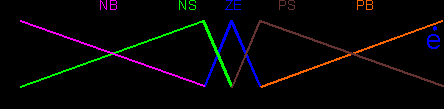Рис. 6б

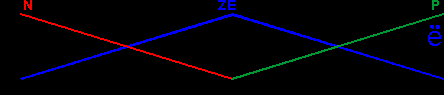Рис. 6в

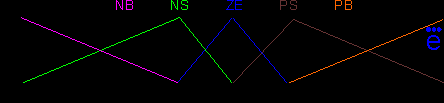Рис. 6г

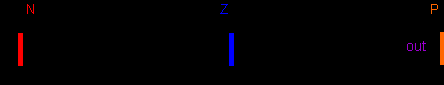Рис. 6д

		e
		NVB	NB	NM	NS	ZE	PS	PM	PB	PVB
... e	NB	P	P	P	Z	Z	Z	Z	P	N
	NS	P	P	Z	Z	Z	Z	Z	P	P
	ZE	P	P	Z	Z	Z	Z	Z	P	P
	PS	P	P	Z	Z	Z	Z	Z	P	P
	PB	N	P	Z	Z	Z	Z	P	P	P

Табл.1

Рис.7

В Таблице 1 приведена база правил нечеткого контроллера, реализующего коррекцию D - терма (на рис. 6 а-д и в Таблице 1 использованы следующие обозначения термов: NVB - отрицательное очень большое,
NB - отрицательное большое, NM - отрицательное среднее,
NS - отрицательное малое, нуль, PS - пололжительное малое,
PM - положительное среднее, PB - положительное большое,
PVB - положительное очень большое, P - положительное,
N - отрицательное).

4. Заключение

Таким образом, в работе продемонстрирована возможность построения систем с нечеткой динамической коррекцией параметров традиционных регуляторов. Использование методов нечеткого управления позволило получить качественный переходный процесс без использования громоздких вычислительных процедур, характерных для классического метода управления с использованием принципа максимума.

Список литературы:

[1] Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф.
Математическая теория оптимальных процессов. М:, Физматгиз, 1961.

Blog