Geum.ru

Структурная модель учебной дисциплины для нечёткого управления индивидуальным обучением

Вид материалаУрок
Подобный материал:
УДК 681.335:004.981

СТРУКТУРНАЯ МОДЕЛЬ УЧЕБНОЙ ДИСЦИПЛИНЫ ДЛЯ НЕЧЁТКОГО УПРАВЛЕНИЯ ИНДИВИДУАЛЬНЫМ ОБУЧЕНИЕМ

Т.Л. Мазурок

Южноукраинский национальный педагогический университет им. К.Д. Ушинского (г. Одесса)


Применение средств информационно-коммуникационных технологий (ИКТ) в обучении – многоаспектный, стремительно развивающийся процесс. Анализ опыта внедрения ИКТ в учебный процесс, развитие различных форм электронного обучения показали, что повышение эффективности их использования связано, прежде всего, с совершенствованием систем управления обучением.

Наиболее перспективным направлением создания таких систем является кибернетический подход, согласно которому необходимо выполнение следующей системы требований: указание цели управления; идентификация исходного состояния управляемого процесса; определение программы воздействия; обеспечение систематической обратной связи; обеспечение выработки регулирующих воздействий и их реализации.

Одной из основополагающих в методологии разработки систем управления обучением является проблема построения адекватной модели учебного материала, которая бы позволила формировать на основе известных взаимосвязей и степени влияния на достижение требуемой компетенции оптимальную траекторию обучения.

Прежде всего, в процессе формирования такой последовательности должны быть учтены логические связи между учебными элементами (УЭ). Входной информацией для блока управления обучением учебной дисциплины (УД) является множество УЭ с соответствующими параметрами, характеризующими достижение цели. Одним из способов повышения адаптации учебного материала к потребностям обучаемого является формирование индивидуальной последовательности УЭ. Целеустремлённость определяется на основе управления степенью взаимосвязей.

Рассмотрим формально е описание структурной модели УД. Пусть задано конечное множество УЭ 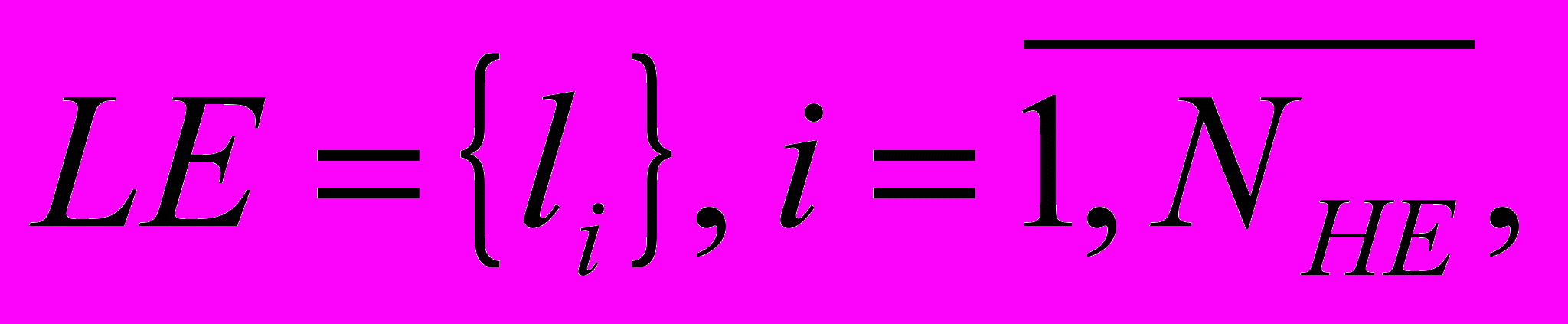нечёткое отношение , которое отображает субъективную меру эксперта-преподавателя по поводу взаимосвязи между двумя УЭ и задаётся функцией принадлежности. 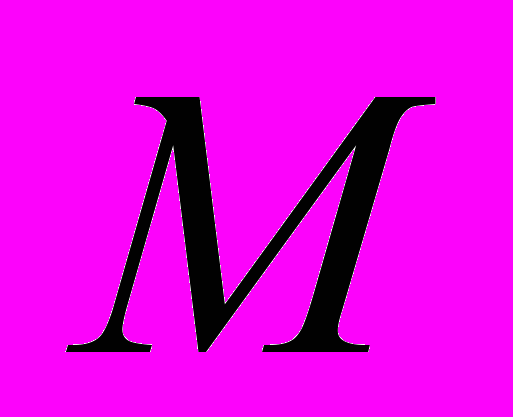- лингвистическая переменная, с помощью которой эксперты имеют возможность оценить степень взаимосвязи между УЭ средствами естественного языка. Множество термов лингвистических значений 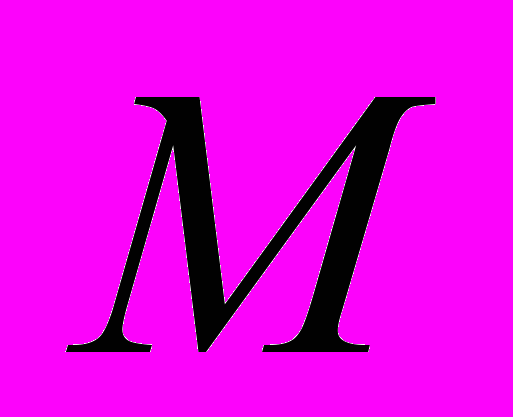следующее:

.

Использование аппарата нечётких множеств обосновано отсутствием точно измерения показателя степени взаимосвязи и субъективным характером его получения. Кроме нечётко заданной степени взаимосвязи необходимо учесть направление связи с помощью соответствующего знака. Таким образом, элементы матрицы инциденций нечёткого графа 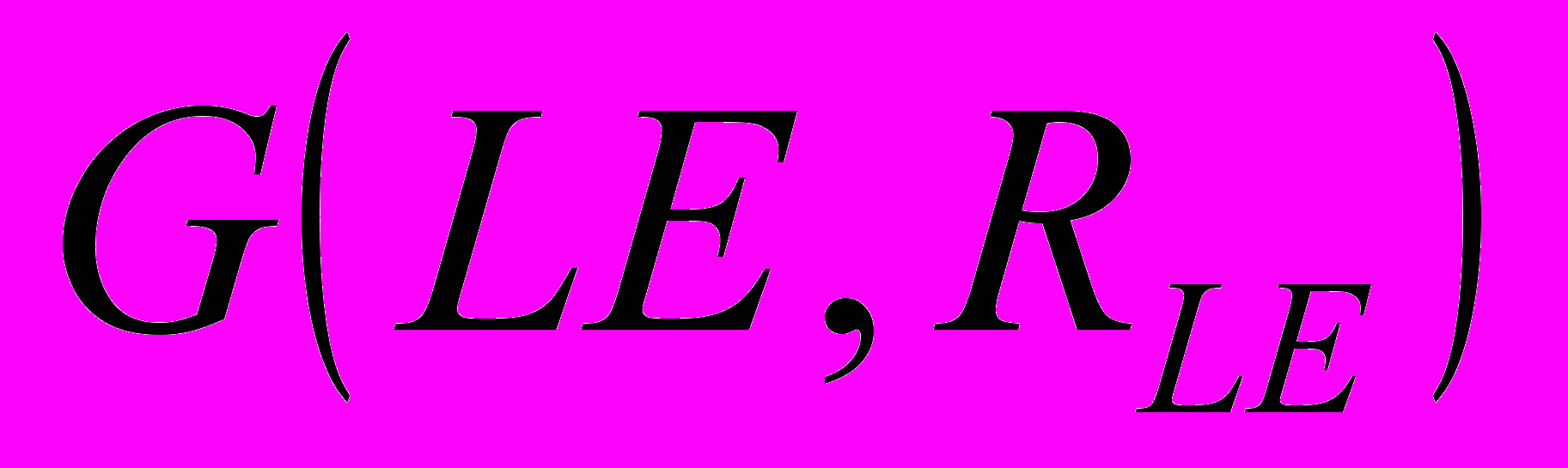образуются по следующей формуле: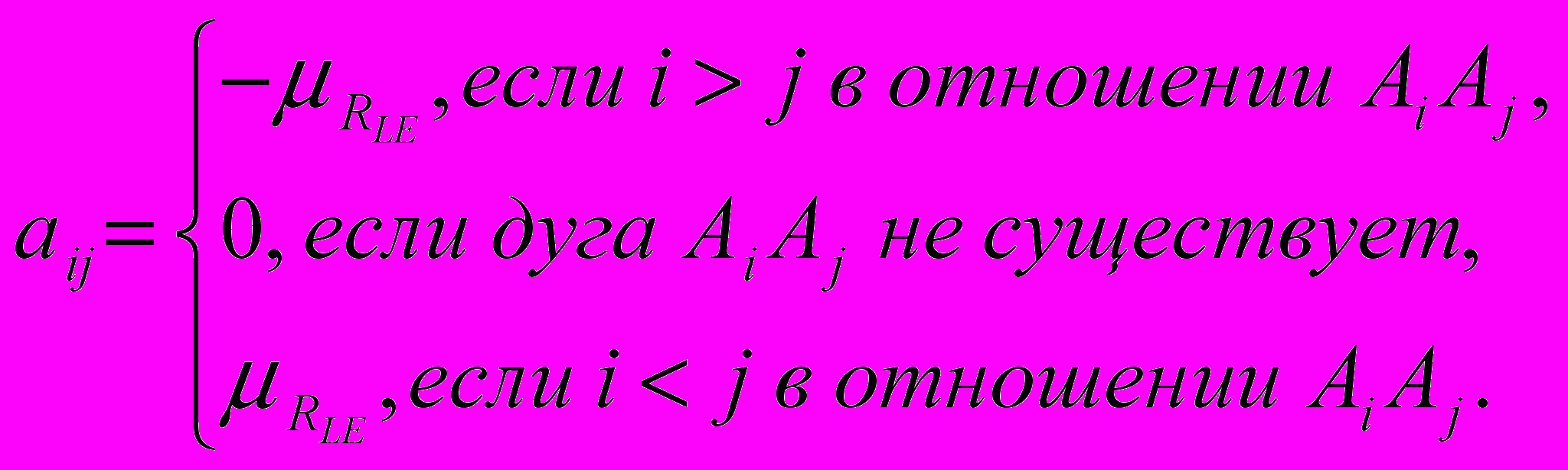



Все вершины нечёткого графа 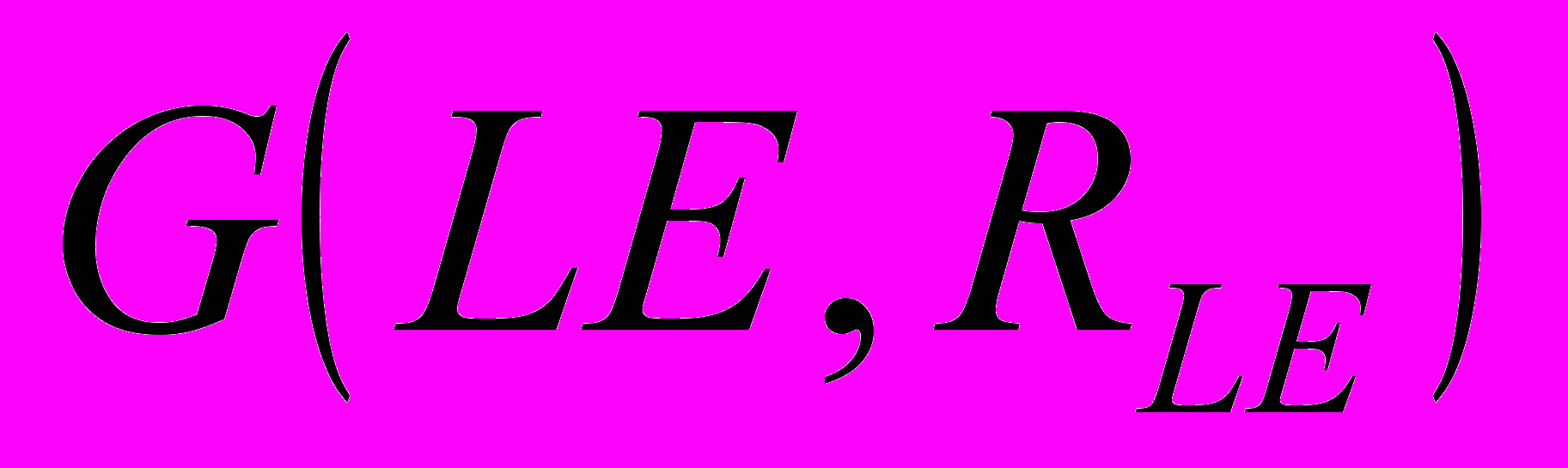делятся на четыре типа вершин в зависимости от их роли в создании структуры УД: базовые, транзитные, конечные (целевые), автономные. Формально условия идентификации могут быть записаны следующим образом:









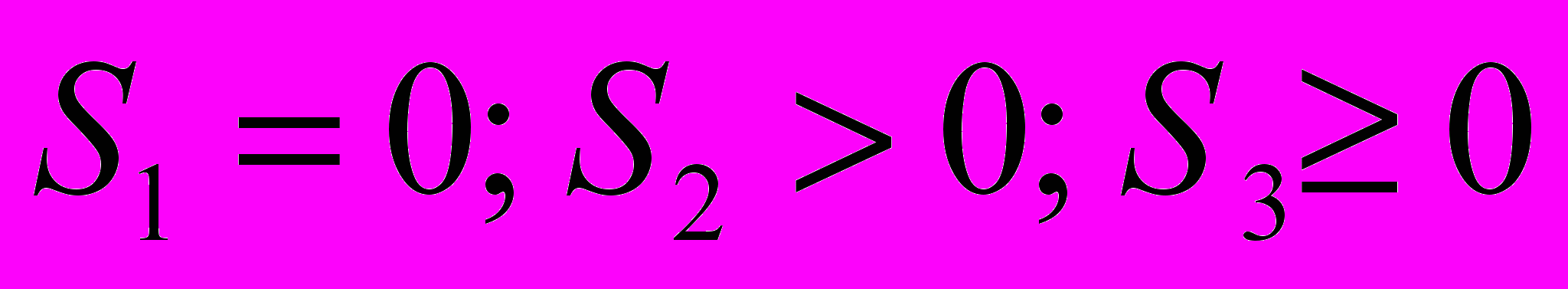
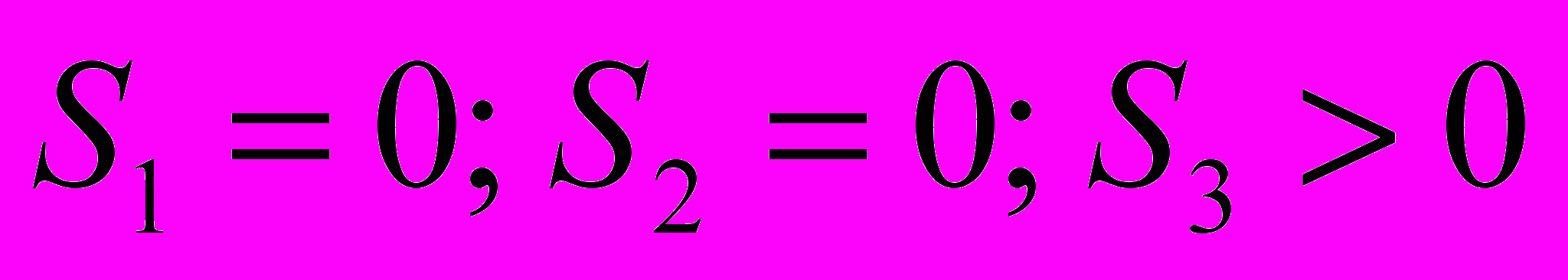
где 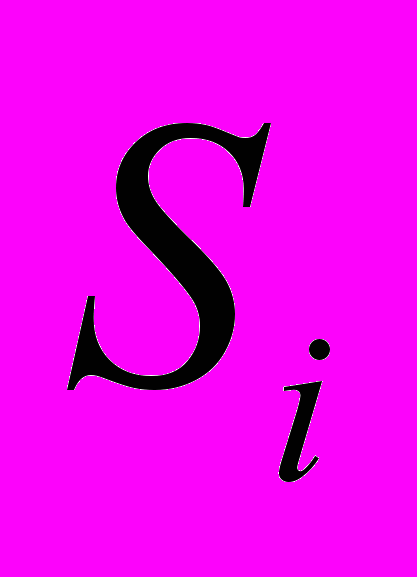, 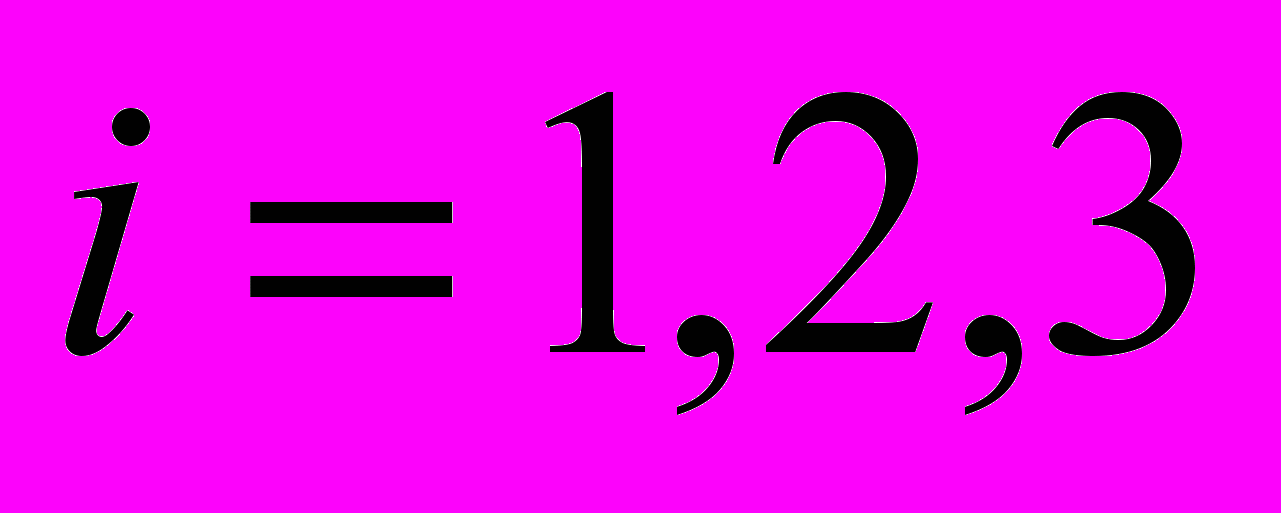- количество вершин, определяемое по таким формулам:





,

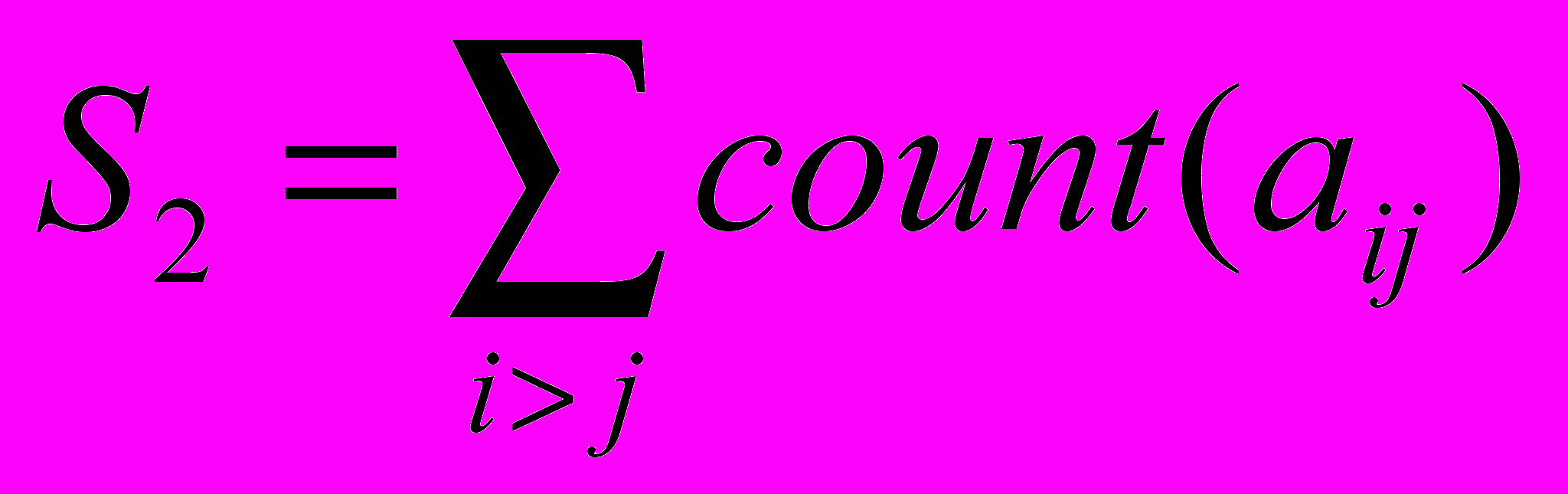
где 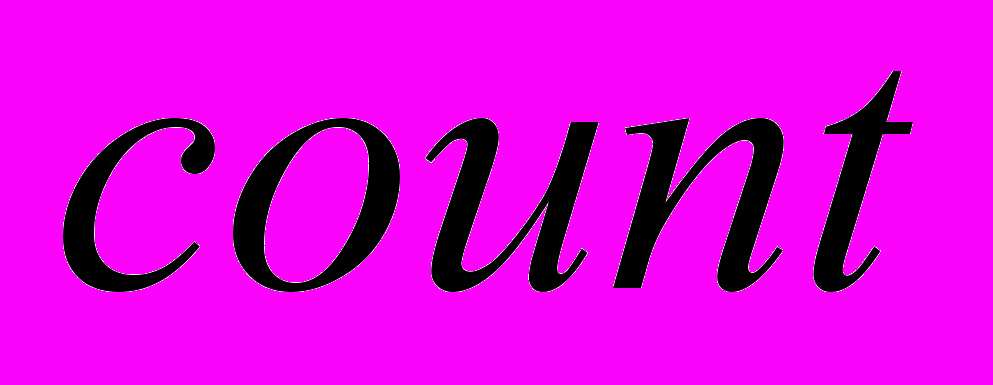- функция, определяющая количество вершин.

Таким образом, построение последовательностей УЭ сводится к процедуре формирования учебных логических блоков определённой структуры. Начало блока задаётся множеством базовых вершин, конец последовательности – конечные вершины, между ними, в общем случае, может быть множество транзитных вершин, кроме того, допустимо добавление автономных вершин при наличии резерва учебного времени. Такие учебные логические блоки являются результатом срабатывания правил нечёткого логического вывода, характеризуются полной выводимостью. Упорядочение последовательности изучения УЭ внутри групп основано на сокращении отрезка времени между временем изучения УЭ, связанных большей степенью взаимосвязи.