Элементарная теория работы полевых транзисторов физической основой работы полевого транзистора со структурой металл-диэлектрик-полупроводник является эффект поля

Вид материала

Документы

Содержание 3.6. Методы определения параметров МОП ПТ из характеристик.

Подобный материал:

• Лекция 4, 201.1kb.
• Методические указания к лабораторной работе по исследованию статических характеристик, 104.56kb.
• Полупроводниковые приборы, 355.8kb.
• Л. М. Чирок Математическая модель электрохимического датчика, 44.36kb.
• "Анализ и расчет статических параметров транзистора в схеме с общим затвором." по курсу, 229.13kb.
• Программа междисциплинарного экзамена для поступления в магистратуру по направлению, 51.62kb.
• Вприближении двухмерной модели атома водорода рассмотрены свойства мелких примесных, 25.62kb.
• Работа № ключевой режим работы транзистора, 358.55kb.
• Аннотация дисциплины, 786.67kb.
• 1. Какие требования предъявляются к транзисторам рэ в стабилизаторах с импульсивным, 463.58kb.

, поскольку ток стока от напряжения на стоке не зависит. Однако эффект модуляции длины канала, как было показано, обуславливает зависимость тока стока I_DS от напряжения на стоке V_DS в виде (3.16). С учетом модуляции длины канала величина дифференциального сопротивления R_i будет




Коэффициент усиления и в области отсечки больше единицы, его величина равна

(3.24)

Для типичных параметров МОП транзисторов W/L=20,

C_ox = 4·10-8Ф/см², =5 В, = 10В, =0,1 получаем омическое сопротивление в области плавного канала R_i= R₀ =125 Ом. Величина дифференциального сопротивления R_i и усиления в области отсечки будут соответственно равны R_i =5 кОм, =40.

Аналогично крутизне характеристики по затвору S можно ввести крутизну переходной характеристики S’ по подложке,

поскольку напряжение канал – подложка также влияет на ток стока.

|= const (3.25)

Подставляя (3.12) в (3.25), получаем

(3.26)

Соотношение (3.26) с учетом (3.8) и (3.17) позволяет по­лучить в явном виде выражение для крутизны передаточных характеристик МДП транзистора по подложке S’. Однако, поскольку в реальных случаях < 1, кру­тизна по подложке S’ ниже крутизны по затвору S.


3.5. Эквивалентная схема и быстродействие МДП транзистора.

Исходя из общефизических соображений, МДП транзис­тор можно изобразить в виде эквивалентной схемы, пред­ставленной на рис.11. Здесь R_ВХ обусловлено сопротив­лением подзатворного диэлектрика; входная емкость С_ВХ -емкостью подзатворного диэлектрика и емкостью перекрытия затвор-исток. Паразитная емкость С_ПАР обусловлена ем­костью перекрытий затвор-сток. Выходное сопротивление R_ВЫХ равно сопротивлению канала транзистора и сопротивлению легированных областей истока и стока. Выходная емкость С_ВЫХ определяется емкостью р-n перехода стока. Генератор тока , передает эффект усиления в МДП транзисторе.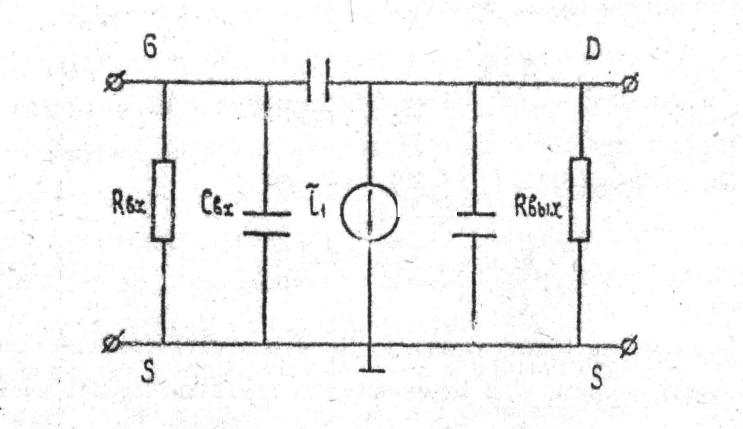





Рис.11. Простейшая эквивалентная схема МДП транзистора.

Определим быстродействие МДП транзистора, исходя из следующих соображений. Пусть на затвор МДП транзистора, работающего в области отсечки, так что

подано малое переменное напряжение .

Тогда за счет усиления в стоковой цепи потечет ток

(3.27)

Одновременно в канал с электрода затвора потечет паразитный ток смещения через геометрическую емкость затвора, равный

(3.28)


С ростом частоты выходного сигнала f паразитный ток будет возрастать и может сравниваться с током канала за счет эффекта усиления. Определим граничную частоту работы МДП-транзистора f= f_макс, когда эти точки будут равны. Получаем с учетом (3.22)

(3.29)


Поскольку напряжение исток-сток порядка напряжения , то, используя определение дрейфовой скорости

(3.30)

можно видеть, что предельная частота усиления f_макс определяется временем пролета электронов через канал транзистора

(3.31)


Оценим быстродействие транзистора. Пусть , длина канала

L = 10мкм =10-3 см, напряжение питания V_ПИТ=10В. Подставляя эти значения в (3.29), получаем, что максимальная частота для МДП-транзистора составляет вели­чину порядка f_макс1ГГц. Заметим, что собственное бы­стродействие транзистора обратно пропорционально квадрату длины инверсионного канала. Поэтому для повышения быстродействия необходимо переходить на субмикронные длины канала.


3.6. Методы определения параметров МОП ПТ из характеристик.

Покажем, как можно из характеристик транзистора определять параметры полупроводниковой подложки, диэлектрика и самого транзистора. Длину канала L и ширину W обычно знают из топологии транзистора. Удельную емкость подзатворного диэлектрика С_ОХ, а следовательно, и его толщину находят из измерения емкости C-V затвора в обогащении. Величину порогового напряжения V_T и под­вижность можно рассчитать как из характеристик в области плавного канала (3.10), так и из характеристик транзистора в области отсечки (3.12). В области плавного качала зависимость тока стока I_DS от напряжения на зат­воре V_GS - прямая линия. Экстраполяция прямолинейного участка зависимости I_DS(V_GS) к значению I_DS = 0 соот­ветствует, согласно (3.10),

(3.32)

Тангенс угла наклона зависимости I_DS(V_GS) определяет величину подвижности .

(3.33)

В области отсечки зависимость корня квадратного из тока стока I_DS от напряжения на затворе V_GS также согласно (3.12) должна быть линейной. Электрополяция этой зави­симости к нулевому току дает пороговое напряжение V_T.

Тангенс угла наклона зависимости определит величину подвижности

(3.34)

На рис.8 были приведены соответствующие зависимости и указаны точки электрополяции. Для определения величины и профиля легирования пользуются зависимостью по­рогового напряжения V_T от смещения канал-подложка V_SS. Действительно, как следует из(3.18), тангенс угла наклона зависимости определяет концентрацию легирующей примеси. Зная толщину окисла и примерное значение (с точностью до порядка для определения ) из (3.18) можно рассчитать величину и профиль распределения легирующей примеси в подложке МДП-транзистора.


(3.35)

Эффективная глубина z , соответствующая данному леги­рованию

(3.36)

Таким образом, из характеристик МДП транзистора можно рассчитать большое количество параметров, характеризую­щих полупроводник, диэлектрик и границу раздела между ними.


Глаза 4. ТОЧНАЯ ТЕОРИЯ РАБОТЫ МОП ПТ


4.1. Зонная диаграмма ОПЗ полупроводника в неравновесных условиях.

Рассмотрим область пространственного заряда (ОПЗ) полупроводника в неравновесных условиях, когда приложено напряжение между областями истока и стока и течет электри­ческий ток. Исток будем считать соединённым с подложкой. В этом случае между каждой точкой инверсионного канала и квазинейтральным объемом, так же как для случая сме­щенного р-n перехода, будет расщепление квазиуровней Ферми для электронов F_n и дырок F_p причем величина этого расщепления F_n - F_p =q V (y) зависит от координаты у, вдоль инверсионного канала. Поскольку в квазинейтральном объеме квазиуровни Ферми для электронов и дырок совпада­ют, то величина отщепления квазиуровня Формн электронов

F_n на поверхности полупроводника по отношению к уровню Ферми в нейтральном объёме будет равна

На рис.12 а) и б) приведены зонные диаграммы ОПЗ полупроводника соответственно в равновесных и неравновесных услови­ях, где указаны величины поверхностного потенциала и квазиуровня Ферми .

Будем рассматривать полупроводник, р-типа. Как следует из статистики заполнения электронами и дырками разрешен­ных зон, концентрация свободных носителей определяется расстоянием квазиуровня Ферми до середины запрещенной зоны.





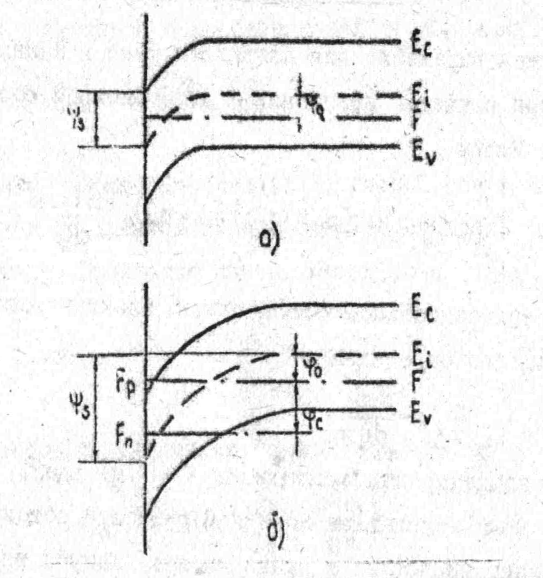
Рис.12. Зонная диаграмма поверхности полупроводника р-типа: а) при равновесных б) при неравновесных условиях.

Имеем, как видно из зонных диаграмм,


(4.1)





Легко проверить, что в (4.1) выполняется фундаментальное coотношение, касающееся произведения концентраций неравновесных носителей

(4.2)


4.2. Учет диффузионного тока в канале.

Запишем выражение для плотности тока в канале МДП транзистора с учетом дрейфовой и диффузионной составляю­щих тока. Имеем

(4.3)

Величина тангенциальной составляющей электрического поля Е_У согласно определению равна

(4.4)

Градиент концентрации электронов вдоль инверсионного канала обусловлен наличием разности потенциалов между областями истока и стока и, как следует из соотношения (4.1), определяется градиентом квазиуровня Ферми . Из (4,1) имеем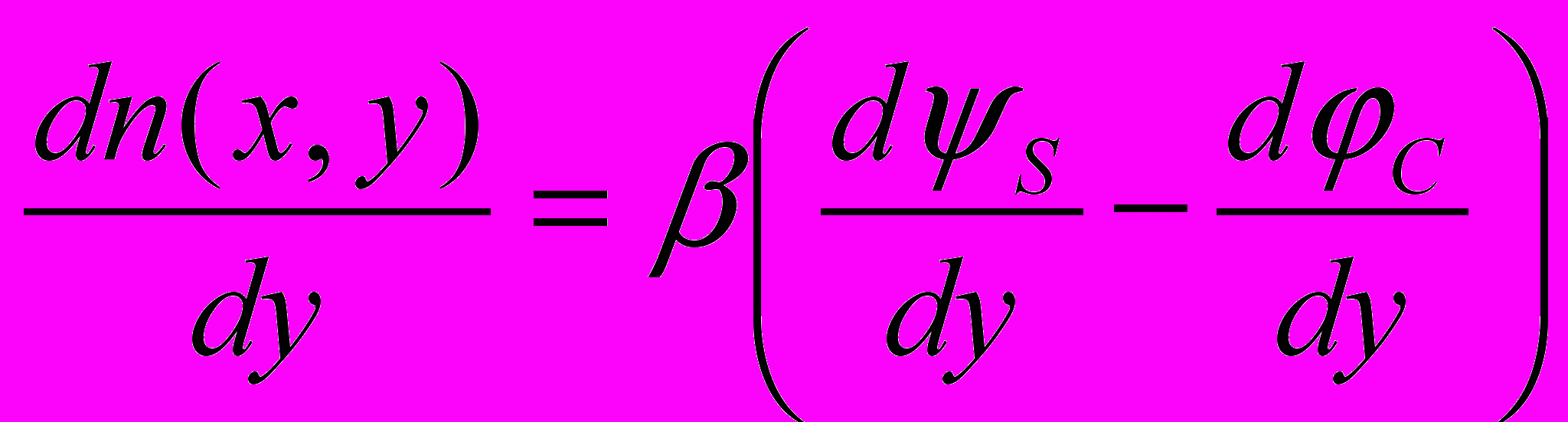




(4.5)


Воспользуемся соотношением Эйнштейна, связывающим подвиж­ность электронов и коэффициент диффузии D_n.



Подставим соотношения (4.4-4.5) в выражение для плотности тока (4.3). Получаем

(4.6)

Проведя интегрирование по глубине z и ширине х инверсионного канала транзистора аналогично рассмотренному в главе 3, приходим к выражению для тока канала I_DS в виде


(4.7)

Как следует из соотношения (4.7), полный ток канала I_DS обусловлен градиентом квазиуровня Ферми вдоль инверсионного канала. Дрейфовая составляющая тока I_др будет

(4.8)

Диффузионная составляющая тока I_диф будет

(4.9)

Если теперь из (4.7- 4.9) выразим доли дрейфовой и диффузионной составляющих тока, в полном токе канала МДП тран­зистора, то получим соответственно

(4.10)


(4.11)

Таким образом, чтобы получить выражение для вольтамперной характеристики МДП транзистора с учетом дрейфовой и диффузионной составляющих, необходимо: а) найти для соотношения (4.7) зависимость заряда неравновесных электронов Q_n как функцию поверхностного потенциала и квазиуровня Ферми , т.е. Q_n( , ); б) найти связь между поверх­ностным потенциалом и квазиуровнем Ферми =() и, на­конец в) найти зависимость поверхностного потенциала от напряжений на затворе V_GS к стоке V_DS.


4.3. Неравновесное уравнение Пуассона.

Запишем уравнение Пуассона для ОПЗ полупроводника р-типа, находящегося в неравновесных условиях в виде

(4.12)

Здесь n и р- неравновесные концентрации электронов и дырок, описываемые соотношением (4.1), и - кон­центрации ионизованных доноров и акцепторов. Подставляя (4.1) в (4.12) и учитывая, что в квазинейтральном объеме

,

получаем аналогично по сравнению с равновесным случаем

(4.13)

Проводя интегрирование уравнения (4.13), получаем первый интеграл неравновесного уравнения Пуассона в виде

(4.14)

Обозначим величину, равную

(4.15)

Знак электрического поля Е выбирается так же, как и в равновесном случае. Если >0 , то Е положительно, если <0 , поле Е отрицательно.

Согласно теореме Гаусса величина электрического поля на поверхности E_S однозначно определяет заряд Q_SC в ОПЗ.

(4.16)

Где L_D – дебаевская длина экранирования, определяемая соотношением



Для области инверсии, в которой работает МДП-транзистор, выражение для заряда Q_SC значительно упрощается. Действительно, поскольку величина положительна и велика, из (4.15) и (4.16) следует, что заряд Q_SC

Равен

(4.17)

заряд электронов Q_n в канале определяется разностью между полным зарядом Q_SC и зарядом ионизированных акцепторов ров Q_В

заряд

(4.18)

Для области слабой инверсии пока ионизованных акцепторов

(4.19)

Для области сильной инверсии, когда , заряд ионизованных акцепторов не зависит от поверхностного по­тенциала . Его величина равна

(4.20)

Здесь и далее мы приняли для простоты, что концентрация основных носителей дырок p_p0 в квазинейтральном объеме равна концентрации легирующей акцепторной примеси N_A. Выражения для заряда свободных носителей Q_n в канале получаем из (4.17- 4.20).

Для области слабой инверсии

(4.21)

Для области сильной инверсии

(4.22)


В начале области сильной инверсии, когда , для выражения заряда электронов Q_n в канале необходимо пользоваться соотношением (4.18), подставляя в него значе­ния Q_SC из (4.17), а значения Q_В из уравнения (4.20).

Таким образом, решение неравновесного уравнения Пуас­сона, даст выражения (4.21,4.22), описывающие зависимость заряда электронов Q_n в инверсионном канале МДП транзистора от поверхностного потенциала и квазиуровня Ферми.


4.4. Уравнение электронейтральности_в неравновесных условиях

Как уже отмечалось в разделе 4.2, для получения в яв­ном виде вольтамперной характеристики транзистора необходимо найти связь между поверхностным потенциалом и квазиуровнем Ферми . Рассмотрим для этого уравнение электронейтральности

(4.23)

Заряд в ОПЗ состоит из заряда свободных электронов Q_n в канале и заряда ионизованных акцепторов Q_В , так показано в (4.18). Разложим заряд Q_В по степеням вблизи порогового значения поверхностного потенциала .

Имеем

(4.24)


(4.25)

Величина - емкость обедненной области при пороговом значении поверхностного потенциала ,.

С учетом (4.24) и (4.25) соотношение (4.23) примет вид

(4.26)

Назовем пороговым напряжением V_Т напряжение на затворе МДП-транзистора V_GS в равновесных условиях () соответствующее пороговому потенциалу .

(4.27)

Из (4.26) и (4.27) следует, что

(4.28)


С учетом написанного для порогового напряжения соотношения (4.28) уравнение электронейтральности примет вид

(4.29)

Где n и будут

;


Множитель n - число, характеризующее отношение емкости поверхностных состояний и емкости обедненной области С_В к емкости подзатворного диэлектрика С_ОХ . Значения n могут лежать для реальных МДП структур в диа­пазоне от (1÷5). Величина характеризует отклонение в данной точке поверхностного потенциала от порогового зна­чения. Слагаемое в уравнении (4.29) соответствует заряду свободных электронов Q_n при пороговом значении поверхностного потенциала и обычно мало по сравнению с ос­тальными слагаемыми, входящими в правую часть уравнения (4.29).

Для области слабой инверсии заряд свободных электро­нов мал и последним слагаемым в (4.29) можно пренебречь. Поскольку напряжение на затворе V_GS и пороговое напряжение V_Т постоянные величины, то из (4.29) следует, что для области слабой инверсии в каждой точке инверсионного ка­нала величина




должна оставаться постоянной. Постоянную величину найдем из того условия, что вблизи истока = 0 и, следовательно


(4.31)

Отсюда следует, что в предпороговой области зависимость поверхностного потенциала от квазиуровня Ферми будет определяться следующим выражением

(4.32)

здесь - значение поверхностного потенциала в точке канала, где = 0 .

Величина m равна

(4.33)

Таким образом, в МДП-транзисторе в области слабой инверсии при отсутствии захвата на поверхностные состояния (; ) поверхностный потенциал не зависит от квази­уровня Ферми и следовательно постоянен вдоль инвер­сионного канала. Этот важный вывод обуславливает целый ряд особенностей в характеристиках МДП транзистора в области слабой инверсии.

Для области сильной инверсии при в уравнении (4.29) в правой части доминирует слагаемое, связанное со свободными носителями заряда Q_W . Поэтому требуется, чтобы вдоль канала в каждой точке величина за­ряда электронов Q_n оставалась постоянной. Поскольку в этой области для Q_n справедливо выражение (4.22), по­лучаем



Следовательно в области сильной инверсии

(4.34)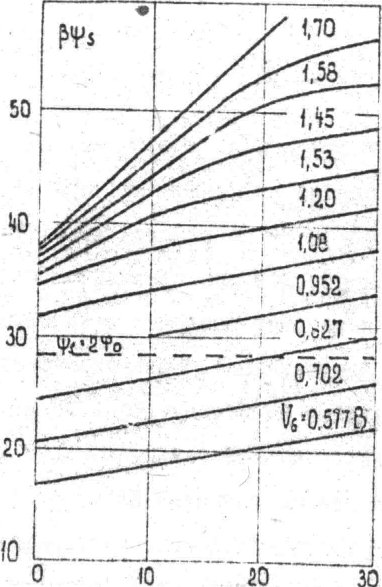





Рис.13. Зависимость поверхностного потенциала от величины квазиуровня Ферми в канале МОП ПТ при раз­личных напряжениях затвора V_G,B.

; ; ; .

Пунктирная линия соответствует условию .

На рис.13 в качестве примера приведен расчет функциональ­ной связи между и по уравнению (4.29), выполненный численным методом. Параметры для расчета указаны в подписи к рисунку.

Зная связь между поверхностным потенциалом и величи­ной квазиуровня Ферми можно получить соотношение между дрейфовой и диффузионной составляющей тока в произвольной точке канала. Действительно, из (4.10, 4.11) и (4.32) следует, что для области слабой инверсии

; (4.35)

В области слабой инверсии при отсутствии захвата ( N_SS=0, m=n) весь ток канала диффузионный. При наличии захвата на поверхностные состояния появляется дрейфовая составля­ющая. Физически она обусловлена появлением продольного электрического поля за счет различия в заполнении поверхностных состояний вдоль канала. При заполнении поверхност­ных состояний основными носителями тока инверсионного ка­нала дрейфовый и диффузионный ток имеют одно и то же на­правление. При условии постоянства плотности поверхностных состояний N_SS () запрещенной зоне полупроводника соотно­шение между диффузионной и дрейфовой составляющей в области слабой инверсии сохраняется.

Для области сильной инверсии из (4.10, 4.11) и (4.34) следует, что диффузионный ток равен нулю и весь ток ка­нала дрейфовый

; (4.36)

В области перехода от слабой к сильной инверсии доля дрей­фовой составляющей в полном токе канала возрастает от значения, определяемого соотношением (4.35), до единицы.


4.5. Вольтамперная характеристика МДП -транзистора в области сильной и слабой инверсии.

После того, как из решения уравнения Пуассона получена зависимость заряда свободных носителей Q_n (,) как функция поверхностного потенциала и квазиуровня Ферми, а из уравнения непрерывности - связь между поверхностным по­тенциалом и квазиуровнем Ферми, можно вернуться к выражению для тока канала (4.7) и получить в явном виде вольтамперную характеристику МДП транзистора.

В области сильной инверсии из (4. 7), (4.32) и (4.34)

следует, что

(4.37)

После интегрирования и учета того, что для области сильной инверсии в уравнении непрерывности (4.29) в правой части доминирует последний член, получаем

(4.38)

Отметим, что для области сильной инверсии, т.е. в приближении плавного канала ВАХ- МДП транзистора в виде (4.38) - совпадает с ВАХ, полученной ранее нами в простейшем случае в виде (3.10).

В области слабой инверсии из (4. 7), (4. 21) и (4.32) следует, что

(4.39)


После интегрирования (4.39) и учета того, что уравнение

непрерывности (4.22) дает для этого случая

(4.40)

получаем

(4.41)

Соотношение (4.41) представляет из себя вольтамперную характеристику МДП транзистора для области слабой инверсии. На рис.14,15 приведены проходные и переходные характерис­тики транзистора в этой области. Обращает на себя внимание тот факт, что в области слабой инверсии зависимость тока стока I_DS от напряжения на затворе V_GS экспоненциальная функция, причем экспоненциальный закон сохраняется на много порядков. Ток стока не зависит практически от напря­жения на стоке, выходя на насыщение при напряжениях исток- сток V_DS порядка долей вольта. Напомним, что при слабом захвате () ток канала имеет диффузионный характер. Для случая, когда МДП- транзистор работает при напря­жениях на затворе V_GS больше порогового напряжения V_T и напряжениях на стоке V_DS больше напряжения отсечки , т.е. в области насыщения тока стока, ситуация усложняется. Точка отсечки соответствует переходу от об­ласти сильной к области слабой инверсии. Слева к истоку от точки отсечки канал находится в области сильной инвер­сии, ток в канале дрейфовый, заряд свободных электронов постоянен вдоль канала. Справа к стоку от точки отсечки область канала находится в слабой инверсии, ток в канале диффузионный, заряд свободных электронов линейно изменя­ется вдоль инверсионного канала. На рис.13 видно, что об­ласть перехода от сильной к слабой инверсии на зависимости () выражается перегибом, что соответствует изменению соотношения между дрейфовой и диффузионными составляющими тока канала. Таким образом, в области отсечки ток в канале вблизи истока в основном дрейфовый, при приближении к сто­ку в области отсечки резко возрастет диффузионная составляющая, которая при нулевом захвате равна у стока полному току канала.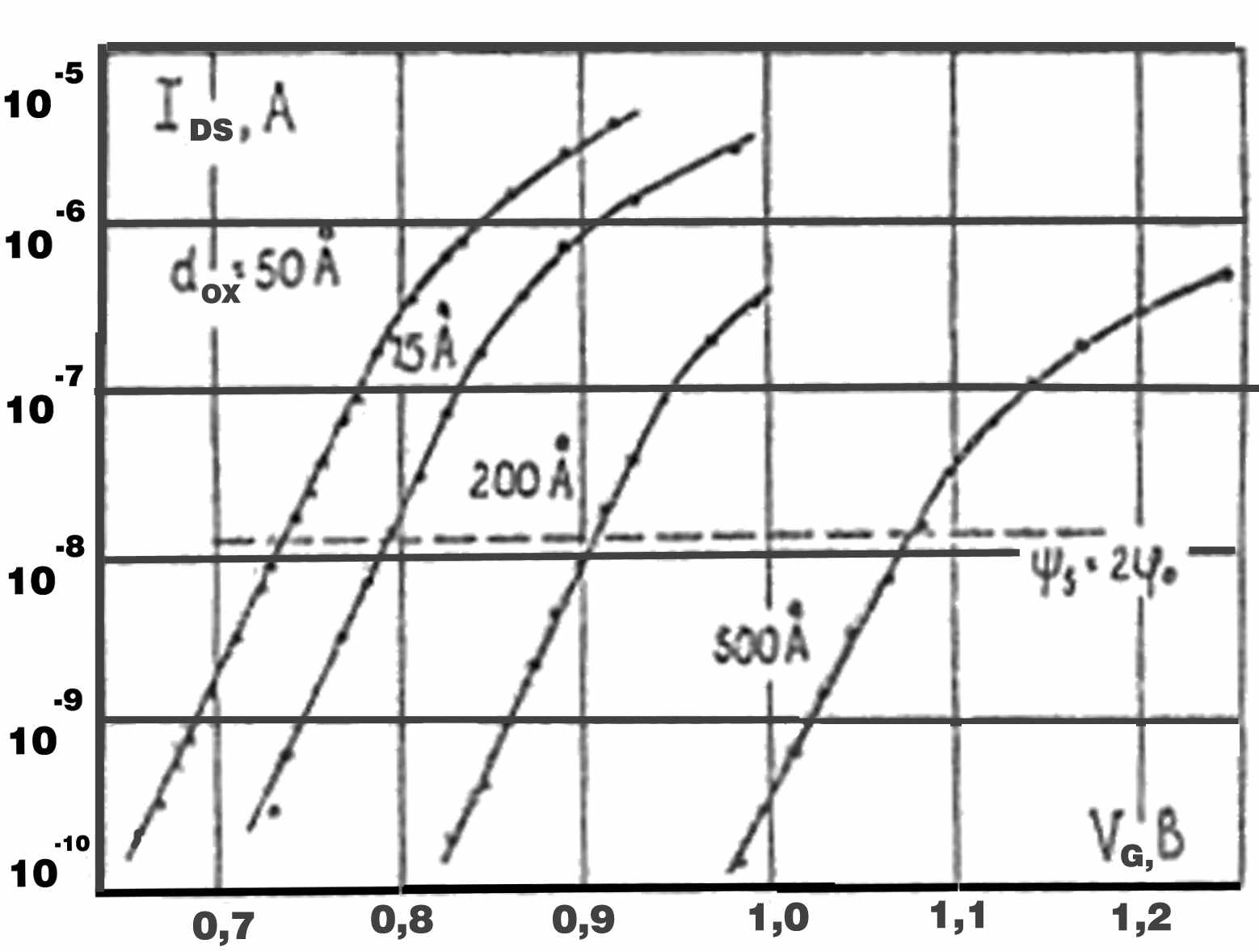





Рис.14. Зависимость тока стока I_DS от напряжения на затворе V_G в предпороговой области для МДП транзисторов с разной толщиной подзатворного диэлектрика. Стрелками на кривых показаны области перехода от экспонен­циальной к более плавной зависимости тока стока I_DS от напряжения па затворе. Напряжение исток-сток V_DS=0.025В.




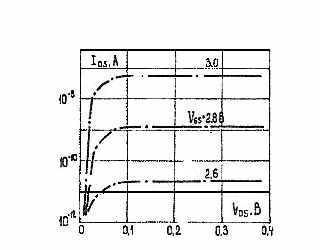
Рис.15. Зависимость тока стока I_DS от напряжения на стоке V_DS в области слабой инверсии при различных предпороговых значениях напряжения на затворе V_G. V_T=2.95В.


4.6. Распределение вдоль инверсионного канала квазиуровня Ферми.


Предыдущий анализ позволяет получить распределение вдоль инверсионного канала квазиуровня Ферми , его градиента и заряда свободных носителей Q_n(у). За основу возьмем Выражение для полного тока в канале в виде (4.7). Будем считать, что подвижность не меня­ется вдоль инверсионного канала. Из условия непрерывности тока следует, что произведение


(4.42)

должно оставаться величиной постоянной вдоль инверсионного канала. Заметим, что при больших величинах напряжения ис­ток-сток V_DS допущение о постоянстве подвижности = const може т не выполняться. Физически зависимость подвижности от положения вдоль канала может быть обусловлена ее зависимостью от концентрации свободных носи­телей. Поэтому в дальнейшем будем считать напряжение исток-сток V_DS малым, когда = const.

Для области слабой и сильной инверсий соотношения (4.21), (4.32), (4.22) и (4,34) дают соответственно

(4.43)

(4.44)

Где Q_n0 - заряд электронов в канале при =0 (или вблизи истока, или при равновесных условиях).

Проведем интегрирование уравнения (4.42) с учетом (4.43) и (4.44) и с граничными условиями

y=0; y = L; ;.

Предполагается, что длина канала L много больше области изменения легирующей концентрации вблизи стока и истока.





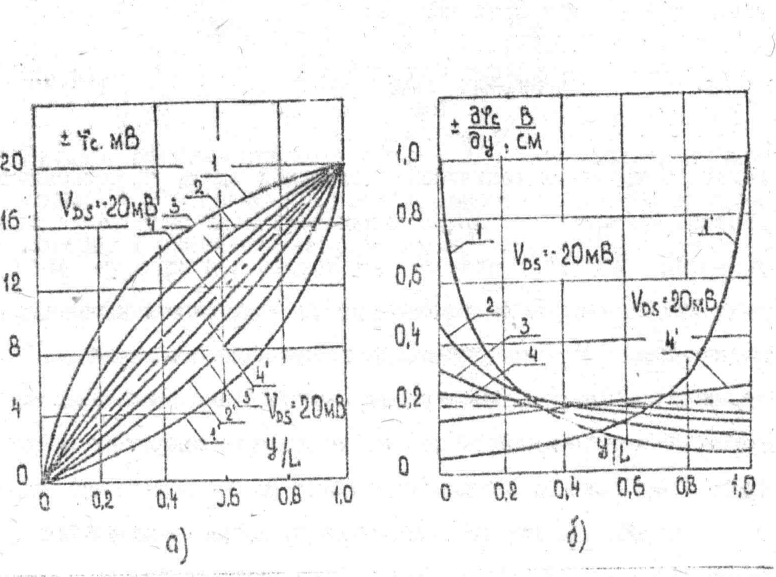
Рис16. а)распределение квазиуровня Ферми и б) гра­диента квазиуровня Ферми вдоль инверсионного канала.

1,1’ – m/n =1; 2,2’-m/n = 0,5; T=80K

3,3’-m/n = 1; 4,4’ – m/n = 0,5; T=290K

Пунктирная линия соответствует линейному распределению квазиуровня Ферми вдоль канала.


Получаем выражения для распределения квазиуровня Ферми вдоль канала в области слабой инверсии

(4.46)

Для градиента квазиуровня получаем после дифференцирования (4.46)


(4.47)

Поскольку вдоль инверсионного канала произведение (4.42) остается постоянным, то, следовательно, заряд свободных электронов Q_n линейно спадает вдоль канала, как вытекает из (4.47)

(4.48)

Ha рис. 16 приведены величины квазиуровня и его градиента как функция координаты вдоль канала у в области слабой инверсии.

Для области сильной инверсии (4.42) с учётом (4.44) и (4.45) дает

; ; (4.49)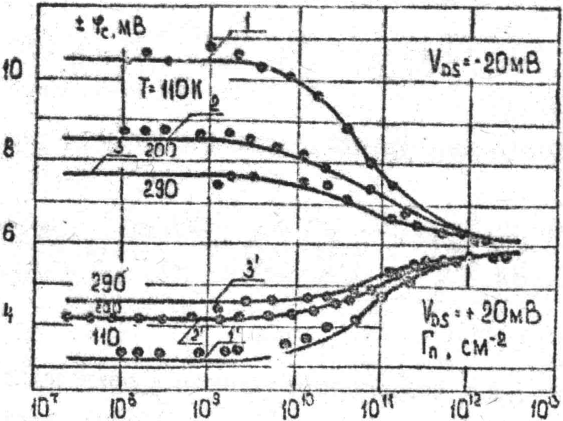



Рис. 17. Зависимость квазиуровня Ферми в точке кана­ла y/L=0.3 в зависимости от избытка электронов Г_n при равных температурах Т и напряжениях V_DS . Точки - эксперимент, сплошная линия - расчет.


Следовательно, в области сильной инверсии квазиуровень Ферми линейно меняется вдоль канала, заряд электро­нов постоянен в каждой точке канала. Отметим, что соотно­шения (4.22), (4.34), являющиеся основой(4.44), справедли­вы в области сильной инверсии, когда . Численный расчет уравнения (4.42) для всего реально изменяющегося диапазона поверхностных избытков Г_n приведен на рис.17. Из .рис.17 следует, что в области избытков Г_n<<109см-2 справедливы соотношения (4.46-4.48), а в области Г_n>1012см-2 соотношения (4.49). В промежуточной области необходим численный расчет .