Удк 004. 89 Реализация системы логического вывода для логики первого порядка на базе структурных функциональных моделей

Вид материала

Документы

Содержание Основные определения Логика высказываний Логика первого порядка Экспериментальные результаты Рис. 1. Результаты сравнения производительности машин вывода (а – на ЛВ, б – на ЛПП)Заключение

Подобный материал:

• «Искусственный интеллект.», 86.69kb.
• Удк 004. 838: 004. 853: 004. 855. 5: 004. 738. 5 Анализ эффективности работы web-сайта, 146.96kb.
• Системы искусственного интеллекта, 15.16kb.
• Лекция: Реализация файловой системы, 382.58kb.
• Задача декомпозиции электронной вычислительной аппаратуры, получившая название компоновки,, 264.9kb.
• Удк ?????? О верификации динамических свойств систем взаимодействующих агентов, 167.14kb.
• Б. Д. Плющенков 1/2 года I. Общая теория дифференциального уравнения (нелинейного), 16.96kb.
• Программа дисциплины Логика для специальности 080102. 65 «Мировая экономика», 146.32kb.
• В. А. Смирнова по теории логического выво­да с учетом их внутренней взаимосвязи и научной, 181.75kb.
• Удк 519. 816 Способ представления термов в логике предикатов первого порядка. Алгоритм, 184.64kb.

УДК 004.89


Реализация системы логического вывода для логики первого порядка на базе структурных функциональных моделей


Implementation of a first-order logic reasoner based on a structural functional model


Пинжин А.Е.

Email: alex_pinjin@tpu.ru


В настоящее время наблюдается повышенный интерес к методам интеллектуальной обработки информации, который проявляется как на уровне отдельных организаций, так и на уровне глобальных информационных систем. Появление и развитие парадигмы Semantic Web [1] также формирует потребность в эффективных средствах представления и обработки знаний. Важной компонентой многих систем обработки знаний является машина логического вывода, эффективность которой остается важной проблемой современных исследований.

Стандартные машины вывода опираются на классический метод резолюций и различные его вариации [2]. Наиболее эффективным и часто используемым (особенно в зарубежных источниках) считается табличный (tableaux) метод, который позволяет добиться линейных затрат на осуществление вывода относительно объема исходной базы знаний [3]. Подход, представленный в [4, 5] предлагает альтернативный алгоритм вывода на основе теории структурных функциональных моделей (С-моделей) [6]. С-модель базируется на определении функциональной связи и изначально разрабатывалась для доказательства теорем с целью последующего синтеза структурных программ. В [7] показано, каким образом функциональные связи могут быть интерпретированы в виде дизъюнктов Хорна. Основной целью доклада является краткое обоснование применимости С-модели для различных логических исчислений: логики высказываний (ЛВ), логики первого порядка (ЛПП). Приведены результаты опытного сравнения производительности предлагаемого алгоритма с существующими реализациями.


Основные определения


Кратко перечислим основные определения, исходя из [6]:

Определение 1. Сигнатурой будем называть четверку =(A,F,P,D), где A, F, P и D – множества (элементарных) имен величин (атрибутов), функциональных символов, селекторных символов и имен схем, соответственно. Считается, что выделено непустое конечное подмножество ED имен примитивных или первичных схем (или типов).

Исходные данные для машины вывода поставляются в виде набора схем отношений. Для упрощения рассуждений будем рассматривать простые схемы без подсхем, вариантной части и рекурсивных вхождений.

Определение 2. Структурная функциональная модель (С-модель), представляет собой конечную совокупность схем М=(T₁,…,T_s).

Определение 3. Простой схемой T объекта t будем называть выражение вида

T(t)=(T₀(a₀),T₁(a₁),…,T_n(a_n) | f_set), (1)

где T – имя схемы, a₀,a₁,…,a_n – собственные атрибуты (величины) схемы T; T_0, T₁,…,T_n  E – собственные (примитивные) подсхемы схемы T, определяющие тип соответствующих им атрибутов.

Выражение f_set в завершающей части описания схемы скрывает множество функциональных связей схемы T.


Определение 4. Функциональная связь (ФС) определяется выражением вида
f: a₁,…,a_na₀, где f – имя, a_i – аргументы, a₀ – результат ФС. Функциональная связь входящая в схему Т, называется допустимой, если и только если a₀,a₁, …,a_n – собственные атрибуты схемы T. В дальнейшем будем рассматривать только синтаксически правильные схемы, где f_set содержит только допустимые ФС.

Постановка задачи планирования в С-модели М может быть представлена следующим образом:

S=(T(t),A₀,X₀), (2)

где t – непервичный атрибут схемы ТМ, на которой ставится задача, A₀ и X₀ – наборы имён соответственно исходных и искомых атрибутов, принадлежащих T.


Логика высказываний


Каждой (примитивной) величине a_ij ставится в соответствие примитивное высказывание A_ij, а функциональный символ интерпретируется как знак логического следствия. Тогда множество ФС схемы может быть представлено в виде следующего выражения:

A₀A₀₁…A_{0n, …,} A_kA_k…A_kn,


либо в виде набора Хорновских дизьюнктов:


A₀A₀₁…A_{0n, …,} A_kA_k…A_kn (3)


Задача планирования (2), при A₀ = {a₁, …, a_i}, X₀ = {a_i+1, …, a_j}, для постановки задачи проверки выполнимости набора высказываний (sat-problem) интерпретируется как X₀A₀ , что, совместно с (3) соответствует:

A₁ (4)

…

A_i

 A_i+1

…

 A_j

Приведенная интерпретация позволяет использовать алгоритмы вывода на С-модели для автоматического доказательства достаточно широкого множества теорем.


Логика первого порядка


Согласно [8] возможно приведение вывода высказываний логики первого порядка (ЛПП) к выводу в логике высказываний.

Приведем некоторый набор высказываний ЛПП, находящихся в стандартной форме и сформулируем задачу вывода:

z(A₀(z)A₀₁(z)…A_0n(z)_{, …,} A_k(z)A_k(z)…A_kn(z)

A₁(z)

…

A_i(z)

 A_i+1(z)

…

 A_j(z))


Вполне очевидно, что пропозиционализация этих высказываний приводит теорему к виду (3, 4), а значит и к (2).


Экспериментальные результаты


Реализация машины вывода на С-модели подробно описана в [5]. Для целей сравнения были разработаны конвертеры формата данных С-модели в различные форматы [9–11], используемые машинами вывода, выбранными для сравнения. В приведенной ниже таблице приведен список реализаций машин вывода, вид логики и формат исходных данных:

Машина вывода	Логика	Формат данных
miniSat (sat4j)	ЛВ	cnf
Darwin 1.4.1	ЛПП	tme
paradox2.2	ЛПП	tptp-fof
iProver0.2	ЛПП	tptp-fof

Поясним выбор реализаций машин вывода. Пакет Sat4j содержит реализацию алгоритма miniSat, который показал максимальную производительность согласно итогам конкурса по решению SAT-проблемы в 2006 г. [12]. Darwin, Paradox, iProver– являются номинантами конкурса CADE ATP System Competition (CASC) 2007, проводимом ежегодно в рамках конференции по автоматизированному логическому выводу (Conference on automated deduction – CADE) [13]. Отметим, что реализацию Vampire 8.0, 9.1 не удалось задействовать по причине закрытого описания входных параметров.

Для целей сравнения выполнялась генерация и последующая конвертация схем числом ФС от 10 до 250 и равным количеством входных атрибутов. Аргументы и цели ФС связывались таким образом, чтобы обеспечить необходимость обработки всех элементов при осуществлении вывода.

Результаты испытаний приведены на рис. 1. Отметим, что при измерении времени работы алгоритмов на ЛПП учитывается время загрузки исходных данных, поэтому на графике а) результаты работы алгоритма вывода на С-модели отличаются от аналогичных результатов на б) и в).


а) б)




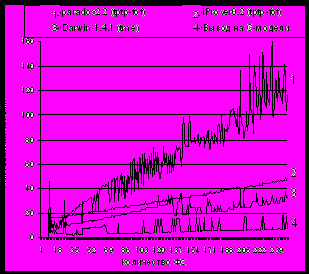
Рис. 1. Результаты сравнения производительности машин вывода

(а – на ЛВ, б – на ЛПП)


Заключение


Безусловно, эмпирические результаты нельзя считать абсолютным показателем относительной производительности разных алгоритмов. Проводя испытания, автор ставил своей целью показать, что предлагаемый алгоритм может быть использован для вывода на различных логиках и показывает хорошие показатели эффективности и может составить конкуренцию существующим реализациям. Особо следует отметить, что в расчет издержек не включались затраты на представление исходной модели в виде специальных структур данных, на которых основан разработанный алгоритм вывода. Эти структуры подготавливаются однократно и могут быть использованы для постановки любых задач, допустимых в данной модели, однако возможность внесения изменений в подготовленные структуры данных остается предметом дальнейших исследований. Из этого следует, что на текущий момент практическое применение предлагаемого алгоритма обосновано и эффективно для достаточно устойчивых моделей.


Список источников

1. Berners-Lee T., Hendler J., Lassila O. The Semantic Web // Scientific American Magazine. –2001. – V. 284. – № 5. – P. 34–43.
   
2. Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем. – М: Наука, 1983. – 358 c.
   
3. Baader F., Sattler U. An overview of tableau algorithms for description logics // Studia Logica. – 2000. – V. 69. – № 1. – P. 5–40.
   
4. Новосельцев В.Б. Синтез рекурсивных программ в системах управления пакетами прикладных программ: Дис. … канд. техн. наук. – Институт теоретической астрономии академии наук СССР. – Л., 1985. – 50 с.
   
5. Новосельцев В.Б., Пинжин А.Е. Реализация эффективного алгоритма синтеза линейных функциональных программ // Известия Томского политехнического университета. – 2008. – Т. 312. – № 5. – С. 32–35.
   
6. Новосельцев В.Б. Теория структурных функциональных моделей // Сибирский математический журнал. – 2006. – Т. 47. – № 5. – С. 1014–1030.
   
7. Новосельцев В.Б. Эффективный нерезолютивный вывод для ограниченного исчисления хорновских дизъюнктов // Известия Томского политехнического университета. – 2008. – Т. 312. – № 5. – С.32–36.
   
8. Рассел С., Норвиг П. Искусственный интеллект: современный подход (AIMA). 2-е изд. – Вильямс. – 2007. – С. 381–384.
   
9. SAT DIMACS Challenge – Satisfiability: Suggested Format [Электронный ресурс]. – 1993. – Режим доступа: ftp://dimacs.rutgers.edu/pub/challenge/satisfiability/doc/ satformat.tex.
   
10. TME input specification [Электронный ресурс]. – Режим доступа: oblenz.de/ag-ki/Systems/Protein/tme-syntax.txt.
    
11. TPTP syntax v3.5.0 [Электронный ресурс]. – Режим доступа: ami.edu/~tptp/TPTP/SyntaxBNF.php.
    
12. SAT-Race 2006: Runtime comparison of all SAT-Race solvers [Электронный ресурс]. – 2006. – Режим доступа: t/sat-race-2006/analysis.php
    
13. The CADE ATP System Competition, part of the The 21st International Conference on Automated Deduction [Электронный ресурс]. – Bremen, Germany. – 17–20th July 2007. – Режим доступа: ami.edu/~tptp/CASC/21/.