Задача декомпозиции электронной вычислительной аппаратуры, получившая название компоновки, решается для разных структурных иерархических уровней: при компоновке функциональных элементов в модули типовых интегральных микросхем;

Вид материала

Задача

Подобный материал:

• Система контроля и анализа технических свойств интегральных элементов и устройств вычислительной, 582.84kb.
• Темы рефератов История развития интегральных микросхем. Факторы прогресса технологии, 23.95kb.
• Основы рациональной компоновки оборудования, 300.67kb.
• Лекции, лабораторные занятия, курсовая работа, консультации, самостоятельная работа, 23.03kb.
• Программа вступительных испытаний в магистратуру кафедры «Проектирование и конструирование, 138.26kb.
• Программа по дисциплине "Технология микросхем и микропроцессоров" разработана на основе, 170.65kb.
• За последние годы в области вычислительной техники произошли существенные изменения, 1117.32kb.
• Программа вступительных испытаний в магистратуру по направлению 210100 68 «Электроника, 119.24kb.
• 10. Статистические параметры логических элементов. К статистическим параметрам, 1066.17kb.
• С. А. Бирюков цифровые устройства на интегральных микросхемах, 1072.73kb.

АВТОМАТИЗИРОВАННОЕ РЕШЕНИЕ ЗАДАЧИ ДЕКОМПОЗИЦИИ СЛОЖНЫХ ОБЪЕКТОВ В САПР.


1.Цель работы. Изучение типовой задачи оптимизации комбинаторно-логического типа и последовательно-итерационных методов её решения.


2.Формулировка задачи декомпозиции.


При решении задач проектирования конструкций современной ЭВА , задач распределения алгоритмов и программ в коллективах вычислителей и микроконтроллерных сетях возникает необходимость разбиения (декомпозиции) аппаратуры на отдельные части , соответствующие унифицированной конструктивно-технологической базе, а также выделения программных блоков, размещаемых в вычислителях с заданными характеристиками. Решение указанных задач требует декомпозиции сложных объектов проектирования (аппаратуры, программ) на блоки по заданным критериям оптимизации и при наличии ограничений.

Так, при декомпозиции программ в качестве критериев оптимальности применяется минимальная стоимость (количество) используемых программируемых БИС или микроконтроллеров, а также минимум числа переключений вычислителей в процессе решения задачи. Ограничениями в таких задачах являются объёмы памяти используемых БИС, число их входов и выходов, а также ограничения на совместную работу параллельных ветвей алгоритмов и программ в одной БИС.

Задача декомпозиции электронной вычислительной аппаратуры, получившая название компоновки, решается для разных структурных иерархических уровней: при компоновке функциональных элементов в модули типовых интегральных микросхем; модулей в ТЭЗы; ТЭЗ в панели, субблоки, блоки, и т.д., до вычислительных комплексов, компонуемых из шкафов, стоек, соединительных кабелей. Решение задачи компоновки на разных уровнях иерархии сводится к объединению модулей низшего (i-1)-го уровня в модули более высокого i-го уровня с учётом ограничений и критериев оптимизации. Подробную характеристику задач компоновки можно найти в работах [1,3].

Рассмотрим постановку задачи декомпозиции сложного объекта на примере задачи компоновки коммутационной схемы, выбрав в качестве критерия суммарное число внешних связей отдельной конструктивной части. Такой подход является наиболее универсальным, так как число внешних соединений между частями коммутационной схемы для любого уровня иерархии определяет надежность ЭВА и упрощение конструкции. Применительно к программному обеспечению данный критерий отражает число прерываний работы отдельного модуля и передачу управления другим программным модулям.

Для алгоритмизации и формального решения задачи производится переход от коммутационной схемы к её графовой модели: мультиграфу или гиперграфу [2].

Задача декомпозиции формируется как задача разбиения графа G(X,U) на части G_i(X_i,U_i), i=1,2,...k, где k-число частей, на которое разбивается граф. Причём, совокупность частей B(G)={G₁,G₂,...,G_k} является разбиением графа G, если: любая часть из этой совокупности не пустая; для любых двух частей из B(G) пересечение множества вершин пусто; пересечение множества рёбер может быть не пустым; объединение всех частей из B(G) в точности равно графу G. Требуется разбить граф G(X,U) на части так, чтобы число рёбер U_ij, соединяющих эти части было минимальным:

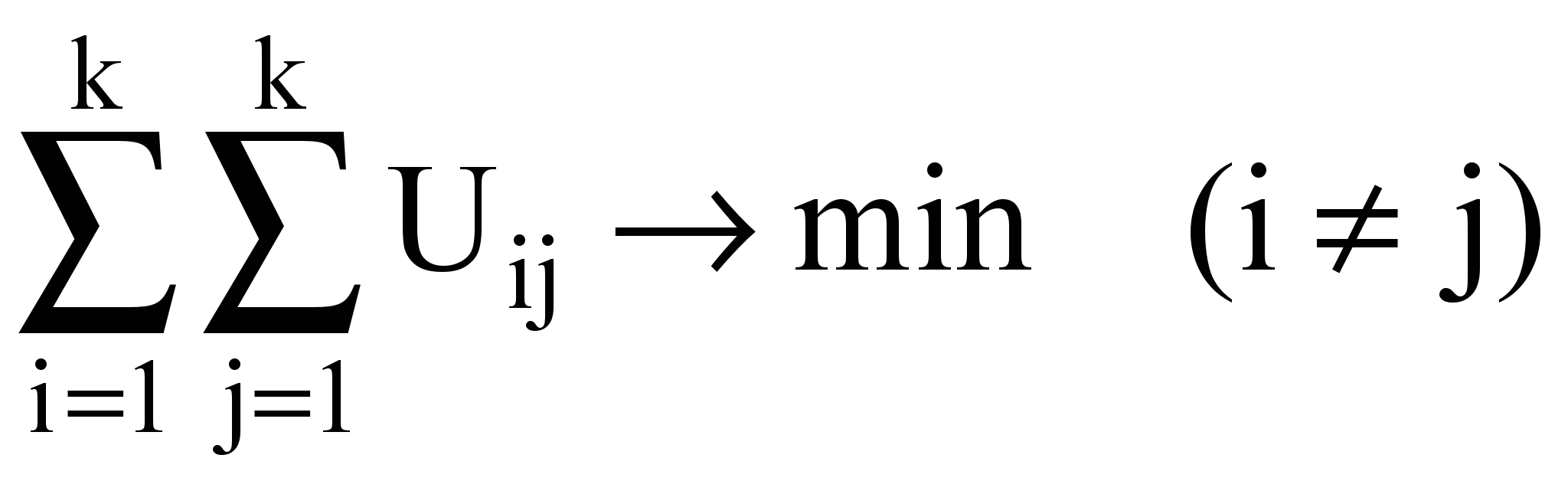(1)

Получение оптимального результата в данной задаче связано с полным перебором различных вариантов разбиения, что практически неприемлемо даже для схемы средней размерности.

Из математических методов для решения данной задачи используют метод ветвей и границ и решение задачи о назначении [1] , однако для реальных устройств они требуют значительных временных затрат.

Практическое применение нашли эвристические алгоритмы разбиения, позволяющие за конечное число шагов получить локальный минимум, который в общем случае достаточен для практических целей.

Эффективными по трудоёмкости являются последовательно-итерационные алгоритмы, в которых на первом этапе выполняется предварительная компоновка частей, а затем итерационное улучшение начального варианта путём парного или группового обмена вершин из разных частей.


3. Последовательный метод декомпозиции.


В предыдущем разделе был сформулирован критерий (1) разрезания графа на подграфы. Запишем его в виде:

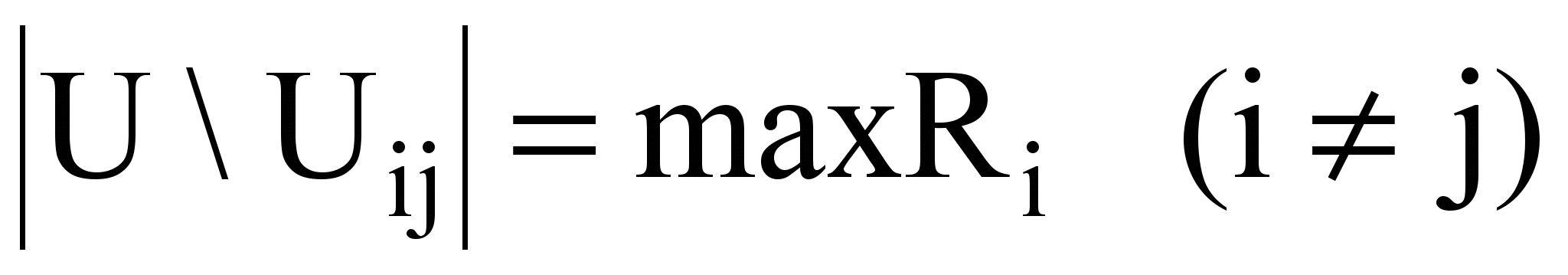(2)

где R_i- число рёбер в подграфе G_i(X_i,U_i). Критерий (2) означает, что подграф G_i должен иметь максимальное число рёбер, т.е. быть максимально связным.

Формирование подграфов в соответствии с критерием (2) составляет суть последовательных алгоритмов разрезания, на каждом шаге которых в очередную часть графа добавляется максимально связная с ним вершина. Получим зависимость для выбора вершины x_j (X\X_t), подсоединяемой к формируемому подграфу G_t(X_t,U_t). Приращение числа внешних связей подграфа G_t после подсоединения к нему вершины x_j будет равно:

DL=L2-L1, где

L1 - число внешних связей подграфа G_t с вершиной x_j до её включения в G_t;

L2 - число внешних связей вершины x_j после её включения в подграф G_t.

Пусть Е множество номеров вершин подграфа G_t , r(x_j) локальная степень вершины x_j.

Тогда ,

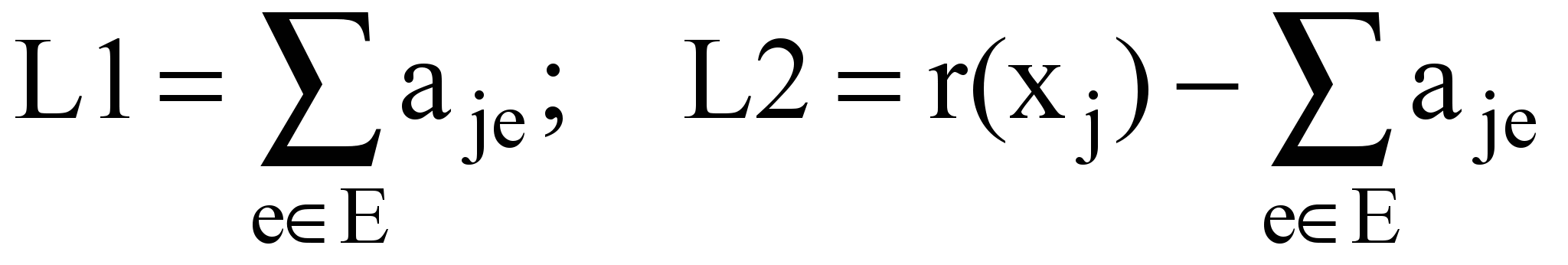где а_je – элемент матрицы смежности А .

Откуда легко получить выражение для DL:

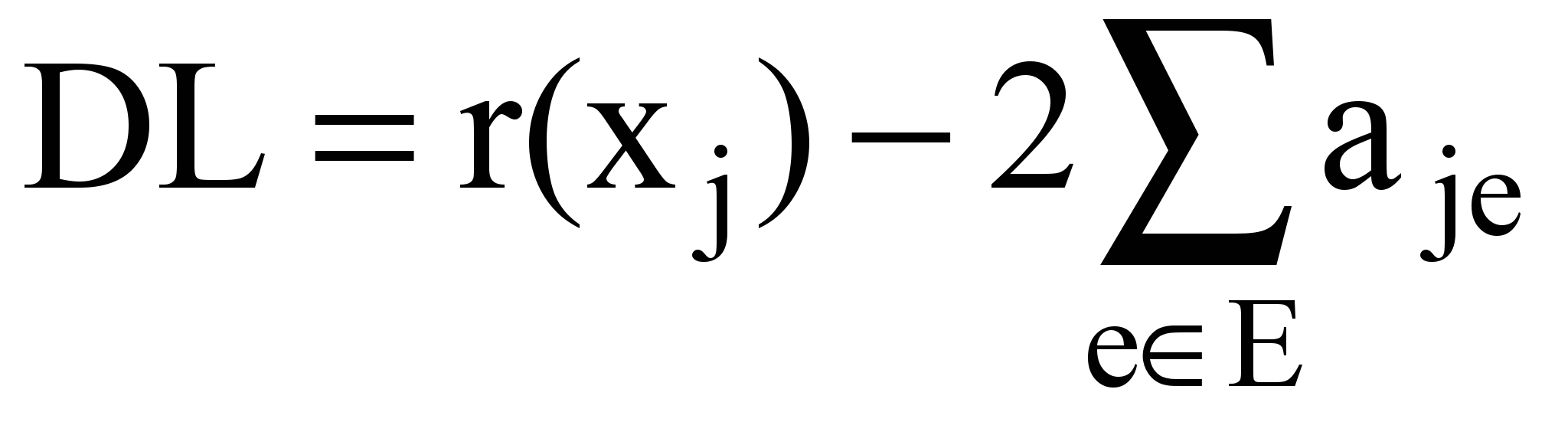(3)

Очевидно, подсоединяться к подграфу должна вершина, дающая уменьшение внешних связей подграфа (DL<0), либо минимальное приращение (DL>0).

Различные последовательные алгоритмы разрезания различаются используемыми ограничениями и требованиями (по числу подграфов, по числу элементов в подграфах, по требованиям на раздельное закрепление вершин за подграфами и пр.) [1,3].

Рассмотрим алгоритм последовательного разрезания мультиграфа G(X,U) на произвольное число подграфов с ограничениями на число n элементов в подграфе (n<=N) и максимально допустимое число m внешних связей подграфа (m<=M).

1. В графе G(X,U) выбирается вершина x_iX с r(x_i)=min. Если таких вершин несколько, выбирается вершина с максимальным локальным числом кратных рёбер и включается в формируемый подграф G_t: X_t=X_t U x_i

2. По матрице смежности А определяется множество Г(X_t) смежных с G_t вершин и определяются их относительные приращения DL по формуле 3.

3. Из множества Г(X_t) выбирается вершина x_j с минимальным приращением DL, а если таких вершин несколько, выбирается вершина с r(x_j)=max и включается в G_t:X_t=X_t U x_j.

4. Определяется и фиксируется число внешних связей подграфа G_t:



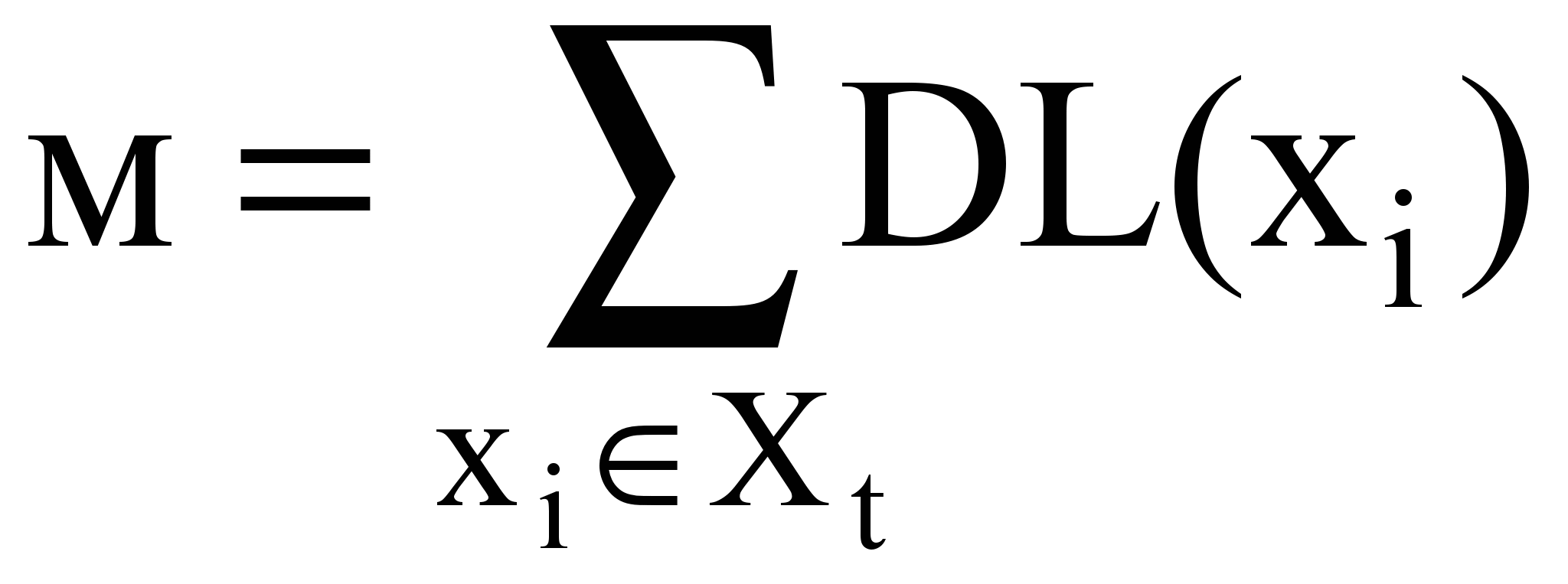
и продолжается формирование подграфа G_t до достижения X_t =n в соответствии с п.п. 2-4.

5. Проверяется условие m<=M. Если оно выполняется, подграф сформирован, если нет, то в качестве окончательного варианта выбирается подграф G_t' G_t с максимальным числом вершин, для которого m<=M (т.е. один из промежуточных результатов формирования подграфа).

Заметим, что согласно приведенному алгоритму формирование подграфа не прекращается даже при нарушении ограничения на число внешних связей до полного укомплектования G_t (до достижения X_t =n). Это объясняется тем, что присоединение очередной вершины к G_t может уменьшить число внешних связей (DL<0) и обеспечить выполнение данного ограничения на последующих шагах.

Рассмотрим пример разрезания мультиграфа на части с числом внешних связей m<=5 и числом элементов в каждой части n<=3. Матрица смежности исходного графа G_t(X,U) имеет вид:

1 2 3 4 5 6 7 r(x_i)




1 0 2 0 3 0 0 0 5

2 2 0 1 1 0 0 0 4

3 0 1 0 0 1 0 4 6

A = 4 3 1 0 0 0 0 1 5

5 0 0 1 0 0 5 1 7

6 0 0 0 0 5 0 1 6

7 0 0 4 1 1 1 0 7


Результаты разрезания представлены в таблице 1.

Таблица 1.

Результаты разрезания графа.

Xt	Ut		Г(Xt)			DL(xi) (xj Xt)			|Xt|
x2	4		x1,x3,x4			DL(x1)=1 DL(x3)=4 DL(x4)=3			1
x2, x1	5		x3,x4			DL(x3)=4 DL(x4)=5			2
x2, x1, x4	2		-			-			3
Формирование G1=(x1,x2,x4) закончено
x6	6			x5,x7			DL(x5)=-3 DL(x7)=5			1
x6, x5	3			x3,x7			DL(x3)=4 DL(x7)=3			2
x6, x5, x7	6>m			-			-			3
Формирование G2=(x5,x6) закончено
x3		6			x7			DL(x7)=-2			1
x3, x7		4			-			-			2
Формирование G3=(x3,x7) закончено

Из рассмотренного примера можно видеть, как отрицательное приращение внешних связей (DL<0) обеспечивает выполнение ограничения на число внешних связей подграфа при подсоединении вершин x₄ и x₇ к подграфам G₁ и G₃. Алгоритмы последовательного типа применяются на начальных этапах декомпозиции для получения начальных вариантов разбиения графа на части.


4. Итерационный метод декомпозиции.


Суть итерационных алгоритмов разрезания состоит в улучшении начального варианта разбиения перестановками вершин из одного подграфа в другой с целью минимизации числа соединительных рёбер.

Так как матрица смежности полностью описывает граф, то нетрудно видеть, что разрезание графа G на k частей эквивалентно разбиению матрицы смежности А графа G на k*k подматриц следующим образом:

		1	. . .	k
	1
	. . .
A=
	k

Подматрицы главной диагонали матрицы А вида А_ij задают подграф G_j, а остальные подматрицы А_ij(ij) определяют наличие рёбер между подграфами G_i и G_j. Из критериев (1) или (2) оптимальное разрезание графа G итерационными методами соответствует такому изоморфному преобразованию матрицы смежности, когда в диагональных подматрицах А_ij(j=1,2,...,k) будет сосредоточено максимальное число ненулевых элементов. Приведение матрицы смежности к указанному виду состоит в отыскании на каждой итерации таких парных перестановок строк и столбцов при которых максимизируется сумма элементов в подматрицах А_ij.

Рассмотрим методику итерационного улучшения начального варианта разрезания с использованием чисел связности.

Под числом связности DS(x_j G_i) вершины x_j понимается числовая характеристика, учитывающая разницу связей вершины x_j  G_t внутри подграфа (внутренняя связность - S(x_j G_t)) и вне его (внешняя связность вершины x_j G_t с подграфами G_i (it)-S(x_j G_i)). Для любой вершины x_j  G_t при разбиении графа на k частей можно определить (k-1) чисел связности по формуле:


DS(x_j G_i)=S(x_j G_i)-S(x_j G_t) (it) (4)


Число связности DS(x_j G_i) (i=1,2,...,k) указывает на приращение внешних связей подграфа G_t после перемещения x_j из G_t в G_i (при этом внешние и внутренние связи вершины x_j поменяются местами).

Внутренняя связность S(x_j G_t) определяется как сумма элементов соответствующей строки в диагональной подматрице А_ti ; внешняя связность - как сумма элементов этой же строки в подматрицах А_ti (i=1,2,...,k);(it).

По значению числа связности можно судить о целесообразности перестановки вершины x_j G_t в другие подграфы . Так, если DS(x_j G_i)<0- число внешних связей подграфов G_t, G_i увеличится на DS, если DS(x_j G_i)<=0 - не изменится, а при DS(x_jG_i)>0 - уменьшится.

Поскольку итерационное улучшение основано на парной перестановке вершин из разных подграфов, то эффективность такого обмена можно определить по формуле :

S(x_ix_j)=DS(x_j G_i)+DS(x_i G_t)-2*a_ij (5),

где S(x_ix_j) - приращение внешних связей подграфов G_i, G_t при парной перестановке вершин x_j G_t и x_i G_i

a_ij- число связей между вершинами x_i и x_j.

Сформулируем алгоритм итерационного разрезания графа на k равных подграфов, используя принцип поэлементных перестановок вершин. Заметим, что если в начальном варианте разрезания подграфы содержат разное число вершин, то перед итерационной перестановкой размерность подграфов выравнивается введением фиктивных изолированных вершин в подграфы с |X_i|i в допустимых пределах по сравнению с первоначальным вариантом.

C учётом сказанного алгоритм итерационного разрезания будет следующим.

1. В матрице смежности А выделить подматрицы А_ij(i,j=1,2,..,k), соответствующие начальному варианту разбиения графа на k подграфов по N вершин в каждом (с учётом изолированных фиктивных вершин).

2. Определить возможные значения чисел связности DS(x_j G_i) для всех вершин при их перестановках в подграфы G_i(i=1,2,...,k) по формуле (4).

3. Определить приращение связей S(x_ix_j) между парами подграфов (G_t, G_i) при всех возможных парных перестановках вершин xi,xj по формуле (5).

4. Выбрать максимальное положительное приращение S(x_ix_j) и переставить соответствующие строки и столбцы исходной матрицы. Приняв полученную матрицу в качестве исходной, перейти к очередной итерации (п.2).

В тех случаях, когда все приращения связей S(x_ix_j)<0 перестановка вершин прекращается. Дальнейшего улучшения варианта разрезания исходного графа можно добиться только изменением начального варианта декомпозиции.

Рассмотрим пример выполнения одной итерации для заданного варианта разбиения графа на три подграфа (вершина x9 - фиктивная):

		x1	x4	x3	x2	x5	x6	x7	x8	x9
	x1			1	1	4	1	4	1
	x4			4					1		G1
	x3	1	4					1	1
	x2	1				1	4		4
A=	x5	4			1		1	4	1		G2
	x6	1			4	1			4
	x7	4		1		4
	x8	1	1	1	4	1	4				G3
	x9

Результаты определения чисел связности для каждой вершины x_i G при её перемещении в другой подграф представлены в таблице 2.

Таблица 2.

Числа связностей вершин

xi	DS(xiG1)	DS(xiG2)	DS(xiG3)
x1 x4 x3	- - -	5 -4 -5	4 -3 -3
x2 x5 x6	-4 -2 -4	- - -	-1 3 -1
x7 x8 x9	5 3 0	4 9 0	- - -

Вычислим теперь приращение связей (уменьшение связей) между парами (G₁,G₂) (G₁,G₃) (G₂,G₃) при всех возможных парных перестановках вершин из разных подграфов. В таблице 3 приведены результаты расчёта S(x_ix_j). Очевидно, S(x_ix_j)=S(x_jx_i).


Таблица 3.

Приращение связей между подграфами.

xj	x1	x4	x3	x2	x5	x6	x7	x8	x9
xi
x1				-1	-1	-1	1	5	4
x4		G1		-8	-2	-8	2	-2	-3
x3				-9	-3	-10	0	-2	-3
x2							3	0	-1
x5					G2		-1	10	3
x6							3	0	-1
x7
x8								G3
x9

Максимальное положительное приращение S(x₅x₈)=10 указывает на необходимость парной перестановки строк и столбцов исходной матрицы А, соответствующих вершинам x₅, x₈. Итерационное улучшение данного варианта разрезания завершается на 3-ей итерации и даёт следующий результат:

X₁={x₉,x₄,x₃}, X₂={x₂,x₈,x₆}, X₃={x₇,x₅,x₁}.

Число внутренних и внешних связей подграфов для исходного и окончательного вариантов разрезания имеют вид:

Исходный вариант Окончательный вариант


G1 G2 G3 G1 G2 G3

G1 5 6 8 G1 4 2 2



G2 6 6 13 G2 2 12 6



G3 8 13 0 G3 2 6 12


Из полученных результатов видно, что итерационная парная перестановка вершин обеспечивает максимальное увеличение внутренней связности формируемых подграфов и соответственно уменьшение связей между подграфами.

Рассмотренная методология может применяться для различных модификаций итерационного алгоритма, а также для других графовых моделей исходных объектов (например для гиперграфа, мультиграфа) [2].


5. Порядок выполнения работы.


Задание 1(2 часа).


1. Построить матричные эквиваленты мультиграфа и гиперграфа для заданной схемы соединения элементов объекта.

2. Выполнить разрезание мультиграфа и гиперграфа схемы с ограничениями на число элементов и внешних связей подграфов последовательным методом и подсчитать число полученных межблочных связей для обоих вариантов моделей схемы.


Задание 2(2 часа).


1. Выполнить итерационное улучшение заданного начального варианта разбиения графа с минимизацией числа межреберных связей в мультиграфе и гиперграфе (2-3 итерации) и подсчитать число полученных межблочных связей.

2. Выполнить автоматическое улучшение начального варианта разрезания и получить число межблочных связей для окончательного варианта.

3. Сопоставить результаты ручных и машинных расчётов. Сравнить число межблочных связей для мультиграфа и гиперграфа. Сделать выводы.


6. Контрольные вопросы и задания.


1. Сформулировать задачу декомпозиции графа.

2. Какие ограничения используются при разрезании графовых эквивалентов коммутационных схем?

3. Получить зависимость для определения приоритета вершин при включении их в формируемый подграф последовательным методом.

4. Сформулировать последовательный алгоритм декомпозиции.

5. Как учитываются ограничения на число внешних связей при формировании подграфа последовательным методом?

6. Дать определение числа связности. Как вычислить внешнюю и внутреннюю связность вершин?

7. Вывести зависимость для определения приращения межблочных связей при парной перестановке вершин.

8. Сформулировать итерационный алгоритм разрезания графа.

9. С какой целью в начальный вариант разрезания добавляются фиктивные вершины.

10. Сформулировать алгоритмы подсчёта числа внутренних и межблочных связей для варианта разбиения мультиграфа и гиперграфа.


ЛИТЕРАТУРА.


1. Мелихов А.Н. и др. Применение графов для проектирования дискретных устройств. - М.: Наука,1984.- 304с.

2. Курейчик В.М. Математическое обеспечение конструкторского и технологического проектирования с применением САПР. - М.: Радио и связь, 1990.- 352с.

3. Деньдобренко Б.М., Малика А.С. Автоматизация конструирования РЭА: Учебник для вузов. - М.: Высш. шк., 1990.-384с.