А. Б. Тазаян Учебно-методический комплекс дисциплины "Юридическая логика" (для студентов дневного отделения) Ростов-на-Дону 2010 Учебно-методический комплекс

Вид материала

Учебно-методический комплекс

Содержание Сложным называется суждение Соединительные суждения Разделительные сложные суждения Строго- разделительное суждение является истинным лишь в том случае, когда одно из простых суждений будет истинным, а второе лож Условное суждение ложно в одном случае: когда истинен антецедент, а консеквент – ложен Суждение эквивалентности образуется из простых суждений, соединенных логическим союзом « если и только если А, то В». Модальность суждений. Условно-категорические умозаключения Разделительно-категорические умозаключения Условно-разделительные умозаключения. Фигуры силлогизма В первой фигуре средний термин выступает в качестве субъекта в большей посылке и предиката в меньшей (Рис. 1.). Barbara, Baroko Bokardo Camenos Общие правила и специальные правила фигур категорического силлогизма Имеется пять правил силлогизма, которые, в свою очередь, делятся на правила терминов и правила посылок. Фигура 1: 1)большая посылка должна быть общим суждением Фигура 3: 1) меньшая посылка должна быть утвердительной 2. Виды индуктивных умозаключений. Неполной индукцией Научная индукция ... Полное содержание

Подобный материал:

• А. Б. Тазаян Учебно-методический комплекс дисциплины "Логика" Ростов-на-Дону 2010 Учебно-методический, 892.49kb.
• А. Б. Тазаян Учебно-методический комплекс дисциплины "Философия права" (для студентов, 524.1kb.
• О. И. Быльченко учебно-методический комплекс по дисциплине «история политических, 1638.27kb.
• И. Л. Литвиненко учебно-методический комплекс по дисциплине международный туризм ростов-на-Дону, 398.8kb.
• Б. В. Мартынов учебно-методический комплекс по дисциплине «логистика» для студентов, 1097.34kb.
• О. А. Миронова Учебно-методический комплекс дисциплины «международная торговля» Ростов-на-Дону, 727.71kb.
• И. Д. Алекперов учебно-методический комплекс дисциплины "информатика" Ростов-на-Дону, 952.05kb.
• Н. В. Брюханова учебно-методический комплекс по дисциплине «История менеджмента», 307.48kb.
• Л. Л. Гришан Учебно-методический комплекс по дисциплине «Аудит» Ростов-на-Дону, 2010, 483.53kb.
• Н. В. Брюханова учебно-методический комплекс по дисциплине «Управление маркетингом», 364.19kb.

3. Сложное суждение, его виды и истинность.

Сложным называется суждение, которое состоит из простых суждений, соединенных между собой логическими связями.

В соответствии с функциями логических связей выделяют следующие основные виды сложных суждений: 1. соединительные (конъюнктивные); 2.разделительные (дизъюнктивные); 3.условные (импликативные); 4. суждения эквивалентности.

Суждение может быть либо истинным, либо ложным. Эти два свойства суждения называются его логическими значениями. Истинностное значение сложных суждений зависит от истинностных значений, входящих в него простых суждений, и логических союзов, связывающих их. Логические союзы «и», «или», « если.., то …» обозначаются определенными символами.

Соединительные суждения образуются из простых с помощью их

соединения логическим союзом «и»( конъюнкцией). Символически: А Λ В. Сложное соединительное суждение истинно, если и только если истинны, составляющие его простые суждения.(Табл.1.) Таким образом, можно утверждать, что конъюнкция, образуя сложное суждение из простых, устанавливает условия его истинности: сложное соединительное суждение является истинным , если каждое из простых суждений, входящих в него, истинно, и ложно, если по крайней мере одно из них ложно.

Таблица истинности соединительных суждений.

А	В	А Λ В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

Табл.1.

Разделительные сложные суждения образуются в результате соединения простых суждений логическим союзом «или» (дизъюнкцией). Логический союз «или» имеет два значения: строго- разделительное и объединительно-разделительное. Строго-разделительная дизъюнкция обозначается символом Ú, а нестрогая V.


Строго- разделительное суждение является истинным лишь в том случае, когда одно из простых суждений будет истинным, а второе ложным ( Табл.2.). Объединительно-разделительное (нестрогая) суждение устанавливает следующие условия истинности : данное сложное суждение будет истинным, если истинным является хотя бы одно из простых, входящих в него суждений (Табл.3.).

Пример строго-разделительного суждения. «Кончил дело – гуляй смело или продолжай работать»(символически А Ú В). В этом суждении дизъюнкция устанавливает строго-разделительную связь, поэтому он истинен лишь в случае, если одно из простых суждений: «Кончил дело – гуляй смело»(«А»)- истинен, а «Кончил дело – продолжай работать»(«В») - ложен, или наоборот.

Таблица истинности строго-разделительных суждений:

А	В	А ÚВ
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

Табл.2.


Пример объединительно-разделительного (нестрогого) суждения: «Кирилл учиться юридическом вузе и занимается спортом»( символически АV B).

Таблица истинности объединительно-разделительных (нестрогой) суждений.:

А	В	АV В
И.	И	И
И	Л	И
Л	И	И
Л	Л	Л

Табл.3.

Условным называется суждением, образованное из простых суждений в результате соединения их логическим союзом « если…, то…» (импликацией). Импликация устанавливает такую логическую связь между двумя событиями, в которой одно событие является достаточным условием для наступления другого события. Суждение, вызывающее другое событие, называется – антецедентом (предыдущим), а вызываемое событие – консеквентом (последующим). Символической форме записывается: А→ В.

Условное суждение ложно в одном случае: когда истинен антецедент, а консеквент – ложен( Табл.4) Пример условного суждения: «Если сессию сдам на отлично, то получу повышенную стипендию».


Таблица истинности условных суждений:

А	В	А→В
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

Табл. 4.


Суждение эквивалентности образуется из простых суждений, соединенных логическим союзом « если и только если А, то В». Символически записывается: А↔ В. В суждении эквивалентности утверждается взаимная обусловленность двух явлений. Суждение эквивалентности истинно только в случае, когда истинностное значение, входящих в него суждений совпадают. (Табл.5). Пример суждения эквивалентности: «Земля круглая, если и только если, неверно, что Земля некруглая».

Таблица истинности суждения эквивалентности:

А	В	А↔В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

Табл.5.


Логический оператор отрицания. С помощью логического оператора отрицания из суждения А образуется новое отрицательное суждение −А( читается: «неверно, что А»), при этом, если первое суждение истинно, то второе – ложно, а если первое суждение ложно, то второе истинно (Табл.6.) . Суждение не-А является сложным суждением.


Таблица истинности логического оператора отрицания.

А	− А
И	Л
Л	И

Табл.6.


Модальность суждений.

Рассматривая ассерторические суждения, мы изучали наличие или отсутствие у предмета определенного признака. Но логика исследует и такие вопросы, как, является ли связь между S и Р суждения необходимой или случай­ной, возможно или невозможно у предмета определенного признака и т.д.

Модальность – это оценочная характеристика суждения. Основания модальной оценки суждения различны. Модальные суждения образуются с помощью специальных модальных связок ( «необходимо, что», «невозможно, что», «возможно, что», «разрешено, что » и т.д.). В зависимости от логической характеристики модальной связки выделяют различные типы модальностей, а те, в свою очередь, делятся на виды. В модальной логике значительных успехов достигло изучения алетических модальностей. Исчисление алетических модальностей полностью формализована, введены логические операторы необходимости ( символически − □) и возможности (символически − ◊ ). Эти модальные операторы , наряду с функционально- истинностными логическими операторами, являются основными выразительными средствами модальных исчислений. То есть они строятся путем расширения или языка логики высказываний, или логики предикатов.

Впервые модальную оценку утверждениям дал Аристотель (384 – 322 г. до н.э.). Он анализировал связь субъекта с предикатом в категорических суждениях на предмет ее необходимости и возможности.

Немецкий философ И.Кант (1724 – 1804), исходя из характера связи субъекта с предикатом, выделил следующие виды простых суждений:

ассерторические(S есть Р), аподиктические ( необходимо, что S есть Р) и проблематические (возможно, что S есть Р).

В настоящее время кантовская классификация суждений претерпела существенные изменения. В современной логике выделяют алетические (необходимо, что; возможно что); деонтические (обязательно, что; разрешено, что; запрещено, что); аксиологические (хорошо, что; плохо, что) ; эпистемические ( верно, что; знаю, что); темпоральные ( будет так, что; всегда будет так, что; и др.) суждения .

Большой вклад в исследование проблем модальной логики внес А.А.Ивин.
В своей работе «Логика норм» (1973, с.29) он дает следующую таблицу логических модальностей:

Логические модальности	Онтологические модальности	Эпистемические модальности
		знание	убеждение
логически необходимо	онтологически необходимо	доказуемо (верифицируемо)	полагает (убежден)
логически случайно	онтологически случайно	неразрешимо (непроверяемо)	сомневается
логически невозможно	онтологически невозможно	опровержимо (фальсифицируемо)	отвергает
логически возможно	онтологически возможно		допускает

Деонтические модальности	Аксиологические модальности		Временные модальности
	абсолютные	сравнительные	абсолютные	сравнительные
обязательно	хорошо	лучше	всегда	раньше
нормативно безразлично	аксиологически безраз­лично	равноценно	только иногда	одновремен­но
запрещено	плохо	хуже	никогда	позже
разрешено

Умозаключения

1. Понятие об умозаключении. Виды умозаключений.

2. Выводы логики высказываний.

а) условно-категорические умозаключения;

б) разделительно-категорические умозаключения;

в) условно-разделительные (лемматические) умозаключения

3. Простой категорический силлогизм.


1.Понятие об умозаключении. Виды умозаключений.

Умозаключение – это способ получения нового знания на основе имеющегося. Умозаключение является основным способом опосредственного получения нового знания, он не опирается непосредственно на показания чувств. Новое знание извлекается из имеющегося знания в процессе рассуждения. Структура умозаключения предстает последовательностью суждений, состоящих из посылок и заключения. Посылки – суждения, представляющие исходное знание. Заключение – суждение, к которому приходим в результате умозаключения.

Понятие умозаключения непосредственно связано с понятием логического следования. Логическое следование устанавливает критерии правильности и неправильности умозаключений. Умозаключение является правильным, если и только если его логическая форма гарантирует при истинностных посылках с необходимостью получать истинностное заключение. Если посылки истинны, а заключение ложно, то умозаключение неправильно. Следует отметить, что истинностное заключение можно получить и при неправильном способе рассуждения и ложных посылках. Основное гносеологическое достоинство логики заключается в том, что он устанавливает отношение логического следования между посылками и заключением и гарантирует истинность заключения при истинности посылок.

По типу логического следования различают дедуктивные и индуктивные умозаключения. Дедукция – есть процесс выведения логических следствий из посылок. Такое знание называется выводным. Выводное знание является демонстративным. Индукция устанавливает такую связь между посылками и заключением, которая обеспечивает лишь некоторую вероятность истинности заключения. Эти заключения называются правдоподобными.

Таким образом, в строгом смысле, правильное умозаключение, устанавливающее отношение логического следования между посылками и заключением, является дедукция. Именно дедуктивные умозаключения (выводы), опираясь исключительно на законы логики, устанавливают логически необходимую связь между посылками и заключением.

2. Выводы логики высказываний.

Условно-категорические умозаключения. Это двухпосылочное умозаключение. Одна посылка является условным суждением, а вторая посылка и заключение, могут быть либо антецедентом, либо консеквентом первой посылки, либо их отрицанием.

К правильным условно-категорическим умозаключениям относятся умозаключения, имеющую следующую логическую форму:

А→ В, А

^{________________}

В

Данный способ умозаключение получил название modus ponens(«утверждающий метод рассуждения»). В утверждающем способе умозаключения устанавливается отношение логического следования между посылками ( условным суждением А→ В, его антецедентом А) и заключением (консеквентом В).

Другим правильным типом условно-категорических умозаключений относятся умозаключения, имеющую следующую логическую форму:


А→ В, − В

^{___________________}

− А

Данный способ условно-категорических умозаключений называется modus tollens («отрицающий способ рассуждения»). В умозаключении данной структуры осуществляется переход от условного суждения А→ В и отрицания его консеквента − В к отрицанию антецедента − А.

Необходимо обратить внимание, что не являются правильными следующие способы условно-категорических рассуждений:


А→ В, В А→ В, − А

^{__________________} ; ^{_________________};

А − В


Разделительно-категорические умозаключения. Это двухпосылочное умозаключение. Одна из посылок - разделительное суждение ( строгая или нестрогая дизъюнкция), а другая и заключение являются одним из членов или отрицание какого-то из членов этого суждения. Основными правильными формами разделительно-категорических умозаключений являются :

А V В, − А А V В, − В

^{__________________} ; ^{____________________}
В А


Эти схемы рассуждений получили название modus tollendo ponens

( «отрицающее-утверждающий способ рассуждения»).


К неправильным относятся следующие схемы разделительно-категорических умозаключений:

А V В, А А V В, В

^{__________________} ; ^{____________________}
− В − А


Но если нестрогую дизъюнкцию заменить строгой дизъюнкцией, то схема умозаключений преобразуется в правильную форму :


А Ỳ В, А А Ỳ В,

^{__________________} ; ^{_________________} .
− В − А


При этом способе умозаключения осуществляется переход от утверждения одного из членов строгой дизъюнктивной посылки к отрицанию другого

её члена. Умозаключения, построенные по этой схеме, называются modus ponendo tollens (« утверждающе-отрицающий способ рассуждения»).


Условно-разделительные умозаключения. Эти умозаключения содержат в качестве посылок несколько условных суждений и одно разделительное суждение. Такие умозаключения называются дилеммами ( ди дважды…+ др.-гр. λήμμα предположение).

Дилеммы делятся на простые, сложные, конструктивные и деструктивные.

Схемы правильных дилемм:


А→ B, C→B, А V C

^{_____________________________ ___} простая конструктивная дилемма;

B


А→ B, C → D, А V C

^{_______________________________ __} сложная конструктивная дилемма;

B V D


A→ B, A → C, −B V −C

^{___________________________________ __} простая деструктивная дилемма;

− A


A → B, C→ D, −B V −D

^{__________________________________ __} сложная деструктивная дилемма.

−A V −C


3. Простой категорический силлогизм:

а) Состав простого категорического силлогизма.
б) Фигуры и модусы силлогизма.

в) Общие правила силлогизма и специальные правила фигур.


Теорию логических умозаключений из категорических суждений называют силлогистикой. Правильные силлогистические умозаключения при истинности посылок гарантируют истинность заключения. Простой категорический силлогизм – это двухпосылочное дедуктивное умозаключение, в котором из двух категорических суждений выводится третье категорическое суждение. Первые два суждения называются посылками, а третье – заключением.
Категорическое суждение включает два понятия, которые называются терминами: субъект- термин, предикат- термин. В простом категорическом силлогизме должно быть три и только три термина. Каждый термин силлогизма должен быть представлен два и только два раза. Термин, входящий в обе посылки, называется средним термином (terminus medius). Средний термин устанавливает связь между остальными двумя терминами, называемыми крайними терминами. Крайний термин, выступающий в заключении субъектом, называется меньшим термином ((terminus minor). Крайний термин, являющийся предикатом заключения, − большим термином (terminus major).

Термины силлогизма принято обозначать латинскими буквами: М – средний термин, S – меньший термин, Р – больший термин. Посылка, включающая наряду со средним термином меньший термин, называется меньшей посылкой. Соответственно, посылка, включающая наряду со средним термином больший термин, большей посылкой.

Пример категорического силлогизма:


Совершивший преступление(M), должен быть подвергнут наказанию(P)

Обвиняемый (S) – совершил преступление (M)

Обвиняемый(S) должен быть подвергнут наказанию (P)

Фигуры силлогизма. Так как правильность силлогизма зависит исключительно от его формы, чрезвычайно важно выявить эти формы правильных силлогизмов.

Силлогизмы отличаются друг от друга расположением среднего термина в структуре посылок. Эти разновидности силлогизма называются фигурами. Имеется четыре фигуры силлогизма.

В первой фигуре средний термин выступает в качестве субъекта в большей посылке и предиката в меньшей (Рис. 1.).

Во второй фигуре средний термин выступает в качестве предиката в обеих посылках (Рис. 2.).

В третьей фигуре средний термин выступает в качестве субъекта в обеих посылках (Рис.3.).

В четвертой фигуре средний термин является предикатом в большей и субъектом в меньшей посылках (Рис.4.).




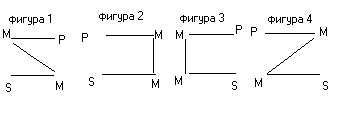
Рис.1. Рис.2. Рис.3. Рис.4.


Модусы силлогизма. Модусы – это разновидности силлогизма внутри каждой фигуры, указывающие возможные сочетания видов категорических суждений в посылках и заключении. Всего модусов 256. Так как видов категорических суждений по объединенной классификации 4, то можно посчитать, что в каждой фигуре 64 модуса (возможные сочетания видов суждений, образующих посылки и заключение силлогизма), а по четырем фигурам силлогизма – 256. Однако не все модусы являются правильными, то есть заключение с логической необходимостью следует из посылок. Правильных модусов – 24 ( по 6 модусов в каждой фигуре). Среди них выделяют 19 сильных модусов и 5 – слабых. Каждому правильному модусу еще в средневековье было присвоено имя.


Фигура 1 Фигура 2 Фигура 3 Фигура 4

Barbara, Baroko Bokardo Camenos

Celarent, Cesare Disamis Dimaris

Darii, Camestres Datisi Camenes

Ferio Festino Ferison Fresison

Barbari Camestrop Darapti Bramantip

Celaront Cesaro Felapton Fesapo

.

Последовательность гласных букв слева направо этих названий указывают вид суждений соответственно большей, меньшей посылок и заключения. Отсюда мы получим следующие сочетания видов суждений по модусам:


Фигура 1 Фигура 2 Фигура 3 Фигура 4

aaa aoo oao aeo

eae eae iai iai

aii aee aii aee

eio eio eio eio

aai aeo aai aai

eao eao eao eao


Следовательно, Barbara, модус фигуры 1, в котором обе посылки и заключение общеутвердительные суждения (этот вид суждений, как мы отмечали, обозначается латинской буквой А) имеет следующую структуру: ааа; Celarent – еае (большая посылка общеотрицательное суждение, меньшая посылка – общеутвердительное, заключение также общеотрицательное суждение)..

Общие правила и специальные правила фигур категорического силлогизма. Определены правила построения правильных категорических силлогизмов. Выполнение каждого правила является необходимым, а всех вместе достаточным основанием правильности модуса. Силлогизм правильный, если все правила, предъявляемые к нему, соблюдены, если не выполнено хотя бы одно из правил, силлогизм – неправильный.

Имеется пять правил силлогизма, которые, в свою очередь, делятся на правила терминов и правила посылок.

Правила терминов:

(1) Средний термин должен быть распределен по крайней в одной из

посылок;

(2) Если термин нераспределен в посылке, то он не должен быть

распределен в заключении;

Правила посылок:

(3) По крайней мере одна из посылок должна быть утвердительной ( из двух

отрицательных посылок нельзя сделать заключения);

(4) Из двух утвердительных посылок нельзя сделать отрицательного

заключения;

(5) Если одна из посылок отрицательное суждение, то заключение должно

быть отрицательным;

Наряду с основными правилами есть два производных:

(6) Из двух частных посылок нельзя сделать заключения ( по крайней мере

одна из посылок должна быть общим суждением);

(7) Если одна из посылок частное суждение, то и заключение должно быть

частным.

Специальные правила фигур:

Фигура 1: 1)большая посылка должна быть общим суждением;

2) меньшая посылка – утвердительной.

Фигура 2: 1) большая посылка должна общим суждением;

2) одна из посылок – отрицательным суждением.


Фигура 3: 1) меньшая посылка должна быть утвердительной;

2) одна из посылок – общим суждением;

3) заключение – всегда частное суждение.

Фигура 4 имеет искусственный характер. В истории предпринимались попытки сформулировать общие правила для нее, но они не принесли желаемых результатов. У четвертой фигуры нет общих регламентирующих специальных правил. Правильность умозаключений четвертой фигуры устанавливается по общим правилам силлогизма и правильным модусам четвертой фигуры. .


Лекция: Правдоподобные умозаключения

1. Понятие индуктивного умозаключения

2. Виды индуктивных умозаключений

3. Умозаключения по аналогии


1. Понятие индуктивного умозаключения.

В логике выделяют способы рассуждения, в которых заключения носят правдоподобный характер. И вся процедура в рассуждениях такого рода решает задачу повышения степени правдоподобия заключения. Подавляющее большинство правдоподобных умозаключений являются индуктивными. Общая познавательная стратегия индукции – переход от частного или единичного факта к общему знанию. Индуктивное умозаключение, всегда есть переход от знания меньшей общности к знанию большей степени общности. В узком смысле индукцию рассматривают как логическую операцию, в результате которой на основании знания об отдельных предметах некоторого множества делается вывод обо всех предметах данного множества. Индуктивные умозаключения, в отличие от дедуктивных умозаключений, не имеют необходимого характера. То есть истинность посылок с необходимостью не переносится на заключение, оно является недемонстративным, правдоподобным. Данная форма связи посылок с заключением называется индуктивным следованием. Всякое индуктивное обобщение опирается на конечное число фактов некоторых признаках предметов множества, а утверждает оно о наличии данного признака у всех возможных предметов данного множества. Отсутствие логического следования между посылками и заключением называется проблемой индукции. Нет логической связи от знания конечного числа фактов к универсальным утверждениям. Индуктивное следование устанавливает соответствие между посылками и заключением. Так как факты подтверждают данное обобщение, оно может быть принято. Расширение фактических свидетельств повышает степень правдоподобия индуктивных умозаключений, но никогда не делает их достоверными.

Таким образом, различие в характере связи между посылками и заключением образует два вида умозаключений: дедуктивное, в котором эта связь выступает в форме логического следования, и индуктивное, - связь в форме индуктивного (правдоподобного) следования.


2. Виды индуктивных умозаключений.

Принято делить индукцию на полную и неполную.

Полной индукцией называется вид индуктивного умозаключения, в котором общее утверждение о предметах некоторого множества сделано на основании обозрения всех без исключения предметов этого множества. Здесь общий вывод является следствием знания всех без исключения предметов искомого множества. Умозаключения полной индукции, с одной стороны, могут быть признаны достоверными, в этом они сходны с дедуктивными умозаключениями, с другой, - они не обладают ресурсом предсказания, не могут быть приняты в качестве универсальных утверждений. Этот недостаток умозаключений полной индукции в значительной мере снижает их научную ценность.

Неполной индукцией называется вид индуктивного умозаключения, в котором общее утверждение о предметах некоторого множества сделано на основании обозрения части предметов искомого множества. Неполная индукция является широко распространенной формой роста естественнонаучного знания. Обобщения в форме утверждений неполной индукции не являются достоверными, они – проблематичные. Вероятность их опровержения всегда существует. Научный статус этих утверждений поддерживается постоянно подтверждающими их новыми фактами.

Неполная индукция делится на популярную и научную. Популярная индукция основана на ограниченном опыте повторяемости некоторого признака у предметов одного и того же множества и отсутствии случая, противоречащего ему. Свидетельство ограниченной повторяемости признака переносится на все предметы данного множества, и делается заключение, что все предметы множества обладают данным признаком. Популярную индукцию в логике также называют индукцией через простое перечисление. В основе данного вида индукции лежит ограниченный опыт, поэтому он практически не используется в науке: нельзя исключить возможности неполностью обозреваемом множестве наличие предмета, не имеющего данного признака. Умозаключения популярной индукции в значительной мере основаны на убеждении. Поэтому, имеющие одинаковую статистическую повторяемость, различные признаки у разных предметов могут быть по-разному оценены в умозаключениях посредством этого метода. Например, утверждение, что «все жидкости – упруги», наделяется большей степенью достоверности, чем «все вороны – черные», хотя оба эти утверждения имеют одинаковую форму обоснования. Но этот вид индукции широко применяется в повседневной жизни. Многие народные приметы (например, народные долгосрочны прогнозы погоды.) строятся на повторяемости некоторых событий при определенных условиях. Но в этих прогнозах, как и в целом в популярной индукции, отсутствует обоснование причинной связи между двумя событиями ( начальными условиями и наступившим событием) .

Научная индукция основана на знании причинных связей предметов и явлений. Научная индукция лежит в основе универсальных утверждений (законов) естествознания. Законы естествознания по сути являются гипотезами, требующими универсального подтверждения. Эмпирически эта процедура не осуществима. Поэтому между универсальными утверждениями (законами) и подтверждающими их событиями устанавливается логическая связь. Из универсального утверждения выводятся логические следствия, которые затем получают опытное подтверждение. Как бы в контекст индукции включается дедукция (переход от общего утверждения к логическим следствиям). Соединение индукции с дедукцией является наиболее продуктивным методом научного познания. Этот «синтез» индукции с дедукцией называется гипотетико-дедуктивным методом. Но так как универсальное утверждение есть результат индуктивного обобщения даже логические следствия, подтверждаемые опытом, не делают его достоверной. Они делают его более правдоподобной.

Методы установления причинных связей.

На уровне здравого смысла в повседневной жизни формируется представление о том, что причинные отношения между событиями можно установить с помощью наблюдения. Такие представления являются ошибочными, в чувственном восприятии нам дана определенная последовательность во времени событий, не более. А причинную связь между событиями мы устанавливаем посредством рассуждения. В философии неочевидность причинности в гносеологическом аспекте впервые поставил шотландский философ Д. Юм. Более того, он рассматривает эту категорию исключительно в контексте психологии восприятия. Не вдаваясь философские дискуссии проблемы причинности, необходимо еще раз подчеркнуть, причинная связь между событиями мы устанавливаем исключительно посредством рассуждений. А рассуждения в своей основе всегда имеют предпосылки, которые принимаются в качестве достоверных, не требующих доказательств.

Индукция как метод научного познания исходит из двух предпосылок: (а) единообразие явлений действительности; (б) всеобщей взаимосвязи и взаимообусловленности явлений действительности; Среди множества взаимосвязей явлений действительности важнейшим является причинная связь. Причинная связь между двумя множествами событий указывает на то, что событие х предшествует событию у и вызывает его . Символически х→у, где х называется причиной, у – следствием этой причины. Знание причинной связи между явлениями действительности лежит в основе научного объяснения.

Основоположник индуктивного метода Ф.Бекон разработал специальные таблицы( присутствия, отсутствия и степеней), которые должны были помочь выявлению причинных связей между эмпирическими событиями. Огромный вклад в повышении научного статуса индуктивного метода внес Дж. Ст. Милль, который усовершенствовал методы установления причинных связей между эмпирическими событиями, а также разработал концепцию пределов совместимости индуктивного и дедуктивного методов в научном познании.

В научной литературе выделяют следующие важнейшие признаками причинной связи: (1) всеобщность, (2) последо­вательность во времени, (3) необходимость и (4) однозначность.

(1) Всеобщность причинной связи указывает на то, что все без исключения события действительности причинно обусловлены.В мире не существует беспричинных событий и каждое событие имеет свою причину.

(2) Последовательность во времени устанавливает, что причина всег­да предшествует следствию, а следствие всегда следует за причиной.

Последовательность причины и следствия во времени есть необходимое, но не достаточное условие причинной связи. Поэтому на основании временной последовательности нельзя утверждать о причинной связи между событиями. Принятие этого признака причинной связи в качестве единственно определяющей приводит к логической ошибке, получившая латинское название: «post hoc, ergo propter hoc» «после этого, значит, по причине этого» ). (3) Причинная связь есть необходимая связь. Это значит, что если два события находятся в необходимой связи и одно из событий является следствием другого, то это другое является причиной. Здесь следует обратить внимание на то, что любая причинная связь есть необходимая связь, но не всякая необходимая связь есть связь причинная.

(4) Однозначный характер причинной связи проявляется в том, что каждая конкретная причина всегда вызывает вполне определен­ное действие. Отсюда следует, что изменение причины с необходимостью влечет изменение действия, а значит, следствия.

Каждый из выделенных признаков является необходимым, а все вместе достаточным условием определения причинной связи.

Для установления причинных связей между событиями в научной индукции применяются пять методов: (1) метод сходства, (2) метод различия, (3) соединен­ный метод сходства и различия, (4) метод сопутствующих измене­ний, (5) метод остатков.

Метод сходств. Если в двух и более случаях исследуемого события одно обстоятельство постоянно предшествует наступлению исследуемого события, то время как другие изменяются, то это обстоятельство есть , вероятно, причина наступившего события. Метод сходства иногда называют методом нахождения общего в различ­ном.

Схема рассуждения по методу сходств имеет следующий вид:

1) АВС — вызывает d

2) MBF — вызывает d

3) МВС — вызывает d

^{________________________________}

По-видимому, В является причиной d.

Схема рассуждения опирается на необходимые признаки причинной связи. Так как d появляется при отсутствии F и М в первом случае, при отсутствии А и С — во втором, при отсутствии А и F — в третьем, то, тем самым обстоятельства А, С, F и М исключаются из возможных причин, ибо признак однозначности причины предполагает наличие одной и той же причины: одна и та же причина вызывает одни и те же следствия, изменение причины влечет изменение действия, а значит, изменение следствия. То есть ни А, ни С, ни F, ни М не являются причиной d. В приведенной схеме рассуждения обстоятельство В повторяется в каждом из обозреваемых случаев. Следовательно, вероятно, что В является причиной d. Из схемы рассуждения следует, что не только установления причинной связи, но и ее большая вероятность напрямую зависит от числа рассмотренных случаев и их репрезентативности. Чем больше случаев исследовано и чем разнооб­разнее обстоятельства, тем выше вероятность достоверности заключения. Но в любом случае, индуктивные умозаключения всегда проблематичны, ибо проблема индуктивного аргумента не имеет логического решения

Метод различия. По методу различия сравнивают два случая, в одном из кото­рых исследуемое событие наступает, а в другом не наступает, предшествующие обстоятельства в обоих случаях отличаются в одном обстоятельстве, а все другие являются сходными. Это различие лежит в основе умозаключения: отсутствующее обстоятельство является причиной, вызывающей исследуемое событие. Таким образом, метод различия - это метод нахождения различного в сходном.

Схема рассуждения по методу различия:

(1) АВСDEМ вызывает d

(2) АВСDE не вызывает d

^{______________________________________}

По-видимому, М является причиной d

В индуктивных обобщениях широко применяется соединительный метод сходств и различий. Соединенный метод сходства и различия: если в двух или более случаях, когда наступает данное событие, сходны только в одном обстоятельстве, в то время как в двух или более случаях, когда это событие не наступает, различаются только тем, что данное обстоятельство отсутствует, то это обстоятельство и есть, вероятно, причина рассматриваемого явления.

Схема рассуждения соединенного метода сходства и различия:

1) АВС вызывает d

2) MFB вызывает d

3) МВС вызывает d

4) AC не вызывает d

5) MF не вызывает d

6) МС не вызывает d

^{__________________________________}

По-видимому, В является причиной d

Сопутствующие изменения: если изменение определенного обстоятельства, при неизменности других, в одном событии вызывает изменение в другом событии, то это обстоятельство, вероятно, устанавливает причинную связь между этими событиями..

Схема рассуждения данного метода:

1) АВС вызывает d

2) ABC¹ вызывает d¹

3) ABC² вызывает d²

4) ABC³ вызывает d<sup>3

__________________________________</sup>

По-видимому, С является причиной d

Метод остатков призван установить обстоятельство, являющееся неотъемлемой частью причины, вызы­вающей следствие, при условии, что обстоятельства, вызывающие другие части этого следствия, установлены.

Схема рассуждения метода остатков:

1) АВС вызывает abсd

2) А вызывает а

3) В вызывает b

4) С вызывает с

^{______________________________________}

По-видимому, существует D, который вызывает d


Рассуждения по методу остатков нередко используются в про­цессе расследования преступлений, главным образом в тех случаях, когда устанавливают явную несоразмерность причин исследуемым действиям. Если действие по своему объему, масштабу или интен­сивности не соответствует известной причине, то ставится вопрос о существовании каких-то других обстоятельств.

3. Умозаключения по аналогии.

Аналогия является видом правдоподобного умозаключения. Таким образом, умозаключения по аналогии являются проблематичными, недемонстративными, в них между посылками и заключением нет отношения логического следования. Аналогией (др.-гр. άναλογία – соразмерность) называют форму рассуждений, в которой от сходства в двух предметах ряда признаков делается заключение о сходстве у этих предметов других признаков. Различают два вида аналогии: аналогию свойств и аналогию отношений. Аналогия свойств — это такой вид аналогии, когда на основе сходства двух объектов по ряду свойств, делается заключение об их сходстве и по другим свойствам. Аналогия свойств, обычно, устанавливается между индивидами. Но так как посредством этой операции устанавливается сходство между предметами, то заключение носит лишь правдоподобный характер. Если тождество между предметами предполагает полное совпадение их свойств, то сходство указывает на наличие у них несовпадающихся свойств. Исключительно средствами логики это несовпадение установить не представляется возможным, а эмпирические свидетельства всегда сохраняют возможность быть опровергнутыми.

Схема рассуждения по аналогии свойств:

1. а имеет признаки .P₁ и b имеет признак P₁

2. a имеет признак P₂ и b имеет признак P₂

3. a имеет признак P₃ и b имеет признак P₃

n. а имеет признак Р_n и b имеет признак Р_n

а и b находятся в отношении подобия

n+1. а имеет признак Q

^{________________________________________}

вероятно, b имеет признак Q.

Где а и b отдельные предметы, Р_1…Р_n, Q – совпадающие свойства предметов.

Аналогия отношений устанавливается между системами предметов. Аналогия отношений – это такой вид аналогии, когда установленные отношения между элементами одной системы переносятся на отношения между элементами другой системы.

Схема рассуждений по аналогии отношений:

1.P₁₍a_1…a_n) и P'₁₍b_1….b_n)

2.P_{2 (}a₁….a_n) и P'₂(b₁…b_n)

.


n. P_n (a₁…a_n) и P'_n (b_1…..b_n)

^{_________________________________________}

(a₁..a_n) и (b₁..b_n) находятся в отношении подобия

n+1 Q(a_1..a_n)

^{_______________________________}

вероятно, Q'(b_1..b_n)

Где (а_1…a_n) и ₍b_1…b_n) – системы объектов, P_1, …P_n и P'_1…P'_n, а также Q и Q' – одинаковые отношения.

Лекция : Логические основы теории аргументации.

1. Аргументация и процесс формирования убеждений.

2. Понятия доказательства и опровержения.

3. Правила и возможные ошибки доказательного рассуждения.


Термин «аргументация» используется в широком и узком значении. В широком значении аргументация – эта деятельность, преследующая цели обосновать или опровергнуть, ценности, научные теории, гипотезы, утверждения и т.д. Обоснование — процедура выявления оснований, в силу которых следует принять к.-л. ут­верждение или концепцию. Совокупность доводов, при­водимых в поддержку обосновываемого положения, называется основанием О. Цель аргументации – формирования убеждения или мнения относительно истинности какого-либо утверждения с помощью других утверждений. В аргументации могут быть использованы различные средства: логико-познавательные, культурные, нравственные, социально-психологические и т.д. Способы осуществления аргументации также многообразны: доказательство, опровержение, теории, дискуссии, споры, полемика и т.д.

Процедура аргументации вызвана способом функционирования знания в социальности. Далеко не все знания ( как в науке, так и в повседневной жизни), которыми пользуются люди, имеют непосредственное, фактуальное подтверждение. Аргументация должна снять сомнения по отношению к знанию, не имеющего непосредственного чувственного свидетельства. Это процесс опосредственного обоснования. Поэтому огромную роль в этом процессе играет доверие к используемым доводам. Доверие лежит в основе формирования убеждения. Убеждение, исключает принуждение, поэтому является наиболее желаемой целью процесса аргументации, ибо открывает широкие возможности управления социальными процессами. Убеждения могут формироваться не только посредством рациональных аргументов или непосредственными свидетельствами, но и путем внушения.

Рациональная аргументация, в отличие от других форм убеждения, влияет на разум людей, на его доверие законам разума, и потому оказывает более сильное и продолжительное воздействие на сознание и поведение людей. Она с самого начала ориентирована, во–первых, на логический анализ отношения между заключениями и аргументами, применяемыми для этого рассуждения. Во–вторых, аргументация опирается на рациональный анализ и оценку данных, с помощью которых подтверждаются и обосновываются ее заключения.

В узком значении аргументация – определяется как форма мыслительной деятельности, цель которой состоит в обосновании утверждения об истинности или ложности некоторого высказывания или теории (или о принципиальной невозможности оценки высказывания как истинного или ложного, т.е. бессмысленного). Все многообразные способы обоснования, обеспечивающие, в конечном счете, «достаточные основания» для принятия утверждения, де­лятся на абсолютные и сравнительные. Абсолютное О. — это приведение тех убедительных или достаточных оснований, в силу которых должно быть принято обосновываемое положение. Сравнительное О. — система убедительных доводов в поддержку того, что лучше принять обосновываемое положение, чем иное, противопоставляемое ему положение. Обоснование представляет собой су­щественный шаг в прибли­жении его к стандартам рациональности. Требования абсолютной и сравнительной обоснованности зна­ния (его обоснованности и рациональности) играют ведущую роль как в системе теоретического и практического мышления, так и в сфере аргументации. В этих требованиях пересекаются и концентрируются все другие темы эпистемологии, и можно сказать, что обоснованность и рациональность являются синонимами способ­ности разума постигать действительность и извлекать выводы, ка­сающиеся практической деятельности. Без данных требований аргументация теряет одно из своих сущностных качеств: она пере­стает апеллировать к разуму тех, кто ее воспринимает, к их спо­собности рационально оценивать приводимые аргументы и на основе такой оценки принимать их или отбрасывать.

2. Понятия доказательства и опровержения.

Термин «доказательство» в эпистемологии ( в теории научного познания) используется в двух смыслах: (1) в качестве дедуктивной процедуры выводного знания, и (2) интеллектуальная деятельность, обосновывающая некоторое неочевидное положение. Второе толкование термина «доказательство» широко используется не только в повседневной практике, но и в науках, не поддающихся формализации ( прежде всего в социально-гуманитарных науках). Результатом доказательства в этом случае могут быть как истинные, так и правдоподобные, а иногда и ложные знания.

В целом невыводное знание, претендующее на достоверность, должно быть фактуальным. Поэтому основная задача аргументов в этом контексте сводится к выявлению степени оправданности перехода от единичных фактов к общим утверждениям. Рациональные аргументы убеждают нас, что некоторые утверждения более вероятны, чем другие. Они помогают в ситуации неопределенности избежать худших решений.

Доказательство( в узком смысле)– рассуждение, устанавливающее истинность некоего утверждения, путем приведения других утверждений, истинность которых доказана или очевидна. Элементами структуры доказательства являются: тезис, аргументы (основания), демонстрация.

Тезис – утверждение, требующее обоснования; аргументы (основания) – совокупность суждений, с помощью которых обосновывается некоторое утверждение; демонстрация – способ логической связи тезиса и его основания.

Доказательства делятся по своей структуре на прямые и косвенные. Прямым называется доказательство, в котором истинность тезиса устанавливается путем его непосредственного выведения из аргументов. Косвенным(непрямым) – называется доказательство, в котором истинность тезиса обосновывается посредством доказательства ложности антитезиса.. Выделяют два вида косвенного доказательства: апагогическое ( доказательство «от противного») и разделительное.

Апагогическое ( др.-греч .άπαγωγή отведение)доказательство – непрямое доказательство. Вместо обоснования тезиса, допускается истинность антитезиса. Антитезис – утверждение, находящееся в отношении противоречия с тезисом. Из антитезиса выводятся следствия, которые находятся в противоречии с ним. Согласно закону противоречия устанавливается ложность антитезиса. Отсюда, согласно другому закону логики, – закону исключенного третьего, − если одно из противоречащих суждений ложно, другое должно быть истинным. Антитезис ложен, значит, тезис – истинен.

Разделительное косвенное доказательство – это процедура выбора из множества исчерпывающего возможные альтернативы данного класса предметов или явлений. Эти процедуры в значительной мере совпадают с процедурами элиминативной логики, – последовательное исключение альтернатив.

Косвенное доказательство имеет более сложную структуру обоснования, поэтому оно менее убедительно, чем прямое доказательство.

Опровержение – рассуждение, направленное против выдвинутого тезиса, имеющее целью установление его или недоказанности, или ложности.

Утверждение, которое надо опровергнуть называется тезисом опровержения. Суждения, с помощью которых опровергается тезис, называются аргументами опровержения. Опровержение может быть осуществлено тремя способами: (1) критикой тезиса; (2) критикой аргументов; (3) критикой демонстрации.

Целью критики тезиса является установление его недоказанности или ложности. Несостоятельность тезиса может быть обоснована посредством: (а) опровержения фактами. Приведение фактов, которые находятся в противоречии с заявленным тезисом. Это способ непосредственного опровержения тезиса; (б)установление ложности следствий, вытекающих из тезиса. Если будет выведено хотя бы одно ложное следствие, то будет доказан ложность тезис ; (в) опровержение тезиса в результате доказательства истинности антитезиса. Согласно закону исключенного третьего, из двух противоречащих суждений одно необходимо истинное. Этот способ опровержения по форме совпадает с косвенным доказательством.

Критика аргументов должна установить их ложность. Она использует те же способы, что и критика тезиса . При выявлении ложности аргументов, можно утверждать, что тезис не доказан. Следует обратить внимание: ложность оснований (аргументов) указывает на не доказанность тезиса, а не на его ложность.

Критика демонстрации призвана показать отсутствие логической связи между тезисом и, обосновывающими его аргументами. То есть установить, что, приведенные аргументы( здесь не ставится вопрос об их истинности) не обосновывают достоверность тезиса. Эта процедура обычно связана с формой доказательства ( форма доказательства – логический способ обоснования тезиса при помощи аргументов). Логическая неправильность формы доказательства свидетельствует лишь о недоказанности тезиса, не более того.

3. Правила и возможные ошибки доказательного рассуждения.

Существуют правила, регламентирующие процесс доказательства. Эти правила устанавливают критерии правильности доказательного рассуждения и касаются всех его составных частей (тезиса, аргументов, демонстрации). Эти правила, организуя процесс обоснования, позволяют избегать возможных ошибок, а значит, неудач в доказательстве.

Правила по отношению к тезису:

• тезис должен быть сформулирован ясно и недвусмысленно. Необходимо четко сформулировать: что предполагается доказать или опровергнуть;
  

тезис должен оставаться одним и тем же на протяжении всего доказательства. Нарушение этого правила называется является «подменой тезиса». Очень часто в процессе доказательства выдвинутый тезис заменяется другим. Подмена тезиса может быть произведена как непреднамеренно, так и сознательно. Очень часто такая подмена остается незаметным, ибо тезисы во многом близки по своему содержанию. Подмена тезиса в науке приводит к фундаментальным заблуждениям, а в политике является универсальным ресурсом манипулирования общественным мнением;

Правила в отношении аргументов:

• аргументы, используемые в доказательстве, должны быть истинными. Очень часто в доказательстве используются аргументы, истинность которых не очевидна. Естественно, недоказанные аргументы, а может быть и ложные, делают обоснование тезиса невозможным или некорректным;
  
• истинность аргументов должна быть установлена независимо от тезиса. Нарушение этого правила приводит к ошибке, называемой «круг в доказательстве». Эта ошибка является следствием того, что не только тезис, но и определенный аргумент, приводимый в его обоснование, доказывается с помощью самого тезиса;
  
• аргументы не должны противоречить друг другу;
  
• аргументы должны быть достаточным основанием для доказательства тезиса.
  

Правило демонстрации:

• в доказательстве тезис должен следовать из аргументов. Нарушение этого правила приводит к ошибке, которое называется – «не следует». Частным случаем нарушения этого правила является подмена тезиса. Само аргументы могут быть истинными, но они или доказывают другое утверждение, или не касаются предмета обоснования. То есть тезис логически не следует из приводимых аргументов.
  

Итак, доказательное рассуждение строится по определенным правилам, нарушение которых приводит к ошибкам. Правильное доказательство должно выполнять правила тезиса, аргументов и демонстрации: тезис должен быть сформулирован ясно и недвусмысленно, в его обоснование должны быть приведены только истинные аргументы, между тезисом и аргументами должна быть установлена логическая связь.


4. Планы семинарских занятий



Занятие 1.

Предмет логики. Логика и язык.
1. Мышление как предмет изучения логики.

а) абстрактное мышление в структуре познания;

б) понятие логической формы ;

в) истинность мысли и формальная правильность рассуждений.

2. Этапы становления и развития логики как науки

а) Аристотель – основоположник традиционной логики;

б) основные логические идеи Лейбница;

в) роль логических работ Дж.Буля и Г.Фреге в становлении

символической логики;

3. Значение логики:

а) теоретическое;

б) практическое.


Занятие 2.

Логика и язык.

1.Язык как знаковая система.

а) функции языка;

б) языки естественные и искусственные;

в) логический анализ языка как средство выявления логических форм;

2. Понятие знака.

а) предметное и смысловое значение языковых выражений;

б) основные аспекты : синтаксис, семантика, прагматика;

3. Семантические категории языка.

а) дескриптивные и логические термины;

б) понятие о языке логики высказываний.


Занятие 3.

Основные законы (принципы) правильного мышления
1. Основные черты правильного мышления.
а)определенность;
б)последовательность;
в) непротиворечивость;
г) доказательность.
2. Основные законы традиционной логики :
а) закон тождества;
б) закон непротиворечия ;
в) закон исключенного третьего;
г) закон достаточного основания.

Занятие 4

Понятие

1. Понятие как форма мышления .
а) выражение понятий в языке;
б) логические приемы формирования понятий: анализ, синтез, сравнение,
абстрагирование, обобщение;
2.Содержание и объем понятия.
а) признаки предметов и их виды; свойства и отношения как признаки ;
б) объем понятия ;
в) логический и фактический объемы и содержания понятий;
г) закон обратного отношения между объемом и содержанием понятий.

3.Виды понятий:
а) пустые и непустые; общие и единичные;
б) конкретные и абстрактные;
в) относительные и безотносительные;
г) положительные и отрицательные;
д) собирательные и несобирательные.
4. Отношения между понятиями.
а) сравнимые и несравнимые понятия; совместимые и несовместимые
понятия;
б) типы совместимости : равнозначность, перекрещивание(пересечение),
подчинение (отношение рода и вида);
в) типы несовместимости : соподчинение, противоположность,
противоречие;
г) круговые схемы Эйлера для выражения отношений между понятиями.
5.Обобщение и ограничение понятий. Деление понятий.
а) обобщение и ограничение понятий;
б) логическая структура деления;
в) виды деления: по видоизменению признака, дихотомическое деление;
г) правила и возможные ошибки в делении;
д) классификация и ее виды.
6.Определение понятий.
а) структура определения;

б) виды определений: явные и неявные; реальные и номинальные;
в) правила определений;
г) возможные ошибки в определении

Занятие 5.

Суждение.

1. Суждение как форма мысли.

а) суждение и предложение;

б) простые и сложные суждения : общая характеристика:

2.Состав простого суждения.

а) виды простых суждений: атрибутивные, суждения с отношениями,

суждения существования (экзистенциальные);

б) категорические суждения и их виды ( деления по количеству и качеству,

объединенная классификация по количеству и качеству);

в) распределенность терминов в категорических суждениях;

г) круговые схемы отношений между терминами в категорических

суждениях;

3.Отношение между суждениями по истинности.

а) отношение совместимости;

б) отношение несовместимости;

в) «логический квадрат».


Занятие 6.

Умозаключение (1^ое занятие).

1. Общее понятие об умозаключении.
а) структура умозаключения: посылки, заключение, логическая связь
между посылками и заключением;
б) понятие логического следования;
в) виды умозаключений : дедуктивные, индуктивные, по аналогии.

2.Простой категорический силлогизм.
а) состав силлогизма;
б) фигуры и модусы силлогизма;
в) общие правила силлогизма и специальные правила фигур.

Занятие 7.