Рабочая программа дисциплина ен. Ф. 01. 04 Математическая логика и теория алгоритмов направление
| Вид материала | Рабочая программа |
- Рабочая учебная программа по дисциплине «Математическая логика и теория алгоритмов», 69.99kb.
- Рабочая программа по дисциплине в 2-Математическая логика и теория алгоритмов шифр, 316.78kb.
- Рабочая учебная программа по дисциплине математическая логика, 72.41kb.
- Рабочей программы учебной дисциплины дв2 Математическая логика и теория алгоритмов, 50.1kb.
- Рабочая программа дисциплины «Математическая логика и теория алгоритмов» Направление, 175.54kb.
- Рабочая программа дисциплины «Математическая логика и теория алгоритмов», 143.48kb.
- В. Б. Гисин Дисциплина по выбору «Математическая логика и теория алгоритмов» Настоящий, 5.87kb.
- Рабочая программа учебной дисциплины «Теория вероятностей и математическая статистика», 165.42kb.
- Рабочая программа учебной дисциплины ен. Ф. 01. 04 Математическая логика и теория алгоритмов, 259.76kb.
- Рабочая программа по дисциплине Математическая логика и теория алгоритмов для специальности, 135.74kb.
1. Высказывания и логические операции над ними
2. Формулы логики высказываний и их классификация
3. Общезначимые формулы
4. Логическое следование
5. Равносильность формул
6. Нормальные формы для формул алгебры высказываний
7. Формализованное исчисление высказываний
8. Теорема о дедукции
9. Полнота, непротиворечивость и разрешимость исчисления высказываний
10. Предикаты и их классификация.
11. Логические и кванторные операции над предикатами
12. Формулы логики предикатов и их классификация
13. Равносильность и логическое следование формул логики предикатов
14. Формализованное исчисление предикатов
15. Классическая логика и клаузальная логика
16. Логическое программирование. Клаузы Хорна и метод резолюций
17. Язык логического программирования Пролог
18. Модальная логика
19. Нечеткая логика
20. Темпоральная логика
21. Задачи и алгоритмы. Свойства алгоритма.
22. Машина Тьюринга
23. Рекурсивные функции
24. Нормальные алгоритмы Маркова
25. Алгоритмически неразрешимые проблемы
26. Сравнительные оценки алгоритмов
27. Классификация алгоритмов по виду функции трудоёмкости
28. Трудоемкость основных алгоритмических конструкций
29. Переход к временным оценкам
30. Сложностные классы задач
31. Построение эффективных алгоритмов. Метод декомпозиции
8. ЗАДАНИЯ НА контрольнУЮ работУ (РАСЧЕТНО-ГРАФИЧЕСКУЮ).
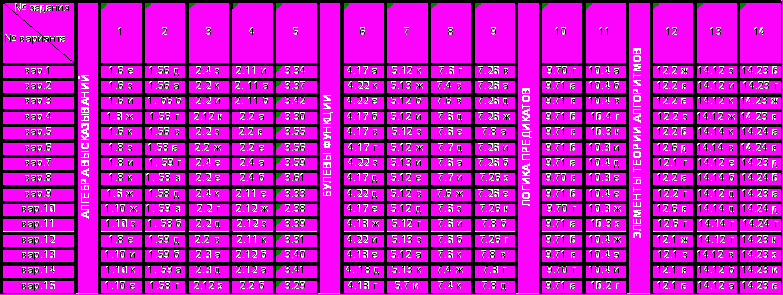
ЗАДАНИЕ: Решить задачи по темам из таблицы 1 согласно своему варианту. Номера задач приведены из учебного пособия: Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов: учеб. пособие для высш. учеб. заведений. – М.: Издательский центр «Академия», 2006. – 304 с. В пособии следует изучить примеры решения задач, аналогичных задачам из таблицы. Номером варианта считать номер фамилии в списке группы. Решение задач оформить в тетради.
Табл. 1
10. ЛИТЕРАТУРА
Основная литература.
- Игошин В.И. Математическая логика и теория алгоритмов: учеб. пособие для студ. высш. учеб. заведений / В.И. Игошин. – 2-е изд., стер. - М.: Академия, 2008. – 448 с.
- Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов: Учеб. Пособие для вузов / В.И. Игошин. – М.: Академия, 2005. – 304с.
- Анкудинов Г.И., Анкудинов И.Г., Петухов О.А. Математическая логика и теория алгоритмов: Учеб. пособие.– 2-е изд. − СПб.: СЗТУ, 2003. - 104 c.
- И.Братко. Программирование на языке ПРОЛОГ для искусственного интеллекта.-М.:Мир,1990.
- Гамова Н. Математическая логика и теория алгоритмов. Саратов; Изд-во СГУ, 1999.-76с.
- Гуц А.К. Математическая логика и теория алгоритмов: Учебное пособие. – Омск: Издательство Наследие. Диалог-Сибирь, 2003. – 108с.
- Ершов Ю.Л., Палютин Е.А. Математическая логика. Учебное пособие. - СПб.: Лань, 2004. -336 с.
- Ковальский Р. Логика в решении проблем. - М.: Наука, 1990. - 280 с.
- Колмогоров А.Н., Драгалин А.Г. Математическая логика. Изд. 3-е, стереотипное. – М.: КомКнига, 2006. 240 с.
- Марков А.А., Нагорный Н.М. Теория алгоритмов. М.: Наука, 1984.
- Мендельсон Э. Введение в математическую логику. М.: Наука, 1984. 320с
- Мощенский С.С. Лекции по математической логике. М.: Наука, 1970
- Л.Стерлинг, Э.Шапиро. Искусство программирования на языке ПРОЛОГ. М.:Мир, 1990
- Судоплатов С.В., Овчинникова Е.В. Математическая логика и теория алгоритмов. Учебник. М.: Инфра-М, 2004. -224 с.
- Ульянов М.В., Шептунов М.В. Математическая логика и теория алгоритмов, часть 1: Математическая логика. – М.: МГАПИ, 2003. – 47 с.
- Ульянов М.В., Шептунов М.В. Математическая логика и теория алгоритмов, часть 2: Теория алгоритмов. – М.: МГАПИ, 2003. – 80 с.
- Эдельман С.Л. Математическая логика: Учебное пособие для институтов / С.Л. Эдельман. – М.: Высшая школа, 1975. – 176с.
Дополнительная литература
- Анкудинов Г.И., Золотов О.А., Петухов О.А. Логическое программирование на языке Prolog: Учеб.пособие. – СПб.: СЗТУ, 2001. – 172с.
- Бердж В. Методы рекурсивного программирования. - М., Машиностроение,1983.
- Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. – М.: Мир, 1982. – 416с.
- Лорьер Ж.-Л. Системы искусственного интеллекта. - М.: Мир, 1991. - 568 с.
- Матросов В.Л. Теория алгоритмов. - М.: Прометей, 1989.
- Минский М.Вычисления и автоматы. - М.: Мир, 1971.
- Нильсон Н. Искусственный интеллект. Методы поиска решений. - М.: Мир, 1973. - 270 с.
- Тей А. и др. Логический подход к искусственному интеллекту: от классической логики к логическому программированию. - М.: Мир, 1990. - 432 с.
- Уинстон П.Искусственный интеллект. - М.-:Мир, 1990.
- Успенский В.А. Машина Поста. - М.: Наука, 1988.
- Успенский В.А., Семенов А.Л. Теория алгоритмов: основные открытия и приложения. - М.: Наука, 1987.
ТЕСТ
1. Квантор общности обозначается символом:
1)¬; 2); 3)
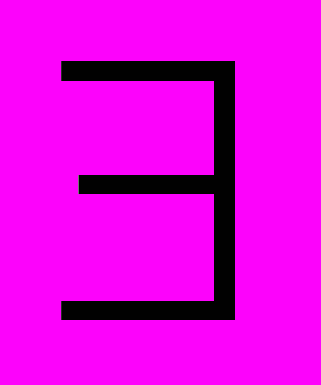 ; 4)
; 4)
2. Контрарными являются суждения:
- совместимые по ложности, но несовместимые по истинности
- несовместимы ни по истинности, ни по ложности
- совместимые по истинности, но несовместимые по ложности
- совместимы и по истинности, и по ложности
3. Формула
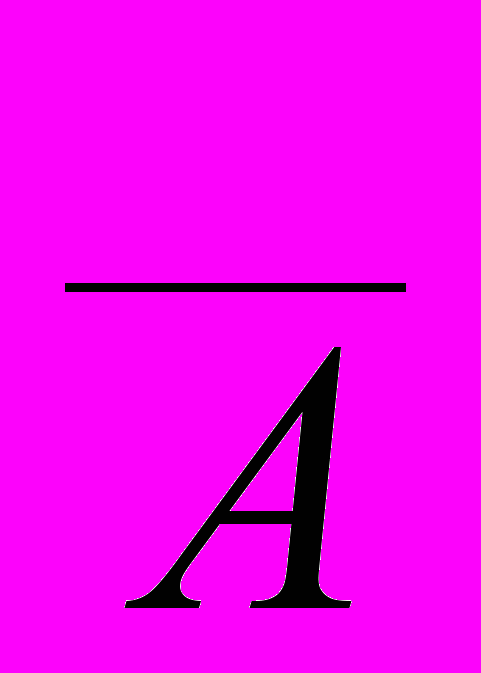 V
V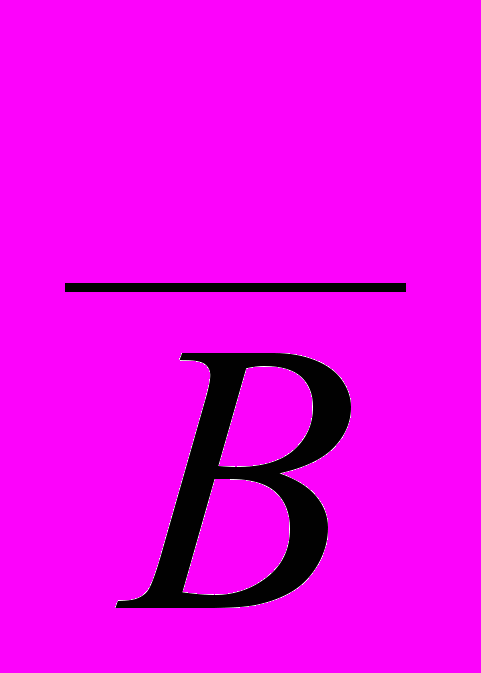
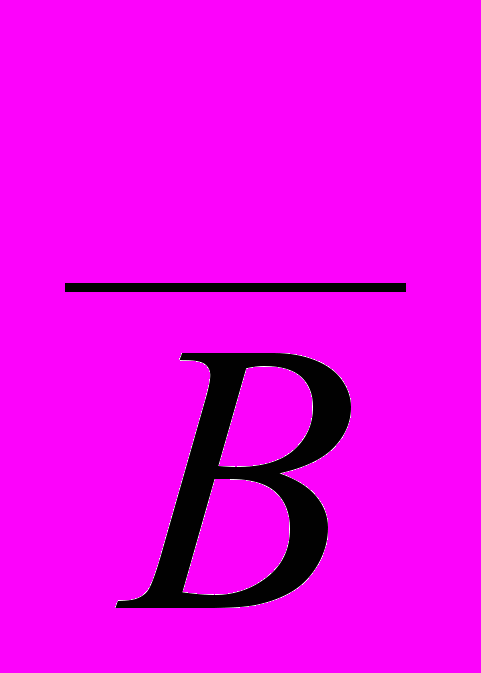 V
V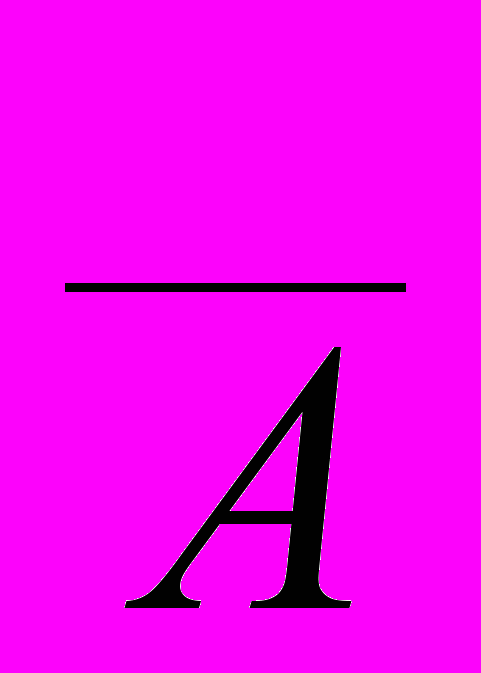 представляет собой закон:
представляет собой закон:1)идемпотентности 3)ассоциативности
2)коммутативности 4)тавтологии
4. Совершенные числа – это числа:
1) которые равны сумме своих делителей 3) простые числа
2) все натуральные числа 4) взятые по модулю
5. Основная проблема теории сложности алгоритмов это:
1) P = NP; 2)P < NP; 3)P > NP; 4)P <> NP
6. Теорема: «Невозможно эффективно распознать точки неопределенности вычислимой частичной арифметической функции» является теоремой
1)Поста; 2)Черча; 3)Тьюринга; 4)Маркова
7. Рекурсивная функция– это:
- функция, значение которой в данной точке нельзя определить через ее значения в предшествующих точках
- функция, значение которой в данной точке можно определить через ее значения в предшествующих точках
- функция, значение которой в данной точке можно определить через ее значения в последующих точках
- невычислимая функция
8. Рациональные числа – это:
- числа, которые можно представить в виде отношения двух целых чисел: p/q, где q не равно 0
- числа, которые являются суммой сходящихся рядов
- упорядоченная пара натуральных чисел (m,n)
- числа, которые являются суммой расходящихся рядов
9. Постовское пространство символов – это:
1) конечная лента ячеек; 3)единичная ячейка;
2) бесконечная лента ячеек; 4)метод параллельного программирования
10. Парадигма для предоставления знаний с целью использования этих знаний компьютером называется:
1) экспертной системой; 2)базой знаний; 3)фреймом; 4) генетическим алгоритмом
11. Структура для представления знаний в виде узлов, соединенных дугами, называется:
1) экспертной системой; 2) базой знаний; 3) фреймом; 4) семантической сетью
12. Компьютерная программа, содержащие накопленные знания специалистов в определенной предметной области, называется:
1) экспертной системой; 2) базой знаний; 3) фреймом; 4) генетическим алгоритмом
13. Объединение множеств обозначается символом:
1) +; 2)–; 3)\; 4)|
14. Какое из следующих равенств с множествами А и В является ложным:
1)
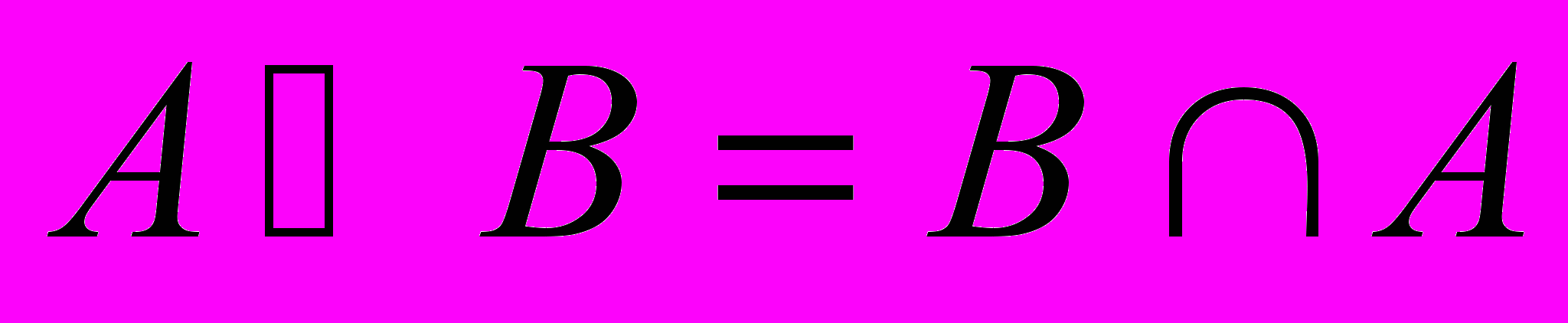 ; 2)(А
; 2)(А В)
В) С=А
С=А (В
(В С); 3) Если
С); 3) Если 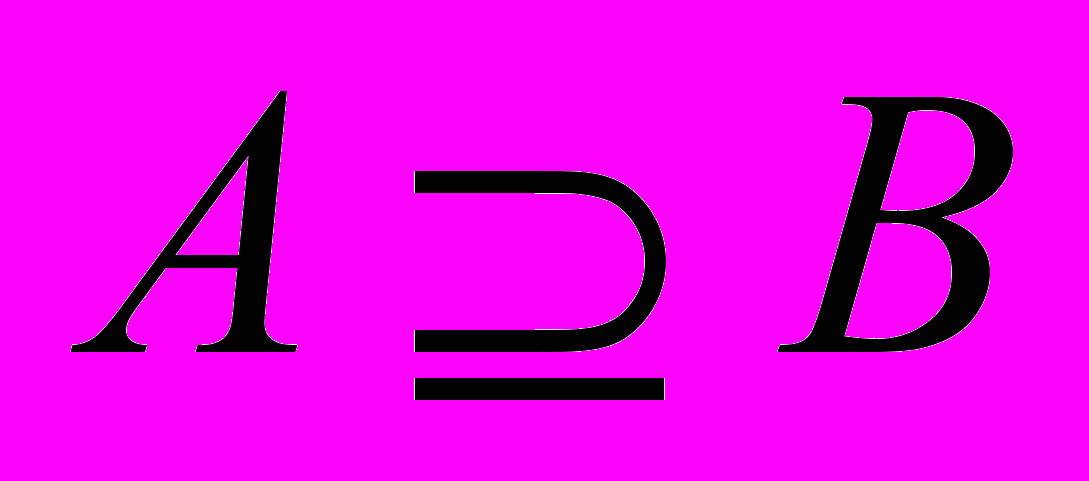 , то А
, то А В= А; 4)А
В= А; 4)А Ø= А.
Ø= А.15. Какое из следующих равенств с множествами А и В является ложным:
1)
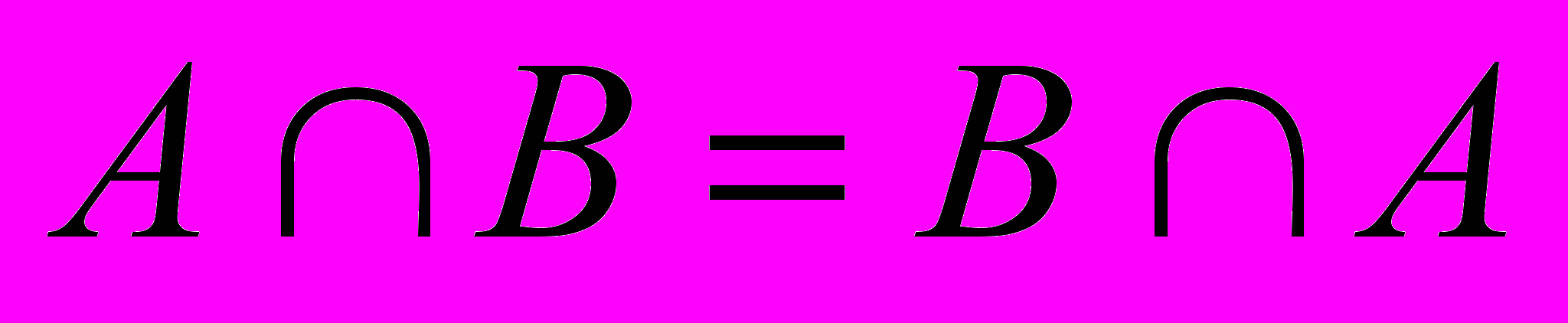 ; 2)(А
; 2)(А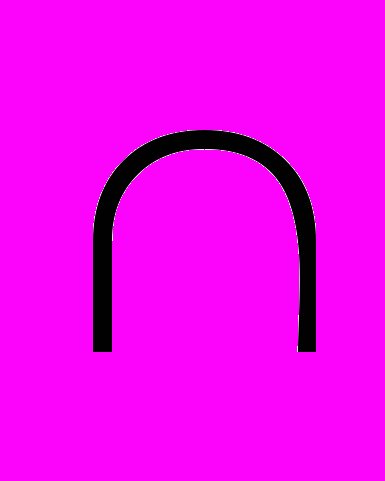 В)
В) 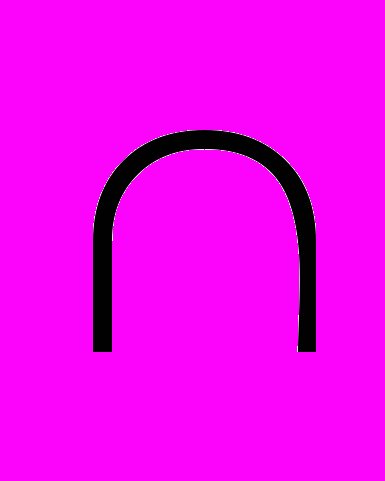 С=А
С=А (В
(В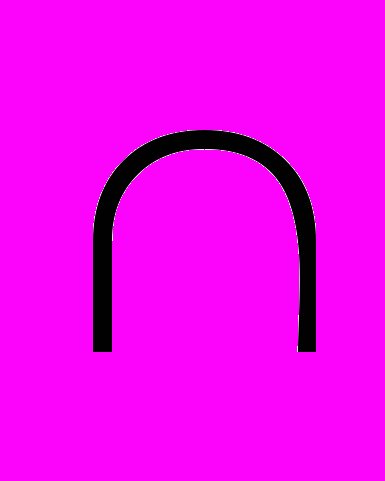 С); 3)Если
С); 3)Если 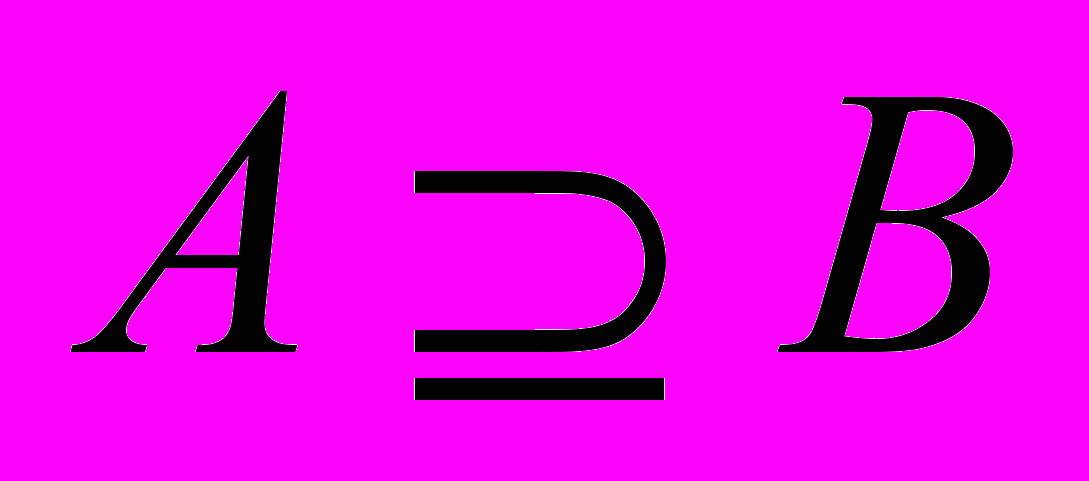 , то А
, то А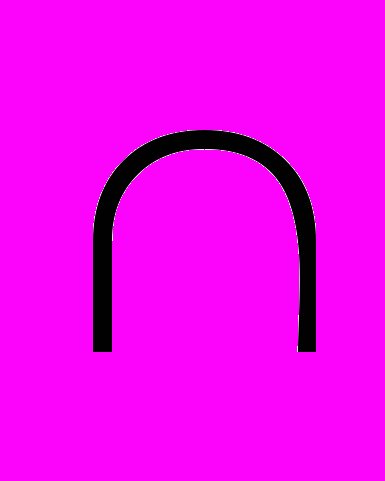 В= В; 4)А
В= В; 4)А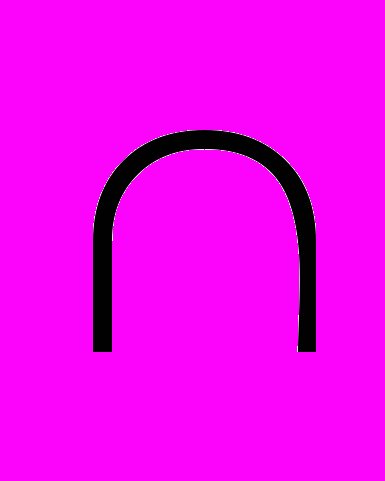 Ø= Ø;
Ø= Ø;16. Множество, эквивалентное множеству натуральных чисел N называется:
1) алгебраическим; 2)тригонометрическим; 3)несчетным; 4)счетным
17. Дизъюнкцией высказываний А и В (обозначение АВ, читается: А или В) называется высказывание:
- истинное тогда, когда истинно хотя бы одно из высказываний А и В, и ложное, если и А и В ложны
- ложное в случае, если А истинно, а В ложно, и истинное в остальных случаях
- истинное тогда, когда истинны оба высказывания А и В, и ложное в остальных случаях
- истинное тогда, когда оба высказывания А и В либо истинны, либо ложны, и ложное если одно из высказываний А, В истинно, а другое ложно
18. Какое из следующих свойств логических операций является неверным:
1) ( А) (А); 2) ( (АВ)) (АВ); 3)( (АВ)) (АВ); 4) ((АВ)С) (А(ВС))
19. К базовым функциям не относится:
1)функция константа; 2)тождества; 3) следования; 4) суперпозиции
20. К числу элементарных операций не относят операцию:
1)константы; 2)суперпозиции; 3)рекурсии; 4)минимизации
21.Пусть g(х)=Ci(х)=0; h(х;у;f (х; у)) = J3,2=y. Пользуясь схемой примитивной рекурсии найти f(3): 1)0; 2)1; 3)2; 4)5
22. Пусть g(x)=J1,1=x; h (х; у; f (х; у)) = (J3,3) = f (x; у) + 1
Пользуясь схемой примитивной рекурсии найти f(3;6):
1)3; 2)6; 3)9; 4)12
23. Пусть g(x) = I1,1 = x; h (х; у; f (х; у)) = -1 (J3,3) = f (x; у) – 1
Пользуясь схемой примитивной рекурсии найти f(6;3):
1)3; 2)6; 3)9; 4)12
24. Информационная ленты, считывающая и записывающая головка и управляющее устройство – это состав машины:
1)Черча; 2)Маркова; 3)Паскаля; 4)Тьюринга
25.. Какое из следующих равенств с множествами А и В является ложным:
1)
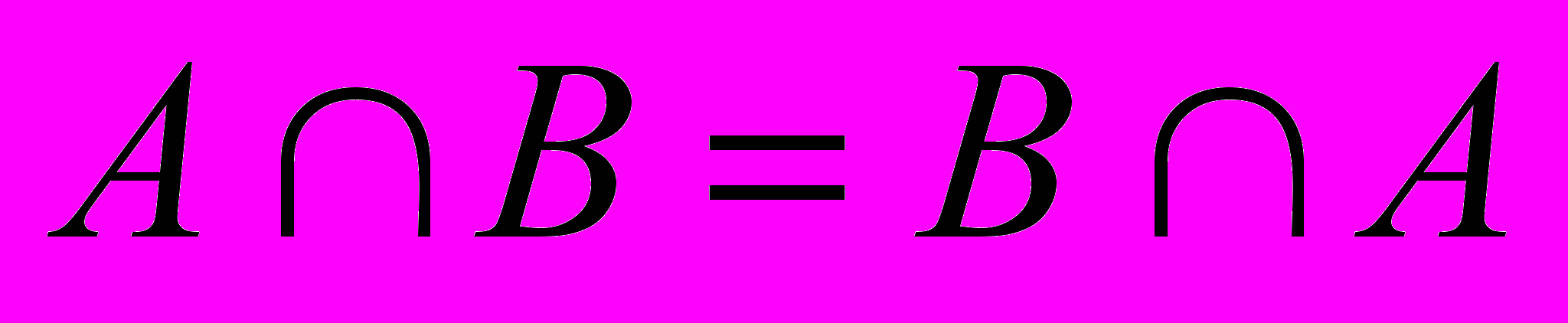 ; 2) (А
; 2) (А В)
В) С=А
С=А (В
(В С); 3) Если
С); 3) Если 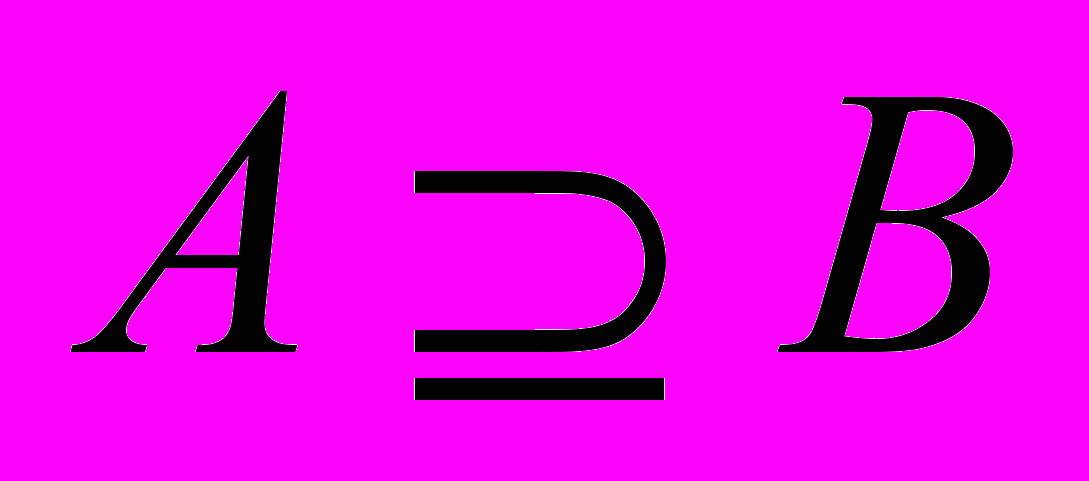 , то А
, то А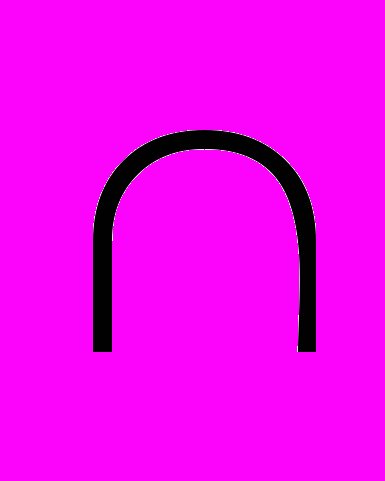 В= А; 4)А
В= А; 4)А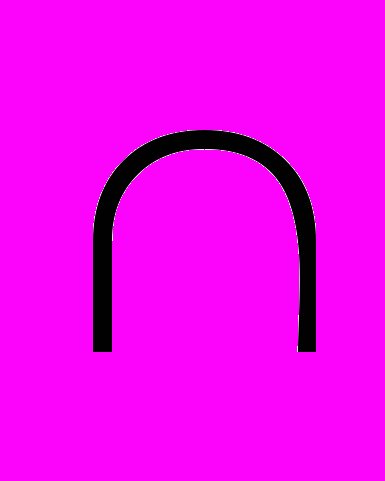 Ø= Ø
Ø= Ø26. В искусственном интеллекте сложились две оппонирующие базовые парадигмы моделирования мышления:
- Репрезентативная и коннекционистская
- Репрезентативная и лингвистическая
- Коннекционистская и лингвистическая
- Рекурсивная и лингвистическая
27. Неразрешимость проблемы разрешения для множества всех истинных предложений логики предикатов установил:
1)Черч; 2) Марков; 3) Паскаль; 4) Тьюринг
28. Упорядоченная последовательность правил подстановки называется:
1)рекурсией; 2)протоколом; 3)детерминантом; 4)алфавитом
29. Функция следования обозначается:
1) Jn,m ; 2) (x); 3) y; 4)R(g(n) ; h(n+2))
30. Оператор минимизации обозначается:
1) Jn,m ; 2) (x); 3) y; 4)R(g(n) ; h(n+2))
| № вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| № отв. | 4 | 1 | 2 | 1 | 1 | 2 | 2 | 1 | 2 | 3 | 4 | 1 | 1 | 1 | 2 |
| № вопроса | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| № отв. | 4 | 1 | 1 | 4 | 1 | 3 | 3 | 1 | 3 | 3 | 1 | 1 | 2 | 2 | 3 |
