Модели эволюции. Генетические алгоритмы

Вид материала

Реферат

Содержание 2.3. Модель "чисто нейтральной" эволюции 1. Имеется популяция черных и белых шаров, общее количество шаров в популяции равно 2.4. Схема гиперцикла. 2.5. Общая схема сайзеров I – полинуклеотидная матрица, Ei I кодирует протеины, фермент   репликации E1 обеспечивает   репликацию матрицы I Самовоспроизводящиеся автоматы Дж. фон Неймана A, предназначенный для изготовления произвольного автомата согласно информации, закодированной в ленте L B , копирующий ленту L 2.6. Гиперциклы или сайзеры? 2.7. NK-автоматы С. Кауффмана: сеть случайно связанных логических элементов K (порядка величины N K не достигнет величины порядка 2. При K  K  2; - если мы сравним число различных аттракторов NK

Подобный материал:

• Доклад «Моделирование эволюции. Генетические алгоритмы», 75.42kb.
• Доклад «Моделирование эволюции. Генетические алгоритмы», 108.9kb.
• Доклад на тему: "Модели эволюций и генетические алгоритмы", 155.74kb.
• Информатика, вычислительная техника и инженерное образование 2011, №1(3) эволюционное, 635.81kb.
• Л. И. Параллелизмы в молекулярной организации генома и проблемы эволюции. В кн.: Молекулярные, 251.18kb.
• Программа дисциплины «Нечеткая логика, генетические алгоритмы и экспертные системы, 228.23kb.
• Дисциплина: Инженерия знаний Доклад Генетические алгоритмы, 371.21kb.
• Курс, 1-й семестр лекции (51 час), экзамен практикум на ЭВМ (68 часов), зачет (с оценкой), 24.4kb.
• Фрагментные генетические алгоритмы, 140.16kb.
• Курсовая работа По дисциплине: «Моделирование систем» По теме: «Генетические алгоритмы, 324.78kb.

2.3. Модель "чисто нейтральной" эволюции

Нейтральный отбор играет важную роль в эволюции популяций конечной численности n. Для того чтобы продемонстрировать особенности нейтрального отбора явно, рассмотрим "чисто нейтральную" эволюционную игру, которую определим следующим образом:

1. Имеется популяция черных и белых шаров, общее количество шаров в популяции равно n.

2. Эволюция состоит из последовательности поколений. Каждое поколение состоит из двух шагов. На первом шаге мы дублируем все шары, сохраняя их  цвета: черный шар имеет два черных потомка, белый шар имеет два белых потомка. На втором шаге мы случайным образом удаляем из популяции ровно половину шаров с равной вероятностью для черных и белых "видов", независимо от их цвета.

Мы говорим, что популяция находится в l -состоянии, если число черных и белых шаров для рассматриваемого поколения равны  l и n - l, соответственно. Будем характеризовать эволюцию вероятностями переходов P_lm . P_lm   есть вероятность перехода из  l -состояния в  m -состояние в течение одного поколения. Используя простой комбинаторный расчет, можно определить значения P_lm :



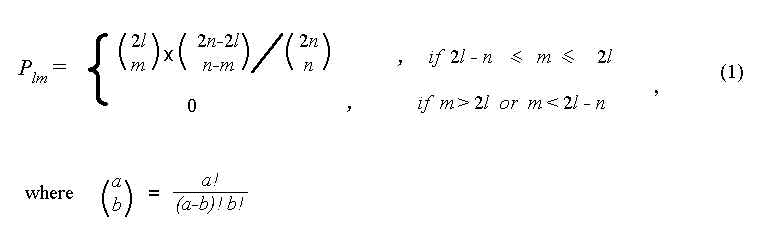
Матрица P_lm  задает случайный Марковский процесс, который может рассматриваться как пример простого стохастического эволюционного процесса [12]. Используя общие методы анализа таких процессов [12], можно показать, что:

1) рассматриваемый процесс всегда сходится к одному из поглощающих состояний, а именно, к 0-состоянию (все шары белые), либо к n-состоянию (все шары черные);
2) при больших  n  характерное число поколений T_n , требуемое для сходимости к какому-либо из поглощающих состояний, равно 2n :

T_n = 2n .                                                                                              (2)

Таким образом, хотя данный эволюционный процесс чисто нейтральный (черно и белые шары имеют равные шансы выжить), однако в результате эволюции отбирается только один вид. Величина T_n характеризует скорость нейтрального отбора, и используется в оценках основного текста.

2.4. Схема гиперцикла.

В была рассмотрена модель квазивидов, в которой изучалась эволюция информационных последовательностей. Одна из содержательных интерпретаций этой модели – эволюция полинуклеотидных цепочек РНК. Такая эволюция могла иметь место на самых начальных этапах происхождения жизни. Цепочки РНК могли самореплицироваться, однако точность копирования примитивных полинуклеотидов была мала, поэтому длина таких цепочек могла быть только небольшой.

В конце 1970-х годов М.Эйген и П.Шустер предложили модель гиперциклов. В гиперцикле к цепочкам РНК добавляются цепочки аминокислот – белки, которые выполняют определенные каталитические функции и вместе с цепочками РНК формируют целостную систему кооперативно взаимодействующих макромолекул. Образно говоря, в гиперцикле цепочки РНК кооперируются, но не сами, а с привлечением примитивных полипептидных ферментов. Ферменты могли способствовать повышению точности копирования, в результате количество информации, которое такие примитивные "особи" могли передавать потомкам, возрастало. Итак, модель гиперциклов интерпретирует гипотетическую стадию эволюции, которая могла следовать за квазивидами.

Схема гиперцикла представлена на Рис.1.

 

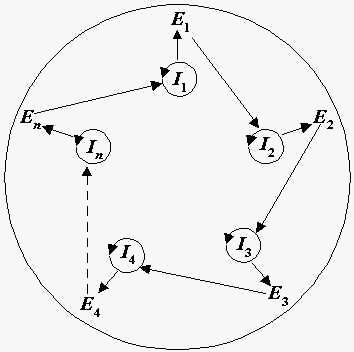
Рис.1. Структура гиперцикла. I_i –  РНК матрицы, E_i –  ферменты репликации (i = 1,2,...,n).

Гиперцикл – это самовоспроизводящаяся макромолекулярная система, в которой РНК и ферменты кооперируются следующим образом: имеются РНК-матрицы (I_i); i-я РНК кодирует i-й фермент E_i (i = 1,2,...,n); ферменты циклически катализируют репликацию РНК,  а именно, E₁ способствует репликации  I₂ , E₂ способствует репликации  I₃ , ..., E_n способствует репликации I₁ . Кроме того, упомянутые макромолекулы кооперативно обеспечивают примитивную трансляцию, так что информация, закодированная РНК- последовательностями, транслируется в структуру ферментов, аналогично обычному механизму трансляции в биологических клетках. Циклическая организация гиперцикла обеспечивает его структурную стабильность.

Схема гиперцикла еще очень далека от схемы самовоспроизводящейся молекулярно-генетической системы живой клетки, тем не менее, гиперцикл – это определенный шаг к живой клетке по сравнению с квазивидами, включающий кооперацию между полинуклеотидами и белками.

Модель гиперциклов характеризует систему кооперативно взаимодействующих макромолекул (полинуклеотидных матриц и кодируемых ими ферментов). М.Эйген и П.Шустер предложили данную модель как следующий эволюционный шаг по сравнению с квазивидами. Приведенный здесь анализ в сжатом виде характеризует математическое описание гиперциклов и их конкуренции. Базируясь на модели квазивидов,  М.Эйген и П.Шустер рассмотрели гипотетическую схему эволюции от отдельных макромолекул до интегрированных клеточных структур.
Эта схема характеризует некий общий сценарий (но конечно, далеко не единственный) предбиологической эволюции. В конце своей книги "Гиперцикл" М.Эйген и П.Шустер приводят цитату из Платона: <<И еще: "Если кто-нибудь может назвать более прекрасный треугольник, лежащий в основе вещей, мы будем приветствовать его не как соперника, но как друга правды".

2.5. Общая схема сайзеров

Сайзер включает в себя (Рис.1): полинуклеотидную матрицу I , фермент репликации E₁ , фермент трансляции  E₂   и дополнительные белки/ферменты E₃ , ..., E_n .



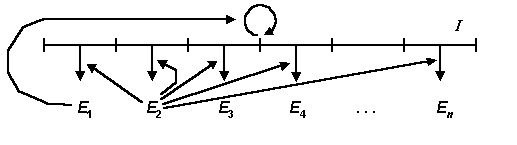
Рис.1. Общая схема сайзера. I – полинуклеотидная матрица, E_i – ферменты / белки. Круговая стрелка над матрицей иллюстрирует процесс репликации. Стрелки, направленные вертикально вниз, иллюстрируют процессы трансляции. Стрелки от ферментов E₁ и E₂ поясняют, что эти ферменты катализируют процессы трансляции и репликации.

Полинуклеотидная матрица I кодирует протеины, фермент   репликации E₁ обеспечивает   репликацию матрицы I , фермент трансляции E₂   обеспечивает синтез белков в соответствии с   информацией, хранящейся в матрице I.

Сайзеры имеют определенное сходство с биологическими клетками. Матрица I хранит "генетическую" информацию; ферменты E₁ и E₂  представляют собой простые аналоги довольно сложных систем репликации и трансляции биологических клеток.

Отметим, что некоторые начальные схемы сайзеров [10,12] включали несколько полинуклеотидных матриц (В.А.Ратнер и В.В.Шамин называют такие объекты сайзерами с несцепленными матрицами). Например, Д. Уайт (D.H.White) [12] рассматривал самовоспроизводящуюся систему, состоящую из двух матриц и двух ферментов: в этой схеме первая матрица кодирует фермент репликации, а вторая матрица -- фермент трансляции. Д. Уайт назвал эту систему "автоген" (Рис.2). Однако существует проблема структурной устойчивости сайзеров с несколькими матрицами [10]. В частности, было показано [15], что автоген структурно неустойчив: для существования автогена  скорости репликации полинуклеотидных матриц должны быть строго равны друг другу, иначе концентрация одной из матриц будет все время уменьшаться по сравнению с другой -- в результате автоген просто вымрет. Поэтому мы ограничим свое рассмотрение только сайзерами с единственной полинуклеотидной матрицей (в терминологии В.А.Ратнера и В.В.Шамина сайзерами со сцепленными матрицами).



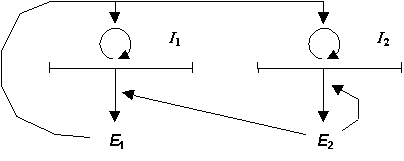
Рис. 2 Схема "автогена" -- Сайзера с несцепленными полинуклеотидными матрицами I₁ , I₂ . Матрица I₁ кодирует фермент репликации E₁ . Матрица I₂ кодирует фермент трансляции  E₂ .

На заре современной компьютерной эры Дж. фон Нейман предложил и исследовал модель самовоспроизводящихся автоматов [20]. Эти самовоспроизводящиеся автоматы состоят из следующих основных компонент (Рис.4):  1) лента L , хранящая информацию, 2) автомат A, предназначенный для изготовления произвольного автомата согласно информации, закодированной в ленте L, 3) автомат B для копирования ленты L, 4) автомат C, координирующий процесс отделения нового изготовленного автомата-потомка от автомата-родителя. И кроме этих необходимых компонент, самовоспроизводящиеся автоматы могут включать дополнительные  автоматы, конструкция которых кодируется лентой L.



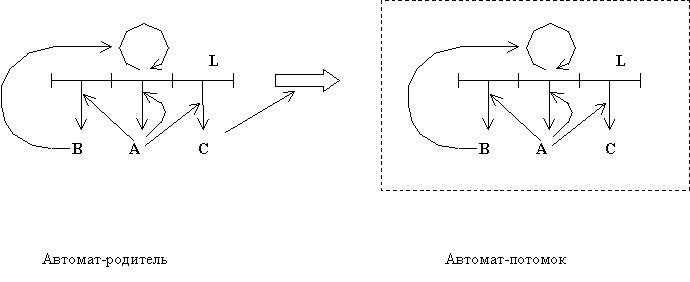
Рис. 4. Схема самовоспроизводящихся автоматов по Дж. фон Нейману.

Общие архитектура и принцип функционирования сайзеров подобны таковым для самовоспроизводящихся автоматов. Компоненты самовоспроизводящихся автоматов и соответствующие им аналоги сайзеров представлены в таблице 1.

Таблица 1. Сравнение архитектур автоматов Дж. фон Неймана и сайзеров

Самовоспроизводящиеся автоматы Дж. фон Неймана	Сайзеры
Запоминающая лента L	Полинуклеотидная матрица I
Автомат A, предназначенный для изготовления произвольного автомата согласно информации, закодированной в ленте L	Фермент трансляции E2
Автомат B , копирующий ленту L	Фермент репликации E1
Автомат C, координирующий процесс отделения автомата-потомка от автомата-родителя	Деление коацерватов в процессе роста сайзеров

Таким образом, модель сайзеров характеризует достаточно общую кибернетическую схему самовоспроизводящихся систем.

2.6. Гиперциклы или сайзеры?

Как модель гиперциклов, так и модель сайзеров предназначена для интерпретации макромолекулярной самоорганизации на предбиологическом уровне. Более того, модель сайзеров была придумана "в противовес" гиперциклам. И действительно, модель сайзеров в большей степени каноническая, т.е. она более естественна,  более проста и содержит меньше допущений по сравнению с гиперциклами. Однако и модель гиперциклов имеет не только историческое значение, но может рассматриваться, как достаточно разумная модель происхождения примитивного механизма трансляции и репликации.   Как уже отмечалось, модель сайзеров ближе к простейшим биологическим организмам, чем гиперциклы. Резюмируя сказанное, соотношение между квазивидами, гиперциклами и сайзерами можно охарактеризовать как последовательное усовершенствование гипотетических макромолекулярных систем (Рис.5):



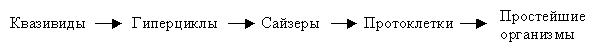
Рис.5.  Схема, иллюстрирующая гипотетический процесс эволюции самовоспроизводящихся макромолекулярных систем.

Таким образом, модель сайзеров характеризует простую самовоспроизводящуюся макромолекулярную систему. Схема сайзеров обладает определенной кибернетической общностью. Модель обеспечивает эффективное математическое описание внутреннюю динамику макромолекул и конкуренции сайзеров разного типа.

Модель сайзеров позволяет анализировать возможные этапы эволюции от простейших мини-сайзеров до макромолекулярных систем, обладающих свойствами реальных живых организмов. Например, модель адаптивного сайзера иллюстрирует процесс эволюционного возникновения простейшей системы управления.

2.7. NK-автоматы С. Кауффмана: сеть случайно связанных логических элементов

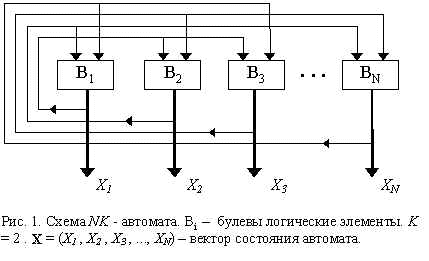
NK-автомат (Рис.1) есть сеть из N булевых логических элементов. Каждый логический элемент имеет K входов и один выход. Сигналы на входах и выходах элементов бинарны, т.е. принимают значения 0 либо 1. Выходы одних элементов поступают на входы других, эти связи случайны, но число входов K каждого элемента фиксировано. Сами логические элементы также выбираются случайно. Автоматы автономны, т.е. внешние входы отсутствуют. Число логических элементов, входящих в автомат, предполагается большим, N >>1.

Автомат функционирует в дискретном времени: t = 1,2,… Состояние автомата в каждый момент времени t определяется вектором X(t) – совокупностью выходных сигналов всех логических элементов. В процессе функционирования последовательность состояний сходится к аттрактору – предельному циклу. Последовательность состояний X(t) в этом аттракторе может рассматриваться как “программа” функционирования автомата. Число аттракторов M и типичная длина аттрактора L – важные характеристики NK-автоматов.



Ряд исследователей анализировали поведение NK-автоматов [2]. Здесь мы не будем излагать методы анализа, а просто приведем основные результаты.

Поведение автоматов существенно зависит от степени связности K.

При больших K (порядка величины N) “жизнь” автоматов стохастична: последовательные состояния аттракторов радикально отличаются друг друга, программы очень чувствительны (существенным образом изменяются) как по отношению к минимальным возмущениям (случайное изменение одной из компонент выходного вектора X(t) в процессе работы автомата), так и по отношению к мутациям (изменение типа элемента или связи между элементами). Длина аттрактора L очень велика: L ~ 2^N/2. Число атракторов M порядка N .

Если степень связности K уменьшается, то такой стохастический тип поведения сохраняется, до тех пор, пока K не достигнет величины порядка 2.

При K  2 поведение автомата принципиально меняется. Влияние минимальных возмущений на программы мало. Мутации обычно вызывают только слабые изменения динамики функционирования автомата. Только отдельные редкие мутации проводят к радикальным, каскадным изменениям программ автоматов. Длина аттракторов L и число аттракторов M уменьшаются до величин порядка N^1/2. Такое поведение характеризуют как жизнь на границе хаоса и порядка (“at the edge of chaos”).

NK-автоматы могут рассматриваться как модель генетической регуляторной системы живых клеток. Действительно, если мы рассматриваем экспрессию определенного гена (синтез соответствующего белка) как зависящую от наличия в клетке других белков, то мы можем аппроксимировать схему регуляции отдельного гена булевым логическим элементом – в результате вся сеть регуляторных связей, определяющая экспрессию генов живой клетки, может быть представлена в виде NK-автомата.

С.А.Кауффман аргументирует, что именно случай K  2 есть адекватная модель молекулярно-генетических систем управления биологических клеточных организмов.

Основные моменты этой аргументации состоят в следующем:

- регуляторные генетические системы на границе хаоса и порядка обеспечивают одновременно как необходимую стабильность жизненных программ клеток, так и потенциал для прогрессивных эволюционных улучшений;

- типичные схемы генной регуляции включают только небольшое число входов от других генов, что согласуется со значением K  2;

- если мы сравним число различных аттракторов NK-автомата M при K = 2 (вычисленное для разных значений N ), с числом различных типов клеток n_cells (т.е. с числом различных программ жизни клетки для фиксированного генома) биологических организмов разного эволюционного уровня, то мы получим близкие цифры (Рис.2). Например, для человека мы имеем (N ~ 10⁵): M = 370, n_cells = 254 [2].



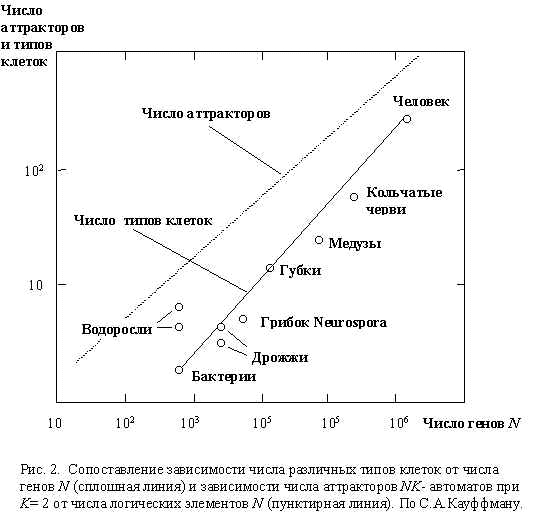
Так как генетические регуляторные структуры на границе хаоса и порядка обеспечивают как стабильность, так и эволюционные улучшения, то вполне разумно предположить, что именно такой тип структуры мог бы быть селективно отобран на ранних этапах жизни на Земле, что в свою очередь могло создать предпосылки для дальнейшего эволюционного прогресса.

Отметим, что метафора “на границе хаоса и порядка”, отражающая сочетание стабильности с предпосылками прогрессивного развития, получила широкое распространение и используется далеко за пределами исследований биологической эволюции: в экологии, в экономике, в истории, в социологии. Например, нынешнюю политическую ситуацию в России можно интерпретировать как смещение в сторону хаоса от разумного сочетания хаоса и порядка.

Итак, теория NK- автоматов С.А.Кауффмана – очень интересный шаг к пониманию кибернетических свойств биологических систем. Эта теория в основном иллюстративна, но, тем не менее, она – очень привлекательный "стимулирующий сценарий" (хорошо развитый математически) для исследования кибернетической эволюции живых организмов.

Список литературы.

1. u/tat_ru/science/aipl/ Страничка Лаборатории Проблем Искусственного Интеллекта АН Татарстана и Казанского Государственного Университета
   
2. .ru:8101/PSI/AIReC/AIReC.ru.phpl Российский Центр Исследований Искусственного Интеллекта
   
3. .newmail.ru/">Каталог ресурсов по компьютерной тематике
   
4. oka.com/algo-rus/index.php Все о программировании и алгоритмах