Модели эволюции. Генетические алгоритмы

Вид материала

Реферат

Содержание 1.2. Модели предбиологической эволюции. Общие представления о моделях 2. Модели эволюции. 2.1. Модель квазивидов 2.1.2. Экспериментальные основы модели 2.1.3. Формальное описание модели – общая схема.

Подобный материал:

• Доклад «Моделирование эволюции. Генетические алгоритмы», 75.42kb.
• Доклад «Моделирование эволюции. Генетические алгоритмы», 108.9kb.
• Доклад на тему: "Модели эволюций и генетические алгоритмы", 155.74kb.
• Информатика, вычислительная техника и инженерное образование 2011, №1(3) эволюционное, 635.81kb.
• Л. И. Параллелизмы в молекулярной организации генома и проблемы эволюции. В кн.: Молекулярные, 251.18kb.
• Программа дисциплины «Нечеткая логика, генетические алгоритмы и экспертные системы, 228.23kb.
• Дисциплина: Инженерия знаний Доклад Генетические алгоритмы, 371.21kb.
• Курс, 1-й семестр лекции (51 час), экзамен практикум на ЭВМ (68 часов), зачет (с оценкой), 24.4kb.
• Фрагментные генетические алгоритмы, 140.16kb.
• Курсовая работа По дисциплине: «Моделирование систем» По теме: «Генетические алгоритмы, 324.78kb.

1.2. Модели предбиологической эволюции. Общие представления о моделях

И на этом пути М.Эйген провел впечатляющие исследования. Он, в частности, предложил и проанализировал модель "квазивидов", описывающую достаточно простую эволюцию полинуклеотидных (информационных) последовательностей, и модель "гиперциклов", описывающую систему каталитически взаимодействующих ферментов и полинуклеотидов. Очень интересная модель – модель "сайзеров" (syser от System of self-reproduction), была предложена новосибирскими учеными В.А. Ратнером и В.В.Шаминым.

В модели квазивидов анализируется эволюция популяции последовательностей символов (информационных аналогов цепочек ДНК или РНК). Последовательности обладают определенными селективными ценностями. В процессе эволюции происходят отбор последовательностей в соответствии с их селективными ценностями и мутации – случайные замены символов в последовательностях.

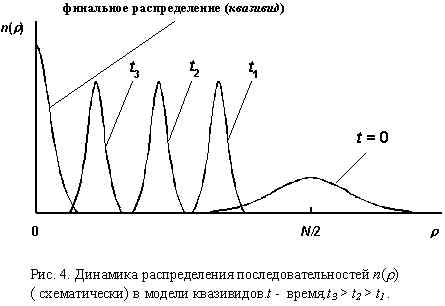
Характерная эволюция распределения последовательностей схематически показана на Рис.4. Для простоты предполагается, что последовательности бинарны, т.е. “геном” каждой “особи” представляет собой последовательность нулей и единиц. Длина последовательностей равна N (N >>1). Есть одна оптимальная последовательность, обладающая максимальной селективной ценностью. Селективные ценности остальных последовательностей тем меньше, чем больше расстояние по Хеммингу  (число несовпадающих символов) между рассматриваемой и оптимальной последовательностями. Исходное распределение (t = 0) случайно. В результате эволюции формируется квазивид: популяция, в которой наряду с оптимальной последовательностью есть множество сходных с ней мутантов.



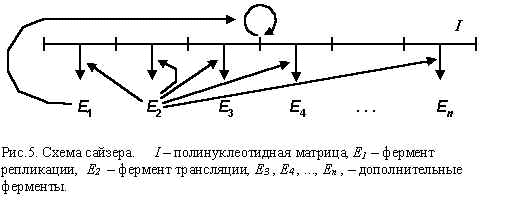
Модель сайзеров (Рис.5) [12,13] описывает самовоспроизводящуюся систему макромолекул, в которую входят: полинуклеотидная матрица I, фермент репликации E₁ и фермент трансляции E₂ . Полинуклеотидная матрица хранит информацию, кодирующую синтезируемые в сайзере ферменты, фермент репликации E₁ обеспечивает копирование полинуклеотидной матрицы, а фермент трансляции E₂ – синтез ферментов в соответствии с закодированной в матрице информацией. Возможны также другие ферменты E₃ , E₄ , ..., E_n , выполняющие какие-либо еще полезные для сайзера функции. По общей структуре модель сайзеров сходна со схемой самовоспроизводящихся автоматов, исследованных на заре развития вычислительной техники Дж. фон Нейманом (J.von Neumann) [14].

2. Модели эволюции.

2.1. Модель квазивидов

2.1.1. Модель квазивидов – простейшая модель эволюции информационных последовательностей.

В 70-х годах лауреат Нобелевской премии из ФРГ Манфред Эйген предпринял впечатляющую попытку построения моделей возникновения в ранней биосфере Земли молекулярно-генетических систем обработки информации [1,2]. Одна из наиболее известных моделей – модель "квазивидов", описывающая достаточно простую эволюцию полинуклеотидных (информационных) последовательностей.

В модели квазивидов рассматривается эволюция информационных последовательностей или векторов S = (S₁ , S₂ , ... , S_N), компоненты которых принимают небольшое число   дискретных значений (для полинуклеотидных последовательностей  = 4). Предполагается, что такие последовательности способны к саморепликации (или к репликации с помощью простейших ферментных систем). Рассматривается популяция последовательностей S₁ , S₂ , ... , S_n и анализируется Дарвиновская эволюция этой популяции, в процессе которой отбирается квазивид: распределение сходных последовательностей, обладающих достаточно большой скоростью репликации.

2.1.2. Экспериментальные основы модели:

1. Синтез малых полинуклеотидов. В экспериментах Л.Оргела было показано, что небольшие цепочки РНК (порядка 10 нуклетидов) способны к самореплицированию. В присутствии ионов цинка (действующего как катализатор) длина воспроизводимых цепочек достигает 40   нуклетидов.

2. Эволюция цепочек РНК в присутствии Q_- репликазы. Вирус Q_ содержит РНК-участок длиной 220 нуклеотидов (спутниковая РНК), который реплицируется ферментом Q_ - репликазой с высокой эффективностью. М. Сумпер из лаборатории М. Эйгена активно исследовал процесс эволюции РНК в присутствии Q_- репликазы. Были исследованы количественные характеристики этого процесса.

Вход: шаблон РНК (спутниковая РНК) + Q_- репликаза + богатые энергией мономеры (АТФ, УТФ, ГТФ, ЦТФ).
Выход: растущая популяция РНК, идентичных шаблону.

3. Синтез РНК de novo. Однажды М. Сумпер сообщил, что если в раствор не вносится шаблон, то синтез РНК также возможен, но он идет значительно дольше и менее стабильно. В результате появляются цепочки РНК, сходные со спутниковой РНК. К.Биебрихер и Р. Луа (сотрудники М.Эйгена) показали, что синтез РНК de novo происходит путем постепенного удлинения РНК-цепочек.

Вход: Q_- репликаза + богатые энергией мономеры (АТФ, УТФ, ГТФ, ЦТФ).
Выход: растущая популяция РНК, сходных с шаблоном.

Вывод. Эксперименты показывают, что есть процессы, которые можно интерпретировать (хотя с некоторыми натяжками) как Дарвиновскую эволюцию полинуклеотидных последовательностей.

2.1.3. Формальное описание модели – общая схема.

Приведем формальное описание модели квазивидов.
Квазивид - модель эволюции информационных последовательностей [1,2,4]. Эволюционирующая популяция есть множество {S_k}, состоящее из n последовательностей S_k , k = 1,..., n. Каждая последовательность представляет собой цепочку из N символов, S_ki, i = 1,..., N. Символы выбираются из алфавита, содержащего  различных букв. Например, мы можем рассматривать алфавит с двумя буквами ( = 2, S_ki = 1, -1 или  S_ki == Г, Ц) или алфавит с четырьмя буквами ( = 4, S_ki  = Г, Ц, A, У). Предполагается, что длина последовательностей N и численность популяции n велики: N, n > > 1.

Последовательности представляют собой геномы модельных "организмов", организмы характеризуются определенными неотрицательными приспособленностями  f(S) (селективными ценностями в терминологии М. Эйгена). В простейшем случае предполагается, что имеется оптимальная последовательность (the master sequence) S_m , имеющая максимальную приспособленность. Приспособленность произвольной особи S определяется расстоянием по Хеммингу  (S, S_m) между S и S_m (числом несовпадающих компонент в этих векторах), причем f(S) экспоненциально уменьшается с ростом  (S, S_m).

Эволюционный процесс состоит из последовательности поколений. Новое поколение  {S_k (t+1)}получается из старого {S_k(t)} путем отбора и мутаций последовательностей S_k (t) ; здесь t  – номер поколения.

Шаг 0. Формирование начальной популяции {Sk (0)}. Для каждого k = 1, ..., n, и для каждого  i = 1 , ..., N , выбираем случайно символ Ski, полагая его равным произвольному символу данного алфавита.

Шаг 1. Отбор

Подшаг 1.1.   Расчет приспособленностей. Для каждого k = 1, ..., n, вычисляем величину f(Sk).

Подшаг 1.2. Формирование новой популяции {Sk (t+1)}. Отбор  n особей в новую популяцию {Sk(t+1)} с вероятностями, пропорциональными f(Sk).

Шаг 2. Мутации особей в новой популяции. Для каждого k = 1, ..., n, для каждого   i = 1, ..., N, заменяем Ski(t+1) на  произвольный символ алфавита с вероятностью P . Параметр P характеризует интенсивность мутаций.

Организация последовательности поколений. Повторяем шаги 1, 2 для t = 0, 1, 2, ...

Схему отбора проиллюстрируем следующим образом. Представим, что у нас есть рулетка. Для каждого поколения отмечаем на рулетке n секторов, долю k-го сектора (отнесенную ко всей площади круга) полагаем равной q_k =  f_k [ _l f_l ]^-1 (Рис. 1). Здесь мы обозначили: f_k =  f(S_k) . Далее n раз крутим рулетку, каждый раз определяем номер сектора, на котором останавливается стрелка, и соответствующую этому номеру особь выбираем в популяцию следующего поколения. Таким образом в следующее поколение будут отобраны  n особей. При этом для каждого вращения рулетки вероятность k-й особи попасть в следующее поколение пропорциональна ее приспособленности f_k .



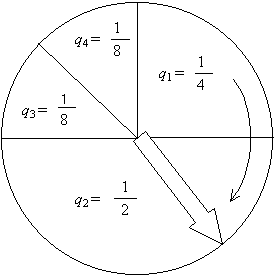
Рис.1. Схема отбора, при которой особи выбираются в популяцию нового поколения с вероятностями q_k , пропорциональными их приспособленностям  f_k . Показан пример, для которого n = 4,  f₁ = 2,  f₂ = 4,  f₃ = 1,  f₄ = 1.