Методические указания для подготовительных курсов Ростов-на-Дону
| Вид материала | Методические указания |
СодержаниеПример Л5. Пример Л6. В является логическим следствием А Пример Л9. Пример Л10. А вс)св(в а) ( а вс) св (в а) |
- Алгоритмы и программы Методические указания для подготовительных курсов Ростов-на-Дону, 1376kb.
- Методические указания для студентов заочной формы обучения Финансового факультета Ростов-на-Дону, 342.26kb.
- Методические указания для студентов заочной формы обучения Финансового факультета Ростов-на-Дону, 205.36kb.
- Методические указания для студентов заочной формы обучения Финансового факультета Ростов-на-Дону, 168.33kb.
- Методические указания курса «культурология» Для студентов биологического факультета, 331.04kb.
- Бюджетное планирование и прогнозирование методические указания для студентов заочной, 174.2kb.
- Методические указания к изучению курса «История зарубежной литературы 19 века» для, 569.78kb.
- Методические указания по выполнению курсовых работ и подготовки к экзамену для студентов, 359.09kb.
- Методические указания по выполнению курсовых работ и подготовки к экзамену для студентов, 320.85kb.
- Методические указания по организации и проведению учебной практики студентов Ростов-на-Дону, 102.61kb.
Пример Л4. Определить, истинна или нет формула (x y) xy, если а) x=1, y=0; б) x=0, y=1.
Решение. Для решения задачи нужно подставить данные значения x и y в формулу и использовать интерпретацию операций, учитывая их приоритет. Так, для а) (1 0) 10 1 0 0 0 1. Ответ: при x=1, y=0 данная формула истинна. Для б) (0 1) 01 (0 0) 0 0 0 1 0 0. Ответ: при x=0, y=1 данная формула ложна. Этот процесс можно представить таблицей:
| x | y | y | x y | (x y) | xy | (x y) xy |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |
Такими таблицами удобно пользоваться, если формула сложная и требуется определить ее истинность для всех возможных значений переменных.
Пример Л5. Определить истинность формулы (xy) xyz xyz для всех значений переменных x, y, z.
Решение. Решаем задачу с помощью таблицы, разбивая исходную формулу на подформулы:
| x | y | z | xy | (xy) 1 | x | y | z | xyz 2 | xyz 3 | 12 4 | 4 3 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Создав такую таблицу, можно ответить на вопрос, является ли данная формула тавтологией? Ответ – нет, т.к. при x=0, y=0, z=0 ее значение есть 0, а тавтология истинна при любых x, y, z. Является ли эта формула противоречием? Нет, т.к. есть наборы переменных, при которых она истинна. Из таблицы видно, что, например, «усеченная» формула (xy) xyz является тавтологией (все ее значения истинны), а соответственно ее отрицание ((xy) xyz ) будет противоречием (все значения ложны).
2.5. Упрощение формул
Следующая важная задача в приложениях логики высказываний – упрощение формул. Под упрощением понимается получение более простой (например, более короткой, не содержащей знаков , скобок, отрицаний над составными формулами) формулы, эквивалентной данной. Для этого используются эквивалентные преобразования формул (правила):
1) А В В А
2) (А В) С А (В С)
3) А А А
4) АВ ВА
5) (АВ)С А(ВС)
6) А А А
7) А(В С) АВ АС
8) А (ВС) (А В) (А С)
9) А А
10) (А В) А В
11) (АВ) А В
12) А В А В
13) А В В А
14) (А В) (В А)
15) А (АВ) А
16) А(А В) А
17) (АВ) В А В
18) А (В С) АВ С
19) А В В В В
20) А В В А
21) А(В В) А
22) А (В В) В В
Здесь А, В, С – (под)формулы, в частности, логические переменные. Обычно при преобразованиях вначале избавляются от импликаций с помощью правила 12, затем от отрицаний над составными формулами (правила 9–11) и скобок. Если в конечном результате преобразований получена тавтология, например хх, то исходная формула также является тавтологией, т.к. она эквивалентна полученной. Аналогично результат xx говорит о противоречивости исходной формулы. Правило 19 говорит о том, что в дизъюнкции подформула-тавтология и будет результатом, т.к. она всегда истинна, а для истинности дизъюнкции достаточно истинности хотя бы одного операнда. Правило 20 говорит о том, что противоречие не влияет на результат дизъюнкции, т.к. оно всегда ложно и результат определяется истинностью или ложностью оставшейся формулы. Соответственно тавтология не влияет на результат конъюнкции (правило 21), т.к. она всегда истинна и окончательный результат зависит только от значения оставшейся формулы.
Пример Л6. Упростить формулу: (xy)(x y)x.
Решение. Проводим цепочку преобразований (в скобках указывается номер применяемого правила):
(xy)(x y)x (12) (xy)( x y)x (11) x y ( x y)x (9, 4, 7) x y xx yx (20) x y yx (15) x y.
Пример Л7. Определить, является ли формула (xy)(x y)x противоречием?
Решение. Проделав упрощения, приведенные в примере 1, получим, что исходная формула эквивалентна формуле x y, которая противоречием не является. Ответ – нет.
Пример Л8. Определить, является формула x ((y z) x) тавтологией?
Решение. Упростим формулу: x ((y z) x) (11) x (y z) x (1) x x (y z) (19) x x. Ответ – да.
2.6. Решение логических задач
Решение логических задач сводится к построению логической формулы и последующему ее упрощению. При этом можно получить ответы на вопросы: является ли рассуждение логически правильным, является ли рассуждение В логическим следствием рассуждения А, совместны ли рассуждения А, В, С, …? Для понимания решения таких задач рассмотрим подробнее эти понятия.
Говорят, что В является логическим следствием А, или А логически влечет В, если формула А В является тавтологией. Из таблицы истинности для операции и определения тавтологии следует, что это условие равносильно следующему: если истинно А, то истинно и В.
Для выяснения, являются ли рассуждения логически правильными, нужно представить каждое предложение в виде логической формулы и проверить, является ли заключение логическим следствием конъюнкции посылок.
Говорят, что множество утверждений совместно, если конъюнкция формул, соответствующих этим утверждениям, не является противоречием.
Пример Л9. Правильно ли рассуждение:
Если Джонс – коммунист, то Джонс – атеист. Джонс – атеист. Следовательно, Джонс – коммунист.
Решение. Обозначим утверждения: А – «Джонс – коммунист», В – «Джонс – атеист». Тогда исходное рассуждение можно представить формулой: (АВ)ВА. Упростим формулу и определим, является ли она тавтологией. Упрощение: избавимся от импликаций, скобок и отрицания по правилам 12, 7, 11, 15: (АВ)В А ((АВ) В)) А В А. Полученная формула тавтологией не является, следовательно, исходное рассуждение логически неверно.
Пример Л10. Совместны ли утверждения: 1) Если инфляция растет, то увеличивается зарплата и увеличиваются налоги. 2) Налоги растут. 3) Зарплата снижается. 4) Если растет зарплата, то инфляция также растет.
Решение. Обозначим простые высказывания: инфляция растет – А, зарплата увеличивается – В, налоги увеличиваются – С. Запишем утверждения в виде формул: 1) А ВС; 2) С; 3) В; 4) В А. Построим их конъюнкцию, упростим и проверим, будет ли окончательная формула противоречием:
(А ВС)СВ(В А) ( А ВС) СВ (В А)
( А ВС)(СВ СВА) АСВ ВСВ СВАА ВСВА АСВ. Полученная формула непротиворечива, следовательно, исходные утверждения совместны.
2.7. Упражнения по теме для самостоятельного решения
Записать с помощью формул:
- Данное отношение есть отношение эквивалентности тогда и только тогда, когда оно рефлексивно, симметрично и транзитивно.
- Для того чтобы число делилось на три, достаточно, чтобы оно делилось на девять.
- Если влажность так высока, то либо после полудня, либо вечером будет дождь.
- Чтобы быть избранным в конгресс, необходимо приложить много усилий.
- Чтобы цены упали, достаточно, чтобы спроса не было и предложение было велико и необходимо, чтобы этого захотел продавец.
Проверить истинность формул:
- Известно, что эквивалентность x y истинна. Что можно сказать о значении x y и x y ?
- Заполнить истинностную таблицу для формулы (PQ)( (PQ)).
- Известно, что x имеет значение 1. Что можно сказать о значениях импликации xy z?
- Проверить истинность формулы ((xy)(yz)) (xz) при x=0, y=1, z=0 и при x=1, y=1, z=0.
- Построить таблицу истинности для функции Ф(x, y, z) ( x y) (x y)x. Является ли она тавтологией?
Преобразование (упрощение) формул:
- Противоречива ли формула P P РР ?
- Является ли тавтологией формула (PQ) P QQ ?
- Пусть Ф – тождественно ложная формула. Доказать, что xyФ
x y.
- Упростить формулу (xy)(x y)x.
- Найти x, если (x a) (x a) b.
- Проверить эквивалентность формул, преобразовав формулы слева и справа от знака к одной и той же формуле: (PQ)(PR) (PQR).
- Противоречива, тавтология или ни то, ни другое формула (PQ) (Q P) QQ ?
- Не строя таблицы истинности, доказать эквивалентность (хy) xy.
- Упростить формулу (x(xx yy) z) x yz (yz).
- Не строя таблицы истинности, доказать эквивалентность x(yz) xy z .
- Построить таблицу истинности: F = А ( В А В).
- Построить таблицу истинности: F = (В А) ( ВА АВ).
- Построить таблицу истинности: F = (А В) (В А) (В А).
- На каких наборах переменных А и В истинна функция F = (А В) (В А) В А (Ответ: <1, 0> , <1, 1>).
- Упростить логическую формулу ( А В) (В С) С А (Ответ: А ).
- Упростить логическую формулу АВС С В (Ответ: А В С).
- Упростить логическую формулу (АВ С)СВ D (Ответ: D).
- Истинность высказываний: «из двух фирм В и С проводит рекламную акцию только одна» и «фирма А проводит рекламную компанию, а фирма С не проводит – означает проведение рекламных акций какими фирмами? (Ответ: Фирмы A и B проводят рекламную акцию (Логическая формула для первого высказывания :
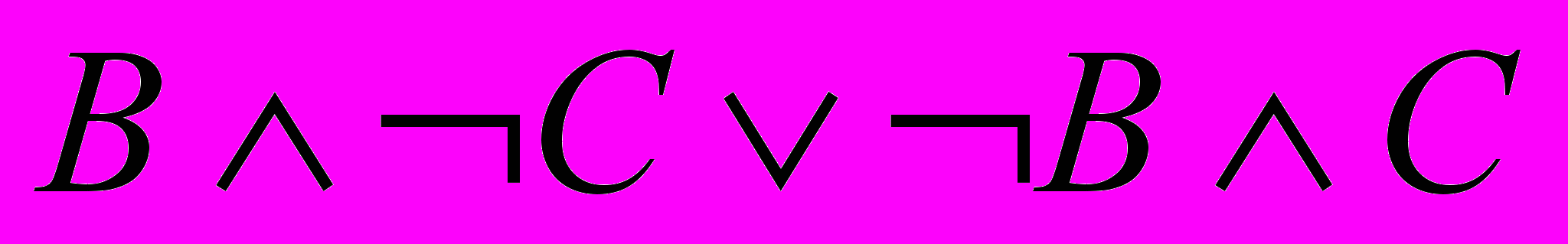 , второго –
, второго – 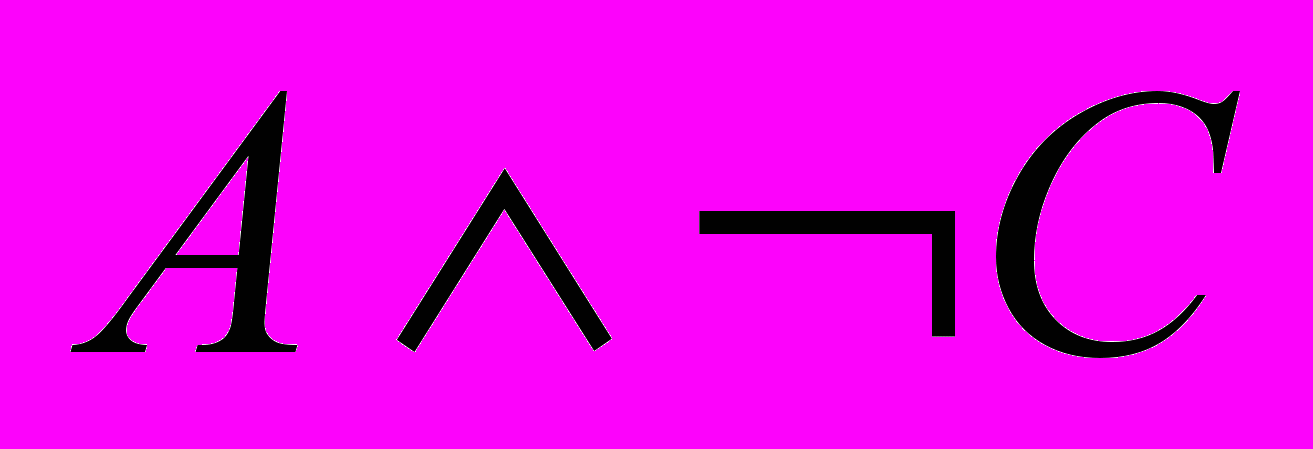 . Тогда из истинности обоих высказываний следует, что (
. Тогда из истинности обоих высказываний следует, что (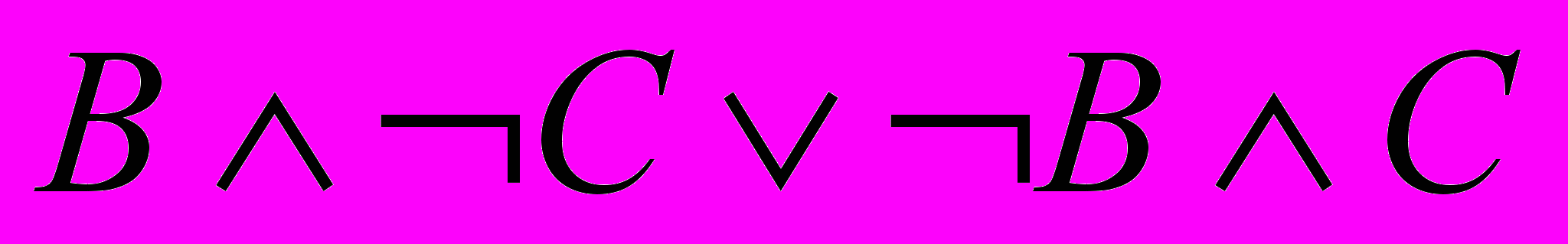 ) (
) (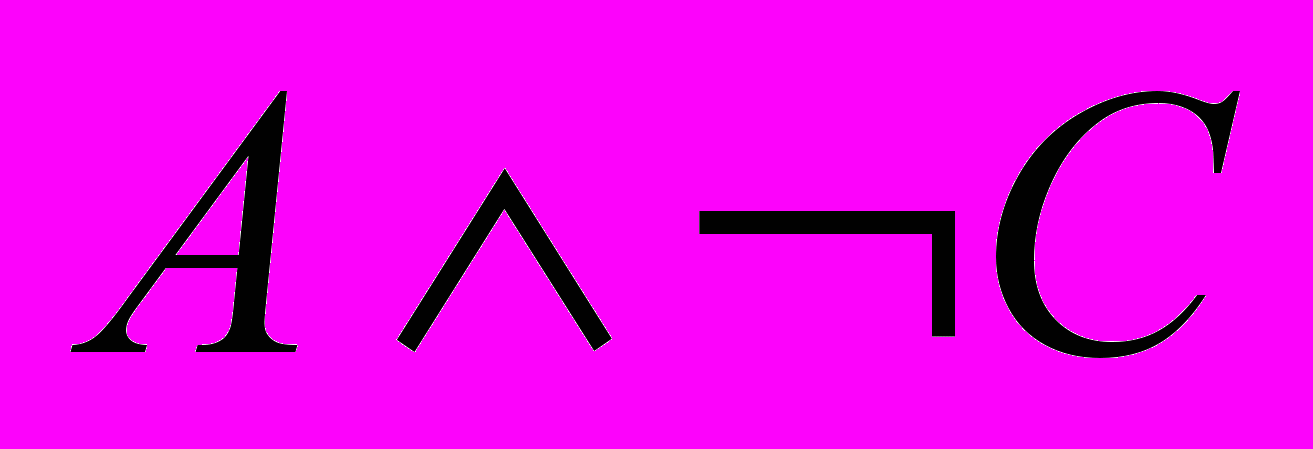 ). Упростим формулу и получим
). Упростим формулу и получим 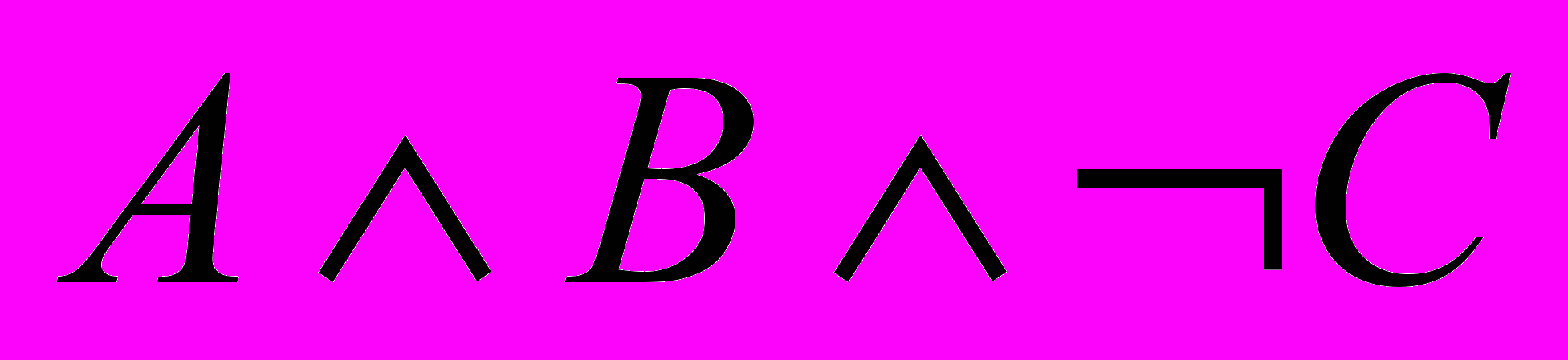 )).
)).
Задания для самостоятельного решения
1. Переведите целые числа из десятичной системы счисления в двоичную:
а) 3204; б) 5100.
2. Переведите десятичные дроби в двоичную систему счисления (ответ записать с шестью двоичными знаками):
а) 0,755; б) 0,787.
3. Переведите смешанное десятичное число в двоичную систему счисления 323,95.
4. Переведите целые числа из десятичной в восьмеричную систему счисления: а) 9080; б) 3090.
- Переведите целые числа из десятичной в шестнадцатеричную систему счисления: а) 2180; б) 4201.
- Переведите числа из десятичной системы счисления в восьмеричную:
а) 9326; б) 814, 562.
- Переведите двоичные числа в восьмеричную систему счисления: а) 1011010011111; б) 111000000100.
- Вычислите сумму чисел x и y, если
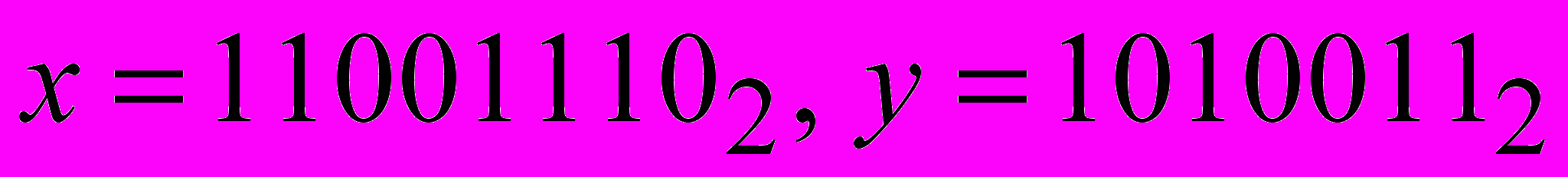 . Результат представьте в виде восьмеричного числа и в виде шестнадцатеричного числа.
. Результат представьте в виде восьмеричного числа и в виде шестнадцатеричного числа.
- Вычислить значение суммы в десятичной системе счисления:
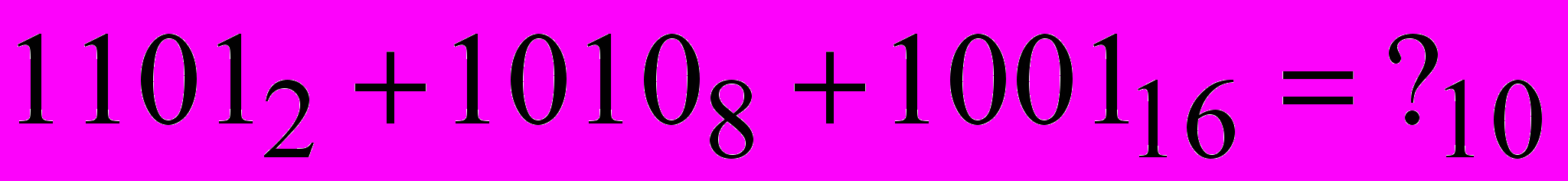 .
.
- B шестнадцатеричной системе счисления сумма чисел 12F16 и 10102 равна?
- Проверить истинность формулы ((xy)(yz)) (xz) при x=0, y=0, z=1 и при x=1, y=0, z=1.
- Является ли тавтологией формула (PQ) P QQ ?
- Упростить формулу (x(xx yy) z) x yz (yz).
- Упростить логическую формулу (А ВС)СА С.
- Упростить логическую формулу (АВ) (АВ)А.
- Упростить логическую формулу АВ(С D) ВСА В ВА.
- Упростить логическую формулу (АВС С) В С.
- Упростить логическую формулу (А В (АВ)) С((АС) С)
Тесты по системам счисления и логике
| ||||||||
| 1)97 | 2) 4B4FB0 | 3) 1650 | 4) 3162 | 5) 324 | 6) 10001 | 7) 4A45 | 8) 1029 | 9) 456 |
| ||||||||
| 1) (0,0); (1,1) | 2) (1,1); (0,1) | 3) (0,0); (0,1); (1,0) | 4) (1,1) | 5) (0,0); (0,1) | 6) на всех наборах | 7) нет наборов | 8) (0,0); (1,0); | 9) (0,1); (1,0); |
| ||||||||
| 1) A B | 2) ABC | 3) CC | 4) BC | 5) CC | 6) Нет варианта ответа | 7) ABC | 8) ABC | 9) A B |
| ||||||||
| 1) x | 2) y | 3) z | 4) z | 5) x | 6) y | 7) x=y=z | 8)x< y, y=z | 9) Нет варианта ответа |
| ||||||||
| 1) (0,1); (1,1); (1,0) | 2) (1,1); (0,1) | 3) (0,0); (0,1); (1,0) | 4) (1,1) | 5) (0,0); (0,1) | 6) на всех наборах | 7) нет наборов | 8) (0,0); (1,0); | 9) (0,1); (1,0); |
| ||||||||
| 1) C | 2) ABC | 3) A B | 4) BC | 5) CC | 6) Нет варианта ответа | 7) B | 8) ABC | 9) A B |

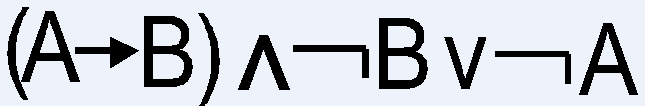 принимает значение Истина:
принимает значение Истина: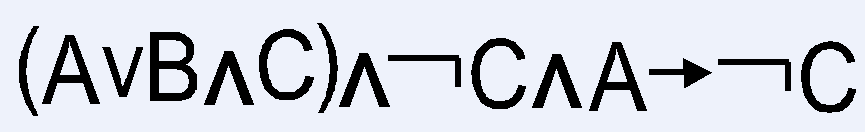 преобразуется к виду
преобразуется к виду принимает значение Истина:
принимает значение Истина: преобразуется к виду
преобразуется к виду