Geum.ru

Методические указания для подготовительных курсов Ростов-на-Дону

Вид материалаМетодические указания

Содержание


Пример С8.
Пример С9.
Пример C10.
Пример С12.
Пример С13.
Пример С14.
Приоритеты операций
Чтение формул
Подобный материал:
1   2   3

Пример С7. Найти сумму чисел 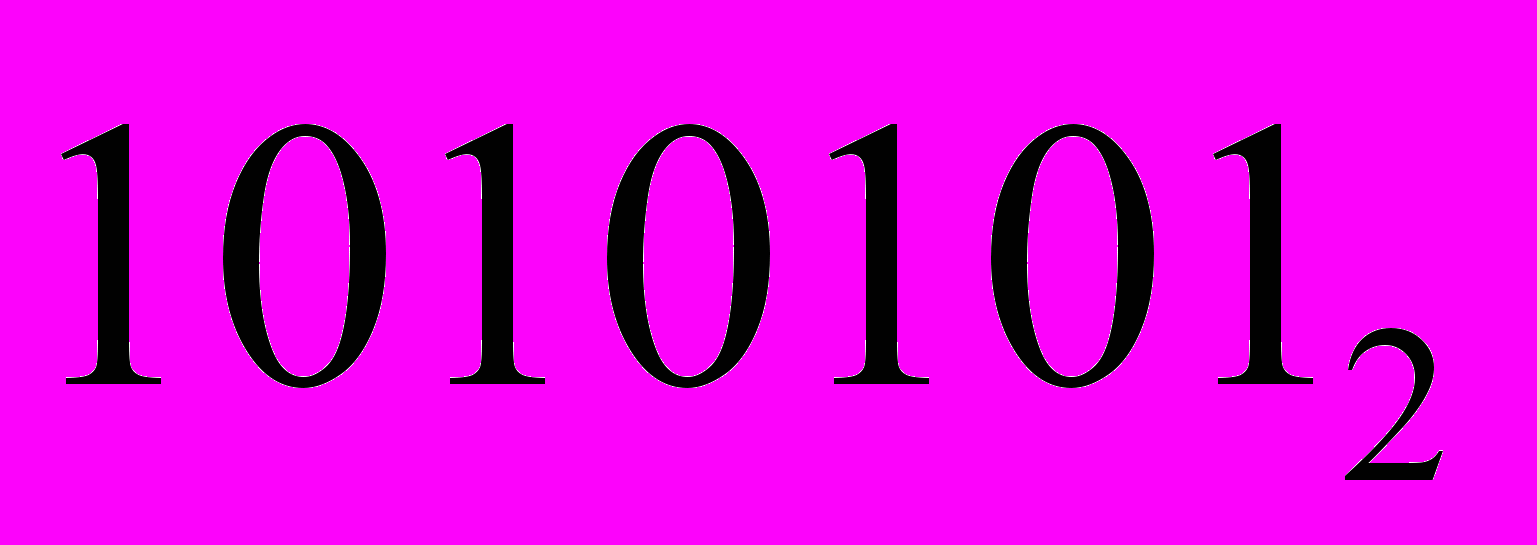и .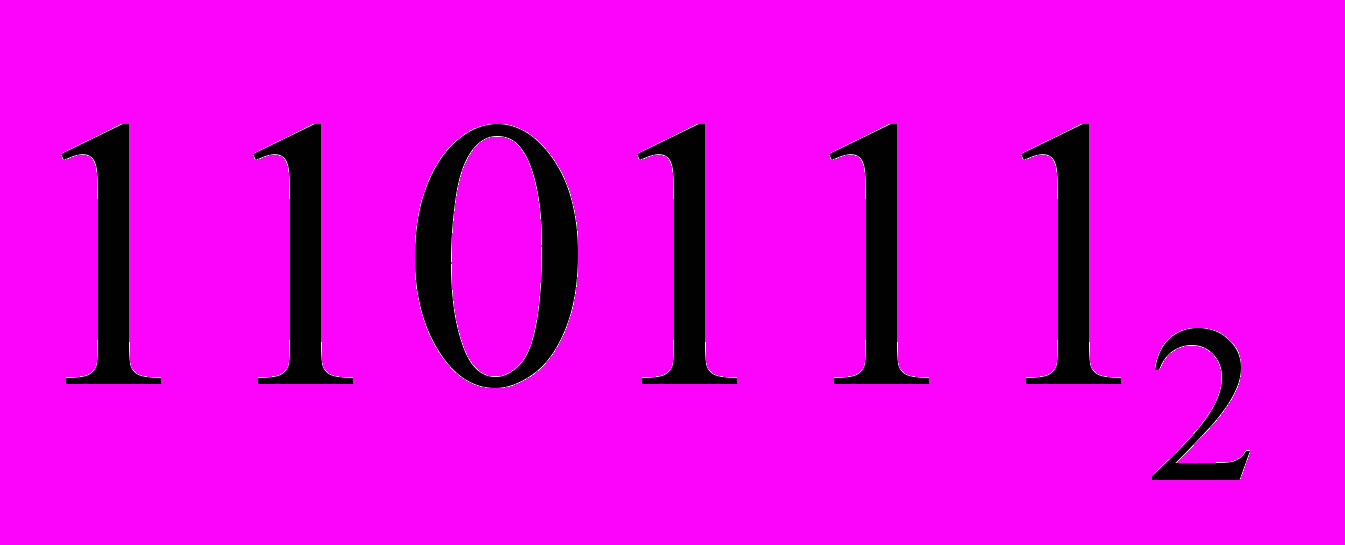

Решение

Первое слагаемое
1010101




+

Второе слагаемое
0110111

Сумма
10001100


Проверим результат нашего сложения, для чего переведем слагаемые и сумму в десятичную систему счисления:









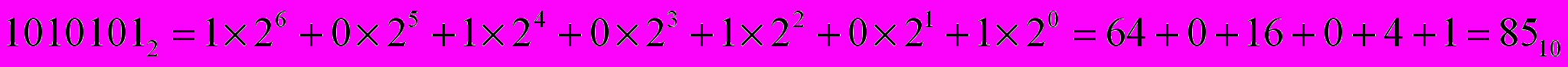
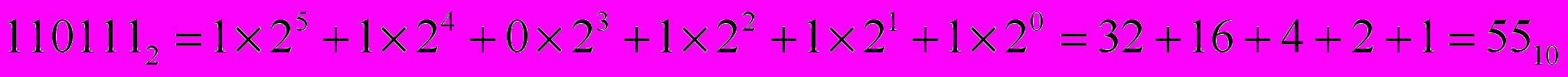
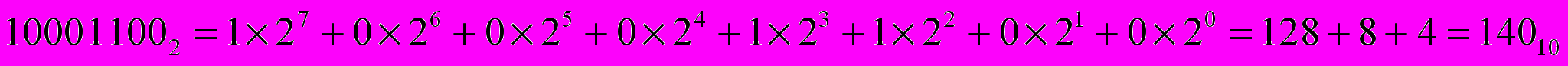
Как видим, действительно 85+55=140. 


Двоичная система, являющаяся основой всей компьютерной арифметики, тем не менее весьма громоздка и не удобна для использования человеком. Поэтому программисты пользуются двумя, кратными двоичной, системами счисления: восьмеричной и шестнадцатеричной.


Приведем в качестве примера запись натуральных чисел от единицы до шестнадцати в четырех системах счисления. Для удобства перевода из двоичной в восьмеричную и шестнадцатеричную системы рассмотрим табл.3.


Таблица 3

Перевод чисел из одной системы счисления в другую


10-я
2-я
8-я
16-я
2-8
2-16

0
0
0
0
000
0000

1
1
1
1
001
0001

2
10
2
2
010
0010

3
11
3
3
011
0011

4
100
4
4
100
0100

5
101
5
5
101
0101

6
110
6
6
110
0110

7
111
7
7
111
0111

8
1000
10
8



1000

9
1001
11
9



1001

10
1010
12
A



1010

11
1011
13
B



1011

12
1100
14
C



1100

13
1101
15
D



1101

14
1110
16
E



1110

15
1111
17
F



1111

16
10000
20
10







Из этой таблицы видно, что в двоичной системе счисления запись второй восьмерки чисел (от 8 до 15) отличается от записи первой восьмерки (от 0 до 7) наличием единицы в четвертом (слева) разряде. На этом основан алгоритм перевода двоичных чисел в восьмеричные «по триадам». Для применения этого алгоритма надо разбить двоичное число на тройки цифр (естественно, отсчитывая справа по три цифры для целого числа и слева для дробного числа) и записать вместо каждой из троек восьмеричную цифру.


Пример С8. Перевести число 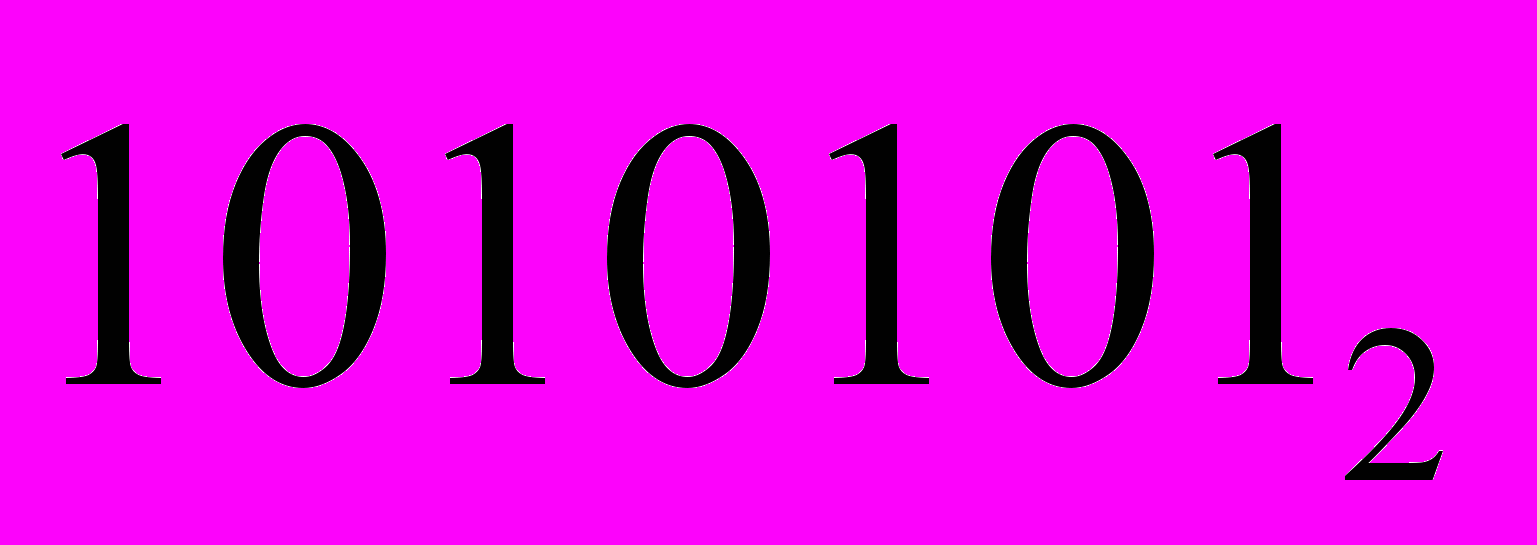в восьмеричную систему счисления.

Решение

Необходимо разбить число справа (т.к. оно целое) на «триады». Если до крайней слева тройки не хватает цифр, то дописываем незначащие нули слева.

.

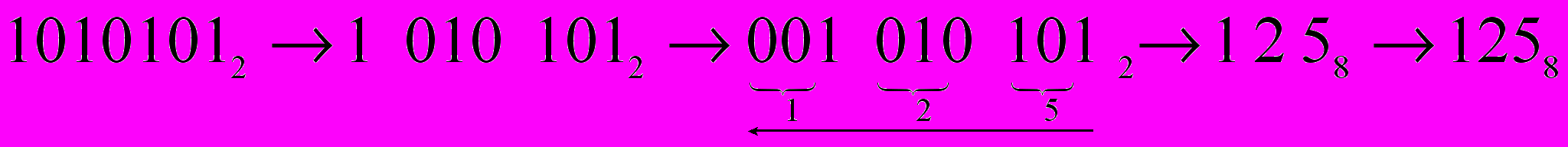Для перевода чисел из восьмеричной системы в двоичную используется обратный алгоритм: восьмеричные цифры заменяются на тройки двоичных цифр.

Например, .

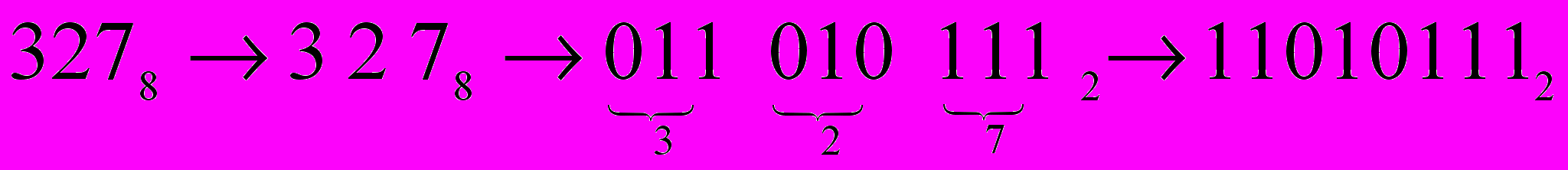Для перевода чисел из двоичной системы в шестнадцатеричную используется алгоритм «по тетрадям». Строка двоичных цифр разбивается на четверки и вместо них записываются шестнадцатеричные цифры.


Пример С9. Перевести двоичное число 110111101011101111,101 в шестнадцатеричную систему счисления.

Решение. Разделим данное число на группы по четыре цифры, начиная справа для целой части числа и слева для дробной части числа. Если в крайней левой группе (для целой части) и в крайней правой(для дробной части) окажется меньше четырех цифр, то дополним их нулями.



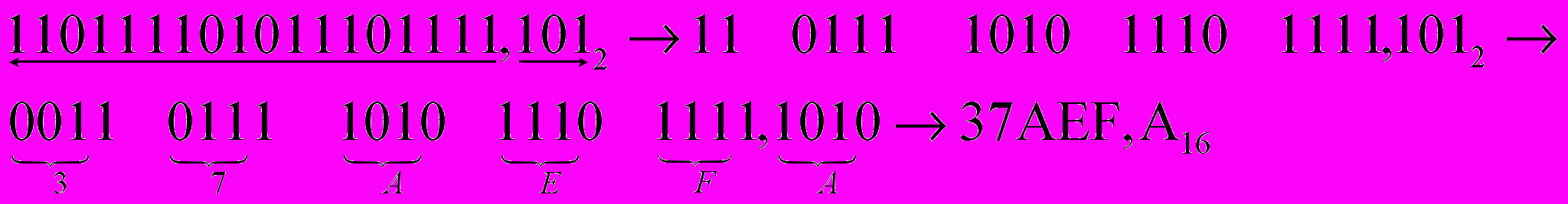
Следовательно, .


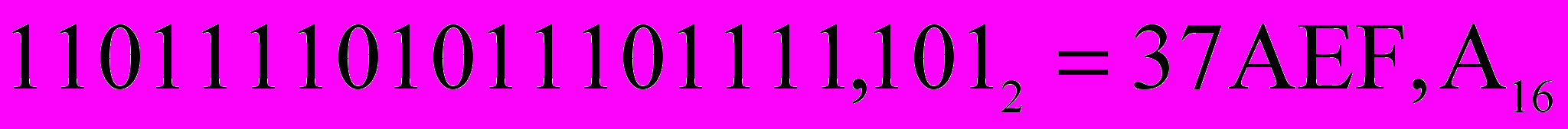Пример C10. Вычислите сумму чисел x и y, если 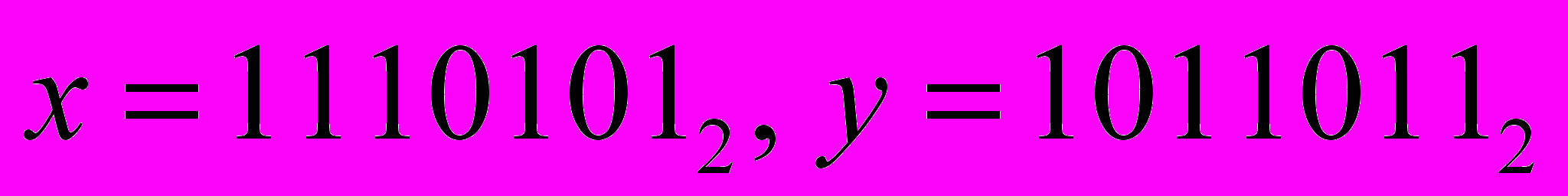. Результат представьте в виде восьмеричного числа.


Варианты ответа:

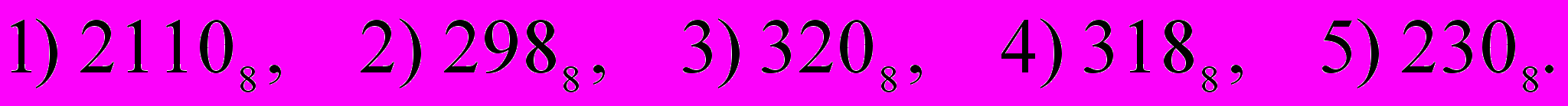
Есть два способа решения. Первый способ – сложить числа по правилам сложения двоичных чисел (столбиком), а результат перевести в восьмеричную систему счисления. Второй способ состоит в том, чтобы сначала числа перевести в восьмеричную систему, а потом сложить их.

Ответ: 3). 


Пример С11. Вычислить значение суммы в десятичной системе счисления:

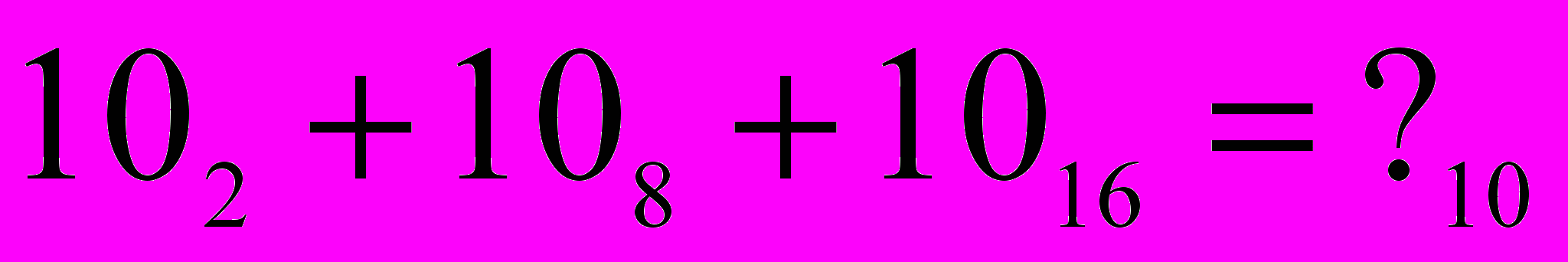
Варианты ответа:

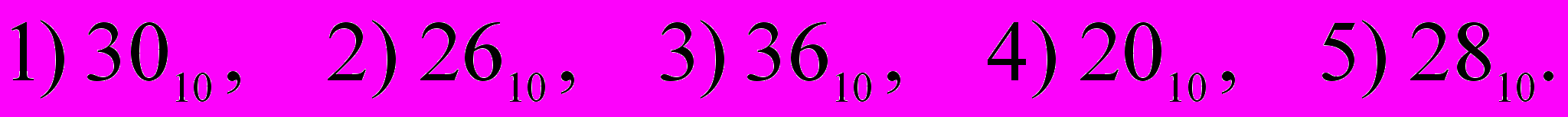
При решении можно перевести все числа в десятичную запись, а затем сложить. Второй способ решения – все числа перевести в двоичную систему, сложить их столбиком, а результат сложения перевести в десятичную систему счисления.

Ответ: 2). 


Пример С12. B шестнадцатеричной системе счисления сумма чисел F16 и 10112 равна

Варианты ответа: 1) 1A16; 2) 3216; 3) 1B16; 4) 2A16; 5) 1C16.

При решении задачи можно число F16 перевести в двоичную систему, затем числа сложить столбиком, а результат перевести в шестнадцатеричную систему.

Ответ: 1). 


Пример С13. B шестнадцатеричной системе счисления произведение чисел A416 и 68 равно

Варианты ответа: 1) 8416; 2) 98416; 3) 8D316; 4) 331816; 5) 3D816.

При решении задачи числа A416 и 68 переводим в двоичную систему, умножаем их по правилу умножения двоичных чисел, результат переводим в шестнадцатеричную систему счисления.

Ответ: 5). 


Пример С14. Какое минимальное основание имеет система счисления, если в ней записаны числа 100, 543, 101?

Варианты ответа: 1) нет верного ответа; 2) 2; 3) 5; 4) 4; 5) 6.

Необходимо ориентироваться на алфавит записи числа, помня что, например, в восьмеричной системе алфавит состоит из 8 цифр (0, 1, 2, 3, 4, 5, 6, 7).

Ответ: 5). 


1.4 Упражнения по теме для самостоятельного решения

  1. Переведите целые числа из десятичной системы счисления в двоичную:

а) 513; в) 600; д) 602; ж) 1000;

б) 2304; г) 5001; е) 7000; з)8192.
  1. Переведите десятичные дроби в двоичную систему счисления (ответ записать с шестью двоичными знаками):

а) 0,4622; в) 0,5198; д) 0,5803; ж) 0,6124;

б) 0,7351; г) 0,7982; е) 0,8544; з) 0,9321.
  1. Переведите смешанные десятичные числа в двоичную систему счисления: а) 40,5; б) 31,75; в) 124,25; г) 125,125.
  2. Переведите целые числа из десятичной в восьмеричную систему счисления: а) 8700; б) 8888; в) 8900; г) 9300.
  3. Переведите целые числа из десятичной в шестнадцатеричную систему счисления: а) 266; б) 1023; в) 1280; г) 2041.
  4. Переведите числа из десятичной системы счисления в восьмеричную:

а) 0,43; б) 37,41; в) 2936; г) 481,625.
  1. Переведите числа из десятичной системы счисления в шестнадцатеричную: а) 0,17; б) 43,78; в) 25,25; г) 18,5.
  2. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основанием 2, 8, 10 и 16.

Основание 2
Основание 8
Основание 10
Основание 16

101010












127












321












2B



  1. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основанием 2, 8, 10 и 16.




Основание 2
Основание 8
Основание 10
Основание 16










101







26






361






10110








  1. Переведите двоичные числа в восьмеричную систему счисления:

а) 1010001001011; в) 1011001101111; д) 110001000100;

б) 1010,00100101; г) 1110,01010001; е) 1000,1111001.
  1. Переведите двоичные числа в шестнадцатеричную систему счисления:

а) 1010001001011; в) 1011001101111; д) 110001000100;

б) 1010,00100101; г) 1110,01010001; е) 100,1111001.
  1. Переведите восьмеричные и шестнадцатеричные числа в двоичную систему счисления:

а) 266; в) 1270; 10,23;

б) 266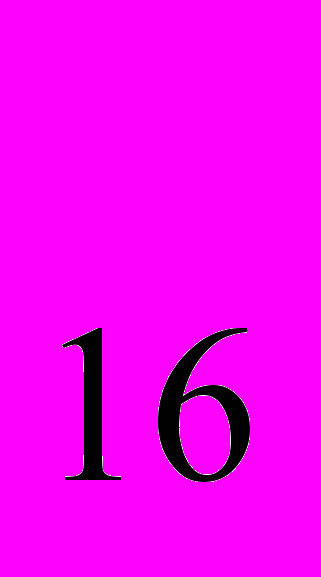; г) 2а19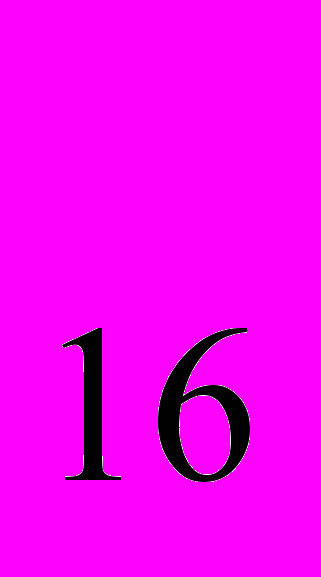; е) 10,23.
  1. Составьте таблицу сложения в восьмеричной системе счисления и выполните вычисления:

а) 3456 + 245; б) 7631-456;

в) 77771 +234; г) 77777-237.
  1. Составьте таблицу сложения в шестнадцатеричной системе счисления и выполните вычисления:

а) FFFF+1; б) 1996+BABA;

в) BEDA-BAC; г) 1998-A1F.

15*. Найти основание q системы счисления и цифру n, если верно равенство:

33m5n+2n443=55424

Пример выполнен в системе счисления с основанием q, m – максимальная цифра в этой системе счисления.


Ответы на некоторые упражнения:

1.a) 1000000001; 1.в) 1001011000;

2.а) 0,011101 2.в) 0,100001;

3.a) 101000,1;

4.а) 20774;

5.а) 10A;

6.а) 0,334; 6.б) 45,321;

7.б) 2B,C7A;

10.а) 12113; 10.г) 16,242.


2. Основы логики высказываний


2.1. Высказывания. Логические операции, выражения


Высказывание – это утверждение (предложение), о котором можно сказать, истинно оно или ложно. Например, высказывание «город Сочи расположен на берегу Черного моря» истинно, а высказывание «город Ростов расположен на берегу Черного моря» ложно. Из простых высказываний А, В можно образовать более сложные высказывания: «А и В», «А или В», «неверно, что А», «если А, то В» («из А следует В»). Зная истинность или ложность утверждений А, В, можно установить истинность или ложность сложного (составного) высказывания.

Высказывание можно формализовать с помощью логической формулы. Логическая формула включает в себя логические переменные и логические связки (знаки логических операций). Переменные представляют утверждения и обозначаются обычно буквами латинского или русского алфавита. Связки – это операции:
  • конъюнкция (обозначения , &, , AND, И);
  • дизъюнкция (обозначения , +, OR, ИЛИ);
  • отрицание (обозначения  , , NOT, НЕ, для высказывания А);
  • импликация (обозначения  , );
  • эквивалентность (обозначения ,).

Далее используются первые из указанных в списках обозначений.


Например, высказывание «если будет дождь, мы не поедем в гости, будем сидеть дома» можно формально представить формулой А  ВС, где переменная А в данном случае представляет высказывание «будет дождь», В – высказывание «поедем в гости», С – «будем сидеть дома». Прочитать такую формулу можно так: «из А следует не В и С».


Операнды дизъюнкции называют дизъюнктами, операнды конъюнкции – конъюнктами. В импликации    левый операнд, формулу , называют посылкой, а если правый операнд, формулу  – заключением. Читают импликацию как «из  следует », или « влечет ».

Приоритеты операций: существует договоренность о порядке выполнения логических операций, если этот порядок не размечен круглыми скобками. Наивысший приоритет имеет отрицание, затем конъюнкция, далее выполняется дизъюнкция и последней – импликация. Если логическое выражение имеет скобки, то они меняют приоритет операций, т.е. сначала выполняются действия в скобках.

Чтение формул. Формулы необходимо читать с учетом приоритетов операций. Например, формулу  (х   у)  z можно прочитать так: из того, что не выполняется условие «из х следует не у», вытекает (логически следует) z. Другой правильный вариант: если неверно, что из х следует не у, то выполняется z. Прочтение «если не х, то не у влечет z» является неверным и неоднозначным, т.к. соответствует формуле  х (  у  z ) и формуле ( х   у)  z. 


2.2. Построение формул по высказываниям


Пример Л1. «Для того, чтобы треугольники были равны, необходимо, чтобы они были подобны». Обозначим простые высказывания переменными: x – «треугольники равны» и y – «треугольники подобны». Тогда формула: x  y соответствует исходному высказыванию. Обратите внимание, что необходимое условие идет справа от операции следования: если треугольники равны, то они точно будут подобны. Обратное, y  x, неверно – из подобия равенства не следует. 


Пример Л2. Высказывание: «Для того чтобы были лужи, достаточно, чтобы прошел дождь». Обозначим x – «были лужи», y – «прошел дождь». Формула y  x формализует исходное высказывание. Обратите внимание, что достаточное условие идет слева от операции следования: если был дождь, то есть и лужи. Обратное x  y неверно, т.к. лужи могут быть вызваны не дождем, а например, водопроводной аварией. 


Пример Л3. Высказывание: «Для того чтобы число было четным, необходимо и достаточно, чтобы оно делилось на два без остатка». Обозначим x – «число четное», y – «число делится на два без остатка». Формула (x  y)  (y  x) формализует исходное высказывание. 


Примеры ошибочного толкования следования

1. Из высказываний «все зебры полосаты» и «это животное полосато» следует, что «это животное – зебра». Так, полосатый кот становится зеброй.

2. Из высказываний «людей много» и «Сократ – человек» следует, что «Сократов много».


2.3. Определение истинности формул


Задача определения истинности формул решается в соответствии с принятыми правилами интерпретации высказываний в логике. Обычно цифрой 0 обозначено значение «ложь», цифрой 1 – значение «истина».

На множестве {0, 1} операции , ,   определены при помощи ниже представленных таблиц.

A
A

0
1

1
0


Другими словами, Отрицание истинно тогда и только тогда, когда исходное высказывание A ложно, и ложно, когда исходное высказывание A истинно.

A
B
A  B

0
0
0

0
1
0

1
0
0

1
1
1


Конъюнкция истинна тогда и только тогда, когда оба операнда А и B истинны.

A
B
A  B

0
0
0

0
1
1

1
0
1

1
1
1


Дизъюнкция ложна тогда и только тогда, когда оба операнда А и B ложны.

A
B
A  B

0
0
1

0
1
1

1
0
0

1
1
1


Импликация ложна тогда и только тогда, когда первое высказывание А (посылка, причина) истинно, а второе высказывание В (заключение, следствие) ложно.

A
B
A  B

0
0
1

0
1
0

1
0
0

1
1
1


Эквивалентность формул означает совпадение их значений истинности для всех возможных наборов входящих в них переменных. Операцию эквивалентности обозначают обычно знаком тождества .

Существуют формулы, имеющие одно и то же значение, при различных значениях входящих в них переменных. К ним относятся тавтология и противоречие.

Тавтология – это формула, истинная при любой интерпретации входящих в нее переменных. Так, формула x  x всегда истинна. Действительно значение дизъюнкции есть истина, если хотя бы один ее операнд истин, а в этой формуле, если x – ложь, то x – истина.

Противоречие – это формула, ложная при любой интерпретации входящих в нее переменных. Так, формула xx всегда ложна. Действительно, значение конъюнкции есть ложь, если хотя бы один ее операнд ложен, а в этой формуле, если x – истина, то x – ложь.

Если заданы значения переменных, то, используя стандартную интерпретацию, можно определить, истинна или нет данная формула.

    1. .Определение истинности формул с помощью таблиц истинности