Н. В. Папуловская Математическая логика Методическое пособие

Вид материала

Содержание

Глава 3. Формализация понятие алгоритма 1. Историческая справка
2. Общее понятие алгоритма
X-Y алгоритмом
Курт Гедель
Aндрей Андреевич Марков
Тезис Черча.
3. Машина Тьюринга
4. Нормальные алгорифмы Маркова.
Определение1. Обычной

Подобный материал:

1 2 3 4 5 6 7 8 9 10 11

Глава 3. Формализация понятие алгоритма

1. Историческая справка

Слово алгоритм содержит в своем составе преобразованное географическое название, а именно слово Хорезм. Хорезм - так назывался город, в котором жил великий ученый средневекового Востока. Имя этого ученого – Мухаммед ибн Муса ал-Хорезми (ал-Хорезми обозначает «Хорезмиец) Он жил приблизительно с 783 по 850 гг. Ал-Хорезми – автор основополагающих трактатов по арифметике и алгебре.

Труды ал-Хорезми были переведены с арабского на латинский в 12 веке, в этих трудах содержалась позиционная система счисления и искусство счета в этой системе (например, алгоритмы сложения столбиком).

В латинских названиях трудов ал-Хорезми его имя писалось как algorismi, арифметический трактат начинался словами «Dixit algorismi», т.е. «сказал ал-Хорезми».

Отсюда и пошло слово «алгоритм» - сначала для обозначения десятичной позиционной арифметики и алгоритмов цифровых вычислений, а затем для обозначения произвольных алгоритмов цифровых вычислений, а затемдля обозначения произвольных алгоритмов.

Позднее город Хорезм ста называться – Хива.

с 1920-1923 гг. – столица Хорезмской Народной Советской Республики,

с 1923-1924 гг.– столица Хорезмской Советской Социалистической Республики

с 1924-1990 гг. – районный центр Хорезмской области Узбекской ССР

Город Ургенч является наследницей древнего Хорезма. Этот город считается колыбелью понятия алгоритма.

2. Общее понятие алгоритма

Понятие алгоритма, подобно понятию множества и натурального числа, принадлежит к числу фундаментальных понятий математики. Оно не может быть выражено через другие, а должно рассматриваться как неопределимое.

Существует не определенное понятие «алгоритм», а только его описание, интуитивный смысл.

Почти во всех сферах жизни мы сталкиваетмся с рецептами решения задач, предписаниями, инструкциями, правилами и т.п. Они однозначно определяют порядок выполнения действий для получения, желаемого результата. Предписание, удовлетворяющее некоторым дополнительным требованиям, называется алгоритмом.

Алгоритм – это определенное на некотором языке конечное предписание, задающее дискретную последовательность исполняемых элементарных операций для решения проблемы. Процесс выполнения предписания состоит из отдельных шагов, на каждом из которых выполняется одна очередная операция.

Под алгоритмом принято понимать конечную последовательность операций, называемых элементарными, исполнение которой приводит к решению любой задачи из заданного множества задач. В это определение входят такие свойства алгоритма, как конечность (конечная длина выполняемых операций), массовость (алгоритм должен быть пригоден для решения всех задач из заданного класса), результативность (в результате получаем решение задачи). Кроме того, должно выполняться ещё одно необходимое свойство алгоритма – детерминизм, которое определяется как однозначное понимание каждой операции, или то же самое, независимость результата выполнения каждой элементарной операции от того, кто её выполняет.

Под это определение подходит широкий круг алгоритмов. Это может быть алгоритм вычисления математической функции, алгоритм технологического процесса, алгоритм проектирования ЭВМ или цеха завода и т.д. Элементарные операции могут быть достаточно сложными: при вычислении функции это может быть, например, нахождение корней уравнения в проектных или технологических алгоритмах – принятие сложных проектных или технологических решений.

Приведенные свойства определяют, конечно, не строгое понятие алгоритма, которое называется интуитивным.

Рассмотренное определение не является формализованным и строгим по двум причинам. Во-первых, в нём не формализовано понятие элементарной операции, и, во-вторых, не формализовано представление последовательности операций. Важность разработки общего для всех алгоритмов формального описания заключается в том, что оно даёт возможность иметь общие инструментарии для сравнения, оценки, преобразования и других действий над алгоритмами.

Формализация операций алгоритмов связано со следующим. Любой алгоритм связан с некоторым объектом действия, и каждый объект представляется в виде описания, причём под описанием понимается не только в виде текстов на языке, но и рисунки, чертежи и т.п. Значит, можно предположить, что объект описан в виде слова в заданном алфавите.

Объект может находиться в различных состояниях, чему соответствуют различные слова. Так, объектом для математических алгоритмов являются математическое описание задачи в форме матриц коэффициентов, графа смежности и т.п.т., для проектных алгоритмов – техническое задание на проектирование или перечень требований и условий к результату.

Операция определяется над описанием объекта и её результатом является новое (изменённое) описание (новое слово). Например, если решается графовая задача, то результатом операции может быть описание графа с промежуточным взвешиванием рёбер и/или вершин. Результатом проектной операции будет более полное, уточнённое описание объекта.

Результатом работы алгоритма в графовой задаче может быть выделенный путь или цепь, частичный подграф или веса вершин или ребер. Результатом работы алгоритма проектирования является описание объекта проектирования, достаточное для его изготовления в заданной технологической базе.

Алгоритмы в интуитивном смысле не являются математическими объектами, к ним не применимы формальные методы исследования и доказательства. Поэтому в XX веке были предприняты усилия в попытке формализовать понятия алгоритм.

Полное описание всякого алгоритма начинается с того, что фиксируются два ансамбля – «ансамбль X-допустимых исходных данных” и «ансамбль Y-допустимых результатов».

X – «ансамбль входов»

Y – «ансамбль выходов»

Произвольный алгоритм называется X-Y алгоритмом. Областью применения, или областью применимости алгоритма, является подмножество ансамбля входов, это подмножество состоит из всех тех входов, для которых алгоритм выдает результат.

Каждый алгоритм задает функцию, определенную на области применимости. Про такую функцию говорят, что она вычисляет рассматриваемый алгоритм. Эквивалентные алгоритмы вычисляют одну и ту же функцию.

Формализация понятия алгоритма необходима по разным причинам. Например. Сравнение двух алгоритмов по эффективности, проверка их эквивалентности, и др. Впервые необходимость формального понятия алгоритма возникла в связи с проблемой алгоритмической неразрешимости некоторых задач.

Задача считается разрешимой, если существует решающий её алгоритм. При отыскании решений некоторых задач долго не удавалось найти соответствующий алгоритм. Примерами таких задач являются следующие:

а) указать способ, согласно которому для любой предикатной формулы за конечное число действий можно выяснить, является ли она тождественно-истинной или нет;

б) разрешимо ли в целых числах любое диофантово уравнение (алгебраическое уравнение с целыми коэффициентами.)

Для решения этих задач найти алгоритмов долго не удавалось, возникло предположение, что такие алгоритмы вообще не существуют. Доказать это с помощью интуитивного понятия алгоритма в принципе невозможно.

В 20-х –30-х годах двадцатого века предпринимались попытки формализовать понятие алгоритма. В результате было предложено несколько моделей формализации понятия алгоритма. Математики С.К. Клини, А.А. Марков, Э. Пост, А. Тьюринг, А. Черч предложили различные математические модели алгоритма.

Курт Гедель определил алгоритм как последовательность правил построения сложных математических функций из более простых, модель рекурсивных функций.

Алонзо Черч использовал -исчисление.

Алан Тьюринг определил алгоритм как программу для вычислительной машины, называемой машиной Тьюринга.

Aндрей Андреевич Марков определил алгоритм как конечный набор правил подстановок цепочек символов.

Удивительным научным фактом является доказательство эквивалентности всех этих формальных определений алгоритма. Эквивалентность двух абстрактных моделей алгоритма состоит в том, что любой класс проблем, которые можно решить с помощью моделей одного типа, можно решить и на моделях другого типа.

Исторически Алонзо Черч первым предложил отождествлять интуитивное понятие алгоритма с одним из эквивалентных между собой точных определений. Алан Тьюринг независимо высказал предположение, что любой алгоритм в интуитивном смысле может быть представлен машиной Тьюринга. Это предположение известно как тезис Черча-Тьюринга.

Тезис Черча. Класс задач, решаемых в любой формальной алгоритмической модели, совпадает с классом задач, которые могут быть решены интуитивно алгоритмическими методами.

Тезис Тьюринга. Любая функция, «вычислимая в естественном» смысле, может быть вычислена универсальной машиной Тьюринга.

3. Машина Тьюринга

Алгоритм есть механический способ обработки информации. В своём вычислительно устройстве Тьюринг смоделировал доведённый до самых элементарных операций процесс выполнения произвольного алгоритма человеком. Человек имеет конечную память, и в этом смысле его можно представить системой с конечным числом состояний. Исходная информация к алгоритму обычно представляется в виде цепочки символов. Можно себе представить, что эта информация представлена в виде слова конечного словаря. Выполняя алгоритм, человек-вычислитель использует дополнительную память для записи информации, она может быть потенциально бесконечной, например, листы бумаги. При вычислении человек может возвращаться к ранее записанной информации, стирать некоторую информацию и т.д.

Таким образом, элементарными операциями при выполнении алгоритма можно считать запись и стирание символа, а также перенесение внимания с одного участка записи на другой.

Машина Тьюринга – это математическая модель идеализированной (примитивной) цифровой вычислительной машины.

Удобно представлять, что машина Тьюринга состоит из четырех частей: ленты, головки, внутренней памяти и устройства управления.

Лента состоит из равных ячеек. Каждая ячейка помечена соответствующим целым числом, и может содержать только один символ из фиксированного конечного множества А.

Множество А называют внешним алфавитом машины. Один символ из А называется пустым или «пробелом» - . Ячейка ленты, в которой записан символ , называется пустой.

Машина работает во времени, которое считается дискретным. В каждый момент времен головка находится над определенной ячейкой ленты и считывает символ.

лента памяти: a_i Є A

а_к

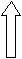
Головка (чтение, запись, перемещение)

УУ (программа)

Рис 1. Машина Тьюринга

В каждый момент времени t_i лента содержит конечное число клеток. Лента потенциально бесконечна, т.е. к ней как справа, так и слева могут быть добавлены новые ячейки.

Головка может остаться на той же клетке (Н-состояние), сдвинуться на одну клетку вправо (П), сдвинуться на одну клетку влево (Л) (Если сдвигается в отсутствующую клетку, то пристраивается новая пустая клетка).

Машина обладает внутренней памятью – некоторое конечное множество состояний Q = {q₀, q₁, … q_k}

q₀– заключительное состояние

q₁– начальное состояние

Движение головки зависит от считываемого символа и внутреннего состояния машины.

Устройство управления в каждый момент времени t:

изменяет считываемый символ a_i на a_j .

передвигает головку в одном из направлений Н, Л, П.

изменяет внутреннее состояние машины q_i на новое q_j, в котором будет машина в момент t + 1

Такое действие УУ называют командой, и она записывается:

q_ia_i a_j Dq_j, где D Є {Н, Л, П}

Выполнение одной команды называется шагом.

Вычисление (или работа) машины Тьюринга есть последовательность шагов. Если после выполнения шага появляется заключительное состояние, то машина останавливается. Результат состоит из содержимого ленты, номера указанной головкой ячейки и содержимого программы в момент остановки. Совокупность этих трех условий называется конфигурацией.

В начальный момент времени конфигурация такова:

на ленте, состоящей из некоторого числа ячеек (рис. 2) записаны символы внешнего алфавита А;
головка находится над первой слева клеткой ленты.
внутреннее состояние машины q₁.

Будем считать машину Тьюринга заданной, если известна ее программа.

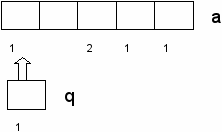
Рис.2 Начальная конфигурация машины Тьюринга

Зная программу и задав начальную конфигурацию, полностью определяем работу машины над словом. Будем считать, что машинное слово M получается из машинного слова М с помощью машины Т, и записывать M_i  ^TM, если существует последовательность преобразований M_i^TM_i₊₁, i=0,1,…,k-1, для которой M₀=M, M_k=M.

Если в работе машины не встречается заключительное состояние, то процесс вычисления будет бесконечным и говорят, что машина неприменима к слову на ленте в начальной конфигурации.

Временем работы машины Тьюринга называется число шагов, выполняемых машиной до получения результата.

Емкостью работы машины Тьюринга называется максимальная длина использованного участка на рабочей ленте. Если вычисления не заканчиваются время и ёмкость считаются бесконечными.

Недетерминированная машина Тьюринга, это такая машина у которой каждый шаг может привести машину в несколько различных состояний. Такая машина является ключевым понятием в теории NP-полных задач.

4. Нормальные алгорифмы Маркова.

Марков Андрей Андреевич (родился в 1903г.), известный русский математик и логик, зав. Кафедрой математической логики МГУ, с 1936 года работал в Математическом институте Академии Наук СССР. Член-корреспондент Академии Наук СССР (с 1953 года). Известен своими работами в области теории алгоритмов. Предложенное им понятие нормального алгорифма явилось крупным вкладом в мировую математическую науку. Ему принадлежит четкое определение таких понятий, как абстракция отождествления и абстракция потенциальной осуществимости. А.А. Марков – основоположник конструктивного направления в математике и математической логике.

Алфавитом называется множество из конечного числа различных символов. Слово в данном алфавите определяется как горизонтальный ряд конечного числа букв этого алфавита. Например, если задан алфавит {a, b}, слова в этом алфавите: a, b, abba, bbba…

Слово без букв – пустое слово. Пустое слово есть в каждом алфавите.

Понятие вхождения слова P в данное слово: слово Р входит в данное слово R, если слово R имеет вид: R₁PR2 (R₁ и R₂ могут быть пустыми словами).

Пример. Пусть в алфавите {a, b} имеем слово R = abaabab, P = ba

R имеет вид R₁PR₂, где R₁ – пустое слово, R₂ – abab;

R₁ = aba, R₂= b

В дальнейшем буем определять только первые вхождения слов и заменять их на другие слова.

Пример. Заменить слова ba в слове aababab на слово а. Результатом будет слово aaaabab.

Если первое вхождение пустого слова в любое слово R заменить на некоторое слово Q, получится слово QR.

Определение1. Обычной формулой подстановки в алфавите А называется слово P  Q где P и Q – слова в алфавите А.

Заключительной формулой подстановки называется слово:

P  Q , где P и Q – слова в алфавите А.

Конечная непустая упорядоченная система подстановок:

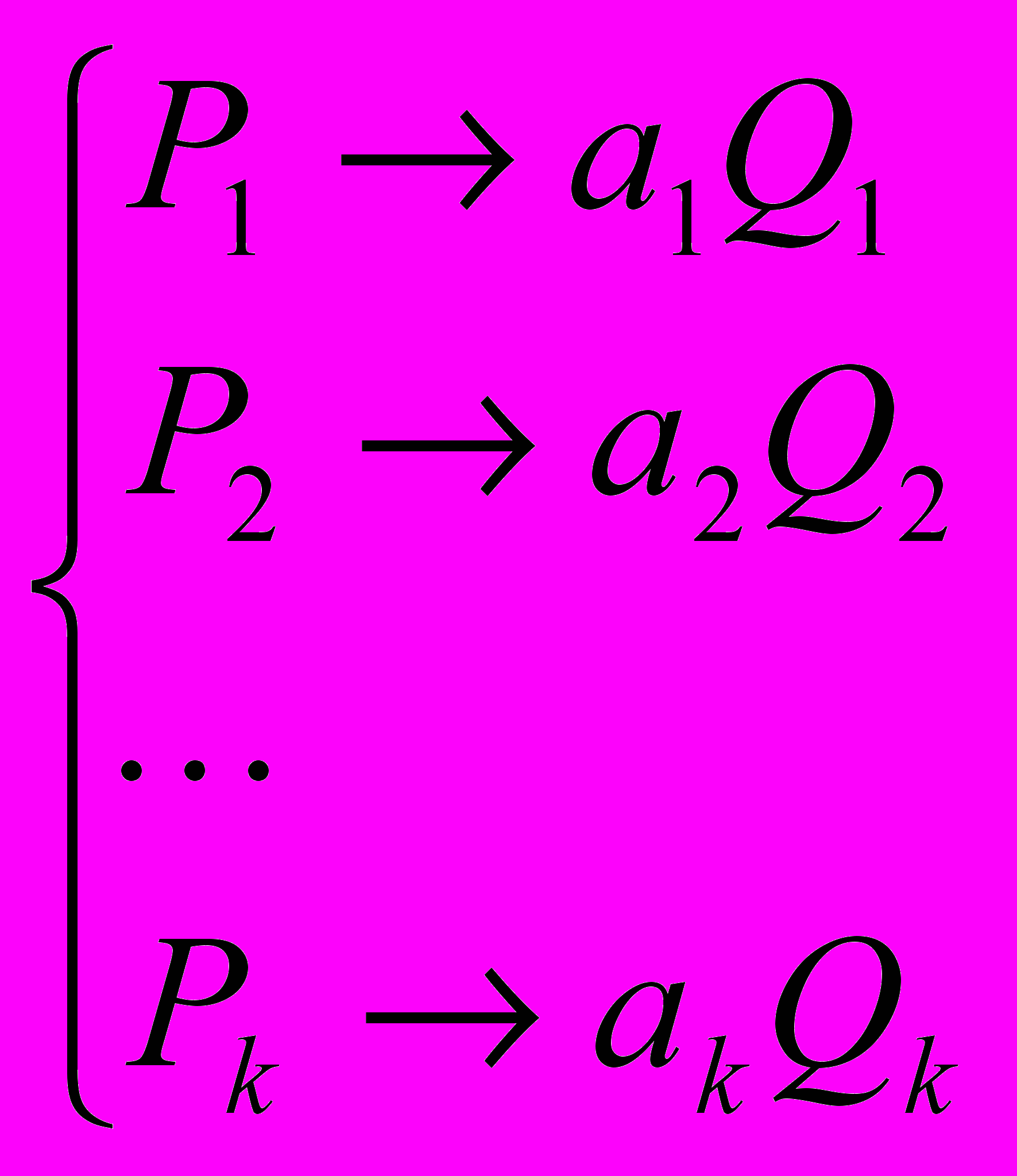
Называется нормальной схемой в алфавите А,

где k 1, a_i = { , пустое слово}, P_iQ_i – слова в алфавите А, i =1, k.

Нормальный алгорифм над алфавитом А (н.а.) задается конечным алфавитом В, не содержащим { ,  } и включающим в себя А или совпадающим с А (BA) и нормальной схемой в алфавите В.

Нормальный алгорифм над алфавитом А преобразует слова в А следующим образом: работа данного н.а. над словом R состоит из отдельных шагов, в результате которых получаются новые слова:

R, R₁, R₂, R₃, …R_i, R_i₊₁… (*)

Слово R_i₊₁ получается из предыдущего слова R_i следующим образом:

просматривается нормальная схема алгорифма, из неё выбирается самая верхняя формула, левая часть которой входит в слово R_i. Пусть это формула P_j a_jQ_j, a_j {, _}

первое вхождение в слово R_i заменяется на слово Q_i, что и даёт слово R_i₊₁.

Работа н.а. над словом заканчивается в двух случаях:

существует такое слово R_i , что слово R_i₊₁ получается из с помощью заключительной формулы подстановки. В этом случае результатом н.а. над словом работы – слово R_i₊₁

Существует R_j из (*), что ни одна левая часть формул подстановок из нормальной схемы не имеет вхождений в слово R_j. Результат работы н.а.– слово R_j.

В остальных случаях работа н.а. над словом не заканчивается, а последовательность (*) будет бесконечной. Говорят, что данный н.а. неприменим к слову R.

Утверждение. Каждая функция, вычислимая при помощи нормальных алгорифмов Маркова вычислима и при помощи машины Тьюринга, и наоборот.

Литература

Колмогоров А.Н. Математическая логика: Учеб. пособие для студентов мат. специальностей вузов / А. Н. Колмогоров, А. Г. Драгалин. Моск. гос. ун-т им. М. В. Ломоносова. - М.: УРСС, 2004. - 240 с.
Андерсон Д. А. Дискретная математика и комбинаторика: Пер. с англ./ Д. А. Андерсон – М.:Издательский дом «Вильямс», 2003 –960с.:ил.
Акимов О.Е. Дискретная математика: логика, группы, графы./ О.Е.Акимов.М.: Лаборатория базовых знаний, 2001. 352с.: ил.
Лихтарников Л. М. Математическая логика: Курс лекций. Задачник-практикум и решения: Учеб. пособие для студентов вузов, обучающихся по мат. спец. / Лихтарников Л.М., Сукачева Т.Г.. - СПб.: Лань, 1999. - 288 с.
Тей А.,. Логический подход к искусственному интеллекту: от классической логики к логическому программированию: Пер. с франц./
А. Тей, П. Грибомон, Ж.М. Луи и др: Мир,1990. 432 с.: ил.
Ершов, Ю. Л. Математическая логика: учеб. пособие / Ю. Л. Ершов, Е. А. Палютин. - 3-е изд., стер. - СПб. [и др.]: Лань, 2004. - 336 с.: ил.

Blog