1. Структура цом, представлення цом як конечного автомата
| Вид материала | Документы |
- Вторая, 374.07kb.
- «Автоматы: модель конечного автомата, распознаватели и преобразователи. Анализаторы, 150.22kb.
- Гражданское право (часть II) в вопросах и ответах батычко Вик. Т., 2008, 1556.04kb.
- Комарова Т. С, 299.71kb.
- Алконос) в русских средневековых легендах райская птица с человеческим лицом (часто, 251.62kb.
- Учебно-тематический план проведения пятидневных учебных сборов с обучающимися образовательных, 107.75kb.
- Урок обж в 10 классе по теме «Назначение и боевые свойства автомата Калашникова», 49.98kb.
- Структура програми Практична робота: «Робота у середовищі програмування», 56.69kb.
- Устройство автомата ак-74, обращение с ним, уход и сбережение Общие сведения Назначение, 10.05kb.
- 3 Последовательность синтеза автоматов с памятью лгоритм работы автомата с памятью, 144.1kb.
5. На підставі одержаних в результаті синтезу булевих виразів ((*) (**)), будуємо функціональну схему автомата. Для цього рівняння ((*) (**)) представимо у вигляді:

Додатково на функціональній схемі показаний сигнал
 , встановлюючий автомат в початковий стан (в даному випадку 00)
, встановлюючий автомат в початковий стан (в даному випадку 00) 
19. Методи усунення гонок в автоматах
Усунути гонки можна апаратними засобами, або використовуючи спеціальні методи кодування .
Одним із способів ліквідації гонок полягає в тестування вхідних сигналів автомата імпульсами певної тривалості, передбачається що окрім вхідних каналів Х1, …,Хе автомата застосовується ще канал С від генератора синхросигналів по якому поступає сигнал С=1 у момент переходу імпульсу і С=0 при його відсутностіУ звязк уз чим вхідний сигнал на переході (am; as) буде не функція Zf , а функція CZf. Тоді Якщо тривалість імпульсу tc менша найкоротшого шляху переходу тактового сигналу зворотного зв’язку по комбінаційній схемі то до номеру переходу в проміжний стан ak сигналу C =0, а отже функція CZf також дор. 0. недоліком методу є складність встановлення імпульсу оскільки вона залежить від багатьох чинників що не піддаються строгому обліку.
Іншим способом ліквідації гонок є використання подвійної пам’яті в цьому випадку кожен елемент пам’яті дублюється причому перезапис з 1-го елемента в 2-й відбувається в момент часу tc=0.
Для усунення гонок використовують кодування. При сусідньому кодування будь які 2-а стани зв’язані дугою на графі автомата кодуються наборами що відмінні станам лише одного елемента пам’яті.
20. Принцип мікропрограмного управління.
ЕОМ переробляє інформацію, виконуючи над нею якісь операції. Для виконання операцій над інформацією використовуються операційні пристрої – процесори, канали вводу-вывода, пристрої управління зовнішніми пристроями і так далі Функцією операційного пристрою є виконання заданої множини операцій F={f1...,fG} над вхідними словами D={d1...,dH} з метою обчислення слів R={r1...,rQ}, які представляють результати операцій R=fg(D), де g=1,2...,G.
Функціональна і структурна організація операційних пристроїв базується на принципі мікропрограмного управління, який полягає в наступному:
1. Будь-яка операція fg(g=1...,G), реалізовувана пристроєм, розглядається як складна дія, яка розділяється на послідовність елементарних дій над словами інформації. Ці елементарні дії називаються мікроопераціями.
2. Для управління порядком проходження мікрооперацій використовуються логічні умови, які залежно від значень слів, які перетворюються мікроопераціями, приймають значення "брехня" або "істина" (1 або 0).
3. Процес виконання операцій в пристрої описується у формі алгоритму, який представляється в термінах мікрооперацій і логічних умов і називається мікропрограмою. Мікропрограма визначає порядок перевірки значень логічних умов і проходження мікрооперацій, необхідний для отримання необхідних результатів.
4. Мікропрограма використовується в якості форма представлення функції пристрою, на основі якої визначається структура і порядок функціонування пристрою в часі.
Тобто з принципу мікропрограмного управління виходить, що структура і порядок функціонування операційні пристроїв зумовлюється алгоритмом виконання операції F={f1...,fG}.
До елементарних дій над словами інформації мікроопераціям відносяться: передача інформації з одного регістра в іншій, узяття зворотної коди, зрушення і так далі
22. Аналіз та синтез автоматів
Проблема синтезу полягає в пошуку та побудові автомата, виходячи з умов, які накладаються до реалізованого ним оператора або до множини, яка ним представляється. Тут мови.
Крім того, вважається, що шуканий автомат належить до заздалегідь окресленого класу автоматів, які дозволяють конструктивний опис. Формальна мова, засобами якої здійснюється цей опис (мова виконавця), також вважається заданою. Коли мова йде про скінченні автомати, зазвичай, опис автомата полягає в представленні системи його команд шляхом графічного або табличного задання функцій Φ, Ψ (матриць перехідних та вихідних імовірностей, якщо автомат імовірнісний). Побудований в результаті абстрактного синтезу автомат може бути використаний надалі як вихідний матеріал на етапі структурного синтезу автомата.
В межах загальної проблеми абстрактного синтеза виникають окремі проблеми:
Існування. Чи існує оператор, який задовольняє умові, заданій формулою U, та такою, що реалізується в автоматі даного типу?
Одиничність. Чи одиничний такий оператор?
Конструкція. Для якого-небудь оператора, який задовольняє умові U, побудувати автомат, який його реалізує та вказати відповідне налаштування: початковий стан, завершальні стани, а в випадку імовірнісного автомата - дозволений рівень надійності.
Мінімізація. Побудований автомат M привести за допомогою еквівалентних перетворень до еквівалентного автомата, який задовольняє деяким критеріям оптимальності. Наприклад, в випадку скінченних автоматів - мінімізація кількості станів шляхом склеювання нерозрізнених та видалення недосяжних станів.
Вирішення цих проблем реалізується в формі алгоритмів, які за заданою формулою U надають відповіді на запитання 1-2 та здійснюють необхідні конструкції та перетворення для проблем 3-4. Відповідна теорія істотно залежить від мов, які застосовуються замовником. В якості мови виконавця зазвичай розглядаються різні класи автоматних діаграм. При обранні мови замовника природньо слід керуватись наступними двома (антагоністичними) вимогами: виразність мови, тобто зручність (для замовника) викладення в ньому умов, яким повинна задовольняти поведінка автомата, простота алгоритмів, які вирішують проблему синтеза в цілому та окремі її завдання (аналогія в програмуванні - виразність вхідної мови та простота транслятора). Ця ситуація докладно вивчена в застосуванні до скінченних автоматів. З точки зору простоти алгоритмів кращими є алгебраїчні мови (див. Регулярні події та вирази). Більш виразними є мови, які базовані на застосуванні фрагментів логіки предикатів (див. Логічна мова для задання автоматів), але й алгоритми синтезу для них стають більш громіздкими.
Проблема аналізу є оберненою до проблеми синтезу: за завданим автоматом потрібно описати його поведінку засобами мови замовника. В певному сенсі аналіз та синтез можна розглядати як переклади з однієї мови на іншу, при цьому переклад, який відповідає аналізові, переважно легший. Розроблено багато алгоритмів синтезу та аналізу, головним чином для скінченних детермінованих автоматів. В якості складової частини алгоритма синтезу детермінованого автомату в нього зазвичай входить побудова недетермінованого автомата з наступним його перетворенням в еквівалентний йому детермінований автомат. Розробка алгоритмів абстрактного синтезу з застосуванням логічних мов виявилась пов'язаною з деякими алгоритмічними проблемами математичної логіки та сприяла їх вирішенню.
23 Мікропрограмні автомати х примусовою та власною адресацією
Мікропрограмні автомати, часто мають більш потужний засіб керування послідовністю виконання: кожна команда автомата має бітове поле, яке включає номер наступного по порядку виконання команди і, таким чином, одночасно є і функціональної командою, і командою безумовного переходу . Методи реалізації умовних переходів в пристроях такого типу відрізняються великою різноманітністю.
Така структура команди полегшує розміщення програми в пам'яті (логічно послідовні команди можуть бути розміщені в будь-яких вільних ділянках), але призводить до значного збільшення довжини команди - і тому застосовується лише в пристроях з дуже невеликою довжиною адреси команди, тобто з маленькою програмної пам'яттю . Мікропрограмні автомати зазвичай компенсують це обмеження складною структурою кожної окремої команди - довжина таких команд досягає декількох сотень бітів і, насправді, вони містять по окремій команді для кожної з функціональних підсистем автомата. Проста ПЛМ не може зберігати попередній стан і здатна тільки перетворювати поточні стану своїх входів до стану своїх виходів. Замкнув деякі з виходів ПЛМ на деякі з її входів через просте запам'ятовуючий пристрій (регістр) ми отримуємо більш складний пристрій, що володіє пам'яттю. Прості мікропрограмні автомати реалізуються на основі ПЛМ і декількох регістрів. Більш складні автомати містять багато регістрів та спеціалізовані функціональні пристрої, такі, як лічильники і суматори.
25. Арифметичні та логічні операції над числами у двійковій системі числення
| X | Y | X+Y |
| 1 | 1 | 0(1) |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| X | Y | X*Y |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| X | Y | X-Y |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1(1) |
| 0 | 0 | 0 |
| | | |
Двійковий полусумматор - пристрій, що виконує арифметичні дії за правилами, які вказані в табл.1. ai bi – розряди операндів А і В відповідно. ci - розряд суми. Пі - перенос із даного розряду в сусідній вищий.
Таблиця 1
| ai | bi | ci | Пі |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Двійковий суматор – прилад що виконує арифметичну дію по правилам вказаним в таблиці 2
Таблиця 2
| ai | bi | Пі – 1 | ci | Пі |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Подвійний «полувычитатель» Z1+1 – позика в старшому розряді
| ai | bi | ci | Z1+1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | -1 |
Подвійний «вычитатель»
| ai | bi | zi |  |  |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | -1 |
| 0 | 0 | -1 | 1 | -1 |
| 0 | 1 | -1 | 0 | 0 |
| 1 | 0 | -1 | 0 | -1 |
| 1 | 1 | -1 | 1 | -1 |
26. Арифметичні операції в десятковій системі
Арифметичних операцій в ЕОМ: прямій, зворотний, додатковий код;
Прямий код
Прямий код — спосіб представлення двійкових чисел з фіксованою комою в комп'ютерній арифметиці. Головним чином використовується для запису позитивних чисел.
При записі числа в прямому коді старший розряд є знаковим розрядом. Якщо його значення рівне 0 — те число позитивне, якщо 1 — те негативне. У решті розрядів (які називаються цифровими розрядами) записується двійкове представлення модуля числа.
Функція кодування двійкових чисел (зокрема цілих чисел і змішаних дробів) в прямому коді має вигляд:

де n — номер знакового розряду. Зокрема, при кодуванні правильних двійкових дробів (тобто чисел _ 1 < A < 1), n = 0 і функція кодування приймає вигляд:
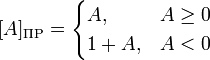
Величина числа A в прямому коді визначається по наступній формулі:

де:
asign — значення знакового розряду;
число A має до розрядів справу ось коми (дробова частина) і n розрядів зліва (ціла частина), тут враховуються тільки цифрові розряди.
Як видно з останньої формули, знаковий розряд в прямому коді не має розрядної ваги. При виконанні арифметичних операцій це приводить до необхідності окремої обробки знакового розряду в прямому коді.
Зворотний код
Зворотний код — метод обчислювальної математики, що дозволяє відняти один число з другого, використовуючи тільки операцію складання над натуральними числами. Раніше метод використовувався в механічних калькуляторах (арифмометрах). В даний час використовується в основному в сучасних комп'ютерах.
Зворотний n-разрядный двійковий код позитивного цілого числа складається з однорозрядної коди знаку (двійкової цифри 0), за яким слідує n _ 1-розрядне двійкове представлення модуля числа (зворотний код позитивного числа співпадає з прямим кодом).
Приклад. Двійкове представлення числа 5 є 101. Зворотний 10-розрядний двійковий код числа +5 є 0000000101.
Зворотний n-разрядный двійковий код негативного цілого числа складається з однорозрядної коди знаку (двійкової цифри 1), за яким слідує n _ 1-розрядне двійкове число, яке інвертоване n _ 1-розрядне представлення модуля числа.
Приклад. Двійкове представлення числа 5 є 101, його 9-розрядне двійкове уявлення — 000000101. Зворотний 10-розрядний двійковий код числа _5 є 1111111010.
Є двох зворотних код числа 0: «позитивний нуль» 0000000000 і «негативний нуль» 1111111111 (приведені 10-розрядних зворотних код).
n-разрядный зворотний код дозволяє представить числа ось _ 2n _ 1 + 1 до + 2n _ 1 _ 1.
Додатковий код
Додатковий код (англ. two’s complement, іноді twos-complement) — найбільш поширений спосіб представлення негативних цілих чисел в комп'ютерах. Он дозволяє замінити операцію віднімання на операцію складання і зробити операції складання і віднімання однаковими для знакових і беззнакових чисел, чим спрощує архітектуру ЕОМ. Додатковий код негативного числа можна отримати інвертуванням модуля двійкового числа (перше доповнення) і збільшенням до інверсії одиниці (друге доповнення). Або відніманням числа з нуля.
Додатковий код (доповнення до 2) двійкового числа виходить додаванням 1 до молодшого значущого розряду його доповнення до 1. [1]
Доповнення до 2 двійкового числа визначається як величина отримана відніманням числа з найбільшого ступеня два (з 2N для N-битного доповнення до 2).[2]
П
 редставление числа в дополнительном коде
редставление числа в дополнительном кодеПри записі числа в додатковому коді старший розряд є знаковим. Якщо його значення рівне 0, то в решті розрядів записано позитивне двійкове число, співпадаюче з прямим кодом. Якщо ж знаковий розряд рівний 1, то в решті розрядів записано негативне двійкове число, перетворене в додатковий код. Для набуття значення, яке протилежне по знаку, всі розряди, включаючи знаковий, інвертуються, а потім до результат додається одиниця.
Двійкове 8-ми розрядне число із знаком в додатковому коді може представляти будь-яке ціле в діапазоні від Г128 до +127. Якщо старший розряд рівний нулю, то найбільше ціле число, яке може бути записане в тих, що залишилися 7 розрядах рівно 27 Г 1, що рівне 127.
П

ри застосуванні той же ідеї до звичної 10-ричной системи числення вийде (наприклад, для гіпотетичного процесора що використовує 10-ричную систему числення):
Перетворення додаткової коди
Перетворення числа з прямої коди в додатковий здійснюється по наступному алгоритму.
- Якщо число, записане в прямому коді, позитивно, то до нього дописується старший (знаковий) розряд, рівний 0, і на цьому перетворення закінчується;
Якщо число, записане в прямому коді, негативно, то всі розряди числа інвертуються, а до результату додається 1. До числа, яке вийшло, дописується старший (знаковий) розряд, рівний 1.
27.Поняття двійково-кодованих ситем (Д-коди)

28. Контроль роботи цифрових автоматів
Система контролю — сукупність методів і засобів, що забезпечують визначення правильності роботи автомата в цілому або його окремих вузлів, а також автоматичне виправлення помилки. Помилки в роботі цифрового автомата можуть бути викликані або виходом з буд якої-небудь деталі, або відхиленням від норми параметрів, наприклад зміна напруги живлення або дією зовнішніх перешкод. Викликані цими порушеннями помилки можуть прийняти постійний або випадковий характер. Постійні помилки легко виявити і виявити. Випадкові помилки, обумовлені короткочасними змінами параметрів, найбільш небезпечні і їх важче виявити. Тому система контролю повинна будуватися з таким розрахунком, щоб вона дозволяла виявити і по можливості виправити будь-які порушення.
При цьому треба розрізняти наступні види помилок результату:
1) що виникають із-за погрішностей у вихідних даних;
2) обумовлені методичними погрішностями;
3) що з'являються із-за возникнованія несправностей в роботі машини.
Перевірка правильності функціонування окремих пристроїв машини і виявлення несправностей може здійснюватися по двох напрямах:
профілактичний контроль, завдання якого — запобігання появі можливих помилок в роботі;
оперативний контроль, завдання якого — перевірка правильності виконання машиною всіх операцій.
