1. Структура цом, представлення цом як конечного автомата

Вид материала

Документы

Содержание 10.Мінімізація функцій алгебри логіки. Методи мінімізації 11 Мінімізація систем функцій алгебри логіки Призначення аналізу і синтезу комбінаційних схем. Або, або-не 13. які критерії якості комбінаційних схем. Або, або-не 14. Кінцеві автомати. Автомати і регулярні мови 15. Автомати Мілі і Мура 17 елементарні автомати 18. Канонічні методи синтезу автоматів. Zi можна поставити у відповідність будь-яку двохрозрядну комбінацію х1

Подобный материал:

• Вторая, 374.07kb.
• «Автоматы: модель конечного автомата, распознаватели и преобразователи. Анализаторы, 150.22kb.
• Гражданское право (часть II) в вопросах и ответах батычко Вик. Т., 2008, 1556.04kb.
• Ко­ма­ро­ва Т. С, 299.71kb.
• Алконос) в русских средневе­ковых легендах райская птица с человеческим ли­цом (часто, 251.62kb.
• Учебно-тематический план проведения пятидневных учебных сборов с обучающимися образовательных, 107.75kb.
• Урок обж в 10 классе по теме «Назначение и боевые свойства автомата Калашникова», 49.98kb.
• Структура програми Практична робота: «Робота у середовищі програмування», 56.69kb.
• Устройство автомата ак-74, обращение с ним, уход и сбережение Общие сведения Назначение, 10.05kb.
• 3 Последовательность синтеза автоматов с памятью лгоритм работы автомата с памятью, 144.1kb.

10.Мінімізація функцій алгебри логіки. Методи мінімізації

Метод Куайна — Мак-Класкі (метод простих імлікант) - табличний метод мінімізації булевих функцій розроблений Уілардом Куайном і Едвардом Мак-Класкі. Функціонально ідентичний карті Карно, але таблична форма робить його більш ефективним для використання в комп'ютерних алгоритмах.

Карта Карно (K-карта скорчено), поліпшення зроблене Морісом Карно в 1953 Діаграм Вейча винайдених Едвардом Вейчем в 1952 , це метод спрощення виразів булевої алгебри. Карта Карно зменшує потребу в обширних обчисленнях, використовуючи перевагу людської можливості розпізнання шаблонів, дозволяє швидке розпізнавання і виключення потенційних станів гонитви.

В карті Карно булеві змінні переносяться (зазвичай з таблиці істинності) і впорядковуються згідно з принципами кода Грея, в якому тільки одна змінна змінюється при переході між сусідніми квадратами. Коли таблиця згенерована, і у відповідні комірки записані вихідні значення, дані організовуються в найбільші можливі групи, що містять 2n комірок (n=0,1,2,3...)[1]. Далі, працюючи з цими групами, отримують мінімізовану ДНФ.

11 Мінімізація систем функцій алгебри логіки

Перетворення логічних функцій з метою спрощення їх аналітичного подання називаються мінімізацією.

Існують два напрямки мінімізації:

1. Найкоротша форма запису (мета - мінімізувати ранг кожного терма). При цьому виходять найкоротші форми КДНФ, ККНФ, КПНФ.

2. Отримання мінімальної форми запису (мета - отримання мінімального числа символів для запису всієї функції відразу).

Існують різні методи мінімізації:

1. Метод безпосередніх перетворень логічних функцій. (1.1)

При застосуванні даного методу:

а) Записуються ДСНФ логічних функцій

б) Форма перетворюється і спрощується з використанням аксіом алгебри логіки. При цьому, зокрема, виявляються у вихідному ДСНФ так звані сусідні min-терми, в яких є по одній не збігається змінної.

Метод невизначених коефіцієнтів. (1.2)

Суть методу полягає в перетворенні ДСНФ в МДНФ.

На підставі теореми Жігалкіна будь-яку ФАЛ можна представити у вигляді трьох змінних змінних

Суть методу зводиться до того, щоб перетворити ДСНФ в МДНФ.

Завдання мінімізації за методом Квайна полягає в попарному порівнянні імплікант, що входять до ДСНФ з метою виявлення можливості склеювання з якоїсь пременной так:

Таким чином, можна знизити ранг термів. Процедура проводиться до тих пір, поки не залишається жодного терма, що допускає склеювання з іншим. Причому склеюючі терми позначаються *.

Для цього:

1. Складаються таблиці, в рядках яких пишуться знайдені первинні імпліканти, а в стовпцях вказуються терми первинної ФАЛ.

2. Клітини цієї таблиці зазначаються в тому випадку, якщо первинна імпліканта входить до складу якого-небудь первинного терма.

3. Завдання спрощення зводиться до знаходження такого мінімальної кількості імплікант, які покривають всі стовпці.

Метод мінімізують карт (для ДСНФ і КСНФ). (1.5)

Одним із способів графічного представлення бульових функцій від невеликого числа змінних є карти Карно. Їхній різновид - карти Вейча, які будуються як розгортки кубів на площині, при цьому вершини куба представляються клітинами карти, координати яких співпадають з координатами відповідних вершин куба.

Для ДСНФ одиниці ставляться в клітці, відповідної номеру набору, на якому значення функції дорівнює одиниці, а нуль не ставиться, а для КСНФ - навпаки.

Карти Карно використовуються для ручної мінімізації функцій алгебри логіки при невеликій кількості змінних. Правило мінімізації: склеювання піддаються 2,4,8,16, клітин і клітини, що лежать на кордоні карти.

При кількості змінних 5 і більше відобразити графічно функцію у вигляді єдиної плоскої карти неможливо. Тоді будують комбіновані карти, що складаються з сукупності більш простих карт. Процедура мінімізації тоді полягає в тому, що спочатку знаходиться мінімальна форма 4-х мірних кубів (карт), а потім, розширюючи поняття сусідніх клітин, відшукують min-терми для сукупності карт. Причому сусідніми клітинами є клітини, що збігаються при поєднанні карт поворотом навколо спільного ребра.

12. в чому полягає аналіз та синтез КС?

Призначення аналізу і синтезу комбінаційних схем.


Технічним аналогом булевої функції в обчислювальній техніці є, так звана, комбінаційна схема, на вхід якої поступають і з виходу знімаються електричні сигнали у вигляді одного з рівнів напруги, що відповідають значенням логічного 0 і логічної 1.

Для з'ясування, що ж таке комбінаційна схема, розглянемо схему S, що має m входів і n виходів (мал. 1). На її входи можуть бути подані набори значень вхідних змінних Xi {0,1} 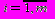, а на виходах формуються вихідні змінні Yj{0,1} .




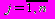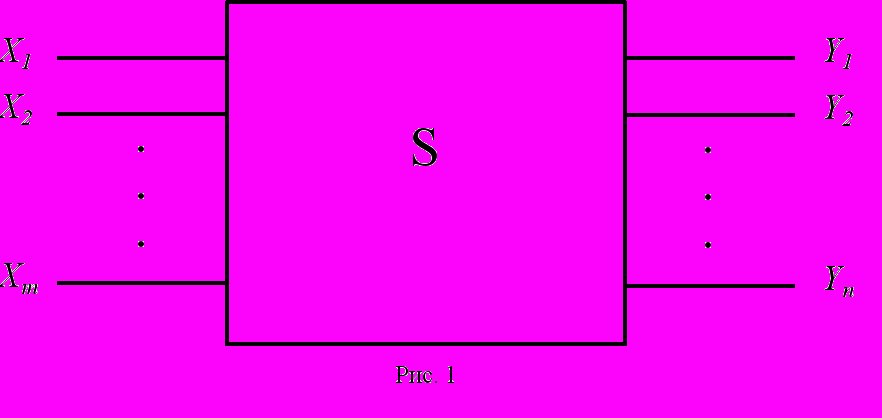
Схема S називається комбінаційною, якщо кожну з n функцій її виходів Y1,Y2 ..., Yn можна представити як булеву функцію вхідних змінних X1, X2 ..., Xm.

Комбінаційна схема описується за допомогою системи рівнянь (1), де Fi – булева функція.


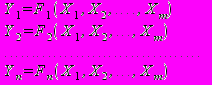
(1)


Як випливає з визначення комбінаційної схеми, значення вихідних змінних Yj в довільний момент часу однозначно визначаються значеннями вхідних змінних Xi.

Структурно комбінаційна схема може бути представлена як сукупність елементарних логічних схем – логічних елементів (ЛЕ). ЛЕ виконують над вхідними змінними елементарні логічні операції типу І-НЕ, І, АБО, АБО-НЕ і т.д. Число входів логічного елемента відповідає числу аргументів відтворюваної ним булевої функції. Графічне зображення комбінаційної схеми, при якому показані зв'язки між різними елементами, а самі елементи представлені умовними позначеннями, називається функціональною схемою.

В ході розробки комбінаційних схем доводиться вирішувати задачі аналізу і синтезу.

Задача аналізу полягає у визначенні статичних і динамічних властивостей комбінаційної схеми. В статиці визначаються булеві функції, реалізовувані комбінаційною схемою по відомій їй структурі. В динаміці розглядається здатність надійного функціонування схеми в перехідних процесах при зміні значень змінних на входах схеми, тобто визначається наявність на виходах схеми можливих небажаних імпульсних сигналів, які не виходять безпосередньо з виразів для булевих функцій, реалізовуваних схемою.

Задача синтезу полягає в побудові із заданого набору логічних елементів комбінаційної схеми, що реалізовує задану систему булевих функцій.

Вирішення задачі синтезу не є однозначним, можна запропонувати різні варіанти комбінаційних схем, що реалізовують одну і ту ж систему булевих функцій, але відрізняються по тих або інших параметрах. Розробник комбінаційних схем з цієї множинаі варіантів вибирає один, виходячи з додаткових критеріїв: мінімальної кількості логічних елементів, необхідних для реалізації схеми, максимальної швидкодії і т.д. Існують різні методи синтезу комбінаційних схем, серед яких найбільш розроблений канонічний метод.


13. які критерії якості комбінаційних схем.

Технічним аналогом булевої функції в обчислювальній техніці є, так звана, комбінаційна схема, на вхід якої поступають і з виходу знімаються електричні сигнали у вигляді одного з рівнів напруги, що відповідають значенням логічного 0 і логічної 1.

Структурно комбінаційна схема може бути представлена як сукупність елементарних логічних схем – логічних елементів (ЛЕ). ЛЕ виконують над вхідними змінними елементарні логічні операції типу І-НЕ, І, АБО, АБО-НЕ і т.д. Число входів логічного елемента відповідає числу аргументів відтворюваної ним булевої функції. Графічне зображення комбінаційної схеми, при якому показані зв'язки між різними елементами, а самі елементи представлені умовними позначеннями, називається функціональною схемою.

Складність схеми оцінюється кількістю устаткування, що складає схему. При розробці схем на основі конкретної елементної бази кількість устаткування звичайно вимірюється числом корпусів (модулів) інтегральних мікросхем, що використовуються в схемі. В теоретичних розробках орієнтуються на довільну елементну базу і тому для оцінки витрат устаткування використовується оцінка складності схем по Квайну.

Складність (ціна) по Квайну визначається сумарним числом входів логічних елементів у складі схеми.

При такій оцінці одиниця складності – один вхід логічного елемента. Ціна інверсного входу звичайно приймається рівною двом. Такий підхід до оцінки складності виправданий з наступних причин:

• складність схеми легко обчислюється по булевих функціях, на основі яких будується схема: для ДНФ складність схеми рівна сумі кількості букв,(букві із знаком заперечення відповідає ціна 2), і кількості знаків диз'юнкції, збільшеної на 1 для кожного диз'юнктивного виразу.
  
• всі класичні методи мінімізації булевих функцій забезпечують мінімальність схеми саме в значенні ціни по Квайну.
  

Практика показує, що схема з мінімальною ціною по Квайну звичайно реалізується якнайменшим числом конструктивних елементів – корпусів інтегральних мікросхем.

Швидкодія комбінаційної схеми оцінюється максимальною затримкою сигналу при проходженні його від входу схеми до виходу, тобто визначається проміжком часу від моменту надходження вхідних сигналів до моменту встановлення відповідних значень вихідних. Затримка сигналу кратна числу елементів, через які проходить сигнал від входу до виходу схеми. Тому швидкодія схеми характеризується значенням r, де  - затримка сигналу на одному елементі. Значення r визначається кількістю рівнів комбінаційної схеми, яка розраховується таким чином. Входам КС приписується рівень нульової. Логічні елементи, пов'язані тільки з входами схеми відносяться до першого рівня . Елемент відноситься до рівня k, якщо він зв'язаний по входах з елементами рівнів k-1, k-2, і т.д. Максимальний рівень елементів r визначає кількість рівнів КС, і називається рангом схеми. Приклад визначення рангу r схеми приведений на рисунку 6.

14. Кінцеві автомати.

Кінцевий автомат — в теорії алгоритмів математична абстракція, що дозволяє описувати шляхи зміни стану об'єкту в залежності ось його поточного стану і вхідних даних, за умови, що загальна можлива кількість станів кінцева. Кінцевий автомат є окремим випадком абстрактного автомата.

Існують різні варіанти завдання кінцевого автомата. Наприклад, кінцевий автомат може бути заданий за допомогою п'яти параметрів: M=(Q,_},q0,F), ду:

Q — кінцева безліч станів автомата;

q0 — початковий стан автомата (q0 є Q);

F — безліч завершуючих (або що допускають) станів, таких що F_Q;

_ — допустимий вхідний алфавіт (кінцева безліч допустимих вхідних символів), з якого формуються терміни, які прочитуються автоматом;

} — задано відображення безлічі Qx_ в безліч P(Q) підмножин Q: _

}:Qx_>P(Q)_

(іноді } називають функцією переходів автомата)._

Автомат починає роботу в змозі q0, прочитуючи по одному символу вхідної терміни. Лічений символ переводить автомат в те, що нове складається з Q відповідно до функції переходів. Якщо після закінчення прочитання вхідного слова (ланцюжки символів) автомат опиняється в одному з допускаючих станів, то слово «приймається» автоматом. В цьому випадку говорять, що оний належить мові даного автомата. Інакше слово «відкидається».

Кінцеві автомати широко використовуються на практиці, наприклад в синтаксичних, лексичних аналізаторах, і тестуванні програмного забезпечення на основі моделей.

Інші способи опису

• Діаграма станів (або іноді граф переходів) — графічне представлення безлічі станів і функції переходів. Навантажений однонаправлений граф, вершини якого — стани АЛЕ, дуги — переходи з одного стану в інше, а навантаження — символи, при яких здійснюється даний перехід. Якщо перехід з полягає q1 в q2 може бути здійснений при появі одного з декількох символів, то над дугою повинні бути надписані всі вони.
  
• Таблиця переходів — табличне представлення функції }. Зазвичай в такій таблиці кожному рядку відповідає один стан, а стовпцю — один допустимий вхідний символ. У осередку на перетині терміни і стовпця записується дія, яку повинен виконати автомат, якщо за ситуації, коли он знаходився в даному перебуванні на вході он отримав даний символ._
  

Детермінована

Кінцеві автомати підрозділяються на детермінованих і недетермінованих.

• Детермінованим кінцевим автоматом (ДКА) називається такий автомат, в якому для кожної послідовності вхідних символів існує лише один стан, в який автомат може перейти з поточного.
  

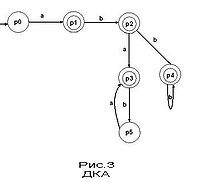
• Недетермінований кінцевий автомат (НКА) є узагальненням детермінованого. Недетермінованість автоматів досягається двома способами:
  

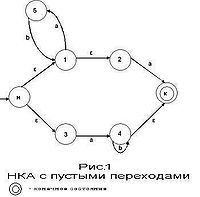
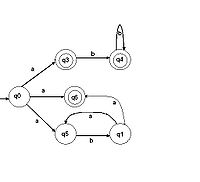
Існує теорема, яка свідчить, що «Будь-який недетермінований кінцевий автомат може бути перетворений в детермінований так, щоб їх мови співпадали» (такі автомати називаються еквівалентними). Проте, оскільки кількість полягають в еквівалентному ДКА у гіршому разі росте експоненціально із зростанням кількості станів початкового НКА, на практиці подібна детерминизация не завжди можлива. Крім того, кінцеві автомати з виходом в загальному випадку не піддаються детерминизации.

Через останні два зауваження, не дивлячись на велику складність недетермінованих кінцевих автоматів, для завдань, пов'язаних з обробкою тексту, переважно застосовуються саме НКА.

Автомати і регулярні мови

Для автомата можна визначити мову (безліч слів) в алфавіті _, який он представляє — так називається безліч слів, при введенні яких автомат переходить з початкового стану в один із станів безлічі F.

Теорема Клини свідчить, що клас мов, уявних кінцевими автоматами, співпадає з класом регулярних мов. Крім того цей клас співпадає з класом мов, які задаються регулярними граматиками.

Спеціалізовані мови програмування

Мова послідовних функціональних схем SFC (Sequential Function Chart) - графічна мова програмування широко використовується для програмування промислових логічних контроллерів (ПЛК).

У SFC програма описується у вигляді схематичної послідовності кроків, об'єднаних переходами.

15. Автомати Мілі і Мура

Основні положення теорії цифрових автоматів Згідно теорії автоматів цифровим автоматом називається последовательностная схема, яка має набір станів, що позначаються зазвичай A 1, A 2 :, A N . У моменти приходу тактових імпульсів автомат переходить з одного стану в інше, визначуване як поточним станом, так і набором вхідних (осведомітельних) сигналів X 1, X 2 :, X N, при цьому формується послідовність наборів вихідних (керівників) сигналів Y 1, Y 2 :, Y N .

Для кожного автомата задається закон функціонування або алгоритм переходів з одного стану в інше під дією різних комбінацій вхідних сигналів з описом комбінацій формованих при цьому вихідних сигналів. Такий алгоритм може бути заданий або у вигляді графа, або у вигляді таблиці переходів. Коли автомат не працює, він знаходиться в початковому стані A 1 . При запуску автомат зберігає стан A 1 протягом одного такту, за час якого формуються відповідні значення вхідних сигналів Х 1 . Після закінчення першого такту автомат перемикається в черговий стан A 2 наказане законом функціонування, і в ОА починає виконуватися наступний набір мікрооперацій. Момент закінчення мікропрограми наголошується поверненням автомата в початковий стан а 1 Прикладом цифрового автомата служить лічильник - автомат, в якого немає взагалі вхідних інформаційних сигналів, а є лише тактовий, на нього подаються рахункові імпульси. Число його станів дорівнює коефіцієнту перерахунку граф цього автомата є кільцем з послідовним переходом від одного стану до наступного. Складніші цифрові автомати можуть мати по декілька можливих переходів з кожного стану під дією різних наборів вхідних сигналів.

Автомат Милі і автомат Мура За способом формування вихідних сигналів автомати підрозділяють на автомати Милі і автомати Мура. Для автомата Милі визначається наступний закон функціонування

A(t + 1) = [A(t), X(t)];

Y(t) = [А (t), Х (t)],

Для автомата Милі, як видно з виразів, вихідні сигнали Y(t) залежать як від стану автомата A(t) у нинішній момент часу t, так і від вхідних сигналів X(t). Аналогічно для автомата Мура

A(t+1) = [А (t), X(t) ];

Y (t) = [А (t)],

Для нього, як видно з виразів, вихідні сигнали Y(t) залежать лише від стану автомата A(t) у нинішній момент часу t. Реалізація автоматів Милі, як правило, простіша, але в них виникають проблеми з синхронністю формування вихідних сигналів.

Алгебра логіки — застосування алгебраїчних методів і символіки для вивчення логічних відношень і розв'язання логічних задач.


17 елементарні автомати

В даний час в обчислювальній техніці, як правило, використовуються елементарні автомати, що мають такі особливості:

1. Елементарні автомати є автоматами Мура з двома внутрішніми станами;

2. Автомат видає два різних вихідних сигналу, що відповідають двом його внутрішнім станам. Надалі стану автомата і його вихідні сигнали будемо позначати однією літерою Q і кодувати цифрами 0 та 1;

3. Елементарні автомати можуть мати в загальному випадку кілька фізичних входів, на кожен з яких можуть подаватися сигнали, закодовані цифрами 0 і 1.

Як елементарних автоматів в обчислювальній техніці використовуються, в основному, тригери різних типів. Розглянемо деякі з них:

Т-тригер D-тригер Rs - тригер Jk тригер (універсальний тригер)

18. Канонічні методи синтезу автоматів.

Приклад канонічного методу структурного синтезу автомата.


Виконаємо структурний синтез часткового автомата А, заданого своїми таблицями переходів і виходів (табл. 23 і 24.).




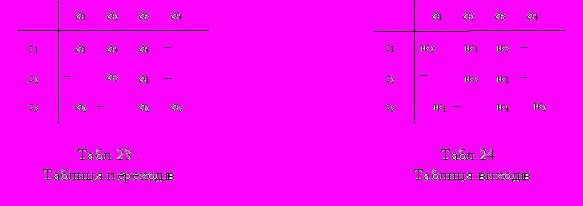
Синтез виконуватимемо в наступному порядку:

1. Виберемо як елементи пам'яті D-трігер, функція входів якого представлена в таблиці стор. 33.

2. Закодуємо вхідні, вихідні сигнали і внутрішні стани автомата. Кількість вхідних абстрактних сигналів F = 3, отже кількість вхідних структурних сигналів L= ]log₂F [ = ]log23[ = 2, тобто х1, х2.

Кількість вихідних абстрактних сигналів G = 4, отже кількість вихідних структурних сигналів N =]log₂G[ = ]log24[ = 2, тобто у1, у2. Кількість внутрішніх станів абстрактного автомата M = 4, отже кількість двійкових елементів пам'яті (трігерів) R = ] log2M [ = ]log24[ = 2.




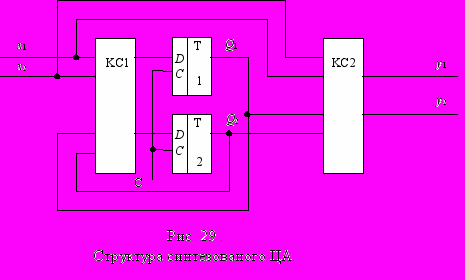
Отже, структура ЦА з урахуванням того, що початковий автомат є автоматом Мілі, як елементи пам'яті використовується D-трігер, може бути представлена у вигляді(мал. 29):

Кодування вхідних, вихідних сигналів і внутрішніх станів представлена в таблицях:

		x1	x2			y1	y2			Q1	Q2
	z1	0	0		w1	0	0		a1	0	0
	z2	0	1		w2	0	1		a2	0	1
	z3	1	1		w3	1	1		a3	1	1
					w4	1	0		a4	1	0

Кодування, в загальному випадку, здійснюється довільно. Тому, наприклад, кожному з сигналів Zi можна поставити у відповідність будь-яку двохрозрядну комбінацію х1, х2. Необхідно тільки, щоб різні вихідні сигнали Zi кодувалися різними комбінаціями х1, х2. Аналогічно для Wi і ai.

3. Одержимо кодовані таблиці переходів і виходів структурного автомата. Для цього в таблицях переходів і виходів початкового абстрактного автомата замість Zi, Wi, ai ставимо відповідні коди. Одержимо таблиці:
   

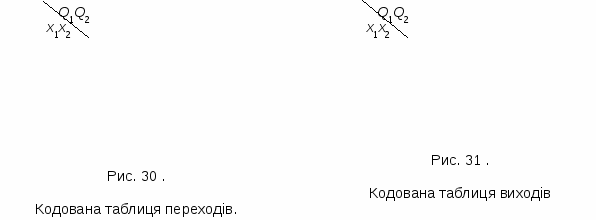			a1	a2	a3	a4				a1	a2	a3	a4
			00	01	11	10				00	01	11	10
	Z1	00	00	10	10	–		Z1	00	01	00	11	–
	Z2	01	–	11	00	–		Z2	01	–	11	00	–
	Z3	11	01	–	01	Q1Q2		Z3	11	00	–	10	y1y2

В кодованій таблиці переходів задані функції



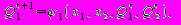
В кодованій таблиці виходів заданні функції:



4. При канонічному методі синтез зводиться до отримання функцій:



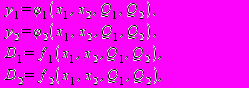
і подальшій побудові комбінаційних схем, що реалізовують дану систему булевих функцій.

Функції у1 і у2 можуть бути безпосередньо одержані з таблиці виходів, наприклад, у вигляді :




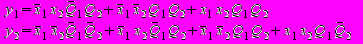
Проте вирази для у1 і у2 можна істотно спростити в результаті мінімізації, наприклад, за допомогою карт Карно:

		00	01	11	10			00	01	11	1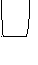0
	00	0	0	1	–		00	1	0	1	–
	01	–	1	0	–		01	–	1	0	–
	11	0	–	1	0		11	0	–	0	1
	10	–	–	–	–		10	–	–	–	–

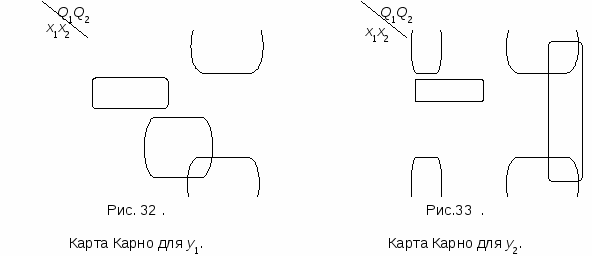
В результаті мінімізації маємо:



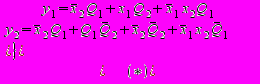
Для отримання виразів для D1 і D2 необхідно одержати таблиці функцій збудження. Для чого в загальному випадку необхідно скористатися таблицею переходів і функціями входів елементів пам'яті. Знаючи код початкового стану автомата і код стану переходу на підставі таблиці входів трігера одержуємо необхідне значення функції збудження, що забезпечує заданий перехід. Проте для D-трігеров, як наголошувалося раніше, таблиця переходів співпадає з таблицею функції збудження. Тоді або безпосередньо з цієї таблиці, або в результаті мінімізації набуваємо необхідні значення Di. Звичайно використовується мінімізація за допомогою карт Карно:

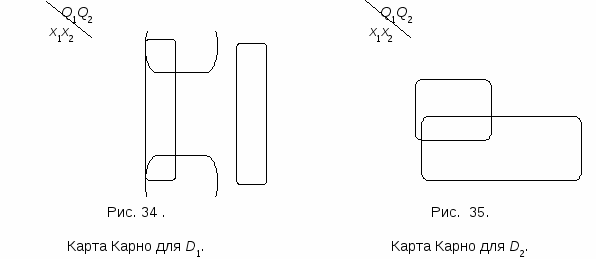		00	01	11	10			00	01	11	10
	00	0	1	1	–		00	0	0	0	–
	01	–	1	0	–		01	–	1	0	–
	11	0	–	0	1		11	1	–	1	1
	10	–	–	–	–		10	–	–	–	–

В результаті мінімізації одержуємо: