Авторефераты по всем темам  >>  Авторефераты по математике

Теория структурных фазовых переходов с несколькими параметрами порядка в кристаллах с октаэдрической анионной подрешёткой

Автореферат докторской диссертации по физико-математическим наукам

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 |

 

Варианты рельефа потенциальной энергии частицы на сечениях по линиям у = 0 и х = 0 дляа такой 1+4-мин. модели будут иметь тот же вид, изображён на рис. 7. В качестве объекта исследования рассматриваем слоистый кристалл с простой тетрагональной решёткойа симметрии D4h, в узлах которого расположены частицы, каждая из которых имеет пять минимумов в плоскостях ортогональных оси 4-го порядка (рис.11). Центральный минимум находится в самом узле, а четыре боковых - немного смещены.

Неравновесный ТП такой пятиминимумной (1+4-мин.) модели в приближении ГБВ имеет вид: 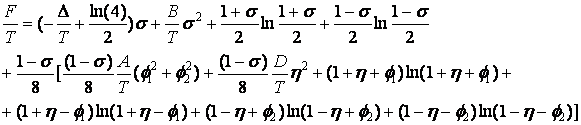(8)

где ?, В - константы, характеризующие те же энергии и взаимодействия, что и в модели 1 + 2-мин. Параметры А и D характеризуют взаимодействие между частицами, находящимися в боковых ямах. D - между подсистемами минимумов, одна из которых состоит из минимумов 1 и 2, а другая - из 3 и 4. Если А < 0, то частицы, стремятся расположиться в боковых ямах одного типа (с одним номером), а если А > 0, то - в разных. Функции ?,?,? выполняют роль параметров порядка (ПП),а ? преобразуется по неприводимому представлению A1g , ? - по В1g, ?1,2 - по E1u. Система уравнений состояния имеет пять типов решений: 1.(?,? =?1= ?2 = 0) - D4h;аа 2. ( ?,?, ?1= ?2 = 0) - D2h;а 3. (?,?, ?1,0) - С2v;а 4.( ?,0, ?,? ) - С2v;аа 5. (?,?, ?1, ?2) - Сs.а

В случае одного и двух ПП особенности термодинамического поведения кристаллов, описываемых моделью 1 + 4-мин. аналогичны особенностям термодинамического поведения кристаллов, описываемых 1 + 2-мин. моделью.

Показано, что в случае трёх ПП в области ? >0, B >0, D >0, A< 0, где k = B/?, s = -A/?, с = - В/D тип упорядочения в пространстве ПП ?,? определяется исключительно соотношением между константами A, D и температурой. Однако появление этих ПП зависит от всех модельных и термодинамических параметров. Необходимым условием возникновения ПП ? является А < 0, но это условие не достаточно, в случае k = 0.4 этот ПП появляется при s ? s* = 7.475. При с = 0.95 решение (?,?,?1,0), возникшее из симметричной фазы, при s* ?а s ? s1(s1 ? 10.5) существует в ограниченном сверху и снизу интервале температур. И сверху, и снизу соседом является та же самая фаза. При s > s0 (s0 = 9.443) в области Т ~ 0, с параметрами ? ~ - 1, ? ~ 1, ?1 ~ 2 появляется вторая ветвь решения (?,?,?1,0)2. В области Т ~ 0 при s ? s1 (s1 = 10.5) термодинамически устойчива фаза (?,0,0,0), а при s > s1 термодинамически устойчивой становится вторая ветвь фазы (?,?,?1,0)2.а

Для решений СУС типа (?,0,?,?) вторая ветвь появляется при s > 8(1+2k). При s > 16 фаза, отвечающая второй ветви решения (?,0,?,?)2, становится термодинамически устойчивой при Т ~ 0.

При понижении температуры реализуются следующие последовательности упорядочений:

дляk = 0.4, s = 8, с = 0.95 - (?,0,0,0) - (?,?,?1,0) - (?,0,0,0);

для k = 0.4, s = 10.4, с = 0.95 -а (?,0,0,0) - (?,?,?1,0)1 - (?,?,?1,0)2 - (?,0,0,0);

для k = 0.4, s = 12, с = 0.95 - (?,0,0,0) - (?,?,?1,0)1;

для k = 0.4, s = 9.6, с = 1.1 -а (?,0,0,0) - (?,0,?,?) - (?,?,?1,?2) - (?,?,?1,0) - (?,?,?1,?2) аЦ (?,0,?,?) - (?,0,0,0).

В первой, второй иа четвёртой последовательностях имеет место возврат в фазу, причём в четвёртой последовательныйа возврат в фазу, при котором фактически возникает целый каскад ФП.

В пятом разделе исследуются ротационные фазовые переходы, один из типов структурных превращений в кристаллах с октаэдрической анионной подрешёткой, в частности в кристаллах семейства перовскита, упорядоченных перовскитах (включая эльпасолиты иа криолиты), слоистых перовскитах и в некоторых других соединениях [A5, A10]. Отмечено, что при таких переходах меняются координация ионов, межионные расстояния и т.п. Эти изменения определяются характером ротационного упорядочения и могут существенно повлиять на физические характеристики соединения.

В подразделе 5.1 исследуются ротационные фазовые переходы в кубических перовскитах и родственных им кристаллах. Вся совокупность ротационных искажений в перовскитах описывается двумя трехкомпонентными параметрами порядка, один из которых - ? относится к трёхлучевой звезде вектора k = (1/2)(b1 + b2), другой - ? принадлежит однолучевой звезде вектора k = (1/2)(b1 + b2 + b3), где bi - базисные векторы обратной решетки. Параметры ? и ? преобразуются соответственно по неприводимым представлениям М3 и R9.

Одна из основных целей этого подраздела выяснение на основе феноменологической теории условий, при которых могли бы быть реализованы указанные ниже наиболее распространённые последовательности ротационных упорядочений [9], а также исследование факторов, влияющих на формирование ФС.

1. 00000?0???1?2? ;а 1a. 00000?0?????;

2. 00000????;аа а 3. 00000?0??а?1,?2,?3 + ?3;а

4. 0000?????;аа а 5. 00000?0?????;

6. 000??????;аа а 7. 000???.аа аа (9)

Модельный термодинамический потенциал для описания всех возможных ротационных ФП, обусловленных конденсацией ПП ? и?,имеет вид:

?(?,?) = ?М +а ?R + ?MR;(10)

?М = ?1MG1M + ?2MG21M +а ?1MG2M + ?MG1MG2M +а ?MG3M + ?2MG22M + ?MG4M Е

?Rа= ?1RG1R + ?2RG21R +а ?1RG2R + ?RG1RG2R +а ?RG3R + ?2RG22R Е;

?MR= ?1G1MG1R + (?2 - ?1)??а+ ?1???а+ ?2G1MG2R +

+ ?3???а+ ?4G1RG2M + Е;

G1M = ?, G2M= ??, G3M = ???,аа

G4M =а ?1?2?3[?14 (?22 - ?32) + ?24 (?32 - ?12) + ?34 (?12 - ?22)],?M3,

G1R= ?, G2R= ??, G3R = ???,?R25

везде берется либо i<j, i =1,2, j=2,3, либо i ? j, i ? k, j<k, i=1, 2, 3 j=1,2, k=2, 3.

Он содержит члены, характеризующие вклад каждого ПП - ?М (?), ?R(?), а также смешанные инварианты, описывающие взаимодействие между этими параметрами порядка - ?МR(?,?). Диаграммы ФС при различных соотношениях между коэффициентами ТП (10) приведены на рис. 11,12. Диаграммы ФС получены при условии: ?1M >> 0, ?1<0, ?2>0, ?2R > 0, ?2M > 0, ?R< 0, ? = ?1 + ?2 < 0, ?R < 0, ?M < 0. На них показаны термодинамические пути, на которых реализуются последовательности фаз из набора (9) под тем же номером. На пути 1 реализуется последовательность фаз, наблюдаемых в CsSrCl3 и CsPbCl3, последовательность фаз 1а, наблюдается в RbCdCl3 и NaTaO3 (рис. 12а); на пути 2 (рис. 11, а и 12, а и б ) - в KCdF3, CsPbBr3; на пути 3а - в NaNbO3; на пути 4 (рис. 12, б) - в KСaF3; на пути 5 (рис. 11б, 12а,б) - в SrZrO3*; на пути 6 (рис. 11, б) - в SmAlO3; на пути 7 (рис. 12, б) - в CaTiO3. Условия реализации последовательностей упорядочений 1, 4, 5 из (9) были получены ранее в работе [14]. Эти результаты согласуются с результатами настоящей работы.

Рисунок 11 - Диаграммы фазовых состояний ТП(10) на ?1,?1 - плоскости:

?1М ? ?1R, Г > 0, ?R< 0 (а); аа?1R??1M, Г > 0, ?R< 0 (б), где ?R = 4?2R ?2R - ?R2,

Г = 4?2M?2R - ?. аЛинии 1, 2, 5, 6 - термодинамические пути, на которых реализуются последовательности фаз из набора (9) под тем же номером

Из проведённого анализа было получено, что ключевым для формирования последовательности фаз является: во-первых, последовательность конденсации ПП, определяемых соотношением между ?1М и ?1R; во-вторых, расположение термодинамического пути относительно мультикритической N-фазной точки ?1= 0, ?1 = 0, определяемое взаимодействием различных компонент каждого ПП, в-третьих, характером взаимодействия параметров порядка между собой.

Аналогичным образом, с учётом упомянутых ключевых моментов, получены диаграммы фазовых состояний для кристаллов со структурой упорядоченных перовскитов (включая эльпасолиты и криолиты) (пр.гр. Op) и слоистых перовскитов (пр. гр. D4p) [9].

Модельный ТП, описывающий ротационные упорядочения в кристаллах со структурой упорядоченных перовскитов (включая эльпасолиты иа криолиты) (пр. гр Op), имеет тот же вид, что и ТП (10), в который помимо инварианта G4? добавлен инвариант такого же вида, но относящийся к другому ПП. Как и в случае кубических перовскитов, наличие таких инвариантов 9-ой степени практически не влияет на вид диаграмм фазовых состояний, но может изменить набор ПП, характеризующих ФС. Поэтому диаграммы ротационно-упорядоченных ФС в кристаллах со структурой упорядоченных перовскитов (пр. гр Op) будут иметь тот же вид, что и диаграммы рис. 11, 12, однако соответствующий этим кристаллам набор ПП, характеризующих ФС, может отличаться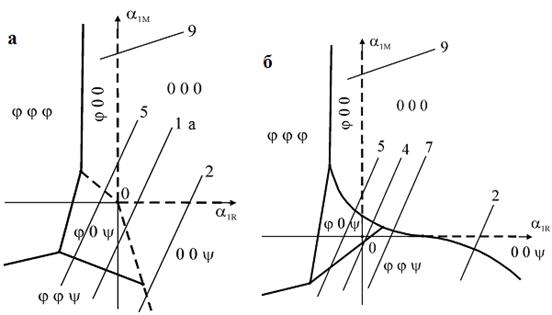.а

а

Рисунок 12 - Диаграммы фазовых состояний ТП (21) на ?1М - а?1R плоскости: ?1R> ~ 0, ?R < 0, Г > 0 (а); ?1R> ~ 0, ?R < 0, Г< 0 (б)

Ротационно-упорядоченные ФС в слоистых перовскитах описываются бо?льшим числом ПП, но меньшей размерности. Поэтому исследование ротационных ФП в этих кристаллах имеет свою специфику. Несмотря на это, использование подхода, который применялся при анализе ротационных ФП в кубических перовскитах, позволило получить диаграммы ФС и определить условия, при которых возникают наиболее распространённые последовательности ротационных упорядочений в кристаллах со структурой слоистых перовскитов [А13].

Из сопоставления характера ротационных упорядочений в кубических перовскитах с величиной фактора толерантности t и зарядом катиона А - ZA получено, чтоа уменьшение t при ZA= const? 0 стимулирует мягкость системы по ПП ? в большей степени, чем по ПП?, аналогично, уменьшение ZA (ZA ?0) при t=constа также стимулирует мягкость преимущественно по ПП ? [A5].

В диссетртации предложена термодинамическая модель [A6, A14], способная на основе феноменологической теории описать всю совокупность ротационных и сегнетоэлектрических ФП, подобных тем, что наблюдаются в твёрдом растворе Na1-xKxNbO3 (NKN) при Т > 300 C, 0.03 < x < 0.2 [15]. Её основные параметры получены из анализа данных по структуре и температурных зависимостей диэлектрической проницаемости для твёрдых растворов NKN различного состава. Это дало возможность определить расположение фазовых состояний на x-T плоскости и на качественном уровне воспроизвести x-T диаграмму фазовых состояний, наблюдаемую в NKN при Т>300 C, 0.03< x< 0.2.

На базе этой модели проанализированы особенности диэлектрических свойств и исследовано влияние внешних воздействий - давления и электрического поля на ФС [A6, A15]. Показано, что вблизи перехода в полярную фазу аномалии диэлектрических свойств, обусловленные ФП между параэлектрическими фазами (ротационные ФП), должны проявляться значительно сильнее чем те, что наблюдаются вдали от него. Это хорошо заметно из сравнения аномалий (изломов) на температурных зависимостях диэлектрической проницаемости при х ~ 0,04?0,06 и при x ~ 0.1.а

Отмечено, что особенности структуры перовскита позволяют посредством изовалентных и гетеровалентных замещений компонент соединений существенным образом влиять на степень их ротационной и поляризационной неустойчивости [А16 - А18].

Показано, что формирование упорядоченного ФС в MnF3 обусловлено совместной конденсацией ротационного ПП и орбитального ПП, характеризующего ориентационное упорядочение октаэдров MnF6, искажённых вследствие эффекта Яна-Теллера. Вклад от орбитального ПП описывается на основе 3-мин. двухподрешёточной модели, вклад от ротационного - на основе феноменологической теории и при этом учитывается нелинейное взаимодействие между обоими параметрами порядка [A10, A19]. Это дало возможность определить условия, при которых фазовый переход из симметричной фазы MnF3 становится фазовым переходом триггерного типа, при котором появление одного параметра порядка стимулирует появление другого.

ЗАКЛЮЧЕНИЕ

аа Основные результаты и выводы:

1. Диаграммы фазовых состояний 4-мин. квадратной, 6- и 8-мин. кубических моделей содержат сегнетоэластическую и три сегнетоэлектрические (полярные) фазы. На границе между сегнетоэластической и одной из полярных фаз, а также на границе между симметричной и этой же полярной фазами имеются трикритические точки, в которых фазовые переходы I рода становятся фазовыми переходами II рода. На линии фазовых переходов II рода из симметричной фазы расположена мультикритическая трёхфазная точка, в которой с симметричной граничат две полярные фазы. В области низких температур на диаграммах фазовых состояний 4-, 6- и 8-мин. моделей имеются по три полярные фазы. В случае 6- и 8-мин. моделей, между аромбоэдрической и тетрагональной фазами расположена либо моноклинная (6-мин.), либо ромбическая (8-мин.) фаза. В случае 4-мин. модели между двумя ромбическими фазами разного типа расположена моноклинная фаза.

2. Учёт одноосных деформаций в 8-мин. кубической модели, приводит к появлению на границе с симметричной фазой ещё одной трикритической точки, в которой фазовые переходы II рода в тетрагональную полярную фазу астановятся фазовыми переходами I рода. Установлено, что последовательность ФП, наблюдаемых в BaTiO3 и KNbO3 может быть описана на основе этой модели.а

3. Учёт сдвиговых деформаций в 6-мин. кубической модели, даже при относительно слабом стрикционном взаимодействии, приводит к тому, что вместо моноклинной СЭ фазы на диаграмме фазовых состояний появляется ромбическая СЭ фаза.

4. Совпадение температур Кюри - Вейсса кристаллов ANbO3 (A = Na, K, Ag), экстраполированных из данных по температурной зависимости диэлектрической проницаемости в кубической фазе, объяснено на основе восьмиминимуной модели для катионов Nb.

5. Получены диаграммы фазовых состояний 12-мин. кубической модели. Они содержат либо три, либо четыре полярные фазы. На границе с симметричной имеются: две трикритические точки, в которых фазовый переход I рода превращается в фазовый переход II рода; мультикритическая трёхфазная точка, в которой сходятся две линии фазовых переходов II рода и линия фазовых переходов I рода между полярными фазами; трёхфазная точка, в которой сходятся три линии фазовых переходов I рода. В области низких температур существуют три полярные фазы: либо ромбоэдрическая и две, отличающиеся по типу, ромбические, либо ромбоэдрическая, тетрагональная и ромбическая.

6. Предложен и применён при исследования статистических свойств многоминимумных, многоподрешёточных моделей метод, включающий следующие этапы:

а. аРазбиение кристаллической решётки на две эквивалентные,аа взаимопроникающие подрешётки, узлы которых чередуются по всем трём направлениям. При этом исходный термодинамический потенциал рассматриваем как сумму термодинамических потенциалов подрешёток и потенциала, характеризующего взаимодействие между подрешётками.

б. Исследование симметрийных и статистических свойств рассматриваемой многоминимумной модели одной из подрешёток.а

в. Построение конфигурационного пространства исходной модели, состоящего из симметричных и антисимметричных комбинаций параметров порядка, описывающих каждую подрешётку.

г. Показано, что статистические свойства исходной модели, описываемые параметрами порядка, образованными симметричной комбинацией, полностью аналогичны статистическим свойствам модели одной из подрешёток. Статистические свойства исходной модели, описываемые параметрами порядка, образованными антисимметричной комбинацией, существенно отличаются.

7. В приближении Горского - Брэгга - Вильямса получены базовые диаграммы фазовых состояний для 3-мин. восьмиподрешёточной кубической (пр. гр. Op) модели, описывающие ориентационные упорядочения антиферродисторсионного типа, характеризуемые параметрами порядка, относящимися к представлениям R3+ и M2+.

8. Диаграмма фазовых состояний 3-мин. двухподрешёточной кубической модели содержит одну сегнетоэластическуюа фазу (фаза I, D4p (Z= 1)) и четыре фазы с антиферродисторсионным типом упорядочения: фазы II и II1 с симметриейа D4p8 (Z = 4), фазу III (D4p7 (Z= 4)) и фазу IV (D2p3 (Z = 4)). Фаза I граничит с симметричной (С) и фазой II по линии фазовых переходов I рода. На границе с симметричной (Oh) и фазойа II имеется трикритическая точка, в которой фазовый переход I рода становятся фазовым переходом II рода. На линии фазовых переходов II рода из симметричной фазы имеютсяа две мультикритические четырёхфазные точки, в которых с фазой С граничат фазы II и III, либо III и II1, а также ромбическая фаза IV. В области низких температур, границы между фазамиаа II - IV,а IV - III иаа III - IV,а IV Ца II1 асимптотически сходятся к двум разным линиям, подобно тому, как они сходились к критическим точкам на границе с симметричной фазой. Поскольку фазы II и II1 имеют одинаковую симметрию и существуют при разныха термодинамических условиях, то может иметь место возврат в фазу, сопровождающийся целым каскадом ФП: С - II - IV - III - IV - II1.

9. Показано, что в кристаллах с несколькими наборами кристаллографически эквивалентных позиций появляются состояния, в которых при Т ~ 0 оказываются частично заполнены позиции с более высокой энергией, то есть алвозбуждённые состояния.а

10. Установлен и описан в рамках статистической теории один из возможных механизмов изоструктурных (изосимметричных) фазовых переходов для кристаллов с несколькими наборами кристаллографически эквивалентных позиций.а

11. Установлено, что основными факторами, определяющими тип и порядок появления ротационных упорядочений, являются последовательность конденсации и взаимодействие параметров порядка между собой, а также характер взаимодействия различных компонент каждого параметра порядка.

12. Влияние кристаллохимических параметров компонент соединений со структурой перовскита (пр. гр. Op) таких, как заряд катиона А (ZA) и соотношение ионных радиусов, характеризуемое фактором толерантности t, на формирование фазовых состояний при ротационных фазовых переходах проявляется следующим образом: при t < ~ 1 температура конденсации моды R25 выше чем моды М3. При фиксированной величине ZA уменьшение t сопровождается более интенсивным ростома температуры конденсации моды М3 по сравнению с температурой конденсации моды R25. При t (t~0,9, ZА=1) моды М3 и R25 конденсируются одновременно. При t~ 0,87 сначала конденсируется М3, затем - R25. С ростом ZA при фиксированном t ав бо??льшей степени стимулируется конденсация моды R25. Поэтому для кристаллов ас ZA а= 2 при t = 0.88 сначала конденсируется мода R25, затем М3. Совместная конденсация мод М3 и R25 имеет место только при t ~ 0.85. Вариант, при котором сначала конденсируется мода М3, представляется маловероятным, так как при t < 0.85 проблематично само существование структуры перовскита.

13. Нелинейные взаимодействия ротационных степеней свободы различного типа с деформационными в потенциале Ландау приводят к появлению промежуточных псевдособственных деформационных фазовых переходов в кубических перовскитах: RbCdCl3, NaTaO3, KСaF3, SrZrO3; в упорядоченных перовскитах: Pb2LuSbO6, Pb2CoTeO6, K2SeCl6, Rb2KMF6 а(M = Sc, In, Lu), Cs2RbDyF6; а также в слоистых перовскитах: K1-xRbxAlF4 и TlAlF4.

14. Предложен модельный термодинамический потенциал, учитывающий вклады от параметров порядка, характеризующих ротационное иа ориентационное упорядочение октаэдров MnF6, искажённых вследствие эффекта Яна-Теллера, а такжеа нелинейное взаимодействие между обоими параметрами порядка. На его основе определены аусловия, при которых фазовый переход из симметричной фазы MnF3 становится фазовым переходом триггерного типа, при котором появление одного параметра порядка стимулирует появление другого.

Список цитируемой литературы

1. Парсонидж Н., Стейвли Л. Беспорядок в кристаллах. Т.1.-М.: Мир, 1982.-434с.

2. Френкель Я.И. Кинетическая теория жидкости.- Л.: Наука, 1975. - 592с.

3. Mason W.P., Mattias В.Т. Theoretical model explaining the ferroelectric effect in Barium titanate // Phys.Rev.-1948.- V.74.- P.1622 - 1636.

4. Comes R., Lambert M., Guinier A. The chain structure of BaTiO3and KNbO3 // Sol. St. Commun.-1968.-V.6.- P.715 - 719.

5. Вихнин В.С., Зайцев О.А. Фазовые переходы и динамические эффекты в кристаллах, обладающих одноячеечными потенциалами с многоямным возбужденным состоянием // ФТТ.- 1997.-Т.39.- С.547- 552.

6. Udovenko A.A., Laptash N. M. Disorder in crystals of dioxofluorotungstates, (Np)2 and Rb2WO2F4 //Acta Cryst. B.- 2008.-V. 64.-P. 645 - 651.а

7. Блат Д. Х., Зиненко В. И. Теория структурных фазовых переходов в цианидах щелочных металлов // ЖЭТФ.- 1980.- Т.79.- С. 974 - 986.

8. Ландау Л.Д., Лифшиц Е.М. Статистическая физика. ч.1.- М.: Наука, 1976.-584с.

9. Александров К.С., Безносиков Б.В. Перовскиты. Настоящее и будущее.- Новосибирск: Изд-во СО РАН,а 2004.- 231с.

10. Pirc R., Blinc R. Off-center Ti model of barium titanate // Phys. Rev. B.-а 2004.- V.70.- 134107-1 - 134107-8.а

11. Lemeshko M.P., Nazarenko E.S., Gonchar A. A., Reznichenko L. A., Nedoseykina N. I., Novakovich A.A., Mathon O., Joly Y., Vedrinskii R.V. EXAFS studies of аthe local atomic structure of lead- free piezoelectric ceramics KxNa1-x NbO3 overа temperature range 10 - 1023 K // Phys. Rev. B.- 2007.- V.76.- 134106-1 - 134106-11.

12. Sicron N., Ravel B., Yacoby Y., Stern E. A., Dogan F., Rehr J. J. Nature of ferroelectric phase transition in PbTiO3 // Phys. Rev.B.- 1994.-V.50.- P. 13168 - 13180.а

13. Сахненко В.П., Таланов В.М., Чечин Г.М. Теоретико-групповой анализ полного конденсата, возникающего при структурных фанзовых переходах // Физика металлов и металловедение. -1986.- Т.62.-а С. 847 - 856.

14. Ларин Е.С. О фазовой диаграмме CsPbCl3 // ФТТ.- 1984.-Т.26.- С.3019 - 3023.

15. Ahtee M., Glazer A.M. Lattice parametrs and tilted octahedra in sodium - potassium niobate solid solutions //Acta. Cryst. A.- 1976.-V. 32.-P. 434 - 446.

Список основных публикаций автора по теме диссертации

А1. Ивлиев, М.П. Фазовые переходы типа порядок - беспорядок, описываемые двумя многоминимумными параметрами порядка (приближение среднего поля)./ М.П. Ивлиев, В.П. Сахненко // Деп. ВИНИТИ № 3418 - 89 от 19.05.89 - Ростовск. гос. ун-т, 1989. - 35с.

А2. Ивлиев, М.П. Формирование сегнетоэлектрических фазовых состояний в KNbO3 и других ниобатах со структурой перовскитов/ М.П. Ивлиев, И.П. Раевский, С.И. Раевская, В.А. Шуваева, И.Н. Пирог // ФТТ.- 2007.- Т.49.- С. 731-740.

А3. Ивлиев, М.П. Сегнетоэластические фазовые переходы в перовскитах, обусловленные орбитальным и ротационным упорядочением / М.П. Ивлиев // ФТТ.- 2009.- С. 1472-1476.

А4. Ивлиев, М.П. Влияние сегнетоэластических параметров порядка на формирование фазовых состояний титаната - цирконата свинца / М.П. Ивлиев // Изв. РАН. сер. физ.- 2010.- аТ.74.- С. 1257 - 1259.

А5. Ивлиев, М.П. Фазовые состояния в ротационно-искажённых перовскитах / М.П. Ивлиев // Кристаллография.- 2002.- Т.47.- С.1065-1071.

А6. Ивлиев, М.П. Фазовые состояния и особенности диэлектрических свойств твёрдых растворов ниобата натрия-калия / М.П. Ивлиев, И.П. Раевский, Л.А. Резниченко, С.И. Раевская, В.П. Сахненко // ФТТ.- 2003.- Т.45.- С. 1886-1891.

А7. Ивлиев, М.П. Возможность существования квадрупольной сегнетоэластической фазы в KTaO3 : Li / М.П. Ивлиев, В.П. Сахненко // ФТТ.- 1986.- Т.28.- С. 632-634.

А8. Ивлиев, М.П. Особенности сегнетоэлектрических упорядочений в перовскитах АNbO3 (А - Na, Ag, K) / М.П. Ивлиев, С.И. Раевская, И.П. Раевский // Труды VIII Междунар. Симпоз. Порядок, беспорядок и свойства оксидов (ODPO - 2005). Сочи, 2005. Ч.2.- С.150 - 153.

А9. Ивлиев, М.П. Теория сегнетоэластических фазовых переходов в KCN / М.П. Ивлиев, В.П. Сахненко // Изв. АНСССР. сер. физ.- 1979. -Т.43. - С.1606-1610.

А10. Ивлиев, М.П. Фазовые состояния трёхминимумной двухподрешёточной модели (приближение среднего поля) / М.П. Ивлиев // Труды Междунар. симпоз. Фазовые превращения в твёрдых растворах и сплавах (OMA - 2003). Сочи, 2003. - С.133-136.

А11. Ивлиев, М.П. Особенности термодинамических свойств кристаллов, описываемых составными многминимумными моделями / М.П. Ивлиев, В.П. Сахненко // Известия ВУЗов. Сев.Кавказский регион.- 2010.- Т.23.- С.41-45.

А12. Ивлиев, М.П. Complex Aggregative Multiminima Models for Ferroelastic Transitions in Crystals / M.P. Ivliev, V.P. Sakhnenko // Ferroelectrics.-2010.-Р.16-21.

А13. Ивлиев, М.П. Soft modes and martensitic transformations in K1-xRbxAlF4 / M.P. Ivliev, V.P. Sakhnenko // Ferroelectrics.- 1996.- V.175.- P.65-71.

А14. Ивлиев, М.П. Получение и исследование монокристаллических твёрдых растворов (Na,K)NbO3 / И.П. Раевский, Л.А. Резниченко, М.П. Ивлиев, В.Г. Смотраков, В.В. Ерёмкин, М.А. Малицкая, Л.А. Шилкина, С.И. Шевцова, А.В. Бородин // Кристаллография.- 2003.- Т.48.- С.531-535.

А15. Ивлиев, М.П. Кристаллохимические аспекты влияния термодинамической предыстории на вид фазовых диаграмм температура - состав твёрдых растворов ниобата натрия - лития и ниобата натрия - калия / М.П. Ивлиев, И.П. Раевский, Л.А. Резниченко, М.Н. Палатников, Л.Е. Балюнис, М.А. Малицкая // ЖТФ.- 2002.- Т. 72.- С. 120 - 124.

А16. Ивлиев, М.П. Влияние модифицирования литием на устойчивость сегнетоэлектрического состояния в пьезоэлектрических, керамических материалах / М.П. Ивлиев, С.И. Раевская,а О.Ю. Кравченко, Л.А. Резниченко, И.П. Раевский//Конструкции из композитных материалов.-2008.-Вып.4.- С.80-87.

А17. Ивлиев, М.П. Влияние несоответствия кристаллохимических параметров катионов Na и Li на диэлектрические свойства твёрдых растворов NaNbO3 - LiNbO3 / М.П. Ивлиев, С.И. Раевская,а О.Ю. Кравченко, Л.А. Резниченко, И.П. Раевский // ФТТ.- 2009.- С. 1988-1993.

А18. Ивлиев, М.П. Влияние модифицирования изовалентными и гетеровалентными ионами на диэлектрические свойства пьезоэлектрических керамических материалов на основе ниобата натрия / М.П. Ивлиев, С.И. Раевская,а О.Ю. Кравченко, Л.А. Резниченко, И.П. Раевский // Конструкции из композитных материалов.- 2009.- Вып.1.- С.61-68.а

А19. Ивлиев, М.П. Взаимодействие ротационного и орбитального упорядочений при формировании фазового состояния в MnF3 / М.П. Ивлиев // Труды VII Междунар. Симпоз. Порядок, беспорядок и свойства оксидов (ODPO - 2004). Сочи, 2004.- С.268 - 269.

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 |

     Авторефераты по всем темам  >>  Авторефераты по математике