Авторефераты по всем темам  >>  Авторефераты по математике

Теория структурных фазовых переходов с несколькими параметрами порядка в кристаллах с октаэдрической анионной подрешёткой

Автореферат докторской диссертации по физико-математическим наукам

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 |

 

Применяя вышеупомянутый подход, в широкой области значений термодинамических и модельных параметров исследованы статистические свойства простых многоминимумных моделей: в главе 2 - четырёхминимумной а(4-мин.) квадратной,а шести-, восьми- и двенадцатиминимуных (6-, 8- и 12-мин.) кубических с одной подрешёткой; в главе 3 - трёхминимумной (3-мин.) кубической с двумя, четырьмя и восьмью подрешётками. В главе 4 проанализированы статистические свойства сложных составныха многоминимумных моделей: 1 + 2-минимуных и 1+4-минимумных, а также исследованы специфические особенности термодинамических свойств кристаллов, описываемых этими моделями.а

В качестве объектов теоретического исследования структурных фазовых переходов в диссертации рассмотрены соединения с октаэдрической анионной подрешёткой. Основу обширной группы таких кристаллов составляют перовскиты, упорядоченные перовскиты (включая эльпасолиты и криолиты), слоистые перовскиты и ряд других соединений [9]. В кристаллах этой группы одним из наиболее распространённых типов структурных превращений являются ФП, обусловленные смещениями анионов, которые можно истолковать как повороты октаэдров (ротационные ФП, "смятие", tilt). В настоящее время накоплен большой объём экспериментального материала по ротационным ФП в этих кристаллах, проведена его систематизация и предварительный теоретико-групповой анализ, позволивший установить ПП, описывающие ротационно упорядоченные фазы. Также был выделен набор наиболее распространённых (базовых) последовательностей ротационных упорядочений [9].

Теоретические исследования ротационных ФП в подавляющем большинстве случаев сводились к описанию ФП в конкретных соединениях. При этом анализировались лишь отдельные типы упорядочений. Такой подход даёт возможность описать термодинамику конкретных структурных превращений, но он не позволяет установить условия, определяющие формирование различных последовательностей упорядоченных фаз, при изменении термодинамических параметров состояния.

Отмечена необходимость исследовать ротационные ФП различного типа на основе феноменологической теории в рамках единого подхода в каждом из рассматриваемых семейств кристаллов. Для решения этой задачи предложен модельный термодинамический потенциал [A5]. С его помощью были получены диаграммы ФС при различных соотношениях между параметрами модели, определяющими последовательность конденсации ПП и характер взаимодействия различных компонент каждого ПП. Это дало возможность определить условия, при которых могли бы быть реализованы наиболее распространённые последовательности ротационных упорядочений.

Для кристаллов со структурой перовскита сопоставление условий реализации различных базовых последовательностей позволило оценить влияние кристаллохимических параметров компонент соединения таких, как заряд катиона А и соотношение ионных радиусов, характеризуемое фактором толерантности, на формирование ФС [A5].

Также исследовано взаимное влияние поляризации и ротационных упорядочений различного типа на формирование упорядоченных ФС. В качестве модельного объекта выбраны твёрдые растворы Na1-xKxNbO3 (NKN), поскольку в них наблюдаются в различных сочетаниях как ротационные, так и сегнетоэлектрические ФП [14]. В диссертации предложена термодинамическая модель [A6], способная описать всю совокупность ротационных и сегнетоэлектрических ФП, подобных тем, что наблюдаются в твёрдом растворе NKN при Т > 300 C, 0.03 < x< 0.2. Её основные параметры получены из анализа данных по структуре и температурных зависимостей диэлектрической проницаемости для твёрдых растворов NKN различного состава. На базе предложенной модели проанализированы особенности диэлектрических свойств и исследовано влияние внешних воздействий - давления и электрического поля на ФС.

Во втором разделе исследуются статистические свойства простых многоминимумных моделей с одной подрешёткой (без мультипликации ячейки): 4-мин. квадратной, 6-, 8- и 12-мин. кубических [A1, A2, A4, A7 - A9]. Такой выбор обусловлен тем, что 6- и 8-мин. кубические модели являются наиболее известными и часто используемыми многоминимумными моделями [3, 4, 7]. аЧетырехминимумная квадратная модель - это, фактически, более простой (плоский) вариант 6-мин. кубической модели. Она является хорошим модельным объектом для демонстрации в деталях всего процесса исследования статистических свойств таких моделей. Статистические свойства 12-мин. кубической модели [7] в широкой области значений термодинамических и модельных параметров ранее никогда не исследовались. Эта модель интересна тем, что её конфигурационное пространство содержит ПП, которые по трансформационным свойствам идентичны поляризации и тензорам одноосных и сдвиговых напряжений.

Исследование в широкой области значений термодинамических и модельных параметров статистических свойств упомянутых моделей проведено в приближении Горского - Брэгга - Вильямса, при этом выявлен ряд общих закономерностей формированияа картины фазовых состояний (ФС).

В подразделе 2.1 проведён анализ 6-мин. кубической модели [A1, A7, A8]. В качестве объекта исследования рассматривается кристалл са кубической решёткойа симметрии Оp, содержащий подсистему частиц, каждая из которых с одинаковой вероятностью может находиться в одной из шести КЭП, отвечающих минимумам их потенциальной энергии в кристаллической решётке. Минимумы немного смещены от узла вдоль направлений типа [001].

Вероятности заполнения минимумов, характеризуются следующим набором

n1,2 = (1 + ?1 ?1);аа n3,4 = (1 Ца ?1 + а?2 ?2)а а n5,6 = (1 Ца ?1 - а?2 ?3).

Функции ?, ? выполняют роль параметров порядка (ПП),а ? преобразуется по неприводимому представлению Eg, а ? - по Т1u. Равновесные значения параметров порядка ?, ? можно найти решив систему уравнений состояния (СУС):аа

аа(i = 1,2),а а(j =1,2,3) аа

и выбрав то решение, которому соответствует абсолютный минимум F приа заданных значенияха A, Bи Т.

Неравновесный термодинамический потенциал (ТП) 6-мин. кубической модели в приближении среднего поля в варианте Горского - Брэгга - Вильямса (ГБВ) в расчёте на одну частицу имеет видаа аа

а= [() + ()]а - ln 6 + [(1 + ?1 ?1) ln (1 + ?1 ?1)+

аа + (1 Ца ?1 + а?2 ?2) ln (1 - ?1 + а?2 ?2) + а аа

а+ (1 Ца ?1 - а?2 ?3) ln (1 Ца ?1 - а?2 ?3)] .а а (1)

Знак л предполагает суммирование выражений сначала со знаком л+, а затем со знаком л-.а Константы А и В - феноменологические параметры теории. ааФункции ?, ? выполняют роль параметров порядка (ПП),а ? преобразуется по неприводимому представлению Eg, а ? - по Т1u. а

Общий вид диаграммы ФС, описываемой термодинамическим потенциалом (1), приведён на рис. 1, где I - кубическая фаза с симметрией Op; II - тетрагональная сегнетоэластическая фаза с симметрией D4p; III, IV, V - сегнетоэлектрические (СЭ) фазы, соответственно, тетрагональная - C4v1, ромбоэдрическая - C3v5 и моноклинная - Сi1. аа Диаграмма ФС (рис. 1) содержит сегнетоэластическую и три СЭ фазы. В области, где критическим является ПП ?, при В < 0 реализуется фаза III Ц(?1,0,?1,0,0), при В > 0 реализуется фаза IV Ц(0,0,?,?,?). Таким образом, с ростом В фаза III либо через промежуточную фазу V - (?1,0,?1,?2,?2), либо непосредственно заменяется фазой IV.

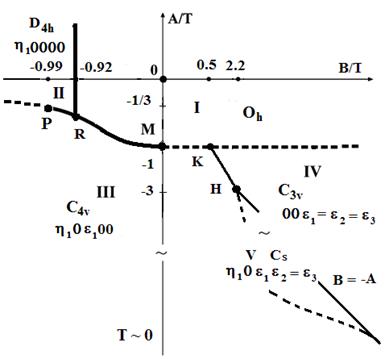
Рисунок 1 - Диаграмма ФС 6-мин. модели, описываемой ТП (1). Здесь и далее сплошными обозначены линии ФП первого рода (ФП 1), штриховыми - второго рода. Линия В = - А - асимптота, к которой сходятся межфазные границы при Т > 0

Диаграмма ФС (рис. 1), это диаграмма для недеформируемой, зажатой решётки. Учёт деформируемости решётки относительно сдвиговых деформаций даже при слабом стрикционном взаимодействии g2/c = 0.04.B (? - константа стрикции, с Цсоответствующий модуль упругости), приводит к тому, что вместо моноклинной СЭ фазы на диаграмме фазовых состояний появляется ромбическая СЭ фаза (рис. 2).

Также в подразделе 2.1 проведён анализ четырёминимумной (4-мин.) квадратной модели [A1]. В качестве объекта исследования рассматривается слоистый кристалл с тетрагональной решёткойа симметрии D4h, содержащий подсистему частиц, каждая из которых с одинаковой вероятностью может находиться в одной из четырёх КЭП, отвечающих минимумам их потенциальной энергии в кристаллической решётке. Минимумы находятся в слоях ортогональных оси 4-го порядка, они немного смещены от узла в направлениях [ 1,0,0] аи [0, 1,0].

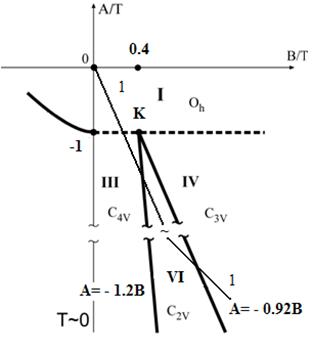
Рисунок 2 - Диаграмма ФС 6-мин. модели при учёте деформируемости решётки относительно сдвиговых деформаций. Тонкая сплошная линия - термодинамический путь, воспроизводящий последовательностьа ФП, наблюдаемых в BaTiO3 и КNbО3

Неравновесный ТП 4-мин. модели имеет вид:аа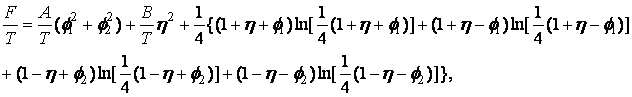

где А, В - параметры модели. Функции ?,? выполняют роль параметров порядка,а ? преобразуется по неприводимому представлению В1g, а ?1,2 - по Eu. Система уравнений состояния имеет пять типов решений, отличающихся по симметрии:а 1.(? =?1= ?2 = 0) - D4h;аа 2. ( ?, ?1= ?2 = 0) - D2h;а 3. (?, ?1,0) - С2v;а 4.( 0, ?,? ) - С2v;аа 5. (?, ?1, ?2) - Сs.

Диаграмма ФС 4-мин. квадратной модели имеет вид подобный тому, что изображён на рис. 1. Она содержит все пять возможных по симметрии фазовых состояний, т.е. фазы I - V. В области, где критическим является ПП ?, при В < 0 реализуется фаза III - (?,?1,0), при В > 0 реализуется фаза IV - (0,?,?). Таким образом, с ростом В фаза III либо через промежуточную фазу V Ца (?,?1,?2), либо непосредственно заменяется фазой IV.

В подразделе 2.2 проведён анализ 8-мин. кубической модели [A2, A9]. Рассматривается кристалл с простой кубической решёткой (пр. гр. Op (Z=1)), содержащий подсистему частиц, каждая из которых с одинаковой вероятностью может находиться в одной из восьми КЭП, отвечающих минимумам их потенциальной энергии в кристаллической решётке. Минимумы немного смещены в направлениях типа [111] от узла в центросимметричной позиции.

Неравновесный ТП 8-мин. модели в приближении ГБВ имеет вид:а

F =а A() + D() + C ?2 +а аа

+[(1+ e1 + e2 +e3 (? + ?1 + ?2 + ?3)) ln(1+ e1 + e2 +e3 (? + ?1 + ?2 + ?3)+

+ (1+ e1 - e2 - e3 (? + ?1 - ?2 - ?3)) ln(1+ e1 - e2 - e3 (? + ?1 - ?2 - ?3))+

+ (1 - e1 + e2 - e3 (? - ?1 + ?2 - ?3)) ln(1 - e1 + e2 - e3 (? - ?1 + ?2 - ?3)+

+(1 - e1 - e2 +e3 (? - ?1 - ?2 +?3)) ln(1 - e1 - e2 +e3 (? - ?1 - ?2 + ?3))],(2)

гдеа A, B, C - модельные константы. Функции ?, ?, е выступают в качестве параметров порядка, ?IT1u, eIT2g, ?IA2u.

Диаграмма ФС 8-мин. кубической модели, описываемая ТП (5) при С = 0 имеет вид, изображённый на рис. 3, где I - кубическая фаза с симметрией Op; II - (0,0,0,e,e,e,0) ромбоэдрическая сегнетоэластическая фаза с симметрией D3d5; III, IV, VI - СЭ фазы, соответственно: ромбоэдрическая - (?,?,?,e,e,e,?), C3v5; тетрагональная - (?1,0,0,0,0,0,0), C4v1; ромбическая - (0,?2,?2,e1,0,0,0), (C2v14) Двигаясь вдоль термодинамического пути 1, обозначенного тонкой сплошной линией (рис. 3), можно воспроизвести последовательность ФП, наблюдаемых в KNbO3: I>IV >VI >III. Отличие от реальной ситуации лишь в том, что на диаграмме ФП I Ца IV - переход второго рода, а в KNbO3 и в BaTiO3 это переход первого рода.

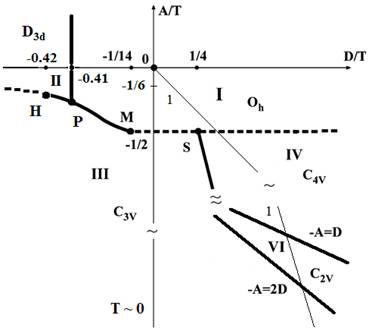
Рисунок 3 Ца Диаграмма ФС 8-мин. модели, описываемая ТП (2) при С = 0

Учёт деформируемости решётки относительно одноосных деформаций приводит к тому, что на диаграмме фазовых состояний, на границе с симметричной фазой появляется вторая трикритическая точка и линия ФП первого рода между фазами I - IV. Показано, что при стрикционном взаимодействии ?2/c0 = 2D а(? Цконстанта стрикции, с0=(1/2)(c11 - c12) - модуль упругости) имеется атермодинамический путь, двигаясь вдоль которого удаётсяа воспроизвести всю последовательность ФП, которая наблюдается в KNbO3, причём все ФП - переходы первого рода.

В подразделе 2.3 проведён анализ статистических свойств 12-мин. кубической модели [7, A4].аа Конфигурационное пространство этой модели содержит ПП, которые по своим трансформационным свойствам идентичны тензорам одноосных и сдвиговых деформаций, а также вектору поляризации. Можно предположить, что такое сочетание ПП позволит в рамках единого подхода описывать ФП первого и второго рода из кубической в наиболее распространённые сегнетоэлектрические фазы - С2v, С3v иа С4v. Фазовые переходы такого типа наблюдаются в твёрдых растворах PbZr1-xTixO3 (ЦТС), (1-х)PbMg1/3Nb2/3O3 - xPbTiO3 (x>0.25), (1-х)PbZn1/3Nb2/3O3 - xPbTiO3 и других. Для оценки возможностей 12-мин. модели, исследована её применимость для описания х-Т диаграммы фазовых состояний, аналогичной наблюдаемой в ЦТС.а Выбор ЦТС обусловлен тем, что его х-Т диаграмма хорошо известна, а кроме того она содержит ряд особенностей, описать которыеа на основе других многоминимумных моделей, не прибегая к введению дополнительных взаимодействий, невозможно.

Рассматривается кристалл с простой кубической решёткой (пр. гр. Op (Z=1)), содержащий подсистему частиц, каждая из которых с одинаковой вероятностью может находиться в одной из двенадцати КЭП, отвечающих минимумам их потенциальной энергии в кристаллической решётке. Минимумы немного смещены в направлениях типа [011] от узла в центросимметричной позиции, в котором пересекаются три оси С4, их расположение и нумерация приведены на рис. 4.

Неравновесный ТП 12-мин. модели имеет вид:

12F =а Aа+ B(6f12 + 2f22) + Dа+ Gа+а аа

+ T[(1 + 2f1 + e3 (?1 + ?2 + ?1 - ?2))ln(1 + 2f1 + e3 (?1 + ?2 + ?1 - ?2)) +

+ (1 + 2f1 - e3 (?1 - ?2 + ?1 + ?2)) ln(1 + 2f1 - e3 (?1 - ?2 + ?1 + ?2)) +

+ (1 - f1 + f2 + e2 (?1 + ?3 - ?1 + ?3)) ln(1 - f1 + f2 + e2 (?1 + ?3 - ?1 + ?3)) +аа

+ (1 - f1 + f2 - e2 (?1 - ?3 - ?1 - ?3))ln(1 - f1 + f2 - e2 (?1 - ?3 - ?1 - ?3)) +

+ (1 - f1 - f2 + e1 (?2 + ? 3 + ?2 - ?3))ln(1 - f1 - f2 + e1 (?2 + ? 3 + ?2 - ?3)) +

+ (1 - f1 - f2 - e1 (?2 - ?3 + ?2 + ? 3))ln(1 - f1 - f2 - e1 (?2 - ?3 + ?2 + ? 3))],(3)

л означает суммирование по верхнему и по нижнему знакам. A, B, D, G - модельные константы. Функции f, ?, e, ?выполняют роль ПП и преобразуются по неприводимым представлениям соответственноа Eg, T1u, T2gиT2u. Параметры порядка f и e можно считать сегнетоэластическими, а ПП ? - сегнетоэлектрическим. Далее полагаем, что критическим является параметр ?. а Из сопоставления результатов исследования ТП (3) вблизи границы с симметричной фазой с экспериментальными данными, получен набор условий, который позволил подобрать модельные константы A(x), B(x), D(x) таким образом, чтобы вид диаграммы фазовых состояний, полученной теоретически, вблизи границы с симметричной фазой соответствовал по основным параметрам экспериментальной х-Т диаграмме твёрдых растворов цирконата-титаната свинца.

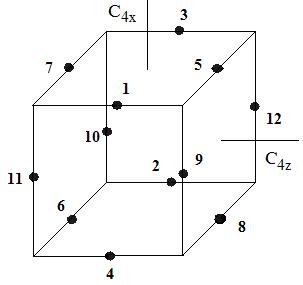
Рисунок 4а - Расположение и нумерация 12-ти аКЭП

Полагая, чтоа

Тс(х) = 450+ 450х - 200х2;аа А(х) = - 4 Тс(х);аа В(х) = (0.4 - 2.4х) Тс(х);а а аD(x) = (- 1.5 + 3.5x) Тс(х)а аа (4)

при G(x) = 0.8(4 - 3x)Tc(x) и G(x) = (4 - 3x)Tc(x) получаем диаграммы ФС а(рис. 5). аНа диаграммах ФС вблизиа линии ФП второго рода из симметричной фазы картина ФС подобна той, что наблюдается у всех рассмотренных ранее моделей. Однако в области x < ~ 1 появляется необычная сегнетоэлектрическая ромбическая фаза Orth II. В области T ~ 0 картина совершенно меняется. Тетрагональная сегнетоэлектрическая фаза либо присутствует в ограниченной области значений модельных параметров, либо отсутствует вообще. Вместо неё присутствуют либо одна Orth II, либо две ромбические сегнетоэлектрические фазы Orth I и Orth II.

Упорядочение, характеризующее фазу Orth II, можно представить следующим образом. Из двенадцати КЭП в бо?льшей степени заполнены четыре КЭП в серединной плоскости, ортогональной оси 4-го порядка. Из этих четырёх две соседние КЭП заполнены одинаково и в бо?льшей степени чем две оставшиеся, которые тоже заполнены одинаково.

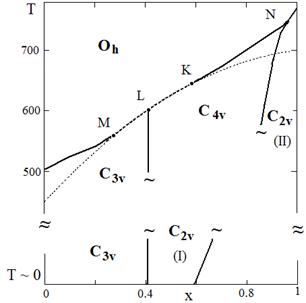
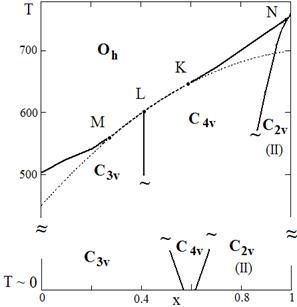
а)аа б)

Рисунок 5 - Диаграммы фазовых состояний, описываемые ТП(3) с учётом (4) при: G(x) = 0.8(4 - 3x)Tc(x) - (а); G(x) = (4 - 3x)Tc(x) -(б)

Появление такой необычной фазы как Orth II обусловлено тем, что она возникает не из кубической, а из тетрагональной сегнетоэластической (D4p). В этой фазе имеет место преимущественное заполнение четырёх КЭП в средней, экваториальной плоскости, ортогональной оси 4-го порядка. Поэтому, когда критическим становится ПП ?, то перераспределение частиц по КЭП происходит по этим четырём позициям. В результате, как следует из анализа 4-мин. квадратной модели, могут появиться две сегнетоэлектрические фазы. При G(x) = 0.8(4-3x)Tc(x)появляются обе. Одна из них фаза Orth II, другая,а Orth I по структуре подобна ромбической сегнетоэлектрической фазе, возникающей из кубической (в данном случае она неустойчива), однако по происхождению это совсем другая фаза.

В третьем разделе на примере трёхминимумной (3-мин.) кубической модели рассмотрены ФП, при которых возникают фазы с несколькими по-разному упорядоченными подрешётками, т.е. фазовые переходы, сопровождаемые мультипликацией ячейки [A3, A10]. Эта модель является одной из наиболее распространённых многоминимумных многоподрешёточных моделей. Известна большая группа ионно-молекулярных кристаллов (CsSH, CsO2), кристаллов, содержащих октаэдры, искажённые вследствие эффекта Яна-Теллера (KCuF3, KCrF3), упорядочения в которых описываются именно этой моделью. Деформирующие ЯТ ионы переходного элемента можно представить в виде частиц в форме вытянутого цилиндра, которые в симметричной (кубической) фазе могут быть ориентированы вдоль трёх направлений типа [001]. На таком уровне исследований ориентационные ФП в ионно-молекулярных кристаллах и ФП, обусловленные статическим эффектом Яна - Теллера, описываются на основе одной и той же статистической модели. В качестве модельной системы рассматривается кристалл, имеющий простую кубическую решётку с симметрией O(Z=1), в её узлах расположены частицы в форме вытянутого цилиндра, которые с одинаковой вероятностью могут быть ориентированы вдоль одного из трёх направлений типа [001], то есть имеют три КЭП.

В подразделе 3.1 анализируется 3-мин. двухподрешёточнаяа модель. Исследуются возможные упорядочения, относящиеся к вектору аk = ()(b1 + b2 + b3), (bi - базисные векторы обратной решётки), то есть к точке R пространства векторов обратной решётки [A10]. В этом случае кристалл можно представить в виде двух одинаковых, взаимопроникающих, по-разному упорядоченных подрешёток, узлы которых чередуются по трём направлениям типа [001].

Функции, характеризующие заполнение КЭП для каждой из подрешёток, имеют вид:а

n1, (I,II) = ,аа n2, (I,II) =

n3, (I,II) =а ,

I, II - номер подрешётки, i= (1,2,3) -а номер КЭП, относящийся к той, или иной подрешётке.а В столбце л знак л+ соответствует первой подрешётке, а знак л - - второй.

Неравновесный ТП двухподрешёточной трёхминимумной (3-мин.) модели в приближении Горского - Брэгга - Вильямса можно представить:

F = + + T.а аа а(5)

Функции ? и ? выполняют роль параметров порядка, где ?Eg(k = 0), ?R2+, k = (1/2,1/2,1/2). Диаграмма ФС, описываемая ТП (5), изображена на рис. 6. Фаза I- (?1,0,0,0), фазы II и II1 - (?1,0,0,?2), фаза III- (?1,0,?1,0), фаза IV- (?1,?2,?1,?2).

аа аа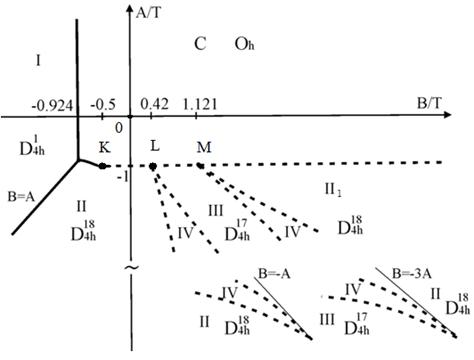

Рисунок 6 - Диаграмма ФС 3-мин. двухподрешёточной модели, описываемая ТП (5). Линии В = - А иB = -а 3A - асимптоты, к которым сходятся межфазные границы при Т > 0

Система уравнений состояния может иметь помимо симметричного ??|???| = |???| = 0 (пр. гр. Op(Z = 1)) ??два набора решений. В первый набор входят два решения типа ?1, ?2 = 0 (пр. гр. D4p(Z = 1)) и ?1, ?2 (пр. гр. D2p(Z = 1)), описывающие сегнетоэластические фазы с упорядочением ферродисторсионного типа [A7]. Во второй набор - три решения типа:а ?1, ?2 = 0, ?1 = 0, ?2 (пр. гр. D4p8(Z = 4));а ?1, ?2 = 0, ?1, ?2 = 0 (пр. гр. D4p7(Z = 4)) и ?1, ?2, ?1, ?2 (пр. гр. D2p3(Z = 4)), описывающие фазы с упорядочением антиферродисторсионного типа с k = (1/2,1/2,1/2). аа

Характерная особенность диаграммы (рис. 6) в том, что фазыа II и II1 имеют одинаковую симметрию. На границе с симметричной фазой С помимо трикритической точки K имеются две четырёх фазные мультикритические точки L и M, а в области низких температур, границы между фазамиаа II - IV,а IV - III иаа III - IV,а IV Ца II1 асимптотически сходятся к двум разным линиям.

В подразделе 3.2 анализируются 3-мин. четырёх- и восьмиподрешёточныеа модели [A3]. Для исследования упорядочений, описываемых 3-мин. восьмиподрешёточной аамоделью предложен следующий метод:

- исходная кристаллическая решётка (пр. гр. Op) разбивается на две эквивалентные, взаимопроникающие подрешётки с симметрией Op;

- исследуются симметрийные и статистические свойства 3-мин. четырёхподрешёточной модели для кристалла с симметрией Op.

Конфигурационное пространство исходной модели формируется из симметричных и антисимметричных комбинаций параметров порядка, описывающих упорядочения в каждой из подрешёток с симметрией Op, а исходный термодинамический потенциал представляется как сумма ТП подрешёток и потенциала, характеризующего взаимодействие между подрешётками. При этом статистические свойства исходной восьмиподрешёточной модели, описываемые параметрами порядка, образованными симметричной комбинацией, будут полностью аналогичны статистическим свойствам 3-мин. четырёхподрешёточнойа модели.

Для параметра порядка,а относящегося к представлению М2+, на различных сечениях получены диаграммы фазовых состояний 3-мин. восьмиподрешёточной модели. Показано, что на границе между симметричной (Op) и фазами (D4p (Z = 2)) и (Tp (Z = 8)) соответственно могут асуществовать атрикритические точки, также ана границе с симметричной фазой имеются мультикритические 3-х фазные точки, в которых граничат симметричная, тетрагональная и ромбоэдрическая фазы. Количество 3-х фазных точек может меняться от нуля до двух.

Используя приближение взаимодействия ближайщих соседей, определены условия, при которых наиболее распространённые упорядочения антиферродисторсионного типа (пр. гр. D4p8 и D4p) могут реализоваться в одном и том же кристалле.

В четвёртом разделе исследуются статистические свойства многоминимумных моделей с несколькими наборами КЭП, отличающимися по энергии (составнымиа многоминимумными моделями) [A11, A12]. Одной из основных целей этого раздела диссертации является выявление на примере наиболее простых Ца 1 + 2-мин. и 1 + 4-мин. моделей, сохраняющих основные черты, присущие кристаллам с несколькими наборами КЭП, особенностей термодинамического поведения, обусловленных перераспределением атомов между различными наборами КЭП.

В подразделе 4.1 исследованы свойства 1 + 2-мин. модели [A11]. Рассмотрена трёхминимумная модель, состоящая из двух подсистем минимумов - центрального и двух боковых (1+2-мин.). На рис. 7 приведены два варианта рельефа потенциальной энергии частицы дляа такой 1+2-мин. модели.

Рассматривается слоистый кристалл с простой тетрагональной решёткойа симметрии D4h, в узлах которого расположены частицы, имеющие три минимума вдоль оси 4-го порядка. Центральный минимум находится в самом узле, в центросимметричной позиции, а два боковых - немного смещены. Возможен ФП, обусловленный резким (скачкообразным) изменением соотношения в степени заполнения центрального и боковых минимумов. Если при этом боковые минимумы остаются заполнены одинаково, тоа симметрия решётки не меняется. Также возможен фазовый переход, связанный с нарушением эквивалентности заполнении боковых минимумов, который сопровождается изменением симметрии решётки.

Функции, характеризующие вероятности заполнения минимумов:а центрального - p = (1+ ?) /2,а боковых - n1 =(1 - ?)(1+ ?)/4, n2 =(1 - ?)(1 - ?)/4. Функции ?, ? выполняют роль параметров порядка, ? преобразуется по неприводимому представлению A1g , аа ? - поA1u.

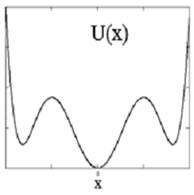
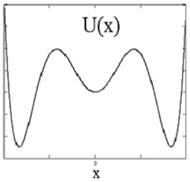
Рисунок 7 - Варианты рельефа потенциальной энергии частицы

дляа 1+2- мин. амодели

Неравновесный термодинамический потенциал трёхминимумной (1+2-мин.) модели в приближении Горского - Брэгга - Вильямса имеет вид:аа

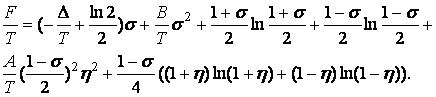(6) а

Параметр ? в основном зависит от разницы глубин потенциальных ям -а центральной и боковых, если ?> 0 то центральная глубже боковых. Параметр В характеризует соотношение между взаимодействиями внутри подсистем минимумов и между этими подсистемами (одна подсистема состоит иза центральных ям, другая - из боковых). Упрощая ситуацию, можно сказать, что при В < 0 частицы стремятся расположиться в одной подсистеме минимумов, а при Ва > 0 - по разным. Параметр Аа характеризует взаимодействие между частицами, находящимися в боковых ямах. Так, если А < 0, то частицы стремятся расположиться в боковых ямах одного типа (т.е. находящихся с одной стороны от центральной), а если А > 0, то - в разных.а

Система уравнений состояния

, (7)

имеет два типа решений: 1. (?,? = 0) - пр. гр. D4h; 2. (?, ?) - пр. гр.C4v.

Показано, что в случае одного ПП в области ? > 0, B < 0 в кристаллах, описываемых этими моделями, наблюдаются следующие особенности термодинамического поведения:а

1. В отсутствие фазовых переходов могут наблюдаться максимумы на температурных зависимостях ряда физических характеристик, в частности упругой податливости ?? и избыточной теплоёмкости Ср (рис. 8).

2. Появляются состояния, в которых при Т ~ 0 оказываются частично заполнены КЭП с более высокой энергией, то есть возбуждённые состояния.а

3. В симметричной фазе имеют место изоструктурные фазовые переходы двух типов: когда фазовый переход происходит между фазами, параметры порядка которых принадлежат одной ветви решений системы уравнений состояния, и фазовый переход между фазами, параметры порядка которых принадлежат разным ветвям системы уравнений состояния. Фазовый переход первого типа связан с появлением локальной неустойчивости у каждой из фаз. Фазовый переход второго типа связан с потерей устойчивости лишь одной из фаз. Другая остаётся устойчивой во всём температурном интервале.а

В случае двух ПП в области ? > 0, B > 0, А < 0 для k = 0.4 (k = B/?) при

0 < s < 1.207 (s = -A/?), несмотря на то, что А < 0 ФП не происходит и ПП ? не появляется. Хотя в области s < ~ 1.207 наблюдаются хорошо заметные аномалии восприимчивости по ПП ? (рис. 9). Ва областиа 1.207 < s < 1.8 СУС (7) имеет только одно решение (?,?)1, ответвляющееся от решения (?,0) в двух точках. Фаза (?,?)1 возникает вследствие ФП второго рода (ФП2) из симметричной и существует в ограниченном интервале температур. Затем снова посредством ФП2 происходит возврат в симметричную фазу, которая остаётся устойчивой при Т ~ 0.

Показано, что при s = 1+ 2k = 1.8 (k = 0.4) в СУС появляется вторая ветвь решений - (?,?)2, возникающая в точке ?= -1,а ?= 1 при Т= 0. В области 1.8 < s ? 2 с ростом s ветви решений (?,?) сближаются, область сосуществования фаз (?,?)1 и (?,?)2 расширяется, а разница между ТП этих фаз уменьшается. Однако фаза (?,?)2 так и остаётся метастабильной, а последовательность упорядочений остаётся той же, что была раньше.

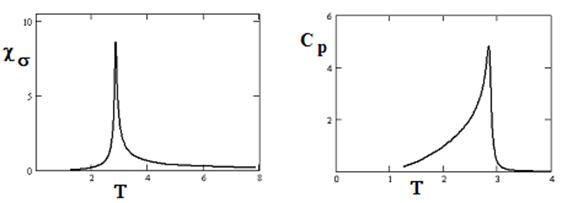
Рисунок 8 - Зависимости от температуры в отсутствие ФП податливости ??а относительно деформации по оси z и избыточной теплоёмкости Ср

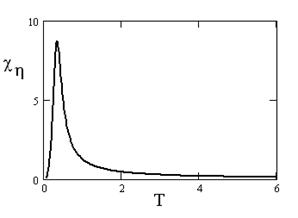
Рисунок 9 - аТемпературная зависимость восприимчивости а??

при k = 0.4, s = 1.15

При s > ~ 2 обе ветви решений смыкаются и уже при s = 2.002 расположение ветвей коренным образом меняется. Теперь каждая из них ответвляется от ветви, описывающей симметричную фазу, и заканчивается в областиа Т ~ 0 при ? ~ 1, одна в точке ? = -1 - первая ветвь, другая в точке ? > 0 - вторая ветвь. При s > 2 реализуется следующая последовательность упорядочений: при высоких Т устойчива фаза (?,0), затем происходит ФП 2 в фазу (?,?). Эта упорядоченная фаза остаётся устойчивой и при Т ~ 0, где ? ~ -1,а ? ~ 1. Именно такой сценарий обычно реализуется в простых многоминимумных моделях.

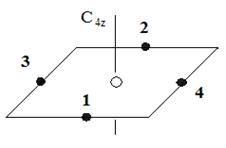
В подразделе 4.2 исследованы свойства 1 + 4-мин. модели [A12]. Рассматривается модель, состоящая из двух подсистем минимумов - центрального и четырёх одинаковых боковых (1+4-мин.). Расположение минимумов приведено на рис. 10.

а аа

Рисунок 10 - Расположение и нумерация минимумов в 1 + 4-мин. модели.

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 |

     Авторефераты по всем темам  >>  Авторефераты по математике