Geum.ru

Технология личностно-ориентированного обучения

Вид материалаУрок
Подобный материал:
Технология личностно-ориентированного обучения.

(Из опыта работы Сыркиной Е.Н., учителя математики МОУ «Вертикосская СОШ»)


«Здравствуйте, ребята. Сегодня на уроке …» И в этот момент несколько пар глаз с любопытством устремляются на меня. Эти ребята хотят знать, чем сегодня будут заниматься на уроке, им интересно, что нового они сегодня узнают. У таких детей высокая познавательная активность, жажда знаний. Но я вижу и другие глаза. Они безучастны ко всему, что происходит в классе. Такие ученики, в лучшем случае, тихонько сидят на уроке и очень хотят, чтобы их не беспокоили никакими премудростями. Ещё три года назад, наблюдая такую картину, я задавала себе извечный вопрос: «Что делать?» Что мне, учителю, нужно сделать, чтоб пробудить интерес к предмету у таких учеников (как правило, это слабоуспевающие ученики), развить их творческие возможности, но при этом не дать остановиться в своем развитии более способным детям? И еще не найдя ответа на поставленный вопрос, передо мной уже возникал другой, более сложный вопрос «Как это сделать?»

Часто учитель просто записывает тему урока и сразу начинает объяснение. Конечно, такой прием не возбуждает у учащихся ни интереса, ни желания познать новое. Я понимала, что формирование познавательной активности возможно при условии, что деятельность, которой занимается ученик, ему интересна. Учащимися совсем по-другому воспринимается цель урока, когда они сами убеждаются в необходимости изучения темы, сами становятся исследователями той или иной проблемы.

Изучая опыт других педагогов, знакомясь с современными педагогическими технологиями, я пыталась найти ответы на мучившие меня вопросы. И среди многочисленных педагогических приемов и технологий мною была выделена и апробирована технология личностно–ориентированного обучения, целью которого является не столько сообщение конкретных знаний (их усвоение, воспроизведение), сколько опора на сложившиеся у школьников способы учебной работы, обеспечивающие им самостоятельность в познании, т.е. умение учиться.

В отличие от традиционной дидактической системы, где центральной фигурой процесса обучения выступает учитель, в центре процесса личностно-ориентированного обучения становится ученик, признается высшая самоценность личности ребенка. Соответственно меняется и роль самого учителя. Учитель управляет познавательной деятельностью ученика, т.е. переходит с позиции носителя знаний (дающего знания) в позицию организатора собственно познавательной деятельности учащихся.

Приведу в качестве примеров уроки, которые по оценке моих учеников, нравятся им больше всего и повторения которых они просят. Вначале представлю опыт проведения спаренного урока в 6 классе по теме «Длина окружности», целиком посвященного изучению нового материала. Урок начинаю с того, что ученикам предлагаю решить задачу по данной теме за 9 класс и, демонстративно показывая учебник «Геометрия 7-9», зачитываю её условие. Ребята в недоумении. И вот звучит вопрос, который я так жду.

- А разве мы сможем решить такую задачу?

- А что мешает вам это сделать? – отвечаю я вопросом на вопрос.

- Так это задача за 9 класс, - настаивают ученики.

- К концу урока вы сможете решить эту задачу, и не только её, - твердо отвечаю я им.

И после недолгой дискуссии, приходим к выводу: нужен либо способ, либо формула для вычисления длины окружности. После чего учеников прошу письменно ответить на вопросы «Что я знаю?» и «Что я хочу узнать» по теме «Окружность». Считаю, этот этап урока очень важным с позиции повторения материала и постановки цели урока.

Конечно, можно было традиционно самой объяснить ученикам новую тему или дать детям для самостоятельного ее изучения. Выбор остановился на практической работе. Дети получали удовольствие, выполняя эту работу. В тетради каждому ученику нужно было начертить окружность, измерить ее диаметр, при помощи нитки и линейки найти длину этой окружности и вычислить отношение длины окружности к ее диаметру (все измерения заносились в таблицу). Когда же ребята сравнили полученные результаты (у всех получилось приблизительно одно и то же число), то поначалу они были очень сильно удивлены («Как такое может быть, если окружности у всех разные?»). Их изумление сменилось восторгом открытия после моего рассказа о том, что число это называют числом π, и открыл его Архимед. Вывод формулы был теперь делом техники и не вызвал у ребят никаких затруднений, как и решение задачи, с которой начался урок. Ребята потом с гордостью делились с родителями, тем, что умеют решать задачи за 9 класс.

Во второй части занятия я предложила ребятам разбиться на группы по интересам: «Знатоки числа π», «Архимед и число π», « Генераторы задач» и творческая группа с целью детального изучения нового материала. Для подготовки 1 и 2 группе были предложены книги, в которых можно были найти ответы на заданную тему. «Генераторы задач» в учебниках разных авторов отбирали задачи, интересные для решения. Творческой группе предстояло сочинить стихотворение, способствующее запоминанию и пониманию формулы. На подготовку отводилось 15 минут. В оставшееся время ребята делились самостоятельно полученными знаниями, решали задачи. На уроке получился равноправный диалог, где каждый ученик смог высказать свое мнение по обсуждаемой теме, не боясь ошибиться.

Продуктивно проходят уроки по закреплению и повторению изученного материала. В классе создаю две- три группы учащихся по 4-5 человек в каждой. Предлагаю им исходя их теоретического содержания и решавшихся на уроках задач, подобрать новые задачи для составления контрольной работы по данной теме. Это является их домашним заданием. На уроке они не только должны презентовать, но и защитить свой вариант контрольной, т.е. объяснить, почему ими выбраны именно эти вопросы и какие знания с их помощью проверяют, какова связь задач с пройденным ранее материалом, каков их уровень трудности. После обсуждения предложенных вариантов, которое всегда проходит очень заинтересованно и горячо, ребята помогают классу решить составленные ими задачи, а я лишь отмечаю типичность каждой и корректирую работу. При этом все знают, что итоговый вариант контрольной работы будет составлен мною с учетом проведенной накануне работы.

Опираясь на инициативу школьников, провожу и урок – праздник знаний. Это обобщающий урок по теме или разделу. Детей к нему готовлю заранее. Каждый ученик самостоятельно выбирает себе дело по желанию. Это могут быть сообщения на пройденную тему, рассказ о научном открытии, экскурс в историю, интересная задача с решением, изготовление модели и т.д. За два дня до урока ученики сообщают мне, что ими готовится (это дает возможность заранее спланировать урок). Но то, что готовит каждый школьник, держится в тайне, и это интригует его одноклассников.

В качестве примера приведу заключительный урок по теме «Теорема Пифагора». Перед началом урока ко мне подошел ученик, которому трудно давалась математика. Им были подготовлены к уроку афоризмы о теореме Пифагора. Я попросила его выписать на доску то изречение, которое понравилось ему больше всего. И урок начался с того, что этим учеником были зачитаны афоризмы по данной теме. Они стали своеобразным эпиграфом к уроку и создали положительный эмоциональный настрой на урок. Галя Сабельфельд подготовила легенды, связанные с именем Пифагора. Одноклассники слушали её, затаив дыхание. Лемешев Павел удивил всех ребят сообщением о том, что теорему Пифагора называют ещё и теоремой невесты, дав этому объяснение. Васютин Паша сформулировал теорему, так, как она звучала во времена Пифагора. Он же заметил, что существует более ста доказательств теоремы и привел одно из них. Оживили урок и рисунки учеников, выполненные на знаменитое высказывание «Пифагоровы штаны во все стороны равны», и пифагоровы головоломки, придуманные детьми. Группа девочек показала практическое применение теоремы Пифагора. Открытием для меня и моих учеников стали «Золотые стихи» Пифагора, подготовленные Чичириной Машей. Получился поистине праздник знаний, творчества и открытий. Дети стремились поделиться друг с другом своими находками. Они чувствовали, что в классе собрались единомышленники, и что урок – их собственное творение. И в этом – одна из главных заслуг такого урока.

Полюбился детям и урок - математический аукцион, и урок - математический банк знаний, и урок защиты ученических проектов.

Так как педагог должен растить ученика, вести его вперед, то для личностно-ориентированных уроков необходимо иметь и наборы индивидуальных карточек-заданий, позволяющих ученику самостоятельно выбирать наиболее значимые для него задания учебного материала. Расскажу более подробно о карточках, которые составлены мною для изучения раздела «Умножение и деление обыкновенных дробей», 6 класс. Принцип работы заключается в том, что каждый ученик должен набрать в сумме 50 баллов за время прохождения всех тем раздела (при этом обязательно оговариваю сроки). Выбор заданий остается за учеником. Карточки раздаю на первом уроке изучения данного раздела.

Все задания поделены на 4 основные блока. I блок «Теория» включает в себя весь спектр вопросов по теоретическому содержанию изучаемого раздела. Например, такие: «Сформулируйте правило нахождения дроби от числа» или «Как выполняется деление смешанных чисел?». В каждой карточке 12 вопросов. Так как задания этого блока носят репродуктивный характер, то ответ на вопрос оценивается в 1 балл. Ответив правильно на все вопросы, ученик соответственно набирает 12 баллов.

II блок «Решение задач» состоит из логически-поисковых задач, решив которые, ученик может набрать 40 баллов. Заданий этого блока также 12, и каждое из них имеет свой уровень сложности. А поэтому любой ученик сможет найти себе задачи «по вкусу». Верное решение задачи: «Из 100 бумажных салфеток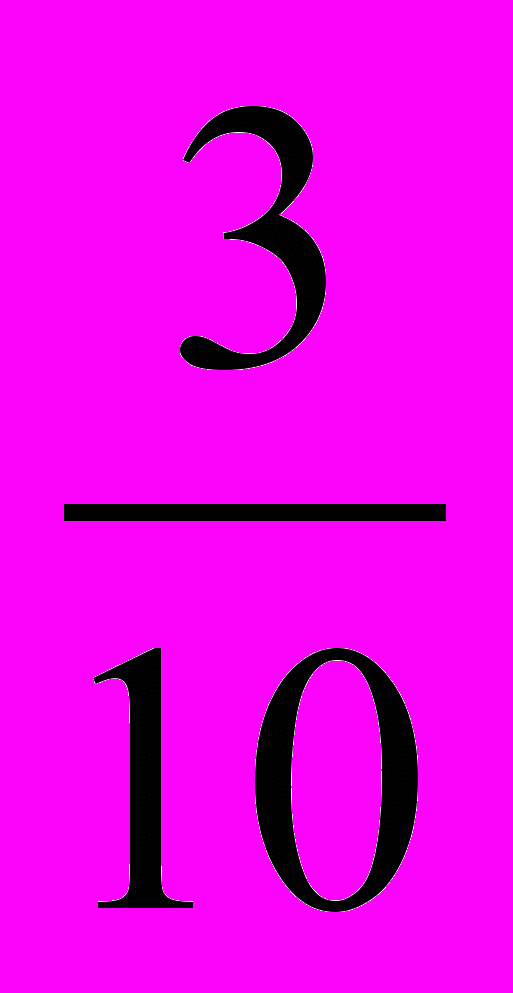остались неиспользованными. Сколько салфеток использовали?» принесет в копилку ученика 2 балла, а задание № 644 учебника Н.Я. Виленкина «Математика – 6» - 6 баллов. Помимо задач, примеров, уравнений в этом блоке учащимся предлагается решить тест, который содержит задания по всем темам изучаемого раздела (12 баллов).

Школьникам, которые любят «поломать» голову над решением сложных задач, предложен III блок «Задачи повышенной сложности», включающий только одну задачу (20 баллов). Например: «Мама дала своим детям конфеты: дочери половину всех конфет и ещё одну конфету, сыну половину остатка и ещё 5 конфет. Сколько всего конфет мама дала детям?». «Сильные» ученики успешно справляются с решением таких задач. Каково же было однажды мое удивление, когда я узнала, что родители, заинтригованные условием задач, предлагали решить их своим родственникам и коллегам по работе.

Название IV блока «Творческие задания» говорит само за себя. Дети всегда активны в создании чего-то нового и задания этого блока дают возможность раскрыть их творческий потенциал. Замечу, что не нашлось ни одного ученика, который бы не выбрал творческое задание IV блока (по условию можно было сделать только одно задание, на выбор самого ученика). Дети составляли кроссворды (5 баллов), придумывали ребусы (5 баллов), писали книжки-шпаргалки (10 балов), а одна из мох учениц разработала урок-игру «Все действия с дробями» (20 баллов). На заключительном уроке была организована выставка. Если бы видели, какая коллекция детских работ получилась!

Особенно важны итоги работы с индивидуальными карточками:
  • Все ученики оказались вовлечены в учебную деятельность, т.к. у них появилась возможность проявить индивидуальную избирательность в работе с учебным материалом.
  • Созданы условия ситуации успеха: ученик начинает верить в собственные силы, справляясь с самостоятельно выбранными заданиями.
  • Созданы условия для опережающего обучения: некоторые из ребят не дожидаются прохождения нового материала, а самостоятельно его изучают. Затем эти учащиеся выступают в роли консультантов.

Лучшим подтверждением того, что личностно-ориентированное обучение можно и нужно практиковать, служат результаты регионального тестирования в тех классах, где применялась данная технология. Так, 6 класс, в котором преподавание было полностью построено на личностно-ориентированном обучении, показал 100% количественной и 64% качественной успеваемости.

К сожалению, в рамках одной статьи невозможно наиболее полно раскрыть все возможности данной технологии. Конечно, при всем многообразии форм уроков и обучения математике было бы опрометчиво навязывать коллегам какую-то одну методику. Хотелось бы подчеркнуть, что преимущество лично-ориентированного обучения состоит ещё и в том, что она включает в себя компетентностый и деятельностный подходы, индивидуализацию и дифференциацию обучения. Выбор, уважаемые коллеги, за вами.