Лекция Анализ данных опыта. Статистические показатели
| Вид материала | Лекция |
- Статистические методы и анализ данных, 190.46kb.
- Программа дисциплины «Методы анализа латентных признаков» для направления 040200., 268.76kb.
- I. Статистические показатели по работе с молодёжью в публичных библиотеках, 1471.37kb.
- Точные науки: математика, физика, химия, 1341.72kb.
- Задачи и виды группировок Статистические ряды распределения Абсолютные показатели, 18.57kb.
- 1352. 08. 02;LS. 01, 19.55kb.
- 2. 2 Производительность труда, 266.71kb.
- Курс лекций "Базы данных и субд" Ульянов В. С. Лекция. Манипулирование реляционными, 276.31kb.
- Лекция на тему: Основы организации баз данных, 393.78kb.
- Анализ и оценка дисциплин обслуживания требований (запросов) с учетом их приоритетов, 20.53kb.
Лекция 3. Анализ данных опыта. Статистические показатели.
Резюме по методам расчета страховых тарифов.
Первая методика расчета основана на концепции постоянной вероятности страхового случая и количестве договоров страхования. Применяется для новых видов страхования, по которым страховая компания еще не имеет репрезентативной статистики и количество договоров сравнительно невелико. В этом случае ширина профиля риска определяется ожидаемым числом страховых случаев.
Вторая методика применяется для массовых видов страхования, где число договоров велико и имеется репрезентативная статистика за ряд лет. Ширина профиля риска обусловлена в этом случае изменчивостью частоты страховых случаев от квартала к кварталу, от года к году. В основе этой методики лежат статистические данные по убыточности страховой суммы.
Понятие тарифа как взноса с единицы страховой суммы имеет ограниченное применение при расчете страховых взносов. Оно используется в личном страховании (НС, жизнь) и в имущественном страховании, т.е. там, где можно ввести страховую сумму как оценку стоимости застрахованного объекта. Если же мы имеем дело с видами страхования, где страховую сумму ввести трудно или вообще невозможно, то производится расчет не тарифных ставок, а непосредственно взносов (МС, путешественники, страхование ответственности).
Пример 1. Страховые выплаты компании по добровольному медицинскому страхованию корпоративных клиентов за год составили 3 млрд. руб. Количество застрахованных составляло 1 млн. Величина страхового нетто-взноса с каждого застрахованного принимается равной суммарной выплате в расчете на одного застрахованного: z=3000 млн.руб./1000000 =3 тыс. руб.
Пример 2. Страховые выплаты компании по ОСАГО за год составили 150 млн. руб. Среднее количество договоров, действовавших в течение года, 150 тысяч. Коэффициент вариации уровня страховых выплат в расчете на один договор страхования составляет: V=0,1. Страховая выплата в расчете на один договор составляет: z=150 млн.руб./150000=1 тыс.руб. Эта величина определяет основную часть нетто-взноса. Размер всего нетто-взноса определяется с учетом рисковой надбавки формулой:
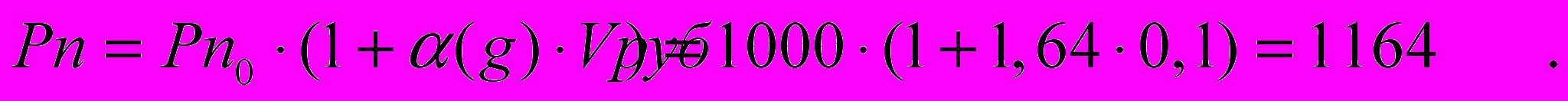
При расчетах мы определили уровень гарантии безопасности g=0,95, α=1,64.
Определение используемых в расчете величин из данных опыта является весьма непростой самостоятельной задачей. Начнем с определения частости страховых случаев, равной отношению числа страховых случаев за период (например, год) к количеству договоров, действовавших в этом периоде. Проблема заключается в том, что часть договоров, действовавших на начало периода, прекращает свое действие до конца периода, а часть договоров будет заключена в течение периода. Чтобы адекватно оценить эффективное число действующих договоров, вводится понятие экспозиции риску (подверженность риску). Полисы, находящиеся под риском в течение той или иной части года, дают вклад в экспозицию, пропорциональный времени нахождения полисов под риском.
Пример (см. табл.1).
| ^ Экспозиция риску, эффективная страховая сумма. | |||||
| | | | | | Таблица 1 |
| Квартал | Число заключенных в начале квартала договоров | Страховая сумма договора | Число действующих договоров на конец квартала | Экспозиция риску | Эффективная совокупная страховая сумма |
| 1 | 100 | 1 | 100 | 100 | 100 |
| 2 | 200 | 2 | 300 | 150 | 300 |
| 3 | 100 | 3 | 400 | 50 | 150 |
| 4 | 100 | 4 | 500 | 25 | 100 |
| | | | | 325 | 650 |
Как видно из табл.1, экспозиция риску составляет 325 полисолет. Если количество страховых случаев за год равно 10, то годовая частость равна
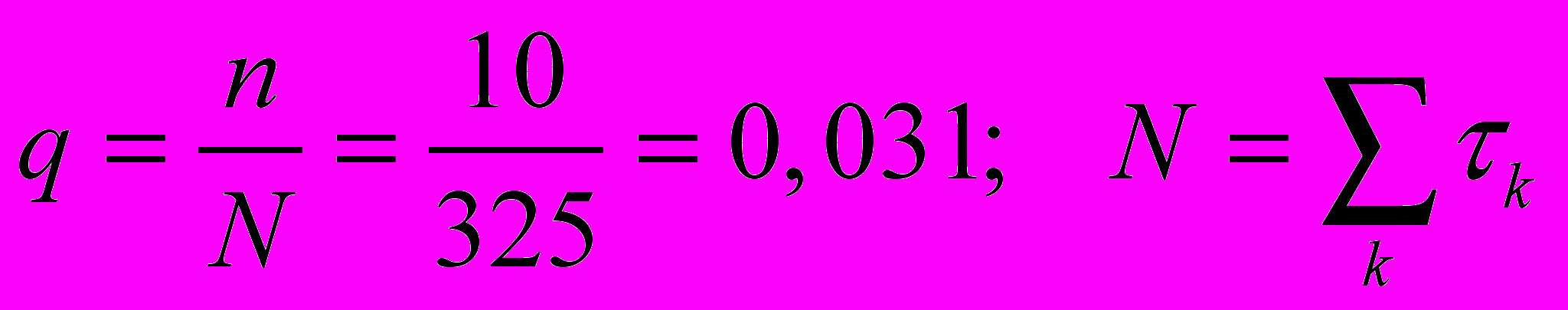
где
–экспозиция риску k-го договора (полиса).Убыточность страховой суммы определяется как отношение убытков за период к совокупной страховой сумме договоров, действующих в течение периода. С учетом экспозиции риску следует ввести понятие эффективной совокупной страховой суммы, равной сумме по всем договорам страховых сумм, умноженных на экспозицию риску каждого договора
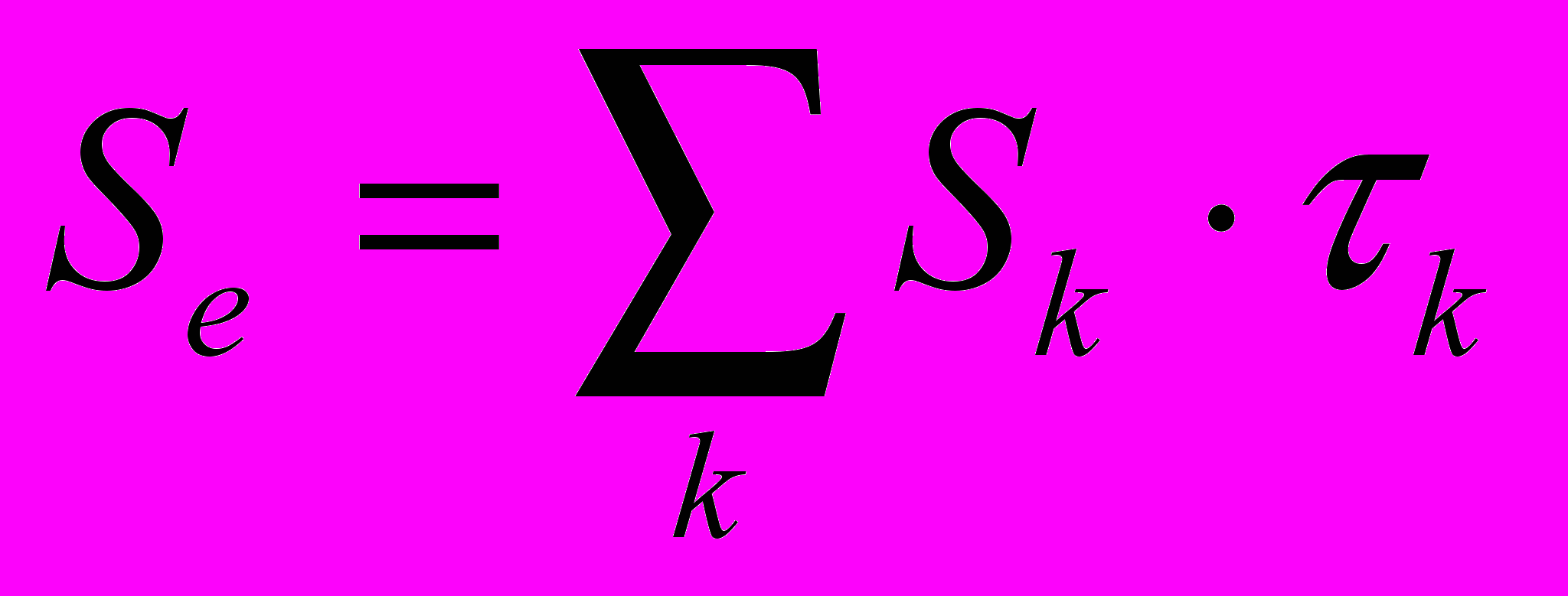
Как видно из табл.1, эффективная совокупная страховая сумма по портфелю договоров равна 650 млн.руб. Если сумма убытков за год составила Z=10 млн.руб., то убыточность страховой сумму равна
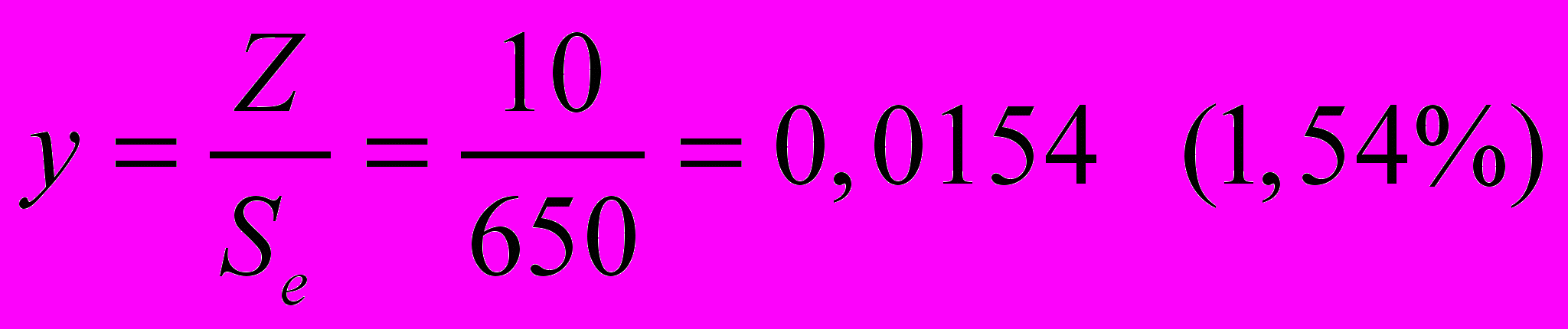
При оценке суммы убытков за период (год) следует учитывать тот факт, что страховые выплаты по страховым случаям данного периода могут происходить и за пределами данного периода (с запаздыванием), поэтому их следует относить не к моменту выплаты, а к моменту наступления страхового случая (allocation, аллокация убытков).
В заключение хочется отметить, что никакие самые точные расчеты не гарантируют того, что фактические выплаты совпадут с предсказанными – мы имеем дело со случайными процессами, а случаем человек не управляет (хотя и очень к этому стремится, создавая науку «риск-менеджмент»). Поэтому важнейшая роль в оперативной деятельности страховой компании отводится мониторингу уровня страховых выплат и принятию решений об изменении тарифов (тарифная политика).
Лекция 4. Основы экономики страхования и страховые резервы.
Особенностью экономики страхования является то обстоятельство, что основную часть расходов при проведении страхования составляют страховые выплаты. Поскольку страховые выплаты являются случайной величиной, их ожидаемое значение оценивается актуарными методами. Таким образом, сфера интересов актуариев включает в себя и вопросы экономики, вплоть до оценки и моделирования ожидаемой прибыли по страховой компании (profit testing). Естественно, что и расходы, связанные с проведением страхования, хотя они и меньше по величине, но должны приниматься во внимание.
Часть страховой премии, равная ожидаемой стоимости страховых выплат, называется нетто-премией. Нетто- премия предназначена для покрытия страховых выплат. Для покрытия издержек страхования сверх нетто-премии взимается еще дополнительная премия, называемая нагрузкой. Сумма нетто-премии и нагрузки называют брутто-премией (Gross Premium). В нагрузке различают расходы на ведение дела, включающие в себя комиссию агентам за продажу полисов, и расходы на превентивные мероприятия для предотвращения страховых случаев. Примерная структура брутто-премии (структура тарифной ставки) имеет следующий вид
| Нетто-ставка, fn x100% | Расходы на ведение дела | Расходы на превентивные мероприятия, fpx100% | |
| Административные расходы, fax100% | Комиссия fcx100% | ||
| 70 | 7 | 15 | 8 |
Предполагается, что вся брутто-премия будет потрачена согласно структуре тарифной ставки и прибыль от страхования будет равна нулю («принцип нуля»). Тогда единственный источник дохода – это инвестиционный доход от инвестирования активов. В действительности имеет место еще и доход от страховой деятельности (за счет того, что фактический уровень выплат меньше нетто-премии) и от экономии на расходах. Совокупность источников прибыли дает структуру прибыли.
Инверсный цикл в экономике страхования.
В обычном цикле сначала производитель несет издержки по производству продукта, затем продукт продается, издержки покрываются, формируется прибыль как превышение доходов над расходами. В страховании продукт сначала продается, а затем в течение срока действия договора происходят страховые выплаты и расходуются средства на ведение страховой деятельности. Поступивший при продаже доход нельзя считать прибылью, эти средства следует зарезервировать для осуществления будущих выплат и расходов. Поэтому основополагающую роль в экономике страхования играют страховые резервы.
Если бы все договора страхования начинались в начале года и заканчивались в конце года, то оценка прибыли за год была бы очень простой. Но ситуация иная: договоры заключаются непрерывно в течение года и срок их действия не всегда равен году. Следует различать календарный год, начинающийся 1 января, и страховой год, начинающийся в момент начала договора. Для каждого договора – своя шкала времени (от начала до конца договора). Результаты деятельности страховой компании оценивают на конец календарного года, промежуточные отчеты – на конец каждого календарного квартала. Поэтому нужно уметь оценивать результат от законченных договоров, действовавших неполную часть года (квартала), от договоров, начавшихся в течение года (квартала), а также и от договоров, не закончивших свое действие в конце года (квартала). Для проведения таких оценок принимается гипотеза о равномерности риска: если убытки за год равны 12 единицам, то убытки за квартал – 3 единицам, за месяц – 1 единице (сезонное распределение риска учитывается при более детальном анализе и требует специального исследования).
Для оценки той части страховой премии, которая может рассматриваться как доход данного периода, по каждому договору вводится понятие заработанной премии. Согласно терминологии МАСН (Международной Ассоциации Страховых Надзоров) заработанная премия (Earned Premium) - премия, в обмен на которую предоставляется страховая защита. Когда премия уплачивается заранее за весь период действия полиса T, компания «зарабатывает» эту премию только по частям по мере того, как истекает время этого периода t:
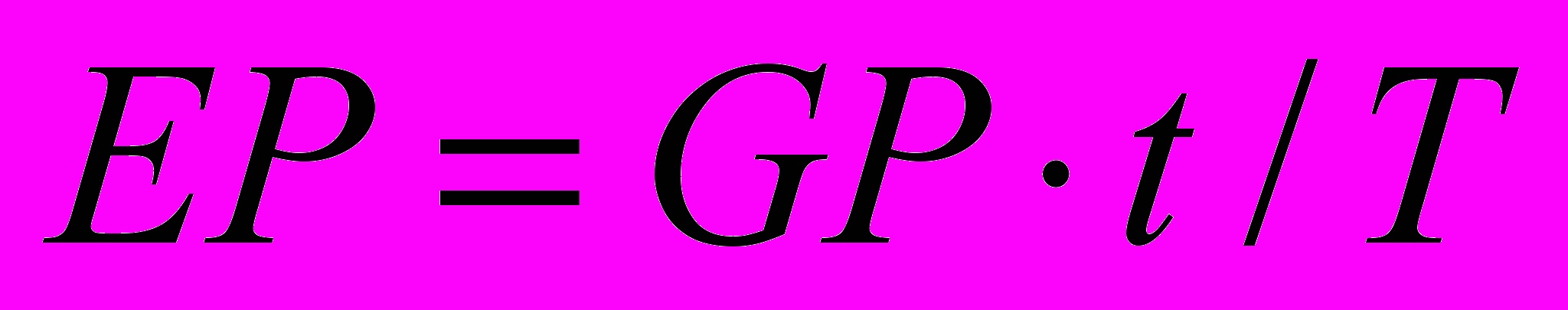
Оставшаяся часть премии называют незаработанной премией (Unearned Premium), или резервом незаработанной премии (РНП):
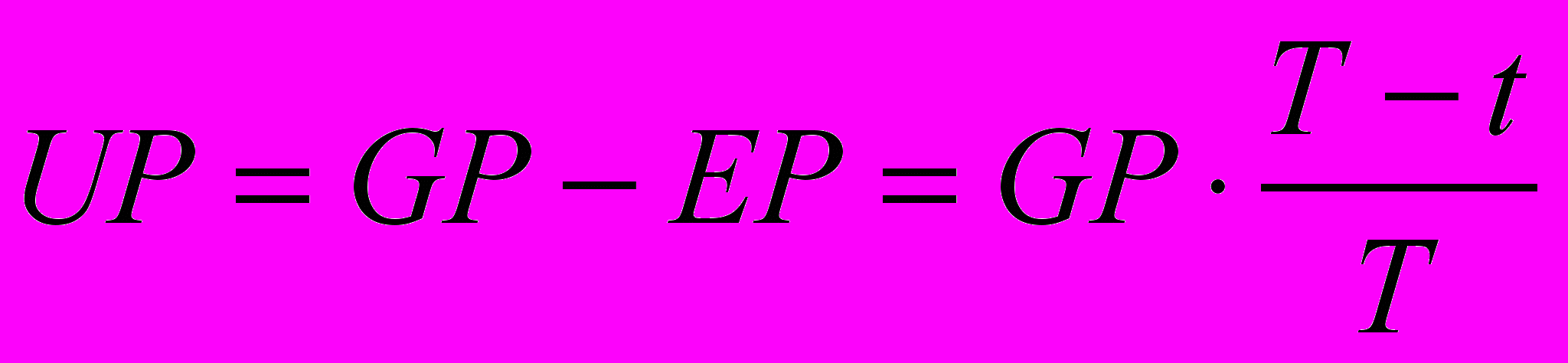
Сам термин незаработанная премия свидетельствует о том, что эту часть денежных поступлений страховой организации нельзя считать прибылью на отчетную дату, поскольку средства эти еще необходимы для выполнения обязательств по осуществлению будущих выплат и будущих расходов по обеспечению страховой деятельности.
В отличие от приведенного выше определения в России принят несколько иной способ определения незаработанной премии, исходя из так называемой базовой страховой премии. Под базовой страховой премией по договору страхования понимается начисленная страховая брутто-премия по договору страхования, уменьшенная на сумму начисленного вознаграждения за заключение договора страхования и отчислений от страховой брутто-премии , предусмотренных действующим законодательством (в частности на финансирование предупредительных мероприятий):
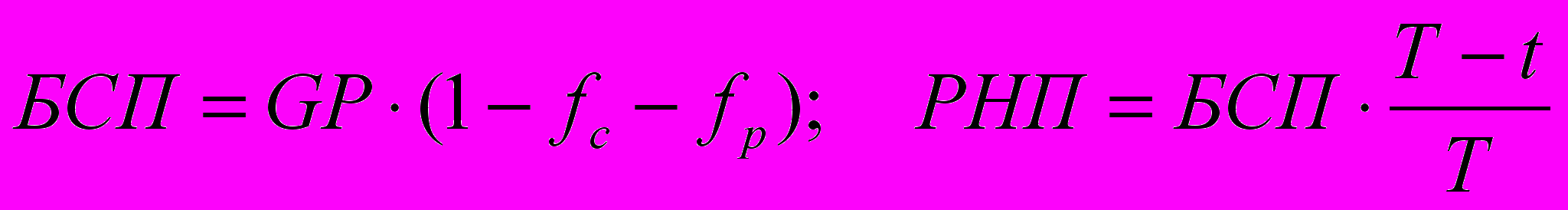
В страховании жизни эту величину называют еще инвентарной премией (Германия, Швейцария), имея в виду, что только эта часть премии остается в страховой компании для обеспечения будущих страховых выплат и расходов по осуществлению страховых операций.
Заработанная премия определяется как разность между брутто-премией и незаработанной премией:
Методы расчета РНП: p.r.t/, 1/8, 1/24.
Метод «pro rata temporis».
В этом методе время в формуле измеряется в днях. Предполагается, что ответственность по договору начинается в 00 часов даты начала договора и оканчивается в 24 часа даты окончания договора. Значение резерва на отчетную дату определяется на 00 часов отчетной даты (01.01, 01.04, 01.07, 01.10).
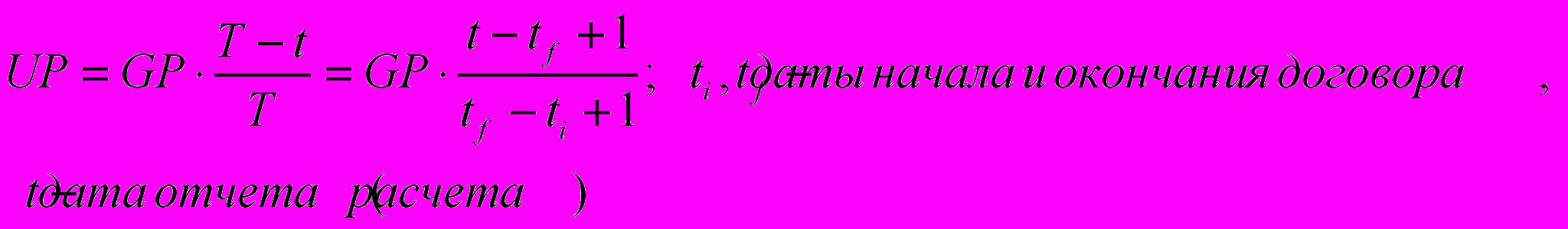
Для России следует заменить в формуле GP на БСП.
Пример. Период действия договора страхования – с 5 марта по 4 мая включительно. Начисленная по договору премия равна 15 млн. руб. Доля комиссионного вознаграждения составляет 15%, доля отчислений в фонд превентивных мероприятий – 8% (
).Определить резерв незаработанной премии на отчетную дату 1 апреля.
Срок действия договора исчисляется с 00 часов 5 марта по 24 часа 4 мая – всего 27+30+4=61 день.
Остаточный срок исчисляется с 00 часов 1 апреля по 24 часа 4 мая – всего 30+4=34 дня.
Базовая страховая премия равна: БСП=15 000 000*(1-0,15-0,08)=11 550 000 руб.
РНП=БСП*34/61 =6 437 705 руб.
Модифицированный метод «pro rata temporis».
Предлагаемые министерством финансов РФ методы расчета резерва незаработанной премии методами «1/24» и «1/8» неоправданно усложнены. Группировка договоров с различным сроком действия и различными датами начала договоров по подгруппам, с последующим умножением суммарной базовой премии на множитель из довольно объемистой таблицы представляет собой довольно громоздкую программу. Кроме того, формирование всякого рода промежуточных таблиц, совершенно необязательных для получения конечного результата, существенно увеличивает объем бумажной информации. Между тем методы «1/24» и «1/8» по своему духу являются методами типа «pro rata temporis», но время в них измеряется не в днях, а в полумесяцах или полукварталах /Кутуков/. По этой причине предлагается производить расчет резерва незаработанной премии для этих методов таким же образом, как и для метода «pro rata temporis», с той только разницей, что даты начала и продолжительность договора будут расчетные, а не фактические.
Для метода «1/24» расчетная дата начала договора всегда будет отнесена к середине месяца начала договора, а расчетный срок действия договора будет равняться ближайшему большему целому числу месяцев. Тогда расчетная дата окончания договора будет отнесена к середине месяца, отстоящего на это целое число месяцев (расчетное!) от начала договора. Так например, если договор заключен 3 марта, а заканчивается 10 апреля, то расчетный срок начала договора будет 15 марта, расчетный срок действия договора – 2 месяца, расчетная дата окончания договора – 15 мая. Если отчетная дата –31 марта, то в соответствии с методом «pro rata temporis» РНП составит ¾ от базовой страховой премии. Расчет по таблицам Минфина дает такой же результат.
Для метода «1/8» расчетная дата начала договора всегда будет отнесена к середине квартала начала договора, а расчетный срок действия договора будет равняться ближайшему большему целому числу кварталов. Тогда расчетная дата окончания договора будет отнесена к середине квартала, отстоящего на это целое число кварталов (расчетное!) от начала договора. Так например, если договор заключен 3 марта, а заканчивается 10 апреля, то расчетный срок начала договора будет 15 февраля, расчетный срок действия договора – 1 квартал, расчетная дата окончания договора – 15 мая. Если отчетная дата –31 марта, то в соответствии с методом «pro rata temporis» РНП составит ½ от базовой страховой премии. Расчет по таблицам Минфина дает такой же результат.
Предложенный модифицированный метод «pro rata temporis» для расчета резерва незаработанной премии дает возможность единым образом производить расчеты для всех трех методов, что существенно упрощает работу с базами договоров.
^ РЕЗЕРВ УБЫТКОВ.
Специфической особенностью страховой деятельности является большой объем незаконченных договоров страхования, премия по которым уже поступила, а убытки еще не произошли или уже произошли, но еще не оплачены. Оценка величины первых дается резервом незаработанной премии, оценка последних дается резервом убытков.
В практике западных страховщиков урегулирование убытков занимает иногда несколько лет. Проблема поздних страховых возмещений (или проблема IBNR от английского «incured but not reported» - «произошло, но не вошло в отчет») может быть весьма существенной при оценке финансового результата от страховой деятельности. При оценке следует учитывать не стоимость выплаченных страховых возмещений на отчетную дату, а те окончательные суммы, до которых они возрастут после полного урегулирования всех претензий. Разность между этими двумя величинами и составляет резерв убытков. Резерв убытков сравним по величине с размером годовой премии, поэтому методам расчета резерва убытков уделяют большое значение.
Существует несколько методов расчета резерва убытков, однако все они используют функцию распределения времени урегулирования убытков, построенную по результатам оплаты убытков в прошлые периоды. Для оценки резерва убытков применяется подход, связанный с группировкой требований выплат по периодам происхождения страховых событий. В основе всех методов расчета лежит статистическое распределение времени урегулирования убытков, характеризуемое соответствующей функцией распределения. Функция распределения времени урегулирования убытков F(t) показывает, какая доля произошедших убытков оплачена спустя время t после наступления страхового случая. Примерный вид функции распределения времени урегулирования убытков по ОСАГО изображен на рис. 1. В приложениях чаще используется дискретный вариант функции распределения, изображенный на рис. 2. Период дискретизации выбирается равным отчетному периоду (году, кварталу), либо (для целей анализа) более коротким. В актуарной науке значения дискретной функции распределения принято называть факторами запаздывания F(t), равными доле произошедших убытков, оплаченной на конец t-го периода оплаты (развития) убытков. На рис.2, где представлена зависимость доли урегулированных убытков от времени, период равен одному месяцу. Если сумму произошедших за месяц убытков принять за 100%, то к концу этого же месяца в среднем будет оплачено 15,8% убытков, к концу второго месяца – 51,2%, к концу третьего месяца – 73,2% и т.д.
Методика расчета функции распределения по данным об оплате убытков в предыдущих периодах состоит в следующем. Идея метода заключается в том, чтобы посмотреть, как увеличивалась сумма оплаченных убытков в прошлом от одного отчетного периода к другому и принять, что эта же схема сохранится и в будущем. Описание процесса урегулирования убытка производится с помощью так называемого треугольника остаточной ответственности. Предположим, что максимальный срок для урегулирования убытков составляет N отчетных периодов (год, квартал). Страховщик располагает информацией за предшествующие N периодов, которая может быть представлена в следующей форме, известной как треугольник дополнительного срока. Для простоты будем считать период равным году, а максимальный срок для урегулирования убытков – 4 годам (N=4). В таблице 2.4.1 приведены данные о динамике оплаты убытков за предшествующие годы. Если страховые случаи произошли в 1999 г., то сумма выплат по ним (нарастающим итогом) составила: на конец 1999 г. – 51 млн.руб., на конец 2000 г. – 75 млн.руб., на конец 2001 г. – 88 млн.руб., на конец 2002 г. – 93 млн.руб.(первая строка). Считаем, что к концу 2002 г. убытки, произошедшие в 1999 году, урегулированы полностью. Поэтому на конец 2002 г. резерв убытков будут представлять не полностью оплаченные на этот момент убытки 2000, 2001 и 2002 гг. Для анализа величины неоплаченных убытков удобнее перестроить таблицу 2.4.1а в таблицу 2.4.1б, используя не календарные годы, а годы развития убытка, отсчитываемые от года события (наступления убытка).
ФР рассчитывается в 2 этапа.
1 этап. Оценка коэффициентов развития.
Если функция распределения содержит ^ N значений, меньших единицы, то вклад в резерв убытков дадут только убытки, произошедшие в N предшествующих периодов. Пронумеруем эти периоды от 1 до N, где N – номер отчетного периода. Пусть i – номер периода наступления убытков, t=N-i+1 –период развития убытка, x(i,t) - сумма убытков, оплаченных к концу t – го периода развития по страховым случаям, произошедшим в i-ом периоде , F(N-i+1) – функция распределения времени урегулирования убытков, показывает, какая доля убытков, произошедших в i-ом периоде, оплачена к концу отчетного периода
Коэффициент развития показывает, во сколько раз средняя величина убытка, оплаченного в последующем периоде развития, больше соответствующей величины в предыдущем периоде:
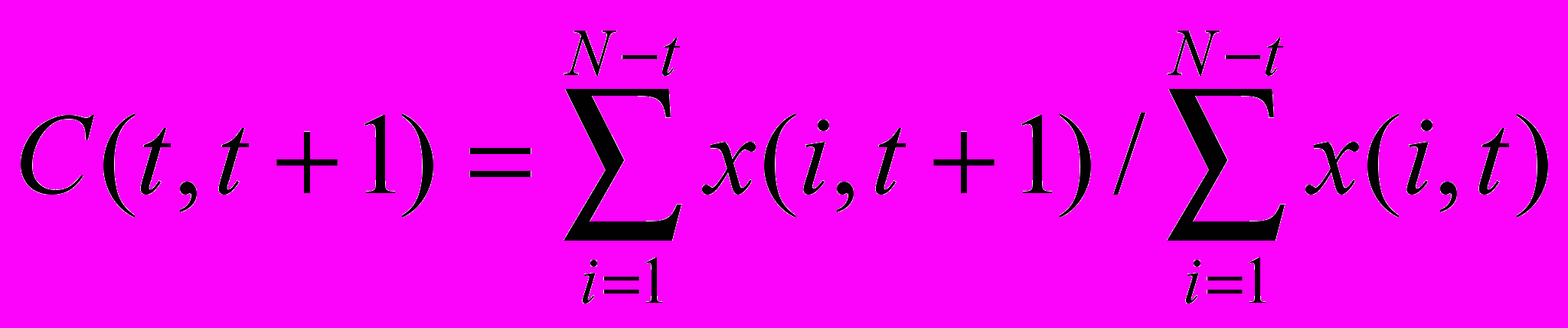
где N – число анализируемых кварталов. Для примера таблицы 2.4.1 С(1,2)=1,4
2 этап. Определяем функцию распределения (фактор запаздывания).
Она показывает, какая часть убытка урегулирована на конец t-го периода:
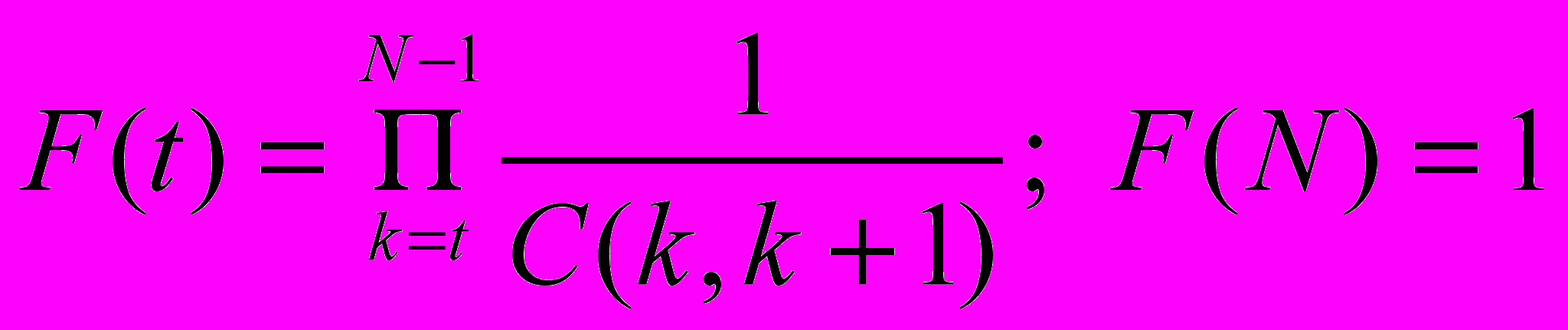
- ^ Метод цепной лестницы.
Один из наиболее простых и надежных методов оценки размера неоплаченных убытков (резерва убытков) заключается в использовании величины уже оплаченных на отчетную дату убытков. Если, например, сумма убытков, оплаченных к концу 2002 года по страховым событиям 2000 года, равна 98 тыс. руб., то полная сумма состоявшихся в 2000 году убытков будет равна 98/0,95=104 тыс. руб. Следовательно, на момент отчета резерв убытков составляет 104-98=6 тыс. руб.
Получим общую формулу для оценки резерва убытков. Если функция распределения содержит ^ N значений, меньших единицы, то вклад в резерв убытков дадут только убытки, произошедшие в N предшествующих периодов. Пронумеруем эти периоды от 1 до N, где N – номер отчетного периода. Пусть i – номер периода наступления убытков, t=N-i+1 –период развития убытка, x(i,t) - сумма убытков, оплаченных к концу t – го периода развития по страховым случаям, произошедшим в i-ом периоде , F(N-i+1) – функция распределения времени урегулирования убытков, показывает, какая доля убытков, произошедших в i-ом периоде, оплачена к концу отчетного периода. При использовании метода цепной лестницы оценка окончательного убытка производится по формуле:
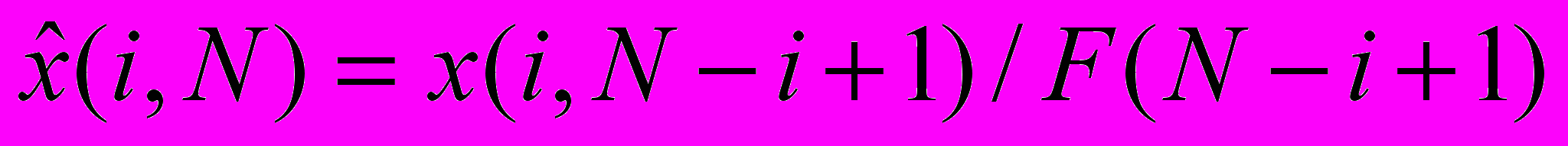
Оценка резерва убытков (^ Claims provision, CP) по страховым событиям i-го периода:
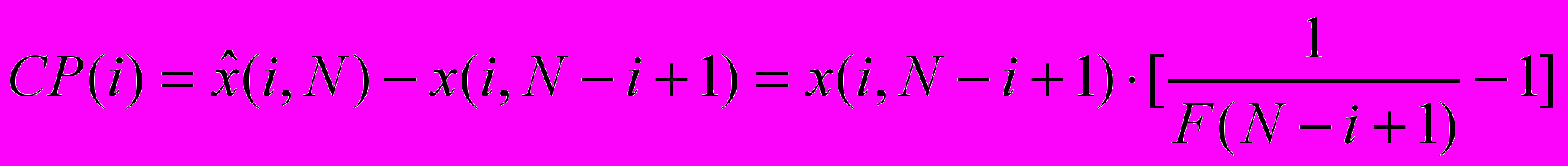
Суммируя по всем периодам событий, получим:
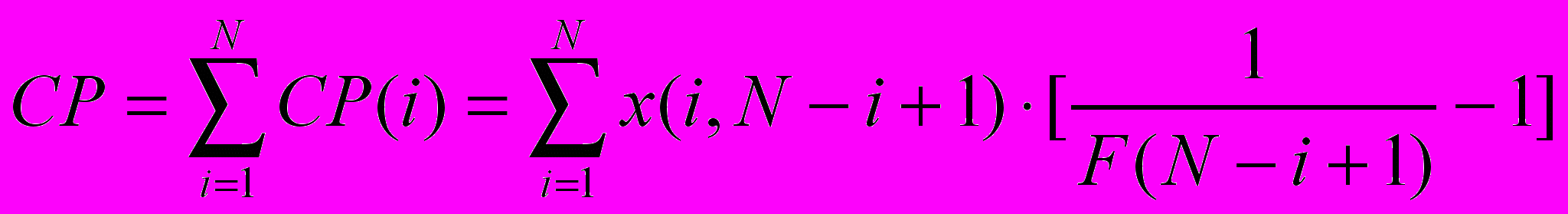
Кроме явных достоинств метода цепной лестницы, таких как простота, доступность и очевидность, у него имеется очевидный недостаток - метод не работает, когда x(1,N-i+1)=0 (т.е. когда еще ни один случай не оплачен).
В ситуации, когда оплаченная сумма убытков, произошедших в данном квартале мала по сравнению с полной суммой возмещений, вряд ли стоит брать ее за основу при оценке ожидаемого размера убытков. В этой ситуации для оценки ожидаемого размера убытков необходимо использовать дополнительную информацию о заработанной за период премии по всем действующим договорам страхования.
- ^ Метод Борнхуэттера-Фергюсона.
В этом методе основой для оценки резерва убытков является не величина оплаченных на дату отчета убытков, а оценка величины окончательного убытка
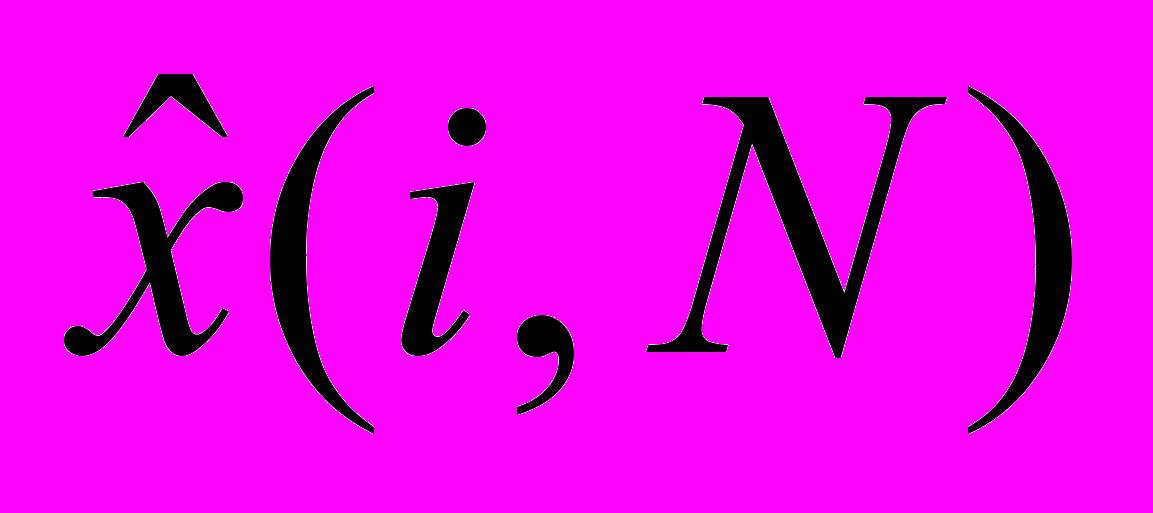, выполненная на основе данных о коэффициенте убыточности и заработанной премии.Основная финансовая характеристика– убыточность, или коэффициент убыточности (^ Loss Ratio, LR)i-го периода:
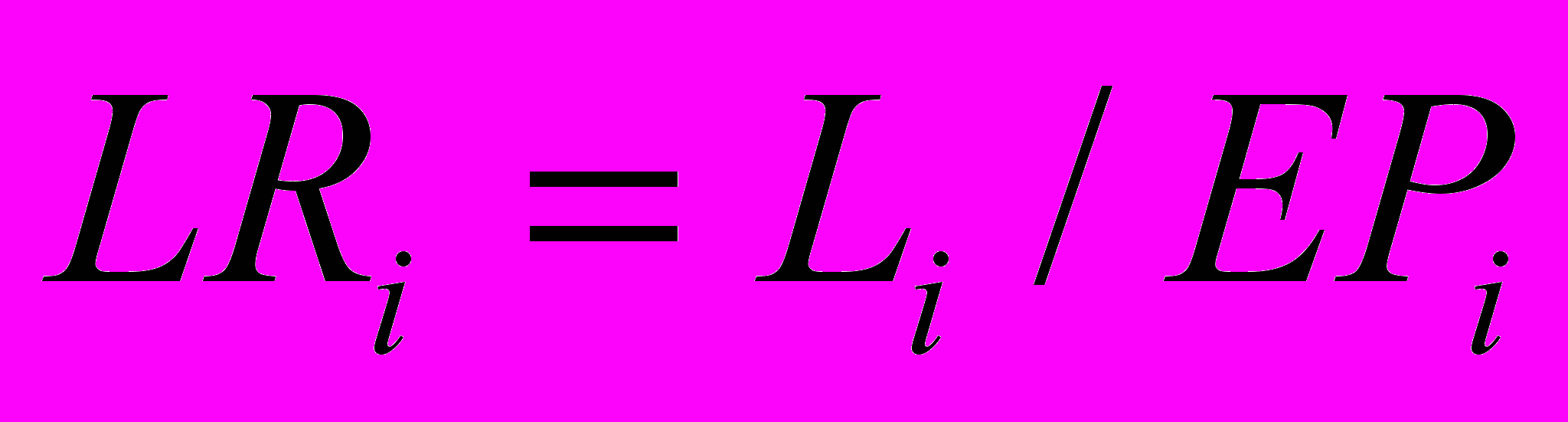
где
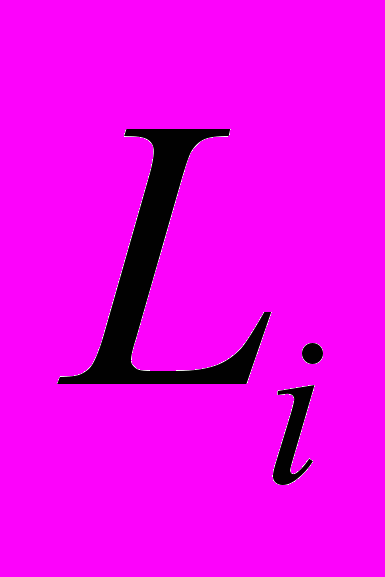- сумма убытков (Loss, L) , а 
- заработанная премия (Earned Premium,EP) i-го периода.При расчете коэффициента убытков следует учитывать все оплаченные убытки по страховым случаям данного периода вне зависимости от того, в каком периоде они оплачены. После расчета коэффициента убытков за каждый период определяется среднее за анализируемый период значение коэффициента убытков:
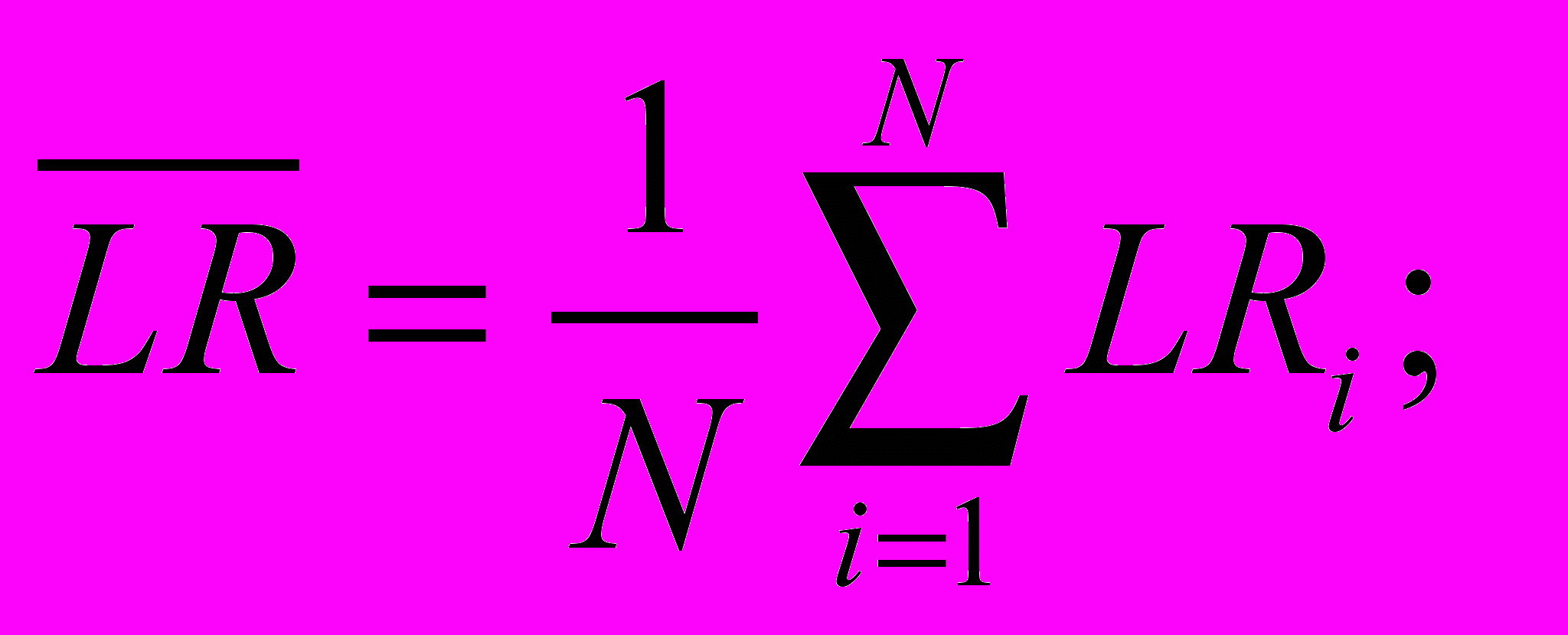
где ^ N – число анализируемых периодов. Ожидаемая величина окончательного убытка по страховым случаям данного i-го периода равна заработанной нетто-премии, умноженной на средний коэффициент убыточности:
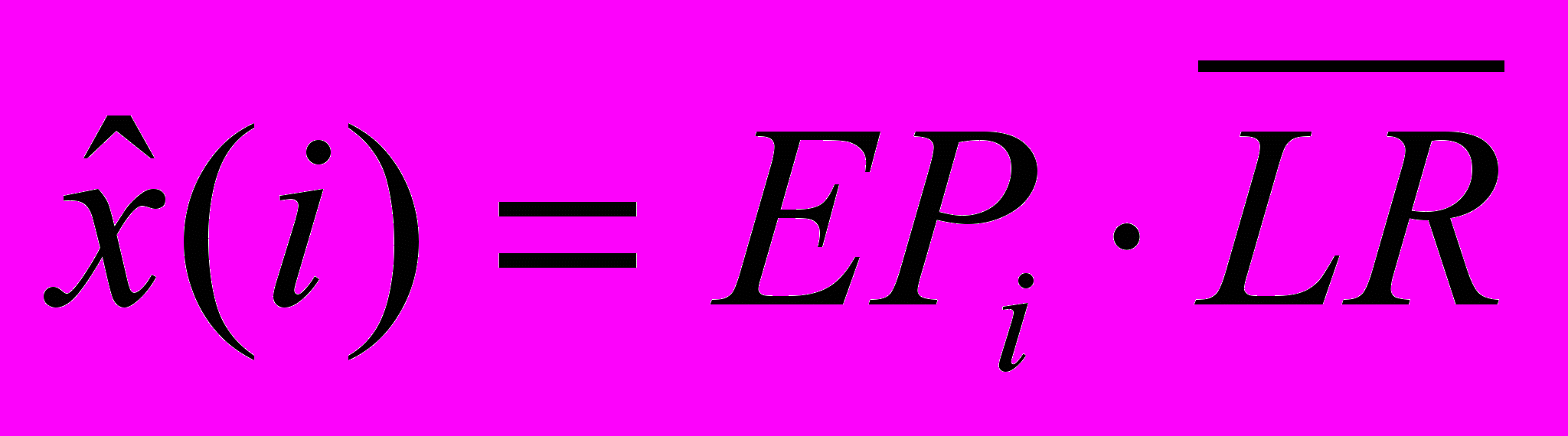
Зная ожидаемую сумму выплат и функцию распределения, легко вычислить ожидаемую величину оплаченных убытков и резерв убытков по страховым событиям i-го периода:
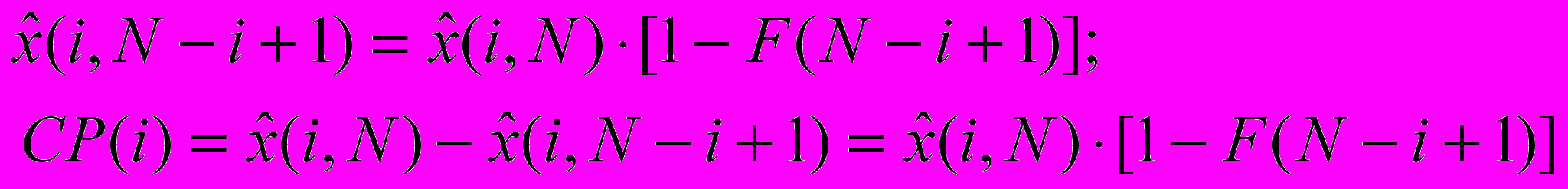
Суммируя по всем периодам событий, получим:
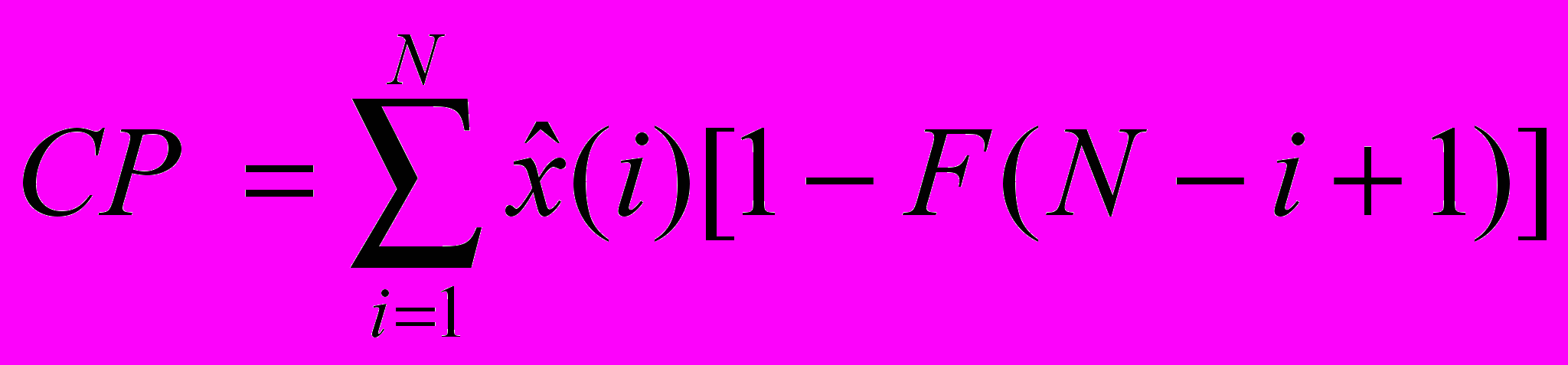
Таким образом, используя приведенный выше метод для расчета резервов, мы используем предположения о будущей величине выплат (основанные на предыдущей статистике) и совершенно игнорируем данные об уже произведенных выплатах. Данный метод был предложен в 1972 г. в статье: BORNHUETTER, R.L., FERGUSON, R.E. The Actuary of IBNR. Proceedings of the Casuality Actuarial Society, Vol. LIX, 181-195. Метод Борнхуеттера-Фергюсона для краткости обычно именуют как метод BF.
Применение как первого, так и второго методов ко всем периодам событий неэффективно. На наш взгляд, оптимальным является расчет резерва убытков методом цепной лестницы для периодов, по которым на момент отчета урегулировано более 30% ожидаемой суммы убытков, и методом BF для периодов, по которым доля урегулированных убытков ниже.
Метод BF не имеет альтернативы при прогнозных расчетах, когда величины убытков еще не известны (финансовое планирование).