А. П. Чехова «репетитор» мотивация: проблемная ситуация в связи с упомянутой в рассказ

Вид материала

Рассказ

Содержание Синее сукно Всего сукна Синее сукно Всего сукна

Подобный материал:

• Рассказ чехова «студент», 695.79kb.
• Анализ рассказа А. П. Чехова «На гвозде». Выполнила ученица 9-е кл. Медведева Дарья., 34.51kb.
• Урок литературы в 8 классе. Предметная тема: «Рассказ А. П. Чехова «О любви», 42.82kb.
• Т. А. Давиденко Функции определений в рассказ, 23.83kb.
• Проблемы коммуникации у Чехова, 5659.83kb.
• Антона Павловича Чехова и главная тема нашего вечера юмористические рассказ, 222.93kb.
• А. П. Чехова Чухаревой Ларисы Александровны, учителя русского языка и литературы мвсоу, 182.74kb.
• Рассказ Чехова «Душечка», 38.76kb.
• А. С. Грибоедов Проблемная ситуация, 181.79kb.
• А. П. Чехова «толстый и тонкий» Приложение №2 Текст относится к жанру рассказ, 60.07kb.

ОБЪЕКТ ЛИТЕРАТУРНО-МАТЕМАТИЧЕСКОГО ИССЛЕДОВАНИЯ:

рассказ А.П.Чехова «РЕПЕТИТОР»


МОТИВАЦИЯ: проблемная ситуация в связи с упомянутой в рассказе задачей.

ЦЕЛЬ: разрешить проблемную ситуацию и найти максимально возможное количество способов решения задачи.

УЧАСТНИКИ САЛОНА: ведущий (учитель), ученики-доверенные лица героев рассказа Удодова-отца и репетитора Зиберова, гости (ученики, учителя, родители).

ХОД МЕРОПРИЯТИЯ.

ВЕДУЩИЙ. Уважаемые гости - знатоки и любители русской словесности и математики – сегодня вы приглашены на творческое заседание в нашем салоне, посвященное рассказу А.П.Чехова «Репетитор».

Как известно, Чехов происходил из семьи торговца. Его отец Павел Егорович держал бакалейную лавку с весьма замысловатой вывеской «Чай, сахар, кофе, мыло, колбаса и другие колониальные товары». Дела шли плохо и, окончательно запутавшись в долгах, отец семейства покидает семью и скрывается в Москве. Вот тогда-то сын Антон, будучи гимназистом в Таганроге, был вынужден зарабатывать средства к жизни репетиторством. Отсюда, по всей вероятности, и возникла идея для будущего рассказа. Послушаем его фрагмент! (Идет чтение рассказа одним из участников.)

Итак. Как явствует из рассказа, задача про сукно оказалась под силу лишь Удодову-отцу. Но вот вопрос: а как именно ему ее удалось решить? И другой вопрос: а как ее вообще можно решить, сколькими способами? Что касается неудавшегося репетитора Зиберова. То он, сделав кучу предположений, так и не справился с задачей. Кстати, вспомните, какие именно предположения он делал? (Ответы с мест: «на неопределенные уравнения», «алгебраическая», «с иксом и игреком решить можно».)

Есть ли среди вас желающие раскрыть секрет решения Удодова-отца? А помочь разобраться с предположениями Зиберова? (Если желающие будут, дать им возможность выступить со своими идеями.) А теперь я хочу предоставить слово специалистам – доверенным лицам героев рассказа!

ПЕРВЫЙ УЧЕНИК. Как вы слышали, Удодов решил задачу «по-неученому», на счетах. Следовательно, задачу он решал арифметически. Возможно, это было так.

1. 138  5 = 690 (руб.) – стоила бы покупка, если бы купили только синее сукно;
   
2. 690-540=150 (руб.) – пришлось бы доплатить;
   
3. 5-3 = 2 (руб.) – разница в цене синего и черного сукна;
   
4. 150:2 = 75 (аршин) – следовало купить черного сукна;
   
5. 138 - 75 = 63 (аршина) – купить синего.
   

Способ, который я вам сейчас показал, называется способом предположений. Этим же способом можно было решать задачу с «покупки» 138 аршин черного сукна. Попробуйте!

ВТОРОЙ УЧЕНИК. Зиберов упомянул, что задача «алгебраическая». И я решил ее, как мы часто решаем. То есть с помощью введения переменной. Вот так:

	Сколько куплено аршин сукна	Сколько рублей стоит 1 аршин	Сколько рублей уплачено
^ СИНЕЕ СУКНО	x	5	5х
ЧЕРНОЕ СУКНО	138-х	3	3(138-х)
^ ВСЕГО СУКНА	138		540

5х + 3(138-х) = 540,

5х + 414-Зх = 540,

2х = 540-414,

2х = 126,

х = 63 – синее сукно, 138 - 63 = 75 – черное сукно.

ТРЕТИЙ УЧЕНИК. А еще, если вы помните, Зиберов сказал, что эту задачу « с иксом и игреком решить можно». И это действительно так! Обратимся к таблице.

	Сколько куплено аршин сукна	Сколько руб. стоит один аршин	Сколько руб. уплачено за товар
^ СИНЕЕ СУКНО	x	5	5х
ЧЕРНОЕ СУКНО	y	3	3y
^ ВСЕГО СУКНА	138		540

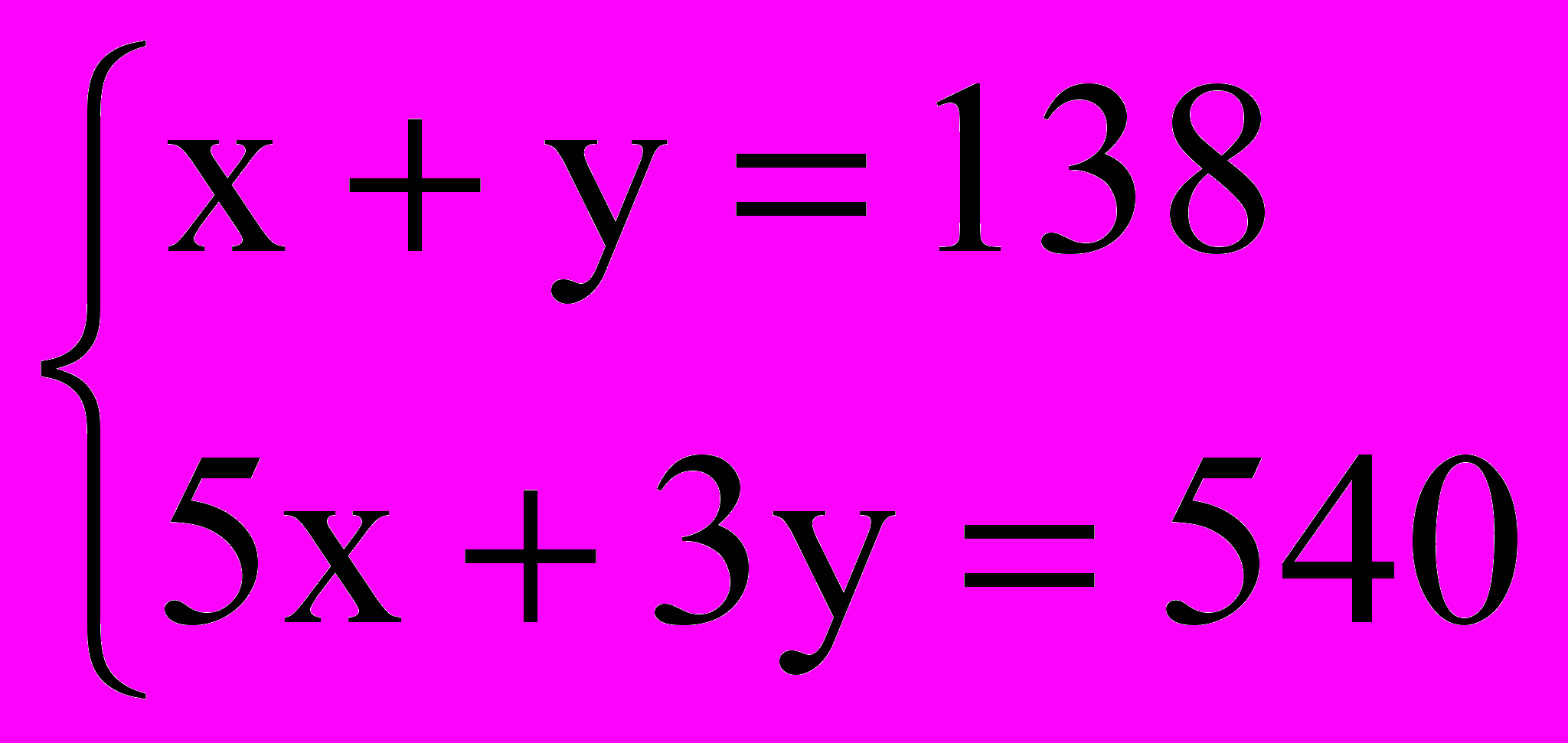
690 - 5у + Зу = 540,

2у= 150,

y = 75,

х= 138 - 75 = 63.

ЧЕТВЕРТЫЙ УЧЕНИК. Я попробовал разобраться, что такое «неопределенные уравнения». Оказывается, что это уравнения, содержащие более одного неизвестного. Обычно решение таких уравнений ищут в целых числах. Возьмем за основу первое из уравнений последней системы:

Х + Y= 138.

Мною был использован метод перебора. Так, X может принимать значения от 1 до 137, а Y - от 137 до 1 соответственно. Всего 137 пар чисел, среди которых пара X = 63 и Y = 75. Чтобы ее отобрать среди прочих, пришлось бы проверять каждую пару по второму условию задачи: 5X + ЗУ = 540! Представляете себе это «удовольствие»? Придется делать вычисления до 63 раз! Не нравится? Ищите другие способы.

ПЯТЫЙ УЧЕНИК. Я тоже решал задачу с X и Y как алгебраическую, но графическим методом.



ВЕДУЩИЙ. Итак, уважаемые гости нашего литературно - математического заседания, наши исследования подошли к концу. Проблема решена. Хотя, наверное, можно было продолжать поиск и дальше. На следующем заседании гостей салона выносится рассказ Л.Н.Толстого «Много ли человеку земли надо. До встречи, друзья!


Приложение (перечень литературных источников для заседаний в салоне)

1. Л.Н.ТОЛСТОЙ, рассказ «Много ли человеку земли надо». (Суть рассказа в том, как крестьянин Пахом, который мечтал о собственной земле и собрал, наконец, желанную сумму, предстал перед требованием старшины: «Сколько за день земли обойдешь, вся твоя будет за 1000 рублей. Но если к закату солнца не возвратишься на место, с которого вышел, пропали твои деньги.»
   
2. М.Е.САЛТЫКОВ-ЩЕДРИН, Роман «Господа Головлевы» (Сын Порфирия Владимировича Петя проиграл в карты казенные 300 рублей и попросил у бабушки эти деньги взаймы. Он говорит: Я бы хороший процент дал. Пять процентов в месяц.»)
   
3. ОНОРЕ БАЛЬЗАК, новелла «Гобсек» (Один из героев, господин Дервиль, взял у ростовщика Гобсека сумму в 150000 франков сроком на 10 лет под 15% годовых.)