Методические указания предназначены для студентов спе­циальности "Электропривод и автоматизация промышленных установок"

1   2   3

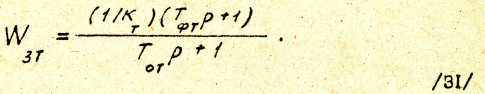
Выражение /31/ используется при расчете внешнего контура –

конту­ра скорости.

Физическая реализация требуемой передаточной функции регулятора тока аналогична рассмотренной ранее для случая отсутствия фильтра в цепи обратной связи /см. п.п.4.1.5.3.1 и 4.1.5.3.2/.

4.1.6.2. Расчет контура скорости при наличии фильтра в цепи обрат­ной связи. Структурная схема контура скорости на основании рис.11 с учетом /31/ будет иметь вид, изображенный на рис.12.



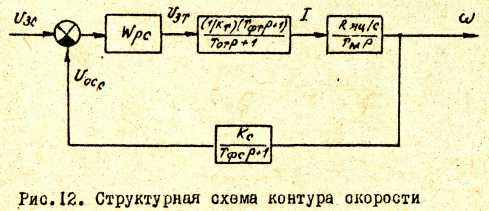
В данном контуре некомпенсируемыми являются форсирующее и апериоди­ческие звенья с постоянными Т_ФТ , Т_ОТ , и Т_ФС. Таким образом, пе­редаточная функция элементов контура, действие которых должен компен­сировать регулятор скорости W_РС, имеет такой же вид, как и при отсутствии фильтров /см. п.4.1.5.4/.


Передаточная функция регулятора скорости при настройке на модуль­ный оптимум с учетом фильтра с постоянной Т_ФС в цепи обратной связи

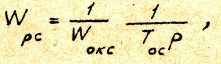
где Т_ОС - оптимизированная постоянная интегрирования разомкнутого контура скорости при настройке на модульный оптимум,



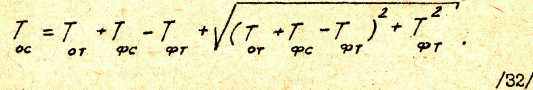
При подстановке W_ОК.С в выражение для W_РС окончательно получаем



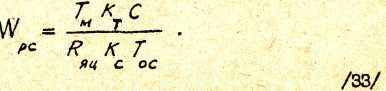
Физическая реализация П-регулятора скорости аналогична рассмот­ренной ранее для случая отсутствия фильтра в цепи обратной связи

/см. пп4.1.5.4.1 -4.1.5.4.3/.

4.1.7. Расчет электромеханических характеристик в двухконтурной СПР с пропорциональным регулятором скорости при отсутствии фильтров. Уравнение электромеханической характеристики двигателя на рабочем участке вытекает из выражения /20/, если последнее разрешить

относительно ω:




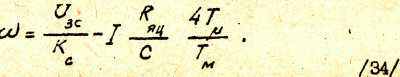
Уравнение /34/ справедливо для токов якоря, удовлетворяющих условию

0≤ I ≤ I_МАКС где I_МАКС - значение тока, при ко­тором напряжение на выходе регулятора скорости достигает напряжения ограничения U_ЗТмакс. Из /34/ следует, что статическое падение скорости Δω_с , обусловленное приложением нагрузки к валу двигателя, определяется вторым членом уравнения, т.е.




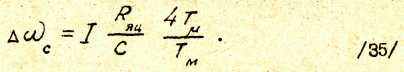
В разомкнутой системе статическое падение скорости

Δω_{с раз} составляет




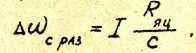
Тогда Δω_с можно представить в виде

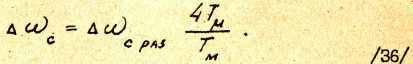
Выражение /36/ показывает, что жесткость электромеханических ха­рактеристик в двухконтурной СПР с пропорциональным регулятором ско­рости выше, чем в случае разомкнутой системы, если Т_М > 4Т_µ

Для большинства реальных приводов электромеханическая постоянная привода Т_М больше учетверенной эквивалентной некомпенсируемой посто­янной контура тока Т_µ. Таким образом, как правило, жесткость электромеханических и механических характеристик двигателя в подобной СПР выше, чем в разомкнутой системе. Однако для многих приводов такая точность поддержания скорости оказывается недостаточной. В этих слу­чаях применяются двухконтурные CПP с пропорционально-интегральным /ПИ/ регулятором скорости. Эти системы называют двукратноинтегрирующими.

При I=I_МАКС электромеханическая характеристика претерпевает

излом и совпадает с вертикалью I=I_МАКС. Таким образом, электромеханические характеристики привода в СПР с пропорциональным регуля­тором скорости имеют вид, изображенный на рис.13.




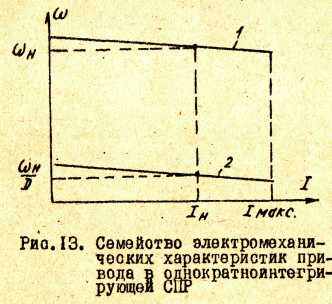
4.1.8. Расчет электромехани­ческих характеристик привода в двухконтурной СПР с П-регулятором скорости при наличии фильтров в це­пях обратных связей по току и ско­рости.

Уравнение электромеханической характеристики на рабочем участке /при 0≤ I ≤ I_МАКС / как следует из сопоставления рис.8 и рис.12 и уравнения /34/, анало­гично уравнению, полученному для СПР без фильтров, и имеет вид

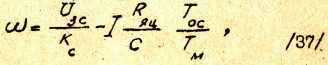
где Т_ОС определяется выражением /32/.


Особенностью электромеханических характеристик привода в системе с фильтрами является еще меньшая жесткость, чем в системе без фильт­ров, так как Т_ОС > 4Т_µ. При I=I_МАКС электромехани­ческая характеристика претерпевает излом и совпадает с вертикалью I=I_МАКС.

Примерный вид электромеханических характеристик привода имеет вид, изображенный на рис.13.

4.1.9. Анализ динамических режимов двухконтурной СПР с

П-регулятором скорости /однократноинтегрирущая СПР/

4.1.9.1. По управляющему воздействию. Как видно из анализа выраже­ний для передаточных функций контуров тока и скорости /3/ и /19/ при настройке регуляторов на оптимум по модулю, которые отличаются толь­ко значением некомпенсируемых постоянных /для контура скорости эта постоянная в 2 раза больше - 2 Тµ против Т_µ / и коэффициентом передачи, переходный процесс в каждом контуре при скачке управляюще­го сигнала на входе будет близким к оптимальному по быстродействию. Перерегулирование будет 4,3 %, а время реакции 4,1σ /3/, где σ -не компенсируемая постоянная контура /для контура тока σ= Тµ, а для контура скорости σ =2Тµ , как изображено на рис.14/.

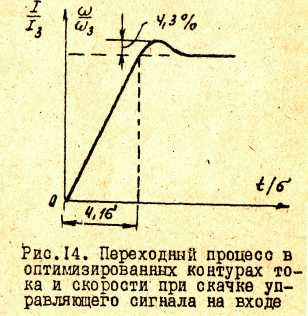
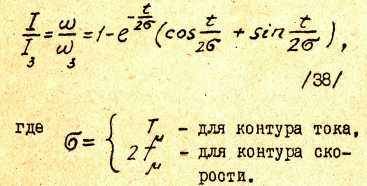
Аналитическое выражение для кривой /рис.14/, которая представляет собой переходную характеристику оптимизиро­ванного контура, легко может быть получено на основании /3/ и /19/

Необходимо иметь в виду, что подобный вид переходного процесса будет только при очень малых скачках управляющего напряжения / U_ЗТ или U_ЗС /, когда оба регулятора РТ и PC на протяжении всего пере­ходного процесса не заходят в область ограничения.

В случае пуска или реверса двигателя в любой реальной СПР при


скачкообразном приложении сигнала задания скорости регулятор скорости очень быстро попадает в область ограничения, т.е. напряжение на выхо­де PC не изменяется при изменении результирующего сигнала на его вхо­де. Поэтому реальный переходный процесс с учетом всех ограничений и нелинейностей может быть получен только с помощью цифровой ЭВМ при использовании более полной и адекватной математической модели, нежели уравнение /38/. Расчет переходных процессов с помощью цифровой ЭВМ будет рассмотрен далее.

4.1.9.2. По возмущающему воздействию. Под возмущающим воздействием для систем электропривода понимают изменение нагрузки на валу двигате­ля. Переходный процесс в рассматриваемой системе при ударном скачко­образном приложении нагрузки к валу двигателя имеет такой же характер и примерно такой же вид, как при управляющем воздействии /3/. Дли­тельность переходного процесса примерно равна утроенной некомпенсируемой постоянной времени контура тока t_рег=3Тµ . Перерегули­рование тока и превышение максимального динамического снижения ско­рости по отношению к статическому не превышает 5%. В качестве базо­вых величин берутся установившиеся значения тока I_c и отклонения скорости Δω_с.

Не следует забывать, что подобный переходный процесс справедлив лишь при очень малых набросах нагрузки, когда регуляторы в течение переходного процесса не заходят в область ограничения. Во всех других случаях простые аналитические выражения для скорости и тока, приве­денные в 3, формулы /7-1/ и /7-9/, для расчета переходных процессов по возмущающему воздействию не применимы. В подобных случаях целесооб­разно использование цифровых ЭВМ для расчета переходных процессов.

4.1.10. Расчет элементов двухконтурной системы подчиненного регу­лирования с ПИ-регулятором скорости /при настройке PC на симметрич­ный оптимум/. Такая СПР называется двукратноинтегрирущей и реализует­ся в схеме на рис.2 при разомкнутом тумблере Р.

В тех случаях, когда статическая и динамическая точность поддержа­ния скорости двигателя при набросе и сбросе нагрузки оказывается не­достаточной в двухконтурной СПР с пропорциональным PC, применяется двукратноинтегрирующая СПР, отличие которой от рассмотренной ранее однократноинтегрирующей заключается в замене П-регулятора скорости ПИ-регулятором, что соответствует настройке PC на симметричный опти­мум. В этом случае, как будет показано далее, статическая ошибка по скорости при набросе и сбросе нагрузки отсутствует.

Расчет параметров контура тока двукратноинтегрирущей СПР совпада­ет с рассмотренным ранее /для однократноинтегрирующей СПР/.


4.1.10.1. Расчет параметров контура скорости /при отсутствий фильтров/. ПИ-регулятору скорости соответствует настройка PC на так называемый симметричный оптимум. При этом пропорциональная часть пере­даточной функции ПИ-регулятора скорости совпадает с передаточной функ­цией W_pc П-регулятора однократноинтегрирующей СПР, полученной ра­нее /18/. Передаточная функция ПИ-регулятора скорости имеет вид

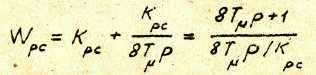
Подставляя в последнее выражение К_РС из /18/, окончательно получаем



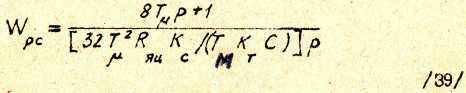
Коэффициент обратной связи по скорости К можно определит*
по /21/.

Физическая реализация передаточной функции регулятора скорости осуществляется аналогично рассмотренному ранее для РТ.

Электрическая схема ПИ-регулятора скорости имеет вид, изображенный на рис.15.

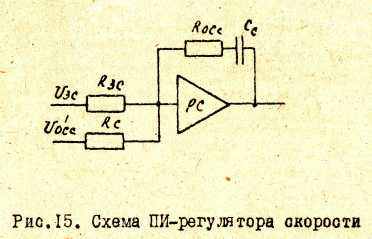
Для определения параметров регулятора скорости необходимо:
а/ задаться емкостью конденсатора С_С . Можно принять

С_С = 0,5...2 мкФ;

б/ найти сопротивление R_ОСС в цепи обратной связи УПТ




в/ рассчитать входное сопротивление регулятора скорости R_З.С



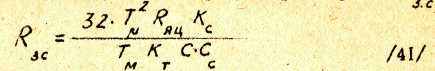
г/ рассчитать сопротивление R_С, на которое заводится сигнал обратной связи по скорости, воспользовавшись формулой /27/, которая справедлива и для случая П-регулятора.

4.1.10.2. Расчет параметров контура скорости /при наличии фильт­ров/, С учетом общепринятых допущений /5/ передаточная функция регуля­тора скорости при настройке на симметричный оптимум имеет вид

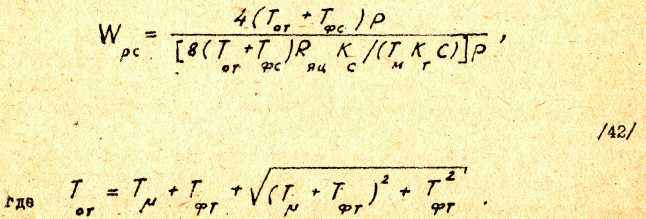
Физическая реализаций этой передаточной функции осуществляется аналогично рассмотренной ранее /см. п.4.1.10.1/.

4.1.11. Расчет электромеханических характеристик в двухконтурной СПР с ПИ-регулятором скорости. Как следует из структурной схемы /см. рис.,5/ с учетом выражения /39/ для передаточной функции PC, в устано­вившемся режиме результирующее входное напряжение PC должно быть рав­но нулю, т.е.



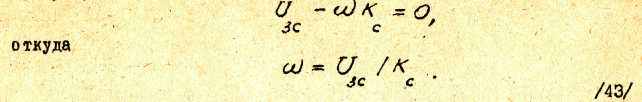
Выражение /43/ представляет собой уравнение электромеханической или механической характеристики. Как видно из /43/, угловая скорость двигателя ω не зависит от тока якоря, т.е. статическая скоростная ошибка, обусловленная набросом или сбросом нагрузки, отсутствует. Та­ким образом, электромеханические характеристики в двукратноинтегри-рующей СПР для 0 ≤ I ≤ I_МАКС представляют собой прямые, параллель­ные оси абсцисс, как изображено на рис.16.



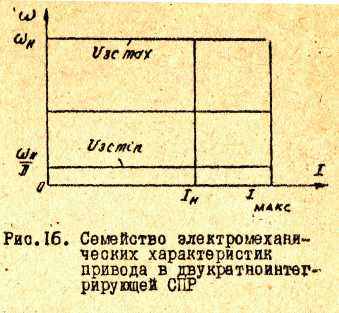
При I= I_МАКС электроме­ханические характеристики претерпе­вают излом, так как PC выходит в область ограничения, и представля­ются отрезком вертикали I= I_МАКС.

В области прерывистого тока в установившемся режиме уравнение /43/ остается в силе. Однако двукратноинтегрирующая СПР в случае прерывистого тока в якоре может стать неустойчивой, если пара­метры регуляторов будут неизмен­ными.

Как показывает практика, для нормальной работы СПР в области прерывистого тока необходимо применение адаптивного регулятора тока РТ. В традиционных системах это требует усложнения схемы регулятора и все же обеспечивает лишь удовлетворительное качество переходных процессов. Для кардинального решения проблемы прерывистого тока в электроприводе весьма перспективным является применение микропроцес­сорных систем, которые позволяют реализовать программным путем зна­чительно более сложные алгоритмы управления, нежели традиционные аналоговые или цифровые системы на жесткой логике.

Другим направлением преодоления нежелательных эффектов, вызыва­емых прерывистыми токами, является сужение зоны этих токов, что тре­бует установки сглаживающих дросселей значительной индуктивности. По­добное решение сильно ухудшает массо-габаритные показатели привода. В последнее время наметилась тенденция к уменьшению использования дополнительных индуктивностей в силовых цепях привода, однако это требует существенного усложнения регуляторов СПР.

4.1.12. Анализ динамических режимов двукратно-интегрирующей СПР

4.1.12.1. По управляющему воздействию. При настройке PC на симмет­ричный оптимум реакция двукратноинтегрирующей СПР на скачок напряжения задания скорости U_З.С оказывается менее благоприятной, чем однократноинтегрирующей. Время регулирования увеличивается примерно вдвое, увеличивается также перерегулирование в контуре скорости, которое пре­вышает 40 %. Для уменьшения перерегулирования до уровня однократно-


интегрирующей системы на входе двукратноинтегрирующей СПР устанавли­вают апериодическое звено либо задатчик интенсивности,

4.1.12.2. По возмущающему воздействию. Реакция двукратноинтег-рирующей СПР на скачок возмущающего воздействия / ΔI_C / более благоприятна, чем однократноинтегрирующей. Хотя время регулирования примерно в 2 раза больше, чем для однократноинтегрирующей t_рег = 8σ, максимальная динамическая скоростная ошибка оказывается меньше. Мак­симальная динамическая скоростная ошибка составляет примерно 80 % установившейся статической скоростной ошибки в однократноинтегрирую­щей СПР.

Перерегулирование в контуре тока достигает 50 %.

В целом можно заключить, что двукратноинтегрирующая СПР для сис­тем стабилизации скорости является предпочтительной по сравнению о однократноинтегрирующей.

4ЛЛЗ. Расчет переходных процессов при пуске, набросе
или сбросе нагрузки в двухконтурной СПР на
цифровой ЭВМ.

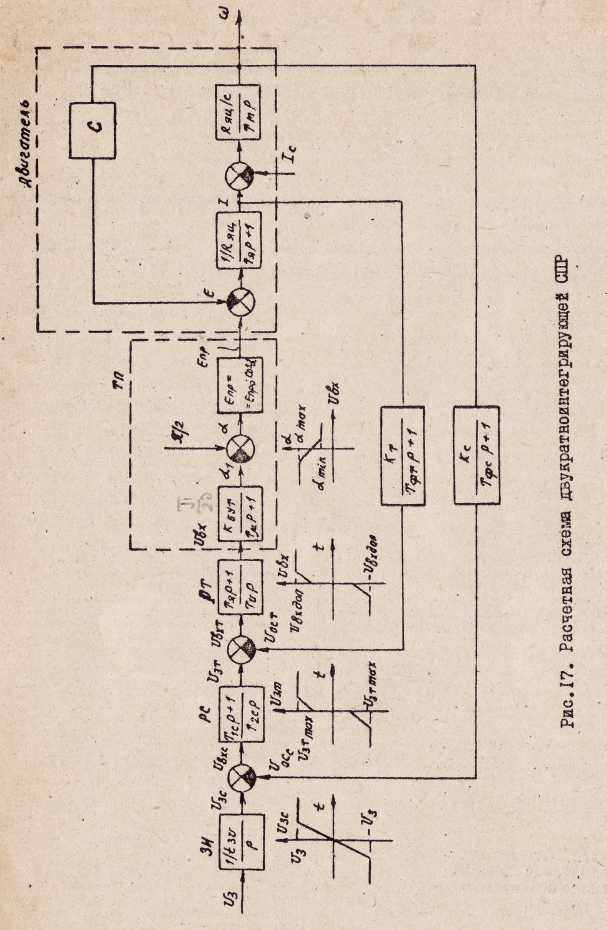
4.1.13.1. Математическая модель. При составлении математической модели можно взять за основу структурную схему на рис.11, дополнив ее задатчиком интенсивности ЗИ, учетом внутренней обратной связи по ЭДС двигателя, нелинейности коэффициента передачи тиристорного преоб­разователя и ограничений отдельных промежуточных координат системы. Тогда получится расчетная схема, изображенная на рис 17.

Схема на рис.17 справедлива при использовании блока управления тиристорами БУТ /см.рис.1/. Графики под блоками ЗИ, PC и РТ представ­ляют собой реакции этих динамических звеньев на скачок входного сигнала. График, расположенный на рисунке справа, является статической ха­рактеристикой вход-выход БУТ с учетом ограничения минимального и максимального углов управления тиристорами.

Переходя от передаточных функций динамических звеньев /рис.17/ к дифференциальным или алгебраическим уравнениям и учитывая ограничения, получаем.

I. Для задатчика интенсивности ЗИ




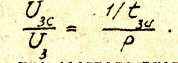
Заменяя р на d/dt, что соответствует переходу от функции комплексного переменного к функции времени, имеем







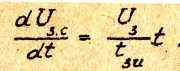
Выражение для определения коэффициентов Рунге – Кутта, необходи­мое при численном решении дифференциального уравнения, имеет вид

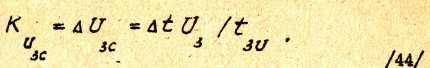
Это выражение получено из исходного дифференциального при замене диф­ференциалов конечными приращениями.

Ограничение выходного напряжения ЗИ на уровне U_З учитывается
в общем случае следующим образом /рис.18/.

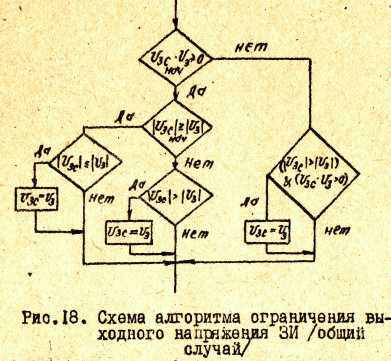
На приведенной структурной схеме использованы обозначения: U_{ЗС нач} - напряжение на выходе ЗИ в начальный момент рассмат­риваемого переходного про­цесса; знак & - логи­ческая функция "И"

В частном случав пуска двигателя от нулевой ско­рости приведенная схема су­щественно упрощается /рис.19/.

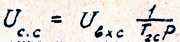
Введем обозначение

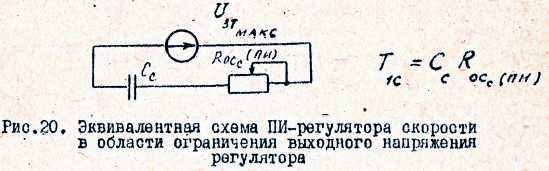
где U_С.С. представляет собой напряжение на емкости С_С регулятора скорости /рис.20/; в то ж время, как следует из последнего выражения для

U_ЗТ ,U_СС является интегральной составляющей выходного напряже­ния ПИ-регулятора скорости.





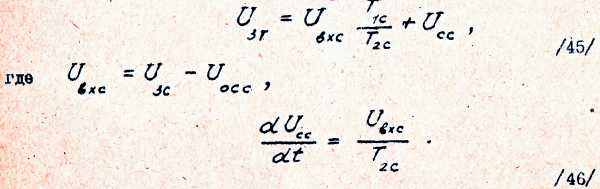С учетом введенного обозначении

Выражение для коэффициентов Рунге – Кутта




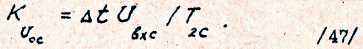
Напряжение обратной связи по скорости связано со скоростью зависимостью

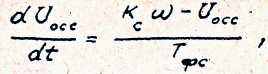откуда выражение для коэффициентов Рунге - Кутта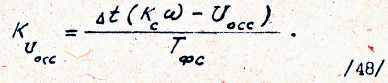

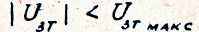Формулы /47/ и /48/ справедливы при

При достижении U_ЗТ уровня ограничения изменяется эквивалентная схема регу­лятора, и схема включения конденсатора С_С принимает вид, изображений на рис.20.


В области ограничения, как следует из рис.20, дифференциальное уравнение для напряжения на конденсаторе С_С принимает вид



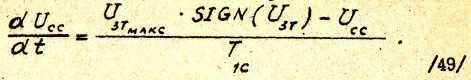
Выражение для коэффициентов Рунге - Кутта

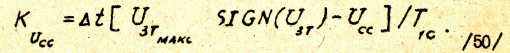
Функция SIGN(x) , где х - переменная, используемая в /49/ и /50/, является функцией выделения знака х , т.е.



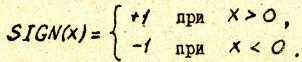
Таким образом, с учетом /48/ и /50/, получим

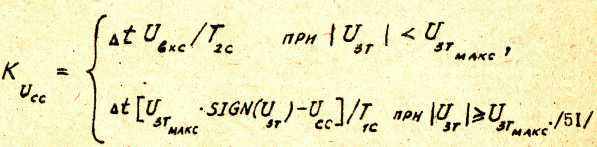
Ограничение выходного напряжения PC учитывается еравенством



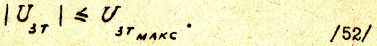
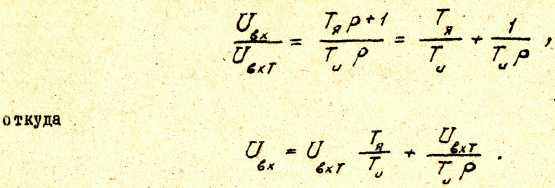3. Для регулятора тока РТ

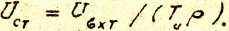Вводим обозначение

U_СТ равно напряжению на емкости С_Т РТ /см.рис.6/ и представляет собой интегральную составляющую выходного напряжения РТ.


С учетом введенного обозначения

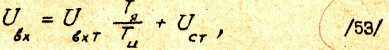
Выражение для коэффициентов Рунге - Кутта /для напряжения U_СТ/



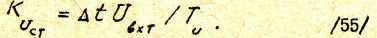
Напряжение обратной связи по току якоря связано с током якоря зависимостью

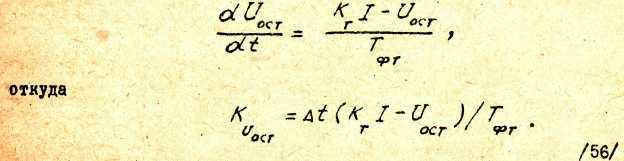
Соотношения /54/ и /55/ справедливы при | U_вх |< U_вх.доп.

При достижении U_вх, уровня ограничения изменяется эквивалентная схема регулятора и схема включения конденсатора С_Т принимает вид,



изображенный на рис.21.

В области ограничения, т.е. при


U_вх = U_вх.доп , как следует из рис.21, дифференциальпое уравне­ние для напряжения на конденсаторе С_Т принимает вид

Таким образом, с учетом /55/ и /56/ получим для коэффициентов Рунге - Кутта