Безошибочное обращение плохо обусловленных матриц в распределенной среде restful веб-сервисов символьных вычислений

Вид материала

Документы

Содержание 2. Блочная декомпозиция и дополнение Шура 3. Эксперимент по обращению матриц Гильберта 4. Сценарий вычислений в среде MathCloud

Подобный материал:

• А. Е. Чуваев научный руководитель В. П. Климов, ст преподаватель Национальный исследовательский, 40.5kb.
• В. В. Климов национальный исследовательский ядерный университет «мифи» модели, методы, 10.26kb.
• Интеграция систем управления содержимым сайта и генерации шаблонов интернет- страниц, 24.69kb.
• В. Н. Коваленко, А. В. Орлов Управление заданиями в распределенной среде и протокол, 311.55kb.
• Календарный план учебных занятий по дисциплине "Высшая алгебра и аналитическая геометрия", 94.97kb.
• Р. М. Алгулиев, М. Ш. Гаджирагимова некоторые аспекты организации и реализации мультиагентной, 90.3kb.
• Принципи доступу до інформації в мережі Інтернет. Поняття про веб-сайт, веб-сторінку,, 85.43kb.
• Технологическая инструкция «Проектирование и развитие веб-сайта детской библиотеки», 120.77kb.
• Теоретический материал дисциплинарного экзамена (бакалавры), 215.88kb.
• Servlet Container Clustering (Tomcat) 13 jvm clustering (Terracotta) 14 Grid-Computing, 287.86kb.

Безошибочное обращение плохо обусловленных матриц в распределенной среде RESTful веб-сервисов символьных вычислений

Авторы статьи: Волошинов В.В., МФТИ, ассистент, vladimir.voloshinov@gmail.com; Смирнов С.А., МФТИ, аспирант, sasmir@gmail.com

Одной из традиционных проблем вычислительной математики являются погрешности при решении плохо обусловленных систем линейных уравнений. Применение символьных вычислений и систем компьютерной алгебры, теоретически, позволяет проводить безошибочные вычисления за счет увеличения продолжительности расчетов и объёма потребляемой памяти. Для повышения производительности был реализован распределённый алгоритм безошибочного обращения матриц на основе программного инструментария MathCloud и RESTful сервисов доступа к системам компьютерной алгебры Maxima, установленным на многоядерных настольных компьютерах. Вычислительный сценарий основан на блочной декомпозиции матриц и вычислении дополнения Шура. Предложенный подход демонстрируется на примере обращения матриц Гильберта (с экспоненциальным ростом числа обусловленности при увеличении размеров матрицы) вплоть до размерности 500x500.

1. Введение

Символьные вычисления в распределённой вычислительной среде за последнее десятилетие стали довольно популярными [1]. В частности, они позволяют выполнять безошибочные вычисления в сложных задачах вычислительной математики, например, решать плохо обусловленные системы линейных уравнений. Для решения этой задачи также применяют системы параллельных вычислений, на основе библиотек «рациональной» арифметики произвольной точности в «традиционных» языках программирования [2], [3]. В докладе [4] мы представили результаты экспериментов с сервисом доступа к системе компьютерной алгебры Maxima (GNU Сomputer Algebra System, maxima.sourceforge.net), реализованном С.А. Смирновым (le.com/p/remote-maxima) при помощи промежуточного программного обеспечения Ice, www.zeroc.com. Данный подход подразумевал, что исследователь самостоятельно реализует, например, на Java, приложение, обеспечивающее выполнение вычислительного сценария решения конкретной задачи. Это сужает возможности применения такой реализации сервиса компьютерной алгебры Maxima.

Здесь мы представляем распределённый и частично параллельный сценарий безошибочного обращения плохо обусловленных матриц в инфраструктуре MathCloud [5], [6], www.mathcloud.org, основанной на парадигме Web 2.0 и RESTful веб-сервисах (HTTP, представление данных на основе JSON, интерактивное веб-приложение в качестве интерфейса пользователя). Для целей работы был разработан RESTful сервис системы Maxima [7]. Сценарий основан на блочной декомпозиции матрицы и на дополнении Шура. Такой подход был анонсирован в [4] и использует параллелизм при умножении промежуточных прямоугольных матриц. Другой целью работы было всестороннее тестирование систем проектирования и управления сценариям среды MathCloud.
^

2. Блочная декомпозиция и дополнение Шура

Предлагается использовать хорошо известный в теории матриц [8] способ их обращения, основанный на блочной декомпозиции и на так называемой формуле Шура (или дополнении Шура). Пусть M квадратная, NxN, матрица, представленная в виде четырёх блоков 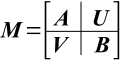, где A, N_AN_A, и B, N_BN_B, N_B=N N_A, квадратные матрицы, а U, N_AN_B; и V, N_B(N N_A), - прямоугольные. Определим квадратную матрицу размера (N N_A)(N N_A), т.н. дополнение Шура блока A матрицы M. Известно [8]: если существует M^-1, тогда (возможно, после перестановок строк и столбцов) существуют A^-1 и S^-1, причем M^-1 может быть поделена на четыре подматрицы того же размера (как A, U, V, B) как показано ниже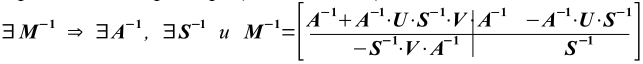

(1)

Такое представление M^-1 позволяет ускорить её вычисление в результате параллельного обращения и умножения подматриц меньшего размера, чем у исходной матрицы M. Упрощённая блок-схема (не все информационные зависимости указаны) сценария показана на Рис. 1. Для обозначения передачи данных между блоками используются два типа стрелок. Сплошная - означает входящие данные необходимы для совершения следующего шага вычислений, например, умножение (A ¹U)S^-1 может быть выполнено лишь после того как будут готовы произведение (A ¹U) и обратная матрица S^-1. Пунктирные стрелки означают, что для следующего шага достаточно готовности хотя бы одного из входов. Например, и VA^-1, и A^-1U достаточно для вычисления VA^-1U=(VA^-1)U=V(A^-1U). Овалами выделены блоки, допускающие параллельное выполнение.



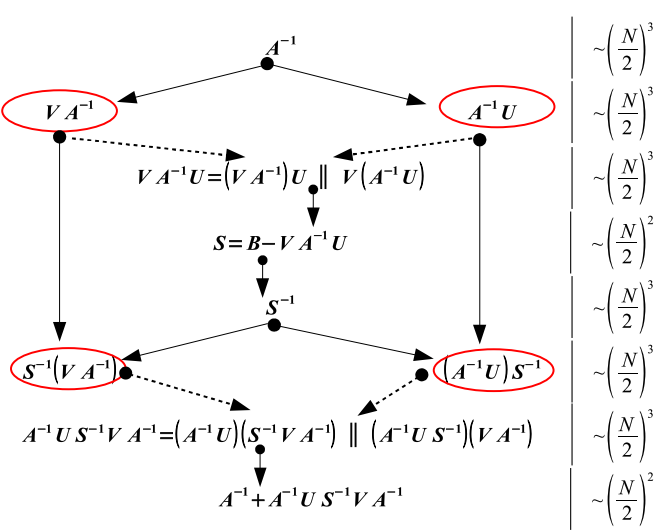
Рис. 1. Оценка эффективности распараллеливания

Оценим потенциальное ускорение для случая, когда этот сценарий работает в параллельной вычислительной среде. Предположим, что мы имеем два вычислительных модуля, использующих арифметику чисел с плавающей точкой фиксированной длины. Также предположим, что модули оснащены стандартными алгоритмами линейной алгебры (включая алгоритмы обращения квадратных матриц методом Гаусса и умножения прямоугольных матриц). Напомним два известных факта вычислительной математики: обращение матрицы размера nn методом Гаусса требует ~n³ операций; произведение двух nn матриц также требует n³ операций (без учёта асимптотически более быстрых алгоритмов Штрассена [9] или Копперсмита-Винограда [10]). Пусть N - четное и N_A=N/2, тогда легко видеть (см. оценки трудоёмкости справа на Рис. 1), что распределённое обращение "стоит" 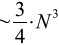арифметических операций против N³ операций при работе одного "вычислителя". Тем самым, стоимость вычислений уменьшается примерно на четверть. К сожалению, такие оценки плохо применимы к символьным вычислениям, т.к. их трудоёмкость зависит ещё от количества цифр в "рациональной записи" операндов. Далее будут представлены только экспериментальные значения временных затрат.

Схема на Рис. 1 может быть использована рекурсивно, для обращения промежуточных матриц A, S и т.д. Кроме того, сценарий содержит операцию умножения прямоугольных матриц, которая тоже хорошо распараллеливается. А именно, рассмотрим две прямоугольные матрицы X, M_XС, и Y, СN_Y, поделённые, соответственно, на пары горизонтальных (X₁, M_X1С, и X₂, (M_X M_X1)С) и вертикальных (Y₁, СN_Y1, и Y₂, С(N_Y  N_Y1)) блоков. Произведение матриц X·Y, M_XN_Y (см. (2)) состоит из четырёх блоков, которые могут быть вычислены параллельно и независимо друг от друга.

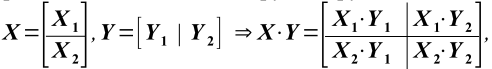(2)
^

3. Эксперимент по обращению матриц Гильберта

Матрица Гильберта размера NN определяется как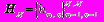, где h_m,n=(m+n-1)^-1. Её можно считать левым верхним квадратным "сегментом" множества коэффициентов Грамма "степенного базиса" в Гильбертовом пространстве L₂[0,1], так как 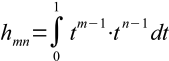. Такие матрицы составляют известный класс плохо обусловленных матриц, где 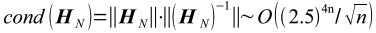. Поэтому, применение вычислительных модулей, работающих с числами с плавающей точкой фиксированной длины, для обращения матриц Гильберта стандартными алгоритмами линейной алгебры (например, методом Гаусса для получения LU-разложения, H=L^U, с последующим решением матричного уравнения L^U^X=E, где E - единичная матрица) становится невозможным даже для относительно небольших значений N.

Табл. 1. Трудоемкость символьного обращения

CPU Intel Xeon E5410 2.33 GHz (на одном ядре из восьми), мин.
N	invH: invert_by_lu(HN)	Проверка, H.invH == E?
200	3	1
300	15	4
400	45	12
500	109	27

Это не так для случая символьных вычислений, работающих с рациональными числами x=^p/_q, где {p,q} - пара целых числителя и знаменателя. С другой стороны, плохая обусловленность матриц означает, что длина символьного представления рациональных коэффициентов обратной матрицы становится очень большой, и время выполнения арифметических операций над ними тоже становится очень большим. В таблице 1, слева, приведены продолжительности обращения матриц Гильберта одной из стандартных процедур Maxima "invert_by_lu" (сочетающей LU-разложение с решением матричного уравнения L^U^X=E после). Во втором столбце приводятся длительности проверок правильности вычислений.

Здесь важно отметить, что Maxima может работать на основе различных реализаций компилятора Common Lisp (мы применяли Steel Bank Common Lisp, www.sbcl.org). Хотя некоторые из них позволяют создавать многопоточные Lisp-приложения, Maxima не использует многопоточность и совершает вычисления в одном потоке даже на многоядерных процессорах. Это и является поводом использования приёмов распределённых вычислений для ускорения расчетов. Далее будет показано, что «параллельная» реализация алгоритма из раздела 2, позволяет уменьшить время вычислений более чем вдвое. Что касается размера точного (!) символьного представления матриц (H_N)^-1, то это ~34 Mb для N=300 (в текстовом формате Lisp) и ~140 Mb для N=500.
^

4. Сценарий вычислений в среде MathCloud

Инфраструктура MathCloud [6] содержит три основных элемента: 1) унифицированный удалённый доступ к существующим приложениям при помощи RESTful веб-сервисов; 2) редактор, реализованный как интерактивное веб-приложение, для быстрой разработки достаточно сложных вычислительных сценариев, которые, в свою очередь, могут быть включены в другие сценарии как «составные» сервисы; 3) система управления сценариями, позволяющая выполнять несколько сценариев одновременно. Каждый RESTful веб-сервис, участвующий в сценарии, представлен на Рис. 2 прямоугольным блоком. Верхние круглые «порты» блоков соответствуют входным параметрам, а нижние - выходным. Поддерживается набор различных типов параметров, из которых для сценария «обращения» используются string и file. Потоки данных представлены «проводами», соединяющими выходные и входные порты. Отметим, что параметры типа file передаются сервисам-получателям в виде URI. Получатель загружает указанные файлы напрямую с сервиса-отправителя независимо от системы управления сценариями, выполняющейся на «третьем» хосте.

В сценарии обращения применялись сервисы двух типов: простой сервис «cat», сшивающий два входных файла в один выходной, и сервис «maxima», предоставляющий доступ к процессу Maxima для проведения вычислений. Сервис Maxima [7] (Рис. 2) имеет три входных параметра: 1) «command» - строка на языке сценариев Maxima, выполняемая экземпляром Maxima; 2) файл с данными (в формате Lisp), которые должны быть использованы во время выполнения команды; 3) файл со вспомогательным сценарием Maxima (например, содержащим определения функций, используемых «command»). Сервис имеет два выходных параметра: 1) файл с данными, записанный в формате Lisp стандартной функцией «save» сценариев Maxima во время выполнения команды; 2) строка с результатом выполнения самой команды.



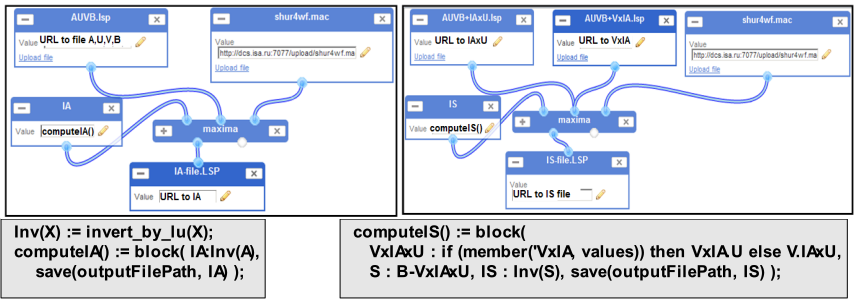
Рис. 2. Примеры «элементарных» блоков сценария обращения в MathCloud и соответствующие функции сценария Maxima

Ниже, на Рис. 3 представлена (во время выполнения) реализация «теоретического» сценария (см. Рис. 1) в редакторе сценариев MathCloud (для простоты, все входные параметры - команды и файлы - скрыты). Детализированный вид верхнего элементарного блока (вычисление A^-1), с соответствующим сценарием Maxima, представлен в левой части Рис. 2 (результат - как переменная с именем «IA» - сохраняется командой «save»). Правая часть Рис. 2 соответствует «центральному» блоку (вычислению S^-1). Здесь демонстрируется нетривиальное поведение сценария (два входных провода к одному порту типа «file»), когда готовность любого из произведений VA ¹ и A ¹U позволяет вычислить дополнение Шура S. В ходе выполнения используется первый пришедшей результат, и альтернативные участки сценария пропускаются (серые блоки «cat» на Рис. 3).

Основной сценарий, показанный на Рис. 3, содержит четыре блока (выделенных овалами), где перемножение матриц может выполняться параллельно. Более того, в соответствии с пояснениями к выражениям (2), каждая из этих операций также может быть распараллелена. На Рис. 4 представлен возможный параллельный сценарий перемножения матриц. Здесь одновременно работают четыре экземпляра Maxima. Данный сценарий был использован в качестве составного сервиса ("VVV_MM_by2x2") в основном сценарии. Таким образом, одновременно работало до восьми экземпляров Maxima.

В таблице 2 время, затраченное на обращение H_N одним процессом Maxima, сравнивается с продолжительностью работы сценария MathCloud на Рис. 3. В таблице 2, в третьем столбце, учтены все "накладные расходы" системы MathCloud (обращения к RESTful сервисам, обмен файлами данных и т.п.). В ходе экспериментов все процессы Maxima запускались сервисом Maxima на одном восьмиядерном хосте. Система управления сценариями MathCloud работала на другом хосте.



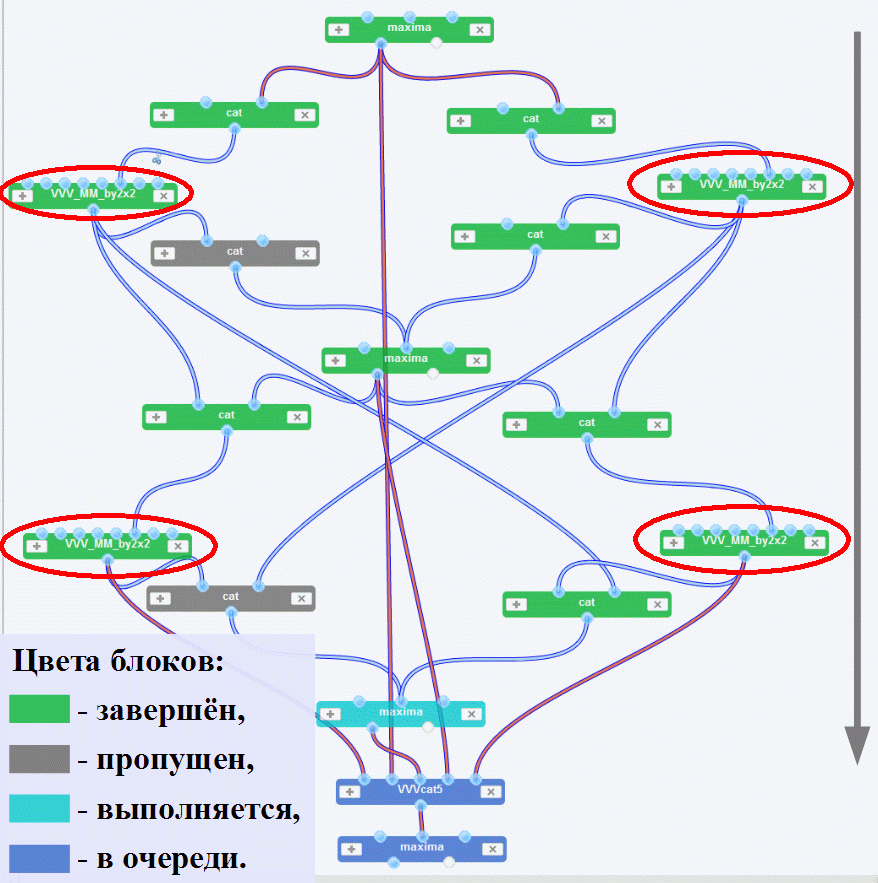
Рис. 3. Основной сценарий (см. Рис. 1) во время выполнения (входные и выходные параметры скрыты)

5. Выводы

1. Распределённый сценарий безошибочного символьного обращения плохо обусловленных матриц был реализован в инфраструктуре MathCloud и проверен на матрицах Гильберта.
   
2. Производительность предлагаемого подхода достаточно хороша для действительно сложных вычислительных задач, когда трудоёмкость вычислений превышает "накладные расходы" (работу системы управления сценариями MathCloud и обмен данными).
   

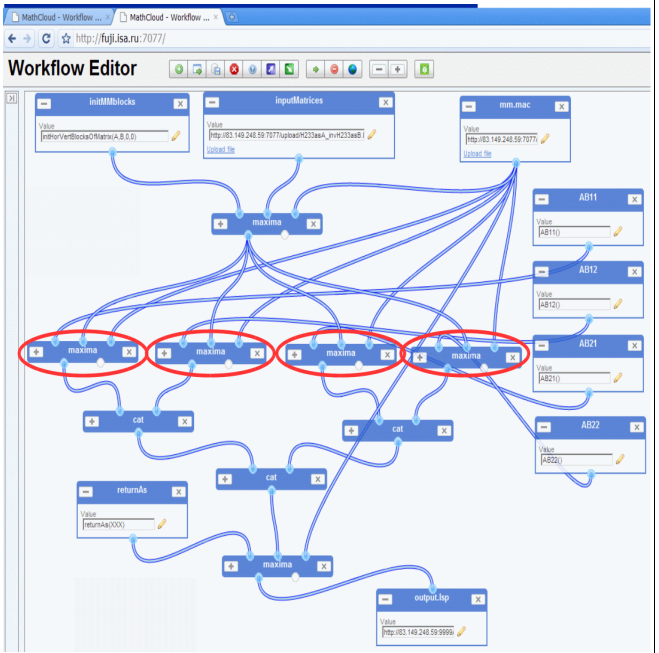
Рис. 4. "Параллельный" сценарий перемножения двух матриц (см. (2)).

Табл. 2. Ускорение обращения матриц H_N в среде MathCloud

CPU Intel Xeon E5410 2.33 GHz (восемь ядер), мин.
N	invH: invert_by_lu(HN)	MathCloud	ускорение, %
200	3	3	134%
300	15	8	191%
400	45	20	218%
500	109	45	244%

Литература

1. K. Hammond, A. Al Zain, G. Cooperman, D. Petcu, and P. Trinder. SymGrid: a Framework for Symbolic Computation on the Grid. In Proc. EuroPar’07 — European Conference on Parallel Processing, LNCS, Rennes, France, 2007. Springer, p. 457-466.

2. Германенко М.И. Программное обеспечение безошибочных дробно-рациональных вычислений и его применение для решения линейных систем // Вестник Нижегородского университета им. Н.И. Лобачевского. 2009. № 4. С. 172-180.

3. [3] Панюков А.В., Германенко М.И. Безошибочное решение систем линейных уравнений // Вестник Южно-Уральского государственного университета. Серия: Математика. Физика. Химия. 2009. № 10. С. 33-40.

4. Волошинов В.В. Символьное обращение плохо обусловленных матриц в Grid-среде сервисов доступа к системе компьютерной алгебры Maxima. Тез. докл. международной конференции "Математическое моделирование и вычислительная физика" - Дубна: ОИЯИ, 2009. c. 175-176., jinr.ru/pdf/Voloshinov.pdf

5. Астафьев А.С., Афанасьев А.П., Лазарев И.В., Сухорослов О.В., Тарасов А.С. Научная сервис-ориентированная среда на основе технологий Web и распределённых вычислений. // Научный сервис в сети Интернет: масштабируемость, параллельность, эффективность: Труды Всероссийской суперкомпьютерной конференции (21-26 сентября 2009 г., г. Новороссийск). – М.: Изд-во МГУ, 2009. – с. 463-467.

6. Лазарев И.В., Сухорослов О.В. Реализация распределенных вычислительных сценариев в среде MathCloud. // Проблемы вычислений в распределенной среде / Под ред. С.В. Емельянова, А.П. Афанасьева. Труды ИСА РАН, Т. 46. - М.: КРАСАНД, 2009. - с. 6-23

7. S.A. Smirnov. On Development of RESTful web Service for a Computer Algebra System in MathCloud Environment // The 4th International Conference "Distributed Computing and Grid-technologies in Science and Education"(GRID'2010), June 28 - July 3, 2010 Dubna, Russia, jinr.ru/files/pdf/maxima.pdf

8. Гантмахер Ф.Р. Теория матриц. - 5-е изд. - М.: Физматлит, 2004. - 560 c.

9. Кормен Т.X., Лейзерсон Ч.И., Ривест Р.Л., Штайн К. Алгоритмы: построение и анализ, 2-е изд.: Пер. с англ. - М.: "Вильямc", 2005. - 1296 с.

10. D. Coppersmith, S. Winograd. Matrix Multiplication via Arithmetic Progressions // J. Symbolic Computation, 1990, No. 9, pp. 251-280.