Списки, очереди, стеки, деревья
| Вид материала | Лабораторная работа |
- Культурология программа курса, 515.05kb.
- М. М. Пришвин «Деревья в плену» Цели урок, 45.79kb.
- Рассказы о деревьях, 1042.66kb.
- Старший дошкольный возраст. Декабрь. Первая–вторая недели Тема: «Лес, деревья, кусты,, 139.55kb.
- Списки для обязательного чтения по программе, 57.64kb.
- Списки для обязательного чтения по программе, 66.45kb.
- Списки для обязательного чтения по программе, 55.84kb.
- Списки для обязательного чтения по программе, 55.48kb.
- Техническое задание на выполнение работы «Реализация мероприятий, направленных на создание, 403kb.
- Понятие вычислительной сети. Основные типы и технологии. Локальные, глобальные и корпоративные, 20.17kb.
Лабораторная работа N 2.5
СПИСКИ, ОЧЕРЕДИ, СТЕКИ, ДЕРЕВЬЯ.
В данной лабораторной работе рассматриваются так называемые динамические структуры данных: списки, очереди, стеки, деревья. Размер и состав структур может изменяться в процессе выполнения программы. Для представления таких структур в компьютере удобно воспользоваться динамической памятью, выделяя память под новые элементы, включаемые в структуру, и освобождая память при исключении элементов.
Каждый элемент динамической структуры данных представляет собой запись, содержащую данные и ссылки (ссылку) на элементы, связанные с ним, - указатели связи. В данных может выделяться специальное поле, идентифицирующее данные, - ключ данных (ключ записи).
Ниже рассматриваются структуры данных и операции над ними.
^ Списки.
Списком называется структура данных, в которой каждый элемент, кроме последнего, содержит ссылку на следующий за ним элемент (рис. 1).
-
ук. нач.
элем.1
элем.2
элем.3
элем.4
рис. 1. Список (однонаправленный линейный список).
Точное название такой структуры - линейный однонаправленный список. Если необходим просмотр «от начала к концу» и «от конца к началу», можно устроить двунаправленный список, дополнив каждый элемент списка ссылкой на предыдущий элемент. Можно закольцевать список, поместив в последний элемент ссылку на начало списка. Мы в дальнейшем под термином “список” будем подразумевать однонаправленный линейный список.
Элемент списка представляет собой запись, содержащую данные и ссылку на следующий за ним элемент (указатель связи). Указатель последней записи списка равен нулю (nil), нулевое значение указателя является признаком конца списка.
Поиск данных в списке. Если список используется для поиска данных, в данных должно быть выделено поле, называемое ключом данных (ключом записи). Поиск данных осуществляется по значению ключа путем просмотра элементов списка, начиная с первого. Средняя длина просмотра - N/2, если ключ содержится в списке, и N, если ключа в списке нет (N - число элементов в списке). Для сокращения длины просмотра на список можно наложить дополнительное условие: элементы списка должны быть упорядочены по значению ключа. В этом случае средняя длина просмотра всегда равна N/2.
Желательно, чтобы функция поиска наряду с ответом «есть - нет» выдавала также и местоположение элемента: указатель на элемент, предшествующий искомому, - если «есть», или указатель на элемент, после которого должен следовать искомый, - если «нет».
^ Вставка элемента в список. Чтобы вставить новый элемент в список необходимо указать данные, составляющие содержание нового элемента, и элемент списка, после которого должен быть помещен вставляемый элемент. Пример вставки нового элемента в список рис.1 рассматривается на рис.2.
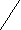

| ук. нач. | | элем.1 | | | элем.2 | | | элем.3 | | | элем.4 | |




-

 нов.эл.
нов.эл.
Рис. 2. Вставка элемента в список.
Новый элемент вставляется после элемента 1. Если до вставки элемент 1 указывал на элемент 2, то после вставки элемент 1 должен указывать на новый элемент и новый элемент - на элемент 2.
Порядок действий при вставке нового элемента:
выделить память для нового элемента;
передать в запись нового элемента данные;
передать указатель связи элемента, предшествующего вставляемому, в указатель связи нового элемента;
передать указатель на новый элемент в указатель связи элемента, предшествующего вставляемому.
Этот порядок действий сохраняется и при вставке нового элемента в конец списка (предшествующий элемент - последний элемент списка). Однако при вставке нового элемента в начало списка этот порядок действий нарушается - отсутствует предшествующий элемент. Для того, чтобы сохранить единообразие действий при вставке/удалении элементов, в начало списка помещается «пустой» элемент, называемый заголовком списка. В этом случае элементу, вставляемому в начало списка, будет предшествовать заголовок списка, порядок действий остается стандартным.
Структура записи заголовка списка такая же, как и у «реальных» элементов списка. Однако информационная часть записи заголовка списка данных не содержит. Она может быть использована для хранения дополнительной информации о списке, например, - о числе элементов списка. Указатель связи записи заголовка указывает на первый «реальный» элемент списка.
При наличии заголовка списка операция «создать пустой список» означает создание заголовка с нулевым значением указателя связи и передачу указателя на заголовок в указатель начала списка.
^ Удаление элемента из списка. Для удаления элемента из списка необходимо указать элемент, предшествующий удаляемому. Пример удаления элемента из списка, указанного на рис.1, рассматривается на рис. 3.
   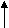 ук. нач. ук. нач. | | Элем.1 | | | элем.2 | | | элем.3 | | | элем.4 | |

Рис. 3. Удаление элемента из списка:
Удаляется элемент, следующий за элементом 2. До удаления элемент 2 указывал на элемент 3, элемент 3 - на элемент 4. После удаления элемент 2 должен указывать на элемент 4, элемент 3 выпадает из цепочки связей. Необходимо только побеспокоиться об освобождении памяти, занятой элементом 3.
Порядок действий при удалении элемента списка:
указатель связи предшествующего элемента передать во вспомогательную переменную - для последующего освобождения памяти;
указатель связи удаляемого элемента передать в указатель связи предшествующего элемента;
освободить память, занимаемую удаляемым элементом.
Этот порядок действий сохраняется и при удалении элемента из конца списка и, - при наличии заголовка, - из начала списка.
Итак для операций вставки и удаления элемента требуется небольшое, не зависящее от длины списка число элементарных действий. Операция поиска требует в среднем просмотра половины списка. Следует отметить, что для определения места вставки/удаления операциям вставки или удаления во многих случаях должна предшествовать операция поиска. В таких случаях операции вставки и удаления требуют просмотра N/2 элементов. Сокращение длины просмотра может быть достигнуто при применении древовидных структур данных (см. ниже).
Очереди.
Очередью называется специальный вид списка, в котором элементы всегда добавляются с одного конца, называемого “конец очереди”, и удаляются всегда с другого конца - “начала очереди”. Говорят, что дисциплина обслуживания очереди - FIFO (ferst in - ferst out). Для работы с очередью наряду с указателем начала удобно иметь также указатель конца очереди (рис. 4).
-
ук. кон.
ук. нач.
элем.1
элем.2
элем.3
элем.4
Рис. 4. Очередь
В очереди в каждый данный момент доступен для работы только элемент в начале очереди. Операции поиска не требуются. Операции добавления и удаления элементов очереди аналогичны соответствующим операциям над списками - с учетом специфических особенностей очереди.
^ Добавление элемента в очередь:
выделить память для нового элемента, передать в запись элемента данные, указатель связи элемента положить равным нулю (nil);
если очередь пуста (указатель начала = nil), указатели начала и конца очереди положить равными указателю на новый элемент;
в противном случае:
в указатель связи последнего элемента (определяется указателем конца очереди), передать указатель на новый элемент;
указатель конца очереди положить равным указателю на новый элемент.
^ Удаление элемента из очереди:
указатель начала очереди передать во вспомогательную переменную для последующего освобождения памяти;
указатель связи первого элемента (определяется указателем начала очереди) передать в указатель начала очереди;
освободить память, занимаемую удаленным элементом.
Признак исчерпания очереди - указатель начала очереди = nil.
^ Стеки.
Стеком называется специальный вид списка, в котором элементы добавляются и удаляются только с одного конца, именуемого вершиной стека (рис. 5). Говорят, что дисциплина обслуживания стека - LIFO (last in - ferst out).
-
ук. верш.
элем.4
элем.3
элем.2
элем.1
Рис. 5. Стек.
В стеке в каждый данный момент доступен для работы только элемент в его вершине.
^ Добавление элемента в стек:
выделить память для нового элемента, передать в запись элемента данные, указатель связи элемента положить равным указателю вершины;
указатель вершины положить равным указателю на новый элемент.
^ Удаление элемента из стека:
указатель вершины передать во вспомогательную переменную для последующего освобождения памяти;
указатель связи элемента в вершине стека передать в указатель вершины;
освободить память, занимаемую удаленным элементом.
Признак исчерпания стека - указатель вершины = nil.
^ Дерево. Двоичное дерево.
Деревом (ориентированным деревом) S=(V,T) называется конечное непустое множество узлов V={vi; i=1, ..., n; n1} и соединяющих узлы ребер T={(v, w) | vV, wV}, для которых:
а) ребра представлены в виде упорядоченных пар узлов (v,w). Узел v называется началом, узел w - концом ребра. Говорят, что ребро идет из v в w;
б) имеется в точности один узел, называемый корнем дерева, в который не входит ни одно ребро;
в) в каждый узел, кроме корня, входит в точности одно ребро;
г) из корня к каждому узлу существует единственный путь. Путем называется последовательность ребер вида (v1,v2), (v2,v3), ..., (vk-1,vk). Число членов последовательности называется длиной пути.
Отметим, что наше определение допускает существование дерева, состоящего только из одного узла (множество T пусто).
Узлы и ребра дерева имеют и другое название - вершины и дуги.
Если существует ребро, идущее из узла v в узел w, узел w называется сыном узла v, узел v - отцом узла w. Узлы, не имеющие сыновей, называются листьями дерева.
Если существует путь из узла v в узел w, узел w называется потомком узла v, узел v - предком узла w. Узел v вместе со своими потомками образует поддерево дерева S. Узел v является корнем этого поддерева.
Глубиной узла в дереве называется длина пути из корня в узел. Высотой узла в дереве называется длина самого длинного пути из узла в лист. Высотой дерева называется высота его корня. Уровнем узла в дереве называется разность между высотой дерева и глубиной узла.
^ Двоичные деревья.
Двоичным (бинарным) деревом называется дерево, у которого:
а) каждый узел имеет не более двух сыновей;
б) каждый сын любого узла идентифицируется как левый либо как правый сын;
в) каждый узел имеет не более одного левого и не более одного правого сына.
В компьютере узлы двоичного дерева представляются в виде записи, содержащей данные и ссылки на правого и левого сыновей. Т.е. ребра дерева представляются в виде ссылок (указателей связи). Нулевое значение указателя означает отсутствие соответствующего сына. Дополнительно к этому в программе должен быть определен указатель корня дерева.
Если дерево используется для поиска данных, то в данных должно быть выделено поле - ключ данных (ключ записи). Поиск данных будет осуществляться по ключу.
Доопределим двоичное дерево. В дополнение к условиям а), б), в) потребуем:
г) ключи узлов (ключи записей) дерева - разные;
д) для каждого узла дерева ключ узла больше ключа левого сына, если он есть, и меньше ключа правого сына, если он есть.
Так определенное двоичное дерево носит название дерева двоичного поиска. Мы в дальнейшем будем называть его двоичным деревом или просто деревом.
Операции над деревом:
^ Добавление элемента в дерево.
выделяем память для нового элемента, передаем в него данные, указатели правого и левого сыновей элемента полагаем равными нулю (nil): новый элемент - всегда лист;
если дерево пусто (указатель корня = nil), новый элемент делаем корнем дерева, положив указатель корня равным указателю на новый элемент;
если дерево не пусто, ищем узел, к которому должен быть подсоединен новый элемент:
полагаем текущий узел равным корню дерева;
если ключ текущего узла больше ключа нового элемента, переходим к левому сыну узла, в противном случае переходим к правому сыну;
повторяем сравнение для нового текущего узла и т.д. Процесс продолжаем до тех пор, пока не получим узел, у которого соответствующий сын отсутствует;
делаем новый элемент сыном этого узла.
Пример: двоичное дерево сформированное для последовательности ключей (40. 80. 20. 60. 10. 70) представлено на рис. 6.

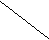
 40
40 

20 80




10 60


70
рис. 6. Двоичное дерево для последовательности ключей
(40, 80, 20, 60, 10, 70).
Можно доказать, что средняя длина просмотра при вставке элемента в дерево по всем деревьям с N узлами равна log2N.
^ Поиск данных в дереве.
в качестве текущего узла выбираем корень дерева;
если ключ текущего узла равен заданному, поиск прекращаем;
в противном случае переходим к левому или правому сыну узла, повторяем сравнения для нового текущего узла и т.д.;
если при очередном сравнении соответствующий (левый или правый) сын узла отсутствует, поиск прекращаем: элемента с заданным ключом в дереве нет.
Как и при вставке элемента, средняя длина просмотра по всем деревьям с N узлами равна log2N.
Желательно, чтобы функция поиска наряду с ответом «есть - нет» выдавала также указатель на отца узла с заданным ключом (ответ «есть») либо на узел, сыном которого должен быть узел с заданным ключом (ответ «нет»).
^ Поиск наибольшего и наименьшего значений ключа в дереве. Для получения наименьшего значения ключа следует, начиная с корня дерева, двигаться по левым сыновьям узлов. Первый узел на этом пути, не имеющий левого сына, содержит наименьший ключ. Для получения наибольшего значения ключа следует двигаться по правым сыновьям узлов.
^ Удаление элемента из дерева. При удалении узла дерева следует побеспокоиться о выполнении условия поиска д). Рассмотрим возможные ситуации:
1) Удаляемый узел - лист. Если этот узел является также и корнем дерева, делаем дерево пустым, полагая указатель корня дерева равным нулю, в противном случае полагаем равным нулю соответствующий указатель отца удаляемого узла. Освобождаем память, занимаемую удаляемым узлом.
2) Удаляемый узел имеет только одного сына. Сына удаляемого узла делаем сыном отца этого узла - тем же (левым или правым), что и удаляемый узел. Если удаляемый узел - корень дерева, новым корнем дерева делаем его сына. Освобождаем память, занимаемую удаляемым узлом.
3) Удаляемый узел имеет двух сыновей. Удалять узел, как это делали ранее, нельзя - мы нарушим условие поиска. В самом деле, даже если отец удаляемого узла имеет одного сына, сделав сыновей узла сыновьями его отца мы отнесем их к правому и левому поддеревьям отца узла - в то время как сыновья узла по отношению к его отцу должны находиться в одном поддереве - левом или правом. Для сохранения условия поиска на место данных, содержащихся в удаляемом узле, следует поместить либо данные из левого поддерева удаляемого узла, содержащие наибольший ключ, либо данные из правого поддерева, содержащие наименьший ключ, затем - удалить узел, содержащий данные. Будем выбирать наименьший ключ правого поддерева: ищем соответствующий узел, передаем данные из записи найденного узла в запись удаляемого узла, удаляем найденный узел. Отметим, что найденный узел будет листом или узлом с одним сыном. Удаление такого узла затруднений не представляет.
Если удаляемый узел - корень дерева, удаление выполняется по тем же правилам.
Пример: на рис. 7 представлены результаты удаления из дерева, изображенного на рис. 6: а) листа (ключ 10), б) узла, имеющего одного сына (ключ 60), в) узла, имеющего двух сыновей (ключ 40).



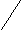
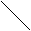
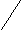
 40 .... 40 ..... 60
40 .... 40 ..... 60 





20 80. .... 20 80 ..... 20 80





60 ..... 0 70 . .... 10 70

70..... .....
а) б) в)
рис. 7. Дерево рис. 6 после удаления элементов: 10 (а), 60 (б), 40 (в).
Обход дерева. Обход требуется в тех случаях, когда необходимо просмотреть все записи дерева. Выбор метода обхода определяется решаемой задачей. Некоторые методы рассматриваются ниже.
^ Обход в глубину. Для каждого узла дерева, начиная с корня, посещаем узел, затем - левое поддерево узла, если оно есть, затем - правое поддерево, если оно есть.
Алгоритм обхода задается рекурсивной процедурой.
procedure ОБХОД_ГЛУБ(узел: элем; ОБРАБ: процедура);
begin
if есть левый сын узла then ОБХОД_ГЛУБ(левый сын, ОБРАБ);
if есть правый сын узла then ОБХОД_ГЛУБ(правый сын, ОБРАБ);
end;
Аргументами процедуры являются указатель текущего узла дерева и имя процедуры обработки записи узла. Первоначальное (из основной программы) обращение к процедуре имеет вид
ОБХОД_ГЛУБ(корень, ОБРАБ);
Пример: для дерева, изображенного на рис. 8, обход в глубину даст следующий порядок обработки узлов: A, B, C, D, E, F, K, L, J, H, I. Подчеркнем, что буквы в узлах дерева - имена (но не ключи!) узлов.




A
B
C
D
H
I
E
L
F


K



J

Рис. 8. Двоичное дерево. Буквы в узлах дерева - имена узлов.
При не рекурсивной реализации алгоритма обхода в глубину для фиксации текущего пути (корней поддеревьев) необходимо использовать стек. Заметим, что аналогичный стек автоматически строится в стековой памяти в процессе рекурсивных обращений к процедуре ОБХОД_ГЛУБ.
Алгоритм обхода имеет вид
создать пустой стек;
поместить в стек корень дерева;
while стек не пуст do
begin
тек. узел := вершина стека;
ОБРАБ(тек. Узел);
удалить вершину стека;
while есть левый сын тек. узла do
begin
if есть правый сын тек. узла then добавить правый сын в стек;
тек. узел := левый сын тек. узла;
ОБРАБ(тек. узел);
end;
end;
Заметим, что пересылка данных в операциях присваивания типа «тек. узел := вершина стека», «добавить узел в стек» не требуется. Соответствующие действия можно выполнить на уровне указателей узлов.
^ Обход дерева в ширину. Обход предполагает посещение узлов дерева слева направо, уровень за уровнем, начиная с уровня корня. Для дерева, изображенного на рис. 8, обход в ширину даст следующий порядок обработки узлов: A, B, H, C, D, I, E, J, F, K, L.
Для реализации алгоритма удобно использовать очередь, Алгоритм обхода имеет вид
создать пустую очередь;
поместить в очередь корень дерева;
while очередь не пуста do
begin
тек. узел := элемент из начала очереди;
удалить элемент из очереди;
ОБРАБ(тек. узел);
if левый сын тек. узла есть then добавить в очередь левый сын;
if правый сын тек. узла есть then добавить в очередь правый сын;
end;
Как и в предыдущем алгоритме, действия над узлами следует заменить действиями над указателями узлов.
^ Обход в порядке возрастания значений ключа. Используем следующие свойства двоичного дерева:
1) Для поиска минимального значения ключа в дереве или поддереве необходимо, начиная с корня, двигаться по левым сыновьям узлов до тех пор, пока не получим узел, не имеющий левого сына.
2) Для любого узла дерева значение ключа узла больше значений ключа узлов его левого поддерева и меньше значений ключа узлов его правого поддерева.
Алгоритм обхода имеет вид
создать пустой стек;
поместить корень дерева в стек;
while стек не пуст do
begin
while есть левый сын вершины стека do
добавить левый сын вершины в стек;
while нет правого сына вершины and стек не пуст do
begin
ОБРАБ(вершина стека);
удалить вершину из стека;
end;
if стек не пуст then
begin
ОБРАБ(вершина стека);
тек. узел := вершина стека;
удалить вершину из стека;
добавить правый сын тек. узла в стек;
end;
end;
Для дерева, изображенного на рис. 8, алгоритм обхода даст следующий порядок обработки узлов: C, B, F, E, L, K, D, J, A, H, I. Напомним, что буквы на рис. 8 обозначают имена (а не ключи!) узлов.
Задания.
В заданиях 1 - 16 узлы двоичного дерева Т представляются записями, содержащими
ключ типа integer;
элемент данных типа real, если не оговорен другой тип;
указатели левого и правого сыновей.
Требуется:
а) Построить дерево Т. Данные для построения (ключи и элементы данных) читаются из текстового файла.
б) Выполнить работу, предусмотренную в задании, все действия выполняются над записями узлов дерева.
1. Составить программу печати ключей и элементов данных из всех листьев дерева Т.
2. Составить программу печати среднего арифметического всех элементов данных дерева Т.
3. Дерево Т содержит элементы данных типа сhar. Составить программу печати количества вхождений прописных букв латинского алфавита в дерево Т.
4. Составить программу, которая заменяет все отрицательные элементы данных в дереве Т на их абсолютные значения . Напечатать ключи и элементы данных дерева по уровням, уровень 0 - уровень корня.
5. Составить программу печати ключей и элементов данных дерева Т, которым соответствуют ключи, меньшие заданного ключа k1.
6. Составить программу, которая удаляет все узлы дерева Т с ключами, большими заданного ключа k1.
7. Составить программу удаления узла дерева Т, ключ которого равен заданному ключу k1. Напечатать ключи и элементы данных полученного дерева по уровням, уровень 0 - уровень корня.
8. Составить программу печати в порядке возрастания значений ключа ключей и элементов данных дерева Т, которым соответствуют ключи, меньшие целой части среднего арифметического наибольшего и наименьшего ключей в дереве Т.
9. Составить программу печати максимального из элементов данных дерева Т по всем элементам, которым соответствуют ключи, меньше заданного ключа k1.
10. Составить программу, которая меняет местами максимальный и минимальный элементы данных в дереве Т, все элементы данных которого предполагаются различными.
11. Составить программу , которая печатает все элементы данных дерева Т по уровням: сначала - из корня дерева, затем ( слева направо) - из вершин, дочерних по отношению к корню, затем (также слева направо) - из вершин, дочерних по отношению к этим вершинам, и т. д..
12. Элементы данных дерева Т имеют тип integer. Составить программу , которая находит длину пути от корня до ближайшей вершины с элементом данных Е. Напечатать ключ вершины и длину пути. Если Е не входит в дерево Т, за ответ принять -1.
13. Составить программу, которая находит число вершин на n- ом уровне дерева Т. Корень считать вершиной 0-го уровня.
14. Составить программу , которая находит высоту дерева Т, т.е. число ребер на самом длинном из путей от корня дерева до листа.
15. Составить программу , которая находит длины путей от корня дерева до листьев. Напечатать длины путей и ключи листьев.
16. Составить программу , которая удаляет листья на n- ом уровне дерева Т. Напечатать ключи и элементы данных полученного дерева по уровням, уровень 0 - уровень корня.
В задачах 17 - 22 многочлен P(x) = anxn + an-1xn-1+...+a1x+a0 представляется в виде списка (рис.9a). Если для некоторых 0 i







n
an
n-1



an-1



1
a1



0
a0



40
52



8
-3



1
1
nil
nil
P
S








а)
б)
Рис. 9. Представление многочлена в виде списка.
17. Составить программу, которая считывает из входного файла безошибочную запись многочлена, формирует соответствующий список-многочлен p, дифференцирует многочлен и печатает математическую запись результирующего многочлена. Например, многочлен из рис.9б программа должна напечатать как 52x**40-3x**8+x.
18. Составить программу , которая считывает из входного файла безошибочную запись многочлена, формирует соответствующий список-многочлен p, вычисляет многочлен в заданной точке х и печатает математическую запись многочлена, знак “=”, числовое значение многочлена, текст “при х=”, числовое значение х. Например, значение многочлена из рис.9б при х=1 программа должна напечатать как 52x**40-3x**8+x=50 при х=1.
19. Составить программу , которая считывает из входного файла безошибочные записи двух многочленов p(x) и q(x), формирует соответствующие списки-многочлены p и q, проверяет на равенство многочлены p и q, печатает их математические записи и знак «=» или «<>» между ними.
20. Составить программу , которая считывает из входного файла безошибочные записи двух многочленов p(x) и q(x), формирует соответствующие списки-многочлены p и q, находит их сумму и печатает ее математическую запись. Например, многочлен из рис.9б программа должна напечатать как 52x**40-3x**8+x.
21. Составить программу, которая считывает из входного файла безошибочную запись многочлена p(x) , приводит подобные члены, располагает его по убыванию степеней х и печатает его математическую запись. Например, многочлен из рис.9б программа должна напечатать как 52x**40-3x**8+x.
22. Составить программу , которая считывает из входного файла безошибочные записи двух многочленов p(x) и q(x), формирует соответствующие списки-многочлены p и q, находит их произведение и печатает его математическую запись. Например ,многочлен из рис.9б программа должна напечатать как 52x**40-3x**8+x.
23. Используя очередь или стек, решить задачу: в файле записан текст, сбалансированный по круглым скобкам. Для каждой пары соответствующих открывающей и закрывающей скобок напечатать номера их позиций в тексте, упорядочив пары номеров по возрастанию номеров позиций закрывающих скобок. Например, для текста a+(45-f(x)*(b-c)) надо напечатать: 8,10; 12,16; 3,17.
24. Используя очередь или стек, решить задачу: в файле записан текст, сбалансированный по круглым скобкам. Для каждой пары соответствующих открывающей и закрывающей скобок напечатать номера их позиций в тексте, упорядочив пары номеров по возрастанию номеров позиций открывающих скобок. Например, для текста a+(45-f(x)*(b-c)) надо напечатать: 3,17; 8,10; 12,16.
25. Предложить и описать на Паскале представление файлов из элементов некоторого типа в виде списков. Определить функцию eof1(f) и процедуры reset1(f), read1(f, x), rewrite1(f) и write1(f, x), реализующие при таком представлении файлов действия соответствующих стандартных функций и процедур.
26. Из заданных n предметов выбрать такие, чтобы суммарный вес был менее 30 кг, а стоимость - наибольшей. Напечатать суммарную стоимость выбранных предметов.
Указание. Определим дерево вариантов следующим образом: На очередном ходе i=1, 2,..., n будем рассматривать предмет с номером i, а вариантов j хода i всегда будет два: j=0 означает брать предмет, j=1 означает не брать его. Получится двоичное дерево, все ветви которого имеют длину n.
При рассмотрении вариантов важно прекращать перебор, как только станет ясно, что он не представляет интереса.
При движении вперед мы пытаемся добавить предмет (если вес меньше 30). В этом случае мы идем по левой ветке. Если же предмет добавить нельзя, то мы его не берем (т. е. движемся по правой ветке, отбрасывая все дерево вариантов, идущих влево). В обоих случаях продолжаем двигаться вперед пока не будет рассмотрен последний предмет. Если все предметы рассмотрены, то вариант получен. Он сравнивается со стоимостью и начинается движение назад и т. д.
Литература.
Литература
1. А.В. Крячков, И.В. Сухинина, В.К. Томшин Программирование на С и С++, практикум , изд-во Радио и связь,1997.
2. Абрамов В. Г., Трифонов Н. П., Трифонова Г. Н. Введение в язык Паскаль. М., Наука, 1988.
3. Касьянов В. Н., Сабельфельд В. К. Сборник заданий по практикуму на ЭВМ. М.: Наука, 1986.
4. Вирт Н. Алгоритмы + структуры данных = программы. М., Мир, 1985.
