Методические рекомендации по подготовке к сдаче государственного экзамена Раздел «Математика»

Вид материала

Методические рекомендации

Содержание Содержание ответа Кольцо многочленов. Теорема Кронекера – Капелли. Неприводимые многочлены. Разложение в произведение неприводимых многочленов. Основная теорема алгебры (без доказательства). Следствия. Формулы Виета. Евклидовы действительные пространства. Процесс ортогонализации. Теорема Лагранжа. Нормальные делители. Фактор-группы. Изоморфизм групп. Теорема Кэли. Рациональные корни целочисленных многочленов. Доказать, что ортогональное дополнение подпространства является подпространством. Представление Евклидова пространства в виде прямой суммы подпространства

Подобный материал:

• Методические рекомендации по подготовке Ульяновск, 1747.38kb.
• Методические рекомендации по подготовке к сдаче государственного экзамена Раздел «Математика», 38.2kb.
• Методические рекомендации по подготовке к сдаче междисциплинарного экзамена по курсу, 557.37kb.
• Методические рекомендации по подготовке к сдаче кандидатского экзамена «История и философия, 864.71kb.
• Методические рекомендации по подготовке к сдаче кандидатского экзамена «История и философия, 868.92kb.
• Методические рекомендации по подготовке к сдаче кандидатского экзамена по дисциплине, 285.36kb.
• Методические рекомендации по подготовке к сдаче кандидатского экзамена по дисциплине, 495.55kb.
• Методические указания для студентов 5 курса лечебного факультета по подготовке к сдаче, 718.25kb.
• Программа государственного итогового междисциплинарного экзамена по специальности 080109., 768.85kb.
• Психолого-педагогические рекомендации по подготовке к сдаче единого экзамена, 94.44kb.

Методические рекомендации
по подготовке к сдаче государственного экзамена


Раздел «Математика»


Выписка из Государственного стандарта по дисциплине «Алгебра»

Понятия группы, кольца, поля. Алгебры, алгебраические системы. Кольца классов вычетов. Поле комплексных чисел. Кольцо многочленов от одной переменной над полем. Теория делимости.

Системы линейных уравнений. Матрицы и определители. Векторные пространства. Евклидовы пространства. Линейные преобразования и их матрицы. Собственные векторы и собственные значения линейных операторов.

Подгруппы. Смежные классы по подгруппе, фактор-группы. Подкольца. Идеалы кольца, фактор-кольца. Кольца главных идеалов. Евклидовы и факториальные кольца. Факториальность кольца многочленов над факториальным кольцом.

Многочлены от нескольких переменных, симметрические многочлены. Алгебраическая замкнутость поля комплексных чисел. Неприводимые над полем действительных чисел многочлены. Расширения полей, алгебраические и конечные расширения, приложение к задачам на построение с помощью циркуля и линейки.


Содержание ответов на экзаменационные вопросы по дисциплине «Алгебра»

1. Однородные системы линейных уравнений (общее решение, фундаментальная система решений). Пространство решений. Связь решений неоднородной и соответствующей однородной систем линейных уравнений.
   

^ Содержание ответа: Общий вид однородной системы m линейных уравнений (СЛОУ) от n неизвестных, матричная запись СЛОУ. Приведение матрицы соответствующей СЛОУ к ступенчатому виду с помощью элементарных преобразований. Определение общего решения и фундаментальной системы решений СЛУ. Умение применять различные методы решения СЛУ в зависимости от количества неизвестных и уравнений. Определение неоднородной системы m линейных уравнений (СЛНУ) от n неизвестных, Связь решений неоднородной и соответствующей однородной систем линейных уравнений. (см. [1], [6], [9])

2. ^ Кольцо многочленов.
   

Содержание ответа: Определение многочлена от одного неизвестного степени 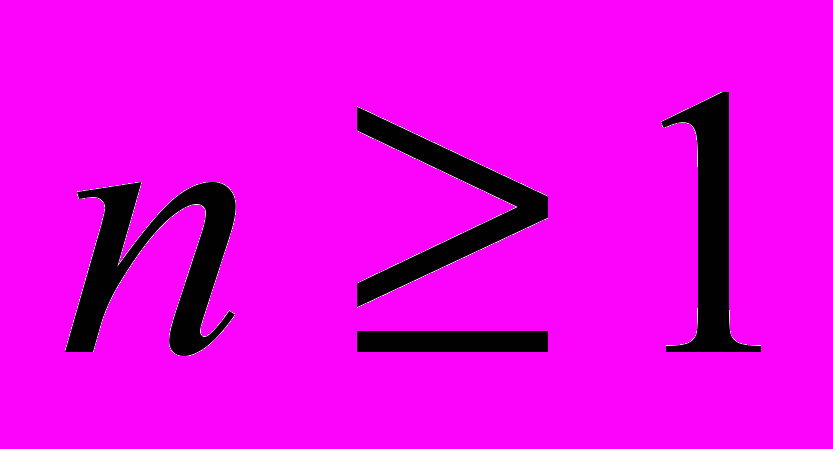, также многочлена нулевой степени. Уметь слаживать и умножать два многочлена разных степеней, уметь определять степень многочлена, полученного сложением и умножением двух многочленов. Алгоритм Евклида при делении двух многочленов. Нахождение наибольшего общего делителя двух многочленов с помощью алгоритма Евклида. (см. [1], [2], [6], [9])

3. ^ Теорема Кронекера – Капелли.
   

Содержание ответа: Сформулировать теорему. При доказательстве теоремы нужно знать: определение ступенчатой матрицы, приведение матрицы к ступенчатому виду с помощью элементарных преобразований строк, ранг эквивалентных матриц. Уметь выделять основную и расширенную матрицы соответствующие данной системе линейных уравнений. Определение совместности СЛУ. (см. [1], [2], [6], [9])

4. ^ Неприводимые многочлены. Разложение в произведение неприводимых многочленов.
   

Содержание ответа: Общий вид многочлена от одного неизвестного степени 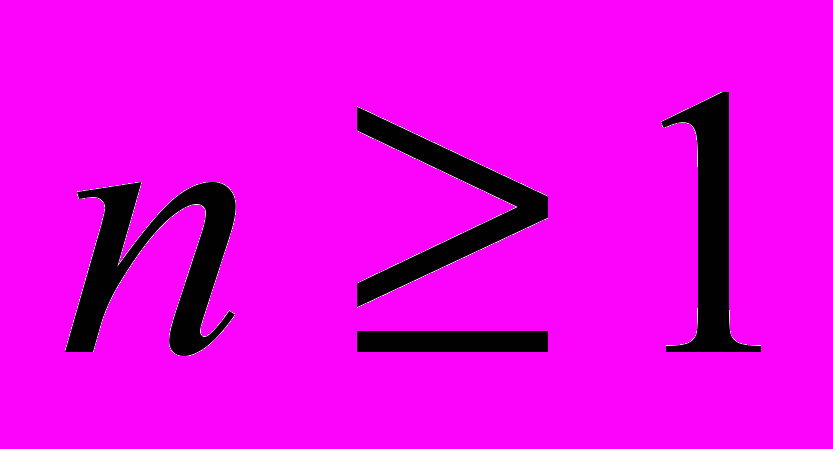, дать определение неприводимого многочлена. Делимость любого многочлена степени 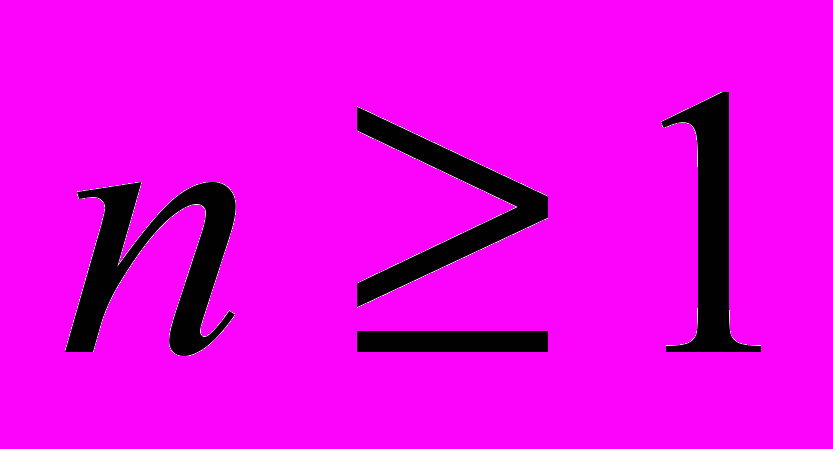по крайней мере на один неприводимый многочлен. Единственность представления всякого многочлена степени 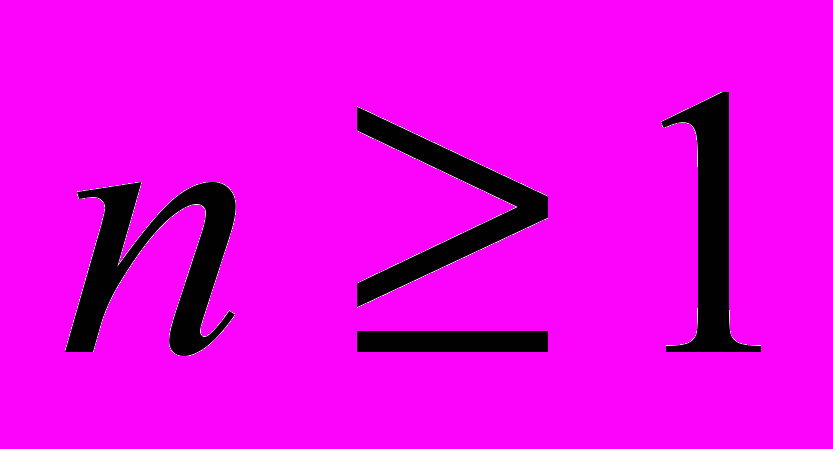в виде произведения неприводимых многочленов и его доказательство. (см. [1], [2], [6], [9])

5. Квадратичные формы. Приведение квадратичной формы к каноническому виду (основная теорема).

Содержание ответа: Определение квадратичной формы 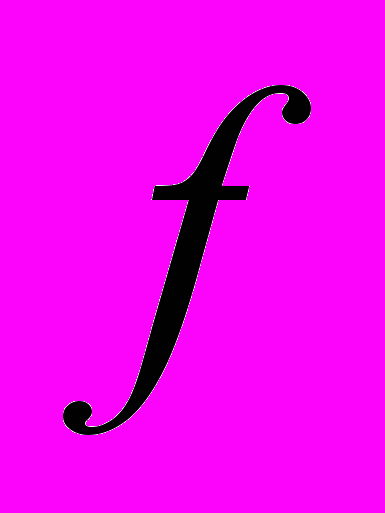от 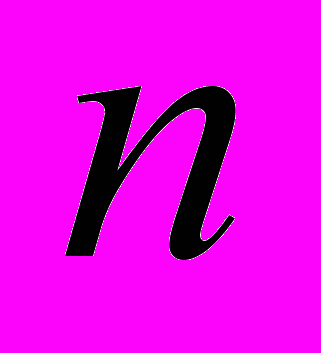неизвестных 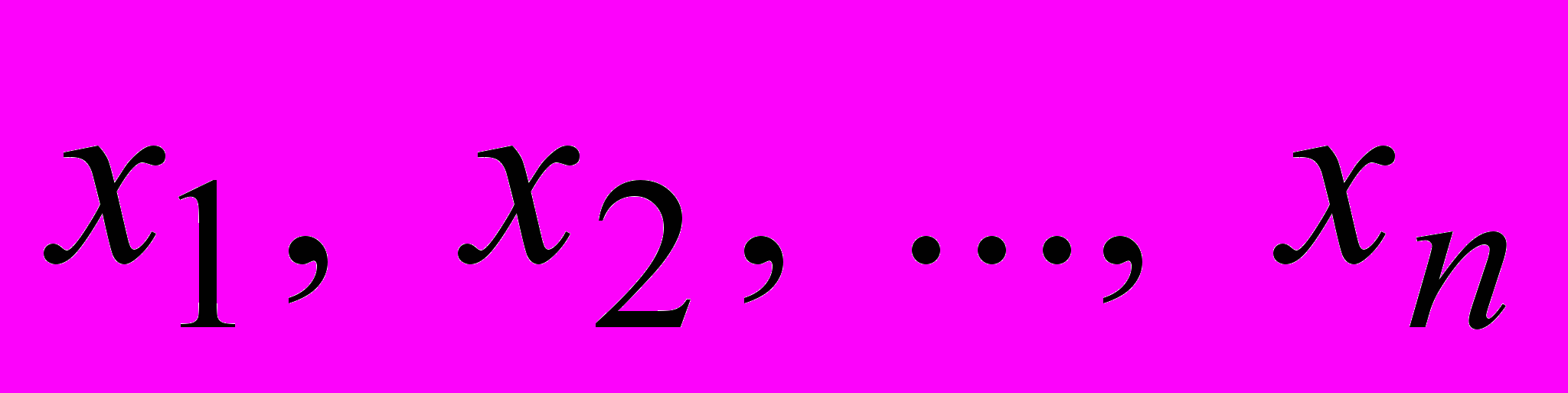, действительные и комплексные квадратичные формы, канонический и нормальный виды квадратичной формы. Теорема о том, что всякую квадратичную форму с помощью некоторого невырожденного линейного преобразования можно привести к каноническому виду и его доказательство. (см. [1], [6], [9])

6. ^ Основная теорема алгебры (без доказательства). Следствия. Формулы Виета.

Содержание ответа: Общий вид многочлена от одного неизвестного степени , дать определение приведенного многочлена. Сформулировать основную теорему, следствия. Дать определение корней многочлена. Написать формулы Виета. И показать применение формул Виета для квадратного уравнения. (см. [1], [2], [6], [9])

7. ^ Евклидовы действительные пространства. Процесс ортогонализации.
   

Содержание ответа: Определение линейного пространства, Евклидова пространства. Дать определение скалярного произведения векторов через координаты сомножителей. Знать понятие ортогональности системы векторов. Показать процесс ортогонализации данной системы векторов, при этом уметь применять свойства скалярного произведения векторов. (см. [1], [6], [9])

7. ^ Теорема Лагранжа. Нормальные делители. Фактор-группы.
   

Содержание ответа: Понятие группы, конечной группы, циклической группы, порядка группы. Подгруппа группы, индекс подгруппы группы. Сформулировать теорему. При доказательстве теоремы надо знать: левосторонние и правосторонние разложения группы по подгруппе; их классы; порядок всякого элемента конечной группы. (см. [1], [2], [6], [9], [10], [11])

7. ^ Изоморфизм групп. Теорема Кэли.
   

Содержание ответа: Определение группы, соотношение между элементами двух изоморфных групп, привести пример абелевой группы. Определение конечной группы, подгруппы группы, симметрической группы, степень группы. Сформулировать теорему. Изоморфное соотношение элементов конечной группы в группу S_n, регулярность подгрупп симметрических групп. (см. [2], [6], [9], [10], [11])

7. ^ Рациональные корни целочисленных многочленов.
   

Содержание ответа: Общий вид многочлена от одного неизвестного степени 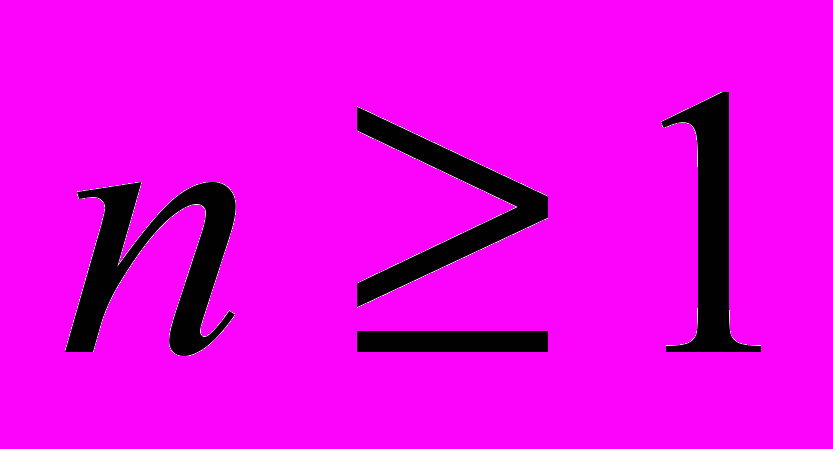, все коэффициенты которого целые числа. Определение корней многочлена. Критерий существования рациональных корней многочлена. Привести пример. (см. [1], [2], [6], [7], [9])

7. Кратные корни. Теорема о кратных корнях.
   

Содержание ответа: Общий вид многочлена от одного неизвестного степени 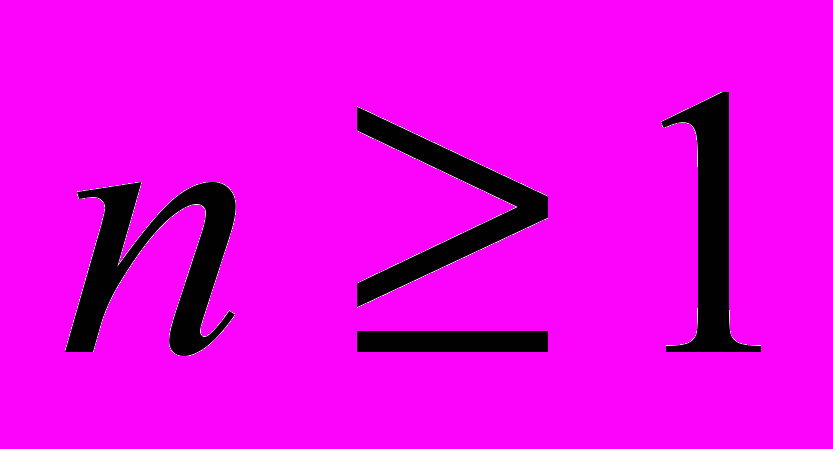. Определение корня многочлена, кратности корня многочлена, простого корня. Определение кратности корня многочлена с помощью схемы Горнера. Сформулировать теорему и его доказательство. Связь понятия кратного корня с понятием производной от многочлена. (см. [1], [2], [6], [7], [9])

7. ^ Доказать, что ортогональное дополнение подпространства является подпространством.
   

Содержание ответа: Понятие скалярного произведения векторов, линейной зависимости векторов. Решение системы линейных однородных уравнений, ранга системы уравнений. Определение ортогонального дополнения подпространства. (см. [1], [6], [8], [10], [11])

7. ^ Представление Евклидова пространства в виде прямой суммы подпространства L и его ортогонального дополнения.
   

Содержание ответа: Понятие скалярного произведения векторов, линейной зависимости векторов. Решение системы линейных однородных уравнений, ранга системы уравнений. Определение Евклидова пространства, подпространства линейного пространства, ортогонального дополнения подпространства. (см. [2], [3], [4], [6], [7], [8], [9])

1. А.Г. Курош. Курс высшей алгебры. СПб.: Лань, 2005.
   
2. Л.А. Скорняков. Элементы алгебры. СПб.: Лань, 2005.
   
3. М.М. Глухов, А.С. Солодовников. Задачник – практикум по высшей алгебре. СПб.: Лань, 2005.
   
4. В.А. Ильин, Э.Г. Позняк. Линейная алгебра. М.:ФИЗМАТЛИТ, 2005.
   
5. И.В. Проскуряков. Сборник задач по линейной алгебре. М.: Бином, 2005.
   
6. Фаддеев Д.К. Лекции по алгебре: Учебное пособие для вузов. СПб.: Издательство "Лань", 2002.
   
7. А.И.Мальцев. Основы линейной алгебры, изд. 2. М.: Гостехиздат, 1956.
   
8. И.А Мальцев. Линейная алгебра. Новосибирск.: Изд-во Ин-та математики, 2001.
   
9. Л.Я.Окунев. Высшая алгебра, изд. 2. М.: Просвещение, 1966.
   
10. Курош А.Г. Теория групп. М.: Наука, 1967.
    
11. Каргополов М.И., Мерзляков Ю.И. Основы теории групп. М., 1972.