Отделение Программной Инженерии программа дисциплины

Вид материала

Содержание

Подобный материал:

Правительство Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

Национальный исследовательский университет
"Высшая школа экономики"

Факультет Бизнес-информатики

Отделение Программной Инженерии

Программа дисциплины

Алгебра

Для направления 231000.62 «Программная инженерия»

подготовки бакалавра

(2010 – 2011 учебный год)

Автор программы:

к.ф.-м.н, доцент И.А. Чубаров

^

Рекомендована секцией УМС Одобрена на заседании кафедры

По бизнес-информатике Высшей математики

на факультете Экономики

Председатель Г.А. Левочкина Зав. кафедрой Ф.Т. Алескеров

__________________ ________________________________

«_____» __________________ 2011 г. «____»__________________ 2011 г

Утверждена Ученым Советом

Факультета Бизнес-информатики

Ученый секретарь В.А. Фомичев

_________________________________

« ____» ___________________2011 г.

Москва 2011

^ Пояснительная записка

Автор программы:

к.ф.-м.н, доцент И.А. Чубаров

Общие сведения об учебном курсе.

Курс читается студентам бакалавриата отделения программной инженерии факультета бизнес-информатики ГУ ВШЭ. Он входит в состав вузовского компонента блока общих математических и естественно-научных дисциплин, определяющих специализацию «Программная инженерия». Курс читается в 1 – 3 модулях первого учебного года. Количество кредитов – 6. Продолжительность курса составляет 104 аудиторных учебных часа (26 недель), в том числе 52 часа лекций, 52 часа семинарских занятий и 112 часов самостоятельной работы, всего 216 часов. Рубежный контроль включает 1 домашнее задание и 2 контрольные работы, зачет по окончании 2 модуля и экзамен по окончании 3 модуля.

Требования к студентам:

Освоение курса не требует никакой предварительной подготовки, помимо школьного курса алгебры и начал анализа, и доступно всем студентам, поступившим на 1 курс.

Учебная задача курса:

Развить математический кругозор и алгебраическое мышление студентов. Обучить студентов важнейшим теоретическим положениям линейной алгебры, началам абстрактной алгебры, матричным методам, выработать у них навыки решения задач, требующих исследования систем линейных уравнений, применения матричных вычислений, многомерной геометрии, линейных операторов.

В результате изучения курса студенты должны:

- знать точные формулировки основных понятий, уметь интерпретировать их на простых модельных примерах;

- знать основные понятия и теоремы о системах линейных уравнений, матрицах и определителях, уметь решать и исследовать системы линейных уравнений при помощи алгоритма Гаусса, вычислять ранги матриц, вычислять определители матриц, пользуясь свойствами определителей, выполнять операции над матрицами.

- знать основные понятия современной алгебры: группы, кольца, поля, важнейшие примеры алгебраических систем, изоморфизмы, гомоморфизмы, теоремы о строении групп, колец и полей, уметь выяснять, является ли данное множество группой, кольцом или полем, устанавливать изоморфизмы, гомоморфизмы между ними.

- знать основные понятия и теоремы, относящиеся к линейным пространствам: примеры пространств, подпространств, операции над подпространствами, линейные отображения и преобразования, собственные векторы, евклидовы пространства, квадратичные формы, уметь находить базисы конечномерных линейных пространств и подпространств, координаты векторов, решать задачи о линейных операторах при помощи матриц, решать простейшие задачи геометрии евклидовых пространств, приводить к простейшему виду квадратичные формы, исследовать их на знакоопределенность.

- знать элементы векторной алгебры и метод координат на плоскости и в трехмерном пространстве, уметь производить операции над векторами, составлять и преобразовывать уравнения прямых и плоскостей, решать метрические задачи о прямых и плоскостях.

Аннотация:

Курс соответствует государственному образовательному стандарту высшего профессионального образования по направлению подготовки бакалавров 231000 – Программная инженерия. Он включает основы теории матриц, современной абстрактной и линейной алгебры, необходимые как для изучения других математических и естественно - научных дисциплин, так и для профессиональной деятельности бакалавра по направлению подготовки 231000 - Программная инженерия.

^ Тематический план учебной дисциплины

№	Название темы	Всего часов	Аудиторные часы		^ Самостоя-тельная работа
№	Название темы	Всего часов	Лекции	Семина- ры	^ Самостоя-тельная работа
	1 модуль
1 2	Системы линейных уравнений, матрицы Элементы общей алгебры	68	16	16	36
	2 модуль
3 4 5	Определители Векторная алгебра. Координаты. Линейные пространства: арифметическое пространство, ранг матрицы, системы линейных уравнений	68	16	16	36
	3 модуль
5	Линейные пространства (окончание) : аксиомы, размерность, подпространства. Билинейные и квадратичные функции. Линейные отображения и операторы Евклидово пространство, линейные операторы и квадратичные формы в евклидовом пространстве.	80	20	20	40
	Итого	216	52	52	112

^ Формы рубежного контроля и правила вывода оценок зачета и экзамена

Предусмотрены 2 контрольные работы (в первом и втором модулях) и 1 домашнее задание (для оценки выполнения домашнего задания проводится контрольная работа в третьем модуле). Во втором модуле проводится зачет, в третьем модуле – экзамен.

Оценки выводятся по следующим формулам.

^ Накопленная оценка за 1 – 2 модули:

«НО1» = 0,4 «О_Кр1мод» + 0,4 «О_{Дз1-2мод}» + 0,2· «О_сем». («О_сем » - оценка за участие в семинарах и выполнение текущих домашних работ).

Результирующая оценка за зачет (2 модуль) «О_Зач» = 0,4 «НО1» + 0,6 «О_{Зач.раб.}».

Накопленная оценка за 3 модуль:

«НО2» = 0,2 «О_Зач » + 0,6 «О_{Дз3 мод}» + 0,2· «О_сем».

Результирующая оценка за экзамен «О_Экз» = 0,4 «НО2» + 0,6 «О_{Экз.раб.}»

по десятибалльной шкале.

В зачетную (экзаменационную) ведомость выставляются три оценки: накопленная, зачетная (экзаменационная) и результирующая (неудовлетворительная оценка за зачет (экзамен) является блокирующей и выставляется как результирующая без учета накопленной оценки). В зачетную книжку выставляется результирующая оценка. В экзаменационную ведомость и зачетную книжку студента выставляется также и оценка по данной дисциплине по пятибалльной шкале, получаемая из оценки по десятибалльной шкале в соответствии с приведенной ниже таблицей соответствия (см. Приложение № 2 к приказу Ректора ГУ-ВШЭ № 1002 от 17.06.2002)

^ Таблица соответствия оценок

по десятибалльной и пятибалльной системам.

По десятибалльной шкале	По пятибалльной шкале
1  неудовлетворительно 2  очень плохо 3  плохо	неудовлетворительно  2
4  удовлетворительно 5  весьма удовлетворительно	удовлетворительно  3
6  хорошо 7  очень хорошо	хорошо  4
8  почти отлично 9  отлично 10 блестяще	отлично  5

Образцы типовых задач приводятся после программы.

^ Содержание программы

Системы линейных уравнений, матрицы

Системы линейных уравнений 2-го и 3-го порядков. Определители 2-го и 3-го порядков, правило Крамера решения системы линейных уравнений 2 и 3 порядков.
Системы линейных уравнений (общий случай). Алгоритм Гаусса. Главные и свободные неизвестные. Общее решение неоднородной системы.
Матрицы. Сложение матриц, умножение матрицы на число, свойства этих операций.
Умножение матриц и его свойства. Обратная матрица. Элементарные матрицы. Вычисление обратной матрицы с помощью элементарных преобразований. Матричные уравнения AX = B, XA = B.

Элементы общей алгебры

Множества, операции над ними, отображения множеств. Бинарные отношения, отношение эквивалентности. Подсчет числа элементов конечных множеств.
Алгебраические операции. Обзор алгебраических систем с одной и двумя бинарными алгебраическими операциями. Полугруппы и моноиды. Примеры.
Группы, подгруппы, изоморфизм групп. Циклические группы и порядки элементов. Группы классов вычетов по модулю n.

Примеры групп: группы вращений на плоскости, группы диэдра, группа кватернионов.

Смежные классы по подгруппе. Теорема Лагранжа. Гомоморфизмы и изоморфизмы групп.
Перестановки и подстановки, их перемножение. Разложение подстановок в произведение транспозиций и независимых циклов. Четность перестановок. Симметрические и знакопеременные группы.
Кольца. Примеры: числовые кольца, кольцо вычетов целых чисел по модулю n. Делители нуля и обратимые элементы. Подкольца в кольцах. Кольцо квадратных матриц.
Кольцо многочленов от одной переменной. Деление многочленов с остатком. Алгоритм Евклида вычисления наибольшего общего делителя. Корни многочленов, разложение многочленов на неприводимые множители (в том числе над R и C). Теорема Виета.
Поля. Поле комплексных чисел. Алгебраическая и тригонометрическая запись комплексных чисел. Формула Муавра. Корни из комплексных чисел. Мультипликативная группа C* и ее подгруппы.
Дальнейшие примеры полей: числовые поля, поле вычетов целых чисел по простому модулю, рациональные дроби. Понятие характеристики поля. Конечные поля.

Определители

Определитель квадратной матрицы (формула полного разложения определителя). Свойства определителей. Миноры, алгебраические дополнения, разложение определителя по элементам строки и столбца. Фальшивое разложение. Способы вычисления определителей.
Решение и исследование квадратной системы линейных уравнений по правилу Крамера.
Вычисление определителя матрицы с углом нулей. Определитель произведения двух квадратных матриц. Критерий существования и формула обратной матрицы.

Векторная алгебра. Координаты.

Векторы на плоскости и в трехмерном пространстве, линейные операции над ними. Базис, координаты вектора в базисе, запись операций над векторами в координатах.
Радиус-вектор точки. Декартова система координат. Полярная, сферическая и цилиндрическая системы координат*. Радиус-вектор точки, делящей отрезок в данном отношении. Применения: середина отрезка, медиана треугольника, биссектриса треугольника.
Скалярное, векторное и смешанное произведения векторов, их свойства и вычисление в координатах. Выражение ортогональной проекции одного вектора на другой. Критерий коллинеарности двух векторов. Объем ориентированного параллелепипеда. Критерий компланарности трех векторов.
Уравнения прямых на плоскости. Уравнения прямых и плоскостей в пространстве. Вычисление расстояний и углов.

Линейные пространства и их преобразования. Билинейные функции.

Арифметическое (координатное) пространство (столбцов или строк): его размерность, примеры базисов. Ранг матрицы. Теорема о ранге матрицы. Вычисление ранга с помощью элементарных преобразований. Базисный минор. Вычисление ранга методом окаймления миноров. Критерий равенства определителя нулю.
Фундаментальная система решений и общее решение однородной и неоднородной систем линейных уравнений. Теорема Кронекера – Капели.
Линейное (векторное) пространство: аксиомы, их простейшие следствия. Примеры. Базис, размерность, координаты вектора в базисе, запись операций над векторами в координатах. Матрица перехода от старого базиса к новому. Изменение координат вектора при изменении базиса.
Подпространства в линейном пространстве. Линейная оболочка конечного набора векторов и ее размерность. Задание подпространства системой линейных уравнений. Сумма и прямая сумма подпространств.
Билинейные функции, их матрицы. Изменение матрицы билинейной функции при замене базиса. Симметрические билинейные и квадратичные формы. Приведение квадратичной формы к каноническому (нормальному) виду методом выделения квадратов (алгоритм Лагранжа). Закон инерции квадратичных форм (формулировка). Положительно определенная квадратичная форма, критерий Сильвестра.
Линейные отображения и преобразования (операторы) линейных пространств. Ядро и образ (множество значений) линейного отображения. Матрица линейного оператора и ее изменение при замене базиса. Действия над линейными отображениями.
Собственный вектор и собственное значение линейного оператора и матрицы. Линейная независимость собственных векторов, отвечающих различным собственным значениям. Характеристическое уравнение и характеристический многочлен квадратной матрицы. Приведение матрицы линейного оператора к диагональному виду путем перехода к базису из собственных векторов, условия диагонализируемости.
Евклидово пространство. Неравенство Коши-Буняковского. Ортонормированный базис, алгоритм ортогонализации (Грама-Шмидта). Ортогональное дополнение. Ортогональная проекция вектора на подпространство, расстояние и угол между вектором и подпространством.
Линейные операторы в евклидовом пространстве: самосопряженные (симметрические) и ортогональные, их свойства и свойства их матриц. Приведение квадратичных форм к диагональному виду (к главным осям) при помощи собственных значений и ортогональной замены координат.

Список литературы

Основная

Умнов А.Е. Аналитическая геометрия и линейная алгебра. – М.: МФТИ, 2006.
Беклемишева Л.А., Беклемишев Д.В., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре.– 3-е изд. СПб.: Лань, 2008 (2-е изд.: М.: Физматлит, 2003, имеется в библиотеке).

Дополнительная

Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры.– М.: Наука, Физматлит, 2000.
Кострикин А.И. Введение в алгебру. Ч. I. Основы алгебры. Ч. II. Линейная алгебра.

Ч. III. Основные структуры алгебры. – М.: Физматлит, 2000 – 2005 или МЦНМО, 2009 -2010.

Сборник задач по алгебре под редакцией А.И. Кострикина. – М.: Физматлит или МЦНМО, 2009.
Данко П.Е., Попов А.Г., Кожевникова Т.Я., Данко С.П. Высшая математика в упражнениях и задачах. 7-е изд. Ч.I. – М.: Оникс, 2009 (или более ранние издания).
Курош А.Г. Курс высшей алгебры. – М.: Наука или СПб.: Лань, 2007.
Шевцов Г.С. Линейная алгебра: теория и прикладные аспекты. М.: Финансы и статистика, 2003.

Образцы задач для контрольных, зачетных и экзаменационных работ по алгебре

Типовые задачи для подготовки к контрольной работе за 1 модуль

Выполнить действия: .
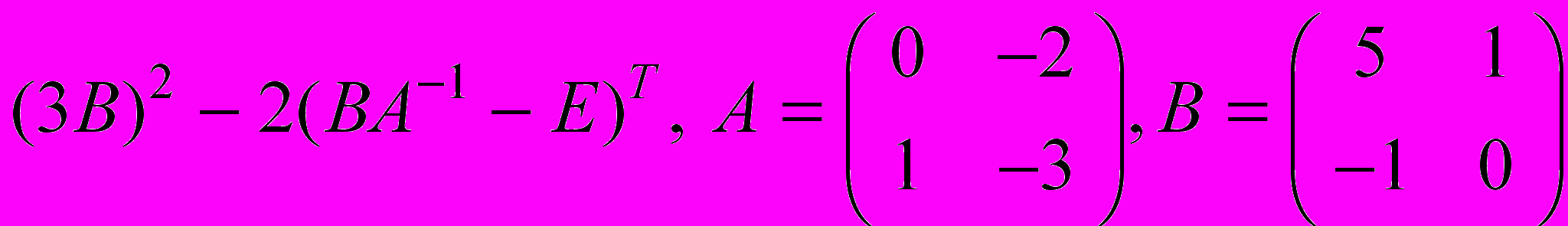Решить систему линейных уравнений с помощью обратной матрицы: .
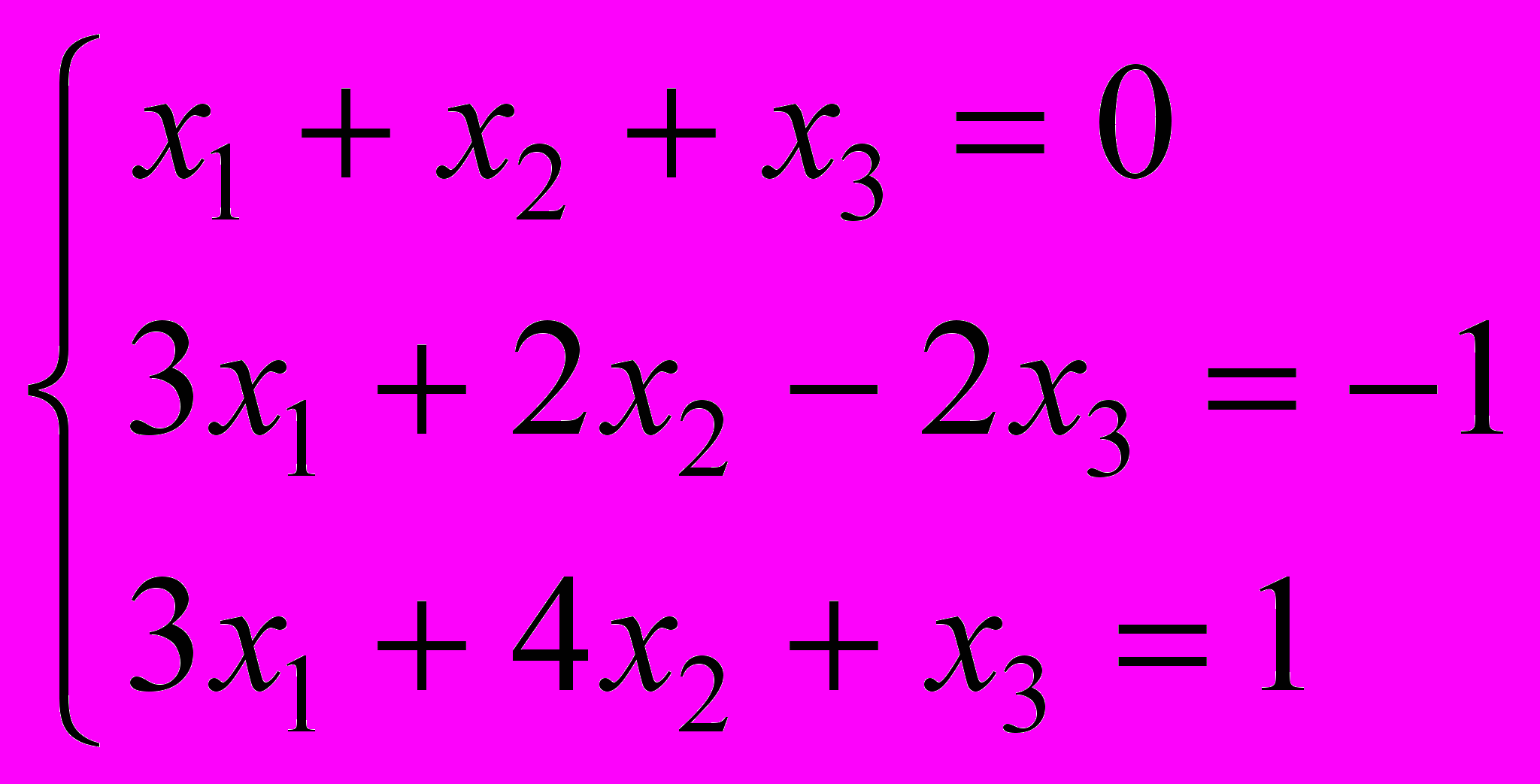Найти все решения системы линейных уравнений .
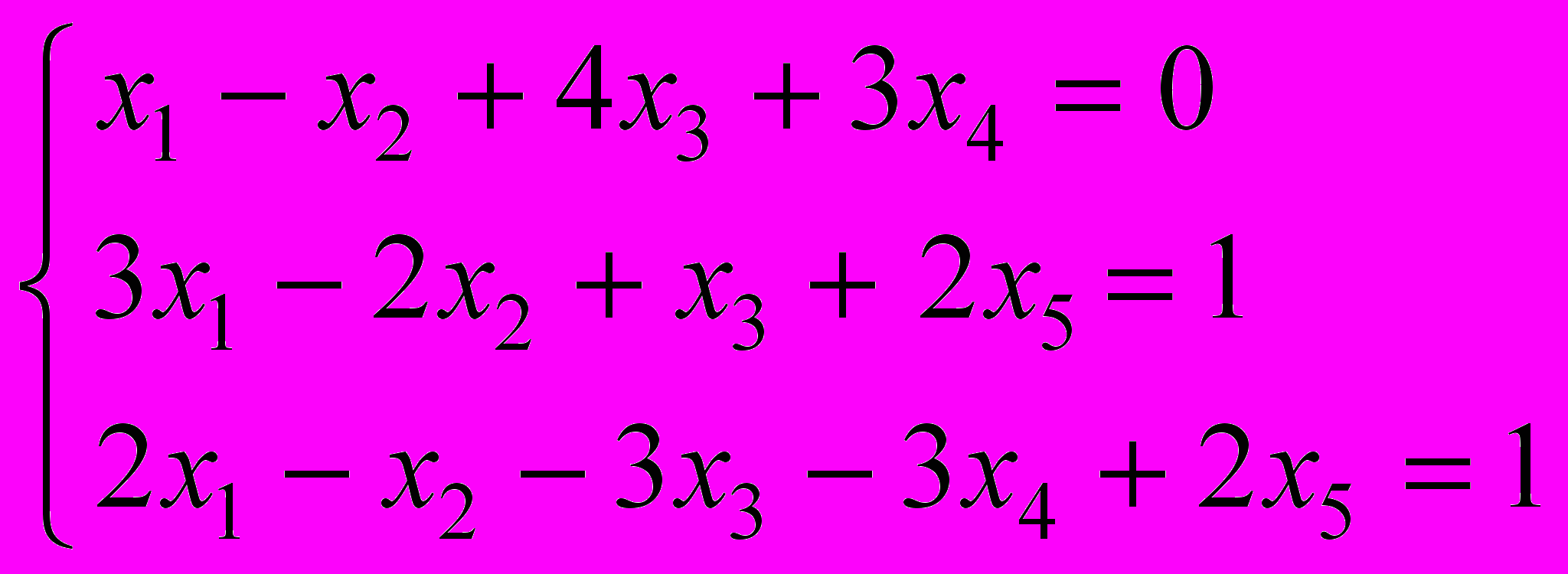Исследовать и решить систему уравнений .
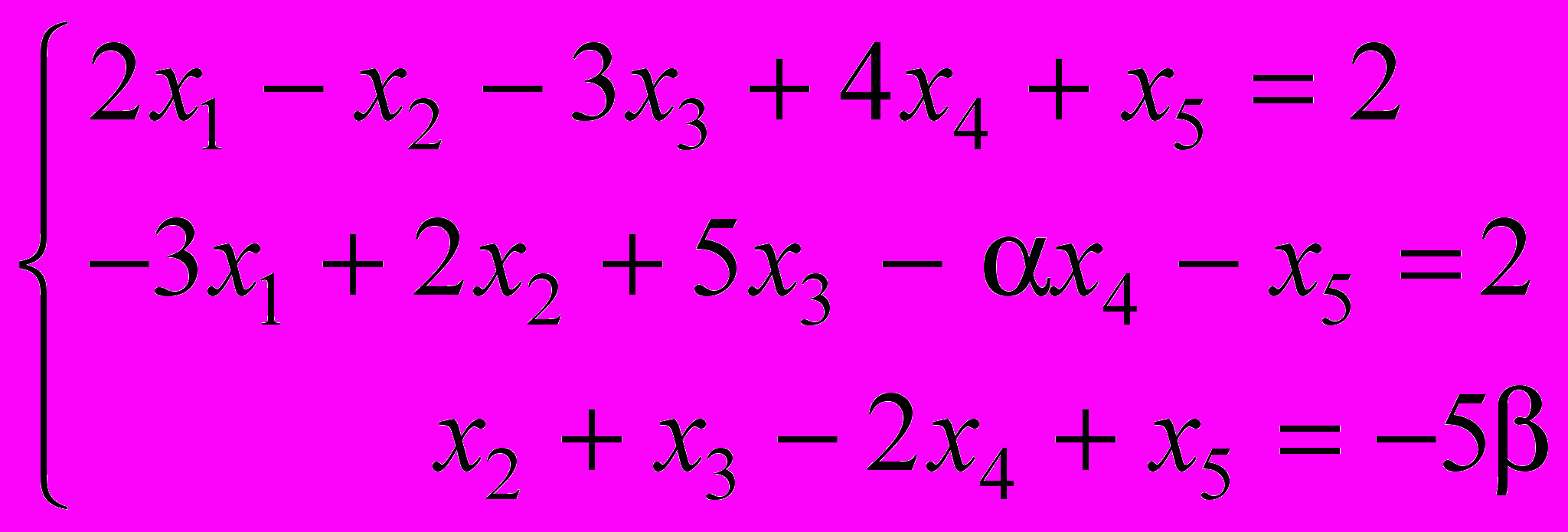Решить матричное уравнение .
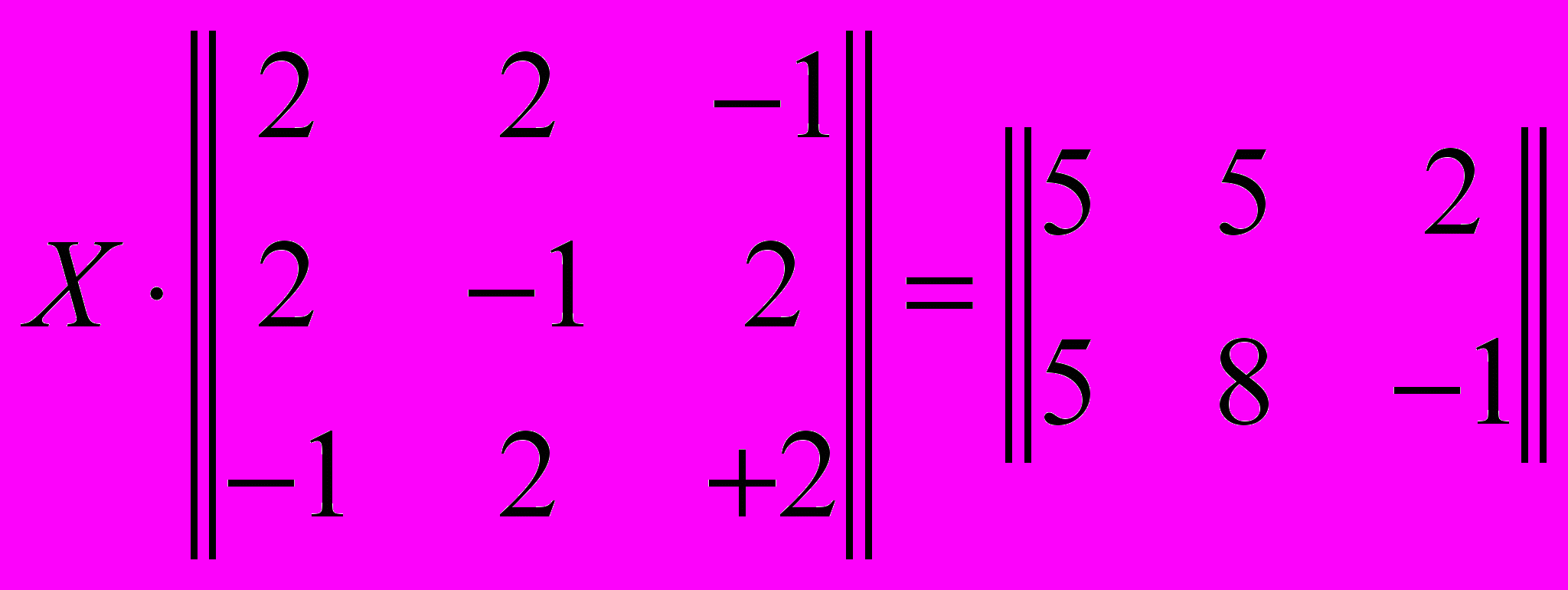Вычислить все значения .
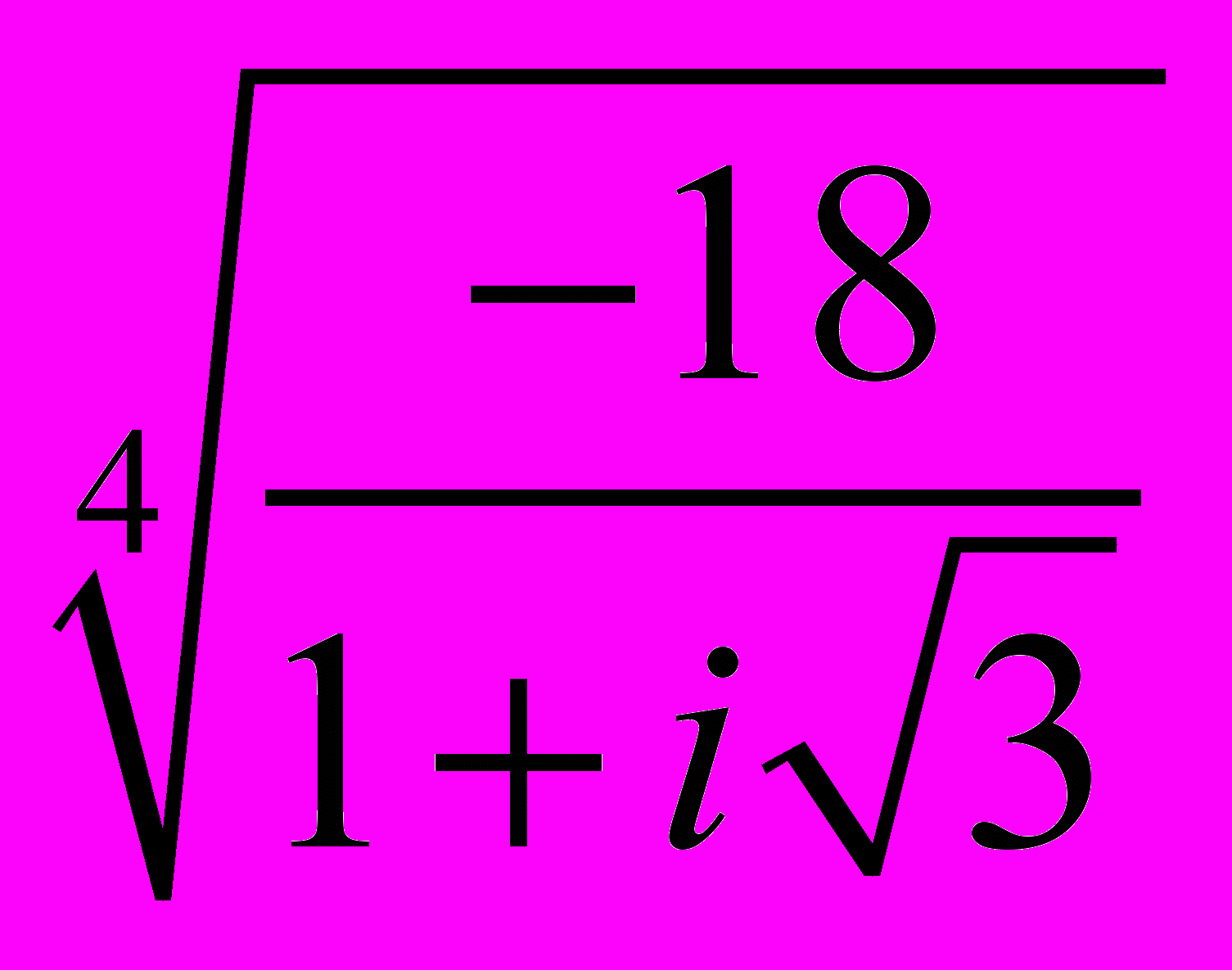Найти корни многочлена и разложить его на множители над R и C .
Образуют ли группу матрицы вида 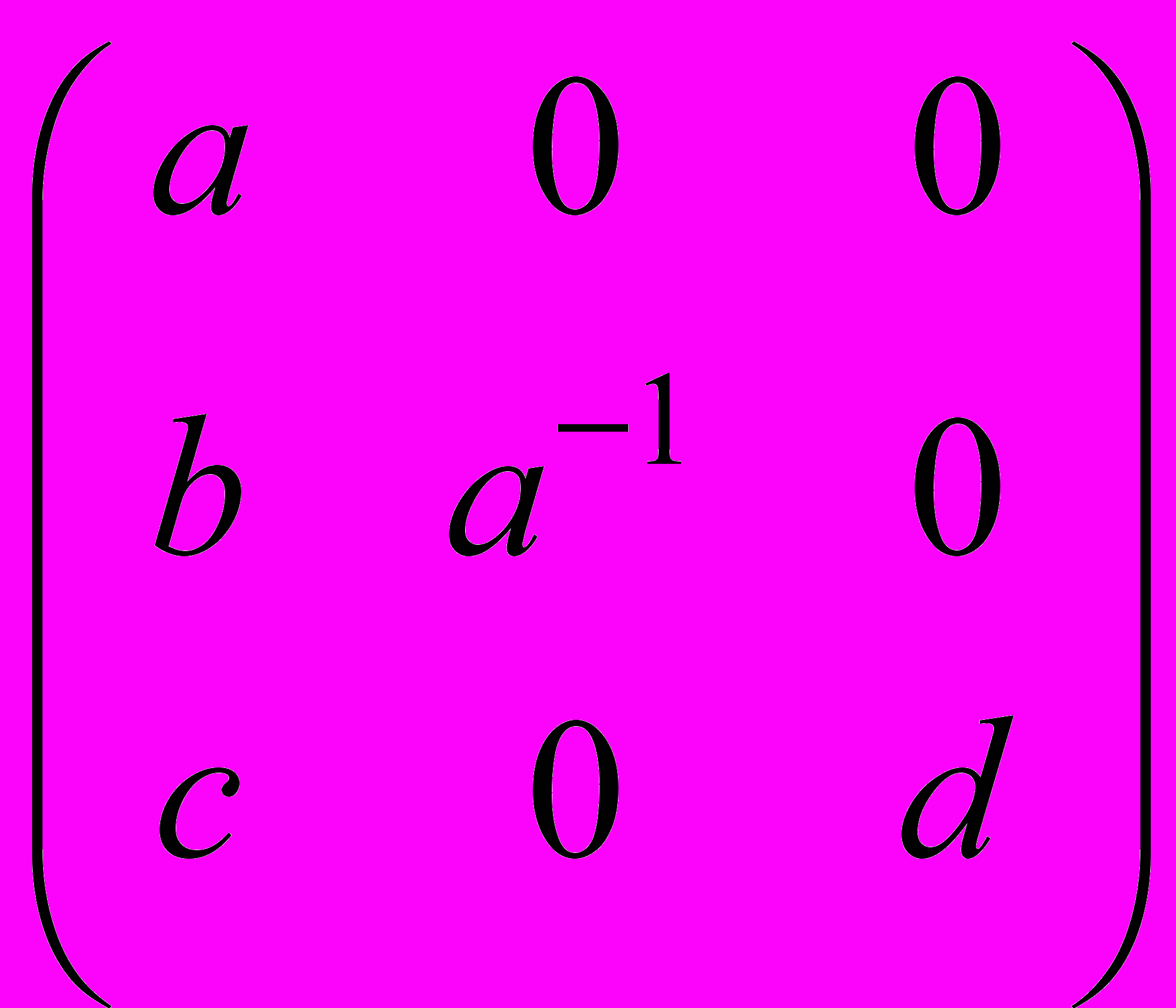относительно умножения (a,b,c,d из некоторого поля К, ad≠0)? Найти число элементов группы, если .
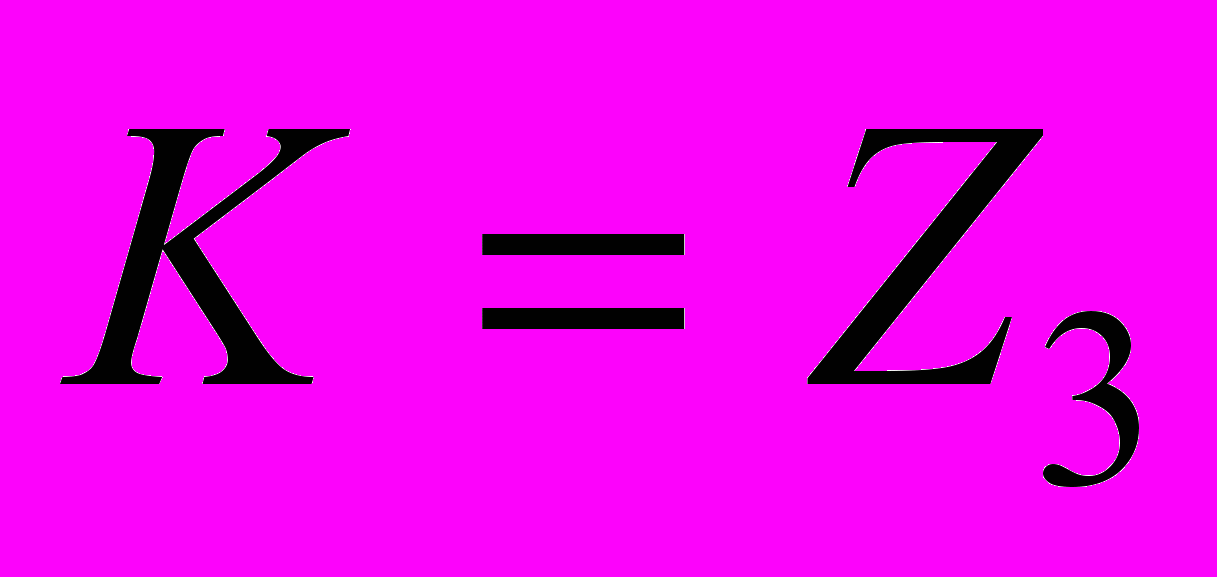В циклической группе G порядка 288 найти: а) все элементы g такие, что g⁹⁰ =1; б) элементы g такие, что 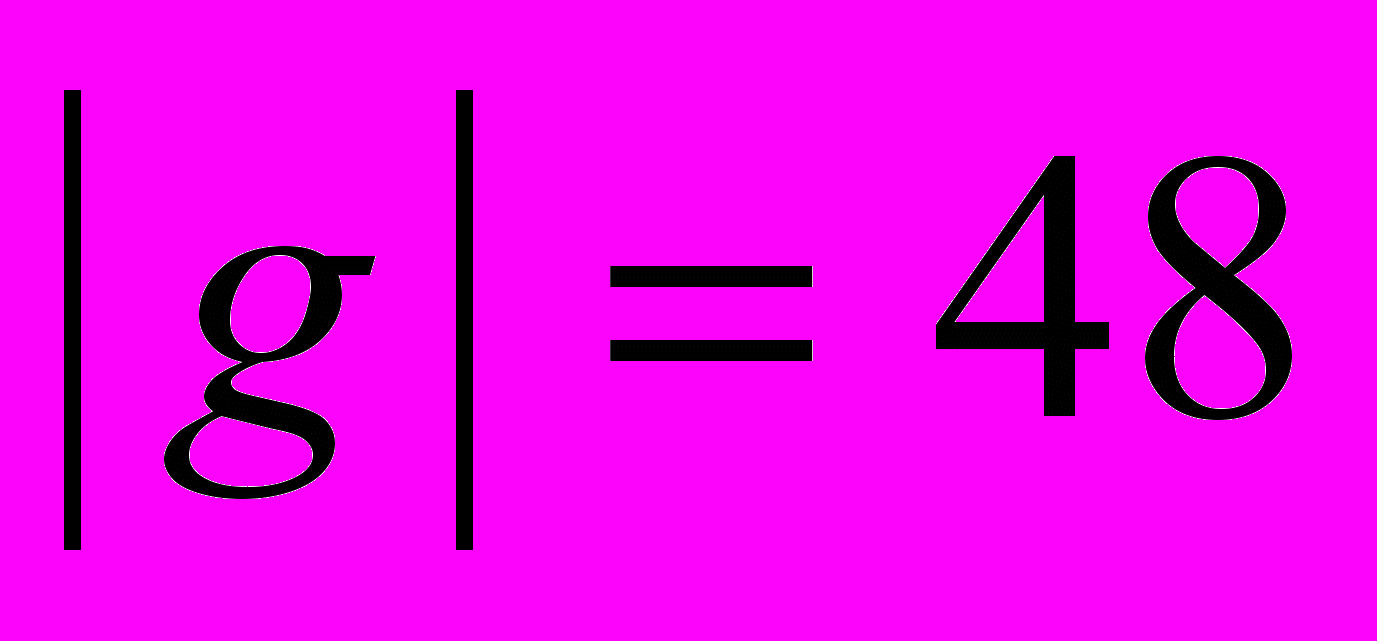, и в каждом случае подсчитать их количество.
Образуют ли кольцо/ поле числа вида 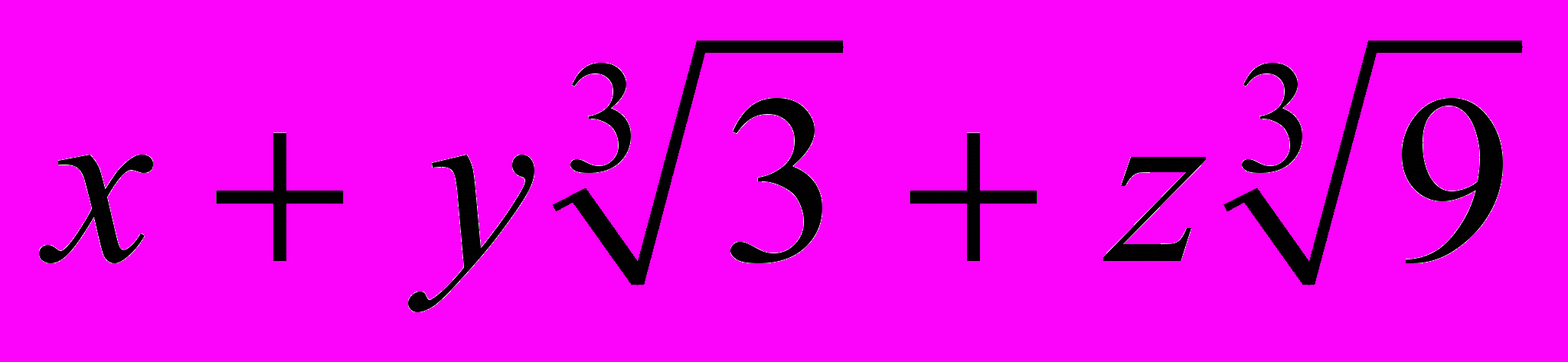(x,y,z Q)?

Типовые задачи для подготовки к контрольной и зачетной работам

за 2 модуль

Решить неравенство
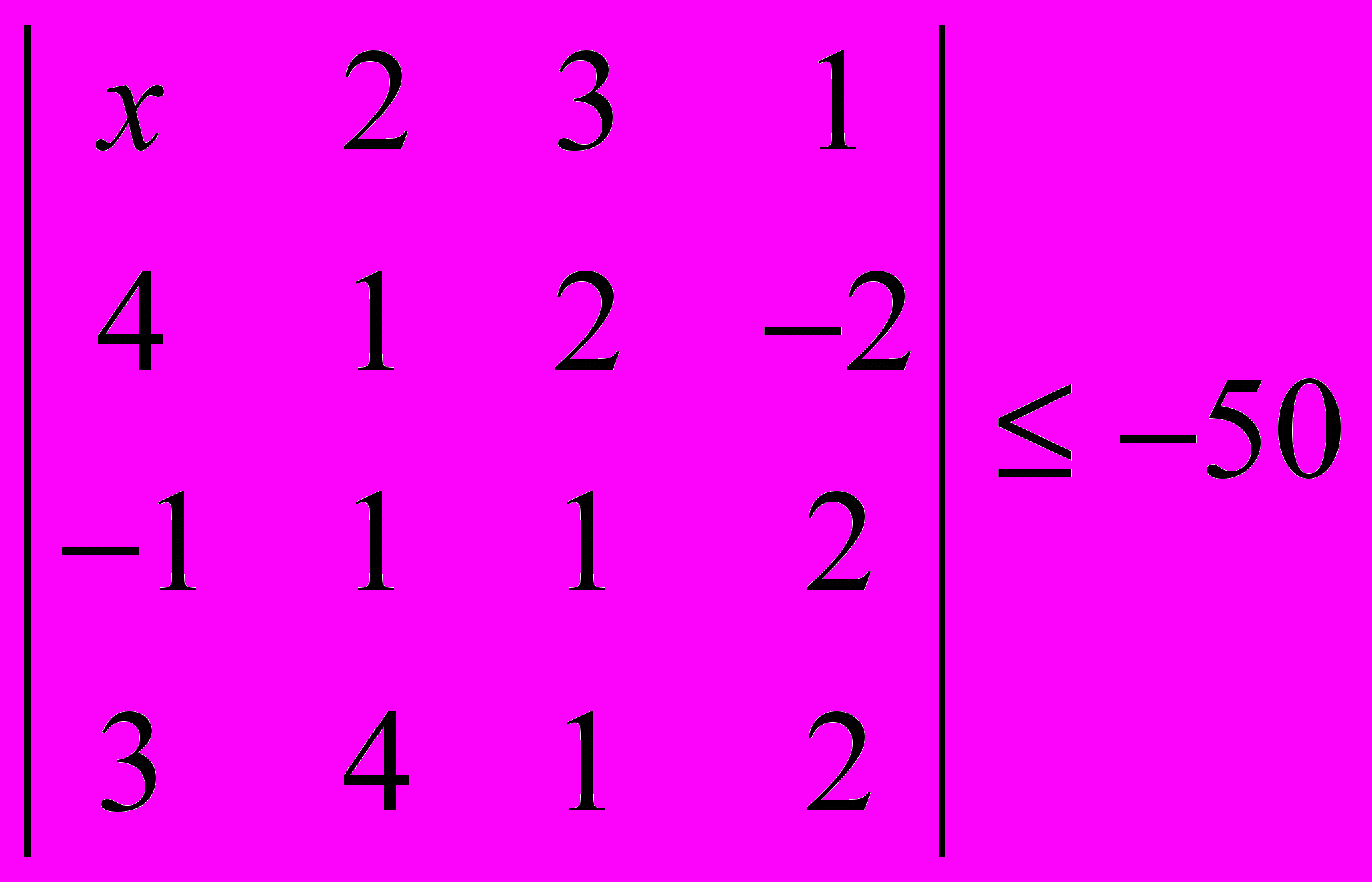
Найти ранг матрицы при всевозможных значениях параметра :
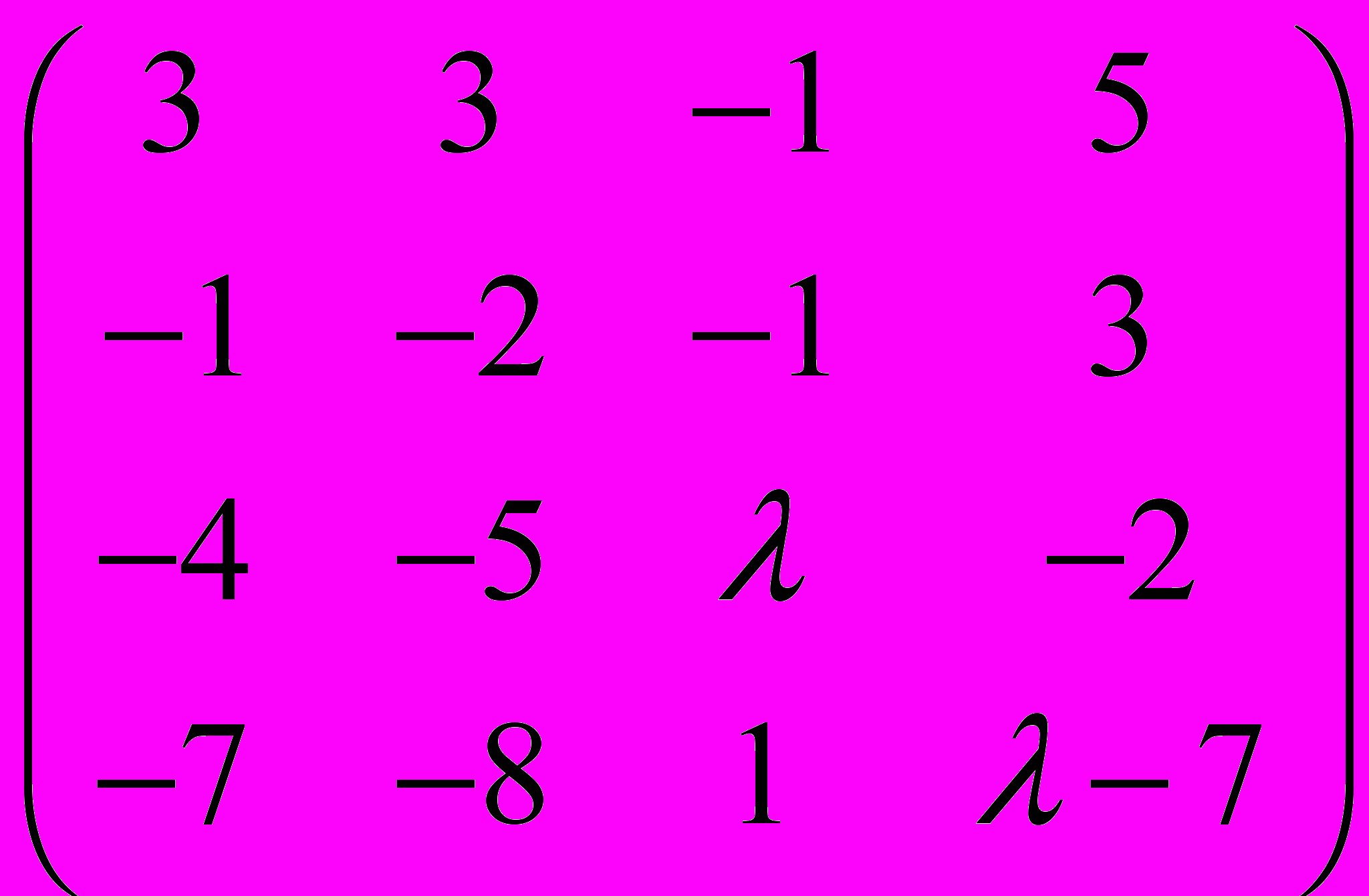
В ортонормированном базисе даны векторы . Найти вектор .

Даны вершины треугольника A(–5,3), B(7,8), C(–2,–1). Составить уравнения медианы, биссектрисы и высоты треугольника, проведенных из вершины А. (Система координат ортонормированная)
Найти точку 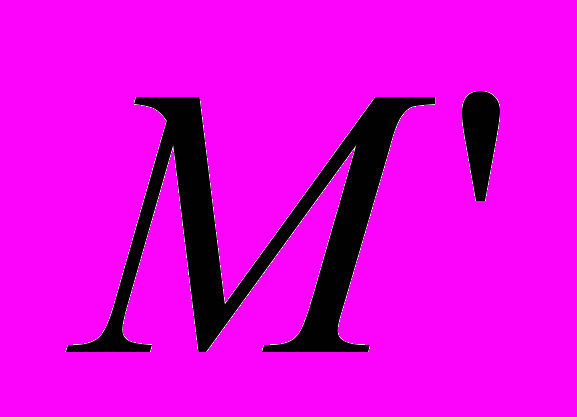, симметричную точке 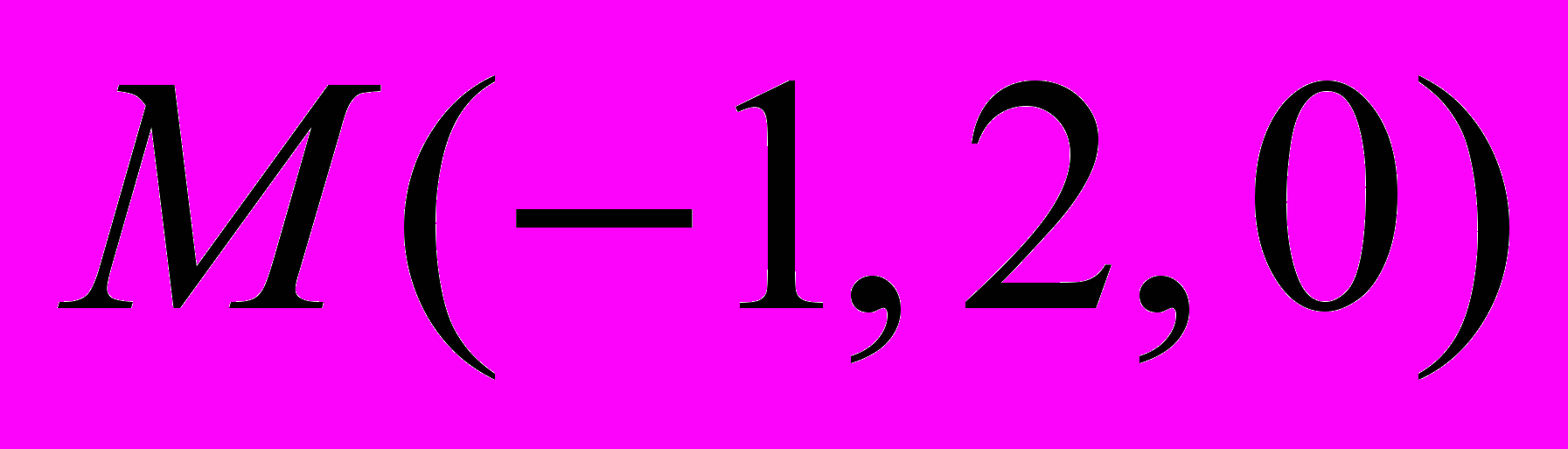относительно прямой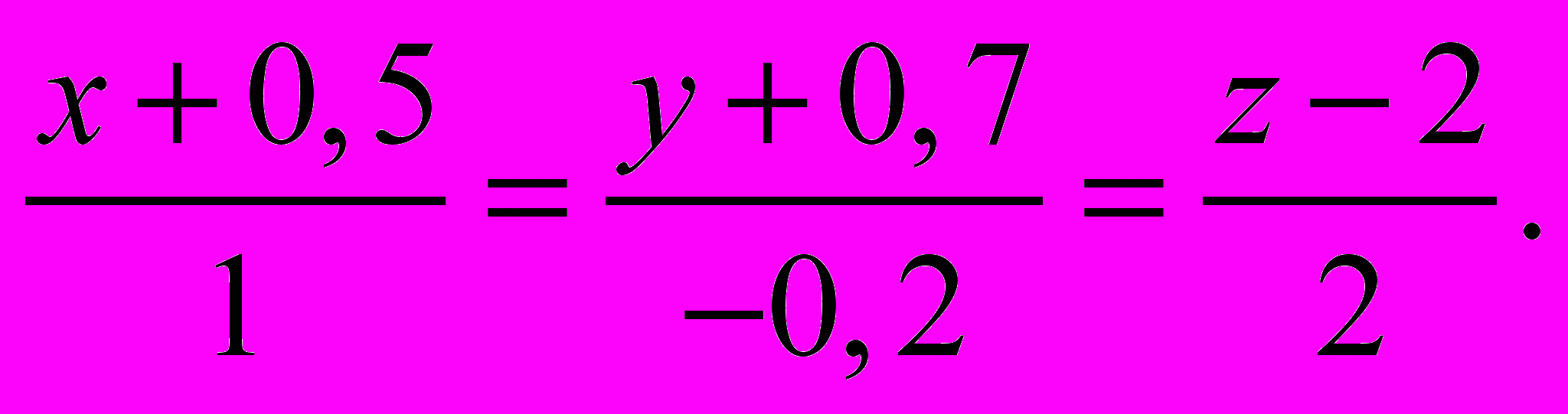

или

5a. Найти точку

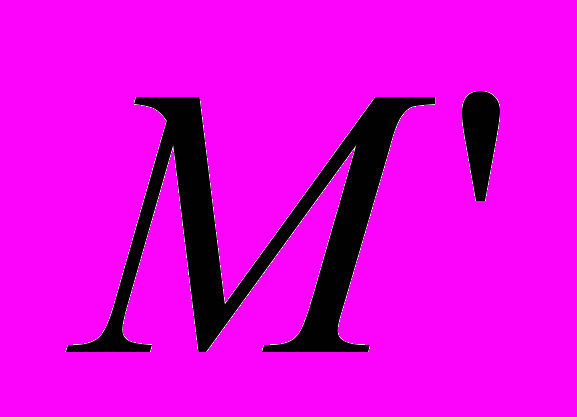, симметричную точке

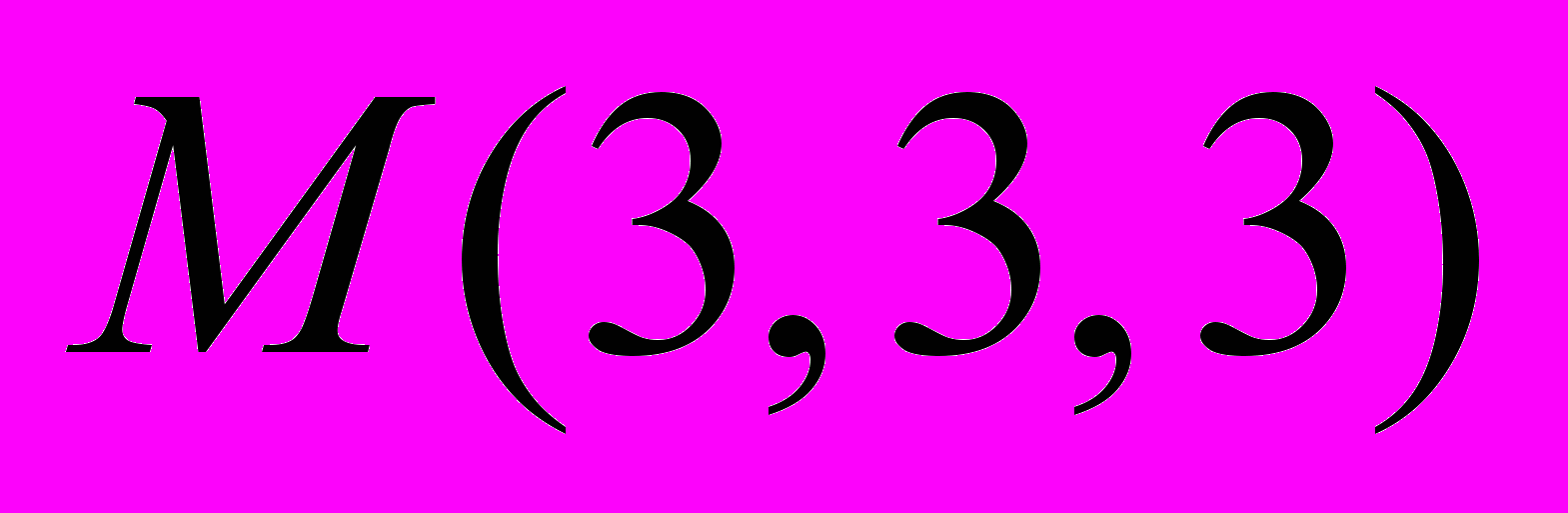относительно плоскости

Даны точки 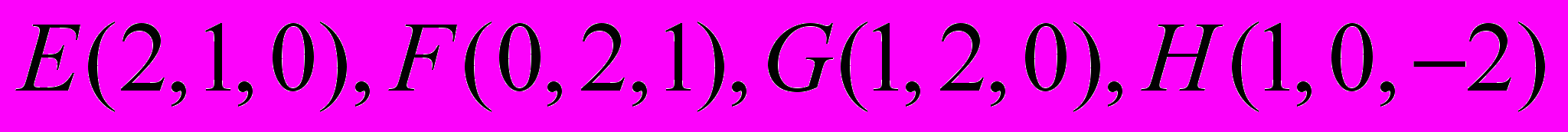. Найти: (а) объем пирамиды EFGH; (б) расстояние между прямыми (EF) и (GH);
Найти общее решение системы линейных уравнений (представить его

как сумму частного решения и линейной комбинации линейно независимых решений соответствующей однородной системы)

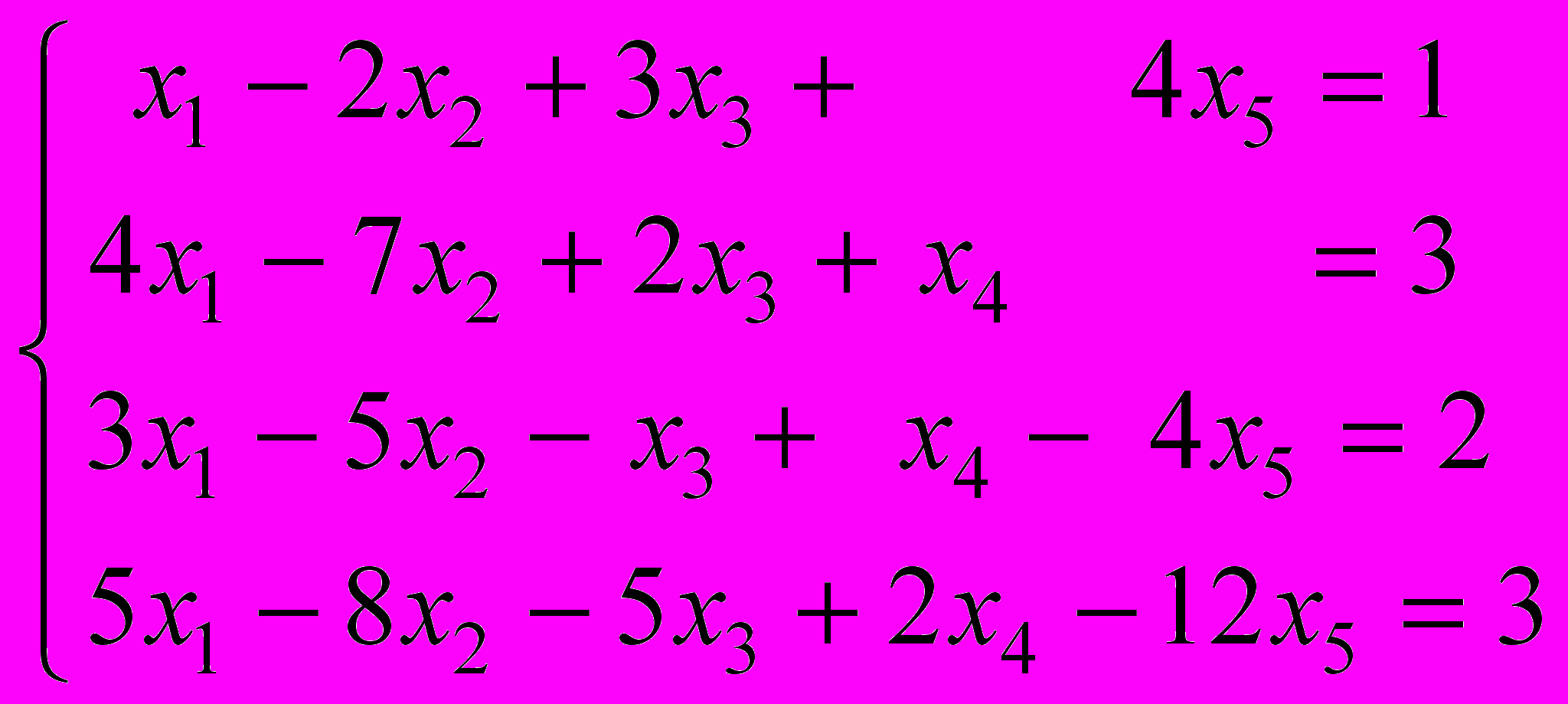Проверить, что данные векторы 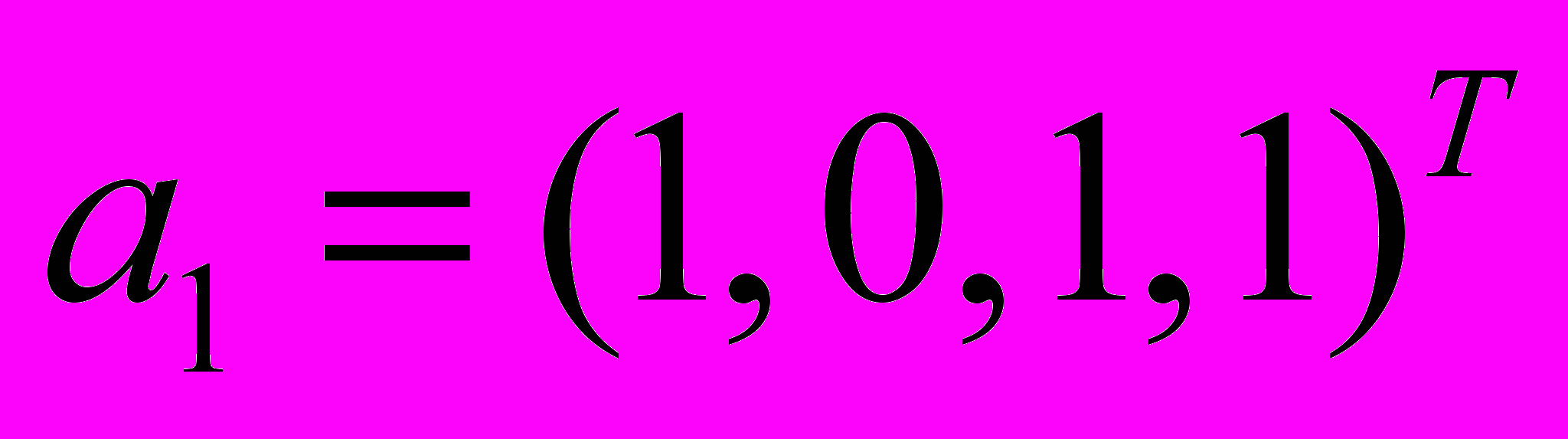,, , 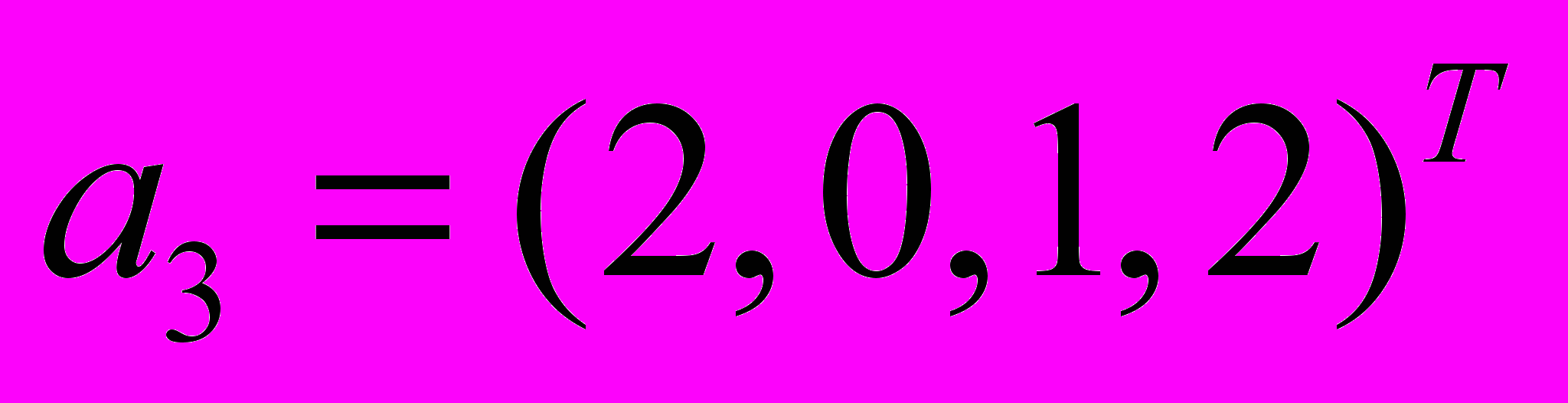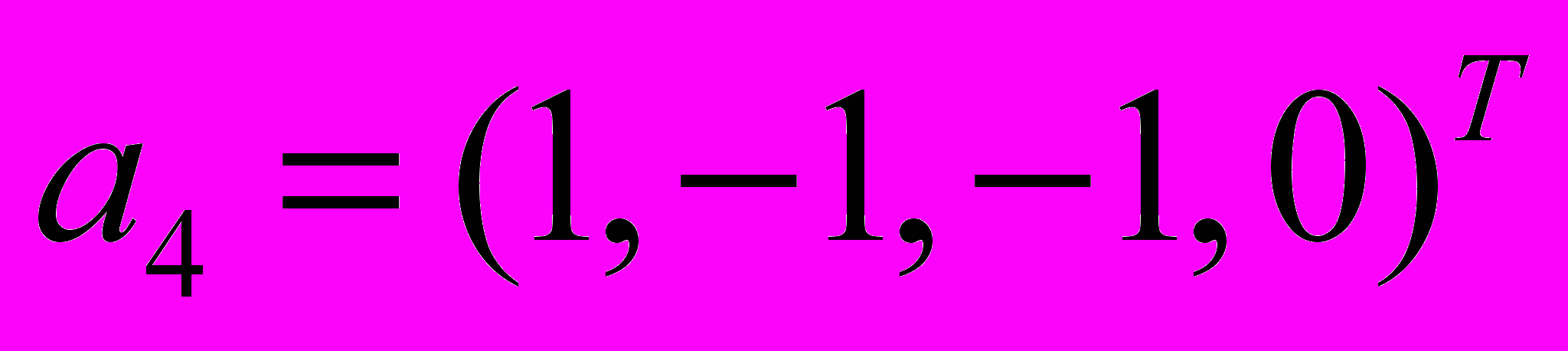образуют базис в пространстве столбцов. Найти координаты вектора 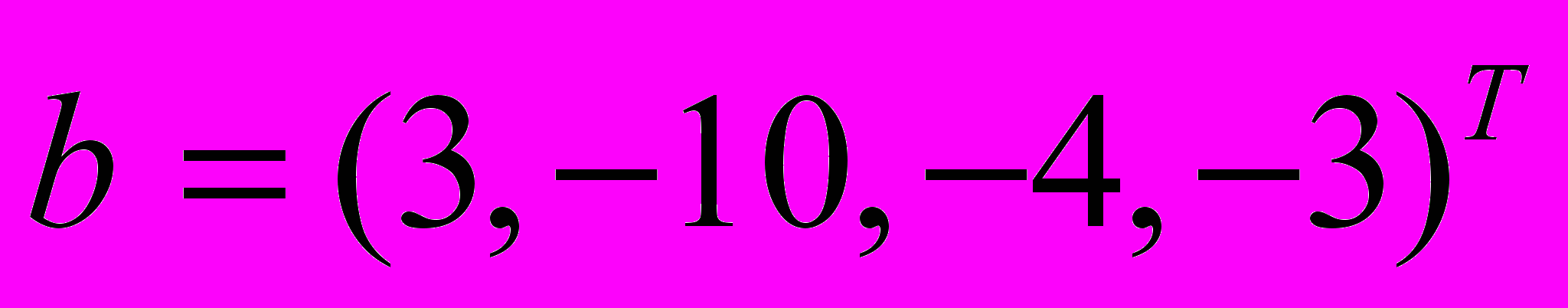в этом базисе.
Найти размерность и базис линейной оболочки векторо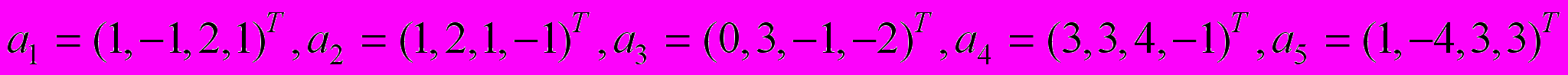в в , выразить небазисные векторы через базисные.
Найти размерность и базис (т.е. фундаментальную систему решений) подпространства решений системы линейных уравнений

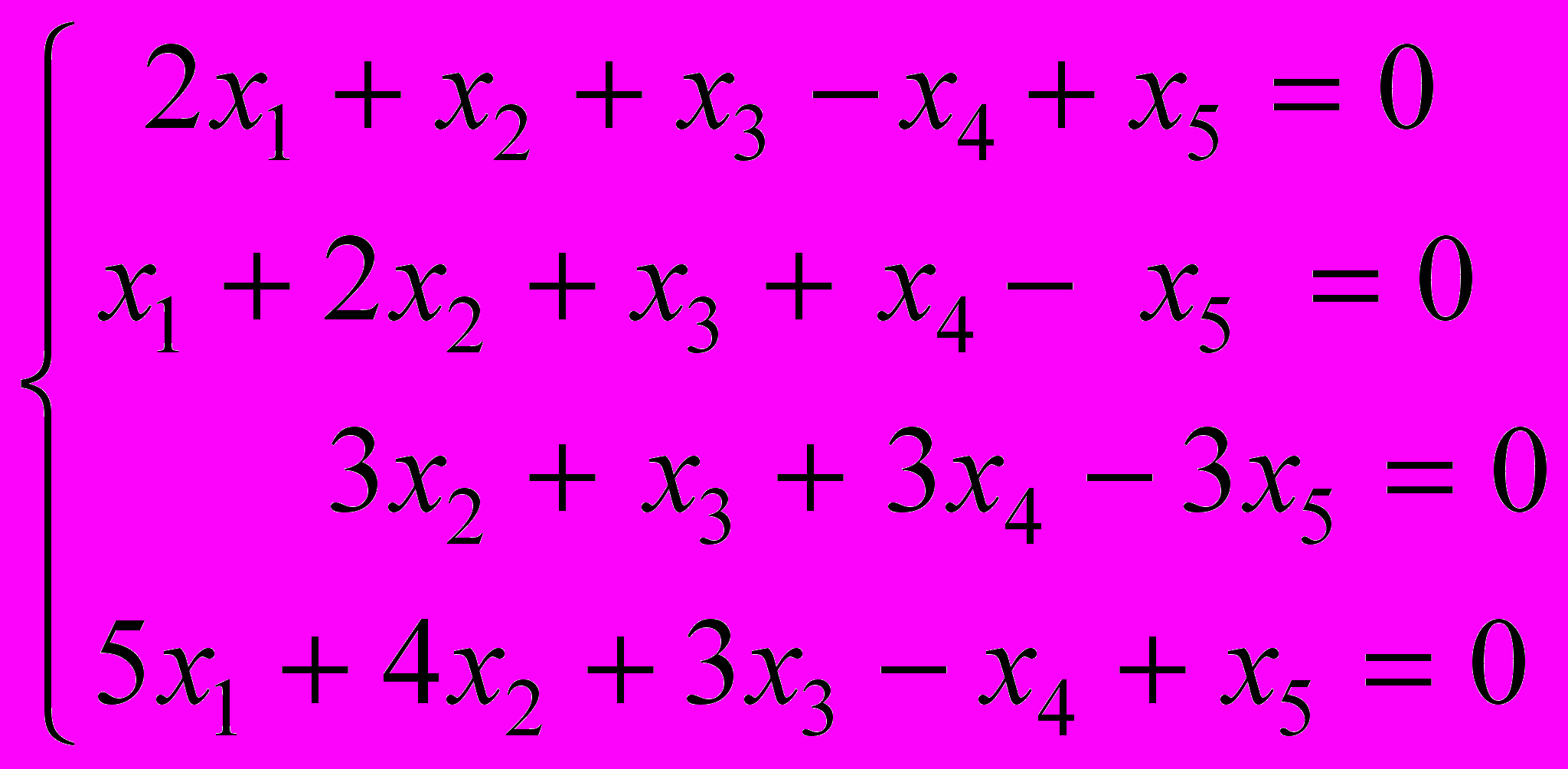
Типовые задачи для подготовки к контрольной и экзаменационной работам за 3 модуль

Найти базис и размерность линейного подпространства L в R⁴, заданного системой уравнений
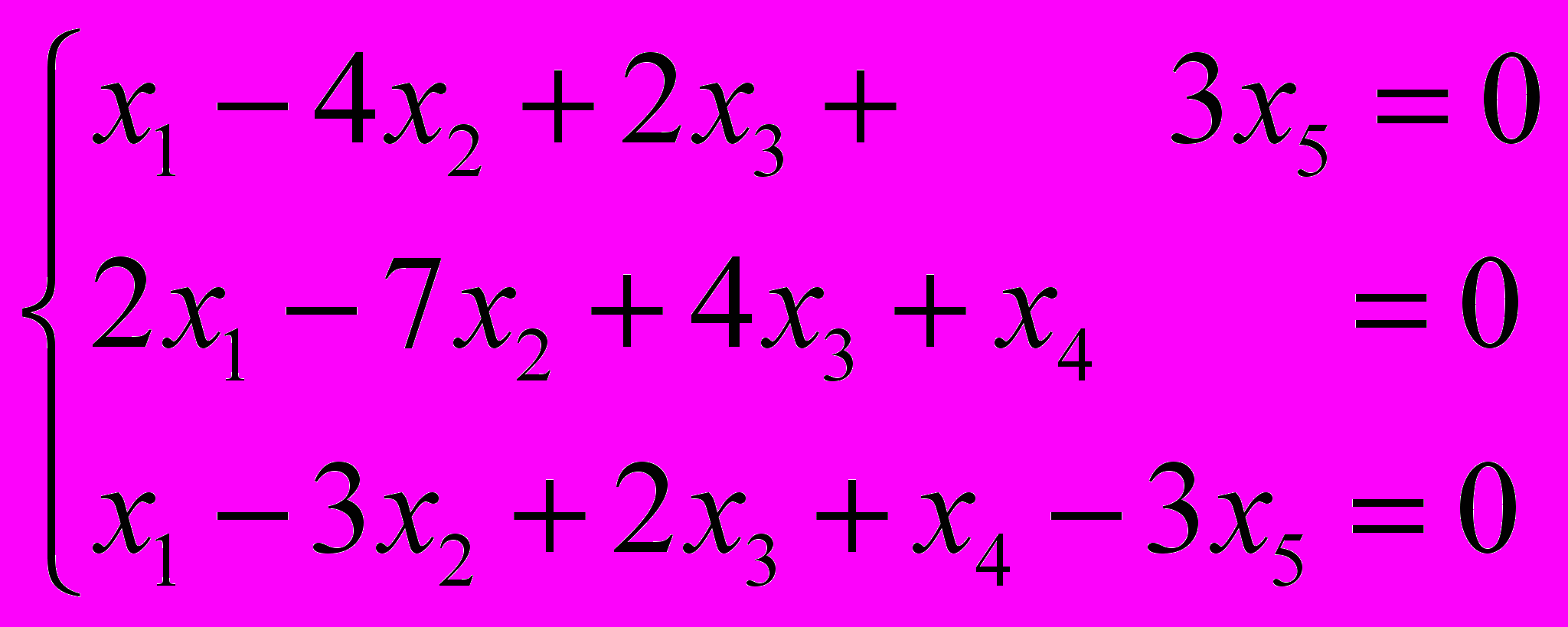
Вычислить все значения .
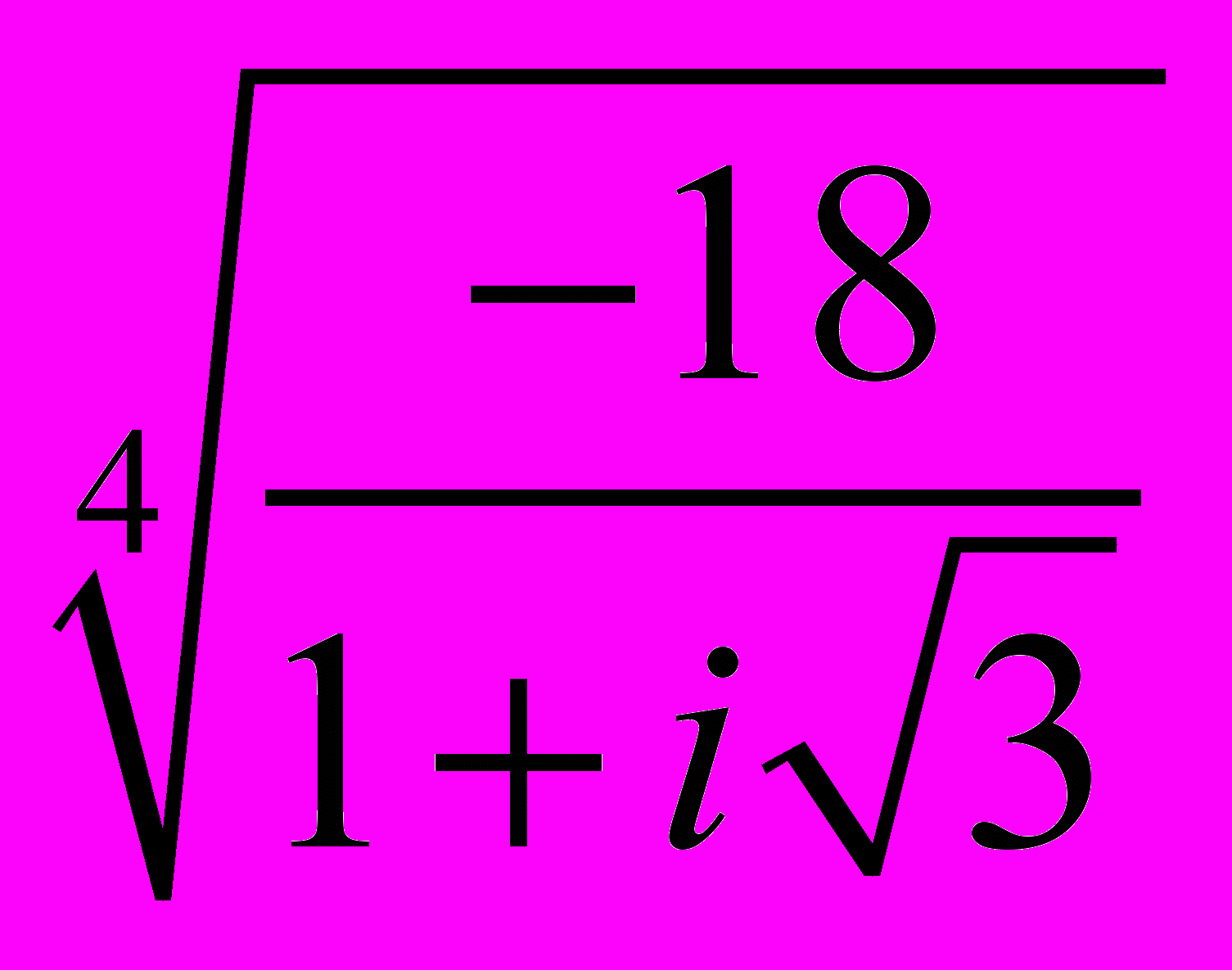Найти комплексные корни уравнения .
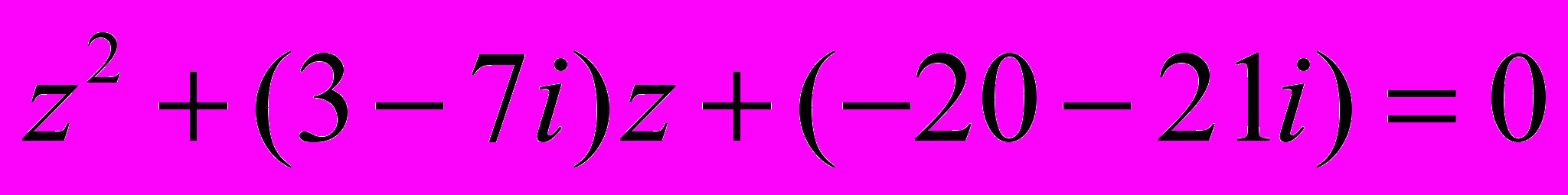Вычислить матрицу перехода от базиса 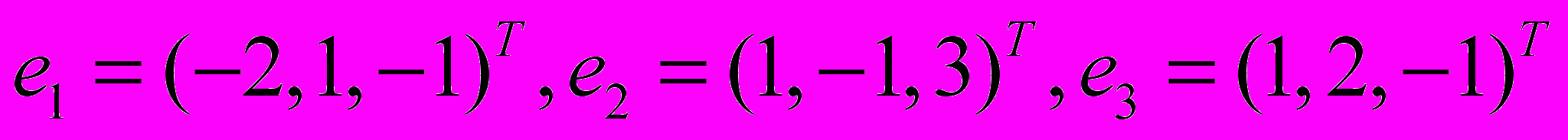к базису 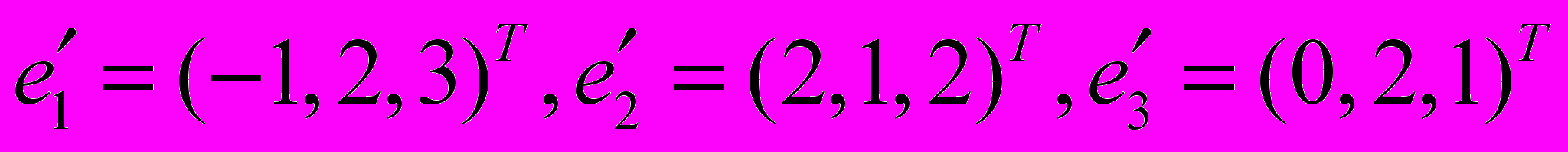в линейном пространстве R³ и определить координаты вектора 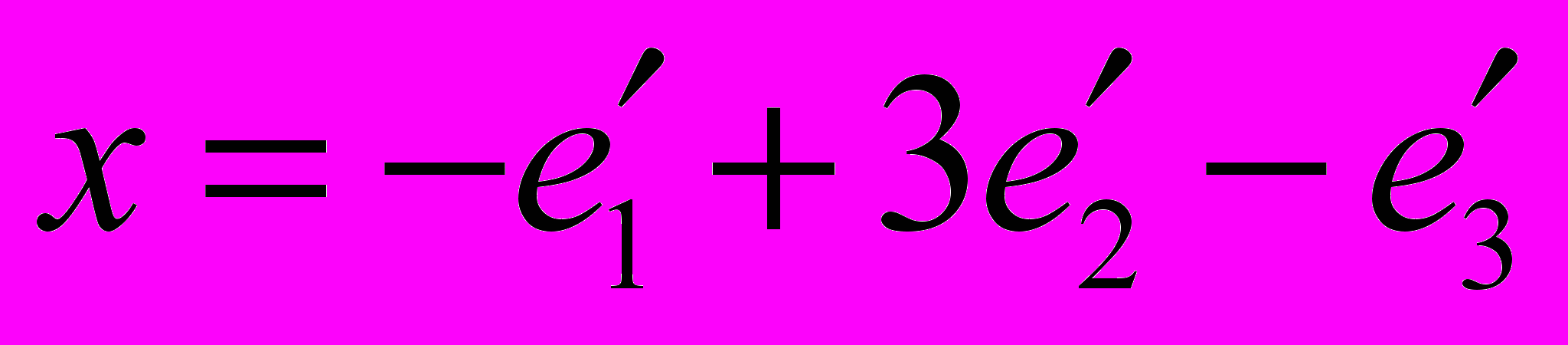в базисе .
Доказать, что пространство является прямой суммой подпространств 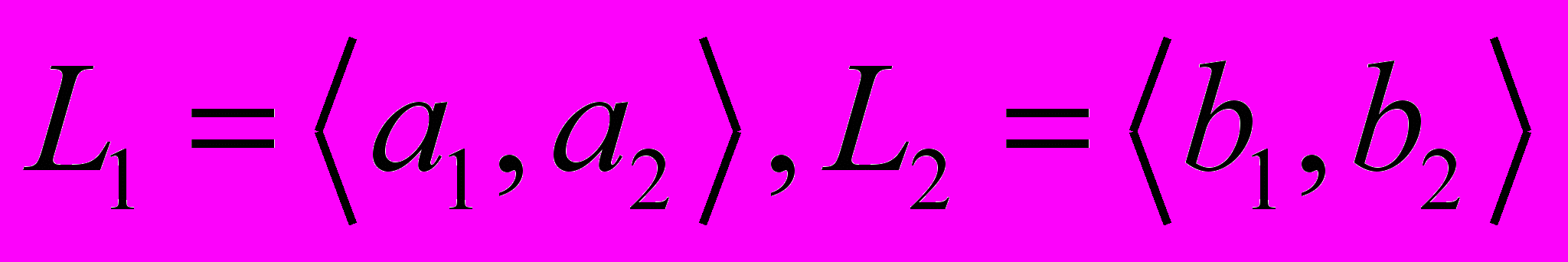и разложить вектор 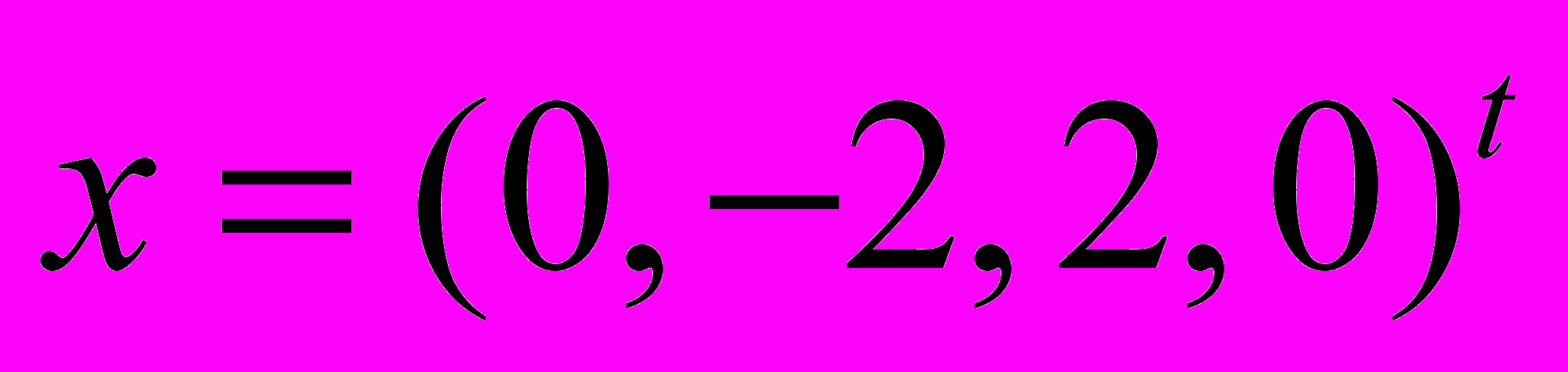на сумму проекций на эти подпространства, где .
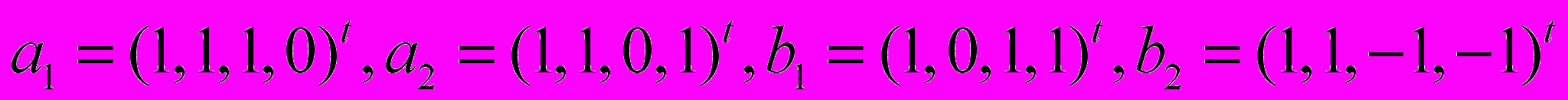Найти матрицу линейного оператора, переводящего векторы 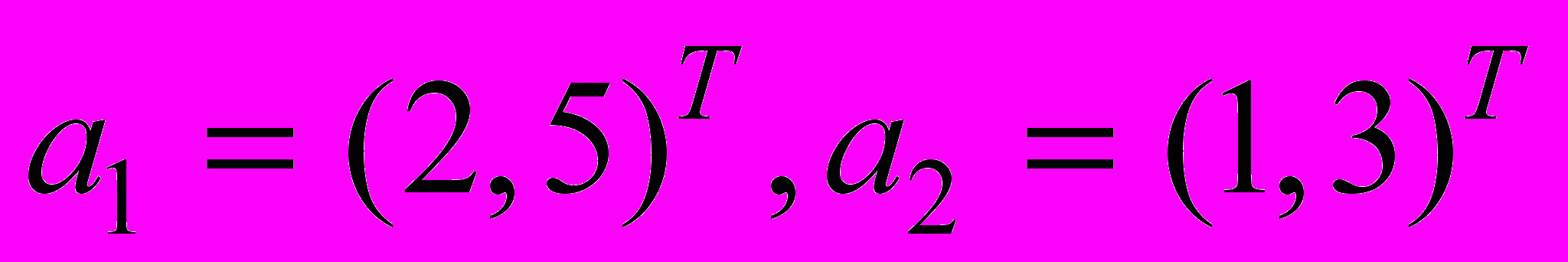соответственно в векторы 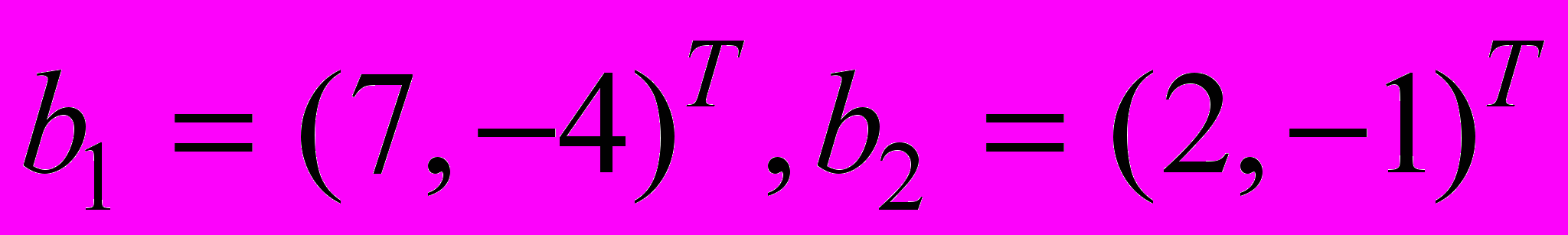в базисе, в котором даны координаты векторов.
В базисе 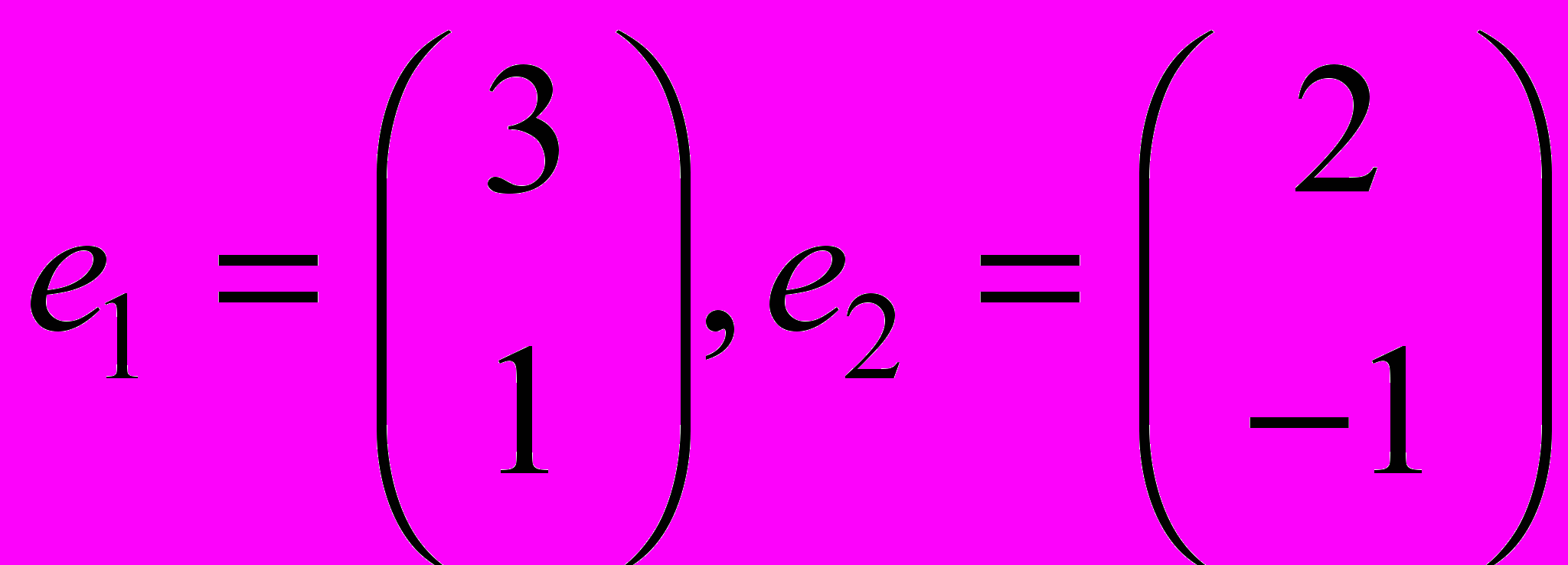линейный оператор  имеет матрицу . Найти матрицу оператора  в базисе .
Найти собственные векторы и собственные значения линейного оператора, заданного в некотором базисе матрицей 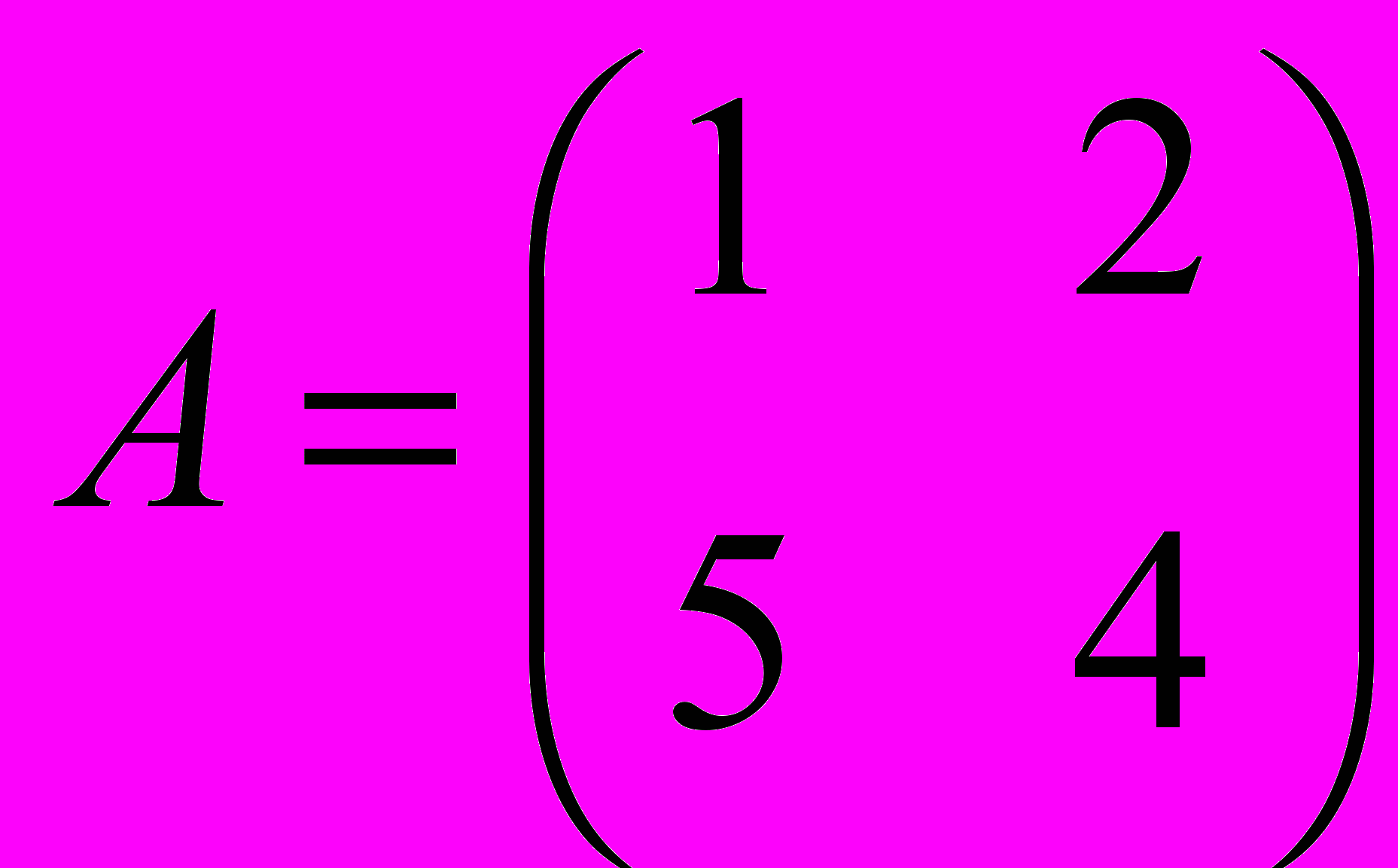, привести ее к диагональному виду.
Вычислить матрицу , где .
В евклидовом пространстве R⁴ (со стандартным скалярным произведением) дано подпространство 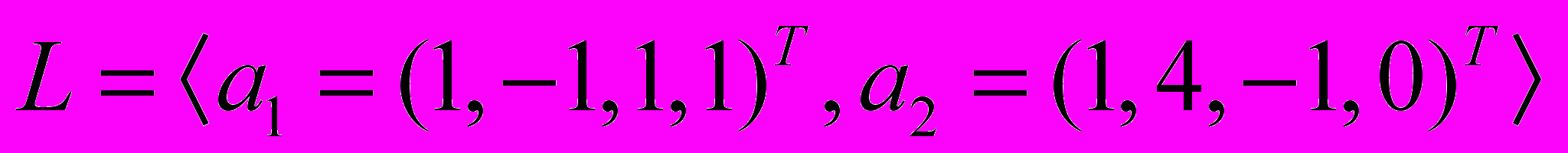. Разложить вектор 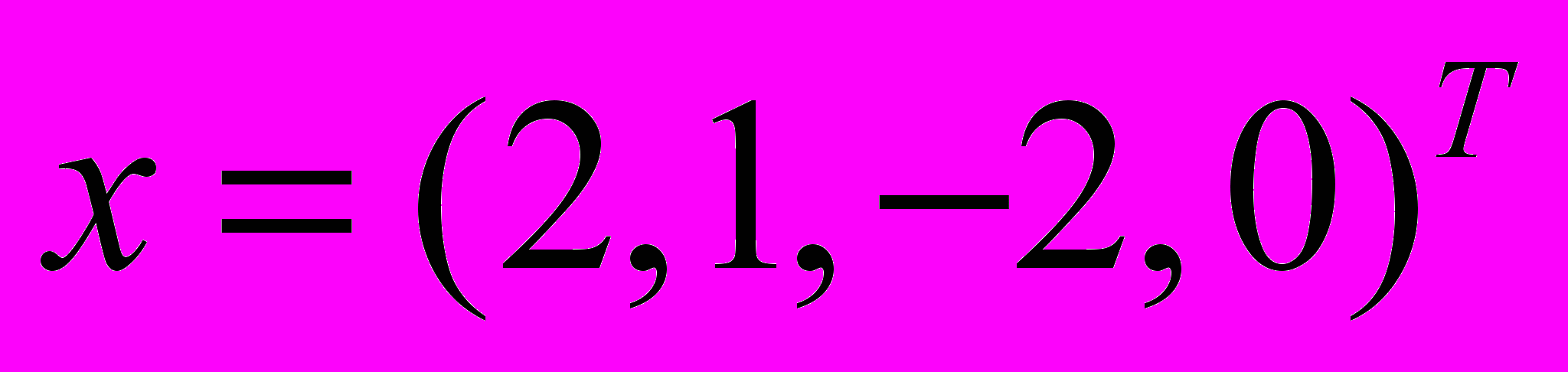на сумму ортогональной проекции на L и ортогональной составляющей; найти расстояние от вектора x до L и угол между x и L.
Построить при помощи процесса ортогонализации ортонормированный базис линейной оболочки векторов .
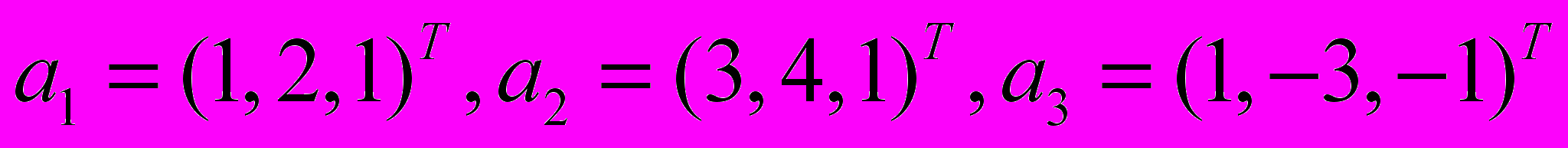Найти ортонормированный базис из собственных векторов симметричной матрицы
Привести квадратичную форму