7. Агрегативное описание систем

Вид материала

Документы

Содержание 7.2. Процесс функционирования агрегата 7.2.2. Функционирование СМО как агрегата Агрегативная система Виды связей между агрегатами

Подобный материал:

• Курсовая работа по курсу "Организация ЭВМ и систем", 136.96kb.
• План-конспект лекций благовещенск 2007 Содержание Основные понятия автоматического, 218.83kb.
• В. А. Геодакян Окружающий нас мир состоит из разных систем: наша галактика система,, 284.73kb.
• Реферат дипломный проект посвящен решению некоторых вопросов реконструкции компрессорного, 54.11kb.
• Тематическое планирование уроков в 7 классе, 894.98kb.
• В. В. Пивоваров московский инженерно-физический институт (государственный университет), 27.99kb.
• Об оценках эффективности систем защиты информации, 19.72kb.
• Руководство по разработке и внедрению систем экологического менеджмента (Краткая версия), 434.61kb.
• Лекция №8. Теоретико-множественное описание систем Вводятся основные понятия теории, 220.04kb.
• Назначение и описание программы optim 29 Заключение 31 Список литературы, 209.35kb.

7. Агрегативное описание систем


7.1. Понятие «агрегат» в теории систем


Пусть T – фиксированное подмножество действительных чисел (множество рассматриваемых моментов времени), X,U,Y,Z – множества любой природы. Элементы указанных множеств назовем: tÎ T – моментом времени; xÎ X; входным сигналом; uÎ U- управляющим сигналом; yÎ Y – выходным сигналом; zÎ Zсостоянием. Состояния, входные, управляющие и выходные сигналы, рассматриваемые как функции времени, обозначим z(t), x(t), u(t) и y(t).

Под агрегатом будем понимать объект (7.1), где H,G – операторы (вообще говоря, случайные). Операторы переходов и выходов H и Gреализуют функции z(t) и y(t). Структура этих операторов собственно и выделяет агрегаты среди прочих систем. Рассмотрим подробнее вид этих операторов. При этом будем считать справедливым следующее предположение.

Предположение 1. За конечный интервал времени в агрегат поступает конечное число входных и управляющих сигналов и вырабатывается конечное число выходных сигналов.

Операторы переходов. Наряду с состоянием z(t) будем рассматривать также точки z(t+0). Договоримся считать, что для любого t₁>tмомент (t+0) Î (t,t ₁]. Вид оператора переходов H зависит от того, содержит ли рассматриваемый интервал времени моменты т.н. особых состояний агрегата или не содержит. Под особыми состояниями будем понимать его состояния в момент получения входного либо управляющего сигналов или выдачи выходного сигнала. Все остальные состояния агрегата будем называть неособыми.

Предположение 2. Из особых состояний агрегат может переходить в новое состояние скачком.

Пусть z(t*) – некоторое особое состояние агрегата, а u_s – последний управляющий сигнал u_sÎ U. Примем следующие обозначения для операторов, являющихся частными видами оператора Hи определяющих состояние агрегата в момент t*+0. Если t* - момент поступления входного сигнала x_, то

z(t*+0)=V¢ [z(t*),x,u_s] (7.2)

Аналогично, если t* - момент поступления управляющего сигнала u, то

z(t*+0)=V¢¢ [z(t*),u] (7.3)

При одновременном поступлении x и u

z(t*+0)=V [z(t*),x,u] (7.4)

Наконец, если t* - момент выдачи выходного сигнала y, то

z(t*+0)=W[z(t*),u_s] (7.5)

В интервале между особыми состояниями, значение z(t) определяется при помощи операторов U, вид которых в общем случае зависит от особого состояния, являющегося для данного интервала времени начальным состоянием:

z(t*+0)=[t,z(t*+0),u_s] (7.6)

Здесь t* - момент особого состояния, являющегося исходным для данного интервала времени. Естественно, замечания о том, что H является случайным оператором, без изменений переносится на его частные виды U,V¢ ,V¢¢ ,V и W.

Оператор выходов. Во множестве Z состояний z(t) агрегата выделим класс подмножеств {Z_y }, обладающих следующими свойствами. Выходной сигнал yвыдается в момент t¢ в тех случаях, когда: 1) z(t¢ )Î Z_y ; z(t¢ -0)Ï Z_y и 2) z(t¢ +0)Î Z_y , но z(t’)Ï Z_y . Тогда, оператор Gможно представить в виде совокупности 2 операторов: G¢ , вырабатывающего выходной сигнал

y=G ¢ [z(t¢ ),u_s] (7.7)

и G ¢¢ , проверяющего для каждого tпринадлежность z(t) к одному из подмножеств Z_y . Заметим, что в общем случае, оператор G¢ является случайным оператором. Это значит, что данным t,z(t),uставится в соответствие не одно определенное значение выходного сигнала, а некоторое множество значений yс соответствующим распределением вероятностей, задаваемых оператором G¢ .

В некоторых случаях в качестве одной составляющих z(t), например z₁(t), можно рассматривать время, оставшееся до выдачи выходного сигнала. Тогда оператор G¢¢ проверяет неравенство z₁(t)>0.


^ 7.2. Процесс функционирования агрегата

7.2.1. Функционирование агрегата общего вида

Агрегат функционирует следующим образом. В начальный момент времени t₀ заданы начальное состояние агрегата z₀ и начальное значение управляющего сигнала u₀.

Пусть t₁ и t₂ – моменты поступления первого x₁ и второго x₂ входных сигналов, t₁ – момент поступления первого управляющего сигнала u₁ и, для определенности t₁12. Рассмотрим полуинтервал (t₀,t₁]. Состояния агрегата изменяются с течением времени по закону

z(t)=[t,z₀,u₀] (t₀1) (7.8)

до тех пор (оператор G¢¢), пока в момент t¢ (пусть t¢1) состояние z(t¢) не окажется принадлежащим подмножеству Z¢_y, хотя состояние z(t¢-0) не принадлежало подмножеству Z¢_y. В этом случае в момент t¢ выдается выходной сигнал y⁽¹⁾, вырабатываемый оператором G¢. Вместе с тем закон изменения состояний (7.6) нарушается и

z(t¢+0)=W[z(t¢),u₀]. (7.9)

Прежде чем рассматривать дальнейшие изменения состояний агрегата во времени, необходимо проверить (оператор G¢¢), не удовлетворяет ли состояние z(t¢+0) условиям выдачи выходного сигнала, или, другими словами, не принадлежит ли (в смысле условий 1) и 2), упомянутых выше) состояние z(t¢+0) некоторому новому подмножеству Z¢¢_y). Если состояние z(t¢+0) удовлетворяет условиям выдачи выходного сигнала (принадлежит подмножеству Z¢¢_y), то в момент t¢¢ выдается второй выходной сигнал y⁽²⁾ (оператор G¢), а состояние агрегата описывается соотношением

z(t¢+0+0)=W[z(t¢+0),u₀]=W{W[z(t¢),u₀],u₀} (7.10)

и т.д. В силу принятого соглашения в любой интервал времени может быть выдано лишь конечное множество выходных сигналов. Это свойство агрегата является ограничением, накладываемым на структуру подмножеств Z_y и оператор W. Предположим теперь, что z(t¢+0) не принадлежит никакому из подмножеств Z_y. Поэтому далее состояние агрегата изменяется в соответствии с законом

z(t)=u_t¢[t,z(t¢+0),u₀]=u_t¢{t,W[z(t¢),u₀],u₀}. (7.11)

Пусть теперь в момент t₁ поступает входной сигнал x_1. Проследим поведение агрегата в момент t₁ при различных вариантах возможных событий.

Если при достаточно малых e>0 в момент t₁-e состояние агрегата не принадлежало подмножеству Z^*_y, а в момент t₁ z(t₁) принадлежит Z^*_y, то условимся, что в момент t₁ выдается выходной сигнал y^*_, а состояние агрегата есть

z(t₁+0)=W[z(t₁),u₀] . (7.12)

Вместе с тем действие входного сигнала x₁ приводит к тому, что

z(t₁+0+0)=V¢[z(t₁+0),x₁,u₀]=V’{W[z(t₁),u₀],x₁,u₁} . (7.13)

Очевидно, что состояние z(t₁+0+0) должно быть проверено (оператором G¢¢) по отношению к условиям выдачи выходного сигнала. Предположим теперь, что в момент t₁ не было оснований для выдачи выходного сигнала y*. Тогда вместо (7.12 и 7.13) в силу действия входного сигнала x₁ состояние агрегата имеет вид

z(t₁+0)=V¢[z(t₁),x₁,u₀], (7.14)

а в дальнейшем, если состояние (7.14) не соответствует выдаче выходного сигнала:

z(t)={t,V¢[z(t₁),x₁,u₀],u₀} (11.13) t₁1,t] (7.15)

Пусть в момент t₁ в агрегат поступает управляющий сигнал u₁. Тогда состояние агрегата имеет вид

z(t₁+0)=V¢¢[z(t₁),u₁], (7.16)

если в момент t₁ не происходит выдача выходного сигнала, или

z(t₁+0+0)=V¢¢{[W[z(t₁),u₀]]u_1,b}, (7.17)

если в момент t₁ выдается выходной сигнал.

Необходимо отметить, что управляющий сигнал u в общем случае является параметром, определяющим операторы V¢,V¢¢,W,U,G¢,G¢¢. Поэтому в дальнейшем вместо начального значения управляющего сигнала u₀ в этих операторах должно использоваться значение u₁ до тех пор, пока не поступит следующий управляющий сигнал u_2. Например, в полуинтервале (t₁, t₂], если нет оснований для выдачи выходного сигнала

z(t)=z(t₁+0),u₁] t₁2 (7.18)

В частном случае, операторы H и G могут оставаться неизменными при поступлении очередного управляющего сигнала. Аналогично, оператор U может быть одним и тем же при любых выходных сигналах (при попадании z(t) в любые подмножества Z_y).

Агрегат представляет собой математическую схему весьма общего вида, частными случаями которой являются функции алгебры логики, релейно-контактные схемы, конечные автоматы, всевозможные классы систем массового обслуживания, динамические системы, описываемые обыкновенными дифференциальными уравнениями и некоторые другие объекты. С точки зрения моделирования агрегат выступает как достаточно универсальный переработчик информации – он воспринимает входные и управляющие сигналы и выдает выходные сигналы.


^ 7.2.2. Функционирование СМО как агрегата

В качестве примера представления систем в виде агрегатов рассмотрим однолинейную СМО следующего вида. В моменты времени t_j, представляющие собой случайный поток однородных событий с заданным законом распределения, в систему поступают заявки, каждая из которых характеризуется параметром a_j. Величина a_j является случайной величиной с условным законом распределения f(a/t) при условии, что t_j=t. Если линия обслуживания занята, заявка попадает в очередь и может находиться там (ждать) не более, чем

t_k^(ж)=j(a_j,b_i) (7.19)

Величина b_i является случайной величиной с условным законом распределения f(b/t) при условии, что t_k=t. Величины t_k образуют случайный поток однородных событий с заданным законом распределения, не зависимый от t_j. Заявка должна быть принята к обслуживанию не позднее, чем в момент времени t_j+t_k^(ж), в противном случае она получит отказ.

Время обслуживания заявки или время занятости линии

t_k^(з)=y(a_j,b_i) (7.20)

Представим эту СМО в виде агрегата. Состояние агрегата будем характеризовать вектором z(t)ÎZ со следующими компонентами:

z₁(t) – время, оставшееся до конца обслуживания заявки (для заявки, которая находится на обслуживании);

z₂(t) – значение величины b_i;

z₃(t) – количеств заявок в очереди;

z₄(t) – оставшееся время ожидания первой заявки из очереди (время до момента отказа);

z₅(t) – оставшееся время ожидания второй заявки из очереди (время до момента отказа);

z_k(t) – оставшееся время ожидания последней заявки из очереди (время до момента отказа).

Входной сигнал x_j поступает в момент t_j и несет с собой информацию об a_j, т.е. x_j=a_j. Управляющий сигнал g_i поступает в момент t_i и несет с собой информацию о величине b_i, т.е. g_i=b_i.

Рассмотрим подмножества Z_y и соответствующие им выходные сигналы y, операторы W и U.

Подмножество Z_y⁽¹⁾. Пусть в момент времени t₁:

z₁(t₁)=0; z_l(t)>0; l=3,4,…,k.

Это означает, что обслуживание заявки закончилось. Выходной сигнал y₁=(y₁⁽¹⁾,y₁⁽²⁾). Здесь y₁⁽¹⁾ – признак «заявка обслужена», y₁⁽²⁾=y₁⁽²⁾(a_j,b_i,t₁) – выходной параметр заявки, зависящий от a_j и b_i. Заметим, что случайный характер оператора G¢ может проявляться в том, что y₁² (a_j,b_i,t₁) представляет собой случайную функцию a_j,b_i,t_1. Оператор W, определяющий состояние агрегата в момент t₁+0, задается следующим образом. Из всех z_l(t₁), где l=4,5,..k=z₃(t), выбирается наименьшее и соответствующая заявка, например номер m, m£k принимается к обслуживанию со временем обслуживания (занятости канала) t⁽³⁾_m=y(a_m,b_i). Поэтому

(7.21)

Количество заявок в очереди уменьшится на 1: z₃(t₁+0)=z₃(t₁)-1 (7.22), а величина z_m(t₁+0) не определяется. Все остальные z_l(t₁+0) при l=4,5,..(за исключением z_m)

z_l(t₁+0)= z_l(t₁) (7.23)

Оператор U, определяющий состояния агрегата для моментов времени t>t₁ (до последующего особого состояния) имеет вид

z₁(t)=z₁(t₁+0)-(t-t₁)

z₂(t)=z₂(t₁+0)=const

z₃(t)=z₃(t₁+0)=const (7.24)

z₄(t)=z₄(t₁+0)-(t-t₁)

............…………

z_k(t)=z_k(t₁+0)-(t-t₁)


Подмножество . Пусть в момент времени t₂:

z₁(t₂)>0; z₃(t₂)>0, z_m(t₂)=0, 4£m£k

Это означает, что время ожидания одной из заявок в очереди истекло. Поскольку заявка до момента t₂ не была принята к обслуживанию, она получает отказ. Выходной сигнал y₂=(y₂⁽¹⁾,y₂⁽²⁾). Здесь y₂⁽¹⁾ представляет собой признак «заявка получила отказ», y₂⁽²⁾= y₂⁽²⁾(a_j,b_i,t₂) – выходной параметр заявки. Оператор W в момент t₂+0 описывается соотношениями:

z₁(t₂+0)=z₁(t₂)

z₂(t₂+0)=z₂(t₂

z₃(t₂+0)=z₃(t₂)-1 (7.25)

............…………

z_l(t₂+0)=z_l(t₂) l=4,5,..k l¹m


Величина z_m(t₂+0) не определяется. Оператор U₍₎ для моментов времени t>t₂ определяется равенствами.

z₁(t)=z₁(t₂+0)-(t-t₂)

z₂(t)=z₂(t₂+0)=const

z₃(t)=z₃(t₂+0)=const (7.26)

............…………

z_l(t)=z_l(t₂+0)-(t-t₂) ) l=4,5,..k l¹m


Подмножество . В момент времени t₃: z₁(t₃)=0, z₃(t₃)=0. Это значит, что очередь заявок отсутствует, и обслуживание закончилось в момент t₃. Выходной сигнал y₃=(y₃⁽¹⁾,y₃⁽²⁾). Здесь y₃⁽¹⁾ – признак «система свободна», а y₃⁽²⁾=t₃ показывает момент освобождения системы. Оператор W: z₁(t₃+0)=0; z₃(t₃+0)=0; другие z_l не определяются. Оператор для всех t>t₃ задается соотношениями: z₁(t)=0, z₃(t)=0; z_l(t) при l>3 не определяются (до следующего особого состояния).

Пусть теперь в момент t_j поступает входной сигнал x_j=a_j (заявка с параметром a_j). Оператор V¢ имеет следующий вид. Если входной сигнал поступил после выходного сигнала y₃ (действовал оператор ) , то это означает, что система была свободной, и заявка сразу поступила на обслуживание с t_j^(З)=y(a_j,b_i). Поэтому

z₁(t_j+0)= t_j⁽³⁾=y(a_j,b_i) (7.27)

z₃(t_j+0)=0

…………………………….

Величины z_l(t_j+0) для l>3 не определяются. Если входной сигнал поступил после выходных сигналов y₁ и y₂, то заявка попадает в очередь, т.е.

z₁(t_j+0)=z₁(t_j)

z₂(t_j+0)=z₂(t_j)

z₃(t_j+0)=z₃(t_j)+1

…………………. (7.28)

z_l(t_j+0)=z_l(t_j); l=4,5,..k

………………….

z_k+1(t_j+0)=t_j^(ж)=j (a_j,b_i)


В дальнейшем (оператор ) состояния z(t) определяются аналогично (7.24)

Пусть теперь в момент t_i поступает управляющий сигнал g_i=b_i+1. При этом изменится только значение z₂(t): вместо прежнего значения b_i должно быть z₂(t)=b_i+1. остальные z_l(t) не зависят от b_i+1. Из этого легко усмотреть содержание операторов W и U.

На этом рассмотрение примера можно закончить. Обзор процесса функционирования такой системы массового обслуживания как агрегата дальше можно сделать самостоятельно.


7.3. Моделирование процесса функционирования агрегата


Целью моделирования в любом случае является получение характеристик, определяемых состояниями системы. Для этого необходимо фиксировать в процессе моделирования достаточно полную информацию о состояниях системы в соответствующие моменты модельного времени. Применительно к агрегату это означает, что необходимо получать значения состояний z(t) для некоторых моментов времени интервала исследования (0,T). Выше было показано, что вид оператора H, решающего эту задачу, зависит от того, поступают или нет входные и управляющие сигналы в течение рассматриваемого интервала времени. Моменты поступления x и uиграют значительную роль с точки зрения построения моделирующего алгоритма. В частности, мы будем рассматривать моделирование как последовательную цепь переходов из одного особого состояния агрегата в другое, причисляя условно к особым состояниям и z(0). Вид моделирующего алгоритма существенно зависит от того, известны ли заранее моменты поступления xи u и вообще моменты последующих особых состояний. С этой точки зрения следует иметь в виду два случая. Первый связан с рассмотрением агрегата, для которого законы поступления входных и управляющих сигналов заданы. В этом случае, очевидно, для моделирования агрегата, кроме описания самого агрегата, необходимо иметь исчерпывающее описание входных и управляющих сигналов, как воздействий внешней среды. Второй случай - рассмотрение агрегата, для которого входные и управляющие сигналы вырабатываются в процессе моделирования как выходные сигналы других агрегатов. Рассмотрим более подробно первый случай.

Итак, изучаем процесс функционирования агрегата в интервале времени (0, Т). Совокупности входных и управляющих сигналов, поступающих в агрегат в течение интервала времени (0, Т), считаем известными. Весьма важным является вопрос о способах ввода в модель входных и управляющих сигналов. Возможные варианты:

1. Входные и управляющие сигналы записываются в памяти машины в виде таблицы, содержащей для всех моментов значения параметров сигналов. Данные из таблицы автоматически выбираются по ходу моделирования (если не очень много сигналов и их параметров).

2. Генерирование сигналов при помощи случайных чисел. Моменты поступления сигналов в агрегат представляются в виде потока однородных событий, задаваемого соответствующим законом распределения интервалов времени между последовательными моментами. Другие параметры сигнала следует при этом задавать условным законом распределения при условии, что момент поступления сигнала задан. Тогда моделирование совокупности сигналов сводится к моделированию потока однородных событий и реализаций случайного вектора, заданного условным законом распределения.

Существенные особенности возникают лишь в том случае, когда входной (или управляющий) сигнал приходит от нескольких источников. Чтобы учесть такого рода обстоятельства, необходимо к подалгоритмам модели, формирующей входные и управляющие сигналы, построить дополнительный подалгоритм – сортировщик, который будет располагать сигналы, вырабатываемые различными источниками, в единую последовательность по времени. Перейдем к рассмотрению структуры моделирующего алгоритма. Введем следующие операторы:

Ф₁ – формирование очередного момента τ_iпоступления в агрегат управляющего сигнала;

Р₂ – проверка условия τ_i ≤ Т, где Т – граница интервала (0, Т) изучения агрегата;

F₃ – подстановка вместо τ_i величины Т+b (b>0);

А₄ – запоминание величины τ_i ;

Р₅ – проверка условия i > 1;

Р₆ – проверка условия t_j< τ_i, где t_j – момент поступления входного сигнала, и определение t_вх = min (τ _i, t_j);

Ф₇ – формирование очередного момента t_j поступления в агрегат входного сигнала;

Р₈ – проверка условия t_j < Т;

А₉ – запоминание величины t_j;

F₁₀ – подстановка вместо t_j величины Т+b (b>0);

F₁₁ – формирование признака μ = 0 – «ближайшим сигналом будет управляющий сигнал», t_вх = τ_i;

F₁₂ – формирование признака μ = 1 – «ближайшим сигналом будет входной сигнал», t _вх = t_j ;

Ф₁₃ – формирование оператора U_{t 0} для определения состояний z(t) агрегата в промежутках между особыми состояниями;

А₁₄ – определение ближайшего момента t _вых выдачи выходного сигнала (реализация оператора G");

Р₁₅ – проверка условия t_вых ≤ t_вх, где под t_вх понимается меньшее из τ _iи t _j ;

Ф₁₆ – определение состояния агрегата в момент t _вых (реализация оператора U_t0);

Ф₁₇ – формирование выходного сигнала у (реализация оператора G');

Ф₁₈ – формирование состояния z( t _вых + 0) после выдачи выходного сигнала (реализация оператора W);

Р₁₉ – проверка принадлежности состояния z( t _вых + 0) подмножеству Z_y (реализация оператора G");

Р₂₀ – проверка условия t _вх < T;

Ф₂₁ – определение состояния агрегата z( t _вх) в момент t_вх(реализация оператора U_t0);

Р₂₂ – проверка условия μ > 0 (ближайшим сигналом является входной сигнал);

Ф₂₃ – формирование управляющего сигнала g;

Ф₂₄ – определение состояния z(τ _i + 0) агрегата после управляющего сигнала (реализация оператора V");

Р₂₅ – проверка принадлежности состояния z(τ _i + 0) подмножеству Z_y (реализация оператора G");

Ф₂₆ – формирование входного сигнала х;

Ф₂₇ – определение состояния z(t _j + 0) агрегата после входного сигнала (реализация оператора V');

Р₂₈ – проверка принадлежности состояния z(t _j + 0) подмножеству Z_y (реализация оператора G");

F₂₉ – подстановка вместо t₀ момента t _ос последнего особого состояния (t_вх, t_вых или t=0);

Ф₃₀ – определение состояния агрегата z(Т) в момент Т окончания моделирования (реализация оператора U_t0);

А₃₁ – фиксация результатов, полученных при моделировании данной реализации процесса;

К₃₂ – счетчик количества N реализаций (выполняет операцию N= N+1);

Р₃₃ – проверка условия N
F ₃₄ - переход к моделированию очередной реализации;

А₂₅ – обработка результатов моделирования;

Я₃₆ – выдача.

При перечислении операторов использованы следующие обозначения:

А – вычислительные операторы;

Ф – операторы формирования реализаций случайных процессов;

F – операторы формирования неслучайных величин;

Р – логические операторы;

Я – оператор, означающий окончание вычислений.

Схема алгоритма приведена на рис.10. Работа моделирующего алгоритма протекает следующим образом. Группа операторов Ф₁-F₁₂ предназначена для формирования моментов поступления входных и управляющих сигналов и определения момента поступления ближайшего сигнала. Операторы Ф₁ и Ф ₇ вырабатывают моменты τ _i и t_j соответственно. Операторы Р ₂ и Р₈ определяют, находятся ли эти моменты в пределах интервала моделирования агрегата. Если это условие выполнено, то моменты τ_i (оператор А ₄) и t_j(оператор А ₉) запоминаются. Если же моменты τ_i и t _j находятся вне интервала (0, Т), то вместо них подставляется граничное значение времени t=Т (операторы F₃ и F₁₀ ) . Оператор Р₆ сравнивает τ_i и t _j и определяет ближайший момент t _вxпоступления в агрегат внешнего сигнала. Результаты сравнения фиксируются операторами F₁₁ и F₁₂; если μ = 0 – ближайшим будет управляющий сигнал, если μ = 1 – входной сигнал. Группа операторов Ф ₁₃ – Р₁₉ моделирует процесс функционирования агрегата в интервале времени между последовательными моментами поступления внешнего сигнала. В этом интервале состояния агрегата определяются оператором U_t0 (оператор Ф₁₃). Единственным видом особых состояний агрегата в этом случае являются состояния выдачи выходных сигналов или, другими словами, состояния, принадлежащие подмножествам Z_y. Задача оператора А₁₄ состоит в том, чтобы путем совместного моделирования состояний z(t) и условий, определяющих подмножества Z_y, определить моменты t_y выдачи выходных сигналов (оператор G" агрегата) и найти наименьший из них. Пути решения этой задачи (реализация оператора А₁₄) зависят от свойств агрегата и способа задания оператора G". В наиболее простых случаях задача сводится к проверке неравенств вида t _вых - t > 0 или к совместному решению уравнений (неравенств), описывающих состояния z(t) агрегата и подмножества Z _y.

Могут быть и более сложные подходы. В худшем случае приходится «прощупывать» состояния агрегата через малые интервалы времени ∆t и проверять принадлежность их подмножествам Z_y на каждом шаге. Выбор минимального t _у, т.е. t_вых = min t _у, обычно не представляет собой проблемы. Если момент t _вых выходит за пределы интервала моделирования (0, Т) или не существует, то t_вых принимается равным Т + b, где b > 0.

Если момент t _вых оказывается внутри интервала между внешними сигналами (оператор Р₁₅), то выходной сигнал у должен быть фактически выдан. Поэтому необходимо найти z( t _вых) (оператор Ф₁₆) и сформировать сам сигнал у (оператор Ф₁₇). Обычно при моделировании оператора G' его расчленяют на две части:

1. 
   формирование для заданного Z _y закона распределения случайного выходного сигнала у;
   
2. выбор самого сигнала по жребию в соответствии с этим законом распределения.
   

Затем, поскольку агрегат находится в особом состоянии z( t _вых), необходимо определить его состояние z(t_вых + 0) (оператор Ф₁₈) и проверить (оператор Р₁₉), не принадлежит ли z(t_вых + 0) одному из подмножеств Z_y. Если это условие выполнено, то управление передается опять Ф₁₇ для формирования второго выходного сигнала, выдаваемого в момент t _вых и т.д. Если же z( t _вых + 0) Z_y, то через оператор F₂₉ управление передается операторам Ф₁₃ и А₁₄ для формирования новых моментов t_вых. Возвратимся к оператору Р ₁₅. Если условие, проверяемое оператором Р₁₅, не выполнено, т.е. t _вх ≤ t_вых, то переходим к рассмотрению поведения агрегата под воздействием внешнего сигнала. Будем считать, что t _вх< Т (оператор Р₂₀). В противном случае наступает конец интервала моделирования и мы переходим к определению состояния z(Т) (оператор А₃₀). Оператор А₂₁ вычисляет состояние агрегата z( t _вх), а Р₂₂ определяет тип внешнего сигнала (входной, управляющий). Группа операторов Ф₂₃ – Р₂₅ моделирует прием управляющего сигнала в момент τ_i, а группа Ф ₂₆ – Р₂₈ - прием входного сигнала в момент t_j . Работа этих групп аналогична работе рассмотренной выше группы Ф₁₇ – Р₁₉. Заметим только, что z( t _вх + 0) сразу может принадлежать одному из подмножеств Z_y. Это условие проверяется операторами Р₂₅ и Р₂₈ соответственно. Если условие справедливо, то управление передается оператору Ф₁₇ для формирования выходного сигнала. Если нет, управление передается оператору Ф₁ (Ф ₇) для формирования очередного момента поступления управляющего (входного) сигнала.

Сложность машинной реализации рассмотренного моделирующего алгоритма зависит, в основном, от сложности реализации операторов, определяющих функционирование агрегата.

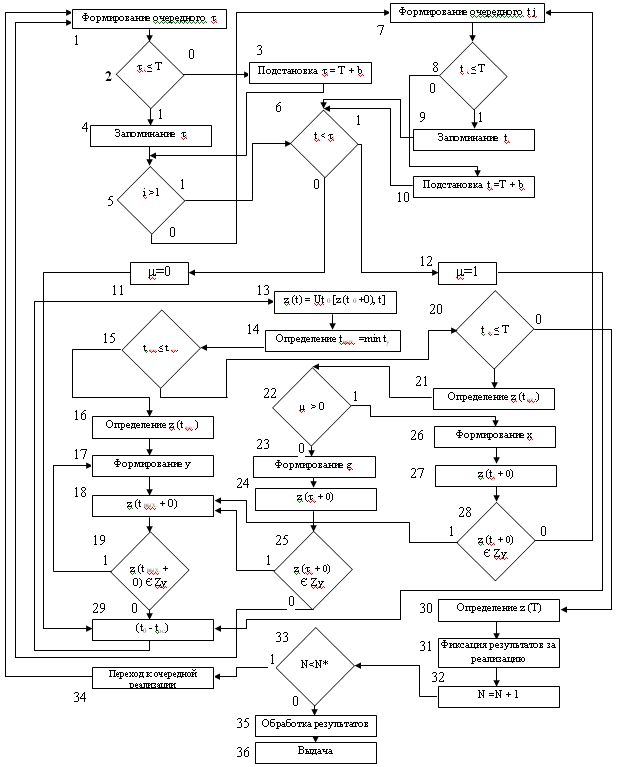
Рис. 7.1. Схема алгоритма функционирования агрегата общего вида

7.4. Кусочно-линейные агрегаты


Как показывает анализ моделирующих алгоритмов, можно добиться их существенных упрощений, если рассматривать объекты чуть более частные, чем агрегат общего вида, но сохраняющие такую важную его особенность, как возможность описания достаточно широкого класса реальных систем. Практически удобным для формализации чрезвычайно широкой совокупности разнообразных процессов и явлений материального мира являются так называемые кусочно-линейные агрегаты (КЛА), к описанию которых мы и приступим.


7.4.1. Понятие о кусочно-линейном агрегате.


Для поставленных здесь задач достаточно считать, что на агрегат не поступают управляющие сигналы u, а поступают лишь входные сигналы x (не ограничивает общности, в качестве x можно рассматривать входной сигнал в широком смысле ()). Итак, мы рассматриваем агрегат как объект, который в каждый момент времени t характеризуется внутренним состоянием z(t), имеет вход и выход. На вход агрегат в изолированные моменты времени могут поступать сигналы, с выхода могут сниматься выходные сигналы. Класс кусочно-линейных агрегатов выделяется с помощью конкретизации структуры множеств Z,X,Y а также операторов H и G. Опишем данную конкретизацию.

Рассмотрим некоторое конечное или счетное множество I. Для определенности предположим, что I={0,1,2,…}, хотя в конкретных задачах I может иметь и другой вид. Назовем I-множеством основных состояний, а элементы nÎI – основными состояниями. Каждому основному состоянию nÎI поставим в соответствие некоторое целое неотрицательное число ||n||, которое назовем рангом основного состояния. Кроме того, каждому nÎI поставим в соответствие выпуклый многогранник Z⁽ⁿ⁾ в евклидовом пространстве размерности ||n||. Будем считать, что Z=UZ⁽ⁿ⁾, т.е. пространство состояний Z можно представить состоящим из всевозможных пар вида (), где nÎI, а z⁽ⁿ⁾ является вектором размерности ||n|| и принимает значения из многогранника Z⁽ⁿ⁾. Вектор z⁽ⁿ⁾ будем называть вектором дополнительных координат. Если ||n||=0 для некоторого nÎI, то это означает, что в данном состоянии n дополнительные координаты не определяются.


7.4.2. Процесс функционирования КЛА.


Опишем сначала динамику КЛА, т.е. процесс изменения внутренних состояний во времени, в предположении отсутствия поступления x. В предыдущей терминологии, определим действия оператора U. Пусть в начальный момент времени t₀ агрегат находится в состоянии z(t₀)=(n,z⁽ⁿ⁾(0)), где z⁽ⁿ⁾(0)- внутренняя точка многогранника Z⁽ⁿ⁾. Тогда при t>t₀ точка z⁽ⁿ⁾(t) перемещается внутри многогранника Z⁽ⁿ⁾ до тех пор, пока не достигнет его границы. Пусть это произойдет в момент t₁, который назовем «опорным». Тогда при t₀1, Dt=t-t₀ «движение» агрегата описывается следующими законами:

n(t)=n=const (7.29),

данному значению n соответствует вектор a⁽ⁿ⁾ размерности ||n|| и

z⁽ⁿ⁾(t)=z⁽ⁿ⁾(0)+Dt×a⁽ⁿ⁾. (7.30)

Значение опорного момента t₁ определяется траекторией z(t), вернее её некоторыми параметрами и может быть найдено из соотношения

t₁=inf{t:z⁽ⁿ⁾(0)+(t-t₀)a⁽ⁿ⁾ÏZ⁽ⁿ⁾, t>t₀}, (7.31)

поскольку Z⁽ⁿ⁾ многогранник, то нахождение t₁ по (7.31) сводится к следующему. Пусть - j-тая грань многогранника Z⁽ⁿ⁾ (предположим, что Z⁽ⁿ⁾ содержит m(n) граней). Эти грани могут быть заданы линейными уравнениями:

j=1,… m(n) , (7.32)

где z_i⁽ⁿ⁾ – компоненты вектора z⁽ⁿ⁾, i=1.. ||n||. Легко понять, что (7.32) может быть записано в виде

или



Обозначим , j=1,…m(n) (7.34)

Пусть t=min{t_j;t_j>0} (7.35)

Тогда из (7.33-7.35) следует, что t₁=t₀+t (7.36)

В момент t₁ состояние рассматриваемого кусочно-линейного агрегата изменяется скачкообразно. Значение z(t₁+0) является случайным, задаваемым распределением P₁, которое зависит лишь от состояния z(t₁). В момент t₁ может выдаваться выходной сигнал (см. оператор G). Содержание (и необходимость выдачи) y зависит от состояния z(t₁). Подмножество Z_y, введенное в общем определении агрегата, в данном случае совпадает с . Для нас важно, указать, что множество Y имеет структуру, аналогичную Z, т.е. выходные сигналы y представляются y=(l,y^(l)), где l-элемент некоторого не более чем счетного множества, y^(l) – вектор, принимающий значения из евклидова пространства размером, зависящим от l. При t>t₁ движение агрегата вновь происходит в соответствии с формулами (7.29) и (7.30) до очередного «особого» момента t₂, где под Dt нужно понимать теперь t-t₁ и т.д. Обратимся теперь к случаю поступления входного сигнала. Подчеркнем, что для КЛА множество X структурно аналогично множествам Z и Y, т.е. x=(m,x^(m)), где m-элемент конечного или счетного множества, а x^(m)- действительный вектор, размерность которого зависит от m. Следующее описание поведения КЛА можно рассматривать как раскрытие действия оператора V^’.

Пусть в рассматриваемый момент t состояние агрегата z(t)=(n,z⁽ⁿ⁾) и пусть в этот момент поступает входной сигнал x=(m,x^(m)). При этом состояние агрегата меняется скачкообразно. Значение z(t+0) является случайным, задаваемым распределением P₂, которое, вообще говоря, зависит от z(t) и x. Будем считать, что в рассматриваемый момент может выдаваться выходной сигнал, содержание и необходимость выдачи которого зависит не только от состояния z(t) (и, быть может, z(t+0)), но и от содержания поступившего входного сигнала x. После рассматриваемого момента времени t движение агрегата происходит в соответствии с формулами (7.29) и (7.30) до следующего момента поступления входного сигнала или выхода вектора состояния на границу допустимых значений.

Динамика КЛА описана полностью. В виде КЛА могут быть формализованы многие реальные процессы: процессы передачи и обмена данными в сетях связи, системы массового обслуживания и материально-технического снабжения, процессы автомобильного движения на дорогах, разнообразные дискретные производственные процессы, вычислительные системы и т.д. При этом всюду основные состояния агрегата указывают на качественно различные состояния моделируемых объектов. Дополнительные же координаты характеризуют происходящие количественные изменения и часто носят сугубо вспомогательный характер, «вбирая» в себя необходимую информацию о предыстории модели. Следует отметить, что представление реальных систем в форме КЛА неоднозначно, поскольку неоднозначно могут быть выбраны состояния агрегатов. Выбор же состояний определяется как целями исследования, так и стремлением уменьшить размерность задачи. При этом всегда приходится идти на компромисс между точностью описания и полнотой получаемой информации с одной стороны и простотой модели – с другой.


7.4.3. Примеры представления систем в виде КЛА.


Пример 1. Вероятностный автомат. Рассмотрим конечный асинхронный вероятностный автомат Мура, т.е. такой, который не имеет «жесткой» тактности, а изменяет свое состояние всякий раз, когда поступает входной сигнал. Синхронный автомат получается, если потребовать, чтобы входные сигналы поступали в моменты t=1,2,… Пусть Z_a – конечное множество внутренних состояний автомата, X_a – его входной (конечный) алфавит, Y_a – его выходной (конечный) алфавит. Для определенности будем считать, что

Z_a={1,2,…N}, X_a={1,2,..K}, Y_a={1,2,..M}.

Динамика автомата описывается следующим образом. Если в момент t состояние автомата z_a(t)=i и поступил входной сигнал, x_a(t)=k, то состояние z_a(t+0)=j выбирается случайно с вероятностью , ³0, при любом k, 1£k£K. Выходной сигнал y_aÎY_a, выдаваемый в этот момент, является однозначной функцией «нового» состояния j: y_a=m=Ф(j), где Ф- некоторая детерминированная функция с областью определения Z_a и множеством значений Y_a. Представим этот автомат в виде кусочно-линейного агрегата. В качестве множества входных сигналов X КЛА возьмем X_a, а в качестве выходных сигналов Y – множество Y_a. За множество I основных состояний КЛА выберем Z_a и будем считать ||n||=0 при всех nÎI, т.е. вектор дополнительных координат z⁽ⁿ⁾ не определяется. При таком выборе состояния КЛА не определяются многогранники Z⁽ⁿ⁾, отпадают вопросы о движении внутри многогранника, выходе на границу и связанного с ним распределения P₁.

Все движение рассматриваемого КЛА состоит из скачков состояния при поступлении входных сигналов, причем ввиду отсутствия вектора дополнительных. координат речь идет лишь о скачках основного состояния n. Т.о., требуется задать лишь распределение P₂. Оно совпадает с рассмотренным выше распределением . Содержание же выходного сигнала, выдаваемого в момент поступления входного, определяется только функцией Ф. Вообще, если предположить, что ||n||=0, ||l||=0, ||m||=0 " n,a,m, то легко видеть, что КЛА превращается в вероятностный автомат весьма общего вида.

Пример 2. Система массового обслуживания. Пусть на обслуживающий прибор поступает ординарный поток требований, причем i-е по счету требование характеризуется параметром q_i, который представляет собой предельно допустимое время ожидания i-м требованием начала обслуживания. Время обслуживания i-того требования равно z_i, причем {z_i} – последовательность независимых одинаково распределенных случайных величин с общей функцией распределения B(x). Искомыми являются вероятностные характеристики длины очереди и времени ожидания.

Представим данный процесс в виде КЛА. За состояние агрегата выберем вектор z=(n,z⁽ⁿ⁾), где n- число требований, находящихся в системе в текущий момент времени, которые дождутся (или дождались) начала обслуживания, ||n||=n, а z⁽ⁿ⁾ – вектор, координаты которого определяются только при n>0 и имеют следующий смысл: z₁⁽ⁿ⁾ – время, оставшееся до окончания обслуживания требования, находящегося на приборе, а z_i⁽ⁿ⁾ (1<i£n) – длительности обслуживания требований, которые стоят в очереди и будут впоследствии обслужены. В соответствие с этим вектор a⁽ⁿ⁾ скоростей изменения дополнительных координат имеет компоненты a₁⁽ⁿ⁾=-1, a_i⁽ⁿ⁾=0 (1<i£n), многогранник Z⁽ⁿ⁾ при каждом n>0 совпадает с первым октантом эвклидова пространства размерности n:

Z⁽ⁿ⁾={z⁽ⁿ⁾: z_i⁽ⁿ⁾³0, i=1,2,.. n} и имеет m(n)=n ограничивающих координатных гиперплоскостей

Z_j⁽ⁿ⁾ ={z⁽ⁿ⁾:z_j⁽ⁿ⁾=0} j=1,..n.

В качестве входного сигнала рассмотрим пару (1,q), где символ 1 просто указывает на факт поступления требования (и, таким образом, дискретная компонента m принимает лишь одно значение 1), а величина q равна допустимому времени ожидания поступающего требования (т.е. ||m||=1).

Рассмотрим динамику данного агрегата. Поскольку между моментами поступления входных сигналов изменяется лишь первая дополнительная координата (если n³1), то нет необходимости рассматривать случаи выхода дополнительных координат на гиперплоскости Z_j⁽ⁿ⁾, j>1 (мы считаем, что z_i>0 с вероятностью 1). Пусть в момент t* выполнено z(t*)ÎZ₁⁽ⁿ⁾. Тогда с необходимостью

z(t*)=(n, 0, z₂⁽ⁿ⁾,..z_n⁽ⁿ⁾), где n>0 (7.37)

Физически это означает, что момент t* является моментом окончания обслуживания и, следовательно, обслуженное требование должно покинуть систему, а его место занимает требование стоящее первым в очереди (если очередь не пуста). Следовательно, из состояния (7.37) агрегат перейдет в состояние



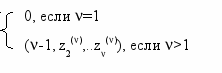
z(t*+0)= (7.38)


Т.о. распределение P₁ является вырожденным и приписывает вероятность 1 состоянию вида (7.38) (если предыдущее состояние имело вид (7.37) и вероятность 0 любому множеству состояний, не содержащему (7.38). Будем считать, что в рассматриваемый момент t* выходной сигнал не выдается.

Рассмотрим теперь случай поступления входного сигнала (1,q) в момент t^**. Пусть при этом состояние агрегата было z(t^**)=(n,z⁽ⁿ⁾), где n³0. Физически поступление рассматриваемого входного сигнала означает приход требования, обладающего предельным временем ожидания q, в систему обслуживания. Рассмотрим 2 случая: n=0 и n>0. В первом из них требование поступает в пустую систему, а во втором – в занятую обслуживанием. При n=0 состояние z(t^**+0) должно отражать тот факт, что поступившее требование сразу принято к обслуживанию и ему случайным образом назначено время обслуживания (с распределением B), т.е.

z(t^**+0)=(1,z), (7.39)

где z - случайная величина, имеющая распределение B(x). При n>0 состояние z(t^**+0) должно отражать тот факт, что требование будет принято к обслуживанию тогда и только тогда, когда его предельное время ожидания q превосходит реальное (т.е. q>) и в случае, если оно принято, ему назначается случайное время обслуживание с распределением B(x).



z(t^**+0)= ( (7.40)


, где z(x) – случайная величина с распределением B(x). Соотношения (7.39) и (7.40) конструктивно задают распределение P₂.

Будем считать, что в момент t^** выдается входной сигнал, фиксирующий имеющуюся длину очереди, время ожидания и факт принятия или непринятия поступающего требования. В соответствии с этим предположим, что y=(l,y^(l)), где l=(l₁,l₂), l₁ – число требований, находящихся в системе в момент t^**. l₂=0 или 1, если поступающее требование не принимается или принимается соответственно к обслуживанию, ||l||=l₂, y^(l)=время ожидания принятым требованиям начала обслуживания.

В данном случае l представляет собой вектор размерности 2 с целочисленными компонентами. Из сказанного следует, что имеют место зависимости:

l₁=n



l₂=


y^(l)=(координата определяется лишь при l₂=1)

На этом описание данной системы массового обслуживания в виде КЛА закончено.


7.5. Агрегативные системы


Рассмотрим класс сложных систем, представляющих собой конструкции из агрегатов, обладающих следующим свойством: существует такое (в общем случае неоднозначное) расчленение системы на элементы, при котором каждый полученный элемент представляет собой агрегат. Такого рода сложные системы будем называть агрегативными или А-системами. Каждый элемент А-системы, будучи в общем случае агрегатом, не обязательно должен обладать полным комплектом свойств агрегата: он может быть и более простым объектом, представляющим собой частный случай агрегата. Вместе с тем среди элементов А-системы не может быть ни одного элемента, который не являлся бы агрегатом (с полным или частичным комплектом свойств). Другими словами, среди элементов А-системы не могут содержаться объекты более общего характера, чем агрегат.

Вся информация, циркулирующая в А-системе, делится на внешнюю (поступающую извне от объектов, не являющихся элементами данной системы) и внутреннюю, вырабатываемую агрегатами самой системы. Обмен информацией между А-системой и внешней средой происходит через агрегаты, называемые полюсами системы. Так имеются входные полюса, представляющие собой агрегаты, для которых вводимая информация, поступающая в виде x-сообщений, является полностью или частично внешней (A₁ и A₄ на рис. 11). Управляющие полюса (A₁,A₃,A₆). Заметим, что А₁ является одновременно входным и управляющим полюсом системы. Выходные полюса (A₃,A₇). Агрегаты, не являющиеся полюсами, называются внутренними агрегатами. В частном случае А-система может не содержать внутренних агрегатов, а состоять только из полюсов. Могут быть также случаи, когда в А-системе отсутствуют входные и управляющие полюсы. Наконец, А-система может состоять лишь из одного агрегата. Этот агрегат одновременно может быть входным, управляющим и выходным полюсом А-системы.



g₂

(x)

(x)

(g)

(g)

(g)


Рис. 11. ^ Агрегативная система


Передача информации в А-системе происходит мгновенно (см 3.2), т.е. момент t¢ выдачи каким-нибудь из агрегатов является также моментом поступления входной или управляющей информации в некоторый агрегат системы или, наконец, моментом выдачи информации выходным полюсом системы. Такое предположение не является стеснительным ограничением. Если в реальной системе передача информации между ее элементами происходит с задержкой по времени, то соответствующая линия передачи представляется как самостоятельный агрегат, осуществляющий задержку. Тогда в формализованной схеме передача информации между элементами будет происходить мгновенно.

^ Виды связей между агрегатами. Свойства А-системы определяются не только свойствами составляющих агрегатов, но также и ее структурой. Рассмотрение структуры начнем с определения соотношений взаимодействия между агрегатами.

Два агрегата B и C называются непосредственно связанными, если между ними осуществляется прямая передача информации, т.е. выходная информация агрегата B является входной или управляющей для агрегата C, или наоборот. Будем также рассматривать просто связанные агрегаты. Агрегаты B и С называются связанными, если существует такая совокупность агрегатов B,D₁,D₂,…,D_S,C, что каждые два соседних агрегата B,D₁,D₂,…,D_S,C непосредственно связаны (в противном случае, несвязанные агрегаты). Рассмотрим некоторые виды связей между агрегатами. Будем говорить, что агрегат С непосредственно следует за агрегатом B (агрегат B непосредственно предшествует агрегату С), если некоторая часть выходной информации агрегата B является частью входной информации агрегата C. Очевидно, что данный агрегат, если даже он является полюсом A-системы, может непосредственно следовать за несколькими (непосредственно предшествовать нескольким) агрегатами А-системы. Аналогичные отношения можно ввести для связанных агрегатов. Будем говорить, что агрегат C следует за агрегатом B (агрегат B предшествует агрегату C), если существует такая совокупность агрегатов B,D₁,D₂,…,D_S,C, каждый из которых непосредственно следует за предыдущим.

Аналогично будем говорить, что агрегат B непосредственно управляет агрегатом C (агрегат С непосредственно подчинен агрегату B), если некоторая часть управляющей информации агрегата С представляет собой часть выходной информации агрегата B. Данный агрегат может непосредственно управлять несколькими агрегатами или быть непосредственно подчинен нескольким агрегатам А-системы. Агрегат B управляет агрегатом С (агрегат С подчинен агрегату B), если существует такая совокупность B,D₁,D₂,…,D_S,C, что каждый из них непосредственно управляет последующим агрегатом.