Адаптивное управление гидроагрегатами гэс с поворотно-лопастными турбинами

Вид материала

Документы

Содержание Исследование электропривода агрегатов для Моделирование сложных систем массового обслуживания Механико-математическая модель рабочего процесса аэродинамического преобразователя температуры Методы определения геометрических параметров шлифовальных зерен Разработка методики расчета оптимальных параметров настройки каскадных систем регулирувания Синтез линейного фильтра для информационных каналов автоматизированных систем управления Принципы построения адаптивных систем автоматического управления многомерными объектами Обработка пространственных данных, полученных с помощью дзз Система автоматического контроля вязкости и плотности Выбор датчиков для экстремальных условий эксплуатации

Подобный материал:

• Анализ факторов, влияющих на режим регулирования водного режима водохранилищ Ангаро-Енисейского, 220.06kb.
• Адаптивное управление социально-экономическим развитием предприятия сферы услуг, 374.74kb.
• Влияние Ангаро-Енисейских гэс на водные биоресурсы и среду их обитания, 73.72kb.
• Недзиев Сергей Николаевич адаптивное управление кадровой политикой предприятия специальность, 188.79kb.
• Адаптивное прогнозирование экономического состояния промышленного предприятия на основе, 344.8kb.
• Адаптивное управление промышленными предприятиями в конкурентной среде, 946.53kb.
• Новосибирская гэс, 25.71kb.
• Межотраслевой центр эргономических исследований и разработок «эргоцентр» Грачев Владислав, 302.22kb.
• Адаптивное управление для станков с чпу н. В. Лищенко, канд техн наук, ассистент;, 232.54kb.
• Оптимизация водно-энергетических режимов приливных электростанций с ортогональными, 286.14kb.

АДАПТИВНОЕ УПРАВЛЕНИЕ ГИДРОАГРЕГАТАМИ ГЭС

С ПОВОРОТНО-ЛОПАСТНЫМИ ТУРБИНАМИ

А. С. Гольцов, ВПИ (филиал) ВолгГТУ; А. В. Клименко, ОАО «Волжская ГЭС»

Прогнозом развития гидроэнергетики, выполненным Ассоциацией «Гидропроект», решением совместного заседания Бюро Научно-технического совета РАО «ЕС России» и Научного совета РАН по проблемам надежности и безопасности больших систем энергетики, предусматривается существенное повышение роли гидроэлектростанций в производстве электроэнергии в ЕЭС России. При этом решение важнейших задач повышения технического уровня и конкурентоспособности отечественной электроэнергетики, выполнение требований, предъявляемых к синхронной параллельной работе с энергообъединениями Центральной и Западной Европы, можно обеспечить уровнем и качеством автоматизации процессов регулирования частоты и мощности ГЭС.

В существующих системах технологического управления гидроагрегатами ГЭС используются технические решения 40-60 годов 20 века, базирующиеся на классических алгоритмах ПИД-регулирования линейными объектами. Основными недостатками всех известных способов регулирования активной мощности многоагрегатных ГЭС является то, что для их осуществления используются линейные математические модели гидроагрегата и одинаковая для всех гидроагрегатов комбинаторная зависимость – зависимость угла установки лопастей рабочего колеса турбины от напора воды и положения лопаток направляющего аппарата, обеспечивающая (теоретически) максимальный КПД. Но комбинаторную зависимость определяют экспериментальными исследованиями макета рабочего колеса гидротурбины на специальном гидродинамическом стенде и реализуют в системе управления с помощью механических, электрогидравлических и электронных преобразователей. При этом указанный макет существенно отличается от реальной турбины, а каждый агрегат имеет свои отличительные особенности, которые влияют на выбор оптимальных параметров системы управления и величину КПД. Среди этих факторов следует выделить существенное отличие конструкции водоводного тракта гидротурбины от трубопроводов экспериментального стенда, различие в зазорах между лопастями рабочего колеса и камерой разных гидроагрегатов, расхождение между расчетными и фактическими значениями положения лопаток направляющего аппарата и угла разворота лопастей рабочего колеса. Поэтому штатные системы регулирования частоты и активной мощности гидроагрегатов обладают существенными (до 2 %) статическими погрешностями регулирования. При этом законы изменения активная мощность гидроагрегатов и углов установки лопаток НА формируют с колебаниями, которые вызывают колебания давления в спиральной камере и в отсасывающей трубе, что приводит к появлению повышенной вибрации и кавитации.

Комбинаторная зависимость согласует угол установки лопастей РК с углом поворота лопаток НА при разных значениях напора воды и должна обеспечивать максимальное значение к.п.д. гидроагрегата. Каждая точка комбинаторной зависимости была определена в установившемся режиме работы экспериментальной установки при фиксированных значениях напора воды и положения лопаток НА модели рабочего колеса с последующим пересчетом на реальную турбину с помощью теории подобия. Однако в реальных условиях комбинаторная зависимость не выполняется. Экспериментальные исследования штатных систем управления частоты и активной мощности гидроагрегатов Волжской ГЭС, оснащенных контроллером EMERSON, показали, что при одном и том же напоре воды одинаковое значение активной мощности формируется при разных углах установки лопастей рабочего колеса и лопаток направляющего аппарата. Оказалось, что за счет корректировки комбинаторной зависимости можно уменьшить расход воды через турбину (и увеличить КПД гидроагрегата) на 2 - 3 %. Кроме того, было установлено, что в установившихся режимах работы отклонение активной мощности гидроагрегатов от требуемых значений (статическая погрешность регулирования) колеблется в диапазоне  3 % ( 3 МВт), а динамическая погрешность достигает 15 МВт.

Колебательный характер изменения положений лопаток направляющего аппарата и значений мощности турбины приводит к вибрациям и колебаниям давления в отсасывающей трубе и возникновению кавитации, а значит и к сокращению межремонтного периода.

Указанные негативные явления можно устранить либо минимизировать за счет применения микропроцессорной системы адаптивного управления частотой и активной мощности с обучаемой моделью гидроагрегата, формирующей задание регулятору в виде гладких опорных траекторий изменений во времени положения лопаток НА и активной мощности гидроагрегата.

В теории адаптивного управления сложились два подхода к описанию априорных неопределенностей математической модели системы управления: стохастический и детерминированный (минимаксный). Правильный выбор математической модели объекта управления является решающим условием, гарантирующим успех в решении задачи адаптивного управления. Этот выбор должен основываться как на понимании самой процедуры идентификации модели, так и на содержательной и формализованной информации об идентифицируемом объекте. Качество полученной модели может быть, в частности, оце­нено по критерию среднеквадратической ошибки, в котором множество проектных переменных включает структуру модели. В последние годы, когда выяснились теоретические и вычислительные трудности, стоящие перед детерминированным описанием неопределенностей, начали разрабатывать вероятностные модели "неизвестных, но ограниченных по абсолютной величине" возмущений. Такой подход используется при синтезе линейных систем адаптивного управления. Однако и в этих системах адаптивного управления применяют П-регуляторы с постоянными параметрами. Кроме того, в этих системах адаптивного управления не учитывают ограничения в форме неравенств на допустимые траектории перехода объекта управления в требуемое состояние.

Поэтому целью работы является разработка метода аналитического проектирования адаптивной системы автоматического управления гидроагрегатом в условиях априорной неопределенности, когда возмущающие воздействия являются сигналами, ограниченными по абсолютной величине, а математическое описание траекторий перехода управляемых переменных в конечное состояние задано неравенствами.

В соответствии с этой теорией в цепь обратной связи системы управления включается обучаемая модель процессов формирования момента движущих сил турбины, активной мощности гидроагрегата и опорных траекторий перехода управляемых переменных в требуемое состояние. Полученная модель будет содержать нелинейные уравнения, описывающие комбинаторную зависимость, и неизвестные входные воздействия, ограниченные по абсолютной величине. В результате задачи оценивания переменных состояния и возмущающих воздействий, коррекции комбинаторной зависимости и формирования траекторий перехода управляемых переменных в требуемое состояние преобразуют в эквивалентные задачи формирования управляющих воздействий с ограниченной энергией для вспомогательных нелинейных систем.

Алгоритмы решения каждой из этих задач управления были получены минимизацией (с помощью принципа максимума) регуляризованных по А. Н. Тихонову критериев обобщенной работы. Возникающие при этом нелинейные двухточечные краевые задачи преобразованы в эквивалентные задачи Коши с помощью инвариантного погружения.

Выполненные исследования, в которых использовались реальные данные, полученные при пусках гидроагрегатов №№ 4, 8 и 19 ОАО «Волжская ГЭС», показывают, что с помощью предлагаемой системы можно уменьшить статическую погрешность регулирования активной мощности на 2 %, снизить уровень вибраций и уменьшить расход воды через турбину, обеспечив в результате увеличение КПД гидроагрегата на 3 - 4 %.


ИССЛЕДОВАНИЕ ЭЛЕКТРОПРИВОДА АГРЕГАТОВ ДЛЯ

ПРОИЗВОДСТВА РЕЗИНОВЫХ РУКАВОВ С КАРКАСОМ

Л. Б. Иванов, ВПИ (филиал) ВолгГТУ

Целью настоящей работы является повышение эффективности процесса сборки напорно-всасывающих рукавов средствами автоматизированного электропривода.

Традиционно, для технологического оборудования в производстве дорновых напорно-всасывающих рукавов применяются регулируемые электроприводы постоянного тока, а соотношения скоростей для задания шага спирали устанавливается смежными шестернями в редукторе привода каретки, на которой расположена бобина с проволокой. Недостатком такой схемы является невозможность плавно менять шаг при сборке одного рукава, в частности, при закреплении спирали в начале и в конце рукава.

На предприятии Волжского научно-технического комплекса ВолгГТУ разработан станок НО 579, предназначенный для навивки спирали из стальной проволоки и хлопчатобумажного шнура на заготовку с заданным шагом. Электропривод станка осуществляется от двух трёхфазных асинхронных двигателей. Первый двигатель (М1) вращает дорн, на котором находится заготовка рукава, а второй (М2) перемещает каретку, на которой располагается барабан с проволокой, вдоль дорна.

Такая конструкция станка свободна от недостатков, обусловленных необходи-мостью смены шестерней в редукторе при неизменном шаге.

Для повышения эффективности производства предложена система частотного управления электроприводами станка, построенная по схеме “частотный преобразователь – асинхронный двигатель”.

Система частотного управления электроприводами станка должна обеспечить выполнение следующих технологических требований : регулирование частоты вращения электродвигателя дорна при постоянном статическом моменте сопротивления в диапазоне 20:1; регулирование частоты вращения электродвигателя каретки при постоянном статическом моменте сопротивления в рабочем режиме сборки с заданным шагом в диапазоне 87,5 : 1; статическая точность стабилизации частоты вращения не более ± 2,8 %; перерегулирование при отработке скачка задания частоты и момента сопротивления не более 5 %;

Шаг навивки спирали в соответствии с программой работы станка 3; 5; 8; 15; 20; 35 мм.

В качестве регулируемых электроприводов выбраны электроприводы с асинхронными двигателями и преобразователями частоты Micromaster 440.

Анализ литературы показал, что для удовлетворения поставленным технологическим требованиям можно использовать

1)ПЧ с АД с регулятором и обратной связью по скорости;

2)в случае применения типовых частотных преобразователей поставленным технологическим требованиям удовлетворяет система управления u/f c IR компенсацией и компенсацией скольжения или векторный бессенсорный режим.

Для оценки пригодности данных режимов управления сепаратной системы для обеспечения заданных показателей качества требуется экспериментальная проверка.

Для достижения цели работы необходимо решить следующие задачи:

1) выбрать типовые проебразователи частоты и электродвигатели для электроприводов станка;

2) теоретически и экспериментально исследовать возможность создания двухдвигательного электропривода по системе “преобразо-ватель частоты – асинхронный двигатель” с согласованной скоростью вращения, обеспечивающего достижение технологических требований при сборке напорно-всасывающих рукавов

Для реализации задачи исследованы варианты математических моделей и для теоретических исследований выбрана упрощённая математическая модель, так как работа электропривода исследуется только в области рабочей зоны мех. характеристики, и следовательно мат. модель может быть линеаризована с достаточной степенью точности.

Результаты теоретического исследования системы с обратной связью по скорости и ПИ - регулятором представлены на плакате :

Для определения возможности использования настроек типовых частотных преобразователей для двухдвигательного электропривода станка выполнены экспериментальные работы.

В установке использованы ПЧ Micromaster Vector и асинхронные двигатели, по своим характеристикам близкие к реальному электрооборудованию станка, нагрузочное устройство, состоящее из двигателя постоянного тока П-21 и устройство однофазное реверсивное тиристорное БУ3609-32Т2У4.

При экспериментальных исследованиях статических режимов для получения механических характеристик измерения частоты вращения двигателя и механического момента на валу использованы показания дисплея преобразователя частоты, параметрированные в соответствии с инструкцией по эксплуатации.

Выполнены экспериментальные исследования статических режимов при различных частотах и получены механические характеристики для двух режимов : u/f с IR компенсацией и векторного режима.

Исследованы способы реализации системы управления скоростями сепаратных электроприводов: последовательный и параллельный. При последовательном режиме была выявлена значительная ошибка в выходных значениях частот электроприводов (до 100 об/мин). Из этого следует что использование аналоговых выходов типовых частотных преобразователей в качестве сигналов задания или обратных связей невозможно.

При экспериментальном исследовании динамических режимов сепаратной системы и при совместном управлении сепаратными использованы показания дисплея и осциллографа, состоящего из аналого-цифрового преобразователя ADB13x100 и персонального компьютера. Входы аналого-цифрового преобразователя подключались к аналоговым выходам преобразователей (A1OUT+; AOUT-), параметрированным так же, как дисплей.

Запись осциллограммы в файл персонального компьютера выполнялась в соответствии с инструкцией к аналого-цифровому преобразователю ADB13x100. Обработка осциллограмм выполнялась в среде MathCAD 12.

Для данной схемы были сняты осциллограммы:

1) изменение момента;

2) реакция скорости на приложение момента;

3) совместные разгоны и торможения двигателей при различных заданных временах;

Для данного станка в целях повышения эффективности процесса сборки рукавов с заданным шагом будет целесообразным применение системы, содержащей асинхронный электропривод с частотным управлением. Исследования показали: для управления электроприводом дорна может быть предложено скалярное u/f регулирование с IR-компенсацией (FCC) и компенсацией скольжения или векторное управление без датчика скорости.

Для управления электроприводом каретки целесообразно применить скалярное u/f - регулирование с датчиком скорости. При некотором снижении диапазона регулирования (до 50: 1) за счёт введения в кинематическую цепь дополнительной ступени редуктора возможно использование скалярного u/f – управления с IR-компенсацией (FCC) и компенсацией скольжения (FCC при P071 = 80) или векторное управление без датчика скорости.

МОДЕЛИРОВАНИЕ СЛОЖНЫХ СИСТЕМ МАССОВОГО

ОБСЛУЖИВАНИЯ

В. И. Капля, ВПИ (филиал) ВолгГТУ

Процесс управления сложным техническим объектом можно представить в виде возникновения и обработки потока заявок (сообщений) между заданным множеством элементов объекта. Например, промышленные объекты высокого уровня автоматизации оснащены распределенной системой интеллектуальных датчиков, которые в зависимости от состояния объекта формируют информационные сообщения для системы управления.

Топология системы управления строится с учетом пространственного расположения датчиков и управляющих элементов объекта (органов управления). Моделью объекта управления является модель формирования входных потоков сообщений, поступающих в систему управления [1-13].

Случайный характер возмущающих факторов, воздействующих на объект, определяет случайный процесс появления сообщений датчиков, различную длительность обработки этих сообщений в процессорных элементах, реализующих логику и законы управления, и различную длительность задействования управляющих элементов.

Возмущающие факторы можно разделить на две категории: локальные факторы – которые отрабатываются короткой последовательностью сообщений (например, нарастание температуры или изменение вязкости перекачиваемого вещества) и глобальные факторы – вызывающие в системе большой поток сообщений, в течение короткого промежутка времени (например, изменение режима работы).

Целью моделирования СМО является статистическая оценка заданного множества параметров СМО. В качестве оцениваемых параметров обычно рассматривают: среднюю длину очереди в обработчике сообщений, коэффициент загруженности элементов системы или среднюю длительность пребывания сообщения в СМО. Структура и параметры модели служат основой организации процесса моделирования, на которой базируется планирование экспериментов. В результате экспериментов формируется вектор оценок параметров системы, обеспечивающих функциональность и адекватность модели для расчета достоверных прогнозов и проектов.



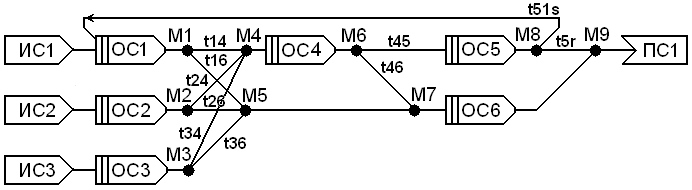
Рисунок 1 – Схема СМО, исследуемая в примере

Матрица входных данных для одного ИС имеет следующий вид:

,

Результаты моделирования СМО

Разработка схемы сложной СМО должна начинаться с определения источников и приемников управляющих сообщений, топологии маршрутов прохождения и обработки сообщений, дисциплин деления и слияния информационных потоков. Свойства информационных потоков целесообразно задавать в виде параметров законов распределения интервалов между сообщениями и длительностей обработки этих сообщений. Рассмотренный подход позволяет построить и проанализировать модель сложного объекта в пространстве случайных дискретных событий.

Введение понятий функции присутствия сообщений в системе и функции деления потоков сообщений в соответствии с заданной дисциплиной позволяет рационально организовать вычислительный процесс. Формирование для каждого сообщения строки параметров, состоящей из номера источника сообщения, приоритета и адреса приемника сообщения, позволяет строить полную модель прохождения каждого сообщения через СМО.

Моделирование многоконтурных систем требует применения рекуррентных алгоритмов вычисления для векторов моментов прибытия и выхода сообщений в каждом обработчике сообщений и в системе в целом. Листинги 1-6 демонстрируют работоспособность предложенных алгоритмов на достаточно общем примере.





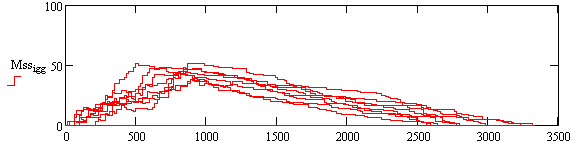
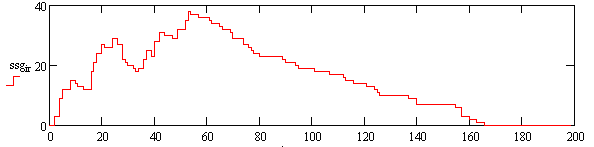
Рисунок 2 – Результаты моделирования

МЕХАНИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАБОЧЕГО ПРОЦЕССА

АЭРОДИНАМИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ ТЕМПЕРАТУРЫ

В. В. Корзин, ВПИ (филиал) ВолгГТУ

Предлагаемый преобразователь целесообразно использовать для измерения температуры протекающих газов в трубопроводах, двигателях внутреннего сгорания, а также при автоматизации технологических процессов в машиностроении и других отраслях промышленности.

Схема чувствительного элемента преобразователя температуры типа «питающий канал  приемный канал» при его работе в ламинарном и перемежаемом режимах течения приведена на рисуноке 1.



L


1 – питающий канал; 2 – струя газа; 3 – приемный канал.

Рисунок 1 – Схема чувствительного элемента струйного преобразователя температуры

При анализе рабочего процесса преобразователя температуры «питающий канал – приемный канал» приняты следующие допущения:

1. Рассматривается струя круглого сечения.

2. Режим течения струи принимается постоянным, с возникающими очагами турбулентности.

3. Потоки в каналах преобразователя и струя, формируемая питающим каналом, являются неизотермическими.

4. В процессе изменения температуры рабочей среды Т, протекающей по питающему каналу, изменяются плотность ρ, динамический коэффициент вязкости μ и число Рейнольдса струи, формируемой питающим каналом.

5. Ламинарный режим течения струи сохраняется на участке L=(10÷15)d_п, в соответствии с данными [1].

6. В переходном режиме течения струи при воздействии температуры могут возникнуть очаги турбулентности.

7. Перепад давлений Δр в питающем и приемном каналах определяется по средней скорости движения рабочей среды v, как принято в [1].

8. Расходы, эжектируемые струей, сформированной в канале питания, на участке ламинарного движения струи L=(10÷15)d_п близки к нулю [1].

9. Принимаем как основной сводный аэрогидродинамический параметр /² в качестве элемента исследования, поскольку динамический коэффициент вязкости µ и плотность ρ являются функцией температуры [2].

Чувствительный элемент преобразователя температуры имеет питающий и приемный ламинарные каналы, диаметром и длиной соответственно d_п, l_п=15d_п и d_в, l_в=(115) d_в, а также рабочую камеру длиной L, в которой осуществляется изменение течения струи при изменении температуры протекающего газа. Газ, температура которого измеряется, подводится к питающему каналу чувствительного элемента, проходит через рабочую камеру и выходит через приемный канал. В питающем и приемном каналах, а также в рабочей камере осуществляется режим перемежаемости струи. Например, при увеличении температуры газа его вязкость увеличивается, а плотность уменьшается, в результате чего изменятся скоростной напор v²/2, а также давление на выходе датчика, по изменению которого можно судить о температуре газа.

Теоретическое обоснование рабочего процесса преобразователя, основано на использовании приведенного параметра /² [2]. Физические величины которого, т.е. плотность и вязкость позволяют проводить исследование влияния температуры на характер режимов протекания струи и потоков рабочей среды.

При проведении теоретического анализа были рассмотрены параметры ламинарного потока рабочей среды в каналах и струи в рабочей камере чувствительного элемента преобразователя. В результате анализа было установлено, что скоростной напор, формируемый питающим каналом, при изменении температуры определяется следующим образом:

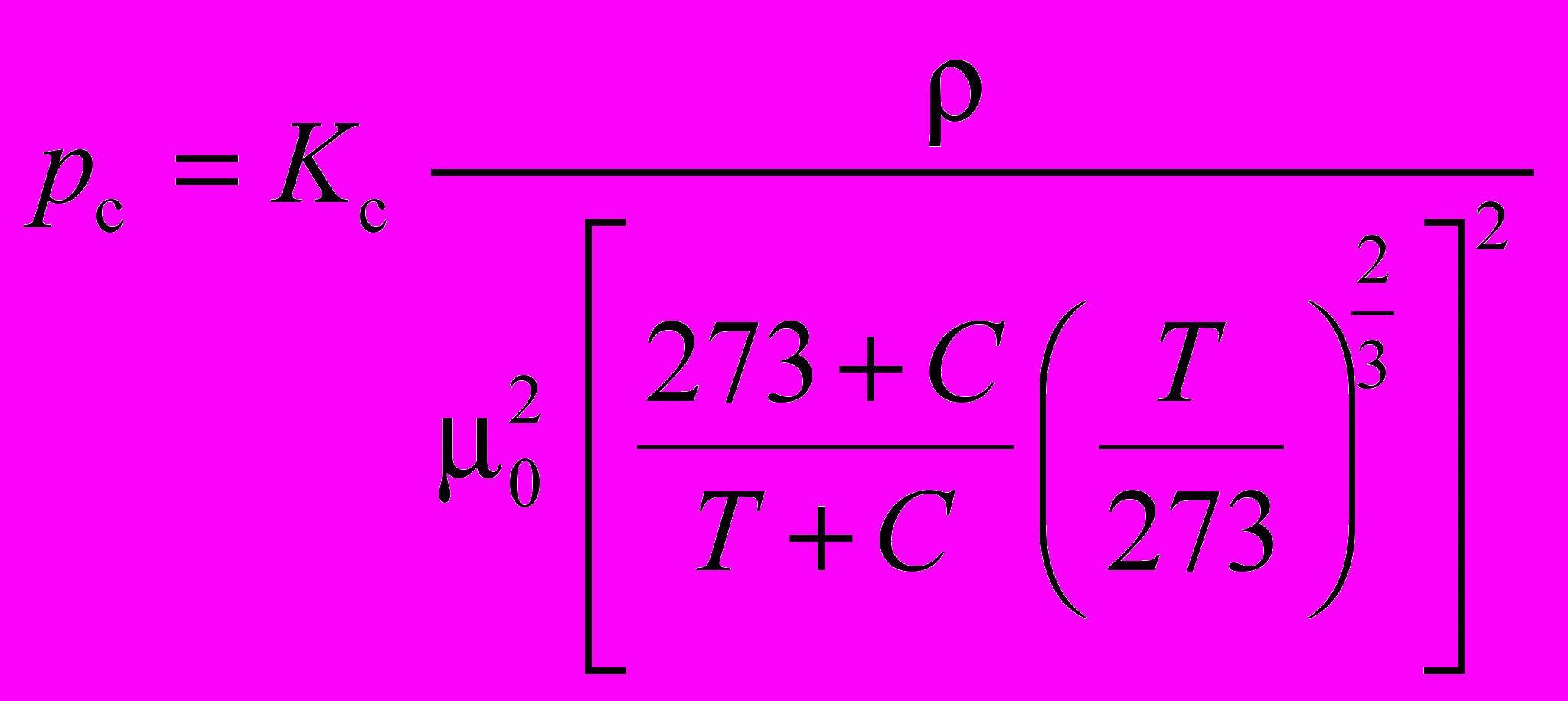, (1)

где К_с=0,510^-3р₀d_п⁴/l_п² – конструктивный коэффициент преобразователя;

α – коэффициент кинетической энергии ламинарного потока;

р₀ – давление на входе в питающий канал.

Из выражения (1) следует, что величина скоростного напора формируемого питающим каналом элемента (рисунок 1) зависит от его длины l_п, диаметра d_п, давления питания р_0, числа Рейнольдса Re, а также от параметра /², определяющего физические свойства среды, то есть плотности  и динамического коэффициента вязкости . Динамический коэффициент вязкости и плотность зависят от рода жидкости или газа, а также от температуры.

Давление на выходе приемного канала чувствительного элемента р_в близко к р_с, но отличается от него за счет условий обтекания входа приемного канала. С учетом выражения для выходного давления, приведенной в [2], и выражения (1) изменение выходного давления р_в в зависимости от температуры может быть представлено в следующем виде:

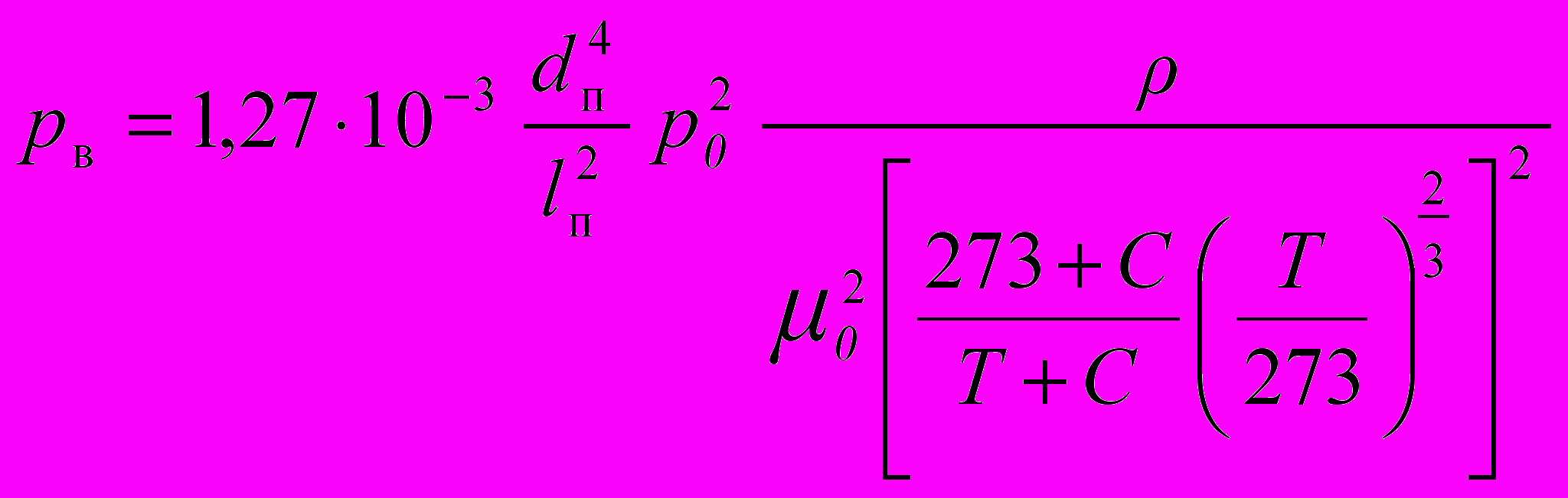, (2)

где С – постоянная для данного газа.

Из полученного выражения следует, что выходное давление является мерой температуры. Проведя преобразования получили выражение для определения температуры:

.

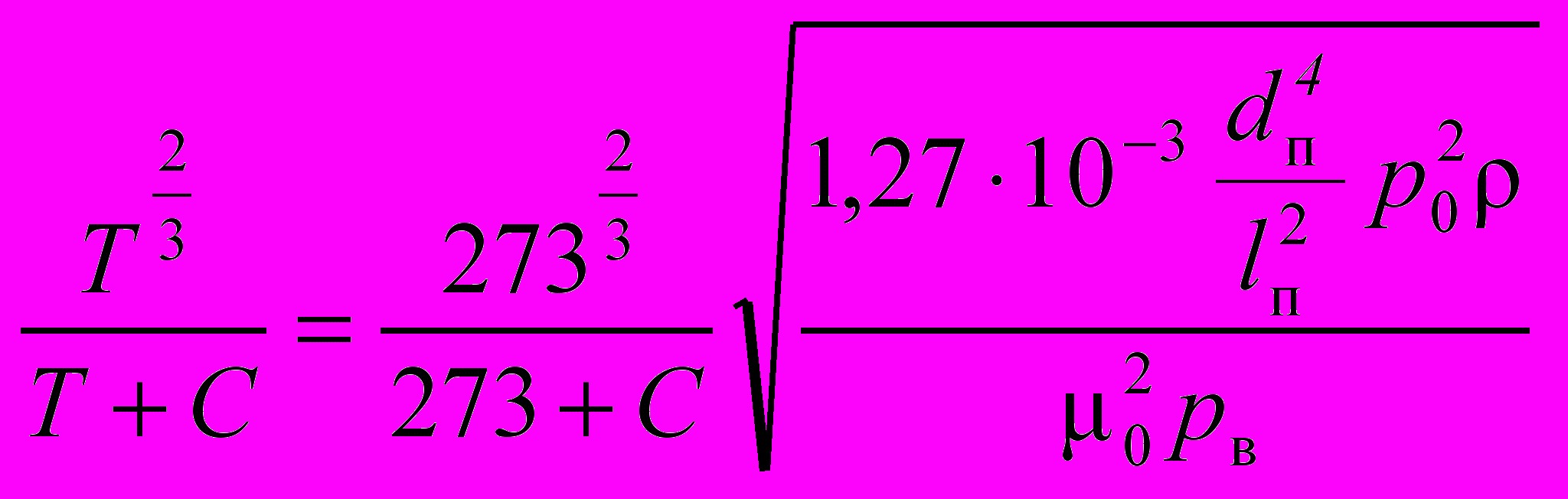Таким образом, на основе проведенного анализа рабочего процесса построена математическая модель рабочего процесса аэродинамического преобразователя температуры, и установлены основные параметры, влияющие на характер этого процесса.

МЕТОДЫ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ

ШЛИФОВАЛЬНЫХ ЗЕРЕН

И. А. Макушкин, ВПИ (филиал) ВолгГТУ

Абразивы – это твердые мелкие частицы, используемые в свободном или связанном виде для механической обработки изделий для удаления материала обрабатываемой поверхности острыми выступами абразива. Основные характеристики абразивных материалов – микротвердость, механическая прочность, хрупкость и размер зерна. Геометрические параметры зерен оказывают заметное влияние на режущую способность шлифовальных инструментов. В настоящее время при производстве зерен из геометрических параметров фактически оценивается только один – наибольшая длина зерна, которая определяется либо при просеивании через контрольные сита, либо микроскопическим способом. В то же для создания шлифовальных инструментов с заданными характеристиками желательно знать больше геометрических параметров полученных зерен, а именно – коэффициент формы, количество режущих кромок зерна и т.д.

Для автоматизации процесса получения геометрических параметров зерна при использовании микроскопического способа было предложено воспользоваться компьютерными методами распознавания фотографических изображений зерен.

Анализируя изображения зерна, можно заметить, что из-за кристаллической структуры вся область изображения, занимаемая зерном, обладает высоким значением градиента, вычисленного для этого изображение. Значение градиента для точки изображения рассчитывается с использованием операции свертки

,

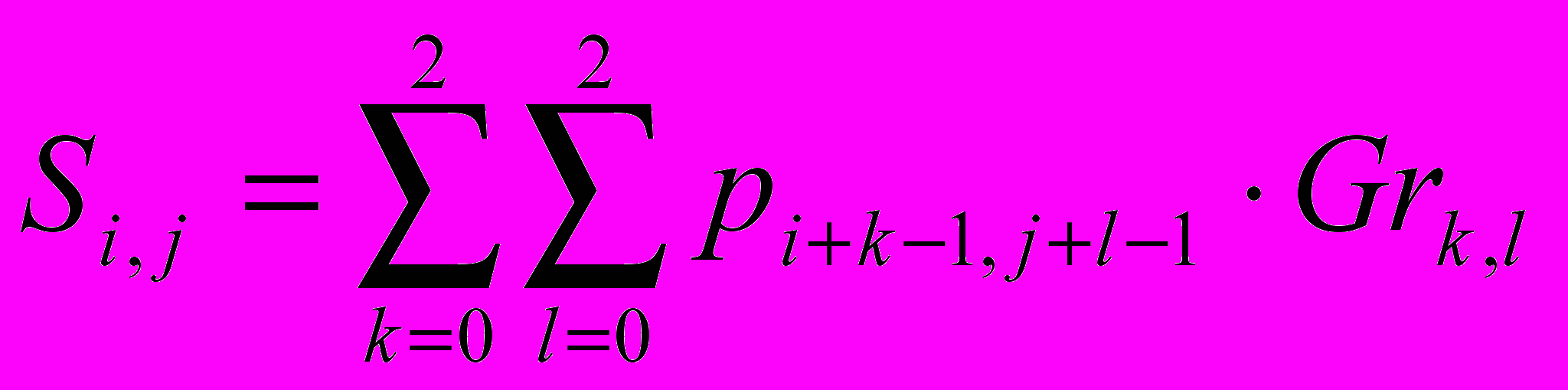где 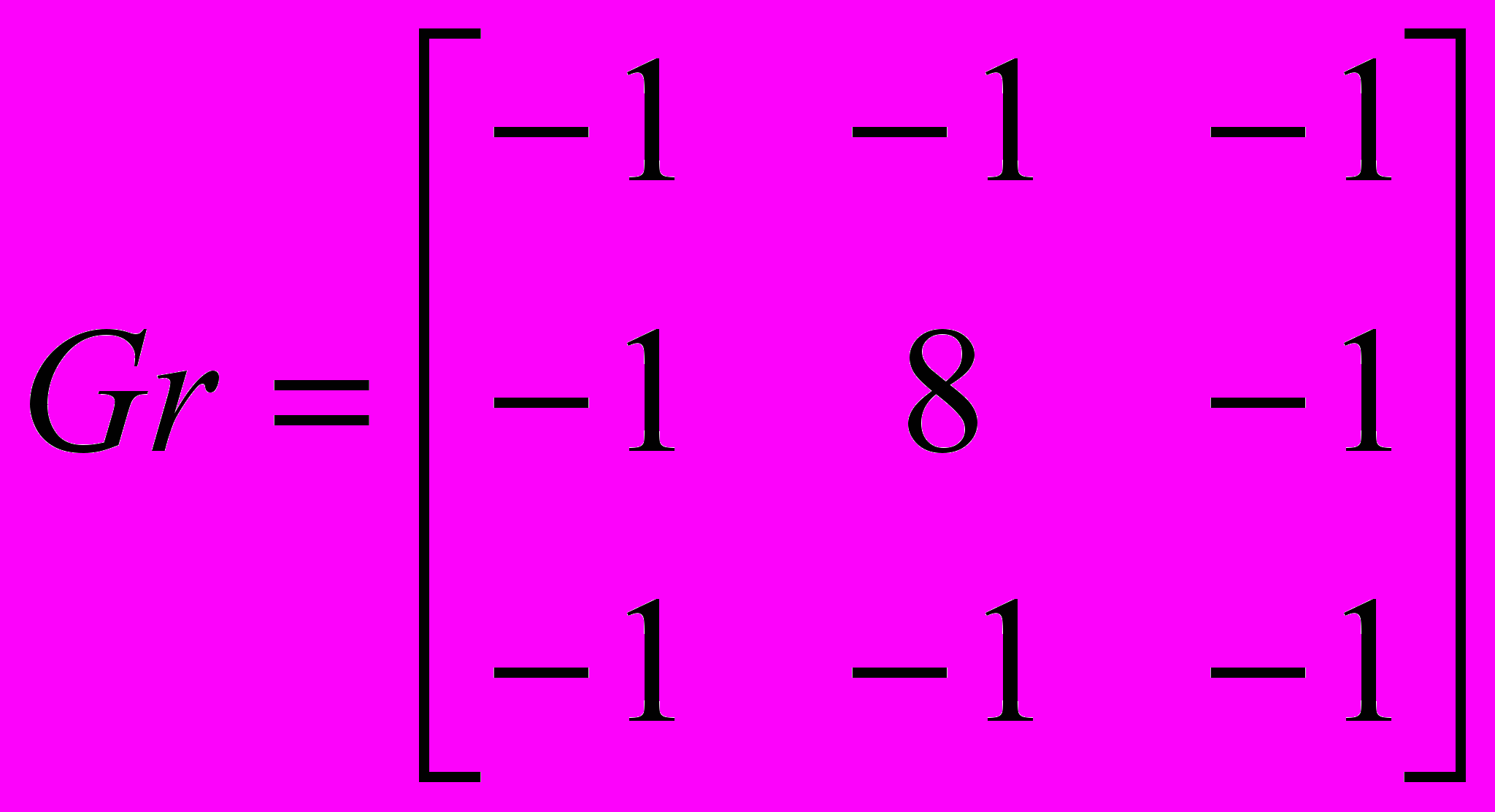– оператор градиента;

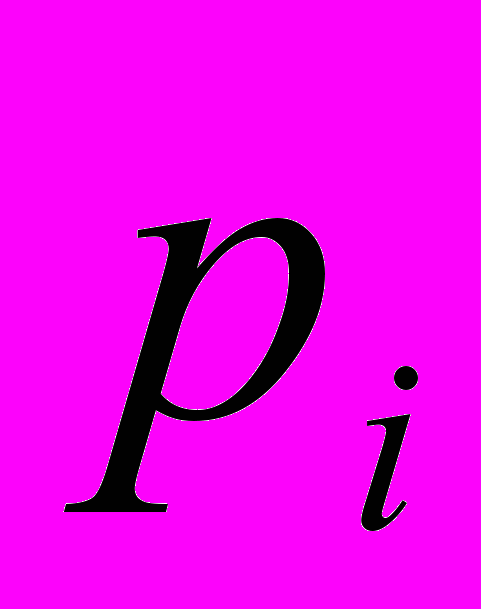– точка исходного изображения.

Полученное изображение сильно зашумлено. Но принимая во внимание тот факт, что значение градиента на границе изображения зерна гораздо выше, чем градиент шума, то применяя простейшую фильтрацию по значению, можно получить изображение, пригодное для дальнейшей обработки.

,

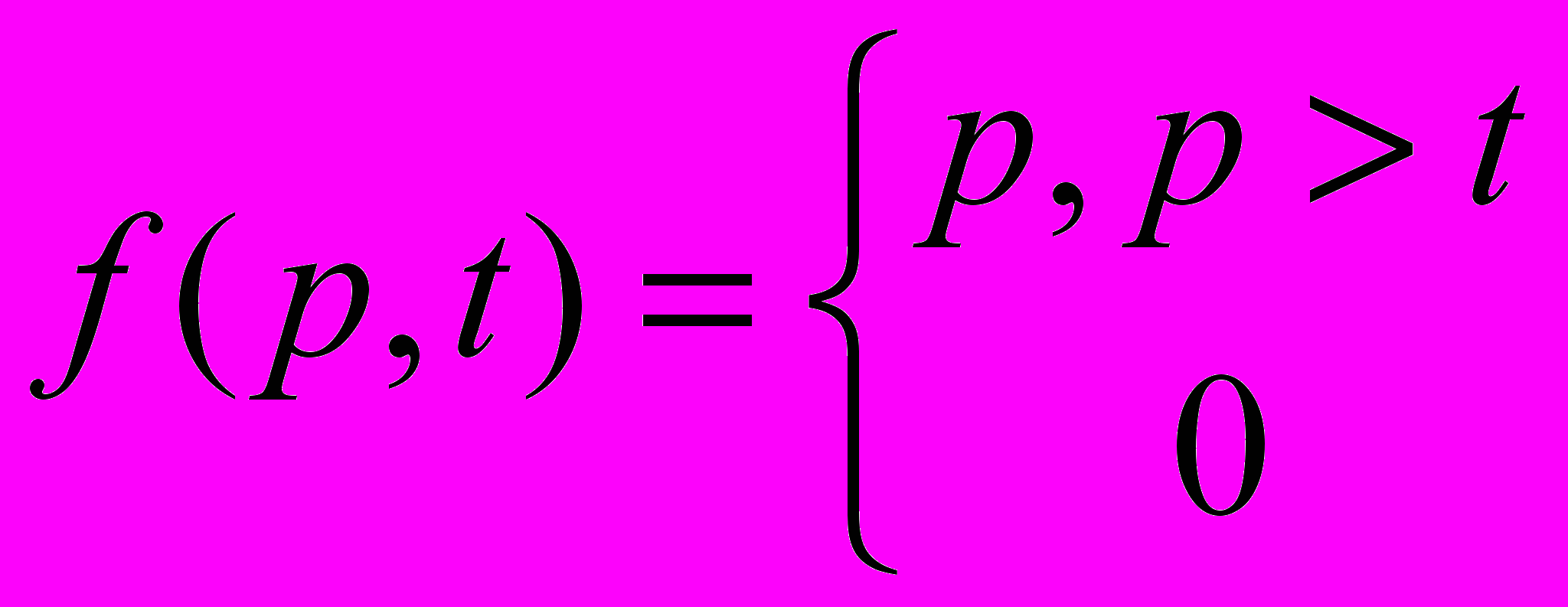где p – значение градиента в точке,

t – пороговое значение фильтра.

Для определения геометрических размеров необходимо выделить контур изображения. Для этого был разработан алгоритм, который основывался на следующих положениях:

1. точка контура имеет высокое значение градиента;

2. контур состоит из связных точек (связность можно принимать равной 4 или 8);

3. точка контура граничит с точкой фона (низкое значение интенсивности и градиента).

Это позволяет существенно упростить и ускорить процедуру выделения контура и определения геометрических параметров зерна.

Данный алгоритм был реализован в виде программы. В дальнейшем, после соответствующей модификации, данную программу можно использовать как аналог измерительного микроскопа при проведении лабораторных занятий, предоставляя возможность проводить измерения геометрических параметров зерен в ручном и в автоматическом режиме.

Библиографический список:

1. У. Претт «Цифровая обработка изображений», том 2, Москва – 1982г.-c.499-500, 564-566.

2. Павлидис Т. Алгоритмы машинной графики и обработки изображений. / М.: Радио и связь, 1986. - 399 с.

3. Путятин Е.П., Аверин С.И. Обработка изображений в робототехнике. М: Машиностроение, 1990. 320 с.

РАЗРАБОТКА МЕТОДИКИ РАСЧЕТА ОПТИМАЛЬНЫХ ПАРАМЕТРОВ НАСТРОЙКИ КАСКАДНЫХ СИСТЕМ РЕГУЛИРУВАНИЯ

Л. И. Медведева, ВПИ (филиал) ВолгГТУ

В основе предложенной методики лежит применение эквивалентных функций, вывод которых осуществляется при помощи структурных преобразований.

Для качественного анализа работы локальных или одноконтурных САУ и определения настроек их управляющих устройств – автоматических регуляторов – в настоящее время существует сравнительно большое число точных и приближенных методов. При исследовании каскадных систем главное внимание уделяется либо последовательному соединению управляющих устройств с объектами управления, либо ограниченному числу контуров управления (чаще всего – это два контура: стабилизирующий и корректирующий).

Таким образом, возникает актуальная задача разработки и исследования методик расчета параметров управляющих устройств n-каскадных или n-контурных систем управления.



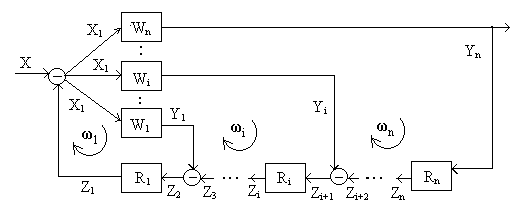
Рисунок 1 – Структурная схема n-контурной САУ (W₁, W_i, W_n – передаточные функции объекта управления по каналам регулирования основной (Y₁) и вспомогательных (Y_i, Y_n) величин; R₁, R_i, R_n – передаточные функции управляющих устройств для поддержания основной и вспомогательных величин на заданном значении; ω₁, ω_i, ω_n – рабочие частоты основного и вспомогательных контуров управления.)

Возможны два варианта определения параметров функционирования управляющих устройств в n-контурных схемах:

- когда рабочая частота основного контура регулирования много больше частот вспомогательных контуров;

- когда рабочие частоты контуров соизмеримы.

При расчете по первому варианту основной контур регулирования рассматривается как независимый и любым известным методом определяются численные значения настроечных коэффициентов регулятора R₁.

Затем находятся значения коэффициентов внешнего вспомогательного регулятора R_n по формуле 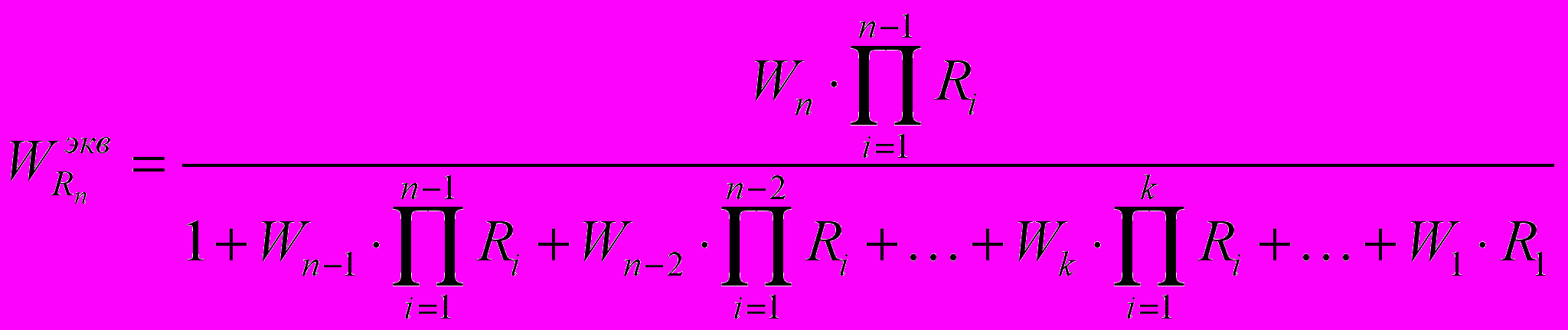(1)

(1)

и с применением вышеописанных структурных и математических преобразований.

Теперь для проверки принятых ранее допущений вновь находятся коэффициенты основного регулятора R₁ с использованием выражения 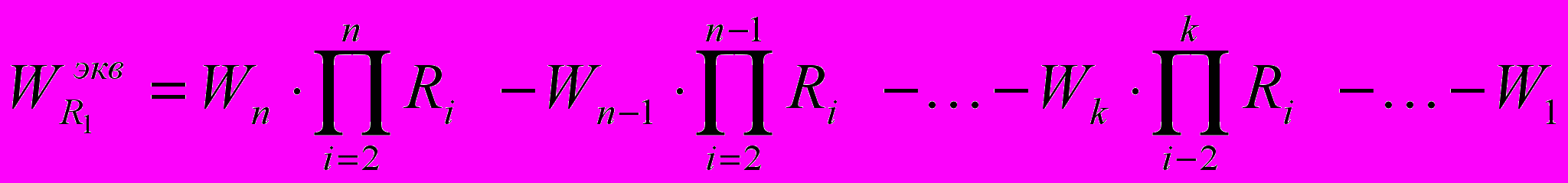(2).

(2)

Результаты проверки при этом должны удовлетворять условию:

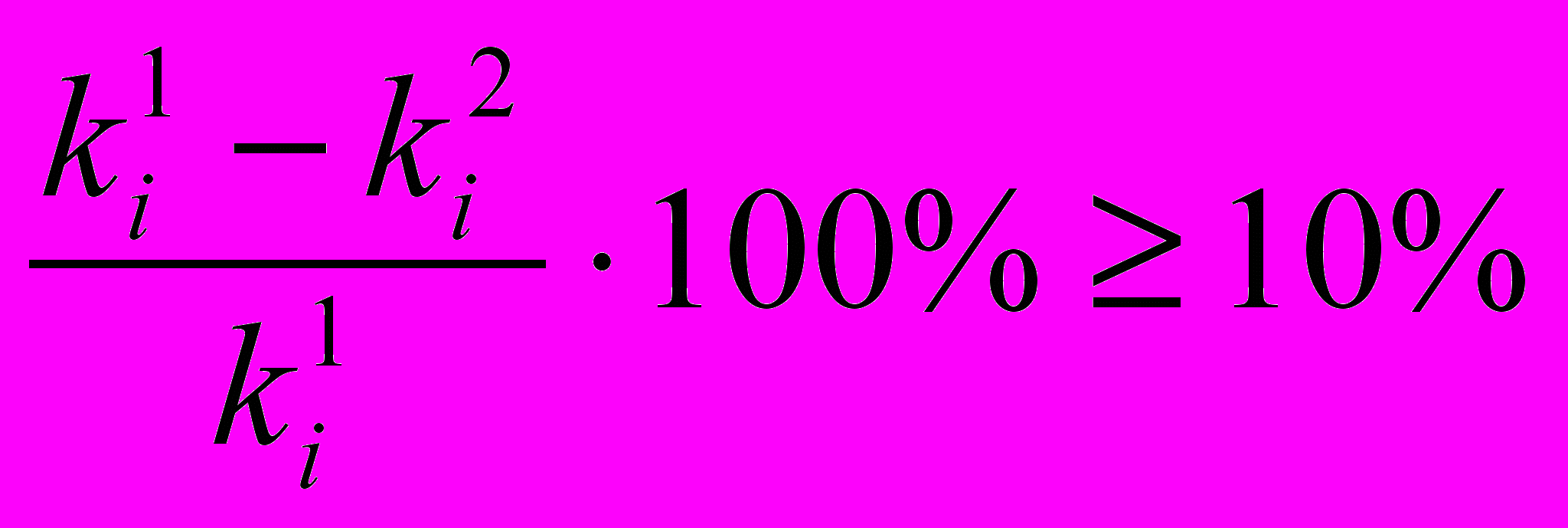, (3)

где k_i¹, k_i² – настроечные коэффициенты внутреннего управляющего устройства, найденные до и во время поверки соответственно.

В противном случае коэффициенты внешнего регулятора R_n изменяются на 10 % и расчет повторяют вновь.

Согласно второму варианту порядок расчета несколько меняется.

Расчет системы управления начинают с внешнего контура и определяют настроечные параметры n-го управляющего устройства. При этом все остальные управляющие устройства принимаются равными единице, и формула эквивалентного объекта будет иметь вид 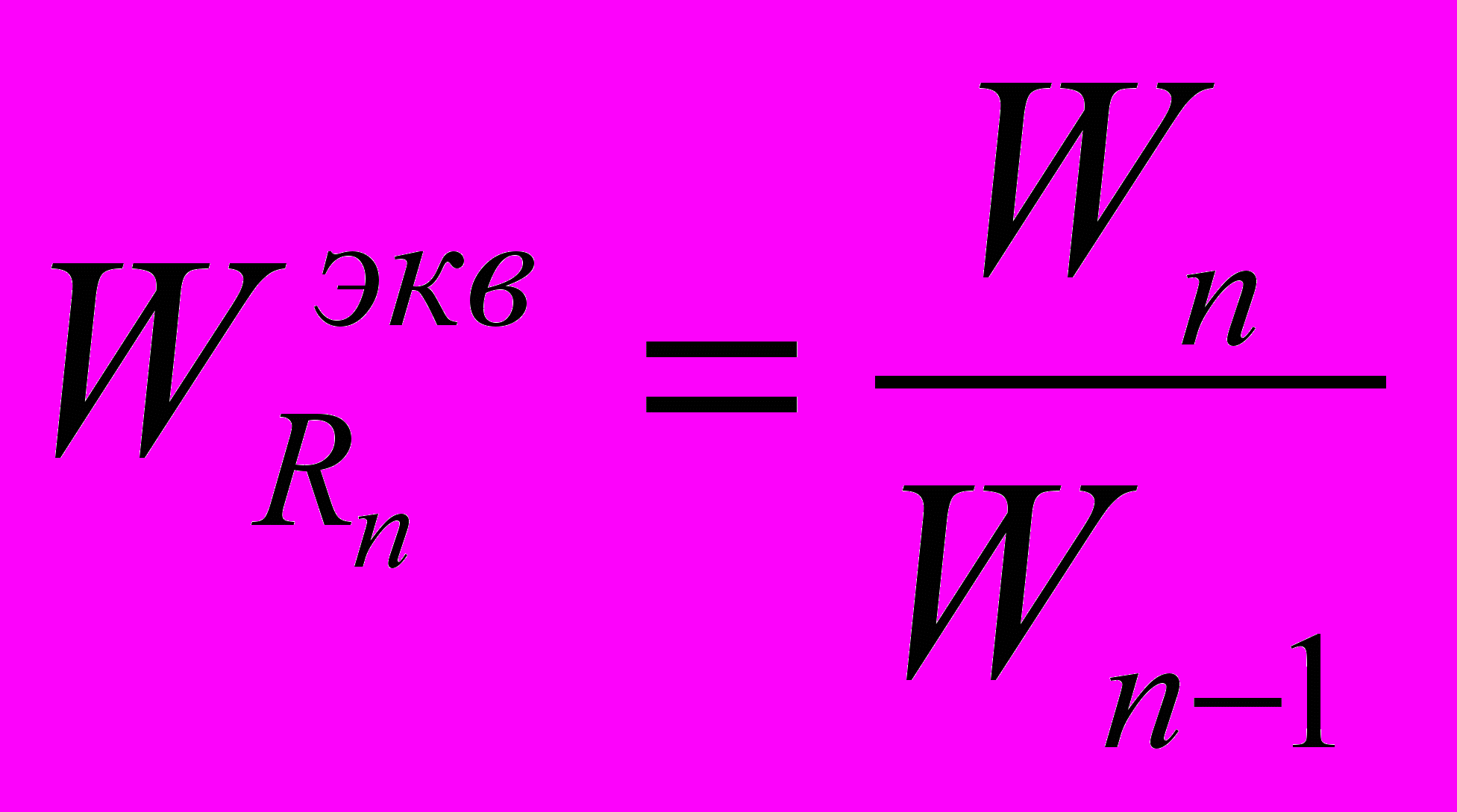(4):

, (4)

где W_n – передаточная функция внешнего объекта управления.

Используя полученную передаточную функцию эквивалентного объекта, определяют параметры внешнего регулятора любым известным методом.

Для нахождения настроечных коэффициентов внутреннего основного контура от исходной схемы зрительно отсекают внутренний регулятор и в качестве объекта управления используют эквивалентную передаточную функцию, найденную по выражению (2). Используя полученную передаточную функцию эквивалентного объекта, определяют параметры внутреннего регулятора любым известным методом.

Для проверки результатов расчета вновь определяют параметры внешнего контура с использованием данных внутреннего управляющего устройства. Для этого регулятор R_n рассчитывают вновь, используя в качестве объекта эквивалентную функцию (1).

Результаты расчетов должны удовлетворять условию (3), в котором используются коэффициенты внешнего вспомогательного управляющего устройства R_n. Если условие (3) не выполняется, то изменяют настройки основного регулятора и расчет повторяют вновь.

СИНТЕЗ ЛИНЕЙНОГО ФИЛЬТРА ДЛЯ ИНФОРМАЦИОННЫХ КАНАЛОВ

АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ

О. В. Свиридова, ВПИ (филиал) ВолгГТУ

Одной из наиболее важных задач автоматизированных систем управления является получение и обработка текущей информации о ходе технологического процесса.

На практике при обработке данных используются три основных критерия построения оптимальных фильтров:

- минимум среднего квадратического отклонения профильтрованного сигнала от его действительного или заданного значения;

- максимум отношения сигнал/шум;

- максимум энергетического отношения сигнал/шум на выходе фильтра.

При анализе и синтезе фильтров используется аддитивная модель входного сигнала:

x(k) = s(k)+q(k),

где s(k) – полезная составляющая сигнала, q(k) – составляющая помех.

Синтез оптимальных фильтров производится с максимальным использованием известной априорной информации как о сигналах, которые необходимо выделить, так и о шумах и помехах. Как правило, используется информация о природе полезного сигнала и шума, об их спектральном составе, о корреляционных и взаимно корреляционных характеристиках. Наличие определенных особенностей (различий) в характеристиках сигнала и шума позволяет реализовать фильтр вообще и оптимальный фильтр в частности. Если такие особенности отсутствуют, постановка задачи становится некорректной.

На практике априорные данные о полезных сигналах, как правило, являются достаточно определенными. Определение характеристик действующих помех представляет собой более сложную проблему, но даже при полной неопределенности можно допустить, что помеха является нормальным стационарным процессом с нулевым средним значением.

При наличии помех абсолютно точное выделение полезного сигнала методами линейной фильтрации, как правило, невозможно. Результат фильтрации y(k) = h(n) _* x(k-n) отличается от s(k) на величины (k) = y(k)-s(k), которые являются абсолютными значениями погрешности воспроизведения полезного сигнала по координатам k. Качество фильтра оценивается средним значением квадрата величины (k):

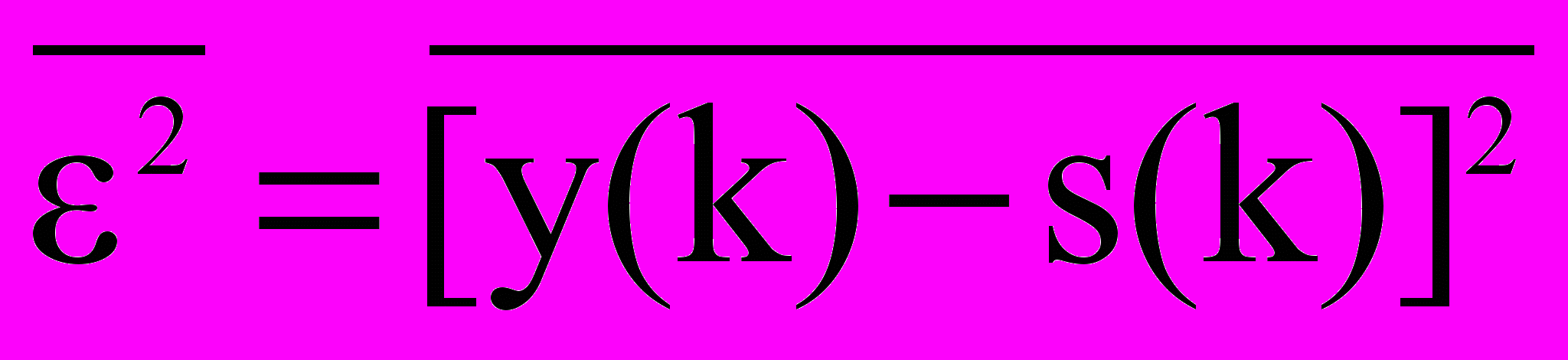. (1)

Во многих задачах обработки данных не требуется восстановления исходной формы сигнала s(k), т.к. в процессе его дальнейшей обработки осуществляется преобразование сигнала s(k) в сигнал z(k), форма которого может быть более удобной для извлечения (измерения) каких-либо информационных параметров сигнала (например - амплитудного значения, ширины сигнала на половине максимального значения и т.п.). В этом случае оптимальный фильтр может проектироваться непосредственно на получение выходного сигнала z(k). Качество таких фильтров, получивших название формирующих, оценивается средним значением квадрата величины (k) получения сигнала заданной формы:

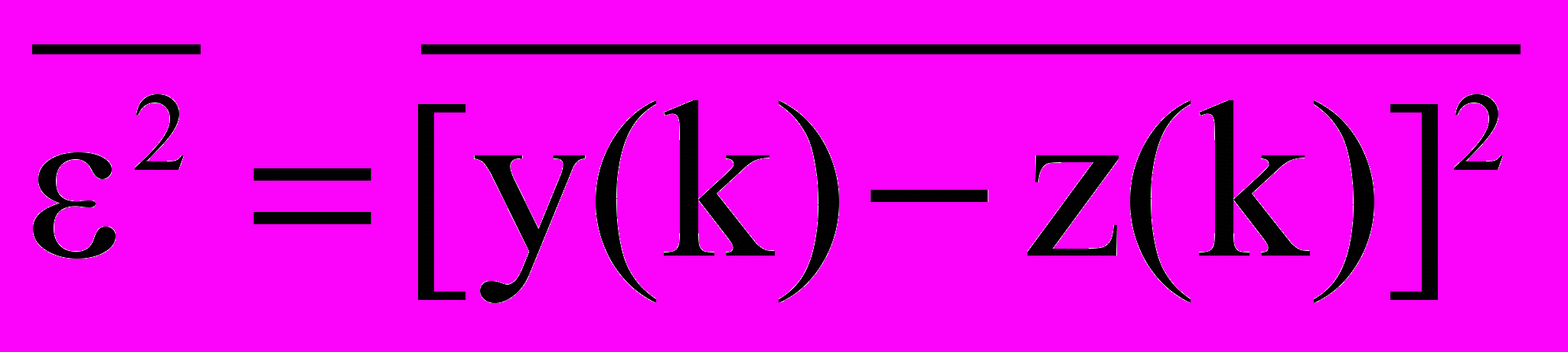. (2)

Выражения (1), (2) дают возможность определить значения h(k) фильтра по критерию минимума среднего квадратического отклонения выходного сигнала от его действительной или заданной формы.

ала в пределах его формы.

При узко конкретной задаче обнаружения сигнала степень искажения самого сигнала может не ограничиваться. Если кроме обнаружения сигнала, как основной цели обработки данных, ставится и задача оценки его формы, то в этом случае для проектирования фильтра обычно используется критерий максимума энергетического отношения сигнал/шум:

Θ= Е_sy/E_qh,

где Е_sу и E_qh – энергия соответственно сигнала и шума на выходе фильтра.

В данной работе были поставлены и решены следующие задачи:

1) фильтрация динамических свойств объекта по каналу X->Y;

2) определение настроек линейного фильтра;

3) применение вероятностно-статистических методов;

В качестве результатов проведенной разработки наибольшую практическую ценность представляют:

1) программа, имитирующая сигналы и помехи, позволяющая проверить искаженные помехами математические модели обрабатываемых сигналов на адекватность;

2) методика синтеза оптимальных динамических компенсаторов.

ПРИНЦИПЫ ПОСТРОЕНИЯ АДАПТИВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ МНОГОМЕРНЫМИ ОБЪЕКТАМИ

А. С. Гольцов, А. А. Силаев, ВПИ (филиал) ВолгГТУ

Принцип действия любой системы автоматического управления состоит в том, чтобы обнаружить отклонение управляемых величин, характеризующих работу машины, или протекание процесса, и при этом воздействовать на машину или процесс так, чтобы устранить возникшие отклонения.

В теории управления сложились два подхода к описанию свойств неопределённостей в уравнении объёкта управления: стохастический и минимаксный.

При стохастической постановке задачи помехам и неизвестным параметрам приписываются какие-либо статические свойства, и достижение цели управления понимается в статическом смысле.

При минимаксной постановке задачи предполагается, что неизвестные параметры уравнения, описывающего объект управления, принадлежат некоторому ограниченному множеству, а последовательность помех ограничена и в остальном произвольна. Цель управления состоит в достижении наилучшего качества управления при наихудшей для выбранного управления реализации последовательности помех. Считается, что целью выбора стратегии управления является минимизация абсолютной величины предельного отклонения выхода объекта от заданной траектории.

В сложных динамических системах показатель эффективности зависит не только от текущих значений выходных переменных, но и от характера их изменения в прошлом, настоящем и будущем, и выражается некоторым функционалом от выходных координат, их производных и времени. Нахождение оптимального уровня управления в таком случае возможно на основе использования математической модели динамической системы и решения задачи методами вариационного исчисления или математического программирования. Для этого используется ЭВМ, в которую поступает следующая информация: о текущих значениях выходных переменных x(t), собираемая системой измерительных преобразователей; об управляющих воздействиях и(t), формируемых управляющим устройством на основе команд, поступающих из ЭВМ; о внешних возмущающих воздействиях q(t). Кроме того, в ЭВМ вводятся данные о граничных условиях.

Адаптивные системы могут приспосабливаться к изменяющимся условиям внешней среды и к своим внутренним изменениям, повышая эффективность функционирования. Адаптивные системы, анализируя изменения воздействий и характеристик процесса функционирования динамической системы, автоматически изменяют значения своих параметров таким образом, чтобы сохранить высокие значения показателей качества и эффективности.

Если адаптивная система способна изменять значения параметров, ее называют самонастраивающейся. При изменении структуры и алгоритма управления систему называют самоорганизующейся.

Адаптивная система содержит устройство управления, реализующее один из фундаментальных принципов управления, и устройство адаптации, взаимодействующее с устройством управления. Непосредственно управляет объектом устройство управления, а устройство адаптации предназначено для обеспечения его оптимальной настройки. Система автоматического управления в этом случае имеет два иерархических уровня.

Устройство адаптации состоит из измерительных преобразователей, вычислительного устройства и блока настройки устройства управления. Последний на основании результатов оценки параметров объекта управления и внешней среды обеспечивает соответствующее изменение параметров устройства управления или его структуры и алгоритма управления. Устройство адаптации может выполняться с разомкнутым контуром воздействий или с замкнутым контуром. В последнем случае устройство адаптации образует цепь обратной связи и реагирует также на изменение управляемой переменной.

Процесс получения информации и расчета алгоритма управления носит непрерывный характер и может протекать в реальном времени.

При этом в первую очередь необходимо определить целевую или стоимостную функцию оптимизируемого процесса. Затем требуется дать соответствующую формулировку задачи в физической форме и осуществить перевод этого физического описания на язык математики. Для осуществления эффективного управления процессом необходимо знать его текущее состояние (задача оценки состояния). Необходимо охарактеризовать процесс с помощью адекватной модели, зависящей от различных внешних факторов (идентификация системы). При условии знания функции стоимости, состояния и параметров системы можно затем определить наилучшее управление, минимизирующее (или максимизирующее) функцию стоимости. Таким образом, можно сформулировать пять взаимосвязанных задач, решение которых даст возможность построить наилучшую, или оптимальную, систему: задача управления; задача оценки состояния; задача стохастического управления; задача оценивания параметра; задача адаптивного управления.

ОБРАБОТКА ПРОСТРАНСТВЕННЫХ ДАННЫХ, ПОЛУЧЕННЫХ С ПОМОЩЬЮ ДЗЗ

А. В. Студеникин, каф. ВАЭиВТ

В рамках выполнения расчёта объёма земельных работ по берегоукреп–лению озера Эльтон (Полласовский район) институтом куплен снимка со спутника. Область интереса охватывает балку Сорочью, пересекающую же–лезнодорожные пути. Полученные данные использованы для вычисления площади георешетки, которой будет укрепляться овраг (рисунок 1).

Параметры снимка: спутник – Quickbird(США), снимок ортоисправленный мультиспектральный (RGB и ближний ИК), пространственное разрешение – 2,5 м, радиометрическое разрешение – 11 бит, облачность – 0 %, площадь – 25 кв.км. В настоящее время работа находится на стадии согласования договора с ОАО «Совзонд» на покупку снимка, удовлетворяющего вышеперечисленные параметры. В архиве компании найден такой снимок, выполненный 6 января 2005 года.



Рисунок 1

В зависимости от пространственного разрешения на снимках можно различать объекты, сопоставимые с величиной единичного элемента разрешения (пиксела) – т. е. объекты величиной до 61 см. Пространственное разрешение - это величина пиксела изображения в пространственных единицах. Эта величина характеризует размер наименьших объектов, различимых на изображении. Панхроматические изображения занимают практически весь видимый диапазон электромагнитного спектра (450-900 нм) и поэтому представляют собой черно-белые изображения. Мультиспектральные (или спектрозональные) изображения – это изображения, которые могут поставляться в виде отдельных спектральных каналов (RGB и инфракрасные каналы) или виде синтеза отдельных каналов для получения цветного изображения. Поочередный синтез отдельных каналов позволяет решать многочисленные тематические задачи, а также помогает при дешифрировании снимков.

Радиометрическая разрешающая способность определяется количеством градаций значений цвета, соответствующих переходу от яркости абсолютно «черного» к абсолютно «белому», и выражается в количестве бит на пиксел изображения. Это означает, что в случае радиометрического разрешения 6 бит на пиксел мы имеем всего 64 градации цвета (2⁶ = 64); в случае 8 бит на пиксел - 256 градаций (2⁸ = 256), 11 бит на пиксел - 2048 градаций (2¹¹ = 2048).  В настоящее время, как правило, сенсоры, установленные на спутниках ДЗЗ, имеют радиометрическое разрешение не хуже 8 бит на пиксел. 

Возможность опознавания объектов на снимке и определения их характеристик зависит как от пространственного, так и от радиометрического разрешения изображения, количества и состава спектральных каналов. Дешифровочные качества снимка можно улучшить с помощью радиометрической (фотометрической) коррекции. Предварительная радиометрическая коррекция проводится поставщиком данных перед предоставлением снимков заказчику; она практически всегда включает в себя нормировку откликов детекторов сенсора. Дополнительные операции – увеличение динамического диапазона, нормализация растра и другие действия – могут быть выполнены как поставщиком, так и заказчиком данных.



Рисунок 2

Выполнена классификация изображения алгоритмом максимального правдоподобия (на рисунках 2 – 5 классов). Затем получена длина оврага – 3032 метра, и площадь – 72858 кв. метров.


СИСТЕМА АВТОМАТИЧЕСКОГО КОНТРОЛЯ ВЯЗКОСТИ И ПЛОТНОСТИ

НЕФТЕПРОДУКТОВ В ПРОЦЕССЕ ИХ ПРОИЗВОДСТВА

К. Ю. Сурганова, ВПИ (филиал) ВолгГТУ

Качество резины, полимеров, красок, машинных масел и других нефтепродуктов определяют в процессе их производства по текущим значениям вязкости и плотности. В процессе синтеза указанных нефтепродуктов их плотность и вязкость в зависимости от температуры непрерывно изменяются. Но на предприятиях химической и нефтеперерабатывающей промышленности России контроль вязкости выпускаемой продукции осуществляют, как правило, один раз в смену с помощью лабораторных вискозиметров. Лабораторный анализ одной порции (пробы) продукта, взятой из трубопровода, длится от 3 до 5 часов, что не позволяет оперативно выполнять коррекцию технологического процесса. Управляют технологическими процессами синтеза этих продуктов, как правило, с помощью автоматизированных систем управления на основе опыта и интуиции оператора (аппаратчика). В результате эти предприятия выпускают большое количество некондиционной продукции.

Рассматривается задача автоматического контроля вязкости, плотности и расхода нефтепродуктов с помощью проточного вискозиметра (рисунок 1).

Измерительный модуль выполнен в виде насоса-расходомера (1), сужающего устройства (2) и диафрагмы (3). При синтезе алгоритма оценивания используют следующую модель вискозиметра. Процесс ламинарного течения нефтепродукта в сужающем устройстве описывается уравнением

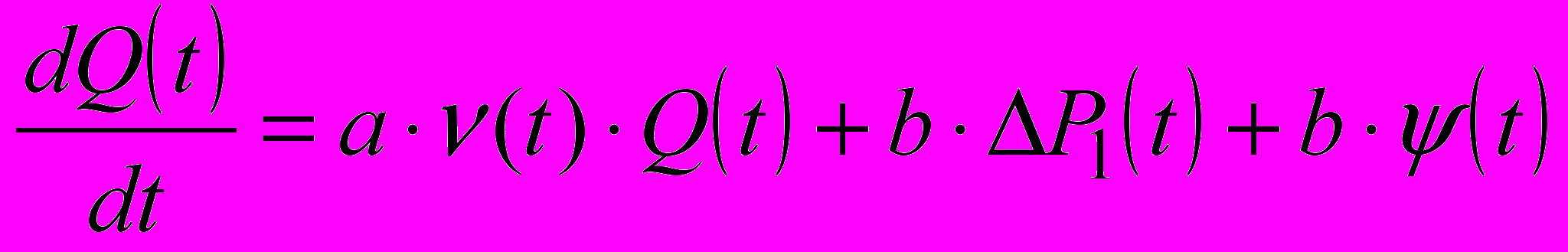(1)


Потери давления ΔP₂(t) при турбулентном течении жидкости через диафрагму описывают уравнением Бернулли:

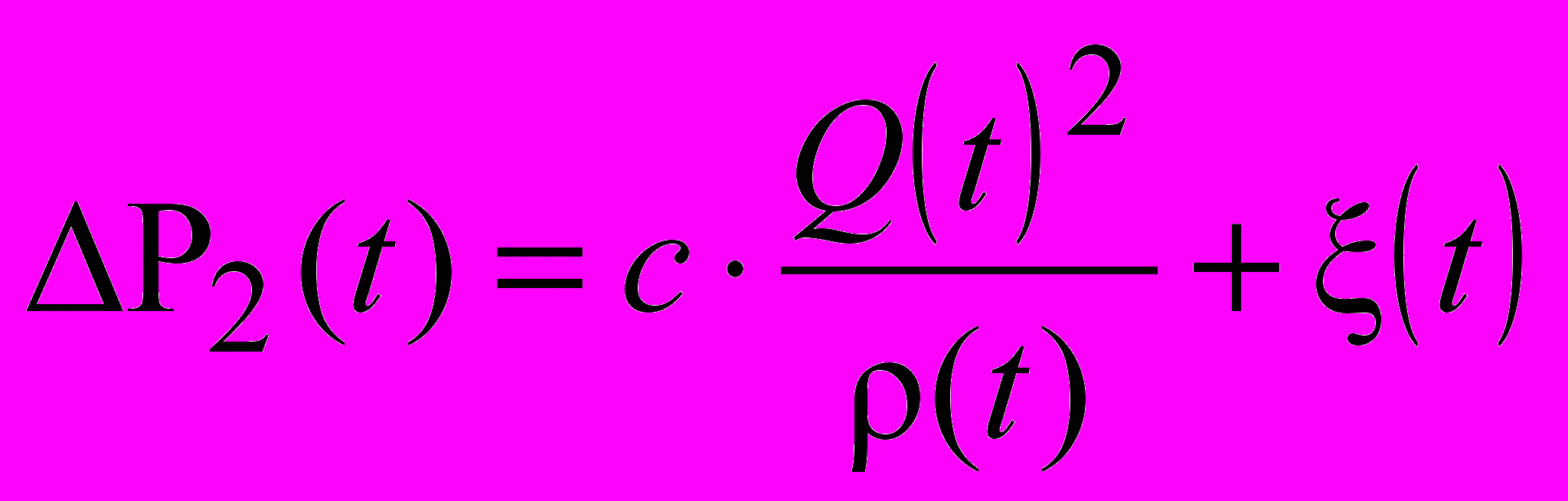, (2)

где: Q(t) – расход массы [кг/с]; a=32/d₁²; b=π·d₁²/4·l₁; c=8/α²·π²·d₂⁴; ξ(t) – погрешность измерений; ψ(t) – погрешность модели процесса ламинарного течения в сужающем устройстве; ΔP₁ – потери давления в сужающем устройстве; d₁ – внутренний диаметр сужающего устройства; d₂ – диаметр диафрагмы; ν(t) и ρ(t) медленно изменяющиеся во времени кинематическая вязкость и плотность.




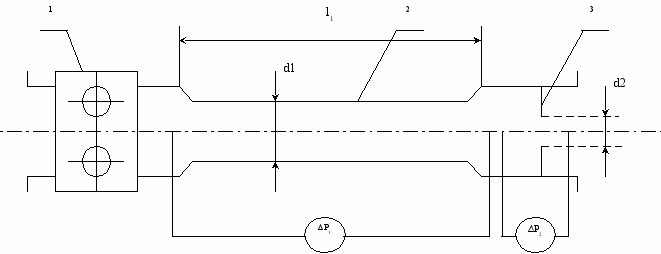
Рисунок 1 – Схема проточного вискозиметра

Текущие значения ν, ρ и Q предлагается определить минимизацией критерия обобщенной работы Красовского с учетом ограничения (1):

,

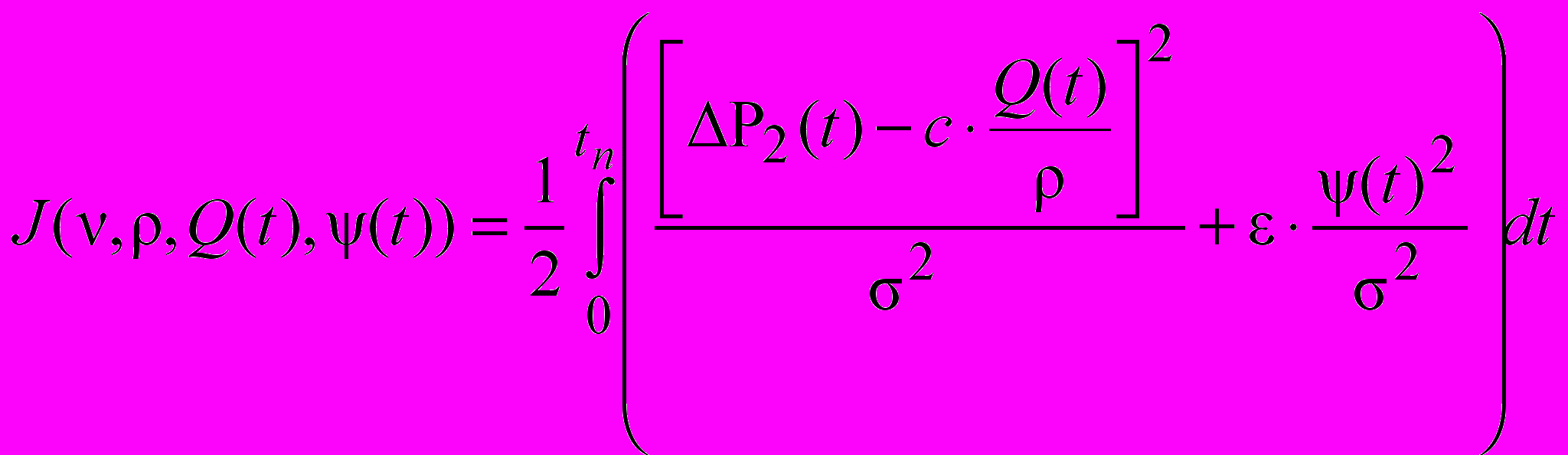где σ – предел допустимой погрешности измерения; ε – весовой коэффициент (параметр регуляризации).

Минимизацию этого критерия осуществляют с помощью принципа максимизации. Полученное уравнение Эйлера-Лагранжа преобразуют в формулы алгоритма рекуррентного метода наименьших квадратов. Имитационным моделированием на ЭВМ выполнен анализ эффективности этой системы. И в результате этого сделан вывод о возможности применения рассматриваемой системы в системах диагностики и автоматического управления технологическим процессом производства нефтепродуктов.

ВЫБОР ДАТЧИКОВ ДЛЯ ЭКСТРЕМАЛЬНЫХ УСЛОВИЙ ЭКСПЛУАТАЦИИ

М. А. Трушников, ВПИ (филиал) ВолгГТУ

Для безопасной работы датчиков в экстремальных условиях необходимо учитывать условия внешней среды еще при разработке конструкции датчика. Взрывоопасные атмосферы могут образовываться на предприятиях различных отраслей промышленности в местах скопления специфических газов, паров или пыли. Последнее вынуждает относить к взрывоопасным такие, казалось бы, «мирные» предприятия, как мукомольные мельницы, хлебозаводы, целлюлозные комбинаты, лесопилки. Поэтому проблемы взрывозащиты это распространенный вопрос не только для нефтяной и химической промышленности, но и для пищевой. Именно поэтому при выборе технических средств нижнего уровня важен правильный выбор измерительных приборов. Взрывобезопасными являются датчики, энергии работы которых недостаточно для детонации окружающей среды. Сертификация датчика означает проверку прибора и определение энергии, необходимой для детонации. При решении вопроса взрывозащиты более часто применяются три наиболее основных подхода: заполнение или продувка оболочки под избыточным давлением, защита вида «e» (повышенная надежность) и искробезопасная электрическая цепь.

Таблица 1 – Виды взрывозащиты

Маркировка	Вид взрывозащиты
	Европейский стандарт (CENELEC)/ Международный стандарт (IEC)/Стандарт РФ	Определение	Области применения
1	2	3	4
Ex o	EN 50 .015/IEC 79-6/ ГОСТ 22782.1-77	Масляное заполнение оболочки Оболочка заполняется маслом или жидким негорючим диэлектриком	Зона 1, Зона 2
Ex p	EN 50 .016/IEC 79-2/ ГОСТ 22782.4-78	Заполнение или продувка оболочки под избыточным давлением Продувка осуществляется чистым воздухом или инертным газом	Зона 1, Зона 2

Окончание таблицы 1

1	2	3	4
Ex q	EN 50 .017/IEC 79-5/ ГОСТ 22782.2-77	Кварцевое заполнение оболочки	Зона 1, Зона 2
Ex d	ЕN 50 .018/IEC 79-1-71/ ГОСТ 2782.6-81	Взрывонепроницаемая оболочка Оболочка, выдерживающая давление взрыва внутри неё и предотвращающая распространение взрыва из оболочки в окружающую взрывоопасную среду	Зона 1, Зона 2
Ex e	EN 50 .019/IEC 79-7/ ГОСТ 22782.7-81	Защита вида «e» Вид взрывозащиты электрооборудования (электротехнического устройства), заключающийся в том, что в электрооборудовании (или его части), не имеющем нормально искрящихся частей, принят ряд мер дополнительно к используемым в электрооборудовании общего назначения, затрудняющих появление опасных нагревов, электрических искр и дуг	Зона 1, Зона 2
Ex i	EN 50 .020, EN 50.039/ IEC 79-3, IEC 79-11/ ГОСТ 22782.5-78	Искробезопасная электрическая цепь Электрическая цепь, выполненная так, что электрический разряд или её нагрев не может воспламенить взрывоопасную среду при предписанных условиях испытания	Зона 1, Зона 2 Зона 0 – после Проведения специальных испытаний
Ex m	EN 50 .028/IEC 79-18	Заполнение веществом (заполнителем) дополнительной оболочки, в которой размещено электрооборудование. Заполнитель не должен иметь трещин, пузырьков, отслаиваться, высыпаться, растрескиваться с течением времени и терять своих свойств во время эксплуатации. Этот вид приблизительно соответствует специальному виду взрывозащиты электрооборудования (электротехнического устройства) Еx s ГОСТ 22782.3-77	Зона 1, Зона 2

При выборе датчика для проведения измерений в экстремальных условиях необходимо обращать внимание на штамп, подтверждающий, что этот прибор прошел соответствующую проверку специализированной организацией. Каждый вид взрывозащиты характеризуется различными видами основного оборудования и вспомогательного оборудования (если оно требуется) и, следовательно, разной стоимостью.

Для решения вопросов их безопасного подключения к АСУ ТП используются различные средства взрывозащиты, среди которых наиболее эффективным и экономичным (от 15 до 50 % экономии по сравнению с другими методами) является метод «искробезопасная электрическая цепь». Искробезопасное подключение отдельно взятого датчика или исполнительного механизма обеспечивают устройства, называемые барьерами искробезопасности. Применение барьеров является широко распространенным решением и обладает рядом достоинств.