Geum.ru

Ся проведение исследований и разработка методов и средств сопровождения учебного процесса с помощью информационных технологий генерации образовательных ресурсов

Вид материалаДокументы

Содержание


Московский государственный технический университет
Д.А. Жуков, А.С. Исанин
Москва МГТУ им. Н.Э. Баумана
1.1 Анализ методов и средств разработки электронных средств обучения
1.2 Технологии открытого образования и дистанционного обучения
2 Разработка курсов дистанционного обучения
Цели дисциплины «Информатика»
Задачи дисциплины «Информатика»: Изучение понятий, образующих теоретический фундамент информатики.
Изучение важнейших алгоритмов и освоения навыков решения конкретных задач с помощью изученных методов.
3.2 Краткое содержание дисциплины
3.2.1 Входной контроль готовности студента к освоению первого семестра
3.2.3 Теоретические занятия
3.2.4 Практические занятия (семинары).
3.3 Создание курса дистанционного обучения дисциплине с использованием системы Lotus Notes
3.3.1 Доступ студентов к курсу дистанционного обучения
CourseRoom (Аудитория)
Менеджер оценки
3.3.2 Работа в «Аудитории»
3.3.3 Процесс интерактивного контроля знаний студента
Created Assessments
...
Полное содержание
Подобный материал:
Серия изданий

«Научно-образовательные и

научно-информационные

материалы

МГТУ им. Н.Э. Баумана —

национального

исследовательского

университета

техники и технологий»

Департамент образования города Москвы

  

Ассоциация московских вузов

  

Московский государственный технический университет

имени Н.Э. Баумана




Кафедра ИУ-8

«Информационная безопасность»


Д.А. Жуков, А.С. Исанин


Научно-образовательный материал

«Курс дистанционного обучения

по дисциплине «Информатика»








Москва

МГТУ им. Н.Э. Баумана

2011

1 Введение

Целью настоящей НИР является проведение исследований и разработка методов и средств сопровождения учебного процесса с помощью информационных технологий генерации образовательных ресурсов. Для решения поставленной задачи проведен анализ содержания дисциплины «Информатика», изучаемой на кафедре «Информационная безопасность» в рамках образовательных стандартов, анализ современных информационных технологий и разработан экспериментальный образец курса дистанционного обучения, сопровождающего учебный процесс кафедры.

На основе проведенного анализа выявлены существенные особенности изучаемой дисциплины, выявленные с учетом задачи разработки электронного учебного пособия:
  1. динамика развития информационных систем требует перманентного совершенствования электронных методических материалов;
  2. особенности методики преподавания дисциплины требуют применения технических средств и программного обеспечения, нуждающихся в постоянном обновлении;
  3. материалы разрабатываемого электронного учебного пособия нуждаются в защите от несанкционированного доступа.

Далее в процессе выполнения настоящей НИР проведен анализ технологий и известных средств создания электронных учебных пособий.

Результаты анализа позволили выработать требования к разрабатываемому учебному пособию.

На основе указанных требований разработан и изготовлен экспериментальный образец курсов дистанционного обучения кафедры «Информационная безопасность».


1.1 Анализ методов и средств разработки электронных средств обучения

Исходя из требований, сформулированных в образовательных стандартах, можно выделить несколько основных направлений наиболее целесообразного информационного сопровождения образовательного процесса, в числе которых:
  1. формирование системы информационных ценностей и развитие индивидуальности в информационной сфере;
  2. формирование общей информационной культуры будущих специалистов, выработка у них адекватных представлений об информационном мире, сути информационных явлений и процессов;
  3. выработка у будущих выпускников навыков информационной деятельности в различных информационных условиях и обеспечение необходимым для этого багажом знаний;
  4. привитие студентам функциональной информационной грамотности;
  5. формирование способности к развитию, в том числе к саморазвитию и самообразованию в информационной сфере.

Очевидно, что успешная реализация подобного информационного сопровождения обучения будет способствовать адаптации субъекта образовательной деятельности к современной информационной среде и формированию у будущего специалиста уровня информационной зрелости, достаточного для обеспечения самостоятельности личности в различных сферах жизнедеятельности информационного общества.


1.2 Технологии открытого образования и дистанционного обучения

Анализ показывает, что открытое образование основано на ряде основополагающих принципов, к числу которых относится свобода обучаемого в выборе учебного заведения, времени, места и темпов обучения, в планировании своих учебных занятий. Предполагается, что открытое образование повысит качество образования и разрешит противоречие между предложением и спросом на образовательные услуги.

Известны и применяются следующие основные технологии дистанционного обучения:

1) кейс-технология, при которой обучаемый получает комплект учебных материалов (кейс) и изучает их, имея возможности периодических консультаций с преподавателями-тьюторами в учебных пунктах (центрах);

2) ТВ-технологии, при которых основные учебные процедуры основаны на прослушивании и просмотре телевизионных лекций;

3) сетевые технологии, при которых доступ к учебным материалам и консультации с преподавателями проводятся посредством телекоммуникационных технологий и вычислительных сетей. Как правило, в качестве сети используется Internet, тогда сетевую технологию называют Internet-технологией (или Web-технологией).


2 Разработка курсов дистанционного обучения

Применение средств электронного дистанционного обучения может позволить сформировать указанные концепции и научить применять их на практике.

Дистанционное обучение (ДО) — совокупность технологий, обеспечивающих доставку обучаемым основного объема изучаемого материала, интерактивное взаимодействие обучаемых и преподавателей в процессе обучения, предоставление обучаемым возможности самостоятельной работы по освоению изучаемого материала, а также в процессе обучения.

Современное дистанционное обучение строится на использовании следующих основных элементов:
  1. среды передачи информации (почта, телевидение, радио, информационные коммуникационные сети);
  2. методов, зависимых от технической среды обмена информацией.

Использование технологий дистанционного обучения позволяет:
  1. снизить затраты на проведение обучения (не требуется затрат на аренду помещений, поездок к месту учебы, как учащихся, так и преподавателей и т. п.);
  2. проводить обучение большого количества учащихся;
  3. повысить качество обучения за счет применения современных средств, объемных электронных библиотек и т.д.
  4. создать единую образовательную среду (особенно актуально для корпоративного обучения).

Дистанционное обучение занимает всё большую роль в модернизации образования. Согласно приказу 137 Министерства образования и науки РФ от 06.05.2005 «Об использовании дистанционных образовательных технологий», итоговый контроль при обучении с помощью ДОТ (дистанционных образовательных технологий) можно проводить как очно, так и дистанционно. Госдума РФ рассматривает проект поправок к закону об образовании, связанных с дистанционным обучением.

Разработанная система представляет собой клиент-серверное приложение на базе ПО LearningSpace LotusNotes. На сервере хранится вся информация о пользователях, их правах доступа, а также содержание курсов. Доступ к серверу осуществляется через клиентское приложение Lotus Notes либо через любой интернет-браузер для инструкторов и пользователей, Domino Admin – для администраторов системы.

Данная система позволяет:
  1. создавать учетные записи пользователей;
  2. создавать группы пользователей;
  3. применять политики безопасности к отдельным учетным записям и к группам пользователей, разграничивая права доступа к определенным курсам (рисунок 2.1);
  4. создавать курсы, которые могут включать в себя различные элементы учебного процесса, такие как:
    1. Schedule (Расписание) – выдаваемая обучаемому «дорожная карта» курса;
    2. MediaCenter (Медиа Центр) – учебная библиотека, содержащая учебный материал для курса, такой как лекции, статьи, образы, звуковые файлы, видеоклипы, ссылки на Web-страницы и т.д.;
    3. CourseRoom (Аудитория) – интерактивно организованная с помощью электронной коммуникации группа, где студенты участвуют во взаимных дискуссиях по обсуждению пройденного материала и можно создать виртуальную команду для того, чтобы поработать совместно над заданиями, предлагаемыми преподавателем;
    4. Assessment Manager (Менеджер оценки) – специализированное средство, позволяющее преподавателю (инструктору) создавать те элементы учебного процесса, которые осуществляют опросы студентов по мере изучения ими материалов курса. Типы проводимых опросов следующие:
      1. тестирование по принципу “да/нет”;
      2. тестирование с несколькими вариантами ответа;
      3. тестирование с развернутым подробным ответом;
      4. самотестирование (вопросы для самопроверки);
    5. Profiles (Профайлы) – это документы, по которым обучаемые знакомятся друг с другом, обмениваясь контактной информацией об их образовании, квалификации и интересах.



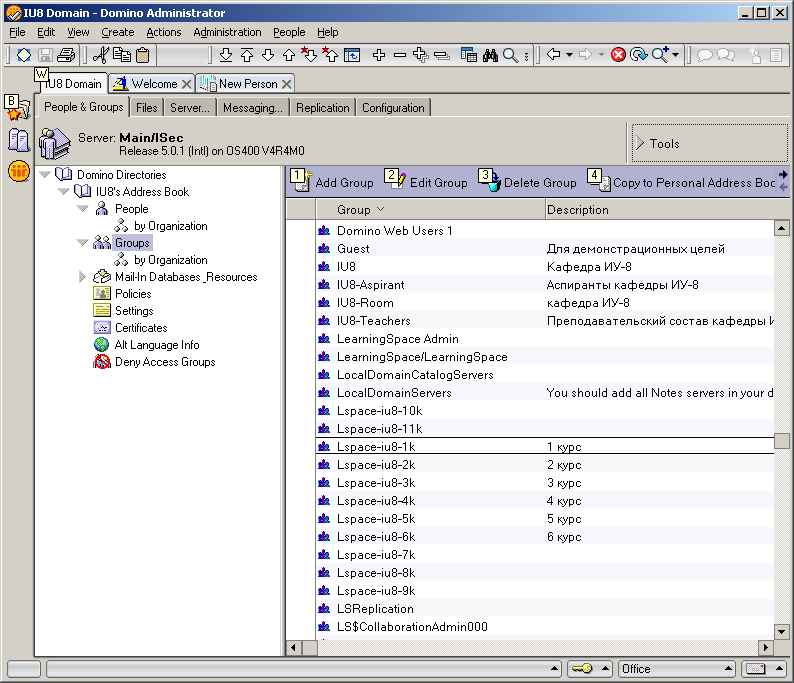
Рисунок 2.1 – Панель администрирования Domino Admin

Формирование курса происходит в базе Медиа Центр. Это совместно используемая студентами база знаний, где расположены материалы учебного курса. Информация может набираться непосредственно средствами Lotus Notes, а может предварительно готовиться в известных автору оболочках и затем уже переноситься в Медиа Центр (рисунок 2.2).

Для проверки знаний студентов существуют возможности, предоставляемые преподавателю базой Assessment Manager (Менеджер оценки).

Типы вопросов следующие:
  1. тестирование по принципу “да/нет”( True / False );
  2. тестирование с несколькими вопросами и единственным ответом (Multiple Choice - Single Answer);
  3. тестирование с несколькими вопросами и несколькими вариантами ответа (Multiple Choice - Multiple Answer);
  4. тестирование с развернутым открытым ответом ( Open - Ended ).

Вопросы первых трех типов могут быть оценены автоматически в базе Assessment Manager, если, конечно преподаватель заложил такую возможность. В противном случае преподаватель должен выставить оценку самостоятельно. Также имеется возможность добавить комментарий к каждой оценке. Оценки, выставленные преподавателем, а также комментарии студент может просмотреть в своем Профиле.



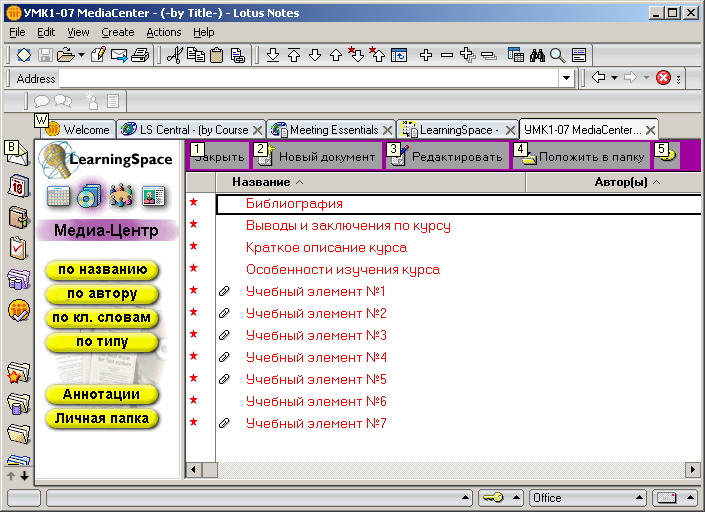
Рисунок 2.2 – Медиа Центр курса «Управление программами и проектами»


3 Разработка курса дистанционного обучения по дисциплине "Информатика"

3.1 Введение

Курс является комплексным учебным пособием. Процесс изучения курса построен на использовании программного продукта LearningSpace, что дает возможность воспользоваться уникальным новаторским опытом обучения, ликвидирует коммуникационный барьер между преподавателем и обучаемыми, дает возможность обучения в любом месте и в любое время, не взирая на пространственные и временные ограничения. Студенты имеют возможность просматривать учебные материалы и упражнения, участвовать в тестах, решать задачи, проводить самотестирование.

Цели дисциплины «Информатика»:

  1. Основная цель дисциплины – комплексная подготовка специалистов по разработке и анализу систем информационной безопасности.

  2. Конкретной целью является знакомство слушателей с понятиями, образующими теоретический фундамент информатики, а также выработка умения строить ту или иную дискретную математическую модель для соответствующей прикладной задачи и формирование навыков по решению этих задач.

Задачи дисциплины «Информатика»:

  1. Изучение понятий, образующих теоретический фундамент информатики.

  2. Изучение подходов к формулировке тех или иных технических проблем в виде соответствующих математических задач.

  3. Изучение важнейших алгоритмов и освоения навыков решения конкретных задач с помощью изученных методов.

  4. Выработка у слушателей не только навыков использования известных алгоритмов применительно к стандартным случаям, но и умения модифицировать эти алгоритмы для решения нестандартных задач.


После освоения данной дисциплины студент подготовлен для изучения следующих курсов учебного плана: «Алгоритмические языки и программирование», «Технология программирования», «Дискретная математика», «Основы теории информации», «Электроника и схемотехника», «Математическая логика и теория алгоритмов», «Алгебраические системы», «Комбинаторика», «Алгебраическая теория кодирования».


3.2 Краткое содержание дисциплины

Первый семестр
  1. Элементы теории множеств
    1. Предмет и задачи информатики и ее связь с современными техническими задачами в том числе с вопросами защиты информации. Дискретная математика как фундамент теоретических основ информатики.
    2. Множества и подмножества. Типы множеств, способы их задания. Операции над множествами и их свойства.
    3. Характеристическая функция множества.
    4. Отображения конечных множеств и их классификация.
  2. Основные комбинаторные понятия и схемы
    1. Основные перечислительные правила.
    2. Схемы выборок из конечного множества.
    3. Бином Ньютона. Свойства биномиальных коэффициентов.
    4. Полиномиальные коэффициенты.
    5. Формула включения-исключения.
    6. Простейшие комбинаторные суммы и их свойства.
  3. Основы теории чисел. Алгоритм Евклида
    1. Арифметика целых чисел Z. Делимость целых чисел, НОД и НОК.
    2. Теоремы Евклида для целых чисел. Свойства НОД и остатков.
    3. Алгоритм Евклида. Расширенный алгоритм Евклида.
    4. Теорема Евклида о НОД для целых чисел.
    5. Китайская теорема об остатках
  4. Модульная арифметика
    1. Сравнимость целых чисел по фиксированному модулю.
    2. Определение множества вычетов Zm и задание в Zm операций сложения и умножения.
    3. Свойства операций в Zm. Обратимость элементов в Zm.
    4. Функция Эйлера
  5. Системы счисления
    1. Позиционные и непозиционные системы счисления.
    2. Перевод целых и дробных чисел из одной системы счисления в другую.
    3. Двоичная система счисления – основа для представления чисел в ЭВМ.
    4. Восьмеричная и шестнадцатеричная системы счисления.
    5. Двоично-дополнительный код.
    6. Непозиционная система счисления, основанная на китайской теореме об остатках.

В первом семестре на изучение данной дисциплины отводится 17 часов лекций и 51 час семинаров (всего 68 часов).


Второй семестр
  1. Элементы дискретной геометрии и комбинаторики
    1. Булев куб как метрическое пространство: двоичный набор (вектор), вес и номер набора, метрика Хемминга и её свойства, связь веса и расстояния, изометрия, соседние и противоположные наборы. Слой номера k, шар, сфера и грань (подкуб), число наборов в них, расстояние между множествами.
    2. Булев куб как частично упорядоченное множество и граф: лексикографический порядок, сравнимые и несравнимые наборы, индуктивное построение и изображение на плоскости, цепи и антицепи, коды Грея.
    3. Булев куб как линейное векторное пространство: линейная (не)зависимость, базис, подпространство, переход от базиса к базису.
    4. Коды Хемминга.
  2. Булевы функции
    1. Определение булевой функции и способы её задания: таблица истинности, вектор значений, помеченный булев куб.
    2. Формула над множеством булевых функций, подформула. Функция, реализуемая формулой. Элементарные связки и их свойства. Построение таблицы истинности булевой функции по заданной формуле.
    3. Существенные и фиктивные переменные. Существенные функции.
    4. Двойственность. Принцип двойственности.
    5. Разложение булевой функции по одной или нескольким переменным. Подфункция.
    6. Нормальные формы булевых функций и их свойства.
    7. СДНФ, СКНФ и АНФ. Теорема Жегалкина.
    8. Алгоритмы вычисления АНФ.
  3. Полнота систем булевых функций. Замкнутые классы алгебры логики
    1. Алгебра логики. Операция замыкания множества булевых функций и её основные свойства.
    2. Функционально полные множества (системы). Замкнутый класс. Базис замкнутого класса.
    3. Классы T0, T1, S, L, M, их замкнутость и основные свойства. Способы определения принадлежности функции основным замкнутым классам и их эффективность.
    4. Нахождение мощности некоторых специальных множеств булевых функций.
    5. Леммы о несамодвойственной, немонотонной и нелинейной функциях.
    6. Функционально полные системы функций в P2. Критерий полноты системы функций алгебры логики (теорема Поста). Шефферовы функции.
    7. Предполные классы и базисы в них. Представление о результатах Поста: решётка замкнутых классов алгебры логики.
    8. Различные оценки числа Дедекинда (числа монотонных булевых функций). Цепи Анселя и лемма Анселя.
  4. Введение в криптографические свойства булевых функций
    1. Коэффициенты Уолша-Адамара булевой функции.
    2. Алгоритмы вычисления преобразования Уолша-Адамара.
    3. Метрический смысл коэффициентов Уолша-Адамара. Свойства полиномов и расстояние нелинейности.
    4. Основные свойства коэффициентов Уолша-Адамара. Формула обращения. Равенство Парсеваля. Тождество Саркара.
    5. Бент-функции.
  5. Элементы теории сложности
    1. Понятие контактной схемы. Её сложность. Функция проводимости.
    2. Реализация булевой функции с помощью контактных схем. Последовательно-параллельные схемы.
    3. Метод каскадов для построения контактных схем.
    4. Понятие схемы из функциональных элементов (СФЭ). Её сложность и глубина.
    5. Простейшие методы синтеза СФЭ, оценка эффективности.
    6. Минимальная схема. Сложность функции. Функция Шеннона.
    7. Нижние оценки сложности. Метод «забивания переменной». Метод обратного анализа схемы. Мощностной метод получения нижних оценок сложности.
    8. Метод каскадов и метод Шеннона как оптимальные по порядку методы синтеза схем.

Во втором семестре на изучение данной дисциплины отводится 17 часов лекций и 34 часа семинаров (всего 51 час).


3.2.1 Входной контроль готовности студента к освоению первого семестра дисциплины сводится к проверке освоения школьного материала.


3.2.2 Входной контроль готовности студента к освоению второго семестра дисциплины сводится к проверке освоения материала первого семестра дисциплины, на котором базируется курс второго семестра. Производится в начале занятий в интерактивной форме.

Пример типового варианта задания для проверки остаточных знаний:
  1. Дать определение сочетания, перестановки, сочетания с повторением.
  2. Найти число различных отображений из множества {0,1}n в себя и число различных обратимых отображений среди них.
  3. Определить, сколько существует различных 20-разрядных натуральных чисел, в десятичной записи которых все цифры следуют в неубывающем порядке.
  4. Чему равна сумма первых n натуральных чисел? Их квадратов?
  5. Найти число всех двоичных последовательностей длины n с чётным числом нулей.


3.2.3 Теоретические занятия возможно проводить в виде презентаций (рис. 3.1)




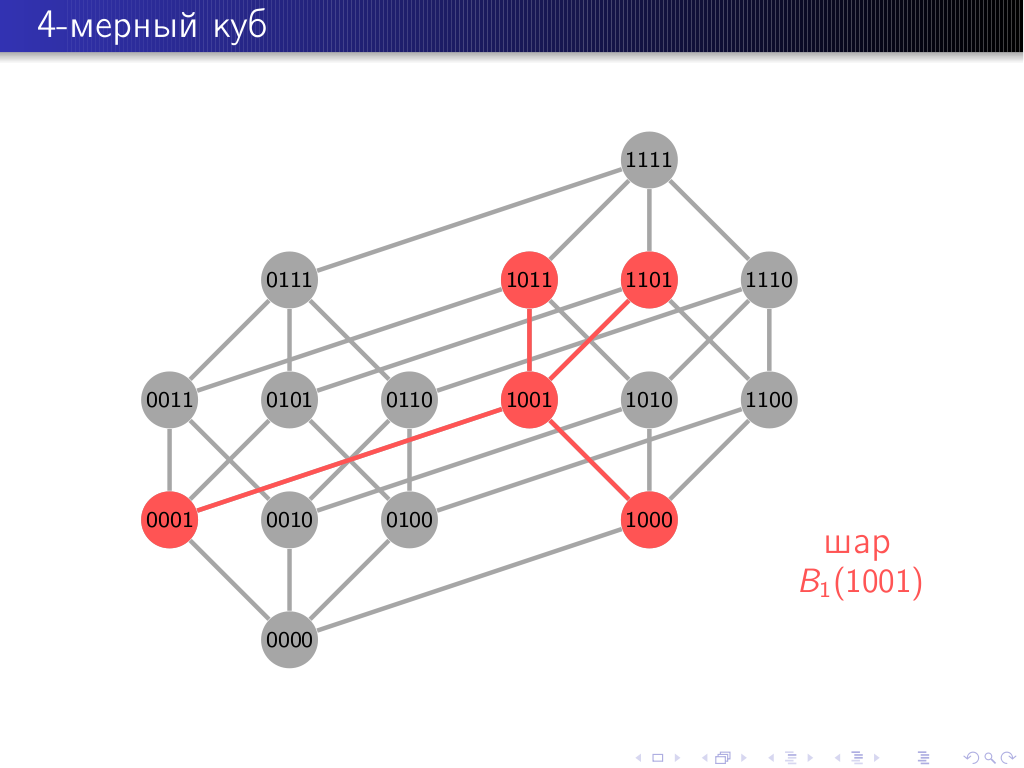
Рисунок 3.1 – Фрагмент первой лекции второго семестра


3.2.4 Практические занятия (семинары).

В начале некоторых из них также целесообразно разобрать несколько задач в режиме презентации. Ниже на рисунках представлены примеры решения некоторых задач 6-го семинара (2-й семестр), посвящённого нормальным формам булевых функций.




Рисунок 3.2 – Заглавный слайд презентации шестого семинара.





Рисунок 3.3 – Вычисление АНФ алгебраическим преобразованием.





Рисунок 3.4 – Пример применения метода неопределённых коэффициентов.





Рисунок 3.5 – Доказательство формулы обращения.


3.3 Создание курса дистанционного обучения дисциплине с использованием системы Lotus Notes

Панель "Administrator Tools" позволяет создать новый курс или отредактировать уже имеющиеся (рис. 3.6).



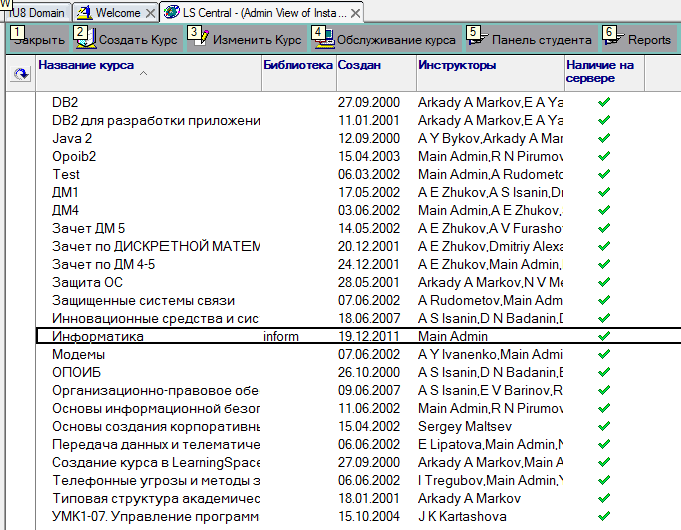
Рисунок 3.6 - Панель "Administrator Tools"


На панели представлен перечень имеющихся курсов и данные, связанные с созданием этих курсов. Среди этих данных информация о нахождении курса на сервере (поле Exists on Server), данные о заглавии курса (поле Course Title), времени его создания (поле Created) и инструкторах (преподавателях), сопровождающих электронный учебный процесс (поле Instructors).

Кнопка "Edit Course" позволяет редактировать описание уже созданного курса, кнопка "Course Tools" раскроет инструменты и средства, связанные с курсом, а кнопка "Return to Student Views" вернет к данную форму к виду, воспринимаемому в студенческой конфигурации LearningSpace.

При нажатии кнопки "Crerate New Course " появляется следующее окно (рис. 3.7):



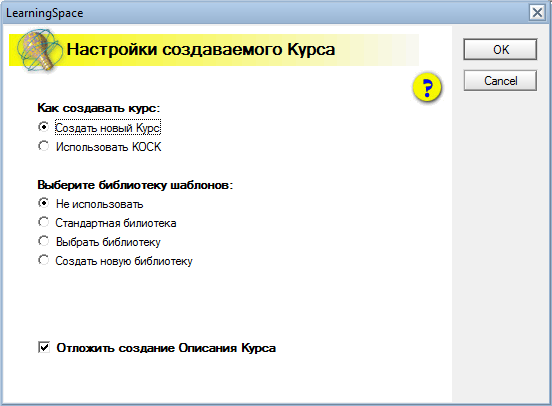
Рисунок 3.7 – Панель создания нового курса


Данные опции позволяют создать новый курс, выбрав опцию "Create new blank course" или распаковать предварительно запакованный курс, выбрав опцию "Create from course pack". Далее необходимо определить возможности подключения дополнительных библиотек курсовых материалов. Допустим, мы решили, что курс будет создан заново совместно с новой библиотекой.

Формирование курса происходит в базе Медиа Центр. Это совместно используемая студентами база знаний, где расположены материалы учебного курса. Информация может набираться непосредственно средствами Lotus Notes, а может предварительно готовиться в известных автору оболочках и затем уже переноситься в Медиа Центр. Список программных сред, в рамках которых могут быть созданы или дополнены информационные модули курса представлен в форме, доступной при открытии опции "Объект", рубрики "Создание" верхнего меню Lotus Notes. Вид формы представлен на рисунке 3.8:





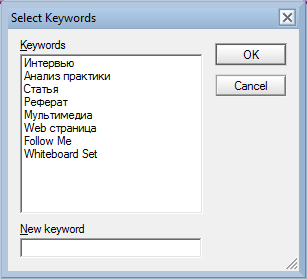
Рисунок 3.8 – Создание объекта в Медиа Центре


Для определенных типов образовательной информации создаются гиперссылки и кнопки, передающие управление другим программным модулям.

Для структурирования информации и лучшей усваиваемости материала для каждого модуля можно определить ключевые слова, которые затем можно просмотреть для каждого раздела (рис. 3.9):





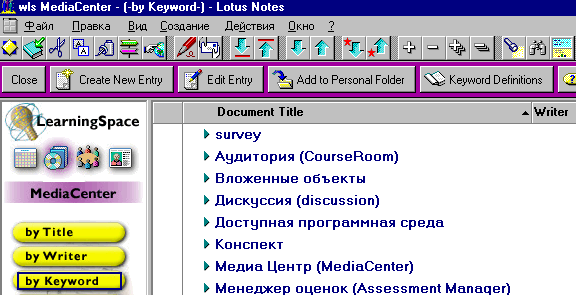
Рисунок 3.9 – Просмотр ключевых слов для основных разделов курса


3.3.1 Доступ студентов к курсу дистанционного обучения

Курс в LearningSpace представляет собой совокупность баз данных, находящихся на сервере, доступ к которым имеют только зарегистрированные пользователи. Получить доступ к курсу можно через любой интернет-браузер, установленный на ПК с выходом в интернет. Для этого, после появления соответствующего запроса от сервера нужно указать имя пользователя и пароль, полученные Вами при регистрации (рисунок 3.10) (Примечание: на данный момент доступ к курсу имеют только пользователя из группы учетных записей Lspace-iu8-1k, т.е. студенты кафедры ИУ8 первого года обучения).





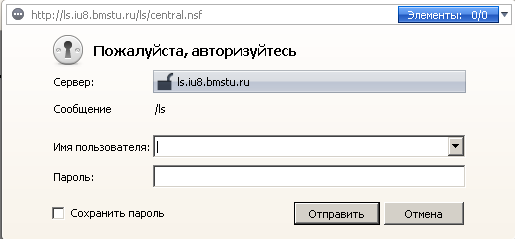
Рисунок 3.10 – Окно авторизация пользователя в системе LearningSpace с использованием браузера Opera


Выбрав курс, пользователь может войти в одну из баз данных (рис 3.11):



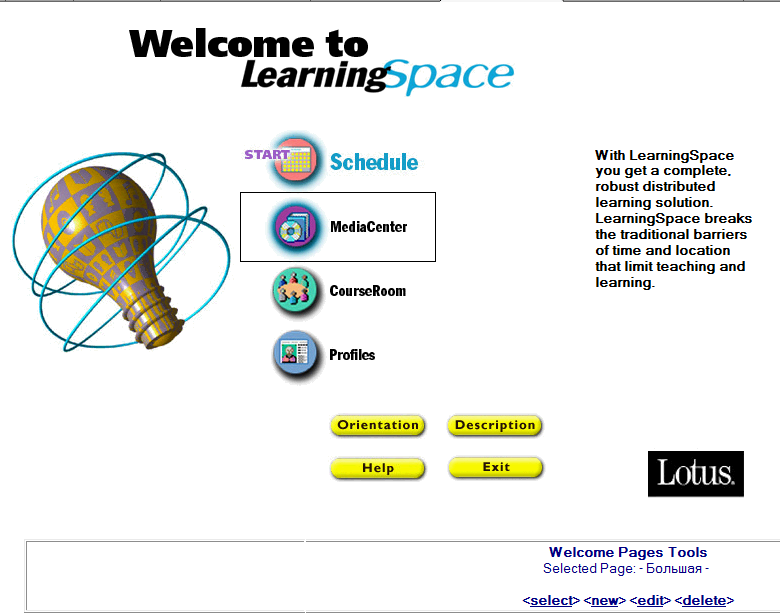
Рисунок 3.11 – Выбор базы данных для входа


Schedule (Расписание) – выдаваемый обучаемому план курса. Он показывает Вам, где предстоит тот или иной вид учебной деятельности (индивидуальной или групповой), назначенной преподавателем. Обучаемый работает с Расписанием на протяжении всего курса, открывая находящиеся здесь документы последовательно и, делая то, что они предписывают делать. Персональное обеспечение учебного процесса достигается рассылкой студентам, изучающим данный курс расписаний время сессий, а также заданий, вопросников и дат, когда они проводятся. Расписание интерактивно связано с базами данных MediaCenter (Медиа Центр) иCourseRoom (Аудитория).

MediaCenter (Медиа Центр) - это учебная библиотека – она содержит учебный материал для курса, такой как лекции, статьи, образы, звуковые файлы, видео клипы, ссылки на Web-страницы и т.д. Содержание Медиа Центра определено в соответствии с Расписанием и структурировано в виде модулей - разделов, охватывающих весь курс. Заполнение разделов может производиться с помощью встроенных возможностей, а также посредством таких программ как Word, Excel, различных графических редакторов, средств создания мультимедиа объектов.

CourseRoom (Аудитория) – интерактивно организованная с помощью электронной коммуникации группа. Это место, где студенты участвуют в дискуссиях по обсуждению пройденного материала, где можно создать виртуальную команду для того, чтобы поработать совместно над заданиями (assignments), предлагаемыми преподавателем. Студенты инициируют эти дискуссии, комментируют их и делают соответствующие выводы. Аудитория интерактивно связана с базами данных MediaCenter (Медиа Центр) и Расписанием.

Assessment Manager (Менеджер оценки) – специализированное средство, позволяющее преподавателю (инструктору) создавать те элементы учебного процесса, которые осуществляют опросы студентов по мере изучения ими материалов курса. Типы проводимых опросов следующие: самотестирование (self - assessment), опрос (quiz), обзор (survey), экзамен (exam). Каждый опрос может быть составлен из вопросов следующих типов:

Вопросы для самопроверки позволяют студенту оценивать свои знания. Когда у Вас как у студента проходит самотестирование, никто не видит этот процесс, – даже преподаватель. Самотестирование может занять у студента столько времени, сколько ему необходимо.

Менеджер оценки доступен только преподавателю.

Profiles (Профили или Профайлы) – это документы, по которым обучаемые знакомятся друг с другом, обмениваясь контактной информацией о их образовании, квалификации и интересах. Желательно также вставить в профайл фотографию студента.


3.3.2 Работа в «Аудитории»

При составлении конспекта доступны любые материалы Медиа Центра и все среды, контакт с которыми поддерживает Lotus Notes.

Подобно тому как происходит написание студентом конспекта, возможно начало и продолжение дискуссии (обмена мнениями) между студентами в Аудитории по поводу изученного материала. Если это разрешено, студенты могут обмениваться мнениями в процессе освоения материалов курса. В качестве своих замечаний они могут помещать вновь набираемый текст, использовать любые вставки, подобно тому, как это они делали при составлении конспекта.

Название своих замечаний (или Топика, как принято в LearningSpace) студент дает самостоятельно. Кроме того, он может определить для кого из его коллег доступны материалы замечаний, а также то, в какой форме он хотел бы получить ответ от тех, к кому обращается (рис. 3.12).

Преподаватель может, при необходимости, корректировать материалы топика (рис 3.13).

Как топики студента так и комментарии преподавателя появляются в Аудитории и доступны там для обозрения и анализа (рис 3.14).



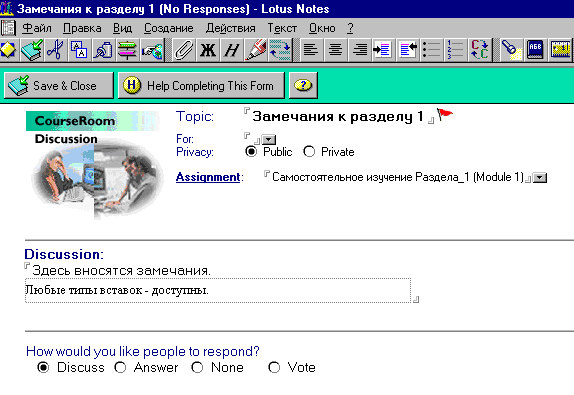
Рисунок 3.12 – Обмен мнениями в «Аудитории»



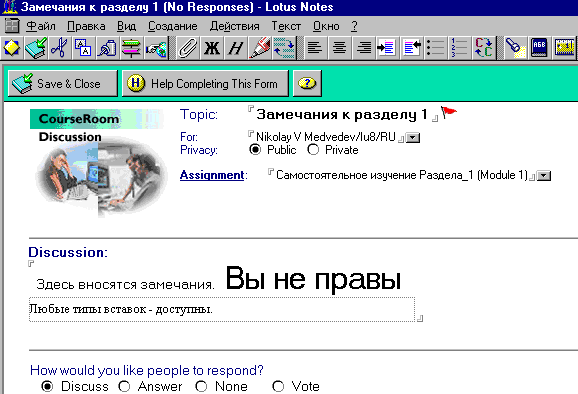
Рисунок 3.13 – Заметка преподавателя в «Аудитории»




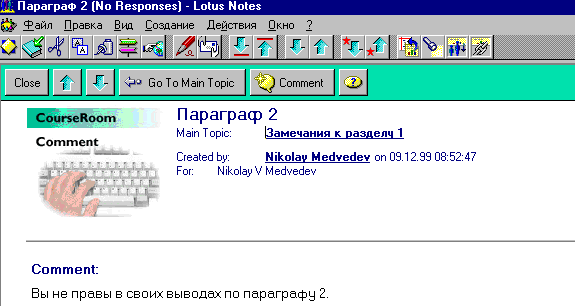
Рисунок 3.14 – Обзор и анализ мнений в «Аудитории»


3.3.3 Процесс интерактивного контроля знаний студента

Для проверки знаний студентов существуют возможности, предоставляемые преподавателю базой Assessment Manager (Менеджер оценки).

Виды, по которым представлена информация в базе Менеджер оценки, следующие:
  1. Created Assessments - созданные вопросники - задания по различным темам, связанным с данным модулем и другими модулями;
  2. Created Questions - созданные преподавателем вопросы по всем темам всех модулей, включая данный;
  3. Returned Assessments - вопросники, возвращенные студентами с ответами на вопросы;
  4. Returned Surveys - отчеты и обзоры, представленные студентами преподавателю;
  5. Graded by Students - оценки студентам;
  6. Graded by Schedule - оценки студентам в соответствии с расписанием

Типы вопросов следующие:
  1. тестирование по принципу “да/нет”( True / False )
  2. тестирование с несколькими вопросами и единственным ответом ( Multiple Choice - Single Answer )
  3. тестирование с несколькими вопросами и несколькими вариантами ответа ( Multiple Choice - Multiple Answer )
  4. тестирование с развернутым открытым ответом ( Open - Ended ).



3.3.3.1 Самотестирование

В конце каждой темы (модуля) студент имеет возможность провести самотестирование и оценить свои знания по пройденному разделу (рис 3.15).



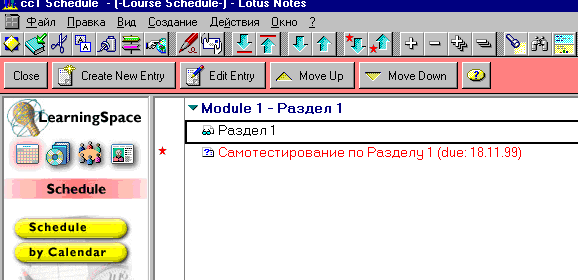
Рисунок 3.15 – Самотестирование

В качестве типа заданий для самотестирования могут быть:
  1. Тестирование (quiz),
  2. обзор (survey)
  3. экзамен с зачетом (exam).



      1. Проверка остаточных знаний в конце семестра

Данная часть курса представляет собой структурированный набор задач для компьютеризированной сдачи контрольных мероприятий по курсу «Информатика».

Каждый студент, изучающий данный курс, автоматически регистрируется в системе LearningSpace и получает логин и пароль для входа в систему.

Во время проведения контрольного мероприятия группа приглашается в компьютеризированное учебное помещение с установленным клиентским программным обеспечением на персональных компьютерах. Студенту предлагается решить ряд задач по определенной тематике (рисунок 3.16).



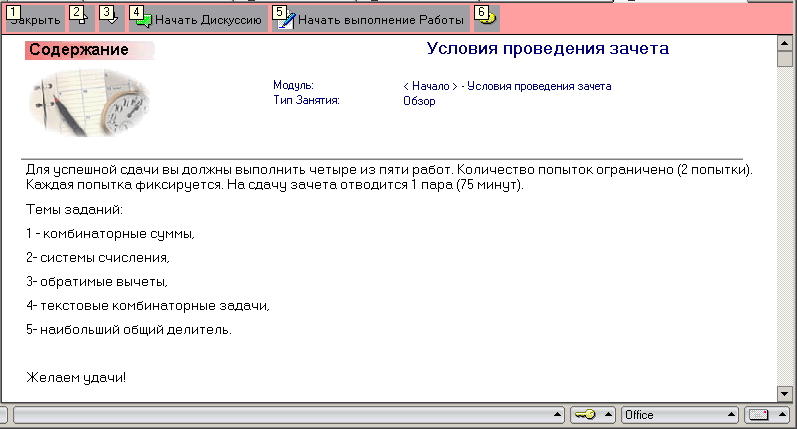
Рисунок 3.16 – Условия проведения компьютерного зачета по курсу «Информатика»

Задачи случайным образом выбираются из существующего набора. Решая каждую, задачу студент отправляет ответ на сервер, где все ответы в дальнейшем автоматически обрабатываются. При наборе определенного количества баллов за правильно решенные задания студент получает зачет.

Данная система имеет ряд настроек безопасности, благодаря которым студент может выполнить только предназначенные для него задания.

Преимущества компьютеризированной сдачи контрольных мероприятий:
  1. все студенты могут сдавать зачет одновременно;
  2. студенты получают различные задания;
  3. тестирование может провести любой сотрудник кафедры;
  4. результаты тестирования выдаются автоматически;
  5. возможна повторная сдача зачета, при этом результаты предыдущих тестирований будут сохранены (рисунок 3.17).



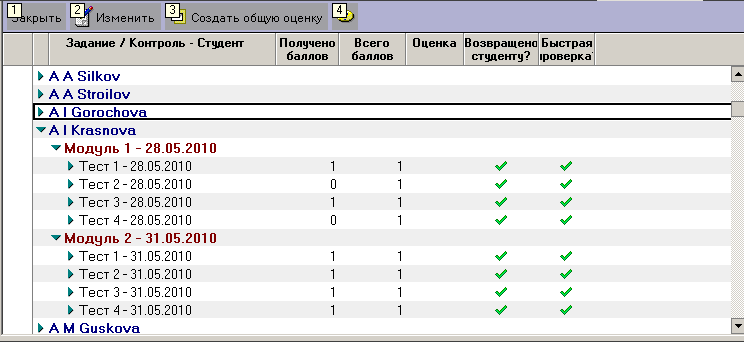
Рисунок 3.17 – Результаты тестирования, обработанные системой LearnigSpace


Заключение

Результаты проведенной работы:
  1. исследованы методы и средства сопровождения учебного процесса с помощью информационных технологий генерации образовательных ресурсов;
  2. проведен анализ содержания дисциплины «Информатика», изучаемой на кафедре «Информационная безопасность» в рамках образовательных стандартов;
  3. на основе проведенных исследований и анализа разработан экспериментальный образец курса дистанционного обучения, сопровождающего учебный процесс кафедры, который позволяет:
    1. создавать учетные записи пользователей;
    2. создавать группы пользователей;
    3. применять политики безопасности к отдельным учетным записям и к группам пользователей, разграничивая права доступа к определенным курсам;
    4. создавать курсы, которые могут включать в себя различные элементы учебного процесса:
      1. выдаваемая обучаемому «дорожная карта» курса;
      2. учебная библиотека, содержащая учебный материал для курса, такой как лекции, статьи, образы, звуковые файлы, видеоклипы, ссылки на Web-страницы и т.д.;
      3. интерактивно организованная с помощью электронной коммуникации группа, где студенты участвуют во взаимных дискуссиях по обсуждению пройденного материала и можно создать виртуальную команду для того, чтобы поработать совместно над заданиями, предлагаемыми преподавателем;
      4. специализированное средство, позволяющее преподавателю (инструктору) создавать те элементы учебного процесса, которые осуществляют опросы студентов по мере изучения ими материалов курса.



Список использованной литературы

Основная учебная литература
  1. Белоусов А.И., Ткачёв С.Б. Дискретная математика. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2001. – 744 с.
  2. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. – 3-е изд. – М.: Физматлит, 2005. – 416 с.
  3. Яблонский С.В. Введение в дискретную математику. – 3-е изд. – М.: Высшая школа, 2010. – 384 с.

Дополнительная учебная литература
  1. Андерсон Дж. Дискретная математика и комбинаторика. – М.: Издательский дом «Вильямс», 2004. – 960 с.
  2. Аршинов М.Н., Садовский Л.Е. Коды и математика (рассказы о кодировании). – М.: Наука, 1983. – 144 с.
  3. Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.: МЦНМО, 2006. – 400 с.
  4. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. – М.: МЦНМО, 2001. – 960 с.
  5. Конспект лекций О. Б. Лупанова по курсу «Введение в математическую логику» / Отв. ред. А. Б. Угольников. – М.: Изд-во ЦПИ при механико-математическом факультете МГУ им. М.В. Ломоносова, 2007. – 192 c.
  6. Липский В. Комбинаторика для программистов. - М.: Мир, 1988. - 200 с.
  7. Логачёв О.А., Сальников А.А., Ященко В.В. Булевы функции в теории кодирования и криптологии. – М.: МЦНМО, 2004. – 470 с.
  8. Лупанов О.Б. Асимптотические оценки сложности управляющих систем. - М.: Изд-во МГУ им. М.В.Ломоносова, 1984. - 138 с.
  9. Марченков С.С. Булевы функции. - М.: Физматлит, 2002. - 72 с.
  10. Марченков С.С. Замкнутые классы булевых функций. - 2-е изд., испр. - М.: Физматлит, 2001. - 128 с.
  11. Нефедов В.Н., Осипова В.А. Курс дискретной математики. – М.: Изд-во МАИ, 1992. – 264 с.
  12. Нигматуллин Р.Г. Сложность булевых функций. – М.: Наука, 1991. – 240 с.
  13. Поздняков С.Н., Рыбин С.В. Дискретная математика: учебник для студ. вузов. - М.: Издательский центр «Академия», 2008. - 448 с.
  14. Таранников Ю.В. Комбинаторные свойства дискретных структур и приложения к криптологии. - М.: МЦНМО, 2011. – 152 с.
  15. Угольников А.Б. Классы Поста. - М.: Изд-во ЦПИ при механико-математическом факультете МГУ им. М.В.Ломоносова, 2008. - 64 с.
  16. Яблонский С.В., Гаврилов Г.П., Кудрявцев В.Б. Функции алгебры логики и классы Поста. - М.: Наука, 1966. - 120 с.

Кафедральные издания и методические материалы
  1. Жуков Д.А., Ключарёв П.Г. Булев куб. Избранные задачи. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2011. (в печати.)