Автоматизация технологической подготовки производства для малых инновационных предприятий в машиностроении

Вид материала

Автореферат

Содержание Четвертая глава P включает 11 основных компонентов: P = P имеет множество значений, например описание формы пластины Pf Сi может быть поставлено в соответствие нечеткое множество A

Подобный материал:

• Учебный план по дополнительной образовательной программе, 38.01kb.
• Методические указания по выполнению дипломных проектов для студентов специальности, 294.98kb.
• Управление венчурным инвестированием малых инновационных предприятий в российских условиях, 342.92kb.
• Семинар Проблемы и перспективы подготовки кадров для высокотехнологичного бизнеса,, 55.18kb.
• Рабочая программа по предмету «Автоматизация производства» Для профессиональной подготовки, 111.79kb.
• Концепция подготовки и проведения VIII всероссийской конференции представителей малых, 265.43kb.
• План введение критерии отнесения предприятия к категории малых предприятий правовые, 364.08kb.
• Вопросы для подготовки к экзамену по Основам технологии получения заготовок деталей, 36.75kb.
• Конкурс инновационных проектов "У. М. Н. И. К.", 185.73kb.
• Автоматизация документального и информационного обеспечения малых предприятий с применением, 297.24kb.

Таким образом, в соответствии с разделом "Система продукций" в табл. 1, для каждой вершины графа декомпозиции Q₁…Q_n имеем систему правил, которую в общем виде можно представить в виде множества:

R = {R₁, R₂,…,R_m} . (6)

В этой системе правил

R_i: если х₁ есть А_i1 и х₂ есть А_i2 и … и х_n есть А_in , то y есть b_i ,(i = 1,…,m), (7)

где х₁, х₂,…, х_n - входные параметры нечеткой модели;

y - выходной параметр;

b_i - значения выходного параметра;

А_ij - нечеткие множества для задания значений входных параметров;

i = 1,…,m; j = 1,…,n.

В соответствии с табл. 1, x₁ = "L", x₂ = "Otn", у = Q₁₃, b₁ = "Цилиндрическая ступень", b₂ = "Канавка прямая" множествами А_ij являются множества, определенные термами "Незначительная", "Много меньше", "Значительная", "Соизмеримое".

Для каждого j множества А_ij имеют единую область определения (т.к. формализуют термы одной и той же лингвистической переменной, связанной с параметром х_j).



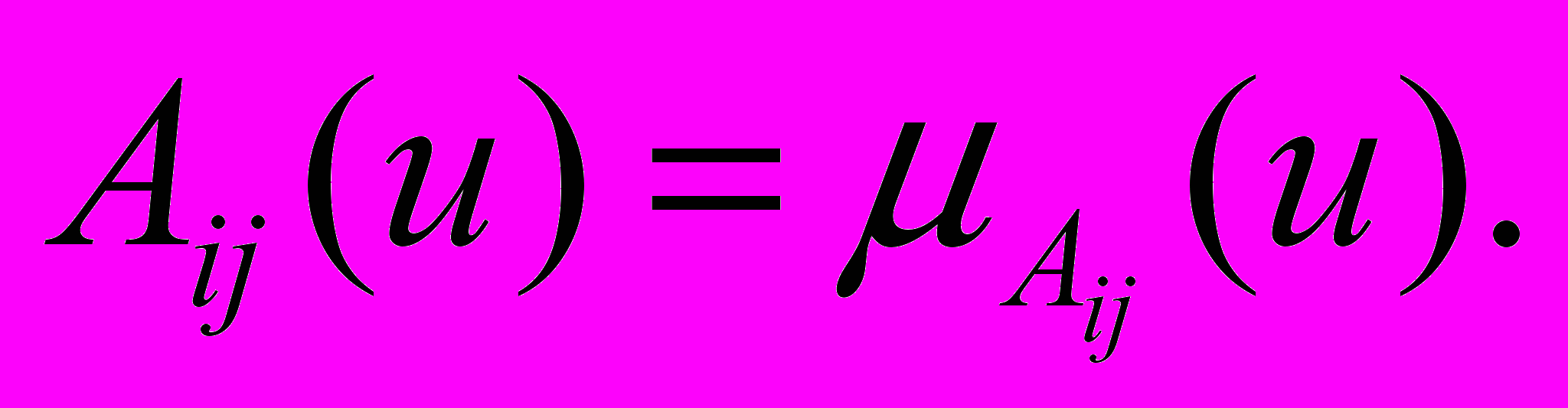
(8)

Пусть U_j - область определения множеств А_ij, обозначим

Для принятия решений был разработан алгоритм приближенных рассуждений. Пусть имеется набор конкретных значений входных параметров (u₁^*, u₂^*,…, u_n^*), где u_j^*  U_j (j = 1,…,n), для которого надо получить значение выходного параметра.

1. Для каждого правила R_i (i = 1,…,n), вычисляется уровень его срабатывания:
   

_i = min (_i1, _i2,…, _in), либо _i = _i1_i2…_in , (9)

где _ij = A_ij(u_j^*) – уровень срабатывания правила R_i по j-му входу.

На основе уровня срабатывания _i определяется вывод из правила R_i (нечеткая точка):


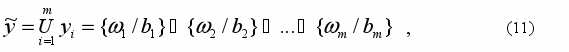
y_i^* = { _i / b_i}. (10)

2. Определяется общий вывод из системы правил R:
   

где 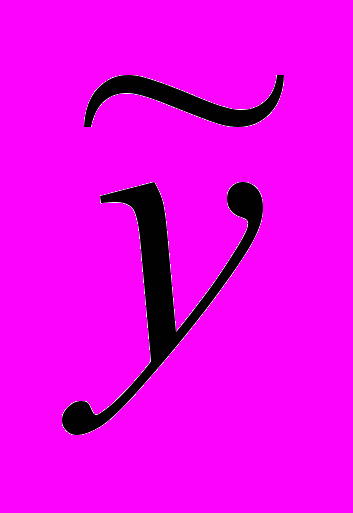- нечеткое множество на множестве возможных значений выходного параметра.

Также, в работе предложена методика сопоставления 3D-модели детали и 2D-чертежа для поиска и идентификации конструкторско-технологических элементов 2 уровня и конструкторских обозначений. Задача сопоставления 2D и 3D появляется после однозначного понимания автоматизированной системой конструкции детали из 3D-модели на основании графа декомпозиции. После завершения поиска каждому элементу 1 уровня, распознанному на основании 3D-модели, сопоставляются линии 2D-чертежа и определяется принадлежность конструкторских обозначений к конкретным КТЭ. Также, сопоставленные 3D-модель и 2D-чертеж детали используются для поиска и распознавания КТЭ 2 уровня.

Для получения параметров качества поверхности, отклонений формы, расположения поверхностей и точности детали анализируется 2D-чертеж, получаемый в формате IGES, и в автоматическом режиме распознаются конструкторские обозначения. Полученная КТМ детали в дальнейшем используется для автоматизации процедур выбора режущего инструмента и стратегий обработки на станках с ЧПУ.

Применение разработанной в диссертационном исследовании автоматизированной системы на основе метода автоматического распознавания КТЭ из 3D-модели и 2D-чертежа на основе графа декомпозиции и передачи КТМ детали в САПР ТП «ТехноПро» в условиях машиностроительных МИП позволяет существенно сократить время на подготовку исходной информации для технологического проектирования, что достоверно подтверждается соответствующими справками о внедрении на ряде МИП региона.

Четвертая глава посвящена автоматизации процедуры выбора рационального режущего инструмента для современного многофункционального технологического оборудования с ЧПУ в условиях МИП, также рассматривается автоматизация выбора стратегий обработки деталей, как новый подход к снижению производственных затрат.

Конструкции современных сборных режущих инструментов одного назначения различаются способами установки и крепления режущих элементов – пластин, т.е. структурной компоновкой и параметрами – размерами пластин, корпусных элементов или элементов крепежа. Количество возможных вариантов в ряде случаев исчисляется тысячами. Выбор подходящей конструкции инженером является постоянно решаемой технической задачей, и осуществляется, в основном, на основании однонаправленных рекламных материалов, личного или коллективного производственного опыта. Наибольшие проблемы в подборе рационального инструмента могут испытывать малые машиностроительные предприятия, в связи с отсутствием коллективного опыта.

С другой стороны, производителями режущего инструмента разработаны базы данных и экспертные системы для выбора инструмента. Однако такие системы не позволяют сравнить между собой однотипные конструкции различных производителей или конструкции, укомплектованные из сборочных элементов различных производителей, а также управлять процессом выбора наилучших вариантов конструкций инструментов.

Таким образом, задача выбора рационального режущего инструмента для обработки изделий на многофункциональном технологическом оборудовании с ЧПУ является актуальной и требующей решения.

В работе разработано математическое обеспечение, алгоритмы и автоматизированная система для выбора рационального металлообрабатывающего инструмента для обработки на основе данных, полученных из ГМ детали, представляемой в виде 3D-модели и 2D-чертежа (процесс получения данных рассмотрен в главе 3), с последующей передачей спецификации на выбранный инструмент в CAM-систему и САПР ТП. Проведенное исследование затрагивает большую часть применяемого в общем машиностроении токарного инструмента. Схема предлагаемого подхода к выбору инструмента рассмотрена на рис. 5.

Согласно стандартам ISO 1832:2004, обозначение режущей пластины P включает 11 основных компонентов:

P =
, (12)

где Pf - множество значений форм пластин, Ab – множество значений заднего угла пластины, Tc - множество значений класса допуска на пластины, Ls - множество значений типа пластины (обозначение фиксации), Pd - множество значений размера пластины (длина режущей кромки), Pt - множество значений толщины пластины, Re - множество значений радиуса при вершине, Cs - множество значений вида режущей кромки, Cd - множество значений исполнения пластины (обозначение направления резания), Cw - множество значений ширины фаски или обозначение стружколома, Ca - множество значений угла фаски.




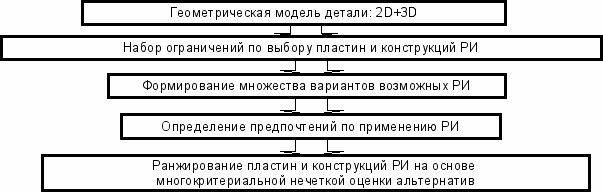
Рис. 5. Предлагаемый подход к выбору инструмента


Каждый компонент обозначения режущей пластины P имеет множество значений, например описание формы пластины Pf:

Pf={Pf₁, Pf₂, … Pf₁₇} ={Ромбическая 35°,

Ромбическая 50°, … ,Восьмигранная, Круглая} . (13)

Рассмотрим задачу выбора рациональной формы режущей пластины Pf из множества выпускаемых пластин. Этот выбор осуществляется на основе степени соответствия альтернатив совокупности требований, определяемых системой 5 различных критериев Ci:

Ci={C₁, C₂, C₃, C₄, С₅}. (14)

где С₁ – эффективность отвода тепла; С₂ – минимальная потребляемая мощность; С₃ – прочность пластины; С₄ – минимум возникновения вибраций;С₅ – универсальность режущей пластины.

В таком случае каждому критерию Сi может быть поставлено в соответствие нечеткое множество

A_Ci = {µ_Ci (Pf₁), µ_Ci (Pf₂), … , µ_Ci (Pf₁₇)}. (15)

Здесь величина µ_Ci (xj) [0,1] представляет собой оценку альтернативы Pf_j по критерию Сi. Иными словами, она выступает характеристикой степени ее соответствия требованию, определяемому рассматриваемым критерием Сi. Множество оценок по критериям приведено в табл. 2.

Данные этой таблицы получены на основе анализа литературных источников. Экспериментальное подтверждение табличных данных является темой для отдельного диссертационного исследования и в работе не выполнялось.

В рассматриваемом случае требуется решать многокритериальную оптимизационную задачу в условиях различной важности критериев достижения максимума целевой функцией. При этом каждому критерию С_i ставится в соответствие некоторый весовой коэффициент λi ≥ 0, причем

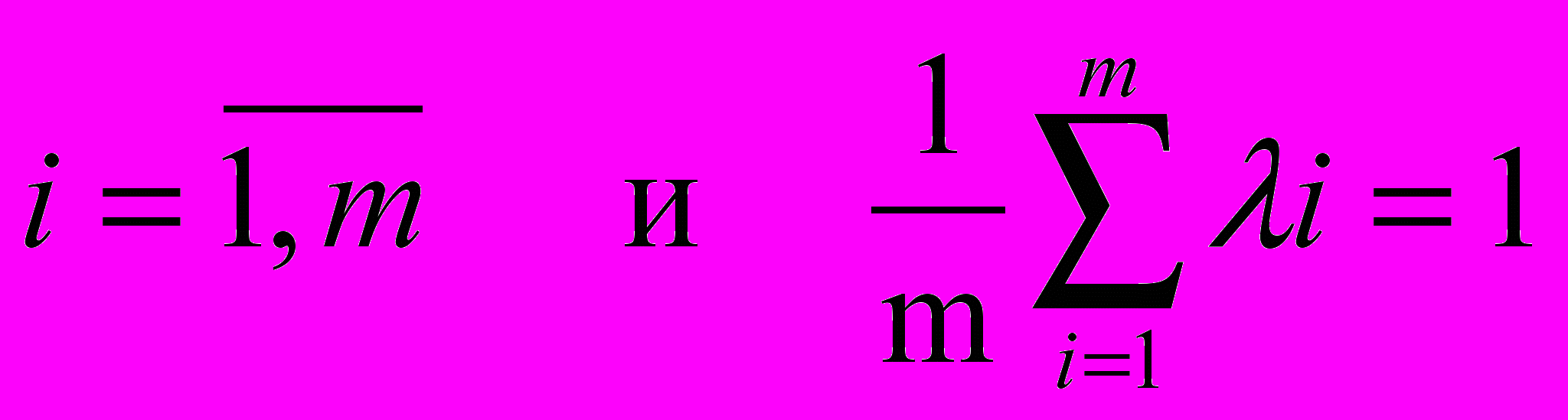. (16)

Таблица 2. Множество оценок форм пластин по критериям

Pfj	Обозначе-ние	Отвод тепла (AC1)	Мощность (AC2)	Прочность (AC3)	Вибрации (AC4)	Универсальность (AC5)
Pf1	V	0,9	0,97	0,1	0,85	0,93
Pf2	F	0,78	0,85	0,22	0,73	0,81
Pf3	D	0,74	0,81	0,26	0,69	0,77
Pf4	К	0,74	0,81	0,26	0,69	0,77
Pf5	Т	0,7	0,77	0,3	0,65	0,73
Pf6	Р	0,604	0,674	0,396	0,554	0,634
Pf7	Е	0,58	0,65	0,42	0,53	0,61
Pf8	С	0,54	0,61	0,46	0,49	0,57
Pf9	W	0,54	0,61	0,46	0,49	0,57
Pf10	В	0,524	0,594	0,476	0,474	0,554
Pf11	А	0,5	0,57	0,5	0,45	0,53
Pf12	М	0,492	0,562	0,508	0,442	0,522
Pf13	S	0,46	0,53	0,54	0,41	0,49
Pf14	L	0,46	0,53	0,54	0,41	0,49
Pf15	Н	0,22	0,29	0,78	0,17	0,25
Pf16	О	0,1	0,17	0,9	0,05	0,13
Pf17	R	0,01	0,05	0,95	0,06	0,07

Решением исходной задачи будет такая альтернатива х, которая в наибольшей мере удовлетворяет требованиям всей совокупности критериев. Решающее правило D выбора наилучшей альтернативы в условиях многокритериальной задачи с неравнозначными критериями С_i, имеющими весовые коэффициенты λ_i, использует процедуру нахождения пересечения нечетких множеств

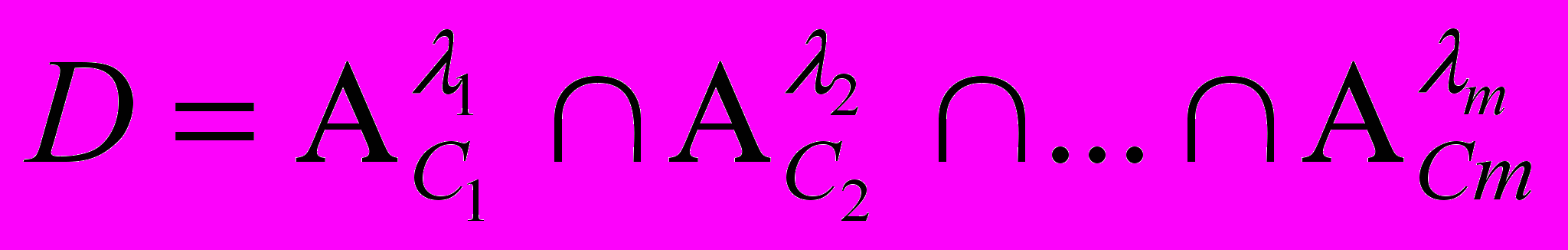. (17)

В соответствии с определением операции пересечения нечетких множеств функция принадлежности искомого решения находится по зависимости:

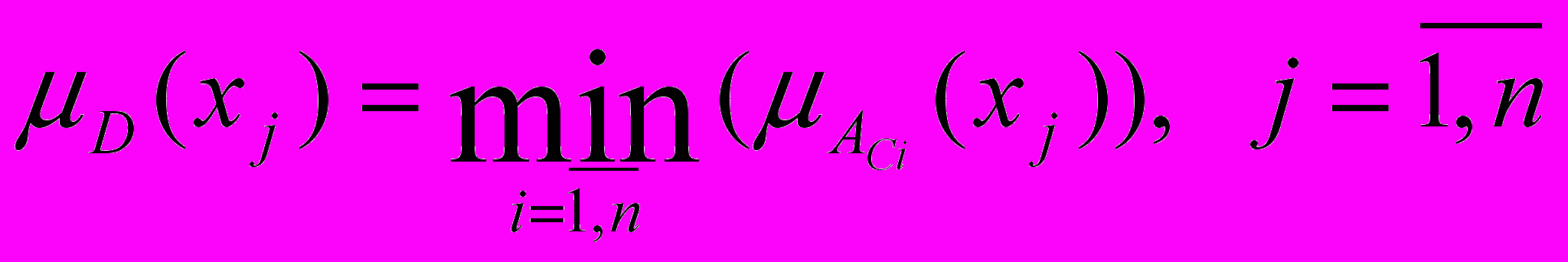. (18)

Таким образом, в качестве наилучшей должна быть выбрана та из альтернатив х_j*, для которой значение функции принадлежности µ_D (x_j) окажется максимальным:

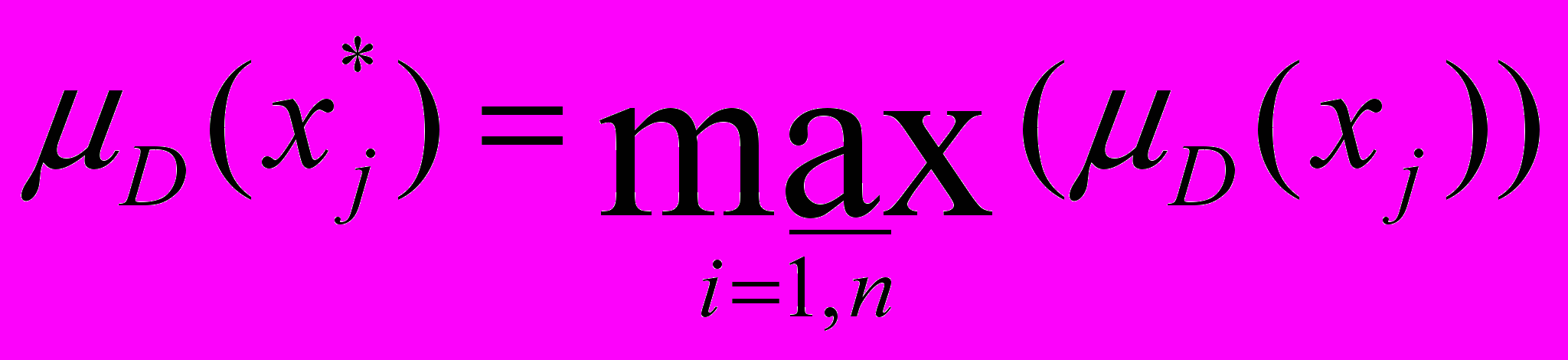. (19)

Именно эта альтернатива и является решением исходной задачи, поскольку она в наибольшей степени удовлетворяет требованиям всей совокупности рассматриваемых критериев.

Значения весовых коэффициентов определяются на основе стандартной процедуры попарного сравнения критериев. С учетом весовых коэффициентов строятся множества A^λi_Ci:

A^λi_Ci = {µ^λi_Ci (Pf ₁), µ^λi_Ci (Pf ₂), … , µ^λi_Ci (Pf ₁₇)}. (20)

Применяя правило выбора искомой альтернативы (оптимальной формы режущей пластины), находится пересечение множеств, которое будет иметь следующий графический вид (рис. 6).

Таким образом, в качестве рациональной должна быть выбрана та из форм пластины Pf_j*, для которой значение функции принадлежности µD(Pfj) окажется максимальным (рис. 6).

Для других параметров пластин, как и для державок, проведены аналогичные математические расчеты.

На основе разработанного математического обеспечения предложены алгоритмы работы системы, состоящей из 4 основных модулей:

• ввода первичной информации;
  
• подбора подходящего режущего инструмента;
  
• выбора рационального инструмента;
  
• модуль вывода.
  

Кроме того, в системе присутствуют модули, отвечающие за отображение чертежа и модели детали, база данных инструмента и ее редактор.

Результатом работы системы является отчет, содержащий необходимую информацию о рациональных инструментах и рекомендуемых режимах резания.


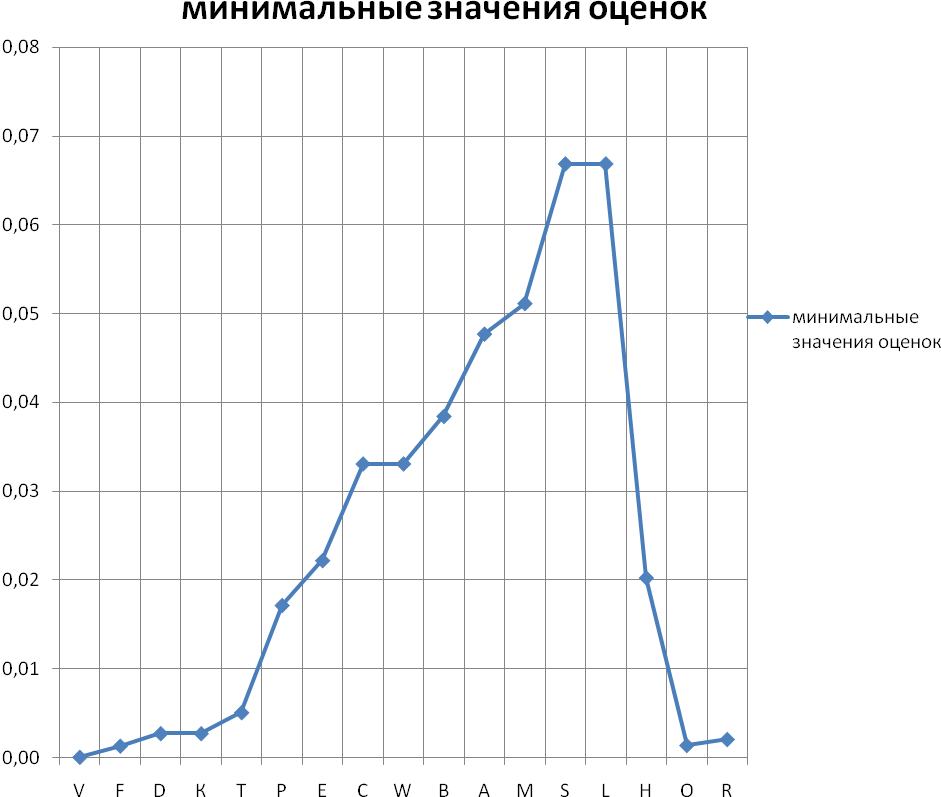
Форма пластины, Pf

µD(Pfj)


Рис.6. Минимальные значения оценок.


При технологической подготовке производства изделий машиностроения одной из важных задач является выбор стратегии обработки деталей. Предпосылками проведения исследований в этой области деталей являются:

• значительное распространение и использование многофункциональных станков с ЧПУ;
  
• увеличение номенклатуры деталей, которые обрабатываются за один установ;
  
• потребность в сокращении сроков подготовки производства деталей;
  
• универсальные CAD/CAM системы больше нацелены на решение геометрических задач и очень мало могут помочь пользователю при решении технологических задач, таких как назначение режимов резания, выбор стратегий обработки, подбор инструмента и т.д.;
  
• недостаточная интегрируемость современных САПР ТП с CAD системами и неспособность данных систем обеспечить сквозную подготовку производства в рамках концепции CALS;
  
• в САПР ТП и CAM-системах отсутствует математический аппарат выбора стратегий обработки детали.
  

Стратегия обработки может пониматься двояко: с одной стороны, под стратегией понимается последовательность обработки поверхностей и выбор инструмента, будем называть ее инструментальная (табл. 3), а с другой стороны – траектории движения инструмента при обработке, будем называть ее кинематическая (табл. 4). В работе рассматриваются оба названных понятия. Выбор стратегий обработки заготовок актуален как для МИП, так и для средних и крупных машиностроительных предприятий.

В табл. 3 для примера приведены только 5 инструментальных стратегий обработки КТЭ из нескольких десятков возможных (в сочетании). Научная проблема выбора инструментальной стратегии обработки возникла сравнительно недавно, с появлением широкого выбора инструмента с новыми возможностями. В отечественной науке этому вопросу уделялось мало внимания по причине ограниченного выбора инструмента для выбора стратегий. В работах Цветкова В.Д. и других авторов упоминается понятие «маршрут обработки поверхности (МОП)», частично схожее с предложенным понятием «инструментальная стратегия обработки». Под МОП понимается последовательность видов обработки (например точение, шлифование, полировка), а под инструментальной стратегией обработки понимается выбор конкретных инструментов и способов их применения. Поэтому, несмотря на схожесть инструментальной стратегии обработки и МОП, принято решение применять первое понятие.

Главный вопрос исследования инструментальных стратегий обработки – «при какой инструментальной стратегии обработки себестоимость детали будет минимальна?»

Исходные данные ID для выбора стратегии обработки можно описать в виде набора:

ID = ,

(21)