Лекции (ч. 4) «Автоматизация измерений, контроля и испытаний»
| Вид материала | Лекции |
- Введение Курс "Методы и средства измерений, испытаний и контроля", 172.41kb.
- Автоматизация измерений и контроля, 15.82kb.
- Рабочая программа дисциплины "Автоматизированные системы испытаний радиоустройств", 531.01kb.
- Курс Семестр Всего зачетных единиц Трудоемкость дисциплины в часах, 33.36kb.
- Рабочая программа По дисциплине «Методы и средства измерений, испытаний и контроля», 457.99kb.
- Организация и технология испытаний, 37.78kb.
- В. В. Черняев московский инженерно-физический институт (государственный университет), 29.9kb.
- Курс семестр Всего зачетных единиц Трудоемкость дисциплины в часах, 26.33kb.
- Программа вступительных испытаний в магистратуру кафедры «Системы автоматического управления, 251.19kb.
- Программа для студентов 4 курса специальности 020302- «Геофизика» Составитель почасовик, 118.38kb.
ЛЕКЦИИ (ч. 4)
«Автоматизация измерений, контроля и испытаний»
СРЕДСТВА АВТОМАТИЗАЦИИ ИЗМЕРЕНИЙ И КОНТРОЛЯ
5.1. Цифроаналоговые и аналого-цифровые преобразователи
Цифроаналоговые (ЦАП) и аналого-цифровые преобразователи (АЦП) являются неотъемлемой частью автоматических систем контроля, управления и регулирования. Кроме того, поскольку подавляющее большинство измеряемых физических величин являются аналоговыми, а их обработка, индикация и регистрация, как правило, осуществляются цифровыми методами, ЦАП и АЦП нашли широкое применение в автоматических средствах измерений. Так, ЦАП и АЦП входят в состав цифровых измерительных приборов (вольтметров, осциллографов, анализаторов спектра и т.п.), программируемых источников питания, дисплеев на электроннолучевых трубках, графопостроителей, радиолокационных систем, установок для контроля элементов и микросхем, являются важными компонентами различных преобразователей и генераторов, устройств ввода-вывода информации ЭВМ. Широкие перспективы применения ЦАП и АЦП открываются в телеметрии и телевидении. Серийный выпуск малогабаритных и относительно дешевых ЦАП и АЦП даёт возможность еще более широкого использования методов дискретно-непрерывного преобразования в науке и технике.
Существует три разновидности конструктивно-технологического исполнения ЦАП и АЦП: модульное, гибридное и интегральное. При этом доля производства интегральных схем (ИС) ЦАП и АЦП в общем объёме их выпуска непрерывно возрастает, чему в значительной степени способствует широкое распространение микропроцессоров и методов цифровой обработки данных.
5.2. Основные понятия
ЦАП — устройство, которое создает на выходе аналоговый сигнал (напряжение или ток), пропорциональный входному цифровому сигналу. При этом значение выходного сигнала зависит от значения опорного напряжения UОП, определяющего полную шкалу выходного сигнала. Если в качестве опорного напряжения использовать какой-либо аналоговый сигнал, то выходной сигнал ЦАП будет пропорционален произведению входных цифрового и аналогового опорного сигналов.
В АЦП цифровой код на выходе определяется отношением преобразуемого входного аналогового сигнала к опорному напряжению UОП, соответствующему полной шкале. Это соотношение выполняется и в том случае, если опорный сигнал изменяется по какому-либо закону. АЦП можно рассматривать как измеритель отношений или делитель напряжений с цифровым выходом.
Э
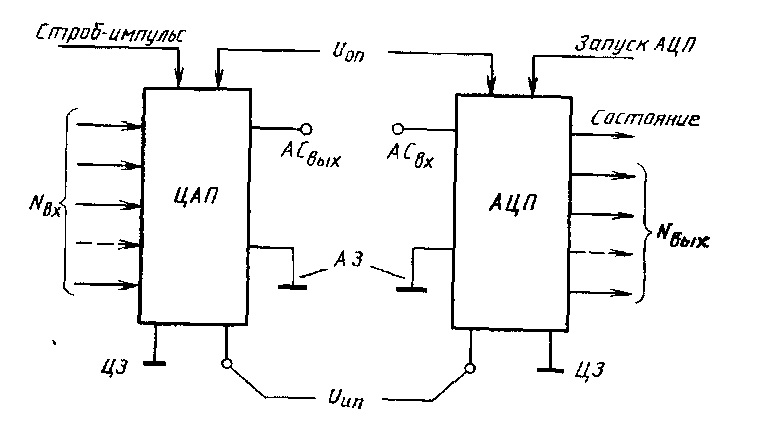лектрические сигналы на входах и выходах ЦАП и АЦП можно обозначить следующим образом: цифровой входной (выходной) код NBX (NВЫХ), аналоговый выходной (входной) сигнал АСВЫХ (АСВХ), напряжение источника питания Uип, сигналы управления (строб-импульс, запуск АЦП), опорное напряжение UОП (рис.5.1). Кроме того, как правило, для обеспечения требуемой помехоустойчивости выводятся две земляные шины: аналоговая земля (A3) и цифровая земля (ЦЗ).Рис.5.1. Типовые входные и выходные сигналы ЦАП и АЦП
Рассмотрим основные характеристики этих сигналов. На выходе ЦАП аналоговый сигнал формируется в форме либо напряжения, либо тока. Обычно ЦАП с выходным сигналом в виде тока (токовый выход) имеют более высокое быстродействие по сравнению с ЦАП, имеющими выходной сигнал в виде напряжения (потенциальный выход), поскольку используемый в этих ЦАП и выполненный на основе операционного усилителя (ОУ) преобразователь тока в напряжение вносит дополнительную инерционность.
ЦАП с потенциальным выходом различают по уровням выходного напряжения. При этом широко распространены унифицированные значения 2,5; 5; 10; 10,24 и 20 В. Наиболее часто встречается значение 10,24 В, которое наиболее удобно при двоичном кодировании поскольку в этом случае значения аналоговых сигналов, соответствующих разрядам преобразователя, описываются простыми цифрами. Так, например, для 10-разрядного ЦАП значение младшего разряда равно 10,0 мВ при шкале 10,24 В.
ЦАП с токовым выходом обычно обеспечивают следующие значения выходного тока: 1; 1,2; 1,5; 2,4; 5,0 и 10 мА.
В прямом двоичном коде старший разряд имеет вес 1/2=2-1 от значения полной шкалы. Следующий за старшим разряд имеет вес 1/4=2-2, и так далее, вплоть до младшего разряда с весом 1/2n, где п — число разрядов преобразователя. Сумма всех разрядов определяет значение полной шкалы преобразователя.
Для определения зависимости входных и выходных сигналов применительно к ЦАП и АЦП с двоичным кодированием удобно оперировать дробным двоичным числом, которое может быть представлено как
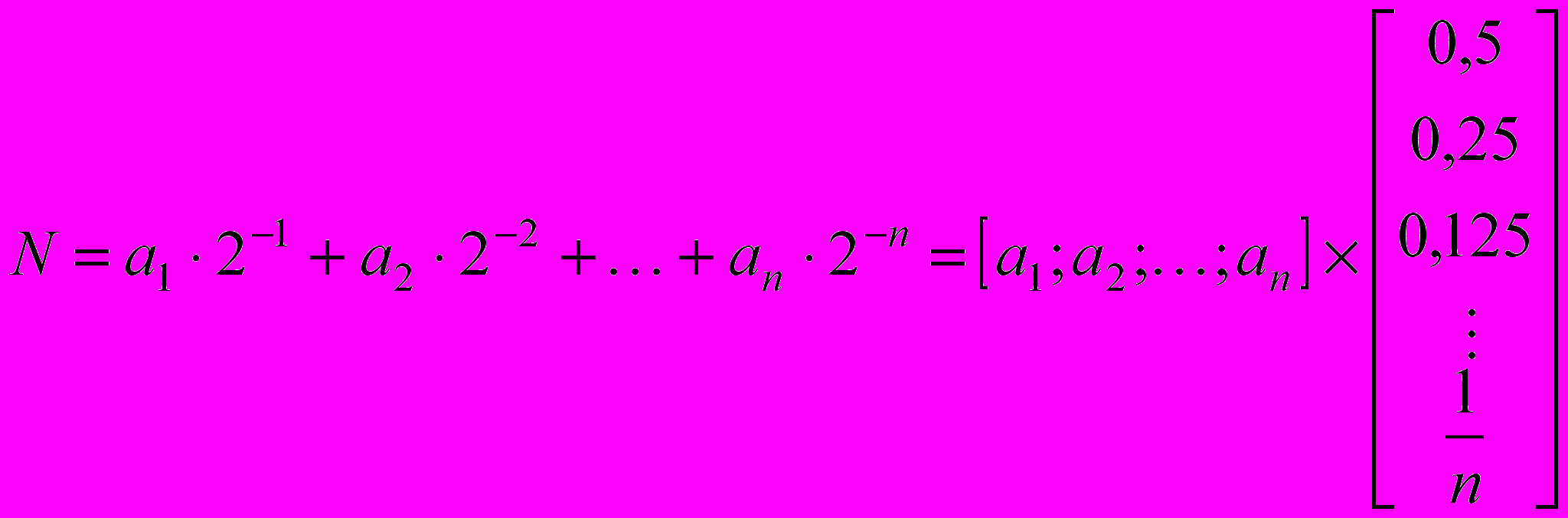.Такая система счисления для преобразователей удобна, поскольку весь диапазон преобразователя условно принимается равным единице, а значение двоичного числа, зависящее от конкретной кодовой комбинации, определяется значением правильной дроби. В этом случае старший (1-й) разряд равен половине полной шкалы, 2-й разряд — четверти полной шкалы и т.д. Самый младший, n-й разряд составляет 1/2n значения полной шкалы.
Пример. Для двоичного кода 1101 дробное кодовое число N имеет значение (1 х 0,5) + (1 х 0,25) + (0 х 0,125) + (1 х 0,0625) = 0,8125
Для ЦАП с п двоичными разрядами в идеальном случае (при отсутствии погрешностей преобразования) аналоговый выход UВЫХ соотносится с входным двоичным числом следующим образом:
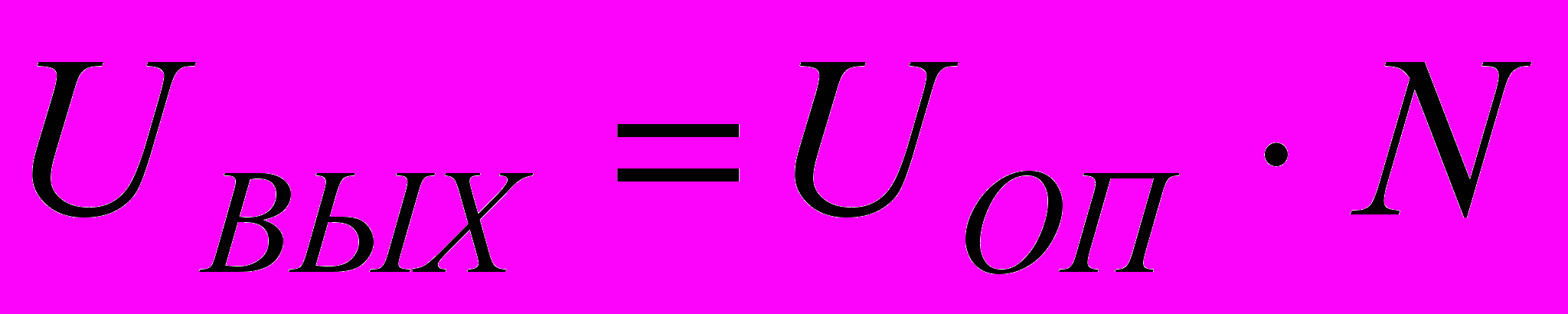,где UОП – опорное напряжение ЦАП (от встроенного или внешнего источника).
Так как
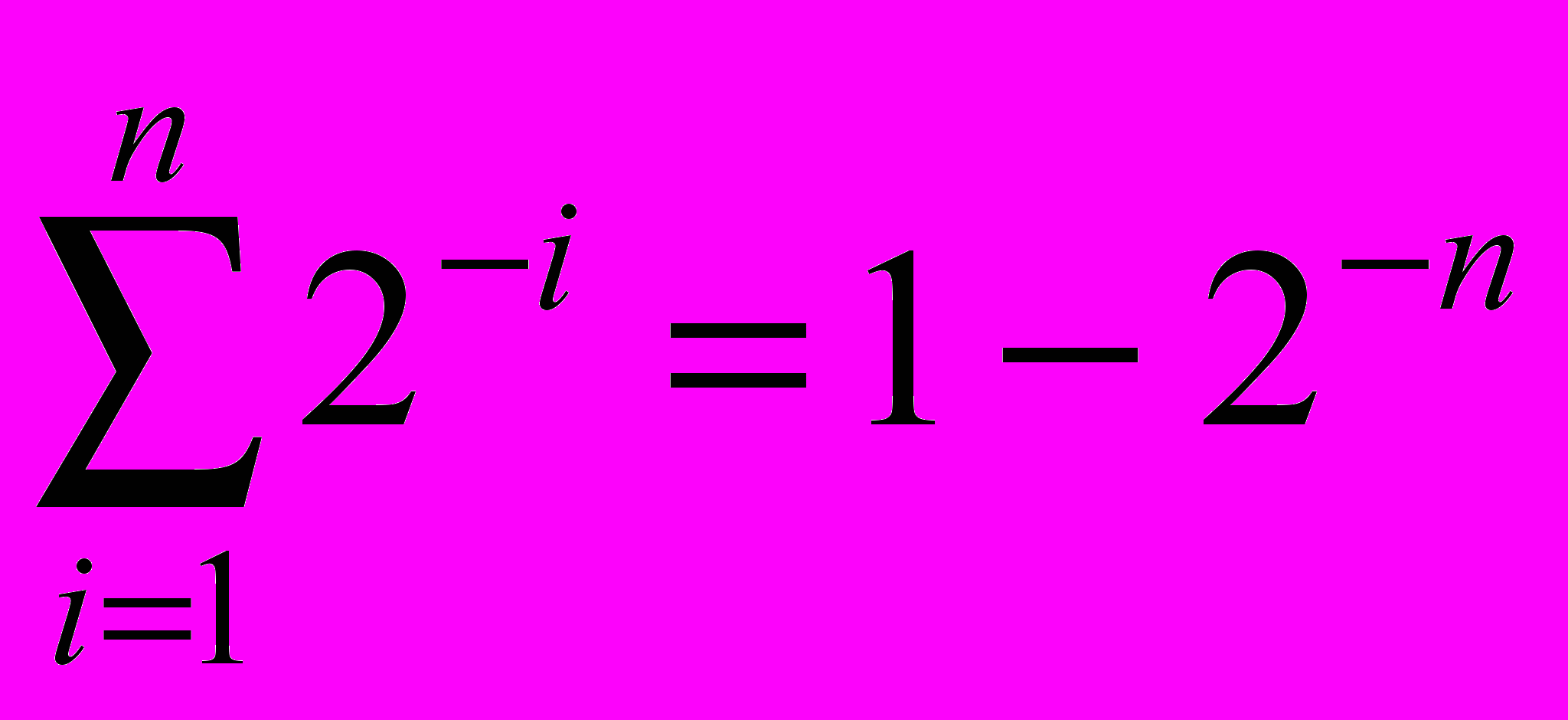,то выходное напряжение ЦАП при всех включённых разрядах называется напряжением полной шкалы и определяется соотношением:
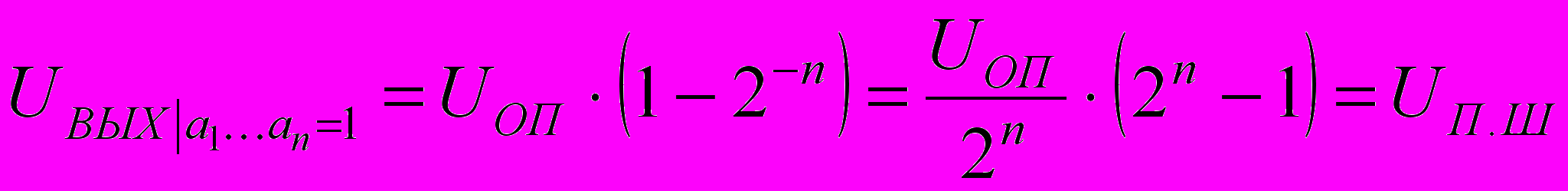.Таким образом, при включении всех разрядов выходное напряжение ЦАП (UП.Ш) отличается от значения опорного напряжения на значение младшего разряда
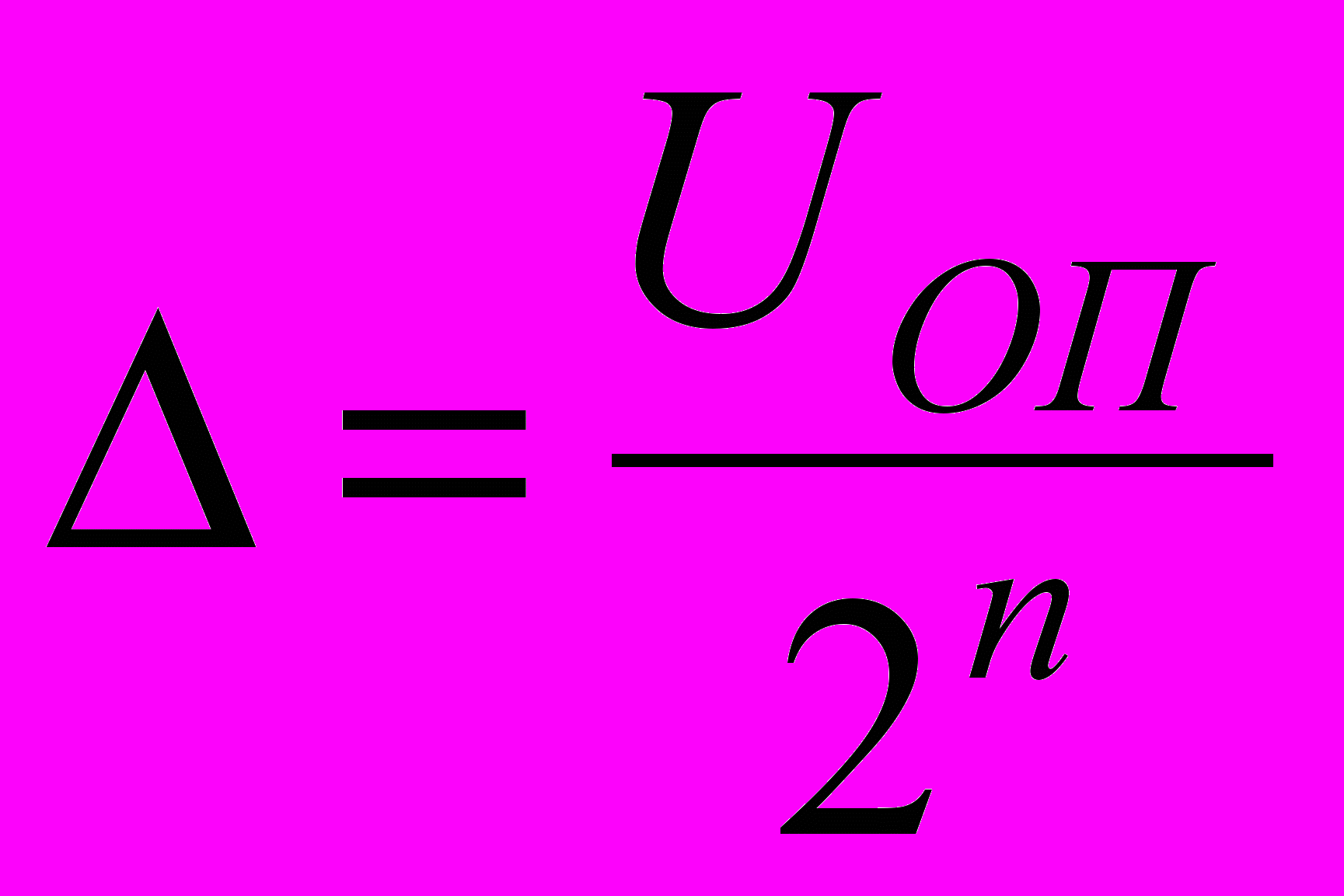.Выходное напряжение ЦАП при включении какого-либо i-го разряда определяется соотношением:
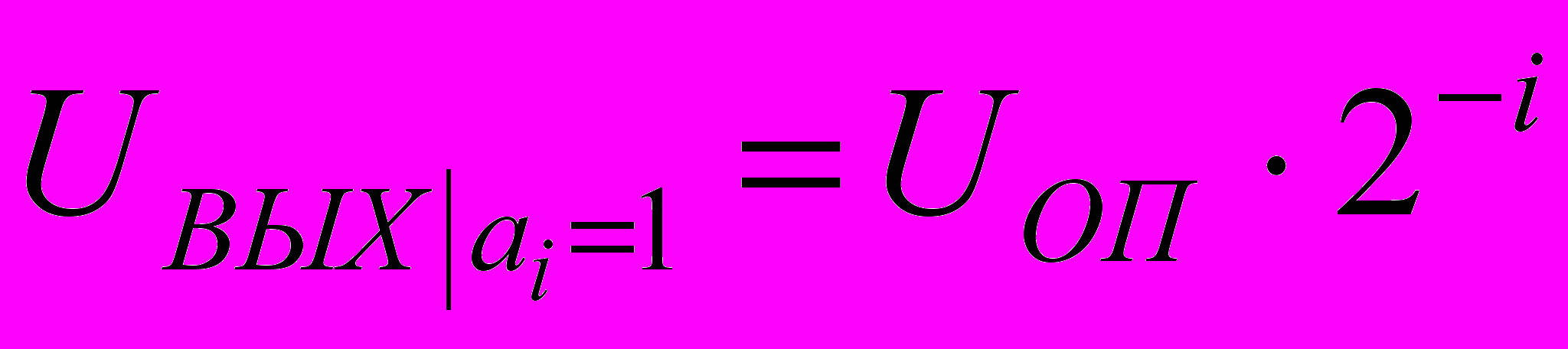
Пример. Если во всех разрядах входного кода ЦАП ai=1 (т.е. все разряды включены), то значение аналогового сигнала на его выходе будет меньше значения полной шкалы на значение , определяемой весом младшего разряда. Так, например, для 4-разрядного ЦАП со значением полной шкалы 10 В при всех включённых на входе разрядах (код 1111) значение аналогового сигнала на выходе ЦАП будет (1 х 0,5 х10) + +(1 х 0,25 х 10) + (1 х 0,125 х 10) + (1 х 0,0625 х 10) = 9,375 В. Вес младшего разряда при этом равен = 10 /24 =0,625 В.
Большинству типов АЦП (за исключением тех, которые осуществляют преобразование в непрерывном режиме) при выполнении преобразования требуется определенный отрезок времени для установления выходного сигнала. Поэтому если производить опрос АЦП в этот промежуток времени, то будет получена ошибочная информация. Для исключения этого в АЦП предусмотрена специальная схема, формирующая выходной управляющий сигнал «Состояние» или «Готов», которая меняет свое состояние каждый раз по окончании цикла преобразования. Этот сигнал можно использовать для запрещения преждевременного считывания и для предотвращения повторного запуска преобразователя до завершения предшествующего цикла преобразования.
ЦАП, как правило, постоянно отслеживает текущее значение входных цифровых сигналов. В случае, когда необходимо отделить основную схему преобразователя от источника цифровой информации, на входе ЦАП ставят буферный регистр, в который записывают цифровую информацию только при наличии разрешающего сигнала «строб-импульс».
5.3. Характеристики цифроаналоговых и аналого-цифровых преобразователей
Основными характеристиками ЦАП и АЦП являются разрешающая способность, нелинейность, коэффициент преобразования (передачи), погрешность нуля (смещение нуля), абсолютная погрешность преобразования и погрешность полной шкалы, дифференциальная нелинейность, монотонность, время преобразования.
Разрешающая способность определяет число дискретных значений выходного сигнала преобразователя, составляющих его предел преобразования. Чем больше число дискретных значений, тем выше разрешающая способность преобразователя. Двоичный n-разрядный преобразователь имеет 2n дискретных значений, а его разрешающая способность равна 1/2n. Однако только по разрешающей способности установить точность преобразования невозможно.
В преобразователях различают наименьший и наибольший значащий разряды. В двоичной системе кодирования наименьшим значащим разрядом считается тот, который имеет наименьший вес. Вес одного младшего разряда определяет разрешающую способность. Наибольший значащий разряд несёт в себе наибольший вес. В двоичном кодировании наибольший значащий разряд имеет вес ½ номинального значения полной шкалы преобразования.
Разрешающая способность может выражаться либо в процентах, либо в долях от полной шкалы. Например, 12-разрядный АЦП имеет разрешающую способность 1/4096 или 0,0245 % полной шкалы. Такой преобразователь с полной шкалой 10 В может обеспечить изменение выходного кода на один двоичный разряд при изменении входного напряжения на 2,45 мВ. Аналогично 12-разрядный ЦАП дает изменение выходного напряжения на 0,0245 % от полной шкалы при изменении двоичного входного кода на один двоичный разряд.
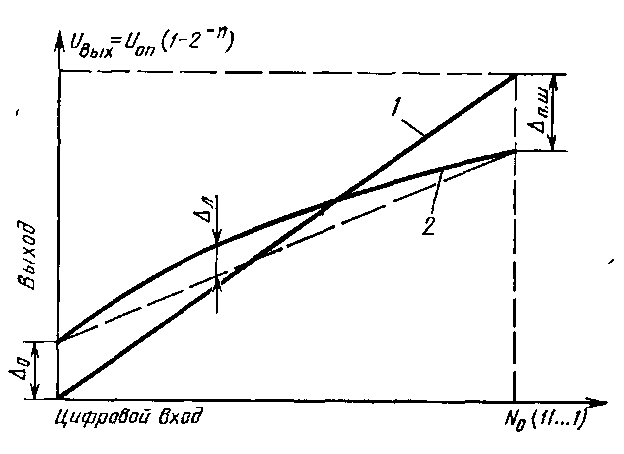
Нелинейность (или, как её часто называют, интегральная нелинейность, или погрешность линейности) л(x) характеризуется отклонением значений реальной характеристики преобразователя fp(x) от прямой (рис.5.2, а). При этом значение л(x) зависит от метода линеаризации, которая может осуществляться по различным критериям, например, критерию граничных точек, когда линеаризующая прямая проходит через начальную и конечную точки реальной функции преобразования fp(x).
На рис.5.2 приведены два способа линеаризации, из которых следует, что способ линеаризации для получения минимального значения л(x), приведенный на рис.5.2, б, позволяет уменьшить погрешность л(x) вдвое.
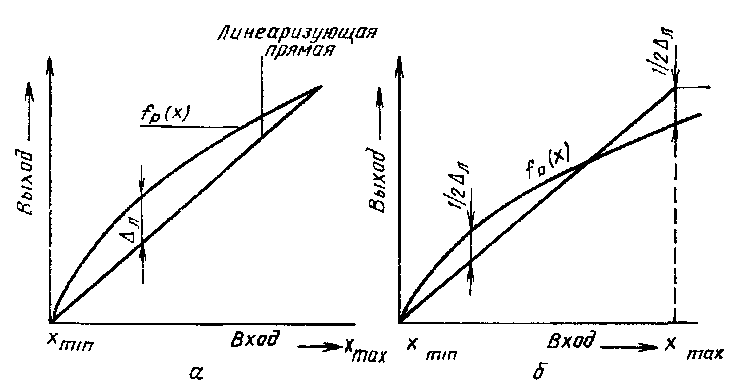
Рис. 5.2. Способы проведения линеаризующей прямой
При изменении входного кода ЦАП на единицу его выходной сигнал меняет своё значение на значение младшего разряда. Дифференциальная нелинейность определяется отклонением приращения выходного сигнала преобразователя от номинального значения младшего разряда при последовательном изменении значений кодового входного сигнала на единицу (рис.5.3). У идеального преобразователя дифференциальная нелинейность равна нулю. Допускаемым значением дифференциальной нелинейности считается
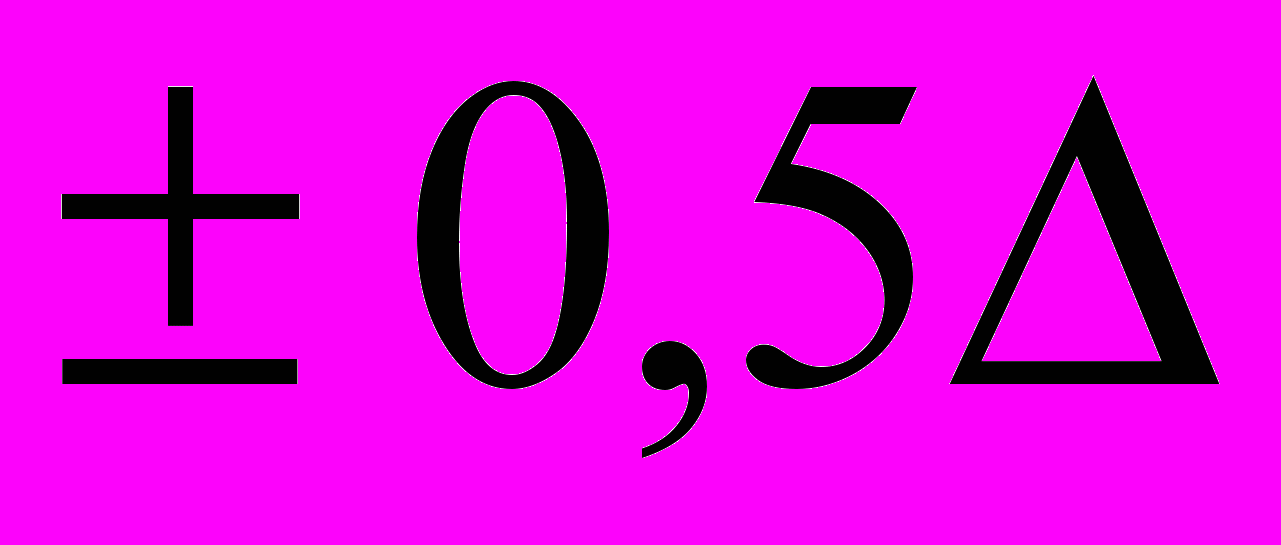.Относительная дифференциальная нелинейность вычисляется по формуле:
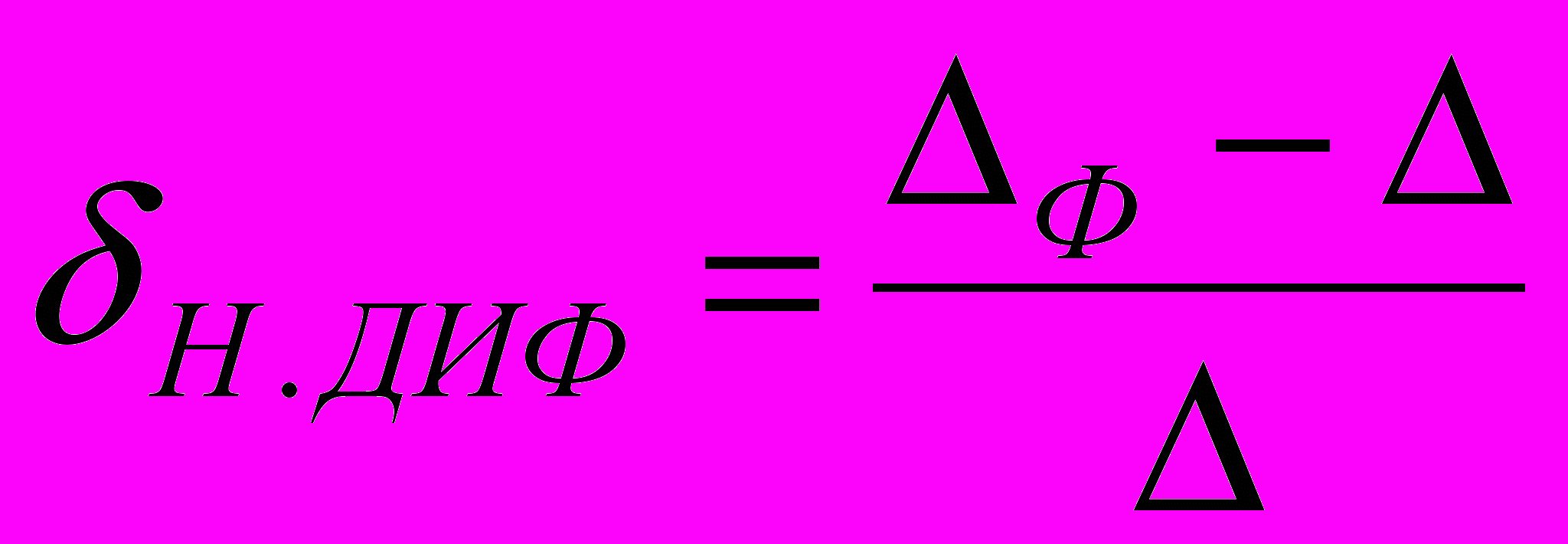,где Ф – фактическое приращение выходного сигнала, вызванное изменением двоичного числа на единицу.
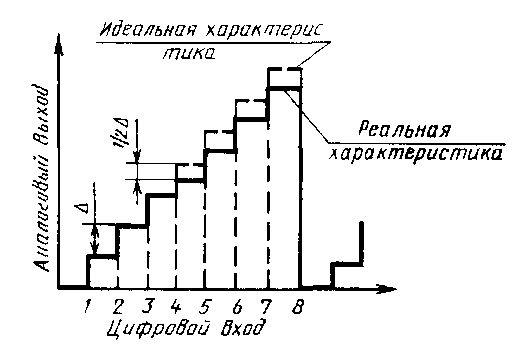
Рис.5.3.
Как правило, наибольшая дифференциальная нелинейность наблюдается тогда, когда происходит выключение всех младших разрядов и включение одного старшего, т.е. при смене кода с 011….1 на 100….0.
Дифференциальная нелинейность может быть выражена в долях младшего разряда или в процентах от полной шкалы.
Нелинейность характеристики ЦАП оказывает незначительное влияние на его дифференциальную нелинейность. Более того, ЦАП может быть линейным, т.е. его реальная характеристика может отклоняться от прямой не более чем на
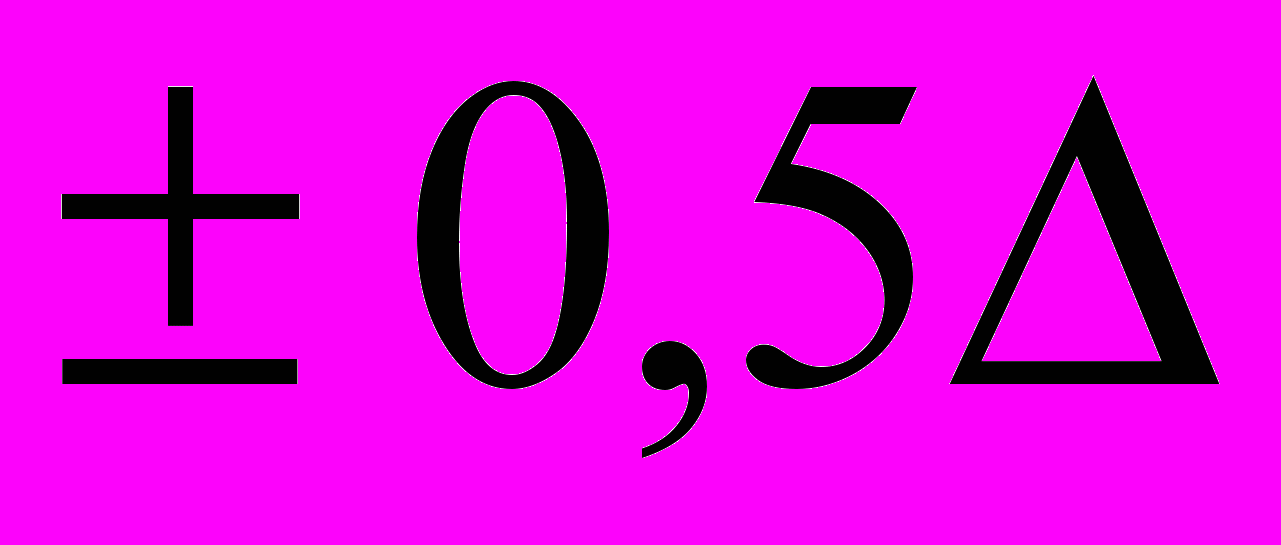, и тем не менее не удовлетворять требованиям дифференциальной линейности (ступеньки 6 и 7 на рис.5.4). И наоборот, даже незначительная накапливающаяся от разряда к разряду дифференциальная нелинейность, не превышающая допускаемое значение, может привести к значительной н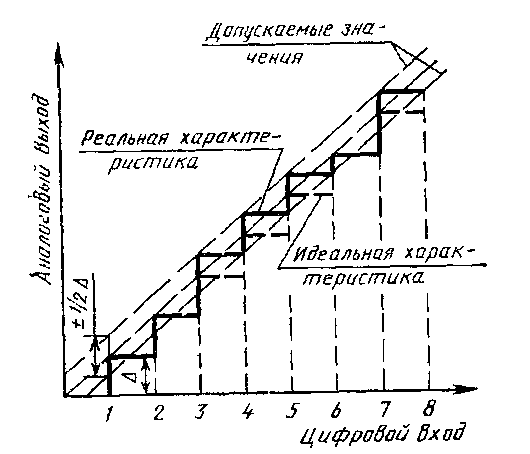
елинейности поеобразователя (рис.5.5).
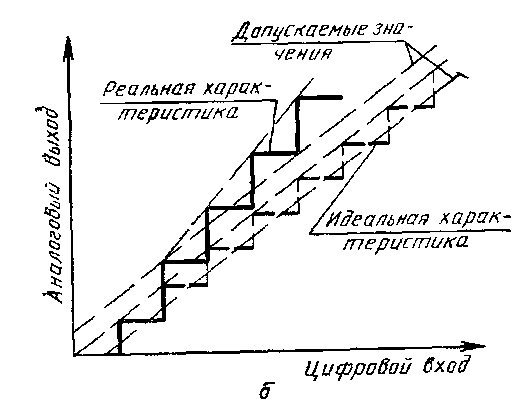
Рис.5.4.
Рис.5.5.
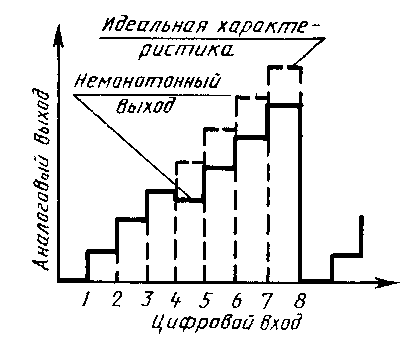
Монотонность преобразователя означает, что при каждом приращении входного сигнала происходит приращение выходного сигнала того же знака, в противном случае преобразователь не является монотонным рис.5.6.
Требование дифференциальной нелинейности, равной
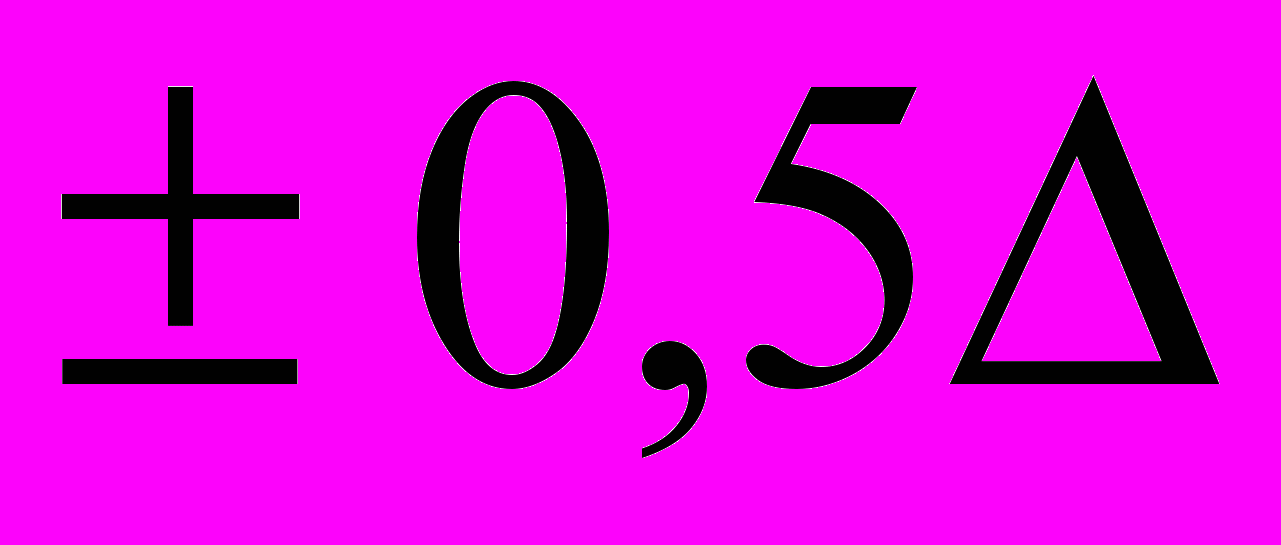, является более жестким, чем требование монотонности, так как немонотонность означает дифференциальную нелинейность большую чем . К
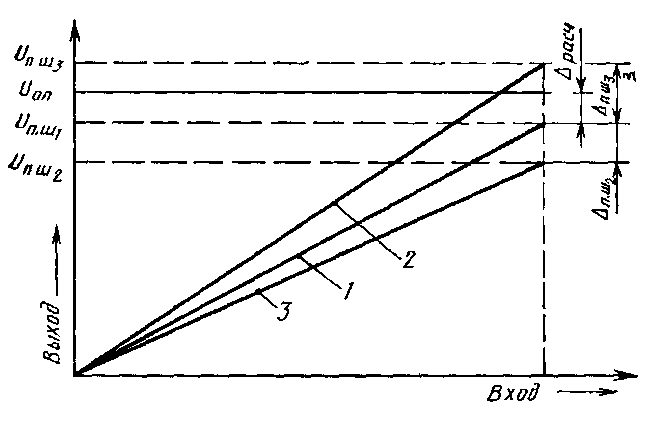
оэффициент преобразования преобразователя определяет угол наклона его характеристики преобразования. Как уже отмечалось, для идеального ЦАП наклон характеристики должен быть таким, чтобы при включении всех разрядов (двоичный код полной шкалы n на его цифровых входах 111 ... 1) выходное напряжение полной шкалы UП.Ш ЦАП было меньше значения опорного напряжения UОП на значение младшего разряда (прямая 1 на рис.5.7).
Для интегральных схем ЦАП с токовым выходом наклон характеристики определяется значением сопротивления резистора Roc, который включен в цепь обратной связи усилителя — преобразователя тока в напряжение. Если значение сопротивления резистора Roc превышает номинальное значение, то коэффициент преобразования возрастает (прямая 2 на рис.5.6), если номинал Roc меньше нормы, то коэффициент преобразования уменьшается (прямая 3 на рис.5.6). Это объясняется тем, что фактические значения младших разрядов Ф2 и Ф3 для характеристик 2 и 3 отличаются от расчётного значения . В этом случае фактические значения младших разрядов преобразователя определяются как
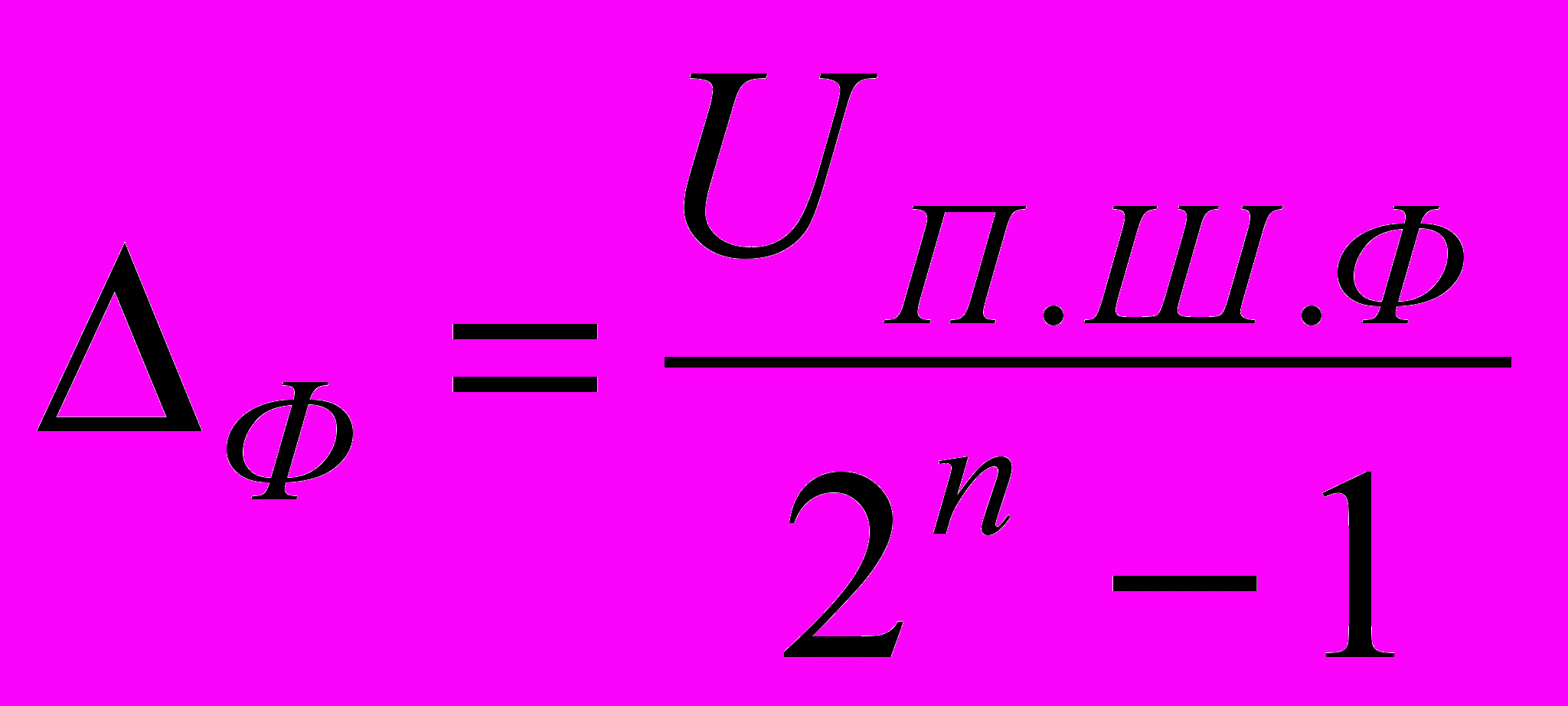,где UП.Ш.Ф — фактическое значение напряжения полной шкалы преобразователя.
Степень отклонения реального значения коэффициента преобразования от расчётного характеризуется абсолютной погрешностью полной шкалы П.Ш , под которой понимают разность между номинальным значением напряжения полной шкалы преобразователя UП.Ш.НОМ, и фактическим его значением UП.Ш.Ф, т.е. для ЦАП:
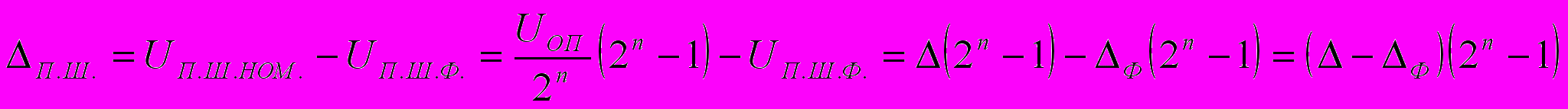
Относительная погрешность полной шкалы П.Ш. ЦАП определяется выражением
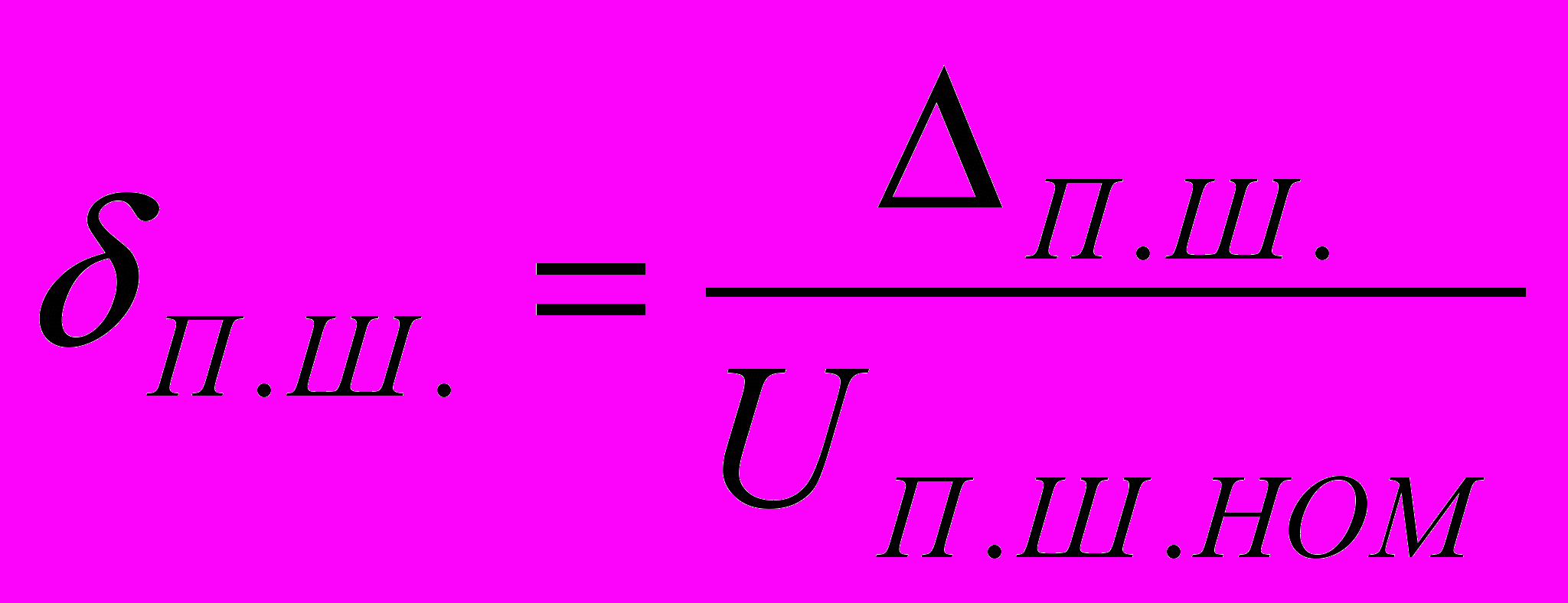
и, следовательно, не зависит от коэффициента преобразования ЦАП.
Погрешности полной шкалы для АЦП характеризуются отклонением действительного входного напряжения от его расчётного значения для полномасштабного выходного кода.
Погрешности полной шкалы для ЦАП и АЦП обусловлены погрешностями:
– опорного напряжения UОП ;
– значений сопротивлений многозвенного резистивного делителя;
– коэффициента усиления усилителя.
Погрешность полной шкалы может быть скорректирована с помощью регулировки коэффициента усиления выходного усилителя (для ЦАП) или значения опорного напряжения (для АЦП).
Погрешность нуля (смещение нуля) 0 для ЦАП — это выходное напряжение ЦАП с нулевым входным кодом, а для АЦП — среднее значение входного напряжения АЦП, необходимое для получения нулевого кода на его выходе. Смещение нуля вызвано током утечки через коммутирующие разрядные ключи ЦАП, входным током или напряжением смещения выходного усилителя (для ЦАП) или компаратора (для АЦП). Данную погрешность можно скомпенсировать с помощью внешней по отношению к ЦАП или АЦП регулировки нулевого смещения. Погрешность нуля выражается в процентах от полной шкалы или в долях единицы младшего разряда.
Погрешность полной шкалы П.Ш., как это показано на рис.5.7, определяется с учётом погрешности нуля характеристики преобразователя 0 , в то время как при определении погрешности линейности Л линеаризирующая прямая реальной функции преобразования fp(x) должна проходить через начало координат. Следовательно, перед тем как определить погрешность линейности необходимо скорректировать погрешность нуля 0.
Абсолютная погрешность преобразования отражает отклонение фактического выходного сигнала преобразователя от теоретического, вычисленного для идеального преобразователя. Значение абсолютной погрешности преобразования выражается обычно в процентах от полной шкалы преобразования и учитывает все составляющие погрешности преобразования (нелинейность, смещение нуля, погрешность коэффициента преобразования). Абсолютная погрешность преобразования находится в прямой зависимости от текущего значения UОП. Изменение значения UОП , например, на 1 % вызывает увеличение абсолютной п
огрешности преобразования также на 1 %.
Рис.5.7.
Время установления ЦАП является важным динамическим параметром и определяется как интервал времени, в течение которого выходной аналоговый сигнал ЦАП при смене кодовой комбинации на его цифровых входах достигает своего установившегося значения (соответствующего статическому режиму преобразования) с допускаемой погрешностью, значение которой выражается как часть от полной шкалы преобразования и обычно равно
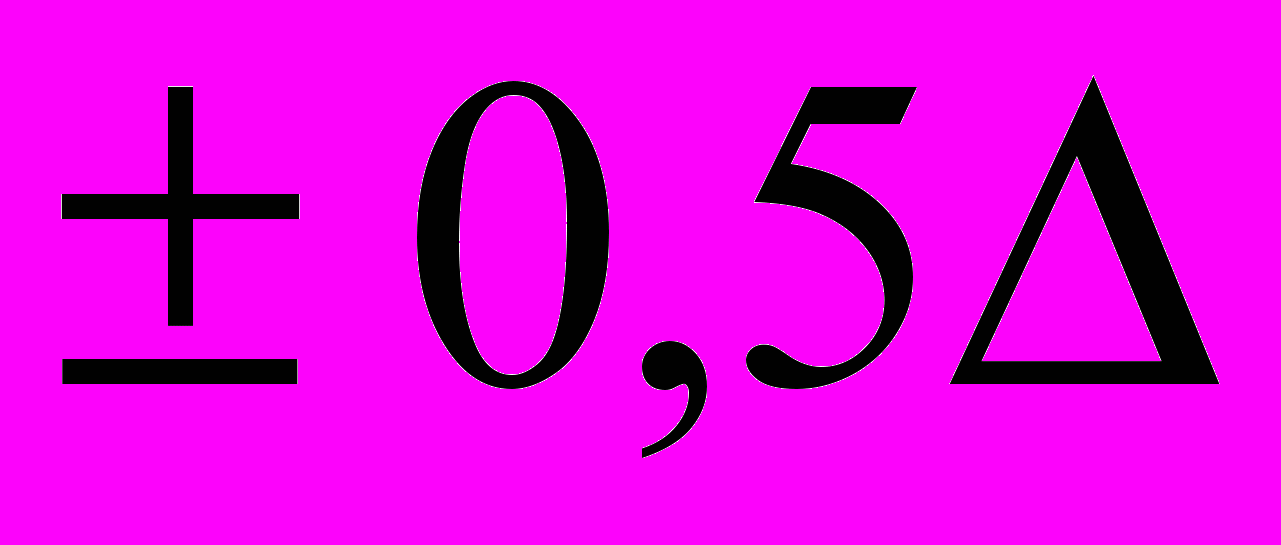. При этом, чем больше изменение входного воздействия и перепад выходного аналогового сигнала, тем продолжительней время установления. Действительно, если погрешность установления не превышает 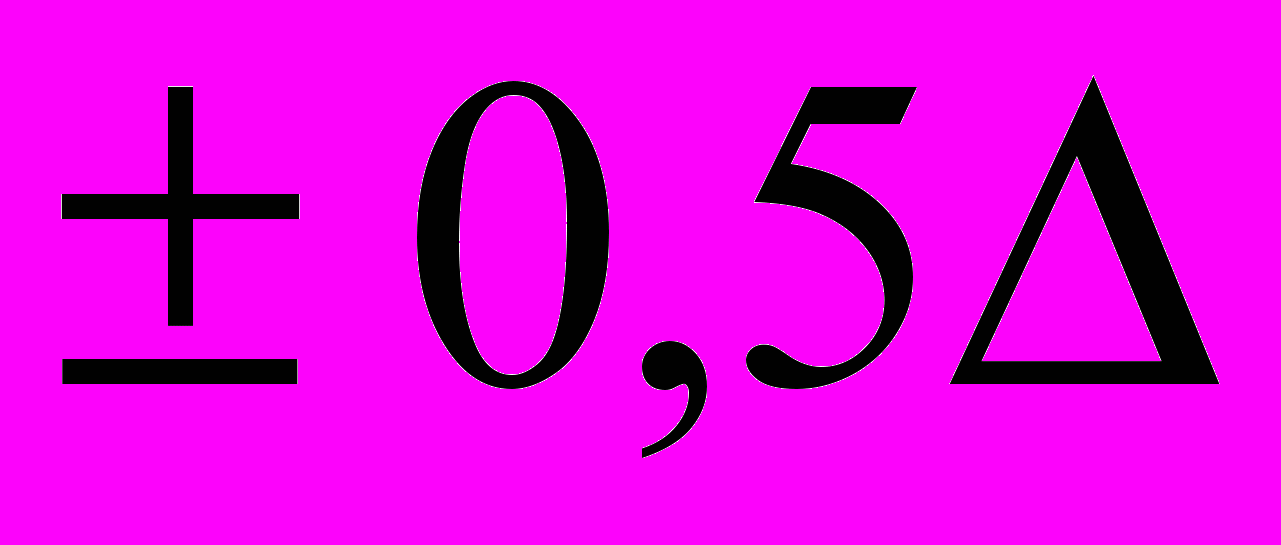, то при включении и выключении, например, младшего разряда перепад выходного аналогового сигнала ЦАП будет составлять всего лишь удвоенную допускаемую погрешность установления. Поэтому время установления будет минимальным. И наоборот, если перепад выходного сигнала ЦАП велик по сравнению с допускаемой погрешностью установления, время установления возрастает. Однако необходимо учитывать следующее обстоятельство. Время установления зависит не только от значения перепада выходного сигнала ЦАП, но и (в большей степени) от того, относительно какого уровня происходят эти перепады, т.е. от того количества разрядов, которые меняют свое состояние при формировании нового значения выходного сигнала ЦАП. Наиболее длительное время установления наблюдается в случае периодического формирования полной шкалы (т.е. при смене кодовых комбинаций на цифровых входах ЦАП с 00…0 на 11…1) и при так называемом главном кодовом переходе, когда меняются кодовые комбинации с 011…1 на 100…0. Это объясняется тем, что выключение разрядов происходит, как правило, быстрее их включения. Поэтому при смене указанных кодовых комбинаций выходной сигнал ЦАП в течение определенного отрезка времени будет иметь нулевое значение, после чего возвращается к предыдущему значению за вычетом единицы младшего разряда.Время преобразования АЦП определяется как интервал времени, в течение которого выходной код преобразователя при скачкообразном изменении входного аналогового сигнала достигает значения, отличающегося от установившегося не более, чем на значение допускаемой погрешности.
Нормирование и определение этого параметра существенно зависит от структуры и назначения преобразователя. Так, время преобразования интегрирующих АЦП вполне определённо и практически не зависит ни от каких внешних факторов. На время преобразования АЦП поразрядного уравновешивания и прямого (параллельного) преобразования влияют многие факторы, и его можно подразделить на время переходного процесса во входных цепях АЦП tBX и время цикла преобразования tЦ , необходимое для отработки всех разрядов АЦП и получения на выходе соответствующего кода. Таким образом, для времени преобразования tПР АЦП можно записать:
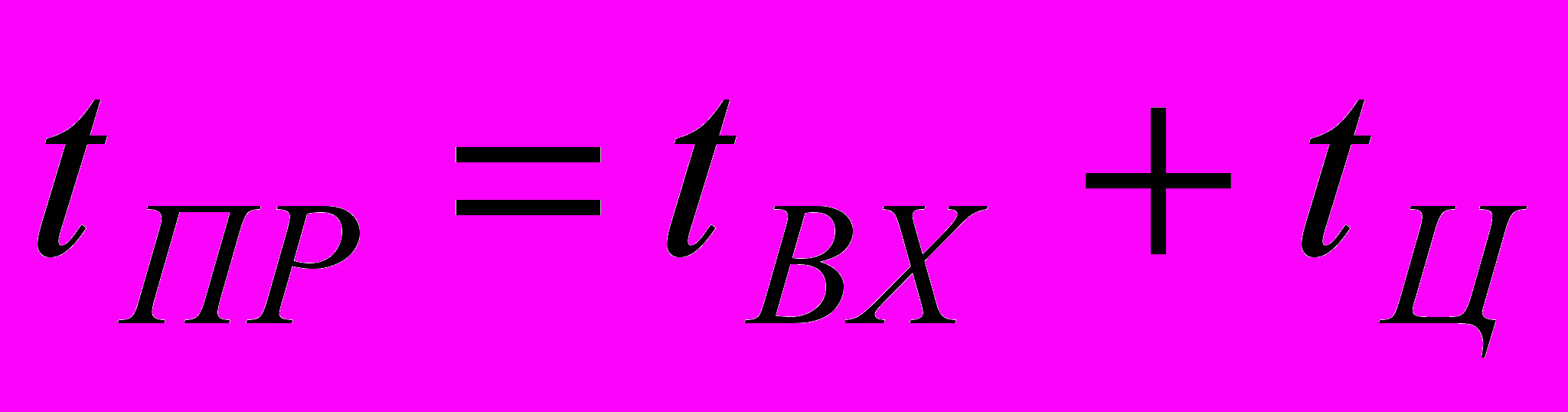
5.4. Основные структуры цифроаналоговых преобразователей (ЦАП)
ЦАП строятся в основном по принципу параллельного преобразования на переключателях тока или напряжения. Такие ЦАП имеют два типа входов: аналоговый, на который подается опорное напряжение UОП постоянного тока, определяющее масштаб цифроаналогового преобразования (в случае отсутствия в ЦАП встроенного источника опорного напряжения), и цифровой, на который подается цифровой код NВХ , подлежащий преобразованию в аналоговый сигнал.
ЦАП, допускающий подачу на аналоговый вход только фиксированного значения опорного напряжения, которое может формироваться как внутри корпуса ЦАП, так и вне его, называется линейным.
В
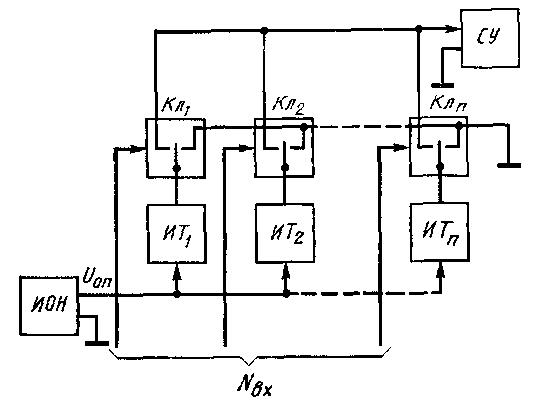
ыходной величиной ЦАП является либо напряжение постоянного тока (при наличии встроенного в ЦАП усилителя— преобразователя тока в напряжение), либо постоянный ток. К ЦАП с токовым выходом необходимо подключать низкоомную нагрузку, падение напряжения на ней должно быть мало для сохранения гарантированной точности ЦАП.
Рис.5.8.
В обобщенной структурной схеме ЦАП с переключателями источников тока (рис.5.8) каждому i-му разряду параллельного входного кода NBX соответствует свой источник тока ИТi. Ток каждой ячейки ИТ, формируется из опорного напряжения UОП от источника опорного напряжения ИОН и соответствует весу данного разряда кода. Выходные токи ячеек, проходящие через отпираемые кодом ключи (Кл), суммируются на входе суммирующего усилителя (СУ).
С
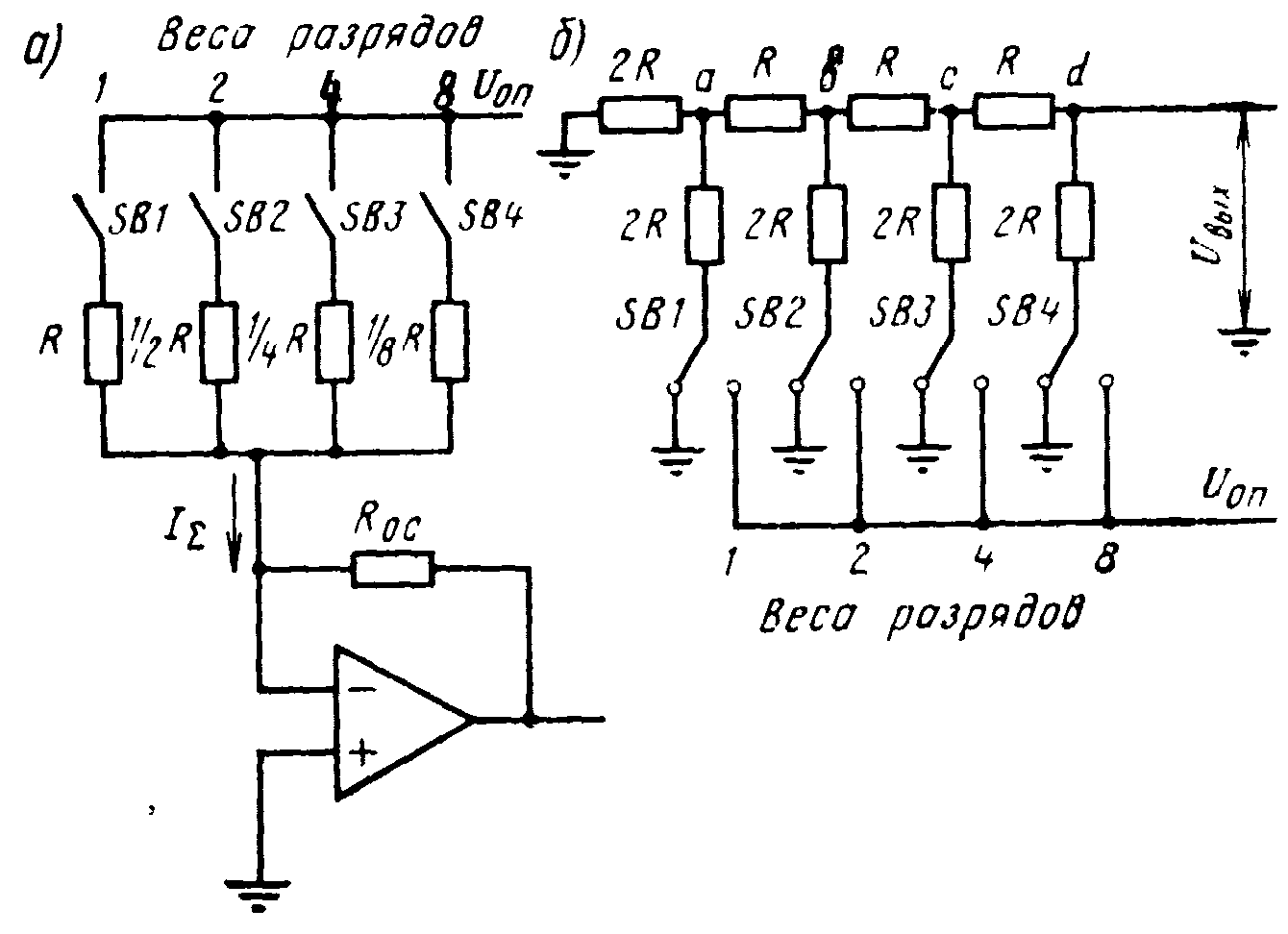
Рис.5.9. ЦАП с помощью суммирования токов (а) и напряжений (б)
уществуют два наиболее широко распространенных метода формирования разрядных токов: с использованием двоично-взвешенных резисторов, номиналы которых изменяются по закону 2n (суммирование токов) , и многозвенной цепочки резисторов R—2R (суммирование напряжения) (рис.5.9).
В схеме (рис.5.9,а) сопротивление входных весовых разрядных резисторов выбирают обратно пропорционально весу разряда, причём, номиналы резисторов должны возрастать от старшего (СР) к младшему (МР) разряду по двоичному закону. Поэтому ток в цепи резистора при его включении пропорционален весу разряда. Ток I равен сумме токов ветвей и, следовательно, сумме весов включённых разрядов:
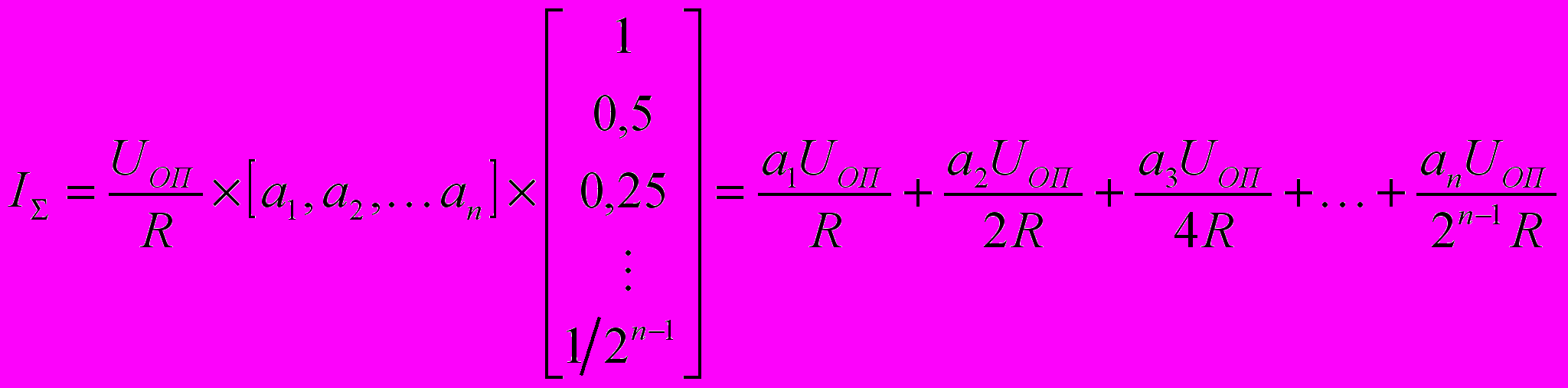.Так, при замыкании ключа SB1 напряжение на выходе ОУ равно
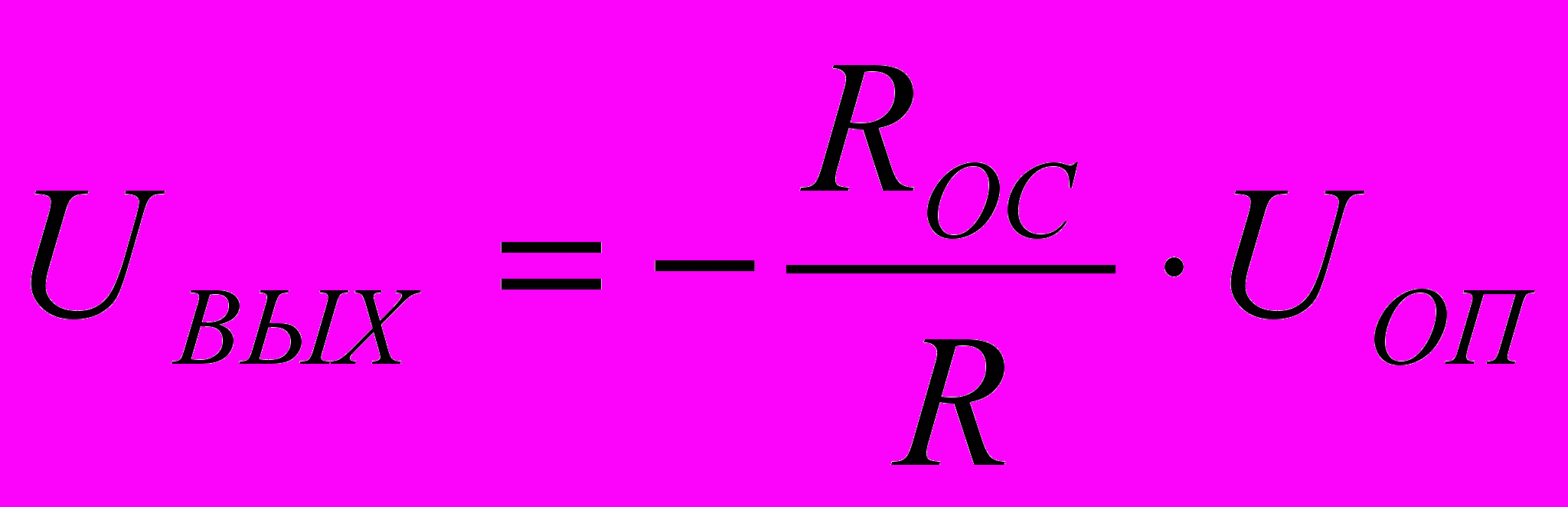, при замыкании ключа SB2 напряжение на выходе ОУ равно 
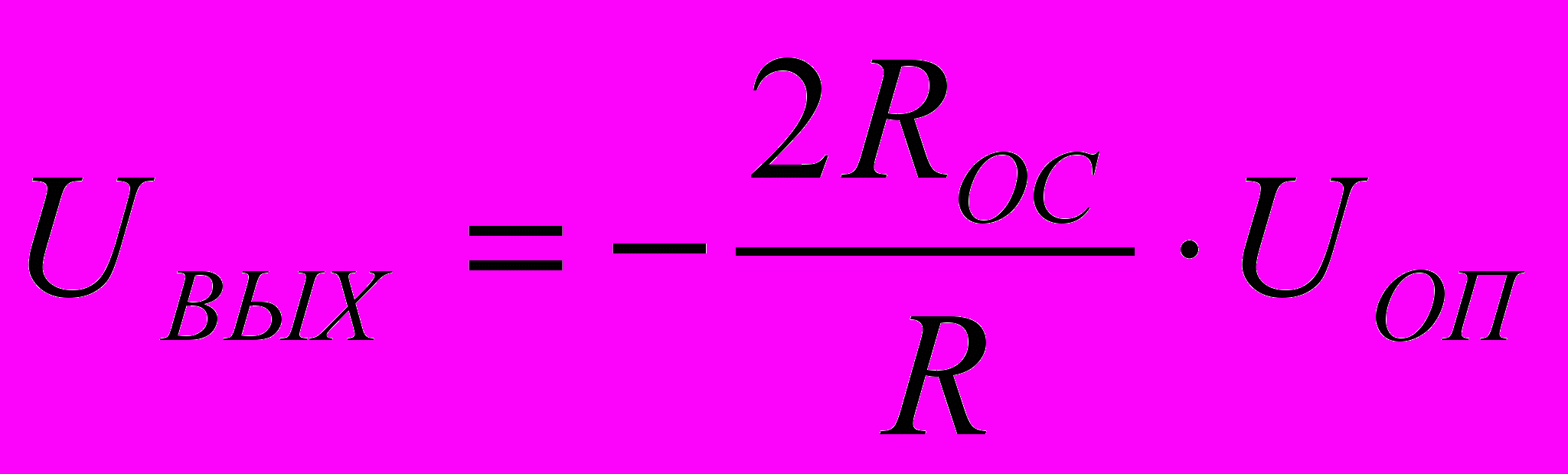, при замыкании ключей SB1 и SB2 напряжение на выходе ОУ будет равно 
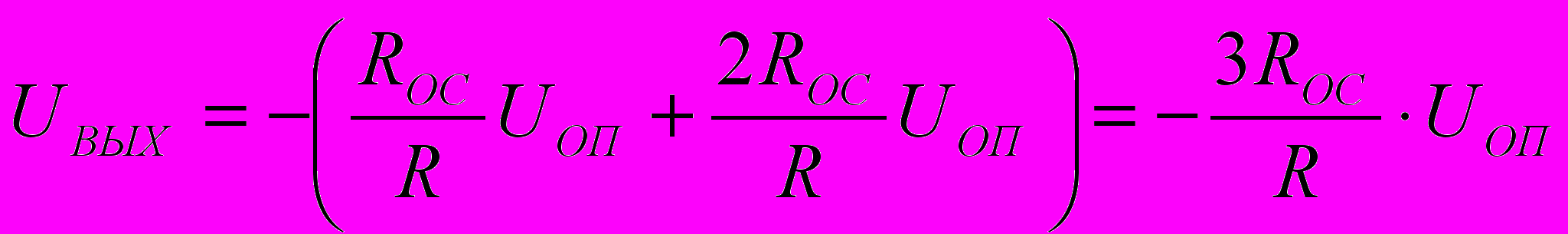и т.д. Таким образом, уровень выходного напряжения прямо пропорционален десятичному эквиваленту двоичного кода, задаваемого ключами SB1 – SB4 .Недостатком рассмотренной схемы является большой диапазон сопротивлений резисторов, особенно при большом числе разрядов входного кода. Так, при 10 двоичных разрядах (
3 десятичных) максимальное и минимальное сопротивления резисторов будут отличаться в 210 раз.Резисторные схемы с сильно различающимися сопротивлениями резисторов трудно изготовить интегральным способом в одном технологическом процессе. Поэтому больший интерес представляет схема (рис.5.9, б) с двумя номиналами сопротивлений резисторов R и 2R.
Напряжение на выходе этой схемы находится для каждого разряда в отдельности (когда ключ только одного разряда подключен к источнику опорного напряжения UОП, а остальные ключи подключены к земле). Результирующее напряжение согласно методу наложения определяется как сумма напряжений от всех разрядов. Результирующее сопротивление слева от каждой из точек а, b, с и d равно 2R. Если сложить это сопротивление с параллельным сопротивлением первого разряда (2R) и прибавить последовательное сопротивление R между точками d и с, то слева от точки с также получим 2R. Аналогично можно найти эквивалентное сопротивление слева от точки а, оно также равно 2R . Поэтому при замыкании ключа SB4 напряжение на выходе схемы будет равно
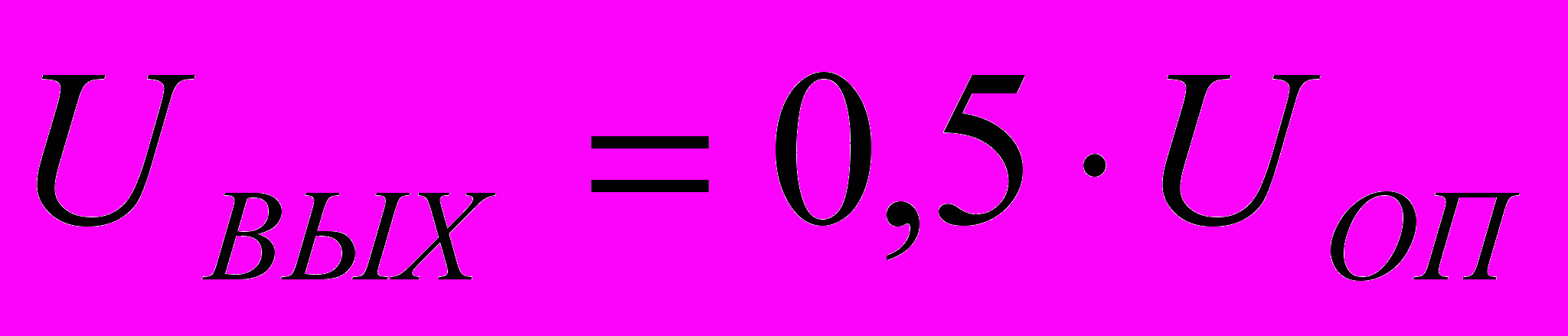, а при замыкании SB3 
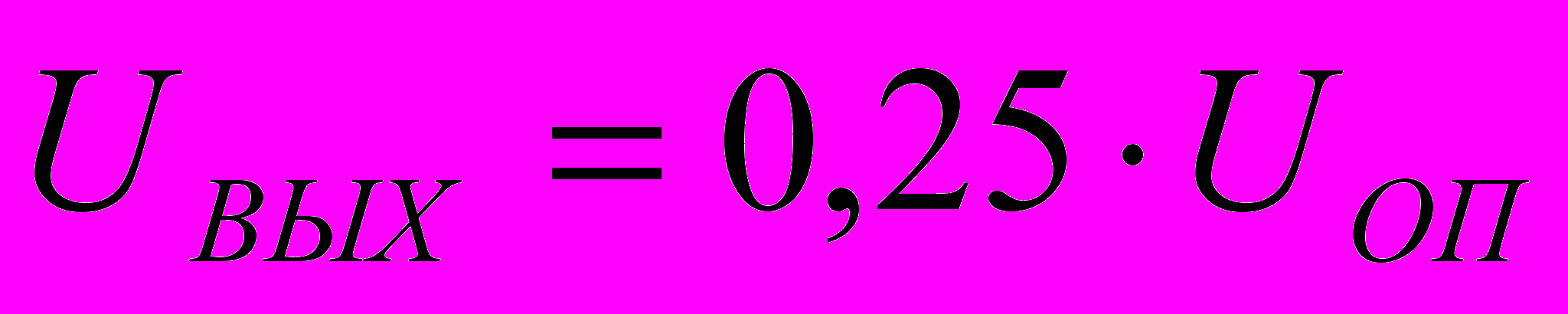. Таким образом, уровень выходного напряжения также как и в схеме рис.5.9,а прямо пропорционален десятичному эквиваленту двоичного кода, задаваемого ключами SB1 – SB4 .5.5. Интегральные ЦАП
С появлением высококачественных и прецизионных интегральных схем (ИС), особенно прецизионных ОУ, быстродействующих компараторов напряжения (КН), преобразователей кода, триггеров, запоминающих устройств и т.п., конструирование ЦАП значительно упростилось – появились гибридные ЦАП, а затем были созданы полностью интегральные ЦАП.
Интегральные ЦАП позволили существенно расширить область их применения в малогабаритных автоматических средствах измерений благодаря их экономичности, небольшим габаритным размерам, малой мощности потребления, высокой надёжности работы при воздействии дестабилизирующих факторов окружающей среды.
Тип микросхемы ЦАП записывается следующим образом: серия ПА номер (К572ПА1). Состоят они из однофазных управляемых переключателей тока, управляющих логических схем и цепочек тонкоплёночных резисторов типа R – 2R.
5.6. Основные структуры аналого-цифровых преобразователей (АЦП)
Исходная непрерывная физическая величина (первоначальные напряжения или ток, уровень жидкости, давление газа, частота вращения и т.д.) сначала преобразуется в электрический аналог (ток или напряжение), который изменяется во времени по тому же закону, что и первичная физическая величина, а затем уже электрический аналог преобразуется в код (в её цифровой эквивалент).
В настоящее время разработано большое количество типов АЦП, удовлетворяющих разнообразным требованиям. В одних случаях преобладающим требованием является высокая точность, в других — скорость преобразования.
В ряде случаев один АЦП используется для одновременного преобразования нескольких аналоговых сигналов. При этом требуется ввести в состав АЦП два дополнительных устройства:
1)мультиплексор, обеспечивающий коммутацию в определенной последовательности соответствующих аналоговых сигналов к общему входу АЦП;
2) устройство выборки и хранения, которое запоминает текущее значение аналогового сигнала в коротком интервале времени и сохраняет это значение постоянным (в пределах допускаемой погрешности) до тех пор, пока АЦП не завершит процесс преобразования.
АЦП можно разделить на программируемые и непрограммируемые.
В программируемых АЦП процесс преобразования состоит из заданного, вполне конкретного числа шагов, каждый из которых тактируется и имеет фиксированную длительность (АЦП последовательного приближения).
Для непрограммируемых АЦП время преобразования определяется только длительностью переходных процессов в цепях преобразования (АЦП с одновременным сравнением или параллельный АЦП).
Также АЦП подразделяютя по наличию или отсутствию цепи обратной связи (в первом случае — это уравновешивающие АЦП, во втором — АЦП прямого преобразования).
По принципу действия все существующие типы АЦП можно разделить на две группы:
АЦП интегрирующего типа;
АЦП со сравнением входного преобразуемого сигнала с дискретными уровнями напряжений.
Принцип работы АЦП интегрирующего типа основан на преобразовании в код времени, необходимого для заряда конденсатора до некоторого уровня опорного или входного напряжения.
АЦП напряжения в частоту является наиболее простым по своей структуре среди интегрирующих преобразователей. Двухпороговый преобразователь (рис.5.10,а) содержит интегратор ИН, два пороговых устройства (компаратора) ПУ1 и ПУ2, выходной триггер Т и коммутирующий элемент на транзисторе VT.
Если к входу такого интегратора приложить постоянное напряжение, то напряжение на выходе интегратора будет возрастать линейно.
Очевидно, чем больше Ux(t), тем круче будет прямая на выходе интегратора и тем быстрее напряжение достигает заданного порогового значения UП1. Интервал времени между срабатываниями пороговых устройств ПУ1 и ПУ2 будет обратно пропорционален, а частота переключения триггера Т прямо пропорциональна входному напряжению Uх(t) (рис.5.10,б).
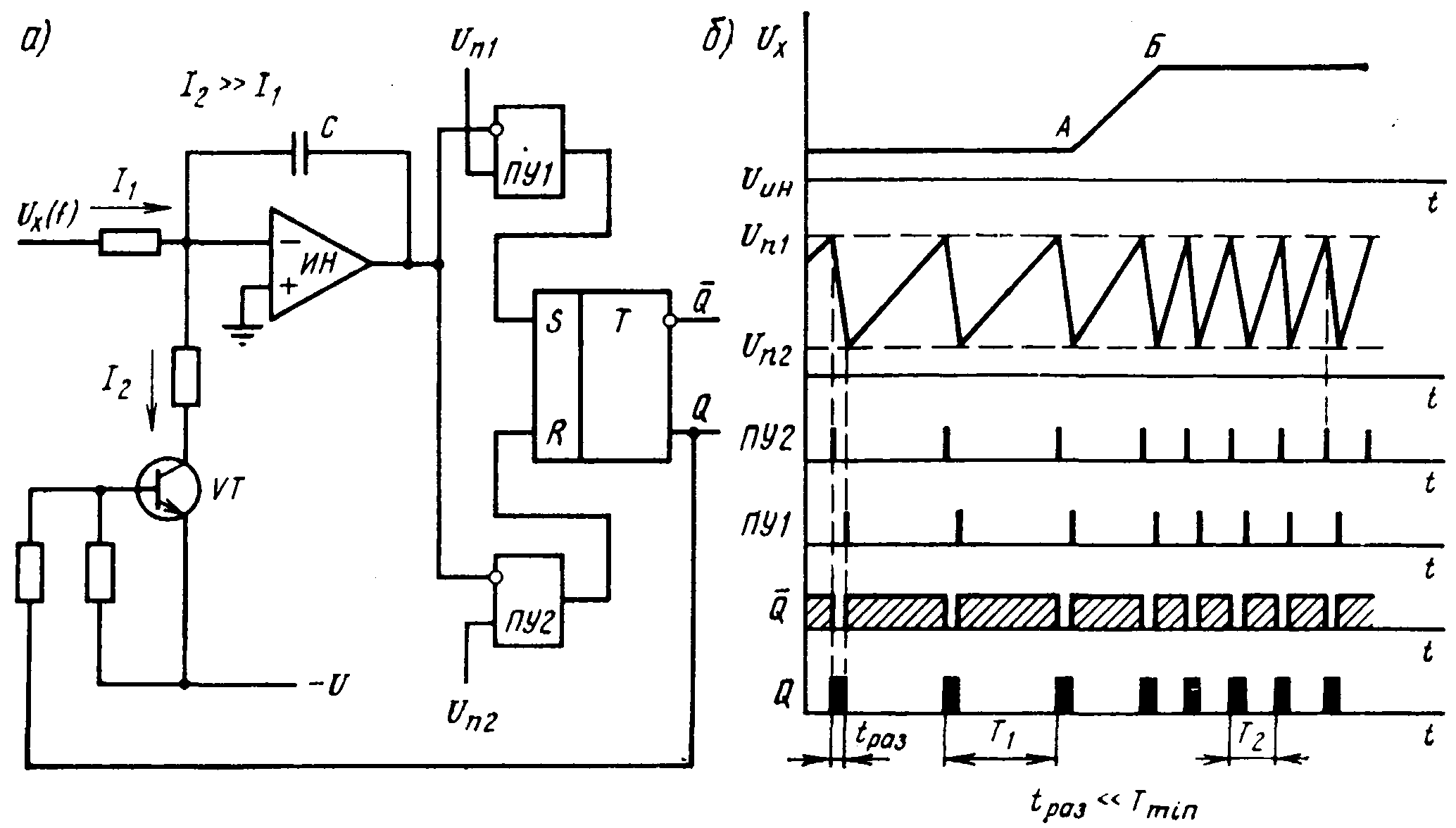
Рис.5.10. Схема простейшего двухпорогового преобразователя
В АЦП со сравнением входного преобразуемого сигнала с дискретными уровнями напряжения используется процесс преобразования, сущность которого заключается в формировании напряжений с уровнями, эквивалентными соответствующим цифровым кодам, и сравнении этих уровней напряжения с входным напряжением с целью определения цифрового эквивалента входного сигнала. При этом уровни напряжения могут формироваться одновременно, последовательно или комбинированным способом.
АЦП последовательного счёта со ступенчатым пилообразным напряжением является одним из простейших преобразователей, в которых используется сравнение дискретных уровней напряжения. Однако эта простота обеспечивается снижением быстродействия этого АЦП (рис.5.11,а), в который входят двоичный Сч, ЦАП, КН, ИОН. Процесс преобразования начинается в момент времени tо с приходом импульса «Запуск», обеспечивающим установку Сч в исходное нулевое состояние. Соответственно на выходе ЦАП, управляемом выходным кодом счётчика, устанавливается напряжение, равное нулю. При этом КН находится в состоянии, разрешающем поступление через логическую схему «И» с генератора Г тактовых импульсов в Сч. По мере возрастания числа импульсов, накопленных в Сч, выходное напряжение ЦАП UВЫХ также возрастает
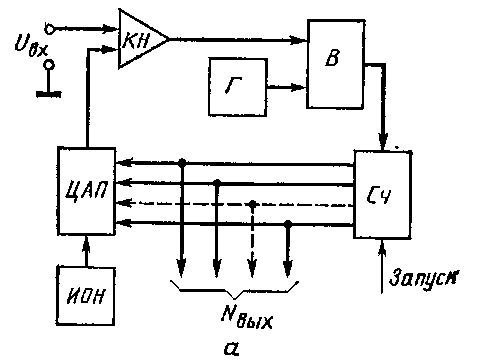
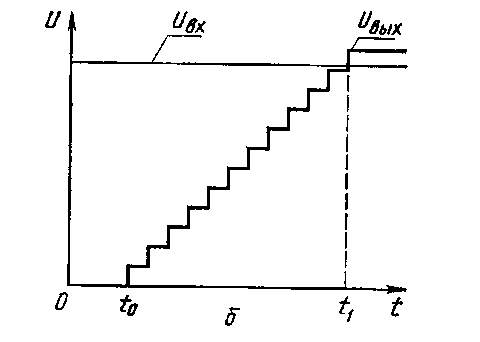
Рис. 5.11. Структурная схема (а) и временная диаграмма (б) работы
АЦП последовательного счёта
(рис.5.11,б). В момент времени t1 , когда число в Сч возрастет настолько, что выходное напряжение ЦАП UВЫХ превысит входное преобразуемое напряжение UВХ , KH изменит свое состояние, закрывая при этом логическую схему «И» и прекращая поступление тактовых импульсов в Сч. В результате полученный в Сч параллельный цифровой код NВЫХ будет цифровым эквивалентом преобразуемого напряжения.
Разрядность и разрешающая способность таких АЦП определяется разрядностью и разрешающей способностью используемого в его составе ЦАП. Время преобразования зависит от уровня входного преобразуемого напряжения UВХ . Для входного напряжения, соответствующего значению полной шкалы, Сч должен быть заполнен и при этом он должен сформировать на входе ЦАП код полной шкалы. Это требует для n-разрядного ЦАП времени преобразования в (2n — 1) раз больше периода тактовых импульсов. Естественно, для быстрого аналого-цифрового преобразования использование подобных АЦП нецелесообразно.
Следящий АЦП характеризуется тем, что в нем суммирующий Сч заменён на реверсивный счетчик РСч (рис.5.12). Благодаря этому становится возможным получать цифровые отсчёты, отслеживающие изменяющееся входное преобразуемое напряжение. Выходной сигнал КН определяет направление счёта (прямое или обратное) в зависимости от того, превышает или нет входное напряжение АЦП UВХ выходное напряжение ЦАП UВЫХ . Для уменьшения среднего времени, необходимого для первого преобразования, перед началом измерений РСч устанавливается в состояние, соответствующее середине шкалы (01 ... 1).
П
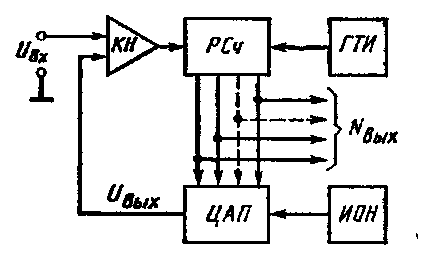
Рис.5.12.
ервый цикл преобразования следящего АЦП аналогичен циклу преобразования в АЦП последовательного счета, т.е. РСч заполняется тактовыми импульсами и на цифровых входах ЦАП формируется параллельный двоичный код, который обеспечивает возрастание выходного напряжения ЦАП UВЫХ . Когда UВЫХ достигнет значения UВХ , KH срабатывает и прекращает счёт импульсов. При этом выходной код NВЫХ соответствует входному напряжению. Как видно, первый цикл преобразования по длительности такой же, как и в предыдущем АЦП. Однако в дальнейшем циклы преобразования существенно сокращаются, так как данный АЦП успевает отследить малые отклонения входного сигнала за несколько тактовых периодов, увеличивая или уменьшая число импульсов, записанное в РСч, в зависимости от знака рассогласования текущего значения преобразуемого напряжения UВХ и выходного напряжения ЦАП. Эта возможность быстрого отслеживания текущего значения входного напряжения и обусловила название подобных АЦП — следящие.
В АЦП параллельного типа входной сигнал одновременно прикладывается ко входам всех КН, число которых m определяется разрядностью АЦП и равно т=2п—1, где n — число разрядов АЦП (рис.5.13). В каждом КН сигнал сравнивается с опорным напряжением, соответствующим весу определенного разряда и снимаемым с узлов резисторного делителя, питаемого от ИОН. Выходные сигналы КН обрабатываются логическим дешифратором (ДШ), вырабатывающим выходной параллельный код NВЫХ , являющийся цифровым эквивалентом входного напряжения UВХ.
Подобные АЦП обладают самым высоким быстродействием по сравнению с другими типами АЦП, поскольку преобразование выполняется за один такт и время преобразования определяется быстродействием компараторов и задержками в логическом ДШ.
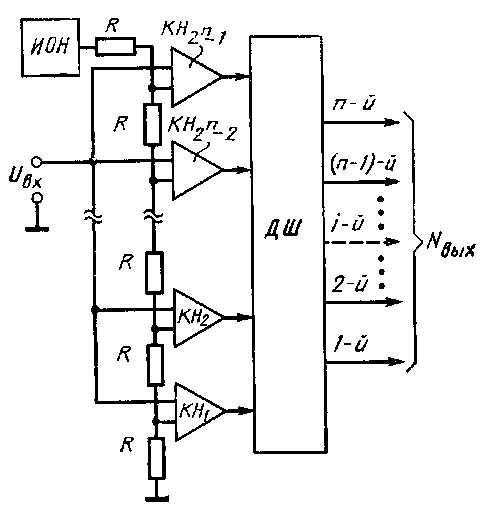
Рис.5.13.
Недостаток таких АЦП заключается в том, что с ростом разрядности количество требуемых элементов практически удваивается (например, для 8-разрядного преобразователя необходимо иметь 255 компараторов, сформировать 255 опорных уровней напряжения и иметь соответствующее число логических схем в дешифраторе). Все это затрудняет построение многоразрядных АЦП подобного типа. Кроме того, точность преобразования ограничивается точностью и стабильностью отдельных КН и резисторного делителя.